Approximate Calculation of Functional Integrals Generated by Nonrelativistic and Relativistic Hamiltonians
Abstract
:1. Introduction
2. Calculation of Functional Integrals Generated by Nonrelativistic Hamiltonians
2.1. Method Based on Expansion in Eigenfunctions of the Hamiltonian
2.2. Harmonic Oscillator
2.3. Anharmonic Oscillator
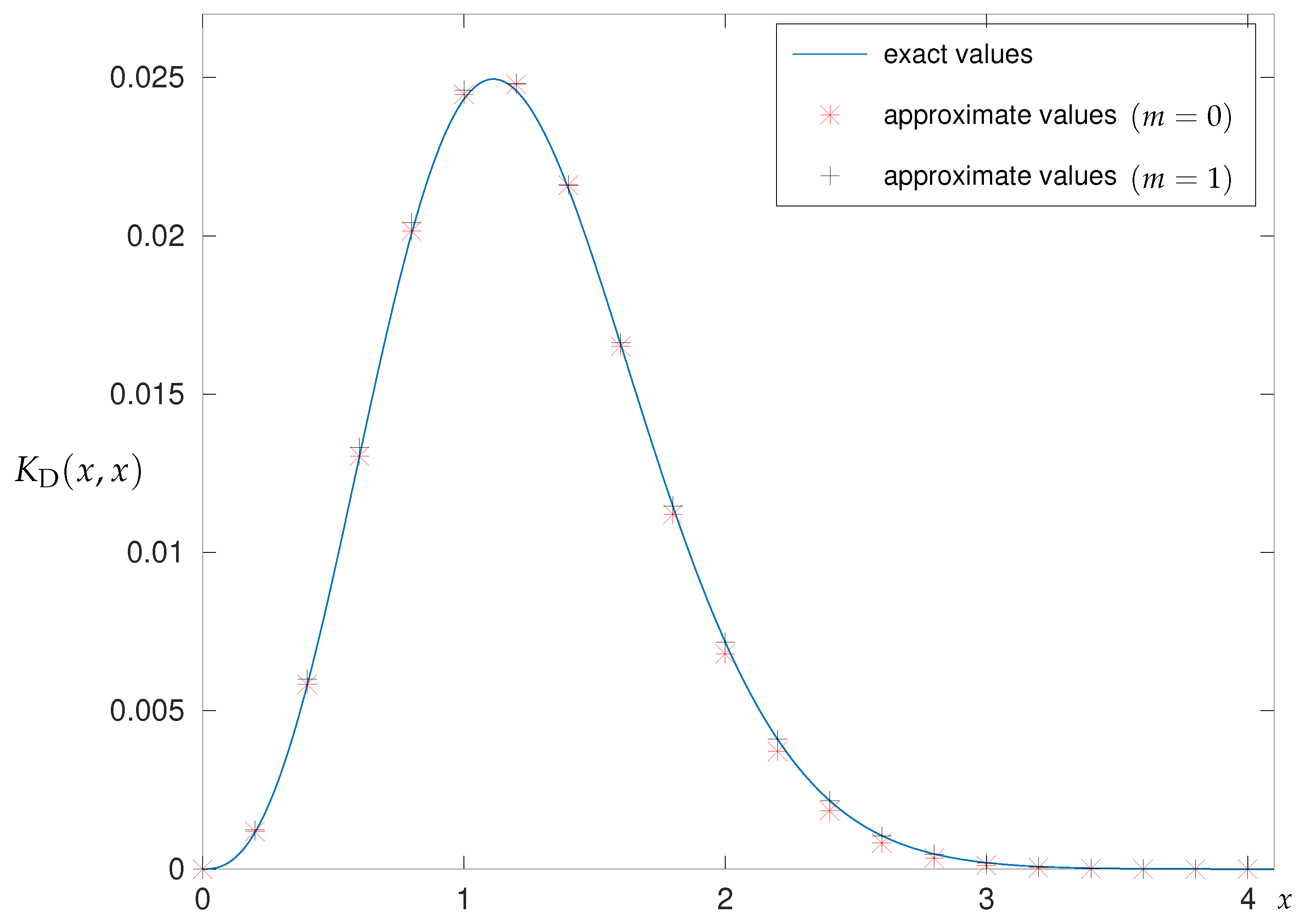
2.4. One-Dimensional Rectangular Potential Well
2.5. Davidson Potential
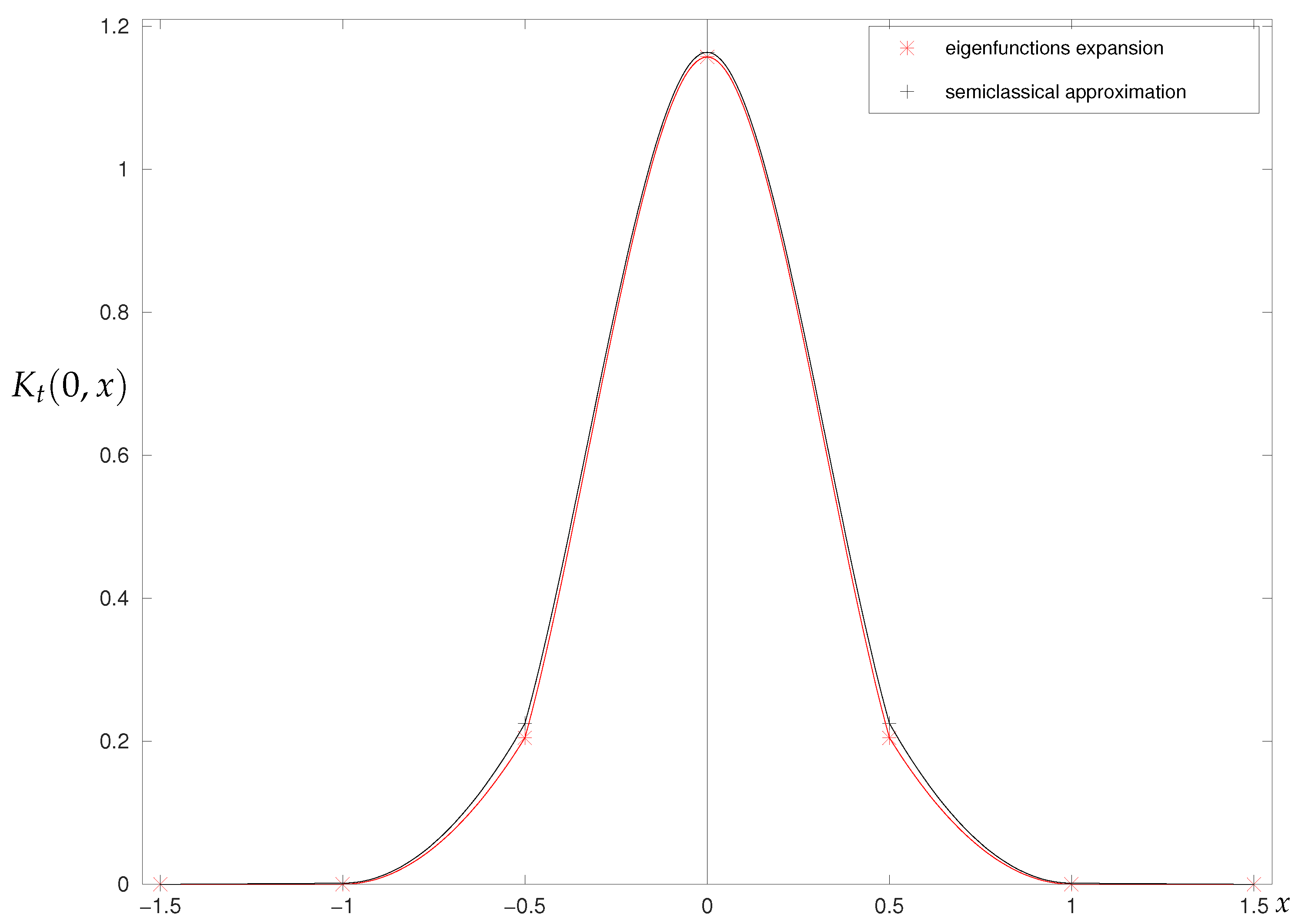
2.6. Semiclassical Approximation for the Calculation of Functional Integrals
2.6.1. Description of the Method
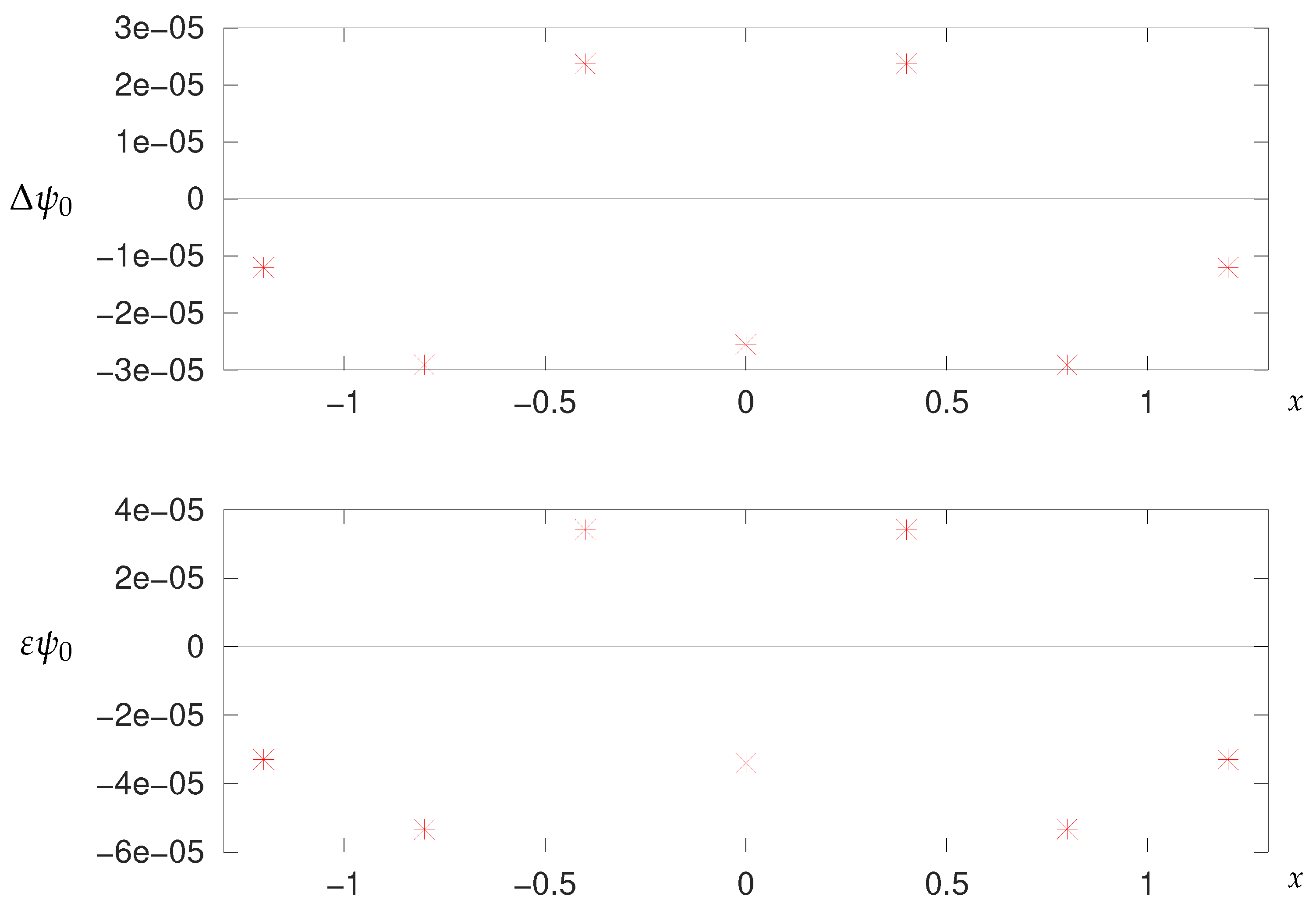
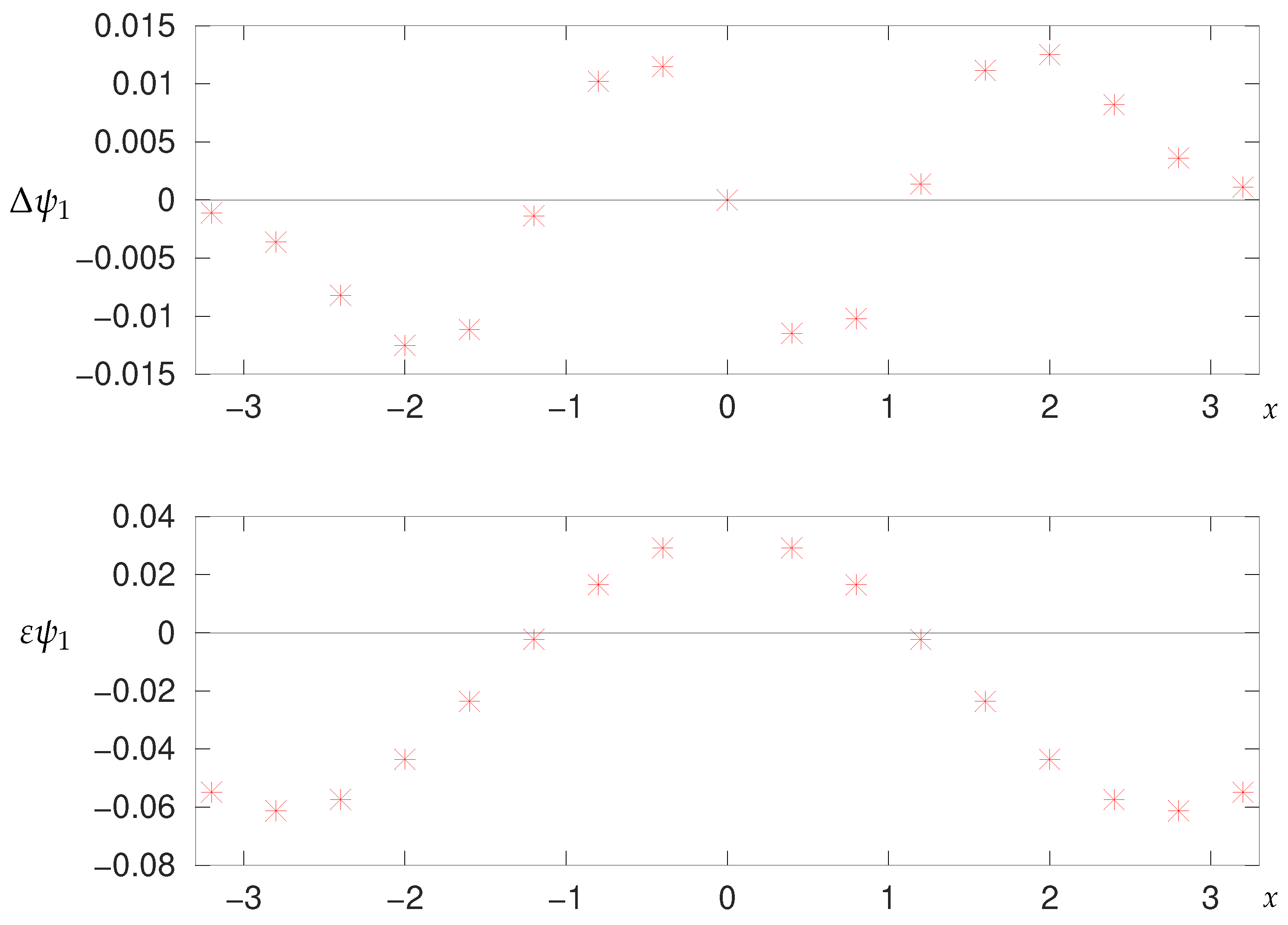
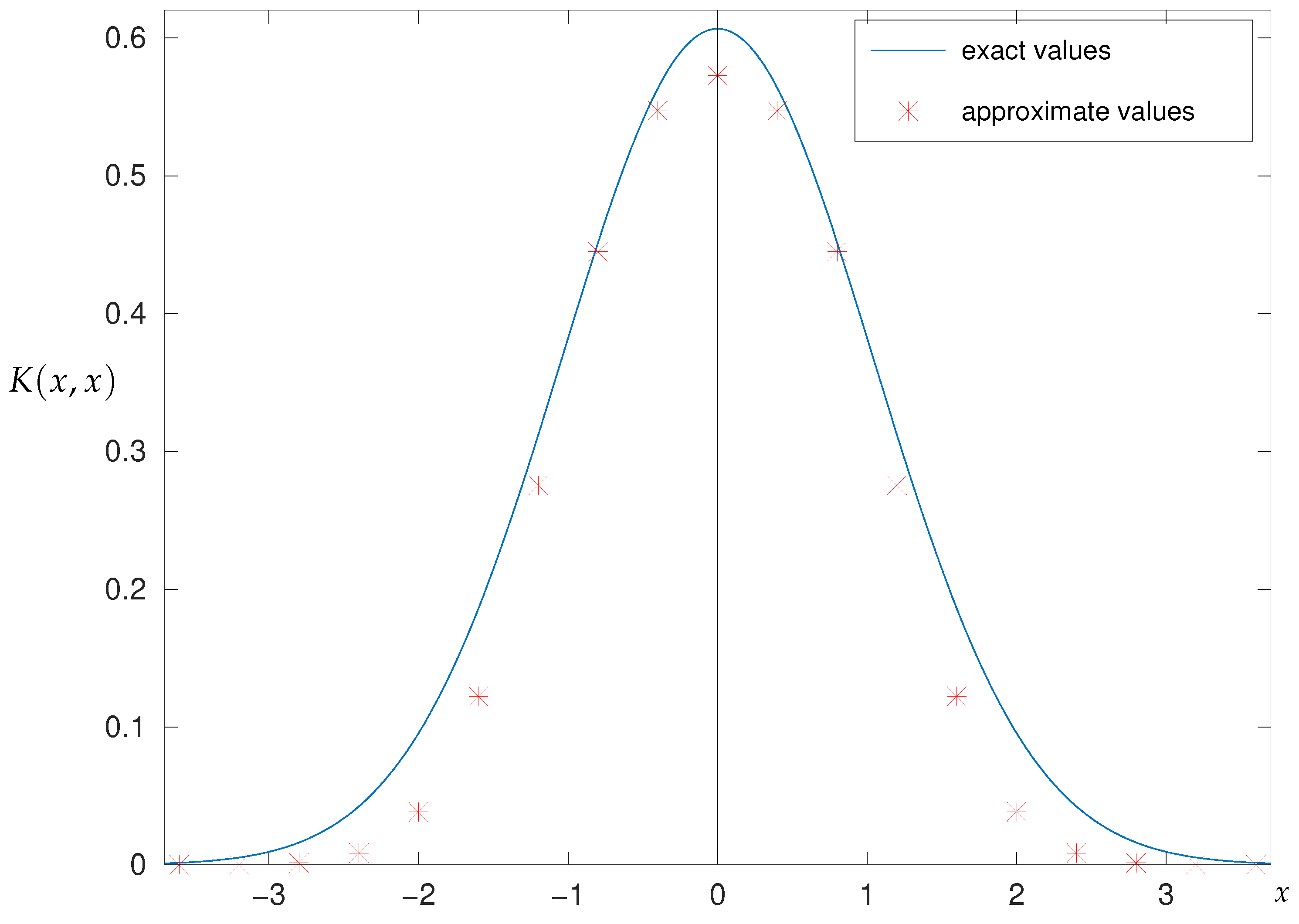
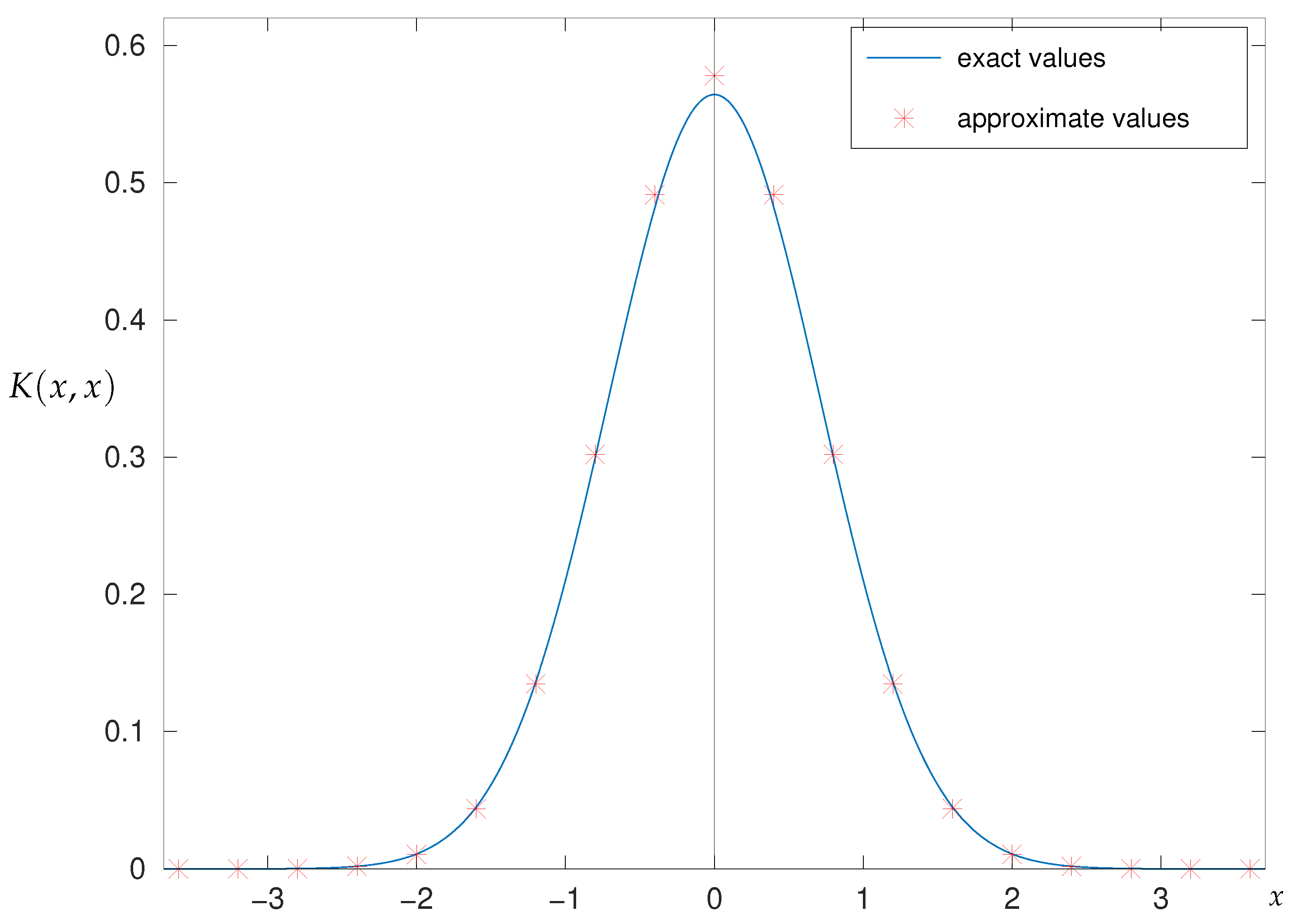
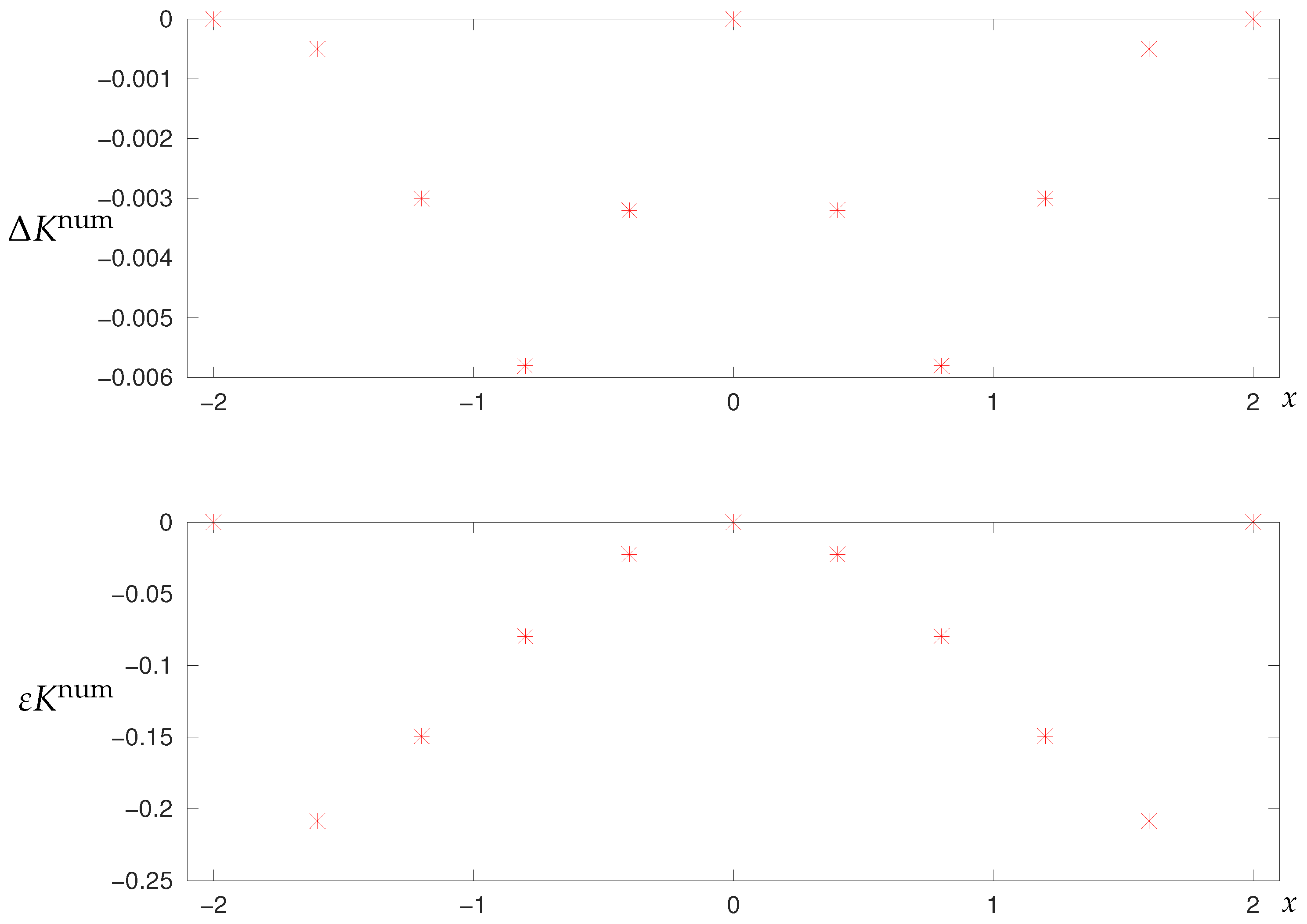
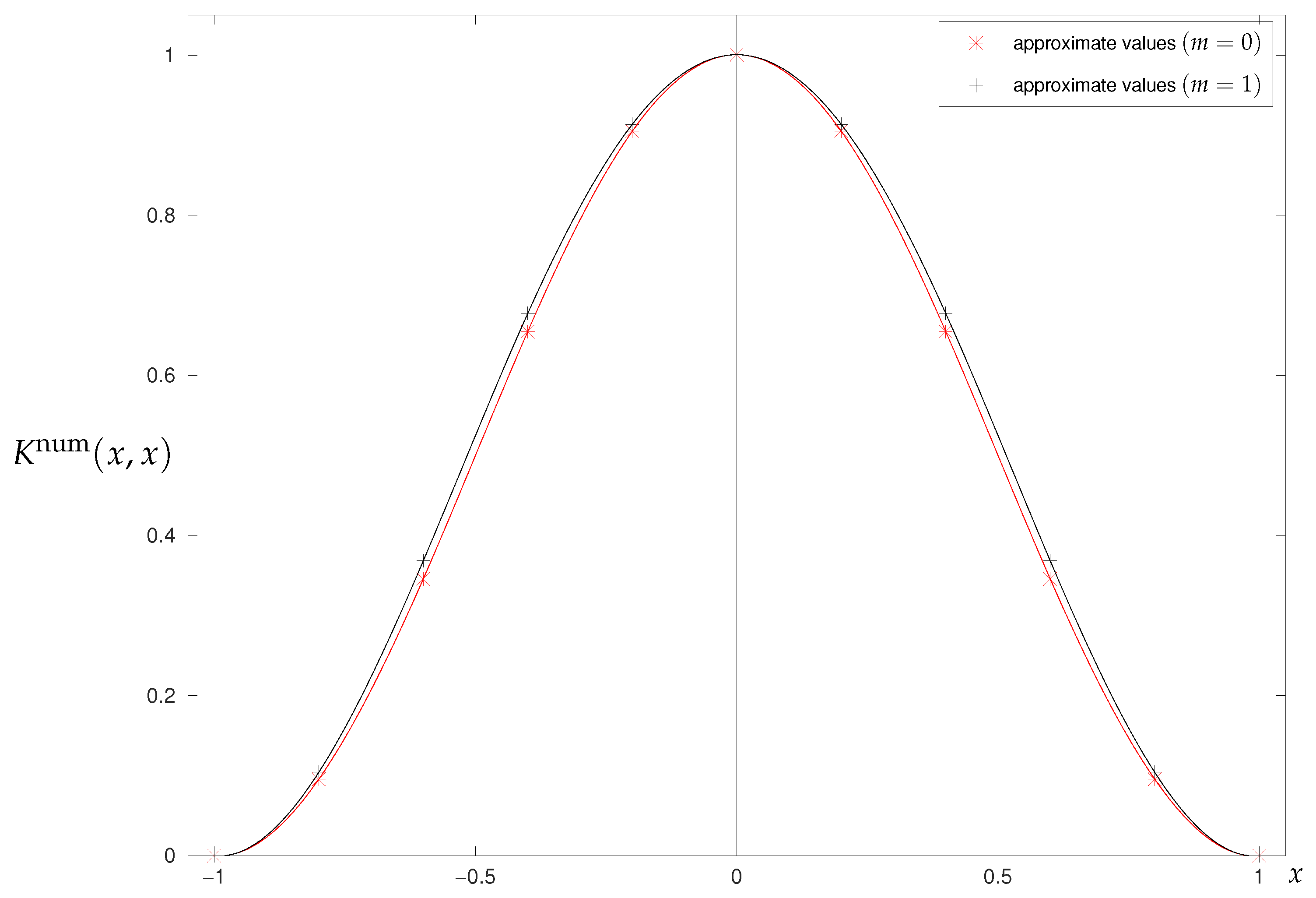
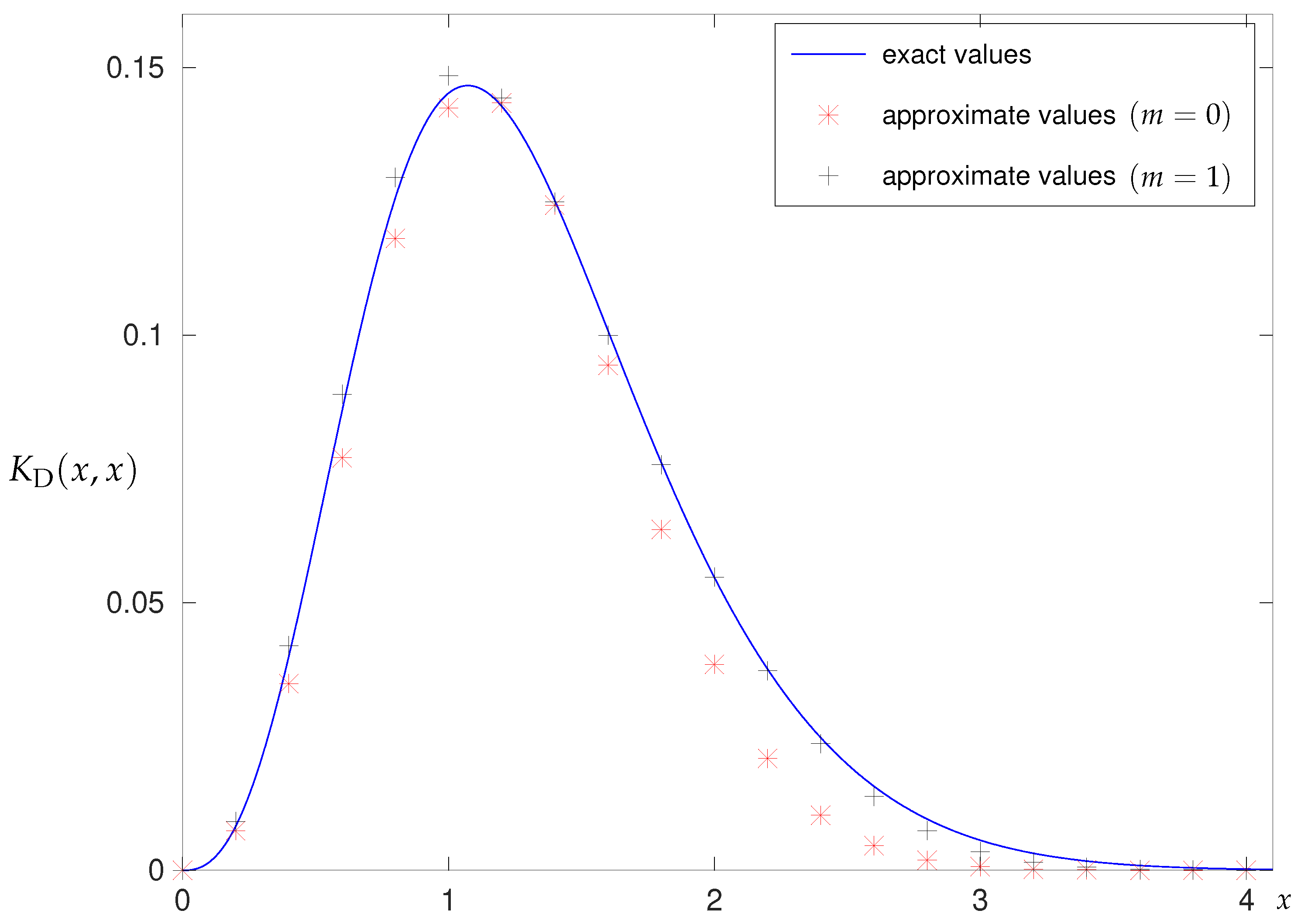
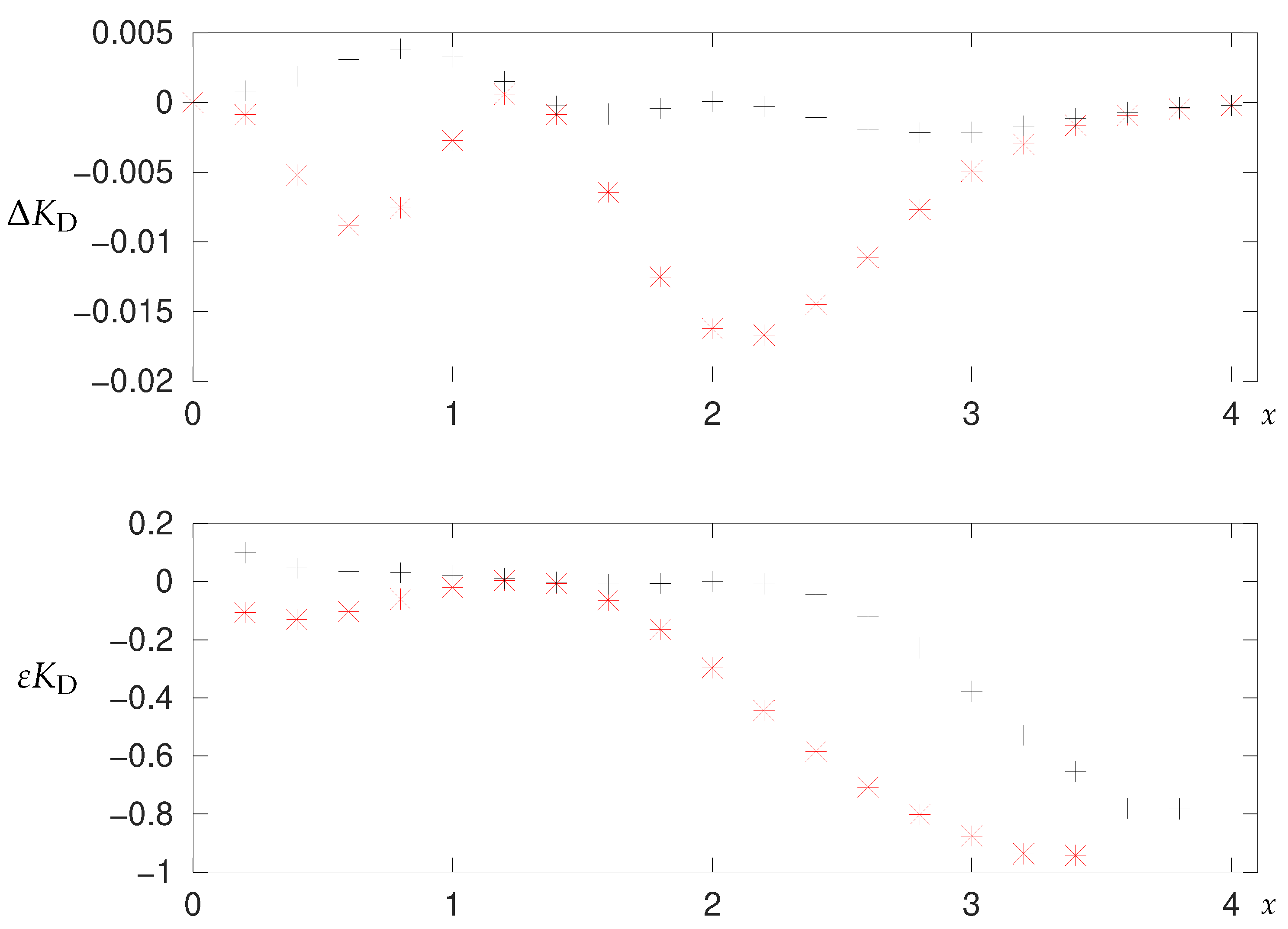
2.6.2. Numerical Results
3. Calculation of Functional Integrals Generated by Relativistic Hamiltonians
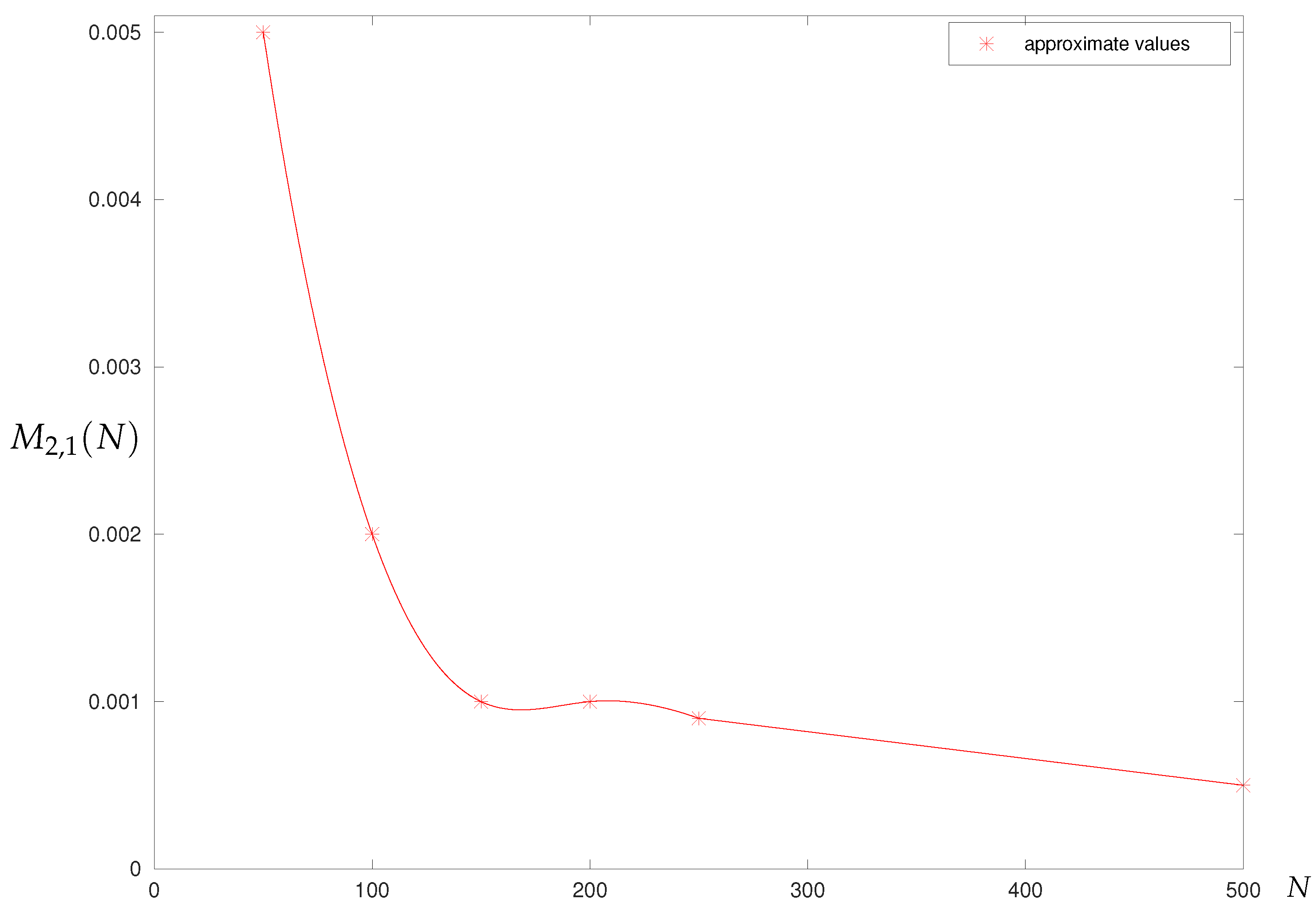
3.1. Method Based on Approximation by Polynomials
3.1.1. Analytical Results
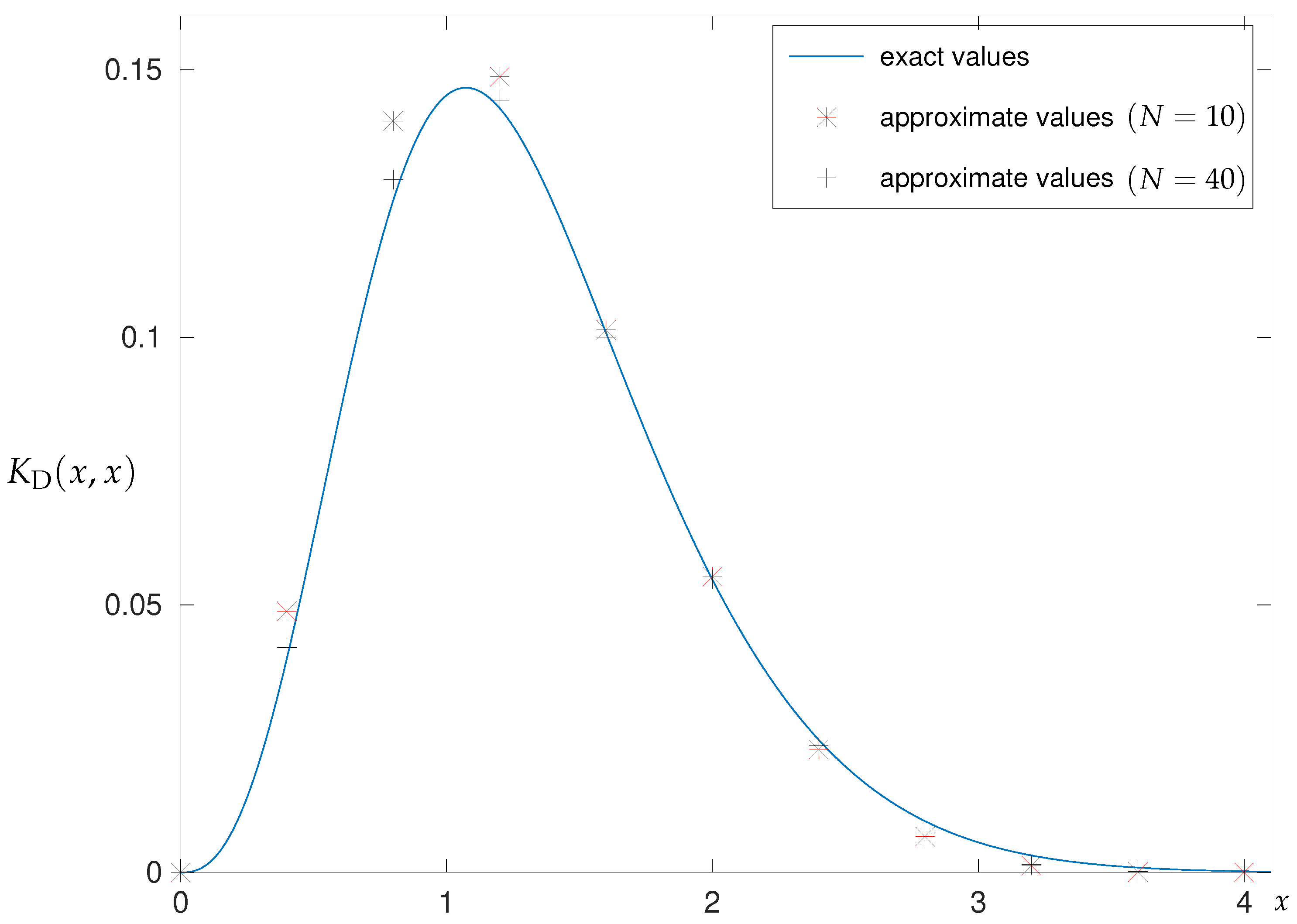
3.1.2. Numerical Results
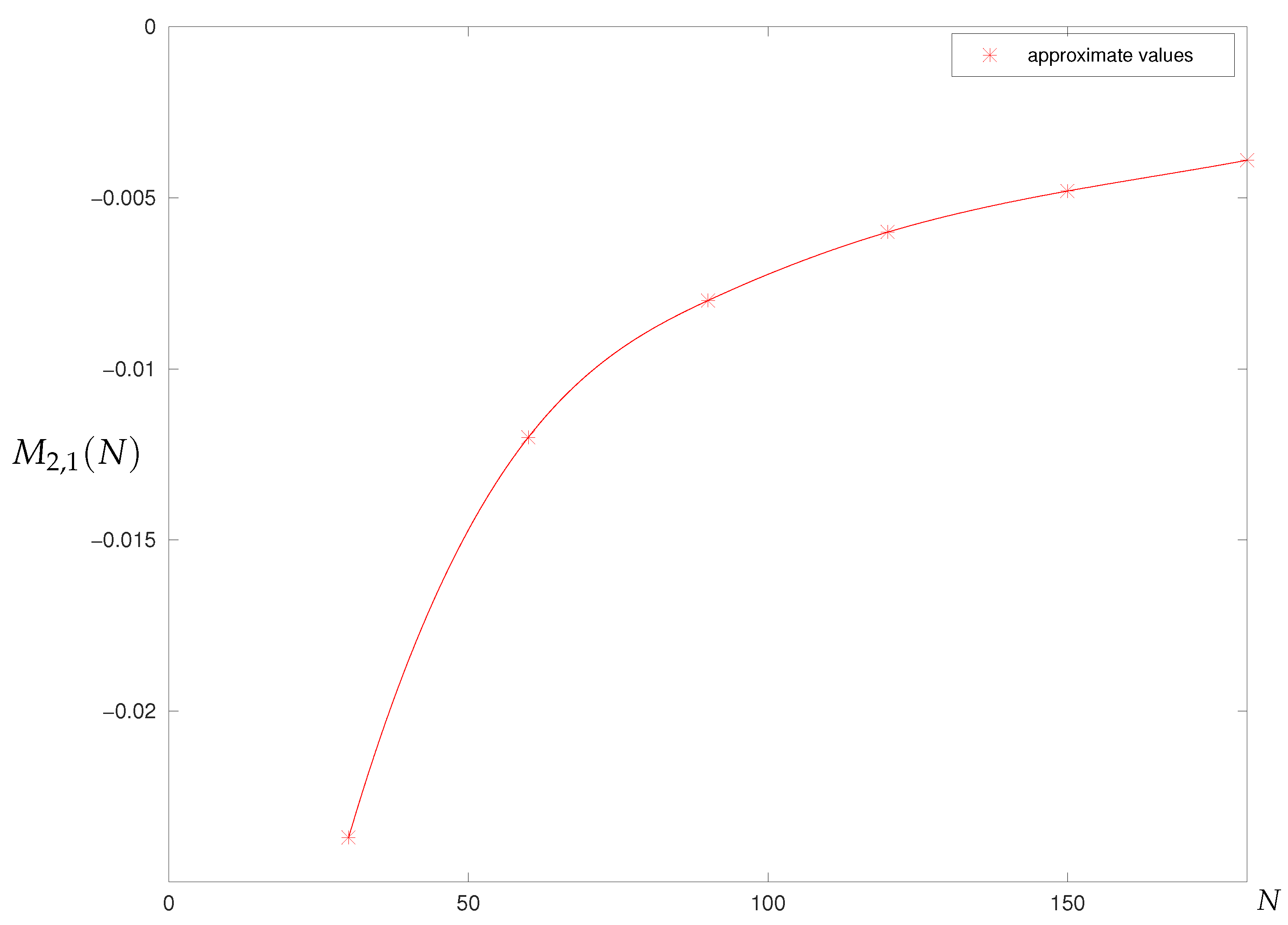
3.2. Functional Integrals Generated by the Matrix Equation
3.2.1. Analytical Results
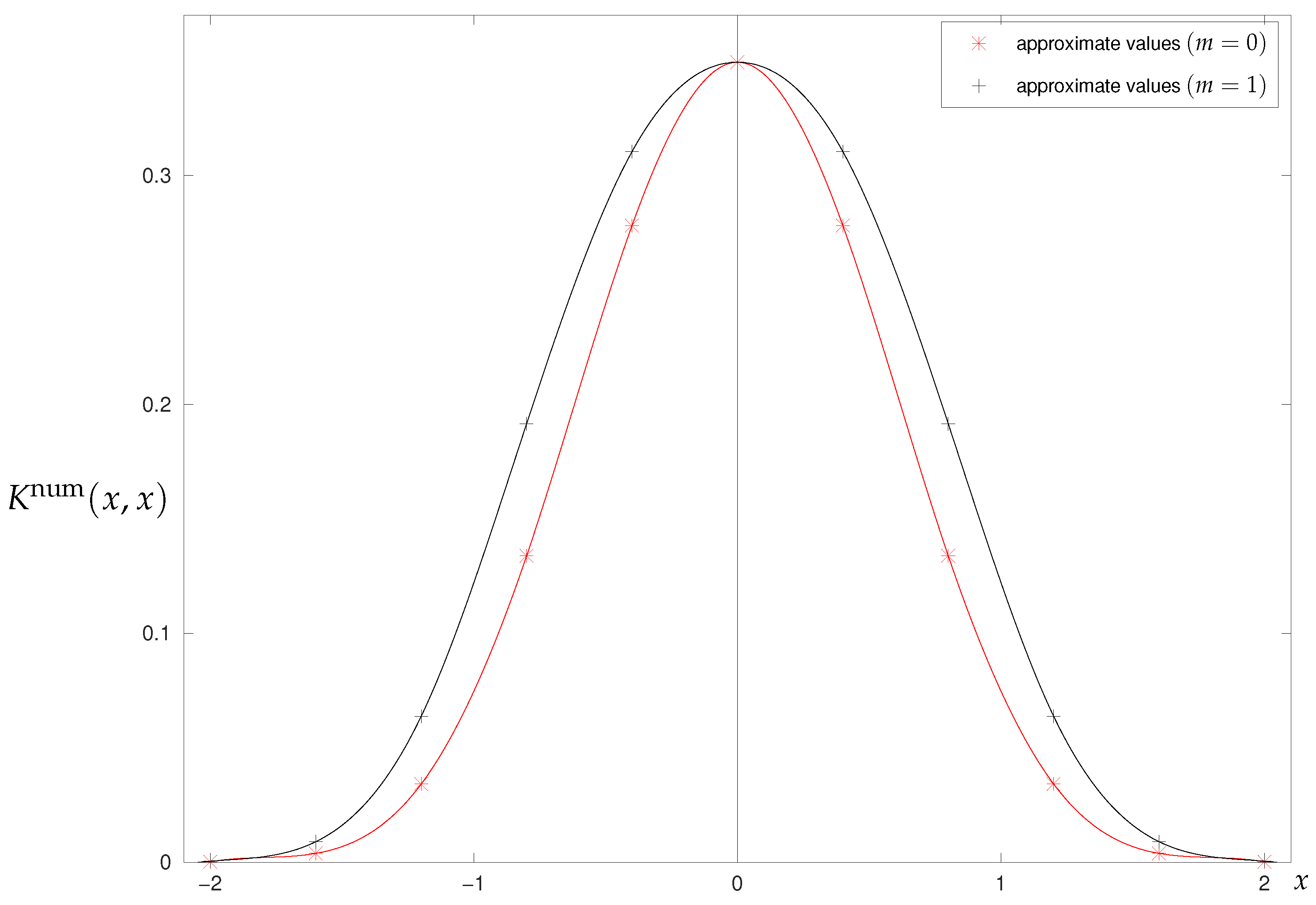
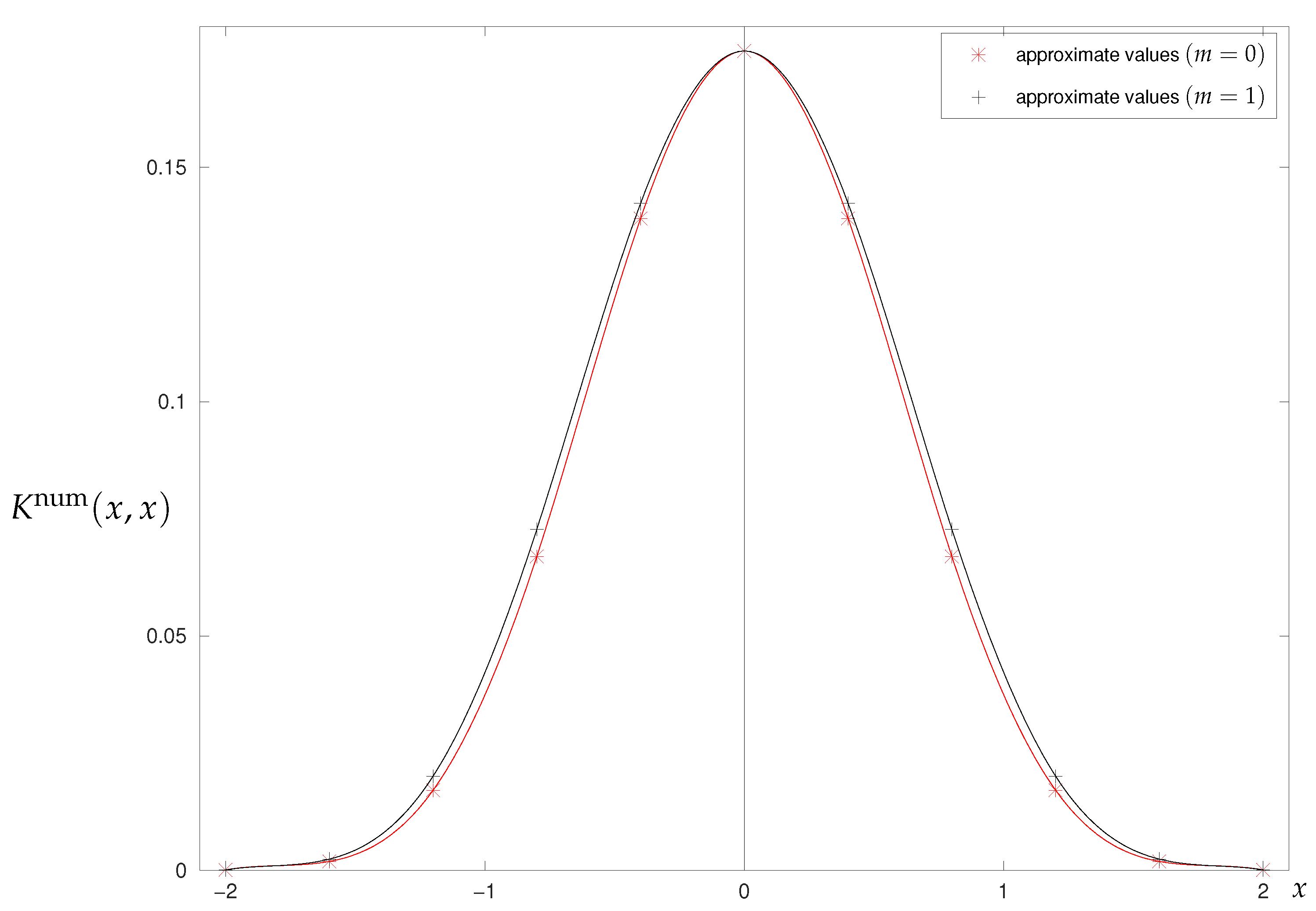
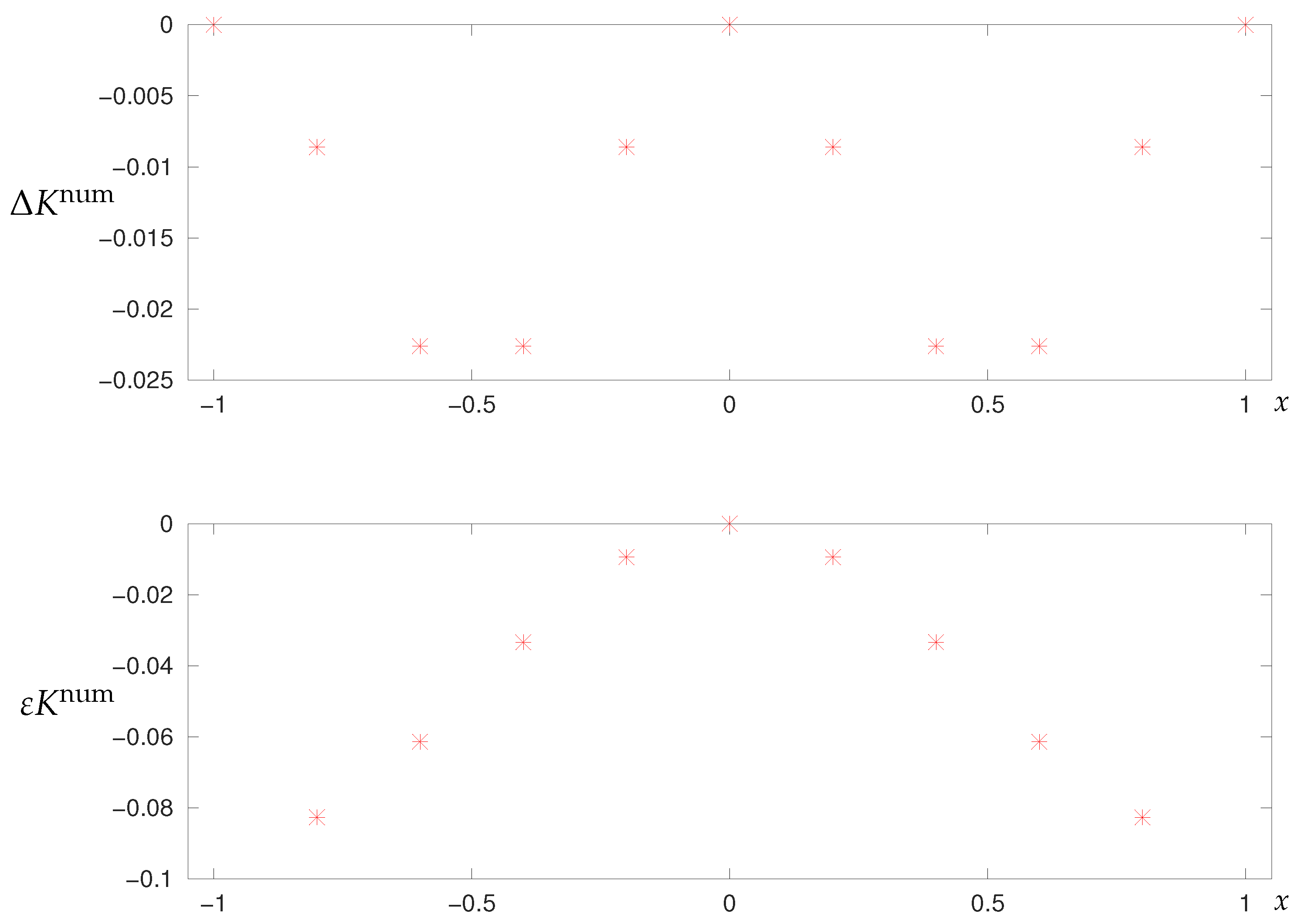
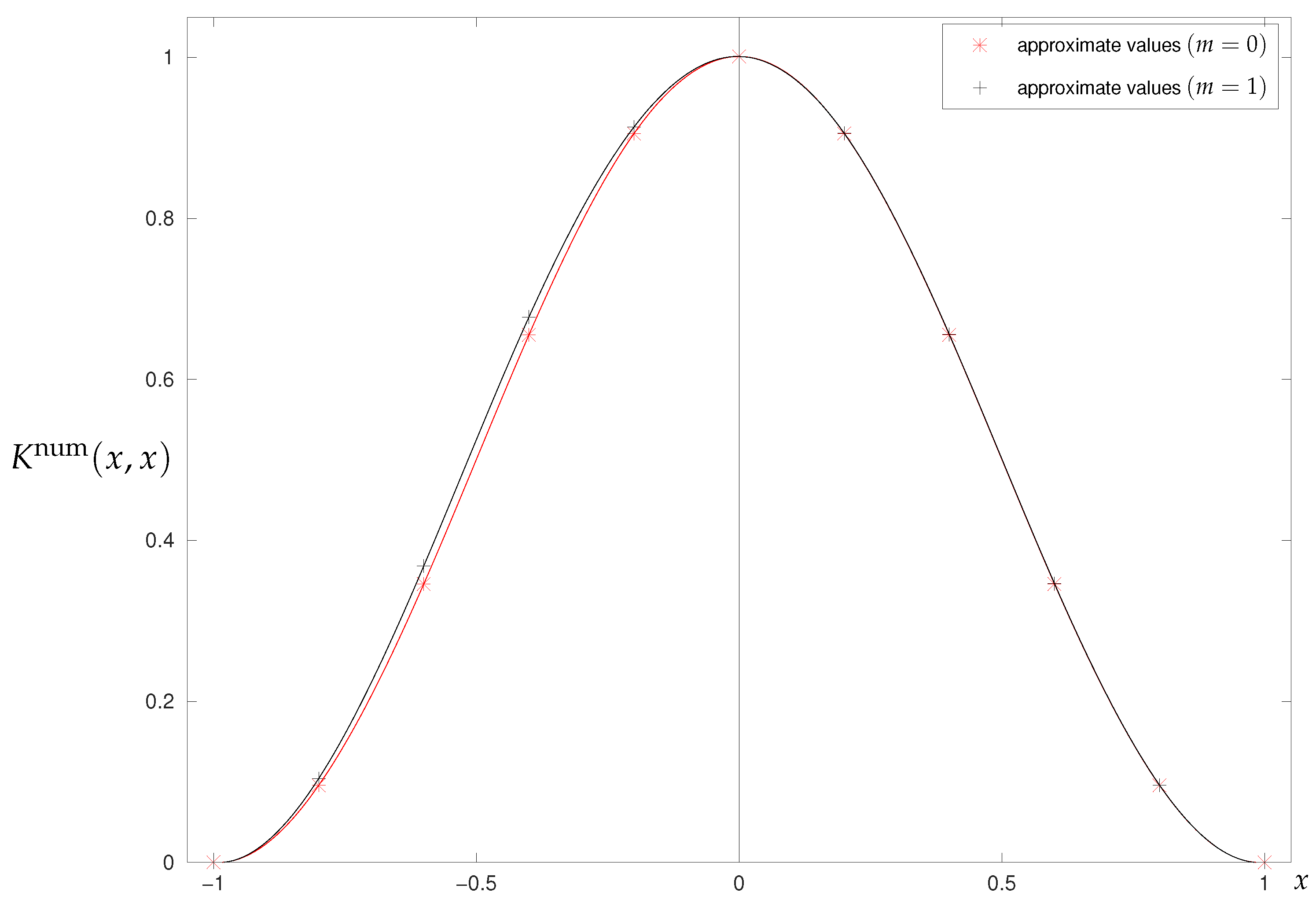
3.2.2. Numerical Results
3.3. Functional Integrals Generated by the Dirac Equation with Pseudospin Symmetry
3.3.1. Analytical Results
3.3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feynman, R.; Hibbs, A. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Glimm, J.; Jaffe, A. Quantum Physics A Functional Integral Point of View; Springer: New York, NY, USA, 1981. [Google Scholar]
- Simon, B. Functional Integration and Quantum Physics; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Roepstorff, G. Path Integral Approach to Quantum Physics: An Introduction; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Bogoliubov, N.N.; Shirkov, D.V. Introduction to the Theory of Quantized Fields, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Vasil’ev, A.N. Functional Methods in Quantum Field Theory and Statistical Physics; Gordon and Breach: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Popov, V.N. Functional Integrals in Quantum Field Theory and Statistical Physics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Mazmanishvili, A.S. Continuum Integration as a Method for Solving Physical Problems; Naukova Dumka: Kiev, Ukraine, 1987. [Google Scholar]
- Langouche, F.; Roekaerts, D.; Tirapegui, E. Functional Integration and Semi-Classical Expansions; D. Reidel Pub. Co.: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Hnatic, M.; Honkonen, J.; Lucivjansky, T. Field theoretic technique for irreversible reaction processes. Phys. Ofparticles Nucl. 2013, 44, 316–348. [Google Scholar] [CrossRef]
- Zhidkov, E.P.; Lobanov, Y.Y. Method of Approximate Continuum Integration in Problems of Mathematical Physics. Phys. Elem. Part. At. Nucl. 1996, 27, 173. [Google Scholar]
- Albeverio, S.A.; Hoegh-Krohn, R.H. Mathematical theory of Feynman path integrals. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1976; Volume 523. [Google Scholar]
- Exner, P. Unstable quantum systems and Feynman integrals. Phys. Elem. Part. At. Nucl. 1984, 15, 121. [Google Scholar]
- Exner, P. Open Quantum Systems and Feynman Integrals; D. Reidel Pub. Co.: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Smolyanov, O.G.; Shavgulidze, E.T. Continuum Integrals; Moscow State University: Moscow, Russia, 1990. [Google Scholar]
- Yanovich, L.A. Approximate Calculation of Path Integrals with Respect to Gaussian Measures; Science and Technology: Minsk, Belarus, 1976. [Google Scholar]
- Elepov, B.S.; Kronberg, A.A.; Mikhailov, G.A.; Sabelfeld, K.K. Solution of Boundary Value Problems by the Monte Carlo Method; Science: Novosibirsk, Russia, 1980. [Google Scholar]
- Sabelfeld, K.K. On the approximate calculation of Wiener path integrals by the Monte Carlo method. Comput. Math. Math. Phys. 1979, 19, 29–43. [Google Scholar]
- Creutz, M. Quarks, Gluons and Lattices; Cambridge University Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Creutz, M.; Freedman, B. A Statistical Approach to Quantum Mechanics. Ann. Phys. 1981, 132, 427–462. [Google Scholar] [CrossRef]
- Shuryak, E.V.; Zhirov, O.V. Testing Monte Carlo methods for path integrals in some quantum mechanical problems. Nucl. Phys. B 1984, 242, 393–406. [Google Scholar] [CrossRef]
- Egorov, A.D.; Sobolevsky, P.I.; Yanovich, L.A. Approximate Methods for Calculating Path Integrals; Science and Technology: Minsk, Belarus, 1985. [Google Scholar]
- Kovalchik, I.M.; Yanovich, L.A. Generalized Wiener Integral and Some of Its Applications; Science and Technology: Minsk, Belarus, 1989. [Google Scholar]
- Egorov, A.D.; Sobolevsky, P.I.; Yanovich, L.A. Functional Integrals: Approximate Evaluation and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Egorov, A.D.; Zhidkov, E.P.; Lobanov, Y.Y. Introduction to the Theory and Applications of Functional Integration; Kluwer Academic: Fizmatlit: Moscow, Russia, 2006. [Google Scholar]
- Malyutin, V.B. On the calculation of functional integrals generated by some nonrelativistic Hamiltonians. Proc. Natl. Acad. Sci. Belarus. Phys. Math. Ser. 2018, 54, 44–49. [Google Scholar]
- Malyutin, V.B. Approximate calculation of functional integrals containing centrifugal potential. Proc. Natl. Acad. Sci. Belarus. Phys. Math. Ser. 2019, 55, 152–157. [Google Scholar]
- Malyutin, V.B.; Nurzhanov, B.O. Semiclassical approximation of functional integrals. Proc. Natl. Acad. Sci. Belarus. Phys. Math. Ser. 2020, 56, 166–174. [Google Scholar] [CrossRef]
- Ayryan, E.A.; Malyutin, V.B. Application of functional polynomials to approximation of matrix-valued functional integrals. Bull. Peoples’ Friendsh. Univ. Russia. Ser. Inform. Phys. 2014, 1, 55–58. [Google Scholar]
- Ayryan, E.A.; Hnatic, M.; Malyutin, V.B. Approximate calculation of functional integrals generated by the relativistic Hamiltonian. Proc. Natl. Acad. Sci. Belarus. Phys. Math. Ser. 2020, 56, 72–83. [Google Scholar]
- Ayryan, E.A.; Hnatic, M.; Malyutin, V.B. Approximate evaluation of the functional integrals generated by the Dirac equation with pseudospin symmetry. Proc. Natl. Acad. Sci. Belarus. Phys. Math. Ser. 2021, 57, 14–22. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Plank Equation: Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Wilkinson, J.H. The Algebraic Eigenvalue Problem; Oxford University Press: Oxford, UK, 1965. [Google Scholar]
- Setare, M.R.; Haidari, S. Solution of the Dirac equation for the Davidson potential. Int. J. Theor. Phys. 2009, 48, 3249–3256. [Google Scholar] [CrossRef]
- Bohm, D. Quantum Theory; Prentice-Hall: New York, NY, USA, 1951. [Google Scholar]
- Schulmann, L.S. Techniques and Applications of Path Integration; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Grosche, C.; Steiner, F. Classification of solvable Feynman path integrals. In Proceedings of the IV International Conference on Path Integrals from meV to MeV, Tutzing, Germany 1992; Grabert, H., Inomata, A., Schulman, L.S., Weiss, U., Eds.; World Scientific: Singapore, 1993; pp. 276–288. [Google Scholar]
- Bennati, E.; Rosa-Clot, M.; Taddei, S. A path integral approach to derivative security pricing I: Formalism and analytical results. Int. J. Theor. Appl. Finan. 1999, 2, 381. [Google Scholar] [CrossRef]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics Polymer Physics, and Financial Markets; World Scientific Publishing: Singapore, 2004. [Google Scholar]
- Wio, H.S. Application of Path Integration to Stochastic Process: An Introduction; World Scientific Publishing Company: Singapore, 2013. [Google Scholar]
- Krylov, V.I.; Bobkov, V.V.; Monastyrny, P.I. Computational Methods of Higher Mathematics; Minsk, Belarus, 1975; Volume 2. [Google Scholar]
- Ichinose, T.; Tamura, H. Propagation of a Dirac particle. A path integral approach. J. Math. Phys. 1984, 25, 1810–1819. [Google Scholar] [CrossRef]
- Ichinose, T.; Tamura, H. The zitterbewegung of a Dirac particle in two-dimensional space-time. J. Math. Phys. 1988, 29, 103–109. [Google Scholar] [CrossRef]
- Schiff, L. Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1949. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory (Course of Theoretical Physics Book 3), 3rd ed.; Elsevier Science: Oxford, UK, 1991. [Google Scholar]
- Berkdemir, C.; Sever, R. Pseudospin symmetry solution of the Dirac equation with an angle-dependent potential. J. Phys. A Math. Theor. 2008, 41, 045302. [Google Scholar] [CrossRef]


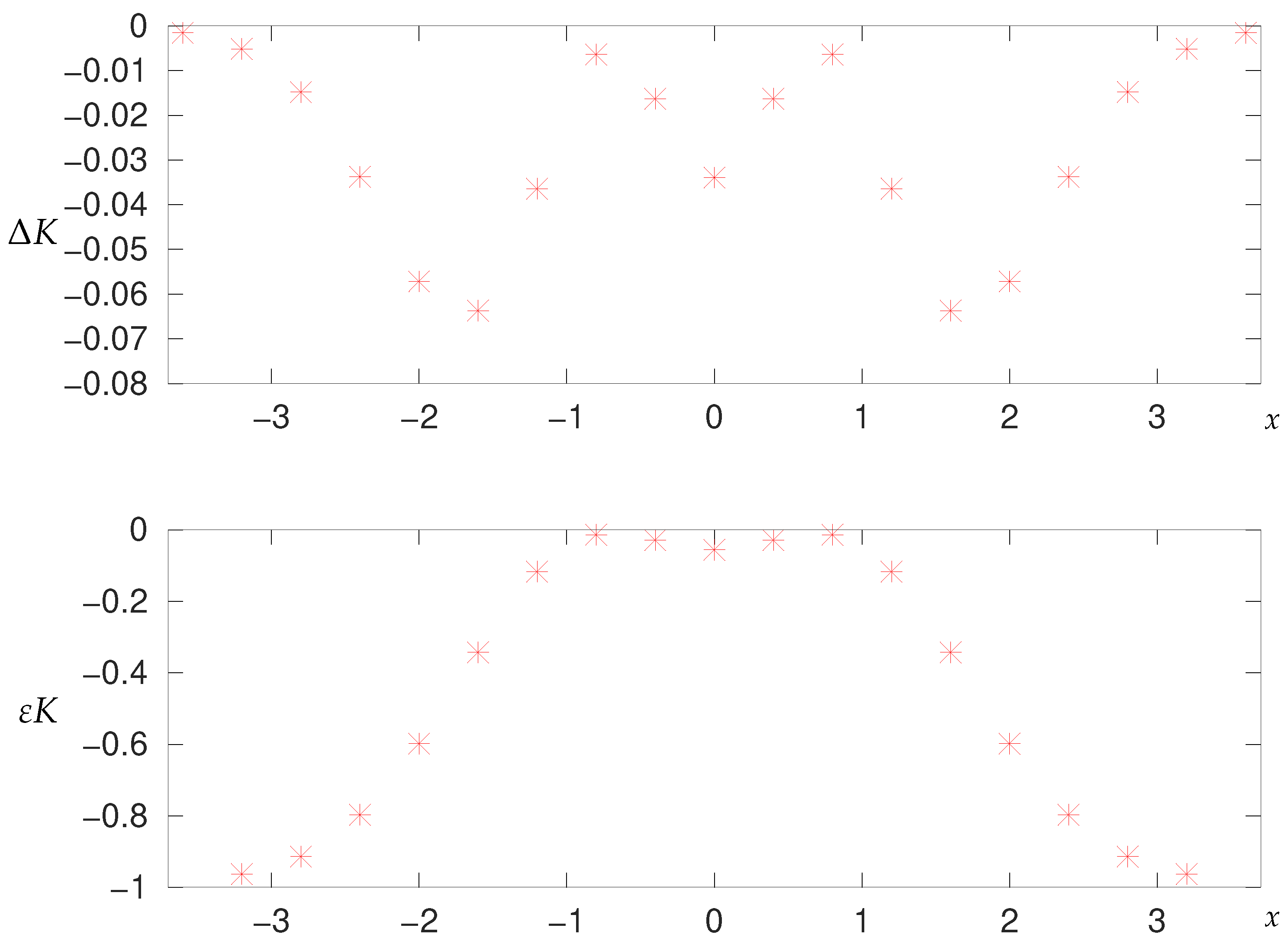
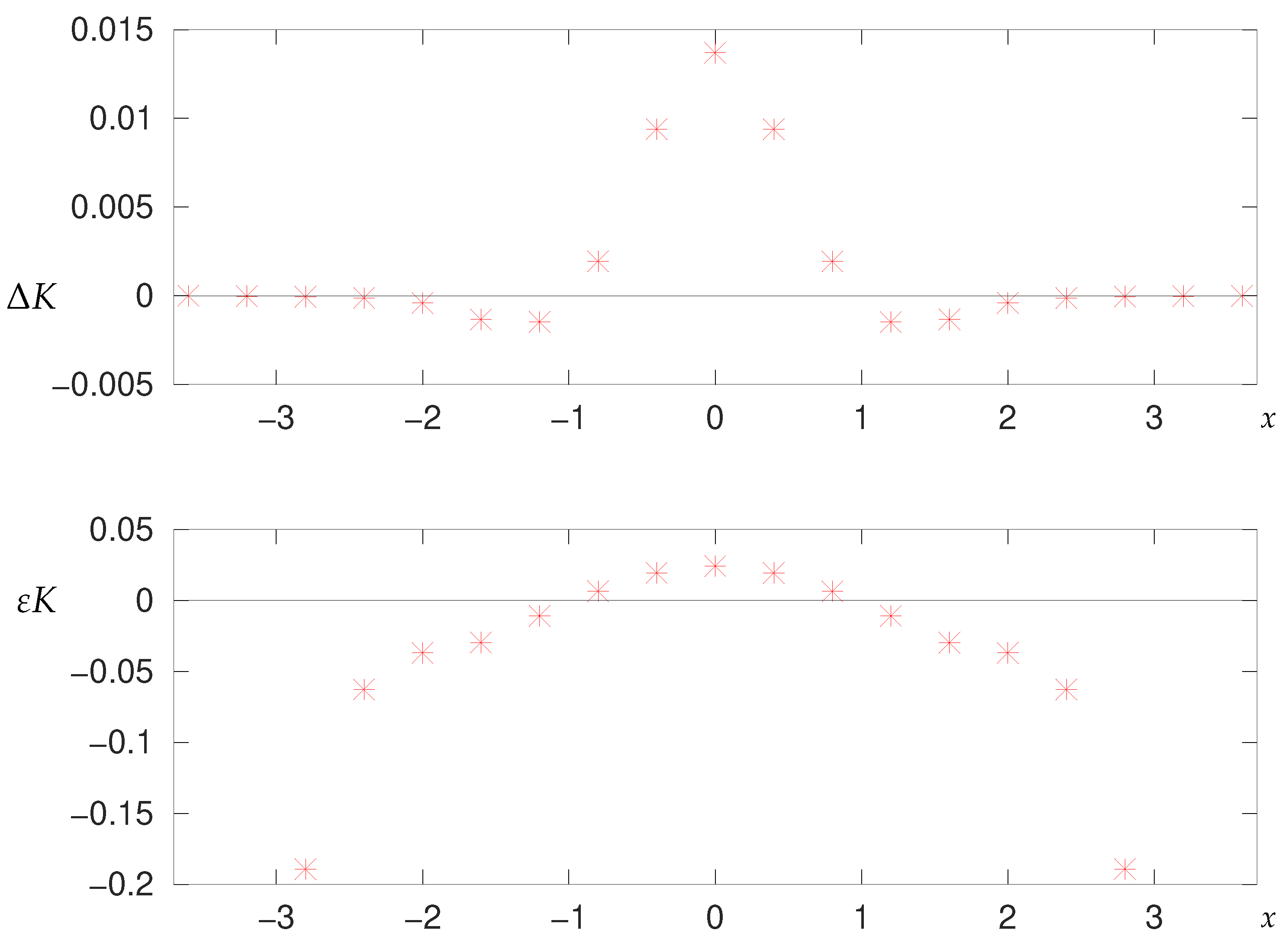


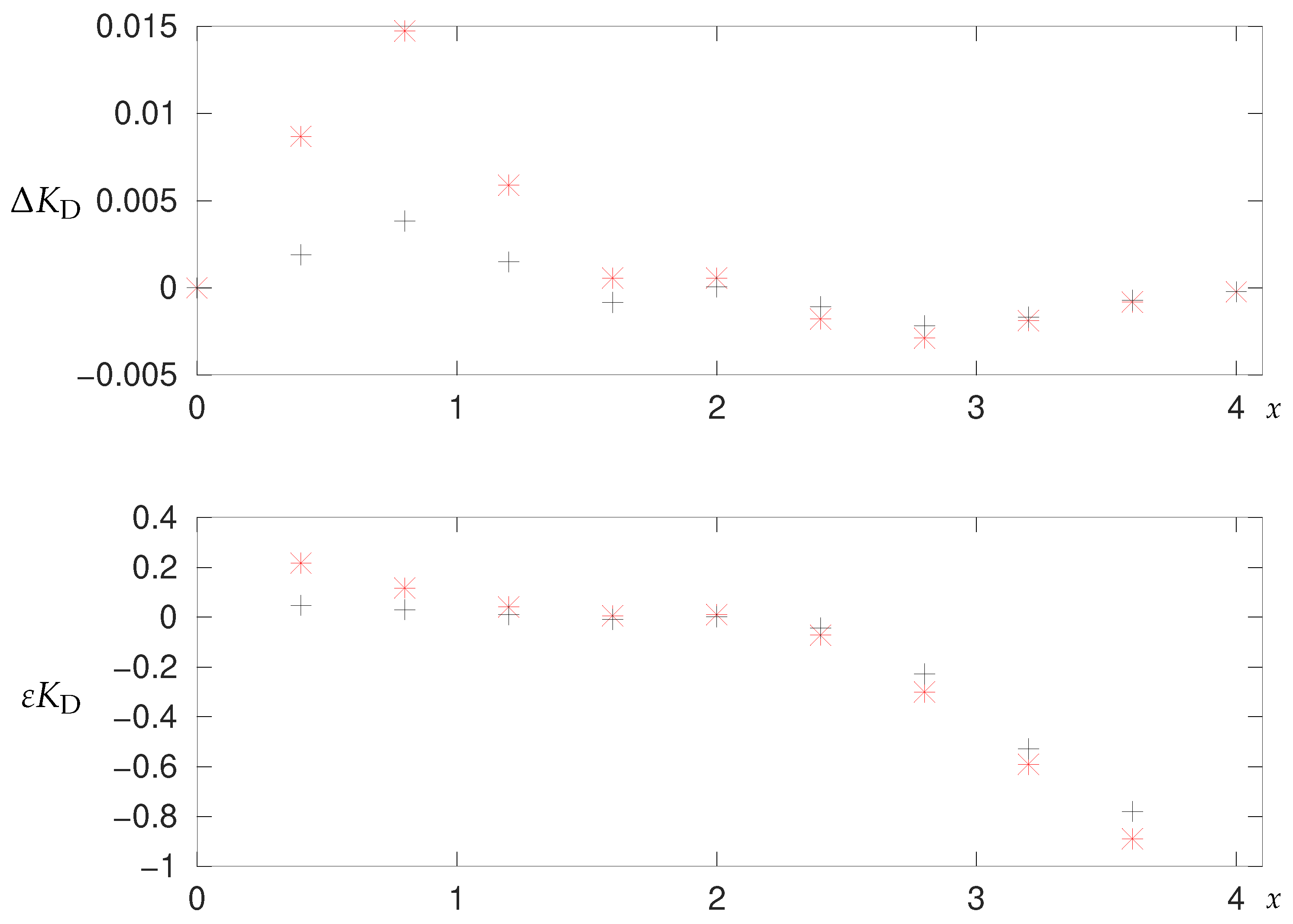





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayryan, E.; Hnatic, M.; Honkonen, J.; Malyutin, V. Approximate Calculation of Functional Integrals Generated by Nonrelativistic and Relativistic Hamiltonians. Symmetry 2023, 15, 1785. https://doi.org/10.3390/sym15091785
Ayryan E, Hnatic M, Honkonen J, Malyutin V. Approximate Calculation of Functional Integrals Generated by Nonrelativistic and Relativistic Hamiltonians. Symmetry. 2023; 15(9):1785. https://doi.org/10.3390/sym15091785
Chicago/Turabian StyleAyryan, Edik, Michal Hnatic, Juha Honkonen, and Victor Malyutin. 2023. "Approximate Calculation of Functional Integrals Generated by Nonrelativistic and Relativistic Hamiltonians" Symmetry 15, no. 9: 1785. https://doi.org/10.3390/sym15091785
APA StyleAyryan, E., Hnatic, M., Honkonen, J., & Malyutin, V. (2023). Approximate Calculation of Functional Integrals Generated by Nonrelativistic and Relativistic Hamiltonians. Symmetry, 15(9), 1785. https://doi.org/10.3390/sym15091785







