Atangana-Baleanu Fractional Dynamics of Predictive Whooping Cough Model with Optimal Control Analysis

Abstract

Whooping cough, or pertussis, is an infectious disease that causes serious threats to people of all ages, specifically to infant and young children, all over the world. Due to the severe impact on health, it is necessary to construct a mathematical model that can be used to predict future dynamics of the disease, as well as to suggest strategies to eliminate the disease in an optimal way. For this, we constructed a new Atangana–Baleanu fractional model for whooping cough disease to predict the future dynamics of the disease, as well as to suggest strategies to eliminate the disease in an optimal way. We prove that the proposed model has a unique solution that is positive and bounded. To measure the contagiousness of the disease, we determined the reproduction number ${\mathcal{R}}_0$ and used it to examine the local and global stability at equilibrium points that have symmetry. Through sensitivity analysis, we determined parameters of the model that are most sensitive to ${\mathcal{R}}_0$. The ultimate aim of this research was to analyze different disease prevention approaches in order to find the most suitable one. For this, we included the vaccination and quarantine compartments in the proposed model and formulated an optimal control problem to assess the effect of vaccination and quarantine rates on disease control in three distinct scenarios. Firstly, we study the impact of vaccination strategy and conclude the findings with a graphical presentation of the results. Secondly, we examine the impact of quarantine strategy on whooping cough infection and its possible elimination from society. Lastly, we implement vaccination and quarantine strategies together to visualize their combined effect on infection control. In addition to the study of the optimal control problem, we examine the effect of the fractional order on disease dynamics, as well as the impact of constant vaccination and quarantine rates on disease transmission and control. The numerical results reveal that the optimal control strategy with vaccination and quarantine together would be more effective in reducing the spread of whooping cough infection. The implementation of the Toufik–Atangana-type numerical scheme for the solution of the fractional optimal control problem is another contribution of this article.

1. Introduction

Whooping cough is a highly contagious disease that is caused by a bacterium called Bordetella pertussis. Many outbreaks of the disease have occurred in different parts of the world. The history of the disease dates back to the late 15th century [1]. However, the first recorded outbreak was witnessed in France in 1578. In 1947, a major whooping cough epidemic occurred in Cape Town that registered 107 deaths [2]. In early 2010, an outbreak occurred in the USA, Ireland and Israel. More than 10,000 whooping cough cases were reported in California in 2014, and it was declared the worst outbreak since 1947. According to a report published in 2014, there were around 24.1 million cases of whooping cough with 160,700 deaths in younger children around the world [3,4]. According to the WHO, there were more than 151,000 pertussis cases worldwide in 2018 [3].

Whooping cough is an extremely infectious disease that has become a serious threat to people of all ages and is especially dangerous to children younger than 5 years. The disease spreads from one infected person to another susceptible person through the droplets released by sneezing or coughing. The symptoms of whooping cough appear gradually and can stay for few weeks to months. Once a person catches the infection, the first disease symptoms appear within 7 to 10 days. Early-stage common symptoms are minor fever, stuffed or runny nose and cough. At this level, it is not easy to tell it apart from the common cold. After early-stage symptoms, the coughing fits start and gradually turn into a hacking cough, which is followed by whooping. Sickness, vomiting and difficulty breathing are the other symptoms of the disease. The people who contract the disease become infectious for up to three weeks. Quarantining such people may help to restrict the spread of the disease. The risk of complications and the spread of the virus to others can be reduced with early whooping cough diagnosis and treatment. Whooping cough vaccines provide the highest level of protection against this highly infectious disease.

Whooping cough is still one of the leading causes of death and illness, especially in infants, around the world. The disease is on the rise again in many parts of the world, including the USA, Australia and Great Britain. There is no definite explanation for this rise, but it is thought to be caused by the vaccine losing its effectiveness, the bacterium becoming more aggressive and improved diagnostics that have resulted in more cases being diagnosed. It is therefore necessary to develop mathematical models that can be used to forecast the dynamics of the whooping cough disease and also to propose strategies for eliminating the disease in the most effective manner. In the existing literature, there are very few mathematical models that have been designed to study the dynamics of whooping cough and to propose effective control strategies. In [5], an effective numerical scheme was presented to simulate a second-order whooping cough model. In 2018, researchers conducted a study on the cost-effectiveness of maternal vaccination for whooping cough in Australia [6]. A whooping cough model with optimal vaccination control was studied in [7]. A whooping cough model was proposed in [8] to analyze disease transmission in Nebraska. An implicit numerical integration method was established in [4] to ensure a consistent dynamic convergence of the SEIR model for the whooping cough epidemic. In [9], the ABC fractional derivative was employed to model phytoplankton nutrients and whooping cough epidemics. In this article, the authors used the homotopy perturbation Elzaki transform method for numerical solutions and proved that the implemented method is an effective technique to handle such fractional models. Among all of the above articles, none used fractional modeling to extensively study the dynamics of whooping cough to determine the most effective control strategies for the disease.

Mathematical modeling is a powerful tool for predicting the dynamics of communicable diseases with prevention measures. The differential equations for the epidemiological compartmental models have symmetry in the sense that they are constructed on the principle that the rate of change for individuals in a particular compartment is equal to the incoming individuals minus the outgoing individuals. In the recent past, fractional calculus has played a significant role in solving physical problems that cannot be solved using integer-order differential equations. For many realistic applications, fractional-order models are always better than integer-order models. For example, the memory effects observed in biological models [10,11,12,13,14,15] cannot be better elucidated using integer-order models. Furthermore, fractional-order operators can be used in mathematical models to solve differential equations without being restricted by the order constraint. This makes fractional-order models more versatile than classical integer-order models and, hence, they provide more precise and accurate information about complex systems. Several fractional differential operators with singular and non-singular kernels are available in the literature [16,17] and have been used in recent studies [18,19,20,21,22] of physical and biological systems. Caputo and Riemann–Liouville fractional derivatives are the most common of these. The singularity property of the kernels in Caputo and Riemann–Liouville derivatives is the fundamental drawback in both derivatives [16,23,24]. Many physical systems are difficult to evaluate with singular kernels, so fractional derivatives with non-singular kernels, such as Caputo–Fabrizo (CF), have been developed and implemented [25,26,27,28,29]. Even though the CF derivative has a non-singular kernel, the function space of CF derivative is not clear and it does not have any memory effects [30]. The authors in [31] introduced a new fractional derivative operator, the Atangana–Baleanu–Caputo (ABC) operator, that uses a Mittag–Leffler (ML) kernel with a single parameter. The ML function is a generalized version of the exponential function and the key feature of this kernel is its non-local and non-singular behavior. Due to this feature, the ABC operator is considered to be the best choice for modeling real world phenomena, including epidemic diseases. The application of the ABC fractional operator to various models can be studied in [32,33,34,35,36,37,38]. Some more features of the ABC operator were latter narrated by authors in [39].

In recent years, many scientists have begun to use fractional models with different fractional operators to include memory effects for better epidemiological disease analysis [40,41,42,43]. Fractional operators have a wide range of uses in modern mathematics, including the complex and significant study of symmetric systems. Furthermore, fractional models work better and are more consistent with the real data. In this study, we develop an Atangana–Baleanu–Caputo (ABC) fractional whooping cough model, $SVEIQR$, to evaluate the effectiveness of different disease control strategies, including vaccination of susceptible and isolation of infected individuals, and to observe the influence of the fractional order on the disease dynamics. The reason for choosing the ABC operator for the proposed model is due to its non-local and non-singular kernel. In addition to this, the operator can capture higher susceptibilities and fewer infections as compared to other fractional operators, such as Caputo and Caputo–Fabrizo [38]. One of the primary objectives of developing a fractional model for whooping cough disease is to figure out potential control strategies that involve constant and time-dependent controls and to understand the evolution of the disease in a more general setup. To achieve the goal, we will first examine the validity of the proposed model by proving the basic properties of the model, such as the existence of a positive and bounded unique solution, and local and global stability analysis at equilibrium points. In addition, this article contributes to developing a fractional optimal control problem to identify optimal vaccination and quarantine rates that will help to limit the spread of whooping cough infection. Symmetry analysis is a robust tool to come up with numerical solutions for certain fractional differential equations. The significance of the present work lies in the use of a previously developed structure-preserving the Toufik–Atangana scheme backward in time for the very first time to evaluate the whooping cough model.

The other sections are arranged as follows: In Section 2, we describe the formulation of a $SVEIQR$ fractional model to express the dynamics of whooping cough disease. The formulation is given with the help of the Atangana–Baleanu fractional derivative. Theoretical aspects of the proposed fractional model are discussed in Section 3, including the existence and uniqueness of the solution, the positivity and boundedness of the solutions, the calculation of equilibrium points, the determination of the fundamental reproduction number ${\mathcal{R}}_0$, the analysis of local and global stability at equilibrium points. In Section 4, Toufik–Atangana type numerical scheme is established and implemented to observe the impact of fractional order on disease dynamics. The effect of vaccination and quarantine rates on disease transmission is also simulated here. In Section 5, we provide sensitivity analysis to identify extremely sensitive parameters for reproduction number ${\mathcal{R}}_0$. In Section 6, the model is further modified with time-dependent controls to form an optimal control problem. The associated optimality conditions, arising from the Pontryagin’s principle, are then numerically solved by applying the Toufik–Atangana numerical scheme to determine the best time-dependent vaccination and quarantine rates for whooping cough control. The results of this study are concluded in Section 7.

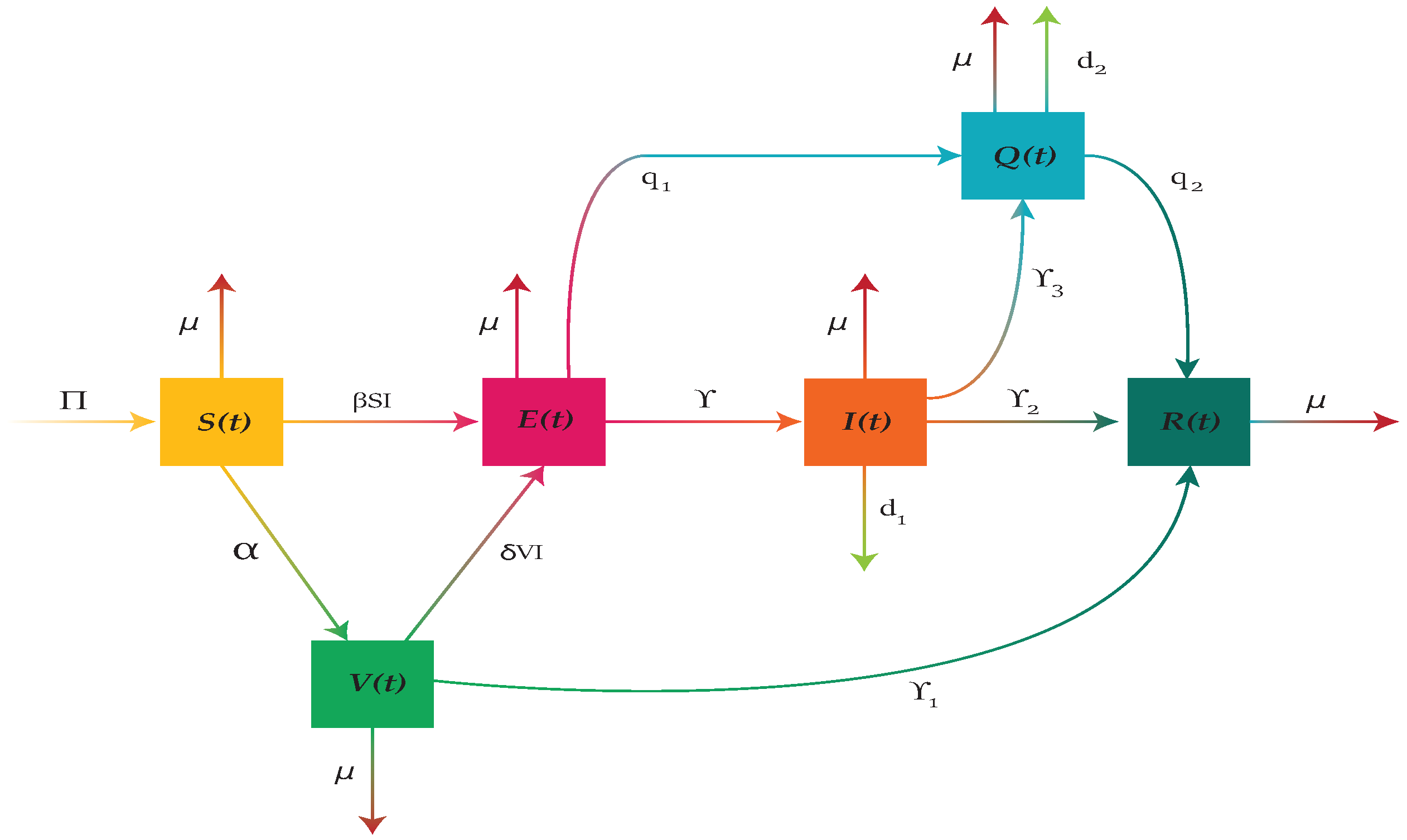
2. Model Formulation

Mathematical models of infectious diseases play a vital role in understanding disease flow patterns and in designing appropriate disease control strategies. Therefore, while developing mathematical models for infectious diseases, it is very important to focus on procedures needed in formulating the epidemiology of the disease and to identify the most important and controllable parameters for disease control. A variety of epidemiological models have been developed based on disease transmission mechanisms and are available in literature, see [44,45,46,47,48,49,50,51,52,53]. These models have played a significant role in formulating and designing control strategies for different diseases.

In this study, we develop a new $SVEIQR$ model for whooping cough infectious disease. The aim is to study the disease dynamics comprehensively and to formulate the most suitable control strategies to restrict the spread of the disease. We divide the total human population $N\left(t\right)$ into six compartments: susceptible $S\left(t\right)$, vaccinated $V\left(t\right)$, exposed $E\left(t\right)$, infected $I\left(t\right)$, quarantined $Q\left(t\right)$ and recovered $R\left(t\right)$. The humans specified by $S\left(t\right)$ are those who are at risk of catching a virus after having contact with an infectious person. Thus, the susceptible who are caught by the virus move to exposed class $E\left(t\right)$, and those who are vaccinated at the rate $\alpha$ move to $V\left(t\right)$. The vaccinated individuals may either move to recovered class $R\left(t\right)$ at the rate ${\gamma }_1$ or to exposed class $E\left(t\right)$ after receiving an infection as a result of having contact with an infectious person. The exposed individuals who become infectious move to infected class $I\left(t\right)$ at the rate $\gamma$. To restrict the spread of disease, we introduce an isolation compartment $Q\left(t\right)$ in the model. The individuals from exposed and infected classes are transferred to quarantined class $Q\left(t\right)$ at rates $q_1$ and ${\gamma }_3$, respectively. The individuals of $I\left(t\right)$ and $Q\left(t\right)$ classes who recovered either by medication or by their natural immunity move to recovered class $R\left(t\right)$, respectively, at the rates ${\gamma }_2$ and $q_2$. We assume that the recovered individuals do not move back to the susceptible class. The rates at which the infected and quarantined die due to disease are $d_1$ and $d_2$. Thus, the whole human population at any time t is given by

$$N\left(t\right)=S\left(t\right)+V\left(t\right)+E\left(t\right)+I\left(t\right)+Q\left(t\right)+R\left(t\right).$$

(1)

The whooping cough disease flow pattern, given in Figure 1, is governed by a mathematical model consisting of the following nonlinear ordinary differential equations:

$$\begin{array}{}\mathrm{(2a)}& {\displaystyle \frac{dS}{dt}}=\Pi -\beta IS-(\mu +\alpha )S,\hfill \mathrm{(2b)}& {\displaystyle \frac{dV}{dt}}=\alpha S-\delta IV-({\gamma }_1+\mu )V,\hfill \mathrm{(2c)}& {\displaystyle \frac{dE}{dt}}=\beta IS+\delta IV-(\mu +\gamma +q_1)E,\hfill \mathrm{(2d)}& {\displaystyle \frac{dI}{dt}}=\gamma E-({\gamma }_2+{\gamma }_3+\mu +d_1)I,\hfill \mathrm{(2e)}& {\displaystyle \frac{dQ}{dt}}=q_{1}E+{\gamma }_{3}I-(q_2+d_2+\mu )Q,\hfill \mathrm{(2f)}& {\displaystyle \frac{dR}{dt}}={\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q-\mu R,\hfill \end{array}$$

subject to the conditions:

$$\begin{array}{}\mathrm{(2g)}& \begin{array}{c}S\left(0\right)=S_0>0,V\left(0\right)=V_0\ge 0,E\left(0\right)=E_0\ge 0,\hfill \\ I\left(0\right)=I_0\ge 0,Q\left(0\right)=Q_0\ge 0,R\left(0\right)=R_0\ge 0.\hfill \end{array}\hfill \end{array}$$

A detailed description of parameters of the model (2) is given below:

• $\Pi$: Recruitment rate of the susceptible.
• $\mu$: Natural death rate of individuals of each compartment.
• $\beta$: Rate of contact of the susceptible with infectious people.
• $\alpha$: Rate at which the susceptible are vaccinated.
• $\delta$: Rate of contact of vaccinated with infectious people.
• $\sigma$: Rate at which the exposed become infectious.
• ${\sigma }_1$: Rate at which vaccinated people recovered.
• ${\sigma }_2$: Rate at which infectious people recovered.
• ${\sigma }_3$: Rate at which infectious people are quarantined.
• $q_1$: Rate at which exposed people are quarantined.
• $q_2$: Rate at which quarantined people recovered.
• $d_1$: Death rate of infected people due to the disease.
• $d_2$: Death rate of quarantined people due to the disease.

Fractional Model

Generally, classical integer order models are neither robust nor more useful for understanding the dynamic behavior of an infectious disease. On the other hand, fractional order models work more appropriately with the real data. Hence, to generalize the system (2) for whooping cough, we use the Atangana–Baleanu derivative ${}_a^{ABC}{D}_t^{\rho }$, defined in (3), in place of the classical integer order time derivative $D_t$. This fractional order formulation will allow us to observe memory impacts and gain further insight into the disease dynamics. For the fractional formulation, we first consider some basics related to the Atangana–Baleanu fractional derivatives [31].

Definition 1

([31]). If the differentiable function $\Phi :[a,b]\to \mathbb{N}$ is defined on $[a,b]$ such that $\Phi \in H^1(a,b)$, $b>a$ and $\sigma \in (0,1]$, then the Atangana–Baleanu derivative of Φ in Caputo sense is defined as

$$\begin{array}{c}\hfill {}_a^{ABC}{D}_t^{\sigma }\Phi \left(t\right)={\displaystyle \frac{F\left(\sigma \right)}{1-\sigma }}{\int }_a^t\dot{\Phi }\left(\xi \right)E_{\sigma }\left[-\sigma {\displaystyle \frac{{(t-\xi )}^{\sigma }}{1-\sigma }}\right]d\xi ,\end{array}$$

(3)

where $E_{\sigma }$ is a well-known one parameter Mittag–Leffler function and $F\left(\sigma \right)$ is a normalizing function such that $F\left(0\right)=1,F\left(1\right)=1$.

Definition 2

([31,43]). The ABC fractional integral with non-local kernal is defined by

$$\begin{array}{c}\hfill {}_a^{ABC}{I}_t^{\sigma }\Phi \left(t\right)={\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\Phi \left(t\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\mathsf{\sigma }\right)}}{\int }_a^t\Phi \left(\xi \right){(t-\xi )}^{\sigma -1}d\xi .\end{array}$$

(4)

For $t\ge 0$ and $\sigma \in (0,1]$, the proposed nonlinear fractional order model for whooping cough, in the sense of the ABC-fractional operator, is given as

$$\begin{array}{}\mathrm{(5a)}& {}_0^{ABC}{D}_t^{\sigma }S\left(t\right)=\Pi -\beta IS-(\mu +\alpha )S,\hfill \mathrm{(5b)}& {}_0^{ABC}{D}_t^{\sigma }V\left(t\right)=\alpha S-\delta IV-({\gamma }_1+\mu )V,\hfill \mathrm{(5c)}& {}_0^{ABC}{D}_t^{\sigma }E\left(t\right)=\beta IS+\delta IV-(\mu +\gamma +q_1)E,\hfill \mathrm{(5d)}& {}_0^{ABC}{D}_t^{\sigma }I\left(t\right)=\gamma E-({\gamma }_2+{\gamma }_3+\mu +d_1)I,\hfill \mathrm{(5e)}& {}_0^{ABC}{D}_t^{\sigma }Q\left(t\right)=q_{1}E+{\gamma }_{3}I-(q_2+d_2+\mu )Q,\hfill \mathrm{(5f)}& {}_0^{ABC}{D}_t^{\sigma }R\left(t\right)={\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q-\mu R,\hfill \end{array}$$

with conditions:

$$\begin{array}{}\mathrm{(5g)}& \hfill \begin{array}{c}S\left(0\right)=S_0>0,V\left(0\right)=V_0\ge 0,E\left(0\right)=E_0\ge 0,\hfill \\ I\left(0\right)=I_0\ge 0,Q\left(0\right)=Q_0\ge 0,R\left(0\right)=R_0\ge 0.\hfill \end{array}\end{array}$$

The system (5) is autonomous, hence, it can be written in the following compact form:

$$\begin{array}{}\mathrm{(6a)}& {}_0^{ABC}{D}_t^{\sigma }\mathcal{V}\left(t\right)=\mathcal{G}\left(\mathcal{V}\left(t\right)\right),\hspace{1em}0<t<t_f<+\infty ,\end{array}$$

along with

$$\begin{array}{}\mathrm{(6a)}& \mathcal{V}\left(0\right)={\mathcal{V}}_0,\end{array}$$

where $\mathcal{V}:[0,+\infty )\to {\mathbb{R}}^6$ and $\mathcal{G}:{\mathbb{R}}^6\to {\mathbb{R}}^6$ are vector valued functions given as

$$\mathcal{V}\left(t\right)=\left(\begin{array}{c}S\left(t\right)\\ V\left(t\right)\\ E\left(t\right)\\ I\left(t\right)\\ Q\left(t\right)\\ R\left(t\right)\end{array}\right),{\mathcal{V}}_0=\left(\begin{array}{c}{S}_0\\ V_0\\ E_0\\ I_0\\ Q_0\\ R_0\end{array}\right),\mathcal{G}\left(\mathcal{V}\left(t\right)\right)=\left(\begin{array}{c}\Pi -\beta IS-(\mu +\alpha )S\\ \alpha S-\delta IV-({\gamma }_1+\mu )V\\ \beta IS+\delta IV-(\mu +\gamma +q_1)E\\ \gamma E-({\gamma }_2+{\gamma }_3+\mu +d_1)I\\ q_{1}E+{\gamma }_{3}I-(q_2+d_2+\mu )Q\\ {\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q-\mu R\end{array}\right).$$

3. Theoretical Analysis of the Proposed Model

This section is devoted to a comprehensive theoretical analysis of the proposed fractional model (6) where we investigate some key characteristics of the model and show that the model is well-posed for numerical approximations.

3.1. Existence and Uniqueness of Solution

First of all, we prove that the solution of the model (6) exists and is unique. We make use of some basic definitions and theorems, stated in [54], to prove the existence and uniqueness of the solution of the proposed fractional model.

Theorem 1

([54]). Every contractive sequence is a Cauchy sequence, and therefore convergent in complete metric space.

Theorem 2

([55]). Let $B\subseteq R$ and $\Psi :B\to R^n$ be a continuously differentiable mapping, $s\in B$. Then, Ψ satisfies a Lipschitz condition on each convex compact subset $\mathcal{B}$ of B with Lipchitz constant L. Where $L>0$ is the supremum of the derivative of Ψ on $\mathcal{B}$, i.e.,

$$L=\underset{s\in \mathcal{B}}{sup}\mid {\displaystyle \frac{d\Psi }{ds}}\mid .$$

Theorem 3.

The function $\mathcal{G}\left(\mathcal{V}\right)$ in Equation (6) is Lipschitz continuous.

Proof. 

Let $\mathcal{S}$ be a convex compact subset of

$$\begin{array}{c}\hfill \mathbb{S}=\left\{(t,\mathcal{V})\right|0\le t\le t_f,\mathcal{V}\in R_{+}^6\}.\end{array}$$

Let ${\mathcal{V}}_1,{\mathcal{V}}_2\in \mathcal{S}$, then by mean value theorem ∃$\zeta \in ({\mathcal{V}}_1,{\mathcal{V}}_2)$ such that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathcal{G}\left({\mathcal{V}}_1\left(t\right)\right)-\mathcal{G}\left({\mathcal{V}}_2\left(t\right)\right)}{{\mathcal{V}}_1\left(t\right)-{\mathcal{V}}_2\left(t\right)}}=& {\mathcal{G}}^{{}^{\prime }}\left(\zeta \left(t\right)\right),\hfill \end{array}$$

or

$$\begin{array}{cc}\hfill \mathcal{G}\left({\mathcal{V}}_1\left(t\right)\right)-\mathcal{G}\left({\mathcal{V}}_2\left(t\right)\right)=& \mathcal{G}{}^{\prime }\left(\zeta \left(t\right)\right).\left({\mathcal{V}}_1\left(t\right)-{\mathcal{V}}_2\left(t\right)\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mid \mathcal{G}\left({\mathcal{V}}_1\left(t\right)\right)-\mathcal{G}\left({\mathcal{V}}_2\left(t\right)\right)\mid & =\mid \mathcal{G}{}^{\prime }\left(\zeta \left(t\right)\right).\left({\mathcal{V}}_1\left(t\right)-{\mathcal{V}}_2\left(t\right)\right)\mid ,\hfill \\ \hfill & \le \parallel \mathcal{G}{}^{\prime }{\left(\zeta \right)\parallel }_{\infty }{\parallel {\mathcal{V}}_1-{\mathcal{V}}_2\parallel }_{\infty }.\hfill \end{array}$$

Since $\mathcal{G}\in C^1[0,t_f]$, so over a convex compact set $\mathcal{S}$, ∃ a constant $\tau >0$ such that

$$\begin{array}{c}\hfill \parallel \mathcal{G}{}^{\prime }{\left(\zeta \right)\parallel }_{\infty }\le \tau ,\end{array}$$

hence,

$$\begin{array}{cc}\hfill \mid \mathcal{G}\left({\mathcal{V}}_1\left(t\right)\right)-\mathcal{G}\left({\mathcal{V}}_2\right)\left(t\right)\mid & \le \tau \parallel {\mathcal{V}}_1-{\mathcal{V}}_2{\parallel }_{\infty },\hfill \\ \hfill \underset{t\in [0,t_f]}{sup}\mid \mathcal{G}\left({\mathcal{V}}_1\right)-\mathcal{G}\left({\mathcal{V}}_2\right)\mid & \le \tau \parallel {\mathcal{V}}_1-{\mathcal{V}}_2{\parallel }_{\infty },\hfill \\ \hfill \parallel \mathcal{G}\left({\mathcal{V}}_1\right)-\mathcal{G}\left({\mathcal{V}}_2\right){\parallel }_{\infty }& \le \tau \parallel {\mathcal{V}}_1-{\mathcal{V}}_2{\parallel }_{\infty }.\hfill \end{array}$$

Thus, $\mathcal{G}\left(\mathcal{V}\right)$ is Lipschitz.   □

Theorem 4.

Suppose that the function $\mathcal{G}\left(\mathcal{V}\right)$ satisfies the Lipschitz condition

$$\begin{array}{c}\hfill \parallel \mathcal{G}\left({\mathcal{V}}_2\right)-\mathcal{G}\left({\mathcal{V}}_1\right){\parallel }_{\infty }\le \tau {\parallel {\mathcal{V}}_2-{\mathcal{V}}_1\parallel }_{\infty },\end{array}$$

then the problem (6) has a unique solution for

$$\begin{array}{c}\hfill \tau \left({\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{T}^{*}\right)<1.\end{array}$$

Proof. 

We shall prove that the function $\mathcal{V}\left(t\right)$ satisfies Equation (6) if and only if it satisfies the relation

$$\begin{array}{c}\hfill \mathcal{V}\left(t\right)=\mathcal{V}\left(0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-\xi )}^{\sigma -1}\mathcal{G}\left(\mathcal{V}\left(\xi \right)\right)d\xi .\end{array}$$

Let $\mathcal{V}\left(t\right)$ satisfy Equation (6). We apply the Atangana–Beleanu fractional integral (4) to both sides of (6) to obtain

$$\begin{array}{c}\hfill {}_0^{ABC}{I}_t^{\sigma }\left[{}_0^{ABC}{D}_t^{\sigma }\mathcal{V}\left(t\right)\right]{=}_0^{ABC}{I}_t^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t\right)\right).\end{array}$$

Simplification yields us the integral equation:

$$\begin{array}{c}\hfill \mathcal{V}\left(t\right)={\mathcal{V}}_0+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-\xi )}^{\sigma -1}\mathcal{G}\left(\mathcal{V}\left(\xi \right)\right)d\xi .\end{array}$$

(7)

Conversely, we suppose that ${\mathcal{V}}_n$ is a sequence of solutions that converges to the solution (7) with Picard successive iteration, i.e.,

$$\begin{array}{c}\hfill {\mathcal{V}}_n\left(t\right)={\mathcal{V}}_0\left(t\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left({\mathcal{V}}_n\left(t\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-\xi )}^{\sigma -1}\mathcal{G}\left({\mathcal{V}}_n\left(\xi \right)\right)d\xi ,{\mathcal{V}}_0\left(t\right)={\mathcal{V}}_0.\end{array}$$

(8)

First of all, we show that the sequence (8) is contractive if $\tau \left({\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{T}^{*}\right)<1,$ where $T^{*}=t_f{\rm Y}$ and ${\rm Y}={sup}_{t\in [0,t_f]}{(t-\xi )}^{\sigma -1}$.

Consider

$$\begin{array}{cc}\hfill \mid {\mathcal{V}}_n\left(t\right)-{\mathcal{V}}_{n-1}\left(t\right)\mid =& \mid {\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}[\mathcal{G}\left({\mathcal{V}}_{n-1}\left(t\right)\right)-\mathcal{G}\left({\mathcal{V}}_{n-2}\left(t\right)\right)]\hfill \\ & +{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-\xi )}^{\sigma -1}[\mathcal{G}\left({\mathcal{V}}_{n-1}\left(x\right)\right)-\mathcal{G}\left({\mathcal{V}}_{n-2}\left(x\right)\right)]d\xi \mid ,\hfill \\ \hfill & \le {\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mid \mathcal{G}\left({\mathcal{V}}_{n-1}\left(t\right)\right)-\mathcal{G}\left({\mathcal{V}}_{n-2}\left(t\right)\right)\mid \hfill \\ & +{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t\mid {(t-\xi )}^{\sigma -1}\mid \mid \mathcal{G}\left({\mathcal{V}}_{n-1}\left(x\right)\right)-\mathcal{G}\left({\mathcal{V}}_{n-2}\right)\mid dx.\hfill \end{array}$$

Using Lipchitz property of function $\mathcal{G}\left(v\right)$, we obtain the following expression:

$$\begin{array}{cc}\hfill \mid {\mathcal{V}}_n\left(t\right)-{\mathcal{V}}_{n-1}\left(t\right)\mid & \le {\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\tau \mid {\mathcal{V}}_{n-1}\left(t\right)-{\mathcal{V}}_{n-2}\left(t\right)\mid \hfill \\ & +{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t\mid {(t-\xi )}^{\sigma -1}\mid \tau \mid {\mathcal{V}}_{n-1}\left(t\right)-{\mathcal{V}}_{n-2}\left(t\right)\mid dx,\hfill \\ \hfill & \le {\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\alpha \underset{t\in [0,t_f]}{sup}\mid {\mathcal{V}}_{n-1}\left(t\right)-{\mathcal{V}}_{n-2}\left(t\right)\mid \hfill \\ & +{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t\tau \underset{t\in [0,t_f]}{sup}\mid {(t-\xi )}^{\sigma -1}\mid \underset{t\in [0,t_f]}{sup}\mid {\mathcal{V}}_{n-1}\left(t\right)-{\mathcal{V}}_{n-2}\left(t\right)\mid dx,\hfill \\ \hfill \mid {\mathcal{V}}_n\left(t\right)-{\mathcal{V}}_{n-1}\left(t\right)\mid & \le \tau \left({\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{T}^{*}\right){\parallel {\mathcal{V}}_{n-1}-{\mathcal{V}}_{n-2}\parallel }_{\infty },\hfill \\ \hfill \underset{t\in [0,t_f]}{sup}\mid {\mathcal{V}}_n\left(t\right)-{\mathcal{V}}_{n-1}\left(t\right)\mid & \le \tau \left({\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{T}^{*}\right){\parallel {\mathcal{V}}_{n-1}-{\mathcal{V}}_{n-2}\parallel }_{\infty },\hfill \\ \hfill \parallel {\mathcal{V}}_n-{\mathcal{V}}_{n-1}{\parallel }_{\infty }& \le \kappa \parallel {\mathcal{V}}_{n-1}-{\mathcal{V}}_{n-2}{\parallel }_{\infty },\hfill \end{array}$$

where

$$\kappa =\tau \left({\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{T}^{*}\right)<1.$$

This implies that

$$d({\mathcal{V}}_n,{\mathcal{V}}_{n-1})\le \kappa d({\mathcal{V}}_{n-1},{\mathcal{V}}_{n-2}).$$

(9)

Thus, from Equation (9), sequence (8) is contractive, hence Theorem 1 implies that it is a Cauchy sequence. Now, for $p,q\in N$ and $p>q$,

$$\begin{array}{cc}\hfill \mid {\mathcal{V}}_p-{\mathcal{V}}_q\mid =& \mid {\mathcal{V}}_p-{\mathcal{V}}_{p-1}+{\mathcal{V}}_{p-1}-{\mathcal{V}}_{p-2}+{\mathcal{V}}_{p-2}\dots -{\mathcal{V}}_{q+1}+{\mathcal{V}}_{q+1}-{\mathcal{V}}_q\mid ,\hfill \\ \hfill & \le \mid {\mathcal{V}}_p-{\mathcal{V}}_{p-1}\mid +\mid {\mathcal{V}}_{p-1}-{\mathcal{V}}_{p-2}\mid +\dots +\mid {\mathcal{V}}_{q+1}-{\mathcal{V}}_q\mid ,\hfill \\ & \le {\kappa }^{p-1}\mid {\mathcal{V}}_1-{\mathcal{V}}_0\mid +{\kappa }^{p-2}\mid {\mathcal{V}}_1-{\mathcal{V}}_0\mid +\dots +{\kappa }^q\mid {\mathcal{V}}_1-{\mathcal{V}}_0\mid ,\hfill \\ \hfill & \le [{\kappa }^{p-1}+{\kappa }^{p-2}+...+{\kappa }^q]\mid {\mathcal{V}}_1-{\mathcal{V}}_0\mid .\hfill \end{array}$$

The right-hand side is a geometric series that is always convergent for $0<\kappa <1$.

$$\begin{array}{cc}\hfill \mid {\mathcal{V}}_p-{\mathcal{V}}_q\mid \le & {\kappa }^q{\displaystyle \frac{1-{\kappa }^{p-q}}{1-\kappa }}\mid {\mathcal{V}}_1-{\mathcal{V}}_0\mid \le {\kappa }^q{\displaystyle \frac{1}{1-\kappa }}\mid {\mathcal{V}}_1-{\mathcal{V}}_0\mid .\hfill \end{array}$$

Since $0<\kappa <1$, $lim\left({\kappa }^q\right)=0$. Therefore, we infer that the sequence $\left({\mathcal{V}}_n\right)$ is Cauchy and hence, by a theorem from [54], it is convergent. Let $lim\left({\mathcal{V}}_n\right)=\mathcal{V}$, then the Equation (8) gives

$$\begin{array}{c}\hfill li{m}_{n\to \infty }{\mathcal{V}}_n\left(t\right)=\mathcal{V}\left(t\right)=v\left(0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-\xi )}^{\sigma -1}\mathcal{G}\left(v\left(\xi \right)\right)d\xi ,\end{array}$$

(10)

which is the required solution.

Uniqueness: For the uniqueness of the solution, we assume on the contrary that the sequence $\left({\mathcal{V}}_n\right)$ converges to two limits, ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$, such that ${\mathcal{V}}_1\ne {\mathcal{V}}_2$. Then, there exist $n_{1}and{n}_2\in N$ such that,

$$\begin{array}{c}\hfill \mid {\mathcal{V}}_n-{\mathcal{V}}_1\mid <{ϵ}_1,n_1\ge n.\\ \hfill \mid {\mathcal{V}}_n-{\mathcal{V}}_2\mid <{ϵ}_2,n_2\ge n.\end{array}$$

Let $n=max\{n_1,n_2\}$. Then,

$$\begin{array}{c}\hfill \mid {\mathcal{V}}_1-{\mathcal{V}}_2\mid =\mid {\mathcal{V}}_1-{\mathcal{V}}_n+{\mathcal{V}}_n-{\mathcal{V}}_2\mid \le \mid {\mathcal{V}}_1-{\mathcal{V}}_n\mid +\mid {\mathcal{V}}_n-{\mathcal{V}}_2\mid <{ϵ}_1+{ϵ}_2=ϵ,\end{array}$$

which implies,

$$\begin{array}{c}\hfill \mid {\mathcal{V}}_1-{\mathcal{V}}_2\mid =0\Rightarrow {\mathcal{V}}_1={\mathcal{V}}_2.\end{array}$$

Hence, it is proved that the solution (10) is a unique solution of (6) or equivalently of the system (5).   □

3.2. Boundedness and Positivity of the Solutions

Next, we prove another property of the model, i.e., we prove that the model (5) has a positive and bounded solution for $t\ge 0$.

Theorem 5.

The solution $y\left(t\right)=\left(S\right(t),V(t),E(t),I(t),Q(t),R(t\left)\right)$ of the model (5) is bounded.

Proof. 

Applying the Atangana–Baleanu–Caputo derivative operator ${}_0^{ABC}{D}_t^{\sigma }$ to (1), we have

$$\begin{array}{cc}\hfill {}_0^{ABC}{D}_t^{\sigma }N\left(t\right)=& {}_0^{ABC}{D}_t^{\sigma }S\left(t\right){+}_0^{ABC}{D}_t^{\sigma }V\left(t\right){+}_0^{ABC}{D}_t^{\sigma }E\left(t\right){+}_0^{ABC}{D}_t^{\sigma }I\left(t\right)\hfill \\ & {+}_0^{ABC}{D}_t^{\sigma }Q\left(t\right){+}_0^{ABC}{D}_t^{\sigma }R\left(t\right),\hfill \\ \hfill =& \Pi -d_{1}I-d_{2}Q-\mu N.\hfill \end{array}$$

Since $d_{1}I+d_{2}Q\ge 0$, so

$$\begin{array}{c}\hfill {}_0^{ABC}{D}_t^{\sigma }N\left(t\right)\le \Pi -\mu N\left(t\right).\end{array}$$

We apply the Laplace transform on both sides of the above inequality to obtain

$$\begin{array}{c}\hfill \mathcal{L}{\{}_0^{ABC}{D}_t^{\sigma }N\left(t\right)\}\left(s\right)\le {\displaystyle \frac{\Pi }{s}}-\mu \mathcal{L}\left\{N\left(t\right)\right\}\left(s\right),\end{array}$$

or

$$\begin{array}{c}\hfill {\displaystyle \frac{F\left(\sigma \right)s^{\sigma }}{\sigma +(1-\sigma )s^{\sigma }}}N\left(s\right)+\mu N\left(s\right)\le \Pi s^{-1}+{\displaystyle \frac{F\left(\sigma \right)N\left(0\right)s^{\sigma -1}}{\sigma +(1-\sigma )s^{\sigma }}},\end{array}$$

(11)

where $N\left(0\right)$ represents the initial value of the total population.

Inequality (11) is solved to obtain

$$\begin{array}{c}\hfill N\left(s\right)\le {\displaystyle \frac{\Pi \Omega }{\mu }}\frac{s^{\sigma -(\sigma +1)}}{s^{\sigma }+\Omega }+\frac{\Omega }{\mu \sigma }\left[\Pi (1-\sigma )+F\left(\sigma \right)N\left(0\right)\right]\frac{s^{\sigma -1}}{s^{\sigma }+\Omega },\end{array}$$

(12)

where $\Omega ={\displaystyle \frac{\sigma \mu }{F\left(\sigma \right)+(1-\sigma )\mu }}$.

Application of inverse Laplace transform on both sides of (12) gives us

$$\begin{array}{c}\hfill N\left(t\right)\le {\displaystyle \frac{\Pi \Omega }{\mu }}{E}_{\sigma ,\sigma +1}(-\Omega t^{\sigma })+\frac{\Omega }{\mu \sigma }\left[\Pi (1-\sigma )+F\left(\sigma \right)N\left(0\right)\right]E_{\sigma ,1}(-\Omega t^{\sigma }).\end{array}$$

(13)

Since the Mittag–Leffler function

$$\begin{array}{c}\hfill E_{\sigma ,\sigma +1}(-\Omega t^{\sigma })={\displaystyle \frac{1}{\Omega t^{\sigma }}}\left[1-E_{\sigma ,1}(-\Omega t^{\sigma })\right],\end{array}$$

is bounded for all $t>0$, so it possesses an asymptotic behavior [31]. It is obvious from (13) that $N\left(t\right)\le {\displaystyle \frac{\Pi }{\mu }}$ as $t\to \infty$. Thus, $N\left(t\right)$ and all other variables of the model (5) are bounded.   □

Theorem 6.

The solution space $y\left(t\right)=(S,V,E,I,Q,R)$ of the system (5) will remain positive forever with any positive initial conditions.

Proof. 

Let us consider Equation (5a) of the model (5).

$${}_0^{ABC}{D}_t^{\sigma }S=\Pi -\beta IS-(\mu +\alpha )S.$$

We have proved that the solutions of the equations of the model (5) are bounded, so we can define $c=max(\beta I+\mu +\alpha )$ as a constant. Then,

$$\begin{array}{c}\hfill {}_0^{ABC}{D}_t^{\sigma }S\left(t\right)\ge -cS\left(t\right).\end{array}$$

(14)

Now, we apply the Laplace transform on both sides of  (14) to obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{F\left(\sigma \right)s^{\sigma }}{\sigma +(1-\sigma )s^{\sigma }}}\left[S\left(s\right)\right]-{\displaystyle \frac{F\left(\sigma \right)s^{\sigma -1}}{\sigma +(1-\sigma )s^{\sigma }}}S\left(0\right)\ge -c\left[S\left(s\right)\right].\end{array}$$

This can be solved to obtain

$$\begin{array}{c}\hfill \left[S\left(s\right)\right]\ge {\displaystyle \frac{F\left(\sigma \right)S\left(0\right)\mathsf{Ϝ}}{c\sigma }}\frac{s^{\sigma -1}}{s^{\sigma }+\mathsf{Ϝ}},\end{array}$$

where $\mathsf{Ϝ}=\frac{c\sigma }{F\left(\sigma \right)+c(1-\sigma )}$.

Now, applying inverse Laplace transform in the above inequality and using property of Mittage–Laffler function, we obtain

$$\begin{array}{c}\hfill S\left(t\right)\ge {\displaystyle \frac{F\left(\sigma \right)S\left(0\right)\mathsf{Ϝ}}{c\sigma }}{E}_{\sigma ,1}\left(-\mathsf{Ϝ}{t}^{\sigma }\right)>0.\end{array}$$

(15)

Thus, the solution variable $S\left(t\right)>0$ for all $t\ge 0$. Similarly, it can be proved that other state variables, corresponding to any non-negative initial data, are also positive for all $t\ge 0$. Thus, the solutions in ${\mathbb{R}}_{+}^6$ remain positive forever.    □

On the basis of above results, the feasible invariant region is defined as

$$\begin{array}{c}\hfill \Xi =\left\{(S,V,E,I,Q,R)\in R_{+}^6:0\le N\left(t\right)\le {\displaystyle \frac{\Pi }{\mu }}\right\},\end{array}$$

with non-negative initial conditions in $R_{+}^6$.

3.3. Equilibrium Points and Threshold Parameter ${\mathcal{R}}_0$

Equilibrium points represent the steady-state prevalence of the disease, where the number of new infections is balanced by the number of recoveries and deaths. We find equilibrium points of the model (5) by solving corresponding steady-state equations. To find steady-state equations, we put

$${}_0^{ABC}{D}_t^{\sigma }S\left(t\right){=}_0^{ABC}{D}_t^{\sigma }V\left(t\right){=}_0^{ABC}{D}_t^{\sigma }E\left(t\right){=}_0^{ABC}{D}_t^{\sigma }I\left(t\right){=}_0^{ABC}{D}_t^{\sigma }Q\left(t\right){=}_0^{ABC}{D}_t^{\sigma }R\left(t\right)=0,$$

in system (5).

3.3.1. Disease Free Equilibrium Point

When no one is infected, the state is known as a disease-free state and the corresponding equilibrium point is called the disease free equilibrium (DFE) point. So, to obtain the DFE point, we put $E\left(t\right)=I\left(t\right)=0$ in steady-state equations of the model (5) and solve them to obtain the following DFE point.

$$P_0=(S^{*},V^{*},E^{*},I^{*},Q^{*},R^{*})=\left(\frac{\Pi }{\mu +\alpha },\frac{\Pi \alpha }{(\mu +\alpha )({\gamma }_1+\mu )},0,0,0,\frac{\Pi \alpha {\gamma }_1}{\mu (\mu +\alpha )({\gamma }_1+\mu )}\right).$$

(16)

It is to be noted that $S^{*}+V^{*}+E^{*}+I^{*}+Q^{*}+R^{*}={\displaystyle \frac{\Pi }{\mu }}$.

3.3.2. Reproduction Number

The reproduction number ${\mathcal{R}}_0$ is a mathematical term used to describe the contagiousness of an infectious disease. Specifically, it represents the average number of new infections that will occur as a result of each infected individual. If the reproduction number is high, it means that the disease is very contagious and will likely require significant interventions to restrict its spread.

We implement the next-generation matrix method [56] to find ${\mathcal{R}}_0$. The recruitment of new infections, and the inside and outside transmission terms of infected compartments are, respectively, represented by the following matrices $\mathcal{F}$ and $\mathcal{V}$, i.e.,

$$\mathcal{F}=\left(\begin{array}{c}-\delta IV\\ \beta IS+\delta IV\\ 0\\ 0\end{array}\right),\mathcal{V}=\left(\begin{array}{c}-\alpha S+({\gamma }_1+\mu )V\\ (\mu +\gamma +q_1)E\\ -\gamma E+({\gamma }_2+{\gamma }_3+\mu +d_1)I\\ -q_{1}E-{\gamma }_{3}I+(q_2+d_2+\mu )Q\end{array}\right).$$

The Jacobian of $\mathcal{F}$ and $\mathcal{V}$, evaluated at $P_0$, are, respectively, given as

$$F=\left(\begin{array}{cccc}0& 0& -\delta V^{*}& 0\\ 0& \beta S^{*}+\delta V^{*}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right),V=\left(\begin{array}{cccc}{k}_2& 0& 0& 0\\ 0& k_3& 0& 0\\ 0& -\gamma & k_4& 0\\ 0& -q_1& {\gamma }_3& k_5\end{array}\right).$$

the reproduction number ${\mathcal{R}}_0$ is computed as the spectral radius of the matrix $F{V}^{-1}$. Thus,

$$\begin{array}{c}\hfill {\mathcal{R}}_0={\displaystyle \frac{\gamma \Pi (\delta \alpha +\beta k_2)}{k_1{k}_2{k}_3{k}_4}},\end{array}$$

(17)

where $k_1=\alpha +\mu$, $k_2={\gamma }_1+\mu$, $k_3=\gamma +q_1+\mu$, $k_4={\gamma }_2+{\gamma }_3+d_1+\mu$. The disease is contiguous and spreads in population if ${\mathcal{R}}_0>1$.

3.3.3. Endemic Equilibrium

The other equilibrium point where the disease is constantly present in the system is called the endemic equilibrium (EE) point. With the consideration that $E\left(t\right)\ne 0,I\left(t\right)\ne 0$, the steady-state equations of model (5) are solved to obtain the following EE point.

$$P_1=(\overline{S},\overline{V},\overline{E},\overline{I},\overline{Q},\overline{R}),$$

where

$$\begin{array}{cc}\hfill & \overline{S}={\displaystyle \frac{\Pi }{k_1{\mathcal{R}}_0}},\overline{V}={\displaystyle \frac{k_1{k}_3{k}_4{\mathcal{R}}_0-\gamma \beta \Pi }{\gamma \delta k_1{\mathcal{R}}_0}},\overline{E}={\displaystyle \frac{k_4({\mathcal{R}}_0-1)}{\gamma \beta }},\overline{I}={\displaystyle \frac{({\mathcal{R}}_0-1)}{\beta }},\hfill \\ \hfill & \overline{Q}={\displaystyle \frac{(q_1{k}_4+\gamma {\gamma }_3)({\mathcal{R}}_0-1)}{\beta \gamma k_5}},\overline{R}={\displaystyle \frac{{\gamma }_1\overline{V}+{\gamma }_2\overline{I}+q_2\overline{Q}}{\mu }}\mathrm{and}{k}_5=q_2+d_2+\mu .\hfill \end{array}$$

3.4. Stability Analysis

Now, we discuss the local and global stabilities of the model (5) at equilibrium points $P_0$ and $P_1$. For local stability, we check signs of eigenvalues of the Jacobian matrix computed at equilibrium points, whereas for global stability, we implement the Lyapunov theory with the LaSalle invariance principle [53] and the Castillo-Chavez theory [57]. The global stability analysis of endemic equilibrium points may suggest public health interventions. If the equilibrium is locally stable, control measures can be implemented to prevent the disease from becoming endemic. On the other hand, if the equilibrium is globally stable, long-term disease control strategies are required.

3.4.1. Local Stability

The purpose of local stability analysis is to identify whether a small perturbation in the disease system will cause the disease to persist or disappear. In epidemiological models, local stability at equilibrium points is an important concept for understanding the behavior of infectious diseases and how they spread through a population. This section investigates the local stability of the whooping cough model (5) at the DFE point and EE point.

Theorem 7.

If ${\mathcal{R}}_0<1$, the model (5) is locally asymptotically stable at $P_0$, and unstable if ${\mathcal{R}}_0>1$.

Proof. 

The model (5) at disease-free equilibrium $P_0$ corresponds to the following Jacobian matrix:

$$J\left(P_0\right)=\left(\begin{array}{cccccc}-k_1& 0& 0& -\beta S^{*}& 0& 0\\ \alpha & -k_2& 0& -\delta V^{*}& 0& 0\\ 0& 0& -k_3& \beta S^{*}+\delta V^{*}& 0& 0\\ 0& 0& \gamma & -k_4& 0& 0\\ 0& 0& q_1& {\gamma }_3& -k_5& 0\\ 0& {\gamma }_1& 0& {\gamma }_2& q_2& -\mu \end{array}\right).$$

Eigenvalues of the Jacobian matrix $J\left(P_0\right)$ are given as

$$\begin{array}{cc}\hfill {\lambda }_1& =-\mu ,\hfill \\ \hfill {\lambda }_2& =-k_1,\hfill \\ \hfill {\lambda }_3& =-k_2,\hfill \\ \hfill {\lambda }_4& =-k_3,\hfill \\ \hfill {\lambda }_5& =-k_5,\hfill \\ \hfill {\lambda }_6& =-(1-{\mathcal{R}}_0)k_4.\hfill \end{array}$$

Here, ${\lambda }_i<0$ for $i=1,2,\cdots ,6$ when ${\mathcal{R}}_0<1$. Therefore, the system (5) is locally asymptotically stable at the point $P_0$. If ${\mathcal{R}}_0>1$, the eigenvalue ${\lambda }_6$ with a positive sign demonstrates the model’s local instability at $P_0$.   □

Theorem 8.

If ${\mathcal{R}}_0>1$, the model (5) is locally asymptotically stable at $P_1$, and unstable if ${\mathcal{R}}_0<1$.

Proof. 

The model (5) at endemic equilibrium $P_1$ corresponds to the following Jacobian matrix:

$$J\left(P_1\right)=\left(\begin{array}{cccccc}-k_1-\beta \overline{I}& 0& 0& -\beta \overline{S}& 0& 0\\ \alpha & -k_2-\delta \overline{I}& 0& -\delta \overline{V}& 0& 0\\ \beta \overline{I}& \delta \overline{I}& -k_3& \beta \overline{S}+\delta \overline{V}& 0& 0\\ 0& 0& \gamma & -k_4& 0& 0\\ 0& 0& q_1& {\gamma }_3& -k_5& 0\\ 0& {\gamma }_1& 0& {\gamma }_2& q_2& -\mu \end{array}\right).$$

We determine the following eigenvalues of the Jacobian matrix $J\left(P_1\right)$.

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_1& =-\mu ,\hfill \\ \hfill {\mathsf{\Lambda }}_2& =-k_3,\hfill \\ \hfill {\mathsf{\Lambda }}_3& =-k_5,\hfill \\ \hfill {\mathsf{\Lambda }}_4& =-\left(k_2+{\displaystyle \frac{\delta ({\mathcal{R}}_0-1)}{\beta }}\right),\hfill \\ \hfill {\mathsf{\Lambda }}_5& =-\left(k_1+{\displaystyle \frac{k_4({\mathcal{R}}_0-1)}{\gamma }}\right),\hfill \\ \hfill {\mathsf{\Lambda }}_6& =-\frac{k_1{k}_2(I\gamma S\beta +I\gamma \delta V)-\gamma S\beta \delta k_1-\gamma \delta V{k}_2\beta +k_3{k}_4(k_2\beta +I\delta \beta -I{k}_2{k}_1+\delta k_1)+\gamma \delta \alpha S\beta }{k_3(\beta k_2+I\beta \delta -I{k}_1{k}_2+k_1\delta )}\hfill \end{array}$$

After plugging in the values of parameters, the eigenvalue ${\mathsf{\Lambda }}_6$ is approximated to give $-0.46232$, a negative eigenvalue. Hence, all of the eigenvalues ${\mathsf{\Lambda }}_i$ for $i=1,2,\cdots ,6,$ are less than zero for ${\mathcal{R}}_0>1$. Therefore, at the endemic equilibrium point $P_1$, the system (5) is locally asymptotically stable.   □

Local stability of the endemic equilibrium point suggests that the disease is likely to persist in the population even after initial outbreaks.

3.4.2. Global Stability

Global stability analysis looks at how the disease system behaves over a long period. This implies that, regardless of the starting points, the system will eventually reach the equilibrium point. To demonstrate that model (5) at DFE state is globally stable, the technique introduced by Castillo-Chavez et al. [57] is applied. Using this technique, we reproduce the model (5) in the form of the following equations.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_0^{ABC}{D}_t^{\sigma }\mathcal{Y}& =\mathcal{K}(\mathcal{Y},\mathcal{Z}),\hfill \\ \hfill {}_0^{ABC}{D}_t^{\sigma }\mathcal{Z}& =\mathcal{G}(\mathcal{Y},\mathcal{Z}),\mathcal{G}(\mathcal{Y},0)=0.\hfill \end{array}\end{array}$$

(18)

where the number of persons who are not affected is indicated by $\mathcal{Y}=(S,V)$, and $\mathcal{Z}=(E,I,Q)$ indicates the number of individuals having an infection. The last equation of the model is ignored because it is independent of the rest. Here, $P_0=({\mathcal{Y}}_0,0)$ is the DFE point. To verify that the DFE point is globally asymptotically stable (GAS), the following two requirements must be fulfilled.

$$\begin{array}{}\mathrm{(19)}& \left(C1\right):{}_0^{ABC}{D}_t^{\sigma }\mathcal{Y}=\mathcal{K}({\mathcal{Y}}_0,0)=0,{\mathcal{Y}}_0\mathrm{is}GAS.\hfill \mathrm{(20)}& \left(C2\right):{}_0^{ABC}{D}_t^{\sigma }\mathcal{Z}=\mathcal{B}\mathcal{Z}-\overline{M}(\mathcal{Y},\mathcal{Z}),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\overline{M}(\mathcal{Y},\mathcal{Z})\ge 0\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l}(\mathcal{Y},\mathcal{Z})\in \Xi ,\hfill \end{array}$$

where $\mathcal{B}=D_{\mathcal{Z}}\mathcal{G}({\mathcal{Y}}_0,0)$ is an M-matrix, and $\Xi$ represents the feasible invariant region. Thus, according to Castillo-Chavez et al., when the system of Equation (18) satisfies the conditions (C1) and (C2), the following theorem holds valid.

Theorem 9.

The DFE point $P_0$ is GAS if ${\mathcal{R}}_0<1$ in the region Ξ and the conditions (C1) and (C2) are satisfied.

Proof. 

Suppose $\mathcal{Y}=(S,V)$ represents uninfected individuals, while $\mathcal{Z}=(E,I,Q)$ symbolize the states having infection, and $P_0=({\mathcal{Y}}_0,0)$ is the DFE. Then,

$$\begin{array}{cc}\hfill {}_0^{ABC}{D}_t^{\sigma }\mathcal{Y}& =\mathcal{K}(\mathcal{Y},\mathcal{Z})=\left[\begin{array}{c}\Pi -\beta IS-(\mu +\alpha )S\\ \alpha S-\delta IV-({\gamma }_1+\mu )V\end{array}\right].\hfill \end{array}$$

(21)

At $P_0=({\mathcal{Y}}_0,0)$, we obtain

$$\mathcal{K}({\mathcal{Y}}_0,0)=\left[\begin{array}{c}\Pi -(\mu +\alpha )S^{*}\\ \alpha S^{*}-({\gamma }_1+\mu )V^{*}\end{array}\right]=0,$$

(22)

where ${\mathcal{Y}}_0=(S^{*},V^{*})=\left({\displaystyle \frac{\Pi }{(\mu +\alpha )}},{\displaystyle \frac{\alpha \Pi }{(\mu +\alpha )({\gamma }_1+\mu )}}\right)$. Thus, ${\mathcal{Y}}_0$ is GAS.

Now,

$$\begin{array}{cc}{}_0^{ABC}{D}_t^{\sigma }\mathcal{Z}& =\left[\begin{array}{ccc}-(\gamma +q_1+\mu )& \beta S^{*}+\delta V^{*}& 0\\ \gamma & -({\gamma }_2+{\gamma }_3+d_1+\mu )& 0\\ q_1& {\gamma }_3& -(q_2+d_2+\mu )\end{array}\right]\left[\begin{array}{c}E\\ I\\ Q\end{array}\right]\\ & -\left[\begin{array}{c}\beta I(S^{*}-S)+\delta I(V^{*}-V)\\ 0\\ 0\end{array}\right],\hfill \\ & =\mathcal{B}\mathcal{Z}-\overline{M}(\mathcal{Y},\mathcal{Z}),\hfill \end{array}$$

(23)

where

$$\begin{array}{ll}\hfill \mathcal{B}& =\left[\begin{array}{ccc}-(\gamma +q_1+\mu )& \beta S^{*}+\delta V^{*}& 0\\ \gamma & -({\gamma }_2+{\gamma }_3+d_1+\mu )& 0\\ q_1& {\gamma }_3& -(q_2+d_2+\mu )\end{array}\right], \mathcal{Z}=\left[\begin{array}{c}E\\ I\\ Q\end{array}\right],\\ \hfill \overline{M}(\mathcal{Y},\mathcal{Z})& =\left[\begin{array}{c}\beta I(S^{*}-S)+\delta I(V^{*}-V)\\ 0\\ 0\end{array}\right].\end{array}$$

Matrix $\mathcal{B}$ is clearly an M-matrix. At DFE point $P_0$, $S\le S_0$ and $V\le V_0$, therefore $\overline{M}(\mathcal{Y},\mathcal{Z})\ge 0$. Consequently, DFE point $P_0$ is GAS.   □

Global stability of DFE implies that the disease will not be able to stay in the population even with the introduction of perturbation of any size in the population.

Theorem 10.

The endemic equilibrium (EE) point $P_1$ is globally stable if ${\mathcal{R}}_0>1$ and unstable if ${\mathcal{R}}_0<1$.

Proof. 

Assume that the basic reproductive number ${\mathcal{R}}_0>1$ so that the endemic equilibrium point exists. We now develop a Volterra-type Lyapunov functional $\Theta$ given as

$$\begin{array}{cc}\hfill \Theta (S,V,E,I,Q,R)=& \left(S-\overline{S}-\overline{S}log\left({\displaystyle \frac{S}{\overline{S}}}\right)\right)+\left(V-\overline{V}-\overline{V}log\left({\displaystyle \frac{V}{\overline{V}}}\right)\right)\hfill \\ & +\left(E-\overline{E}-\overline{E}log\left({\displaystyle \frac{E}{\overline{E}}}\right)\right)+\left(I-\overline{I}-\overline{I}log\left({\displaystyle \frac{I}{\overline{I}}}\right)\right)\hfill \\ & +\left(Q-\overline{Q}-\overline{Q}log\left({\displaystyle \frac{Q}{\overline{Q}}}\right)\right)+\left(R-\overline{R}-\overline{R}log\left({\displaystyle \frac{R}{\overline{R}}}\right)\right).\hfill \end{array}$$

Applying ${}_0^{ABC}{D}_t^{\sigma }$ on both sides, we obtain

$$\begin{array}{cc}\hfill {}_0^{ABC}{D}_t^{\sigma }\Theta =& \left({\displaystyle \frac{S-\overline{S}}{S}}\right){}_0^{ABC}{D}_t^{\sigma }S+\left({\displaystyle \frac{V-\overline{V}}{V}}\right){}_0^{ABC}{D}_t^{\sigma }V+\left({\displaystyle \frac{E-\overline{E}}{E}}\right){}_0^{ABC}{D}_t^{\sigma }E\hfill \\ & +\left({\displaystyle \frac{I-\overline{I}}{I}}\right){}_0^{ABC}{D}_t^{\sigma }I+\left({\displaystyle \frac{Q-\overline{Q}}{Q}}\right){}_0^{ABC}{D}_t^{\sigma }Q+\left({\displaystyle \frac{R-\overline{R}}{R}}\right){}_0^{ABC}{D}_t^{\sigma }R.\hfill \end{array}$$

Using equations of the model (5), we obtain

$$\begin{array}{cc}\hfill {}_0^{ABC}{D}_t^{\sigma }\Theta =& \left({\displaystyle \frac{S-\overline{S}}{S}}\right)\left(\Pi -\beta IS-(\mu +\alpha )S\right)+\left({\displaystyle \frac{V-\overline{V}}{V}}\right)\left(\alpha S-\delta IV-({\gamma }_1+\mu )V\right)\hfill \\ & +\left({\displaystyle \frac{E-\overline{E}}{E}}\right)\left(\beta IS+\delta IV-(\mu +\gamma +q_1)E\right)+\left({\displaystyle \frac{I-\overline{I}}{I}}\right)\left(\gamma E-({\gamma }_2+{\gamma }_3+\mu +d_1)I\right)\hfill \\ & +\left({\displaystyle \frac{Q-\overline{Q}}{Q}}\right)\left(q_{1}E+{\gamma }_{3}I-(q_2+d_2+\mu )Q\right)+\left({\displaystyle \frac{R-\overline{R}}{R}}\right)\left({\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q-\mu R\right),\hfill \end{array}$$

After rearranging the terms, we obtain

$$\begin{array}{cc}\hfill {}_0^{ABC}{D}_t^{\sigma }\Theta =& [\Pi +\left(\beta I+(\mu +\alpha )\right){\displaystyle \frac{{\overline{S}}^2}{S}}+\alpha S+(\delta I+{\gamma }_1+\mu ){\displaystyle \frac{{\overline{V}}^2}{V}}+\delta IV+\beta IS+\left(\mu +\gamma +q_1\right){\displaystyle \frac{{\overline{E}}^2}{E}}\hfill \\ & +\gamma E+\left({\gamma }_2+{\gamma }_3+\mu +d_1\right){\displaystyle \frac{{\overline{I}}^2}{I}}+q_{1}E++{\gamma }_{3}I+\left(q_2+d_2+\mu \right){\displaystyle \frac{{\overline{Q}}^2}{Q}}+{\gamma }_{1}V+{\gamma }_{2}I\hfill \\ & +q_{2}Q+\mu {\displaystyle \frac{{\overline{R}}^2}{R}}]+[\left(\beta I+(\mu +\alpha )\right){\displaystyle \frac{{(S-\overline{S})}^2}{S}}+\left(\beta I+(\mu +\alpha )\right)\overline{S}+\Pi {\displaystyle \frac{\overline{S}}{S}}\hfill \\ & +(\delta I+{\gamma }_1+\mu ){\displaystyle \frac{{(V-\overline{V})}^2}{V}}+(\delta I+{\gamma }_1+\mu )\overline{V}+\left(\alpha S\right){\displaystyle \frac{\overline{V}}{V}}+\left(\mu +\gamma +q_1\right){\displaystyle \frac{{(E-\overline{E})}^2}{E}}\hfill \\ & +\left(\beta IS+\delta VI\right){\displaystyle \frac{\overline{E}}{E}}+\left(\mu +\gamma +q_1\right)\overline{E}+\left({\gamma }_2+{\gamma }_3+\mu +d_1\right){\displaystyle \frac{{(I-\overline{I})}^2}{I}}+\gamma E{\displaystyle \frac{\overline{I}}{I}}\hfill \\ & -\left({\gamma }_2+{\gamma }_3+\mu +d_1\right)\overline{I}+\left(q_2+d_2+\mu \right){\displaystyle \frac{{(Q-\overline{Q})}^2}{Q}}+\left(q_{1}E+{\gamma }_{3}I\right){\displaystyle \frac{\overline{Q}}{Q}}\hfill \\ & +\left(q_2+d_2+\mu \right)\overline{Q}+\mu {\displaystyle \frac{{(R-\overline{R})}^2}{R}}+\mu \overline{R}+\left({\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q\right){\displaystyle \frac{\overline{R}}{R}}].\hfill \end{array}$$

It is now easier to write it as

$${}_0^{ABC}{D}_t^{\sigma }\Theta ={\delta }_1-{\delta }_2,$$

where

$$\begin{array}{cc}\hfill {\delta }_1=& \Pi +\left(\beta I+(\mu +\alpha )\right){\displaystyle \frac{{\overline{S}}^2}{S}}+\alpha S+(\delta I+{\gamma }_1+\mu ){\displaystyle \frac{{\overline{V}}^2}{V}}+\delta IV+\beta IS+\left(\mu +\gamma +q_1\right){\displaystyle \frac{{\overline{E}}^2}{E}}+\gamma E\hfill \\ & +\left({\gamma }_2+{\gamma }_3+\mu +d_1\right){\displaystyle \frac{{\overline{I}}^2}{I}}+q_{1}E++{\gamma }_{3}I+\left(q_2+d_2+\mu \right){\displaystyle \frac{{\overline{Q}}^2}{Q}}+{\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q+\mu {\displaystyle \frac{{\overline{R}}^2}{R}},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\delta }_2=& \left(\beta I+(\mu +\alpha )\right){\displaystyle \frac{{(S-\overline{S})}^2}{S}}+\left(\beta I+(\mu +\alpha )\right)\overline{S}+\Pi {\displaystyle \frac{\overline{S}}{S}}+(\delta I+{\gamma }_1+\mu ){\displaystyle \frac{{(V-\overline{V})}^2}{V}}\hfill \\ & +(\delta I+{\gamma }_1+\mu )\overline{V}+\left(\alpha S\right){\displaystyle \frac{\overline{V}}{V}}+\left(\mu +\gamma +q_1\right){\displaystyle \frac{{(E-\overline{E})}^2}{E}}+\left(\beta IS+\delta VI\right){\displaystyle \frac{\overline{E}}{E}}+\left(\mu +\gamma +q_1\right)\overline{E}\hfill \\ & +\left({\gamma }_2+{\gamma }_3+\mu +d_1\right){\displaystyle \frac{{(I-\overline{I})}^2}{I}}+\gamma E{\displaystyle \frac{\overline{I}}{I}}-\left({\gamma }_2+{\gamma }_3+\mu +d_1\right)\overline{I}+\left(q_2+d_2+\mu \right){\displaystyle \frac{{(Q-\overline{Q})}^2}{Q}}\hfill \\ & +\left(q_{1}E+{\gamma }_{3}I\right){\displaystyle \frac{\overline{Q}}{Q}}+\left(q_2+d_2+\mu \right)\overline{Q}+\mu {\displaystyle \frac{{(R-\overline{R})}^2}{R}}+\mu \overline{R}+\left({\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q\right){\displaystyle \frac{\overline{R}}{R}}.\hfill \end{array}$$

Since all of the parameters in the model are non-negative, we have ${}_0^{ABC}{D}_t^{\sigma }\Theta <0$ when ${\delta }_1<{\delta }_2$ and ${}_0^{ABC}{D}_t^{\sigma }\Theta =0$ if and only if ${\delta }_1={\delta }_2$. The later case implies that $S=\overline{S}$, $V=\overline{V}$, $E=\overline{E}$, $I=\overline{I}$, $Q=\overline{Q}$, and $R=\overline{R}$. Thus, by LaSalle’s invariance principle, the EE point $P_1$ is GAS.   □

Global stability of endemic equilibrium point means that, under certain conditions, the disease will stay forever in the population.

4. Numerical Investigations and Implementations

To approximate the solution of the proposed ABC fractional model for whooping cough, we use the Toufik–Atangana type numerical scheme [58]. We employ the technique to investigate the dynamical behavior of whooping cough pandemic for various fractional order values $\sigma$.

4.1. Toufik–Atangana Discretizations

In this section, we present a brief overview of the numerical scheme that will be used to approximate the solution of the fractional model (5). Derivation of the scheme is based on the Toufik–Atangana scheme [58] for fractional order differential equations with an ABC-derivative operator. The scheme is implemented to discretize each differential equation of model (5).

Application of the fundamental theorem of fractional calculus to model (6) gives us

$$\begin{array}{c}\hfill \mathcal{V}\left(t\right)-\mathcal{V}\left(0\right)={\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-\xi )}^{\sigma -1}\mathcal{G}\left(\mathcal{V}\left(\xi \right)\right)d\xi ,\end{array}$$

and in discrete form:

$$\begin{array}{c}\hfill \mathcal{V}\left(t_{q+1}\right)-\mathcal{V}\left(0\right)={\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}{\int }_0^{t_{q+1}}{(t_{q+1}-\xi )}^{\sigma -1}\mathcal{G}\left(\mathcal{V}\left(\xi \right)\right)d\xi ,\end{array}$$

where $t=t_{q+1},q=0,\cdots ,N\mathrm{with}h=\frac{t_f}{N}$.

This can be equivalently put in the form:

$$\begin{array}{c}\hfill \mathcal{V}\left(t_{q+1}\right)=\mathcal{V}\left(0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}\sum _{p=0}^q{\int }_0^{t_{q+1}}{(t_{q+1}-\xi )}^{\sigma -1}\mathcal{G}\left(\mathcal{V}\left(\xi \right)\right)d\xi .\end{array}$$

(24)

We use interpolation polynomial to approximate the function $\mathcal{G}\left(\mathcal{V}\right(\xi \left)\right)$ to obtain

$$\begin{array}{c}\hfill \mathcal{G}\left(\mathcal{V}\left(\xi \right)\right)=\frac{\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{h}(t-t_{p-1})-\frac{\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{h}(t-t_p).\end{array}$$

We substitute approximation of $\mathcal{G}\left(\mathcal{V}\right(\xi \left)\right)$ in (24) to obtain

$$\begin{array}{cc}\hfill \mathcal{V}\left(t_{q+1}\right)=\mathcal{V}\left(0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)\mathsf{\Gamma }\left(\sigma \right)}}\sum _{p=0}^q[\frac{\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{h}{\int }_{t_p}^{t_{p+1}}{(t_{q+1}-t)}^{\sigma -1}(t-t_{p-1})dt& \hfill \\ \hfill -\frac{\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{h}{\int }_{t_p}^{t_{p+1}}{(t_{q+1}-t)}^{\sigma -1}(t-t_p)dt].\end{array}$$

(25)

The integrals in (25) are evaluated to obtain the following numerical scheme for the equations of type (6).

$$\begin{array}{cc}\hfill \mathcal{V}\left(t_{q+1}\right)=\mathcal{V}\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}].\end{array}$$

Thus, the model (5) in discrete form is given as

$$\begin{array}{cc}\hfill S\left(t_{q+1}\right)=S\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}],\end{array}$$

$$\begin{array}{cc}\hfill V\left(t_{q+1}\right)=V\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}],\end{array}$$

$$\begin{array}{cc}\hfill E\left(t_{q+1}\right)=E\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}],\end{array}$$

$$\begin{array}{cc}\hfill I\left(t_{q+1}\right)=I\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}],\end{array}$$

$$\begin{array}{cc}\hfill Q\left(t_{q+1}\right)=Q\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}],\end{array}$$

$$\begin{array}{cc}\hfill R\left(t_{q+1}\right)=R\left(t_0\right)+{\displaystyle \frac{1-\sigma }{F\left(\sigma \right)}}\mathcal{G}\left(\mathcal{V}\left(t_q\right)\right)+{\displaystyle \frac{\sigma }{F\left(\sigma \right)}}\sum _{p=0}^q\left[\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_p\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\right\{(q-p+2+\sigma ){(q+1-p)}^{\sigma }& \\ \hfill -(q-p+2+2\sigma ){(q-p)}^{\sigma }\}-\frac{h^{\sigma }\mathcal{G}\left(\mathcal{V}\left(t_{p-1}\right)\right)}{\mathsf{\Gamma }(\sigma +2)}\left\{{(q+1-p)}^{\sigma +1}-(q-p+1+\sigma ){(q-p)}^{\sigma }\right\}].\end{array}$$

For numerical simulations, we shall consider days as time unit. The model parameters are assigned following appropriate numerical values: $\Pi =0.4,$ $\mu =0.22,$ $\alpha =0.01,$ $\beta =1.15,$ $\delta =0.2,$ $\gamma =0.5,$ ${\gamma }_1=0.15,$ ${\gamma }_2=0.02,$ ${\gamma }_3=0.15,$ $q_1=0.02,$ $q_2=0.015,$ $d_1=0.004,$ $d_2=0.01$ where $\mu$ is the natural death rate, $d_1$ and $d_2$ are disease-induced death rates of infected and quarantined individuals, respectively.

Fractional Order Effect on Disease Dynamics

We employ the aforementioned approximations to present a graphical representation of the proposed fractional model and investigate the influence of order $\sigma \in (0,1]$ on solution curves.

From graphical curves of the state variables shown in Figure 2, we observe a decrease in exposed, infected, and quarantined individuals with a decrease in the fractional order of the differential equations. However, the susceptibles increase with a decrease in fractional order. Thus, a reduction in fractional order values will reduce whooping cough infection in humans.

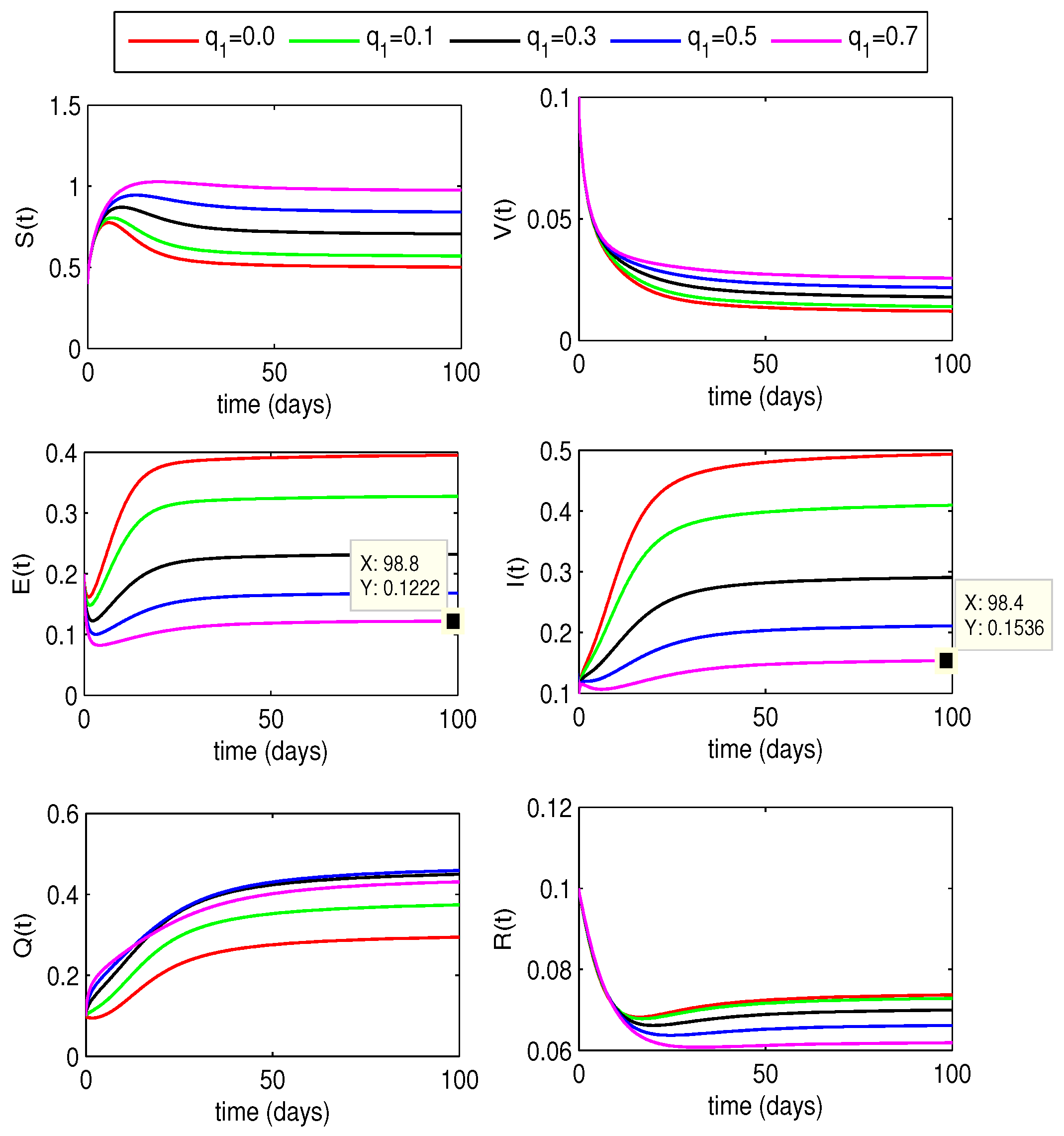
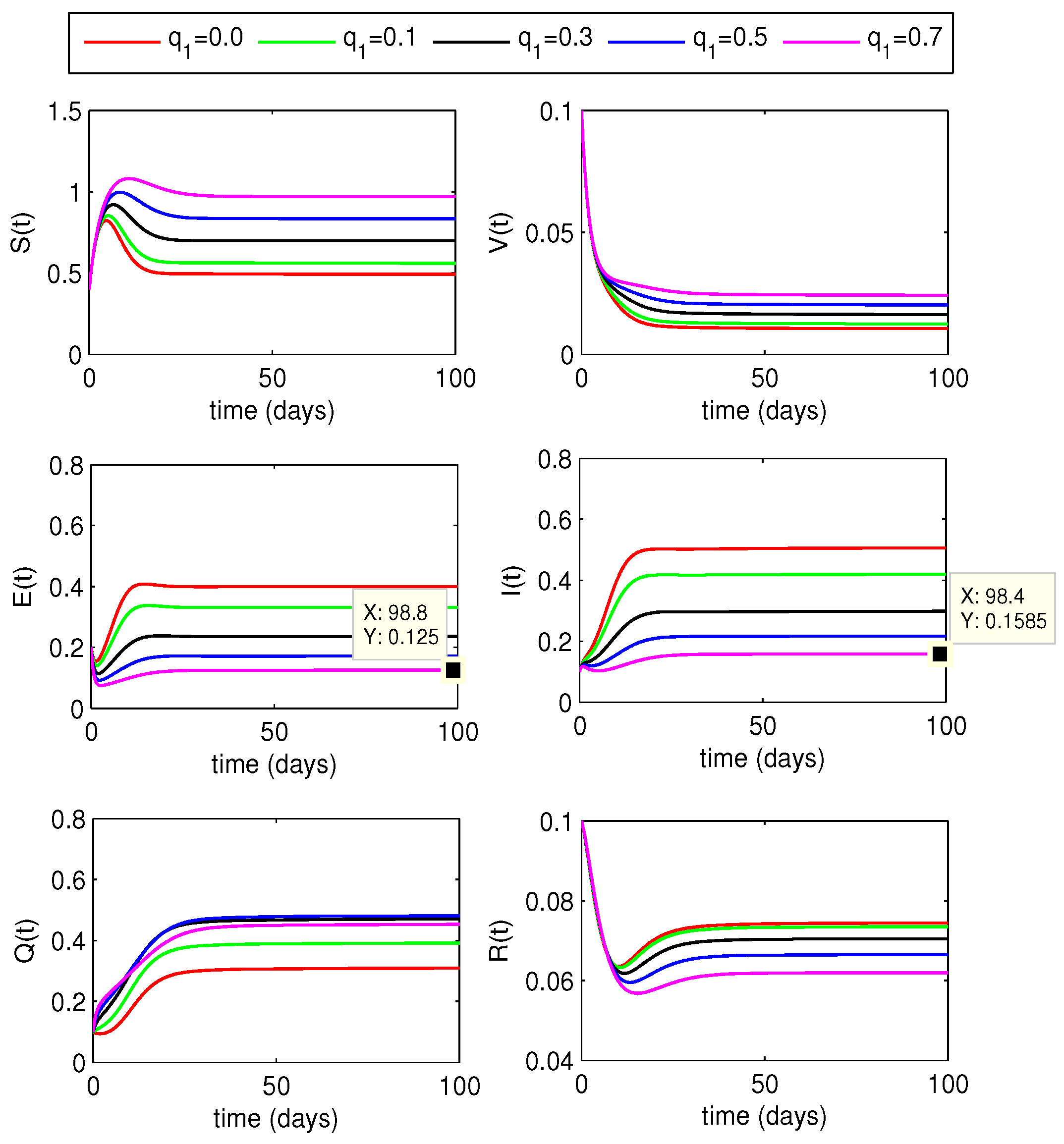
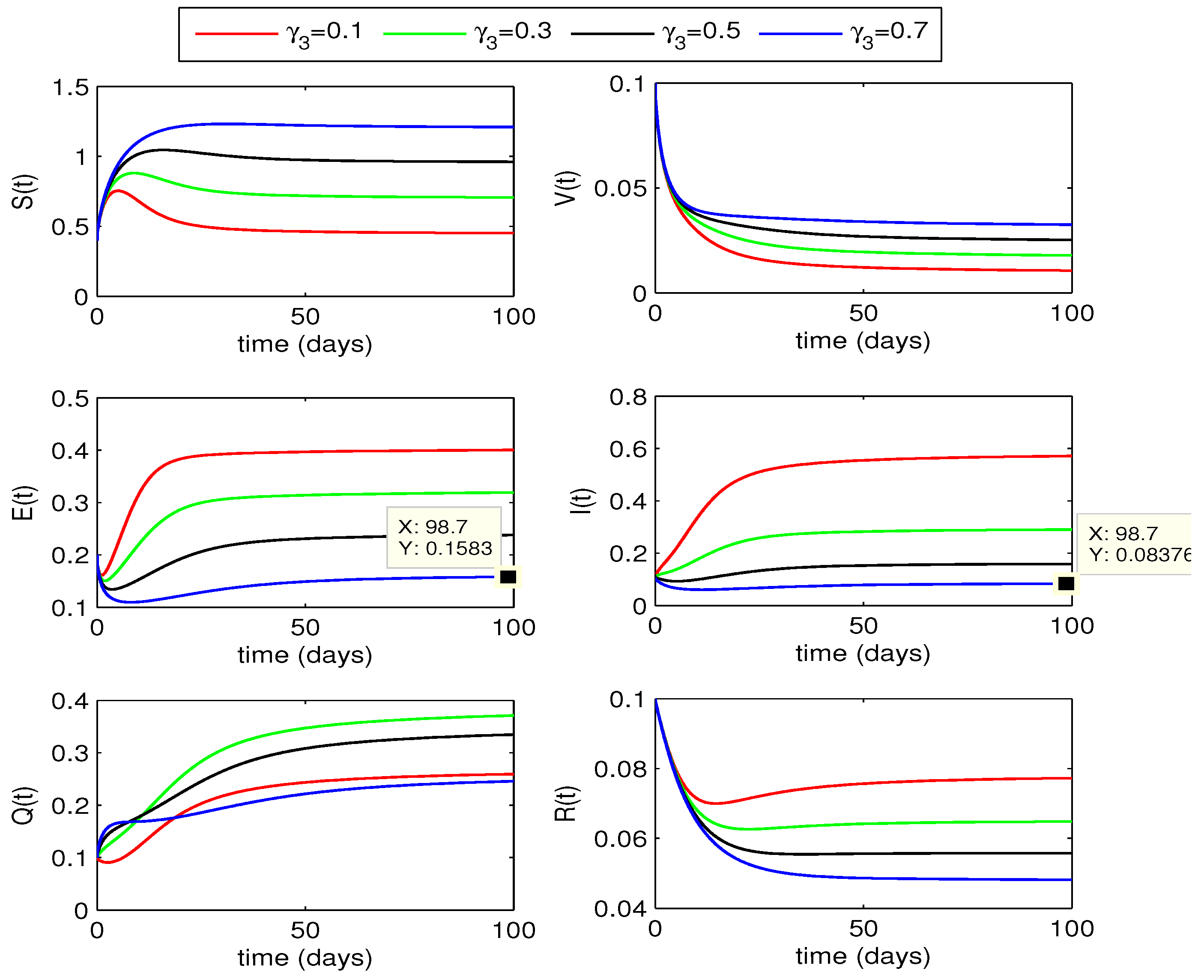
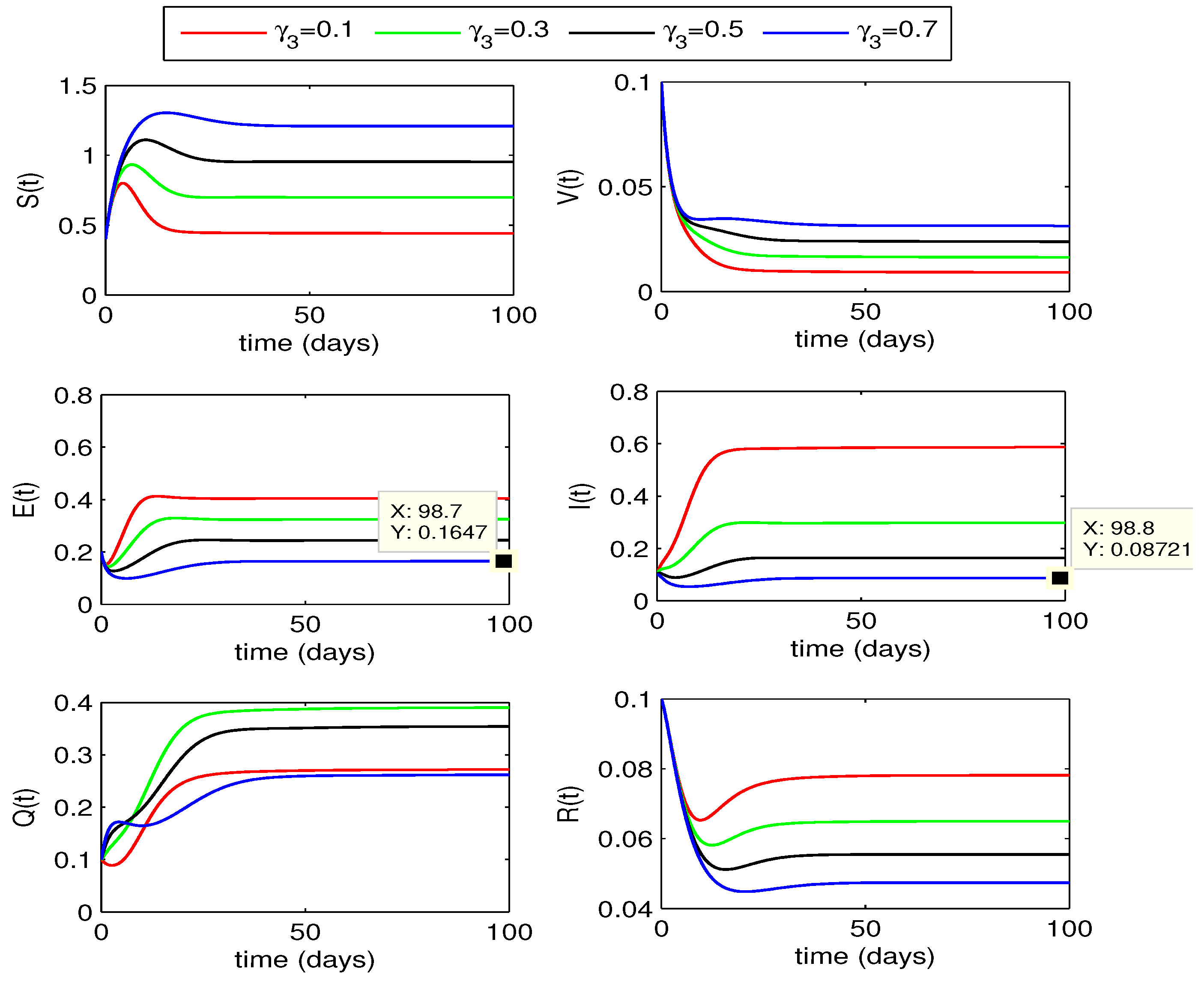
4.2. Quarantining Effects on Disease Dynamics

In model formulation, we had considered quarantining both the exposed and infected individuals, respectively, at rates $q_1$ and ${\gamma }_3$. In this section, we study the effect of both rates on disease control for two different values of fractional order, i.e., for $\sigma =0.8$ and $\sigma =0.95$.

4.2.1. Effect of $Q_1$

The impact of quarantining exposed individuals on disease dynamics can be seen in Figure 3 and Figure 4. The curves for exposed and infected individuals decrease with an increase in the quarantine rate $q_1$ from 0 to 0.7. In this case, the recovered individuals also decrease but the susceptible rise with the increase in the value of $q_1$. We also observe that, for $\sigma =0.8$, the decline in infection is more as compared to the decline in curves for fractional order $\sigma =0.95$.

4.2.2. Effect of ${\gamma }_3$

The impact of quarantining infected individuals, on disease dynamics, can be seen in Figure 5 and Figure 6. If the quarantining rate ${\gamma }_3$ is gradually increased up to 0.7, the curves for exposed and infected individuals gradually decrease. From this declining behavior, we may conclude that the disease may move to a disease-free state if the quarantining rate is increased further, that is more than $70\%$ of infected people should be quarantined to reach a disease-free state. The decline in infection for fractional order $\sigma =0.8$ is more as compared to the case for $\sigma =0.95$.

From the above two quarantining studies, we observe that the quarantine rate $q_1$ has more effect in the reduction of exposed cases, whereas the impact of quarantine rate ${\gamma }_3$ is more on infected individuals.

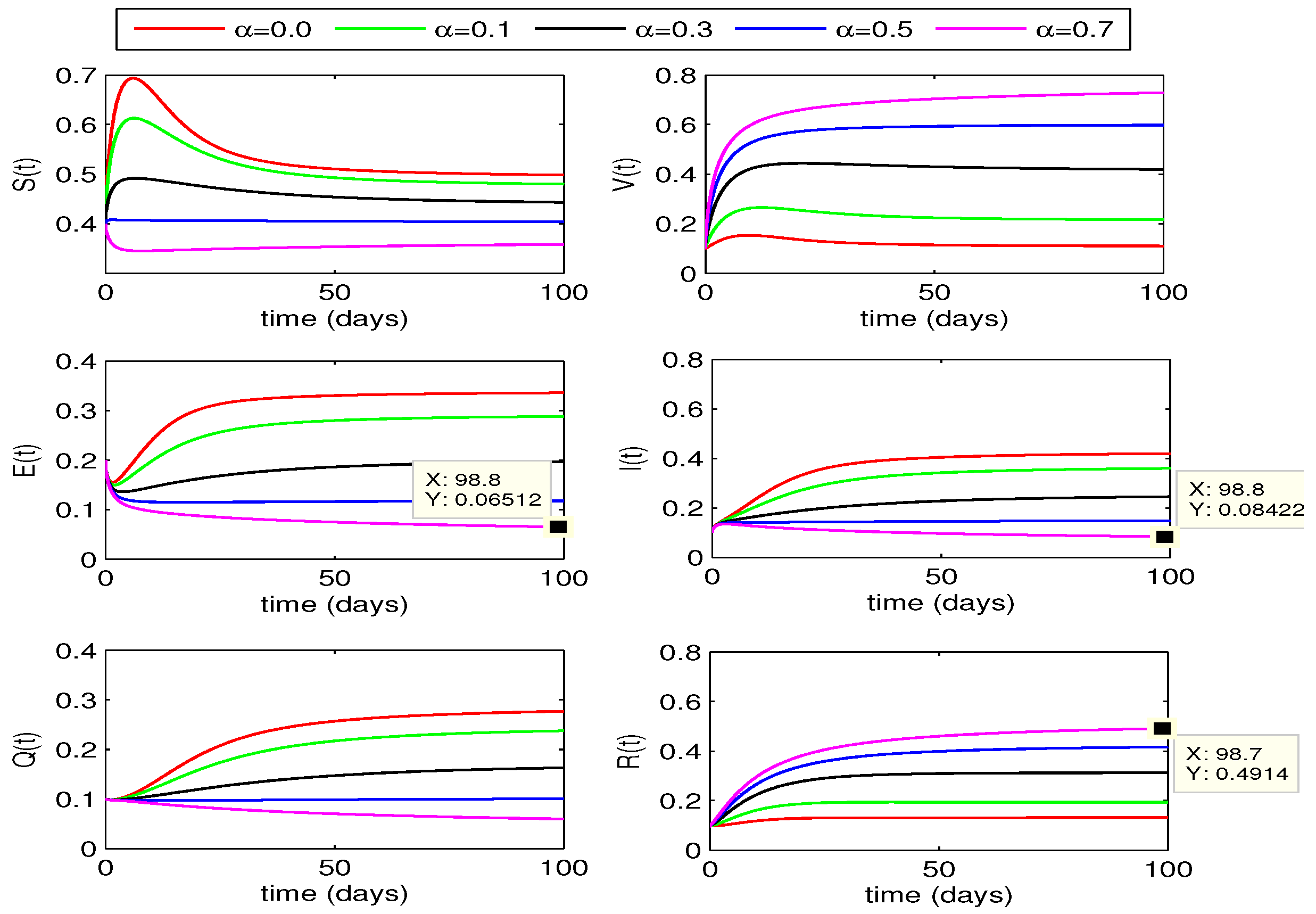
4.3. Vaccination Effect on Disease Dynamics

In this section, we look at how varying vaccination rates affect the dynamics of the whooping cough model quantitatively. From Figure 7 and Figure 8, we observe that the infection in the population decreases as the vaccination rates increase from 0 to 0.7. If the rates are increased further, the curves for infected classes may further decline to move to disease-free states. We also notice a remarkable rise in the recovered individuals in this case. The curves for exposed and infected individuals slightly decline more with the increase in the value of fractional order $\sigma$.

5. Sensitivity Analysis

In this section, we find the sensitivity index for each parameter of the reproduction number ${\mathcal{R}}_0$. On the basis of these indices, we determine the sensitivity of the parameter to ${\mathcal{R}}_0$. A parameter with a high index value is more sensitive to ${\mathcal{R}}_0$. The sensitivity analysis may help to design optimal control strategies for disease control. Parameters having high sensitivity indices may be considered as control variables for the control problem.

We implement the approach given in [52] to compute sensitivity indices of the parameters of ${\mathcal{R}}_0$. The approach is to use the following formula to compute the sensitivity index of a parameter $\zeta$ of ${\mathcal{R}}_0$.

$${\mathcal{I}}_{\zeta }^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial \zeta }\frac{\zeta }{{\mathcal{R}}_0}.$$

Evaluated sensitivity indices for each parameter of ${\mathcal{R}}_0$ are listed in

Table 1. Sensitivity indices for each parameter of $R_0$.

Parameter	Sensitivity Index	Parameter	Sensitivity Index
$\Pi$	1.0000	$\mu$	−1.8150
$\alpha$	−0.0388	$\beta$	0.9953
$\delta$	0.0046	$\gamma$	0.3243
${\gamma }_1$	−0.0018	${\gamma }_2$	−0.0507
${\gamma }_3$	−0.3807	$q_1$	−0.0270
$d_1$	−0.0101	$d_2$	0.0000

. Other than $\Pi$ and $\mu$, transmission rate $\beta$ has the highest sensitivity index. Thus, this parameter is highly sensitive to ${\mathcal{R}}_0$. A unit change in $\beta$ will produce a change of $0.9953$ in ${\mathcal{R}}_0$. Other parameters having comparatively high sensitivity index are $\gamma$ and ${\gamma }_3$. Since ${\gamma }_3$ is a controllable parameter, it will be considered as one of the control variables for disease control strategy.

6. Optimization of the Whooping Cough Model

In this section, we construct an optimal control problem to determine optimal quarantine and vaccination rates to restrict the spread of whooping cough infection. For this, we first update the disease model (5) to adjust time-dependent controls and then define an objective functional. We formulate the Hamiltonian function by introducing adjoint variables and develop optimality conditions by implementing the Pontryagin’s principle [59,60,61]. The conditions will be evaluated by following the steps of an algorithm to produce optimal solutions to the control problem.

6.1. Optimal Control Problem and Optimality Conditions

The objective of defining an optimal control problem is to optimally investigate the effect of quarantining infected individuals and vaccination of susceptible on the spread of whooping cough disease. To achieve this objective, we formulate control strategies for the minimization of exposed and infected individuals at the lowest cost.

First of all, we update model (5) by considering vaccination rate $\alpha$ and quarantining rates $q_1$, ${\gamma }_3$ as time-dependent controls, respectively, denoted by $u_1\left(t\right),u_2\left(t\right)$, and $u_3\left(t\right)$. With these controls, the updated whooping cough model is given below:

$$\begin{array}{}\mathrm{(26a)}& {}_0^{ABC}{D}_t^{\sigma }S\left(t\right)=\Pi -\beta IS-(\mu +u_1)S,\hfill \mathrm{(26b)}& {}_0^{ABC}{D}_t^{\sigma }V\left(t\right)=u_{1}S-\delta IV-({\gamma }_1+\mu )V,\hfill \mathrm{(26c)}& {}_0^{ABC}{D}_t^{\sigma }E\left(t\right)=\beta IS+\delta IV-(\mu +\gamma +u_2)E,\hfill \mathrm{(26d)}& {}_0^{ABC}{D}_t^{\sigma }I\left(t\right)=\gamma E-({\gamma }_2+u_3+\mu +d_1)I,\hfill \mathrm{(26e)}& {}_0^{ABC}{D}_t^{\sigma }Q\left(t\right)=u_{2}E+u_{3}I-(q_2+d_2+\mu )Q,\hfill \mathrm{(26f)}& {}_0^{ABC}{D}_t^{\sigma }R\left(t\right)={\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q-\mu R,\hfill \end{array}$$

along with conditions:

$$\begin{array}{}\mathrm{(26g)}& \begin{array}{c}S\left(0\right)=S_0>0,V\left(0\right)=V_0\ge 0,E\left(0\right)=E_0\ge 0,\hfill \\ I\left(0\right)=I_0\ge 0,Q\left(0\right)=Q_0\ge 0,R\left(0\right)=R_0\ge 0.\hfill \end{array}\hfill \end{array}$$

The objective functional consisting of infected states and controls is defined as

$$\begin{array}{c}\hfill J(z,u)=\underset{0}{\overset{t_f}{\int }}\left[a_{1}E\left(t\right)+a_{2}I\left(t\right)+\frac{1}{2}{b}_1{u}_1^2\left(t\right)+\frac{1}{2}{b}_2{u}_2^2\left(t\right)+\frac{1}{2}{b}_3{u}_3^2\left(t\right)\right]dt,\end{array}$$

(27)

where $t_f$ is the terminal time, $z=(E,I)$ represent state variables, $u=(u_1\left(t\right),u_2\left(t\right),u_3\left(t\right))$ represent control variables, $a_1,a_2$ are non-negative weights associated with state variables and $b_i\ge 0,i=1,2,3$ are the cost of controls.

Our aim is to determine an optimal control variable $u^{*}\in \mathcal{U}$ that minimizes the objective functional $J(z,u)$, i.e.,

$$\begin{array}{c}\hfill {\displaystyle \underset{u\left(t\right)\in \mathcal{U}}{min}J(z,u)\mathrm{subject}\mathrm{to}\mathrm{model}\left(26\right),}\end{array}$$

(28)

where $\mathcal{U}$ is an appropriate space of control variables.

Now, we define a Hamiltonian function and implement Pontryagin’s maximum principle to derive the optimality conditions that are necessary for the solution of optimal control problem (28).

$$\begin{array}{cc}\hfill \mathbb{H}\left(\mathcal{V}\right(t),\Psi (t),u(t\left)\right)=& a_{1}E\left(t\right)+a_{2}I\left(t\right)+\frac{1}{2}{b}_1{u}_1^2\left(t\right)+\frac{1}{2}{b}_2{u}_2^2\left(t\right)+\frac{1}{2}{b}_3{u}_3^2\left(t\right)+\hfill \\ \hfill & +{\Psi }_1\left[\Pi -\beta IS-(\mu +u_1)S\right]+{\Psi }_2\left[u_{1}S-\delta IV-({\gamma }_1+\mu )V\right]\hfill \\ \hfill & +{\Psi }_3\left[\beta IS+\delta IV-(\mu +\gamma +u_2)E\right]+{\Psi }_4\left[\gamma E-({\gamma }_2+u_3+\mu +d_1)I\right]\hfill \\ \hfill & +{\Psi }_5\left[u_{2}E+u_{3}I-(q_2+d_2+\mu )Q\right]+{\Psi }_6\left[{\gamma }_{1}V+{\gamma }_{2}I+q_{2}Q-\mu R\right],\hfill \end{array}$$

(29)

where $\mathcal{V}\left(t\right)=\left(S\right(t),V(t),E(t),I(t),Q(t),R(t\left)\right)$ is a vector of state variables, ${\Psi }_j\left(t\right),j=1,\cdots ,6$ are adjoint variables associated with the state equations of system (26).

Theorem 11.

Let ${\mathcal{V}}^{*}\left(t\right)$ be the optimal solution for model (26) corresponding to the optimal control variable $u^{*}\left(t\right)$ for the control problem (28). Then, there exists a system of linear adjoint equations given as

$$\begin{array}{}\mathrm{(30a)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_1\left(t\right)=-{\displaystyle \frac{\partial \mathbb{H}}{\partial S}},\hfill \mathrm{(30b)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_2\left(t\right)=-{\displaystyle \frac{\partial \mathbb{H}}{\partial V}},\hfill \mathrm{(30c)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_3\left(t\right)=-{\displaystyle \frac{\partial \mathbb{H}}{\partial E}},\hfill \mathrm{(30d)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_4\left(t\right)=-{\displaystyle \frac{\partial \mathbb{H}}{\partial I}},\hfill \mathrm{(30e)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_5\left(t\right)=-{\displaystyle \frac{\partial \mathbb{H}}{\partial Q}},\hfill \mathrm{(30f)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_6\left(t\right)=-{\displaystyle \frac{\partial \mathbb{H}}{\partial R}},\hfill \end{array}$$

along with the conditions:

$$\begin{array}{c}\hfill {\Psi }_1\left(t_f\right)={\Psi }_2\left(t_f\right)={\Psi }_3\left(t_f\right)={\Psi }_4\left(t_f\right)={\Psi }_5\left(t_f\right)={\Psi }_6\left(t_f\right)=0,\end{array}$$

and the control variable $u^{*}\left(t\right)=(u_1^{*},u_2^{*},u_3^{*})$ is characterized by

$$\begin{array}{cc}\hfill u_1^{*}\left(t\right)& =min\left\{1,max\left\{\frac{({\Psi }_1-{\Psi }_2)S}{b_1},0\right\}\right\},\hfill \\ \hfill u_2^{*}\left(t\right)& =min\left\{1,max\left\{\frac{({\Psi }_3-{\Psi }_5)E}{b_2},0\right\}\right\},\hfill \\ \hfill u_3^{*}\left(t\right)& =min\left\{1,max\left\{\frac{({\Psi }_4-{\Psi }_5)S}{b_3},0\right\}\right\}.\hfill \end{array}$$

□

Evaluation and simplification of Equations (30a)–(30f) lead us to the following system of linear adjoint equations:

$$\begin{array}{}\mathrm{(31a)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_1=(\beta I+\mu +u_1){\Psi }_1-u_1{\Psi }_2-\beta I{\Psi }_3,\hfill \mathrm{(31b)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_2=(\delta I+{\gamma }_1+\mu ){\Psi }_2-\delta I{\Psi }_3-{\gamma }_1{\Psi }_6,\hfill \mathrm{(31c)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_3=-a_1+(\mu +\gamma +u_2){\Psi }_3-\gamma {\Psi }_4-u_2{\Psi }_5,\hfill \mathrm{(31d)}& \begin{array}{cc}{}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_4=\hfill & -a_2+\beta S{\Psi }_1+\delta V{\Psi }_2-(\beta S+\delta V){\Psi }_3\hfill \\ & +({\gamma }_2+u_3+\mu +d_1){\Psi }_4-u_3{\Psi }_5-{\gamma }_2{\Psi }_6,\hfill \end{array}\mathrm{(31e)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_5=(q_2+d_2+\mu ){\Psi }_5-q_2{\Psi }_6,\hfill \mathrm{(31f)}& {}_t^{ABC}{\mathcal{D}}_{t_f}^{\sigma }{\Psi }_6=\mu {\Psi }_6,\hfill \end{array}$$

along with the conditions

$$\begin{array}{}\mathrm{(31g)}& {\Psi }_1\left(t_f\right)={\Psi }_2\left(t_f\right)={\Psi }_3\left(t_f\right)={\Psi }_4\left(t_f\right)={\Psi }_5\left(t_f\right)={\Psi }_6\left(t_f\right)=0.\end{array}$$

Differentiation of the Hamiltonian with respect to controls gives us the expressions for control variables, i.e.,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \mathbb{H}}{\partial u_1}}=0\Rightarrow u_1\left(t\right)={\displaystyle \frac{{\Psi }_1-{\Psi }_2}{b_1}}S\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{\partial \mathbb{H}}{\partial u_2}}=0\Rightarrow u_2\left(t\right)={\displaystyle \frac{{\Psi }_3-{\Psi }_5}{b_2}}E\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{\partial \mathbb{H}}{\partial u_3}}=0\Rightarrow u_3\left(t\right)={\displaystyle \frac{{\Psi }_4-{\Psi }_5}{b_3}}I\left(t\right),\hfill \end{array}$$

and the optimal characterizations for controls are given as

$$\begin{array}{}\mathrm{(32a)}& u_1^{*}\left(t\right)=min\left\{1,max\left\{\frac{({\Psi }_1-{\Psi }_2)S}{b_1},0\right\}\right\},\hfill \mathrm{(32b)}& u_2^{*}\left(t\right)=min\left\{1,max\left\{\frac{({\Psi }_3-{\Psi }_5)E}{b_2},0\right\}\right\},\hfill \mathrm{(32c)}& u_3^{*}\left(t\right)=min\left\{1,max\left\{\frac{({\Psi }_4-{\Psi }_5)S}{b_3},0\right\}\right\}.\hfill \end{array}$$

To approximate solutions of the state model (26), we employ the Toufik–Atangana method described in Section 4.1, and for the corresponding adjoint system (31), we implement Toufik–Atangana scheme backward in time together with the conditions (31g).

6.2. Solution Algorithm

Optimality conditions for the control problem (28) are approximated for optimal solutions by the following steps of the Algorithm 1 given below.  

Algorithm 1: Algorithm to find minimizer of the control problem (28)

(1) Make an initial guess for control $u_s\in \mathcal{U}$ for $s=0$. (2) Use values of control $u_s$ to approximate solutions of the state system (26) and the adjoint system (31). (3) Determine $u^{*}$ from (32). (4) Refine control $u_s$ by using $u_s=(u_s+u^{*})/2$. (5) Stop iterations when $\parallel {\Theta }_s-{\Theta }_{s-1}\parallel <\epsilon \parallel {\Theta }_s\parallel$ for $s>0$, otherwise$s+1⟵s$ and jump back to step 2.

Where $\Theta$ represents each of the state variables, adjoint variables and control variables and $\epsilon >0$ is the tolerance set as per accuracy requirements.

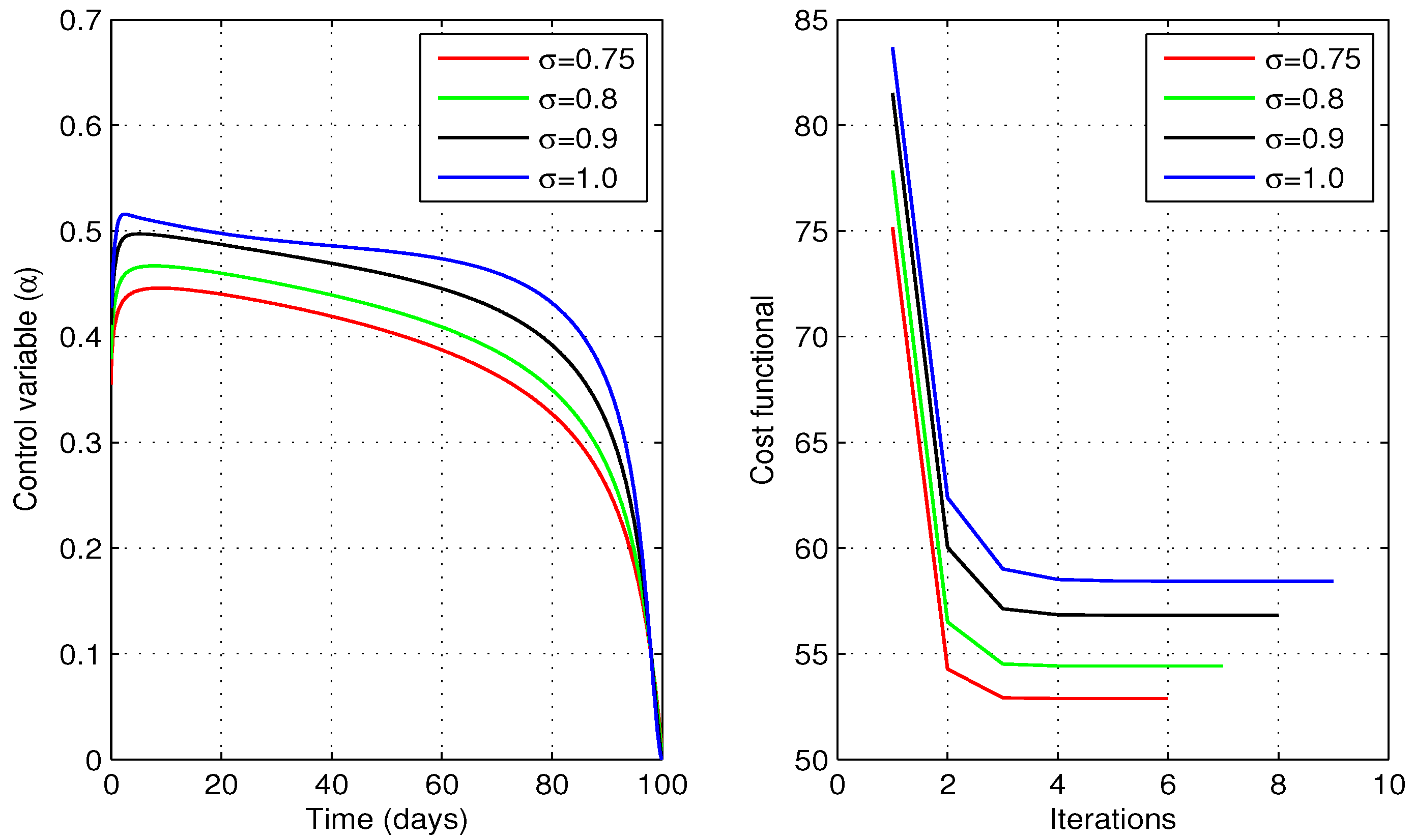
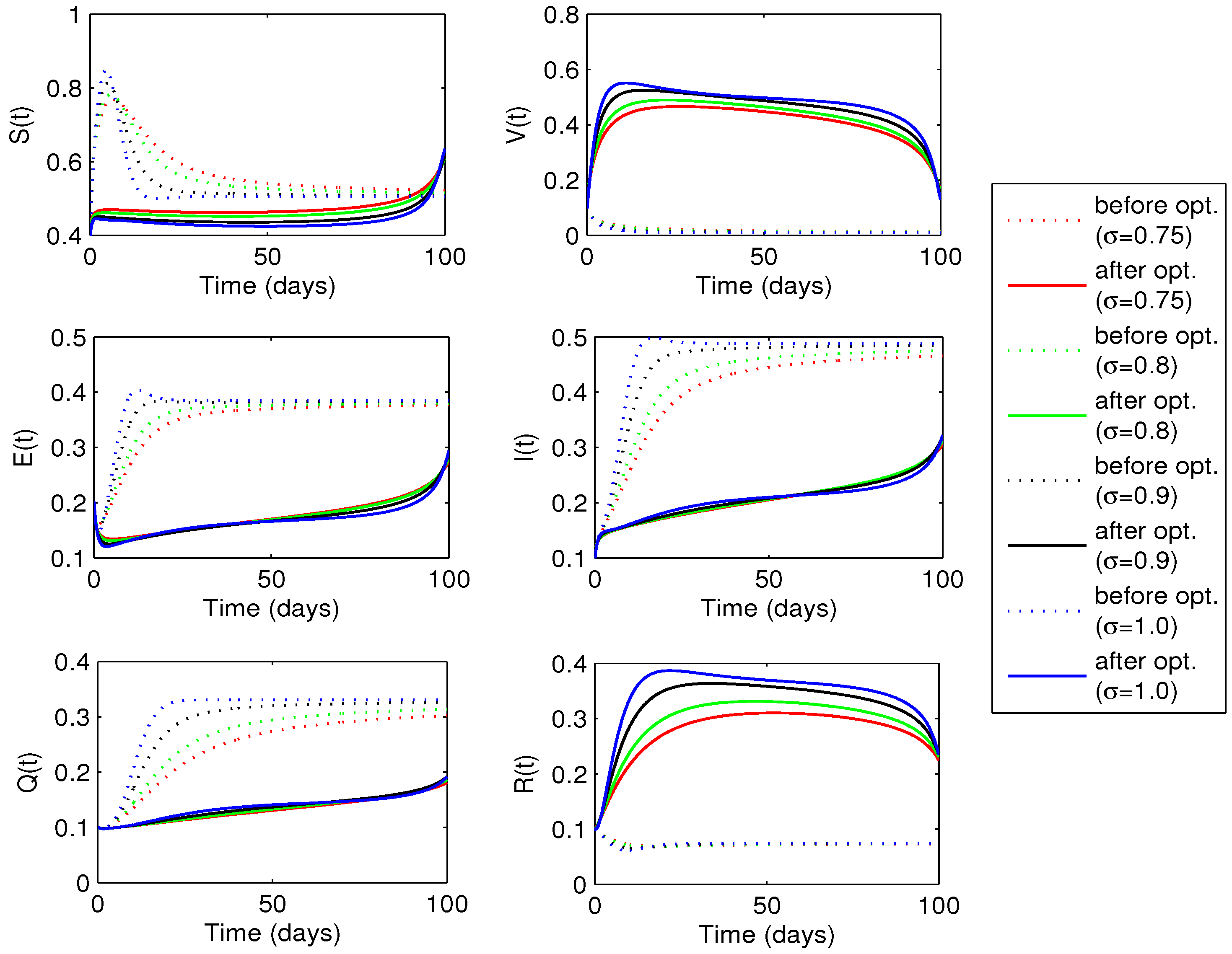
6.3. Optimal Solutions

Simulation results of the optimal control problem (28) are presented and discussed in this section. To obtain these results, we implemented steps of Algorithm 1 through MATLAB code. We discretize the domain $[0,t_f]$ into $N+1$ discrete points $t_q=qh,q=0,1,\cdots ,N$ where $h=\frac{t_f}{N}$ and approximate the state and adjoint equations using the approximating scheme, explained in Section 4.1. We use Simpson’s rule to approximate the cost functional (27) at the discrete points. The results are simulated for different values of fractional order, i.e., for $\sigma =0.75,0.8,0.9,1$.

The objective of this study is to determine the optimal quarantine rates $q_1$, ${\gamma }_3$, and the vaccination rate $\alpha$ that will not only minimize the cost functional, but will also reduce the whooping cough infection in society. For detailed analysis, we discuss here three different cases. In the first case, we keep quarantine rates $q_1$, ${\gamma }_3$ fixed in time and determine the optimal vaccination rate $\alpha \left(t\right)$ for disease control. In the second case, we determine the best quarantine rates $q_1\left(t\right)$, ${\gamma }_3\left(t\right)$ that will reduce the spread of whooping cough infection. In this case, the vaccination rate will be considered as time independent. In the last strategy, we deal with time-dependent vaccination rate and quarantine rates together to determine their optimal profiles that will help to reduce the cost functional to its minimum and to curtail the whooping cough disease infection.

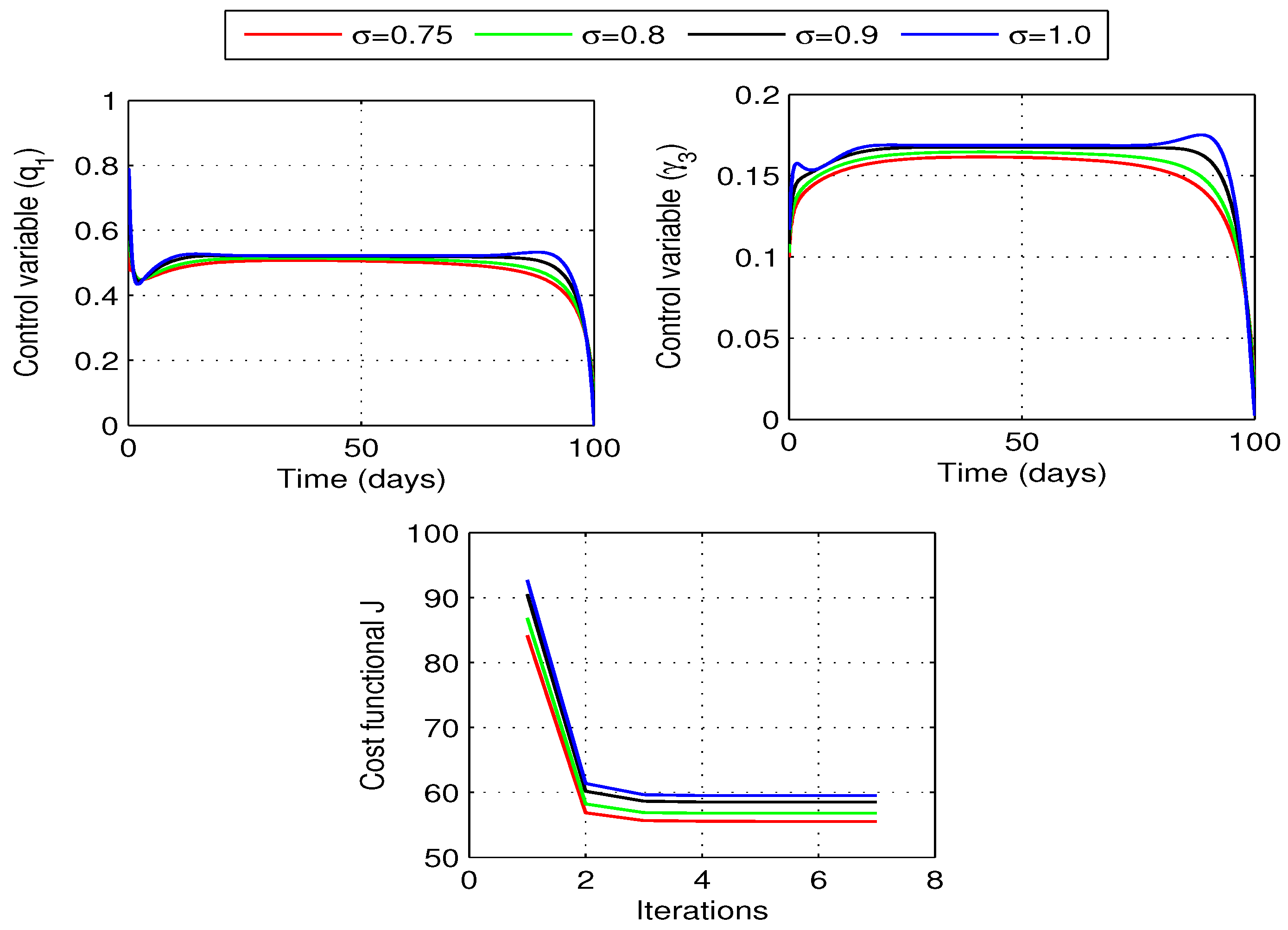
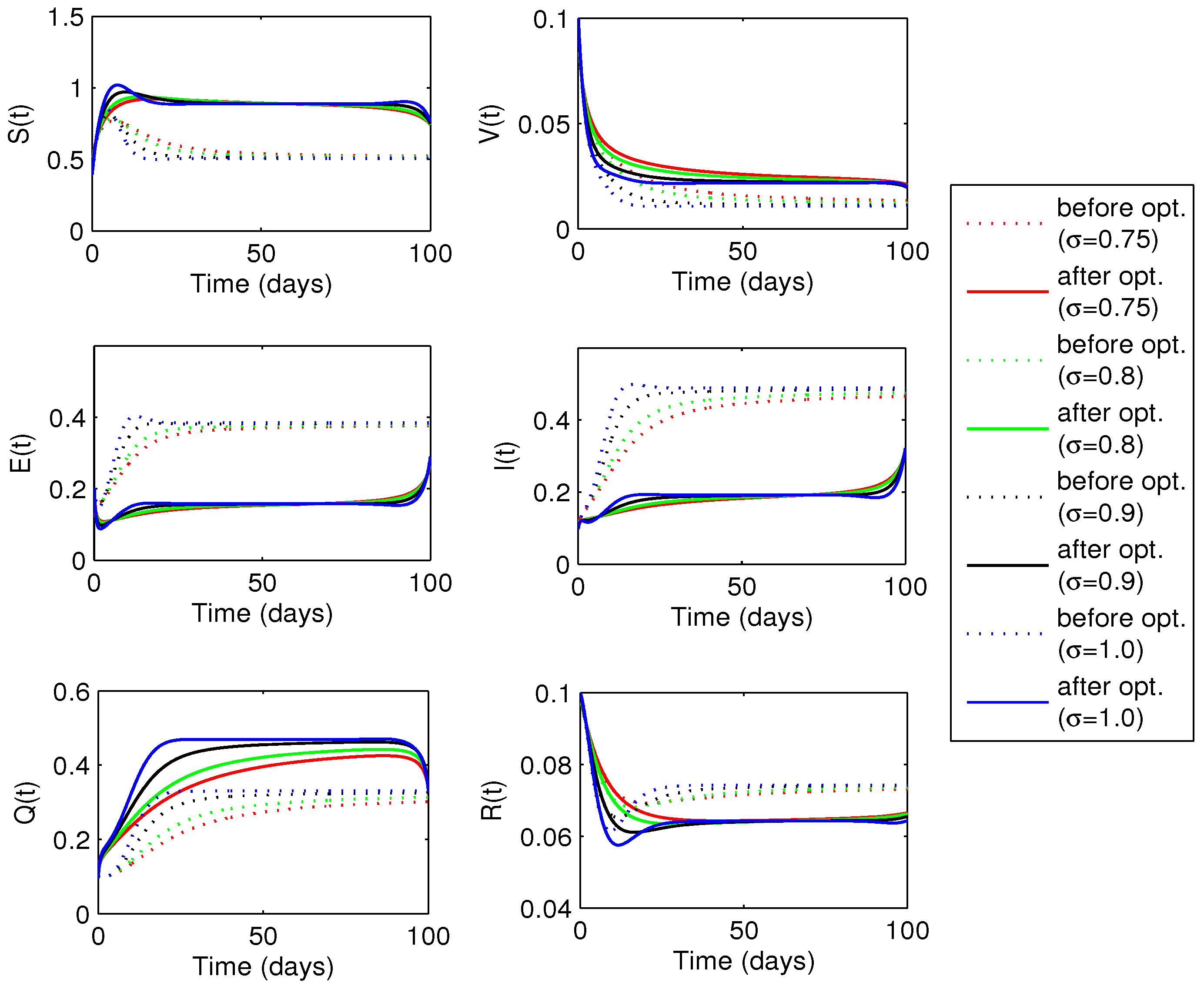
6.3.1. Optimal Vaccination Rate

In the first case, we consider optimization of the problem (28) by considering only vaccination rate $\alpha \left(t\right)(=u_1\left(t\right))$ as the time-dependent control variable. Figure 9 shows profiles of the optimal vaccination rate $\alpha \left(t\right)$ and the associated cost functional J for different values of fractional order $\sigma$. From the figure, we conclude that there is a need to vaccinate almost $40\%$ to $50\%$ of the susceptible at the start of the pandemic and then the vaccination percentage decreases gradually with days. We also note that as the fractional order $\sigma$ decreases, the corresponding cost of implementing the vaccination strategy reduces to its minimum in each case. The minimum cost is observed for fractional order $\sigma =0.75$. The dynamical behaviors of the state variables before and after optimization for each value of the fractional order $\sigma$ are shown in Figure 10. A sufficient decrease in the exposed and infected individuals is noticed in this figure; however, there is a significant rise in the number of recovered individuals. Thus, the strategy is successful in reducing the disease infection and increasing the number of recovered individuals.

6.3.2. Optimal Quarantine Rates

Now, we take quarantine rates $q_1\left(t\right)(=u_2\left(t\right))$ and ${\gamma }_3\left(t\right)(=u_3\left(t\right))$ as the time-dependent control variables for the problem (28). Optimal curves for the control variables and the corresponding behavior of the cost functional for different values of fractional order is shown in the Figure 11. In each case, the curves for the cost functional reach to their minimum in seven iterations. The figure illustrates that there is a need to quarantine almost $50\%$ of the exposed individuals and $17\%$ of the infected individuals to have optimal control of the disease. The optimal quarantine percentage slightly varies with the fractional order $\sigma$. We also note that as the fractional order $\sigma$ decreases, the corresponding cost of implementing the quarantine strategy reduces to its minimum in each case. Figure 12 shows the curves for state variables before and after optimization. Once again, we observe a decrease in the number of exposed and infected individuals in this case. However, the decrease, in this case, is comparatively more to the case when only vaccination rate $\alpha \left(t\right)$ is considered as a single control variable. This means quarantining exposed and infected individuals is more effective for disease control. The computational cost is also less in this case. We also notice a decrease in the number of recovered individuals, but an increase in the susceptible for each value of fractional order $\sigma$.

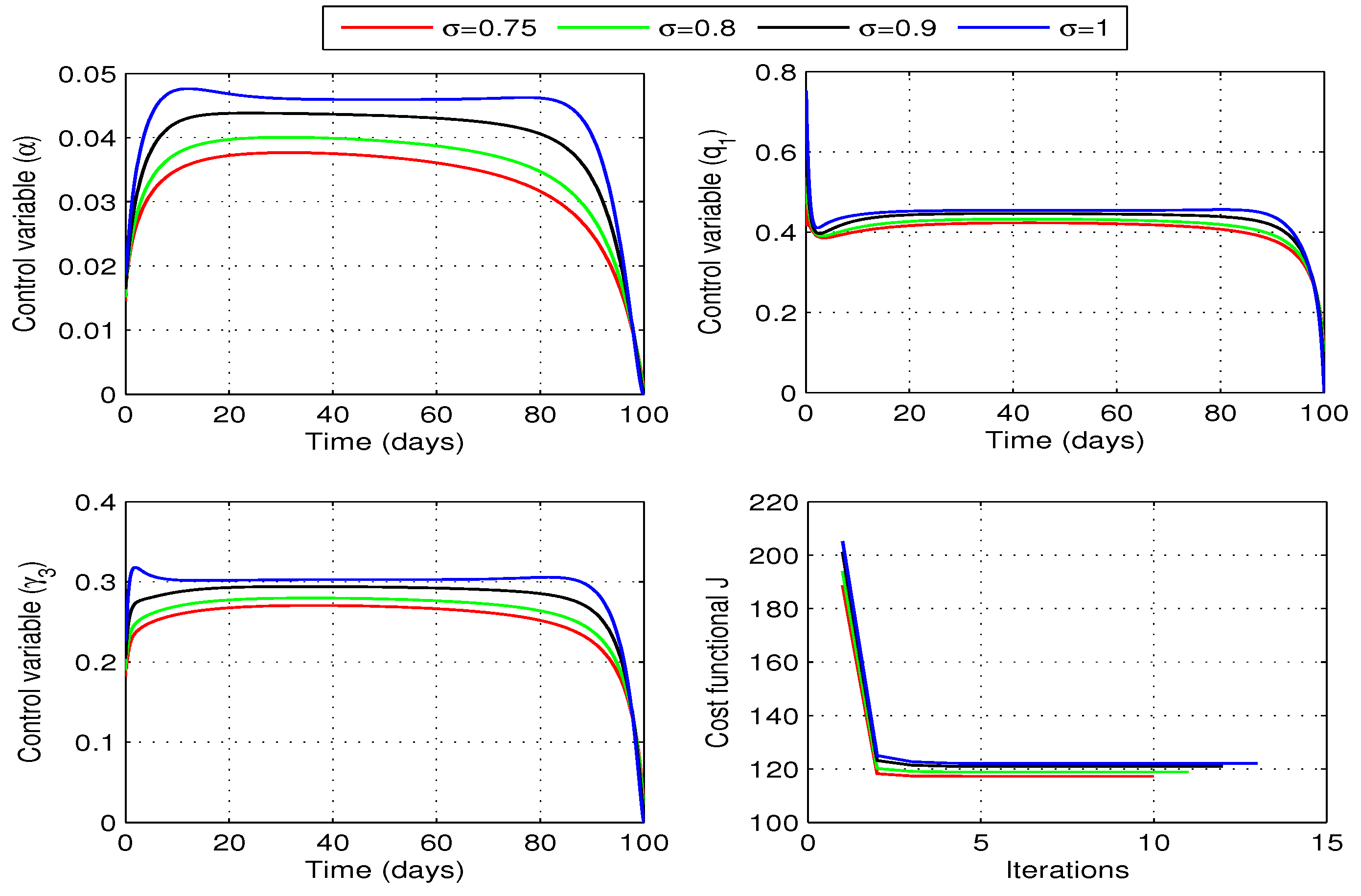
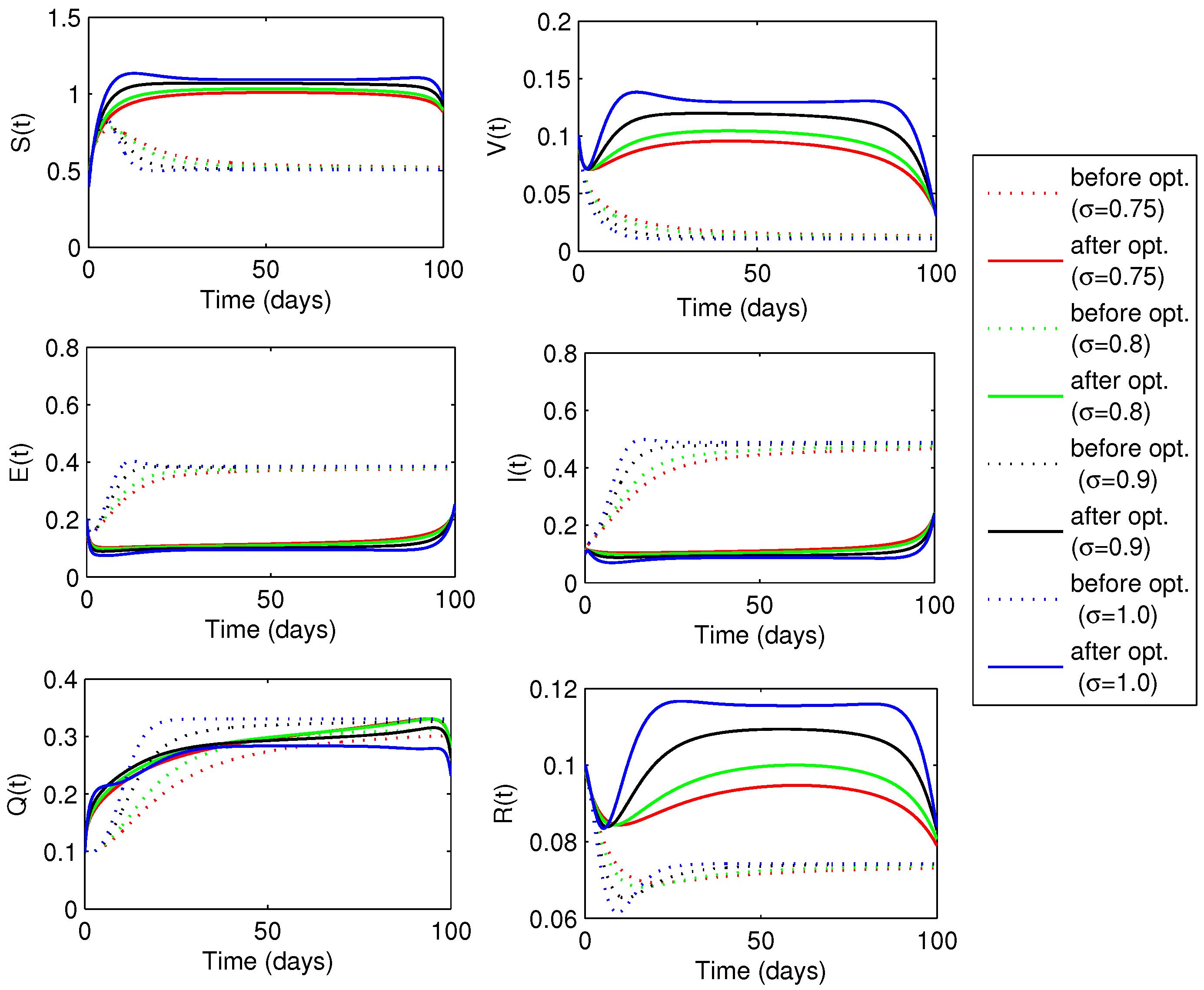
6.3.3. Optimal Vaccination and Quarantine Rates

In the last case, we consider vaccination rate $\alpha \left(t\right)$ and the quarantine rates $q_1\left(t\right),{\gamma }_3\left(t\right)$ as control variables for the optimal control problem (28). For this case, the optimal behavior of the control variables and minimization of the related objective functional J are shown in Figure 13. We observe that there is a need to vaccinate only $5\%$ of the susceptible, quarantine $80\%$ of the exposed in the beginning and later up to $45\%$, and quarantine $30\%$ of the infected individuals. We also note that as the fractional order $\sigma$ decreases, the corresponding cost of implementing the strategy reduces to its minimum in each case. The best cost is attained for $\sigma =0.75$. The cost functional in this case takes more iterations to attain its minimum value, i.e., the computational cost is more for this strategy. Profiles of state variables before and after optimization are shown in Figure 14. the number of exposed and infected individuals decreases more in this case as compared to the previous two control strategies. We also notice a sufficient rise in the susceptible and recovered curves for each value of the fractional order $\sigma$.

The analysis of the three cases reveals that considering all three controls together is more effective in reducing the infection of whooping cough disease. However, the implementation of this strategy requires more resources and infrastructure. Moreover, the vaccination strategy seems to be less effective as compared to the quarantine strategy in controlling the spread of the disease.

7. Conclusions

In this work, we formulated a new ABC fractional disease model for whooping cough infection to analyze the dynamics of the disease and to suggest optimal control strategies for minimizing the effect of the disease. The choice of the ABC operator is due to its non-local and non-singular kernel. First of all, we analyzed the model theoretically by establishing biologically significant aspects of the model. We proved that the proposed model has a unique solution that is positive and bounded. It is also verified that the equilibrium points are locally and globally stable with restriction to threshold parameter ${\mathcal{R}}_0$. These results concluded that the proposed model is well-posed for further numerical investigations. Through sensitivity analysis, we determined that the disease transmission rates $\beta$ and $\gamma$, and the quarantine parameter ${\gamma }_3$ are the most sensitive to ${\mathcal{R}}_0$. Due to their significant impact on ${\mathcal{R}}_0$, the parameters may be considered as control variables for optimal control analysis.

Another objective of this study was to suggest an optimal control strategy to restrict the spread of whooping cough infection. For this, we considered vaccination rate $\alpha$ and quarantine rates $q_1$$(E$ to $Q)$, ${\gamma }_3$$(I$ to $Q)$ as control variables, and studied their impact on disease control. First of all, we took different levels (0 to 0.7) of these parameters and explored the impact of each on disease control. We determined that the disease can be controlled significantly by increasing the values of these parameters. However, it is concluded that vaccination of the susceptible is more effective as compared to quarantining the exposed or infected individuals. The impact of memory index (fractional order) $\sigma$ on disease dynamics was also investigated here. We visualized a decrease in the infection cases with a decrease in the memory index.

For optimal control analysis, we considered the parameters $\alpha ,q_1$, and ${\gamma }_3$ as time-dependent controls and formulated an optimal control problem by defining a cost functional. The aim was to determine optimal values of the control variables that minimize the cost functional. By implementing Pontryagin’s principle, we derived the necessary optimality conditions for the optimal solution to the problem. In this study, we discussed three different optimal control approaches. In the first case, we determined optimal solutions by considering only the vaccination rate $\alpha$ as a control variable. In the second approach, we considered quarantine rates $q_1,{\gamma }_3$ as the time-dependent controls and determined optimal solutions for the given problem. In the last case, all the three parameters $\alpha ,q_1,{\gamma }_3$ were taken as time-dependent controls for optimal solutions. Graphical results show that each of the considered strategies is very effective in reducing the exposed and infected individuals and hence may be implemented to reduce whooping cough infection in society. The graphical results also revealed that the case where we considered all three controls together is more effective in reducing the spread of whooping cough infection. However, implementation of this approach requires more resources and infrastructure. It is also concluded that the simulation results from time-dependent controls are more cost-effective as compared to the results produced by time-independent controls.

The objective of the mathematical analysis, in this study, was to gain an understanding of the dynamics of whooping cough disease. It is important to note that the proposed fractional disease model offers a more precise understanding of the disease’s behavior compared to the integer-order model. We are confident that the findings in the present research work will be beneficial for the health authorities to make better decisions to combat the disease.

The optimal controls for the implementation of compulsory disease control measures will be identified in the future by the analysis of a general stochastic optimum control problem for whooping cough. In addition, a COVID-19 and whooping cough co-infection model will be developed and explored for various optimal control strategies with cost-effective analysis.