Abstract
Our paper considers the possibility of the emergence and control of non-equilibrium states of a quasi-homogenous condensed medium with energy and particle flows in the phase space, which, first of all, manifest themselves in the explosive development of the asymmetry in the initially symmetric equilibrium system. This symmetry breaking and the appearance of non-equilibrium in the system are controlled by the coherent acceleration of the system. Dependencies of thermodynamic parameters of a strong nonequilibrium system on the indices of disequilibrium in coherently correlated states are given, and the estimates of the dielectric permittivity in a non-equilibrium system and modes of plasma acoustic oscillations are made. An estimate of the superconducting transition temperature under nonequilibrium conditions has been made. It is demonstrated that the superconducting transition temperature can approach the limiting value, corresponding to a quantum with its plasma frequency of the medium.
1. Introduction
Advances towards creating methods for controlling the direction of evolutionary processes are largely based on the development of nonequilibrium thermodynamics, and interest in these issues continues unabated [1,2,3,4,5]. The emerging understanding that evolution under certain conditions can be influenced by very insignificant impacts [6,7,8] makes it clear that there is growing concern about the possible existence of unconscious, unpredictable controlling influences of random electromagnetic pollutants on the ecology of the external environment and on biological systems. There is a pressing need to solve problems of managing self-organization in various complex systems.
It should be noted that despite huge achievements, Prigogine’s nonequilibrium thermodynamics [1] is limited by an approximation of local equilibrium states, the strong non-equilibrium of which lies only in the strong spatial dependence of the parameters of equilibrium distributions (density, temperature, etc.). Naturally, the management of system evolution and phase transitions, in this case, is carried out through variations of these thermodynamic parameters. The peculiarities of strongly nonequilibrium states in quasi-homogeneous systems and the peculiarities of non-locality influence in coherently correlated states of complex systems on the sequence of phase transitions and, therefore, on the evolution of their internal structure are insufficiently studied. The key role of correlations in many-particle systems was first clearly demonstrated in the fundamental works of N. Bogoliubov on kinetic equations and hydrodynamics [9] (the results of which are detailed, for example, in Refs. [9,10]).
A peculiar theory of kinetic equations considering the growth and evolution of structures in a particle system and non-locality of system states was obtained and analyzed by Vlasov et al. [11,12,13] using Cartan geometry (the physical meaning of Cartan geometry is thoroughly demonstrated in Penrose’s work [14]). Vlasov’s nonlocal statistical mechanics of a many-particle system and the theory of structure growth are set out in [15,16,17], where the non-locality of particle states is the main axiom of his evolutionary theory.
To verify the non-locality of physical phenomena, Bell proposed a theorem (see, for example, [18]) with inequalities, which now bear his name. The fundamental importance of this theorem is emphasized in [19]: “What Bell’s theorem, together with the experimental results, proves to be impossible (subject to a few caveats we will attend to) is not determinism or hidden variables or realism but locality, in a clear sense. What Bell proved, and what theoretical physics has not yet properly absorbed, is that the physical world itself is non-local.” The experimental proof of violations of Bell’s inequalities, and therefore the objective non-locality of particle interaction, was awarded the Nobel Prize in 2022 [20]. The official formulation of the Nobel Committee is more specific and reads—“for experiments with entangled photons, establishing violations in Bell’s inequality, and for innovations in quantum informatics”.
Non-locality in the dynamics and kinetics of particles leads to the fact that the influence on physical processes is not limited to the infinitesimal vicinity of the considered point but requires accounting for the finiteness of the interaction region and considering all orders of differentials of variables describing the system state. There are two qualitative approaches to describing these effects:
- Operator regularization method: Instead of differential operators for describing the evolution of the system, for example, functional, integrodifferential equations ([21,22,23]) and flows in the phase space are used (see, for example, in the Refs. [24,25,26,27,28,29,30,31,32,33]).
- Regularization method for the evolution of systems: instead of the four-dimensional spacetime, for example, the Cartan space is used (see, for example, the works of Vlasov [15,16,17]).
In the nonlocal theory of Vlasov, the spacetime in which the statistical theory of dynamic systems should be formulated is not the usual four-dimensional Riemann spacetime but the Cartan space. The Cartan space is a combination of points in the four-dimensional Riemann spacetime and tangent surfaces of different orders at each point.
The main variables in the statistical theory are not only coordinates, time, and velocities (momenta) but also accelerations of all orders. In his covariant kinetic equation in the Cartan space (see Ref. [16]), Vlasov obtained the exact power-law solution for non-inertial reference systems, i.e., systems in strong nonequilibrium with coherent acceleration.
Physically equivalent descriptions of non-inertial systems with coherent acceleration are spatially homogeneous systems of particles with phase space flows [24,25,26,27,28]. Exact power-law solutions for kinetic equations of Boltzmann, Landau, Balescu-Lenard [25,26,27], and kinetic equations in fractal media (see [24]) have been obtained for such physical models.
In all the mentioned cases, strongly nonequilibrium particle distributions in phase space exhibit power-law behavior, which reflects the common physical nature of evolution control—coherent acceleration and phase space flow (see [28]). It is important to note that coherent acceleration and the corresponding inertial forces are associated with the variation of the system’s structure, i.e., its binding energy and inertia [28,29,30].
Energy flows in the system arise either due to changes in the environment or due to internal changes in the structure of the system itself (see [28,29,30]). Importantly, environmental changes can influence both through the boundary between the designated system and the environment and uniformly throughout the system if the considered system is fully immersed in the environment. Each element of the system experiences the influence of the environment.
Section 2 of this study presents the Vlasov equations on the first tangent bundles after the corresponding averaging over higher accelerations. In these Vlasov equations, we explicitly account for the mentioned dependencies between variations in the system’s structures, coherent acceleration of many-particle systems, and particle and energy fluxes, which affect the distributions of charged particles and the characteristics of phase transitions (see for example, Refs. [31,32]). They can lead to a significant change in the phase transition temperature, the estimation of which is provided at the end of this article.
Together with the averaged kinetic equations, we obtain the dynamic transport equations. The dynamic equations in non-inertial reference systems, when averaging over higher orders of acceleration and considering the evolution of the internal structure of the system, can exhibit positive feedback that is consistent with the results obtained in [33]. In the same section, we present the covariant Vlasov kinetic equation with the evolution of the internal structure considered, along with its exact power-law solution expressed through non-extensive generalizations of Tsallis exponentials [34,35,36,37]. The obtained non-equilibrium distributions in systems with coherent acceleration are consistent with the general properties of accelerated reference systems [38] and the geometric properties of systems with constraints [39,40,41,42].
The processes of system evolution from an equilibrium system to a non-equilibrium quasi-stationary state with energy flows and/or the number of particles in the phase space of the system (non-equilibrium phase transitions) are accompanied by the emergence and explosive power-law growth of the asymmetry of the system’s phase space, the structure of the phase space and the corresponding evolution of the order parameter .
Section 3 of this study presents the fundamental thermodynamic properties of systems in strongly non-equilibrium states close to spatial homogeneity. The physical situation where each element of the system experiences the same influence from its surrounding environment is crucial for the system’s evolution and corresponds to the action of a mass force (and the corresponding flow ), leading to coherent acceleration of the entire system [28,29,30]. This mass force can result from changes in the environment’s structure or contributions from changes in the internal structure of the system itself, which occur under the influence of mass forces and coherent acceleration. The properties of nonlinearity, nonlocality, and nonextensiveness [34,35,36,37] are closely related to the thermodynamic properties of coherently correlated systems (see [43,44,45,46]).
The properties of nonlinearity, nonlocality, and nonextensiveness (coherent parameter q) [34] are closely related to the thermodynamic properties of coherently correlated systems (see [47,48]), anisotropy, and the properties of thin films [49]. In [50], the role of local nonequilibrium of electron states in the processes of increasing the temperature of the superconducting transition is shown. The non-equilibrium phase transition of evolution to a non-equilibrium quasi-stationary state is accompanied by a certain dependence between the coherence parameter , the order parameter and flows in its phase space.
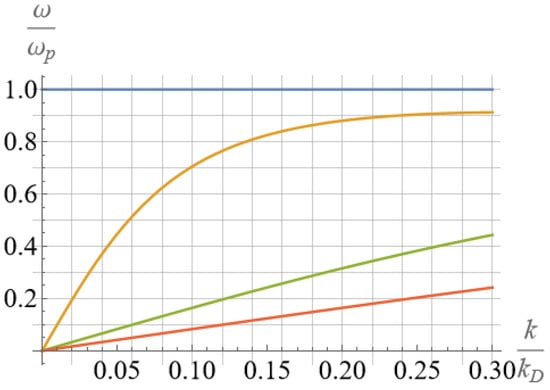
In Section 4 of this study, the obtained relationships for non-equilibrium states and particle distributions are utilized to estimate the dielectric permeability of the non-equilibrium medium and the parameters of acoustic modes in these non-equilibrium states. At the end of the section, using the “jelly” model [51] and Ginzburg’s relations for the temperature of the superconducting transition [52], temperature estimations for the superconducting transition in these non-equilibrium states are derived.
2. On the Vlasov Kinetic Equations in Systems with Varying Internal Structure
The body forces and coherent accelerations of all orders cause the non-locality and evolution of the system (changes in its internal structure, see, for example, [15,16]). The geometric representation of particle dynamics leads to the general Vlasov kinetic equation for the distribution function , which has the form of a continuity equation in Cartan space:
The divergent character of the kinetic equation corresponds to the free motion of particles in this complete space. From the kinetic Equation (1) for the distribution function in the full space, by successive averaging over higher-order accelerations, one can obtain a set of averaged physical quantities:
describing a reduced description, a chain of linking equations containing several divergent terms that correspond to the number of tangent bundles over which no averaging has been performed. Together with the sequence of kinetic equations that correspond to the hierarchy of averaging, the dynamic equations for the main average kinematic quantities (the corresponding equations of motion) also follow [10,16].
Below, we present the Vlasov kinetic equations [16,17] considering the variation of the internal structure during evolution [28] at the first three main levels of the averaging hierarchy.
2.1. Averaging over all Tangent Spaces, Averaging over Speeds and accelerations of All Orders
With this averaging, we obtain the continuity equation for the density and the equation of motion in a dissipative medium:
Vlasov called the resulting particle dynamics equation the Aristotelian equation of motion—the average speed when moving in a dissipative medium is proportional to the force.
2.2. Averaging over Tangent Spaces of Accelerations of all Orders
In this case, we obtain the Vlasov kinetic equation for the distribution function in the phase space (in terms of coordinates and impulses or velocities) and the averaged equations of dynamics, which coincide in inertial reference frames with Newton’s dynamic equations in the first tangent bundle:
This approximation is sufficient in inertial frames of reference, but in non-inertial frames of reference, Equation (4) must include evolutionary processes with a change in the internal structure of the system (entropy). In non-inertial systems, the left-hand side should contain the change in momentum, taking into account viscous dissipative losses when interacting with the medium and variations in bonds and internal structure (and, therefore, entropy) in the base space and the first tangent bundle takes the form . And the dynamics equation from (4) takes the form:
where is external mass force acting on the system, —effective self-consistent viscosity, and is the averaged self-consistent force of viscosity between particles and the medium, taking into account the entropy force arising due to the variation of inertia (see, for example, [18,19,20]). It can be seen that, under certain conditions, bond variations can make the effective self-consistent viscosity negative [53,54].
Let us now consider the kinetic equation from (4). The mass force initiating the evolution process creates an initial coherent acceleration for the subsystem in the coherence region with the scale: [39,40,41,42]. As a result, the subsystem becomes coherent and homogeneous within the region with the specified scale, and variations in the structure and binding energy of the system occur, contributing to the self-consistent viscous force.
We write the entropy forces that modify the Vlasov equation in the form of a collision integral in the divergent form:
The action of the mass entropy force on a system of particles and the acceleration of the system, which is inextricably linked with it, force the system to rebuild its internal structure and, thus, evolve in the tangent bundle of space-time in accordance with the variational principle of dynamic harmonization.
The kinetic Equation (5) for the particles included in the subsystem in the eight-dimensional space of the supporting elements can be represented in the covariant form:
Given that:
we write (6) by components:
Let us analyze the solutions of the kinetic equation in an important particular case, when the explicit contribution of the divergence into the kinetic equations can be ignored, and the covariant equation of quasi-stationary states takes the form:
This approximation is valid in two cases:
- when there are no external forces in the system and no flow in the phase space (this case corresponds to complete equilibrium in the system);
- when external forces do not act directly in the system, but the flow of energy, particles or entropy is constant in the phase space (this corresponds to a strong deviation from equilibrium).
Let us consider solutions of the kinetic Equation (7) isotropic in the space of velocities and stationary in laboratory time, i.e., Let’s pretend that:
We emphasize that this stationarity does not imply independence of proper time. In this approximation:
Separating the variables, we represent the distribution function in the form:
After these relations, from (8) follows the system of equations, which is exactly solved, and the solution can be expressed in terms of the generalized exponential [34]:
The dependence of the distribution function on energy and coherence index q is shown in Figure 1 and Figure 2.
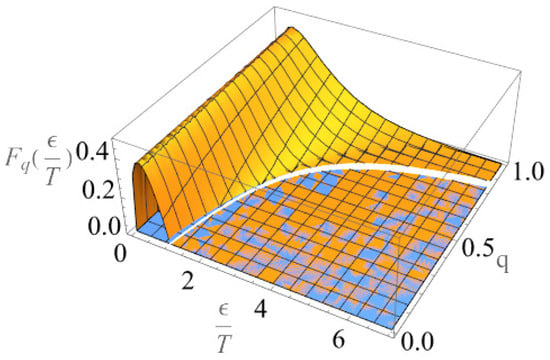
Figure 1.
Dependence of the distribution function on energy and coherence parameters . With increasing deviation from equilibrium, there is an increase in localization. (The function values are represented in one color, and the zero value is represented in blue. The surface rises above the zero value.)
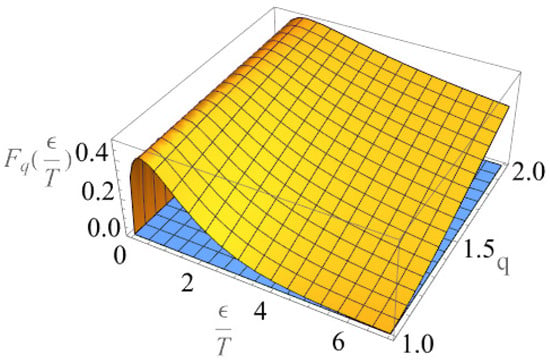
Figure 2.
Dependence of the distribution function on energy and coherence parameter . With increasing deviation from equilibrium, there is an increase in delocalization. (Non-zero function values are represented in a single color, and a zero value is represented in blue. The surface rises above the zero value.)
These solutions reflect that in the absence of an entropy flow (i.e., at ), a homogeneous equilibrium case is realized. The distribution function for velocities (or energies) passes into the Maxwell distribution function, the distribution function into the Boltzmann distribution, and the function becomes a constant. There is no difference between local and laboratory time. To the extent that entropy flows are present in the system (), the distribution functions over energies and coordinates change from an exponential dependence to a quasi-power one.
An analysis of the behavior of the solutions shows that for , the distribution is localized with an increase in the deviation from 1, and for , an increase in the deviation leads to an increase in the delocalization of the distribution function and with it an increase in the characteristic dispersion of physical quantities that depend on momenta and energies.
Exact solutions of the kinetic equations of a function with power asymptotic were studied in [24,25,26,27], and the thermodynamic properties of similar functions and states were obtained in many works [5,28,29,30,34,35,36,37]
An analysis of the exact solutions of the kinetic equations and thermodynamic functions in nonequilibrium states leads to the conclusion about the relationship between the coherence parameter and fluxes in the phase space in accordance with the relation [29,30]. In this case, the sign of the flow in the phase space determines the region and region . The coherence parameter also can be related to the order parameter using the relations:
2.3. Averaging over Tangent Spaces of Higher-Order Accelerations
With this averaging, we obtain the kinetic equation, taking into account the dynamics of the system in the base space and the first two tangent bundles:
In a non-inertial frame of reference, the equation of dynamics (13) for the average value of acceleration, considering the variation of inertia, takes the form:
Within the coherence scale, the system can be considered homogeneous with high accuracy, and the term in the kinetic equation can be neglected. In this case, of course, the main evolution now occurs in tangent bundles—spaces of velocities (energy space) and accelerations, which form a layered energy phase space and satisfy Equations (11) and (12). In Equation (12) is the external force averaged over the derivatives of accelerations above the first and acting on the system in the energy phase space with coordinates , and the corresponding value of the coherent velocity acceleration (averaged coherent value of the third derivative of the coordinate of the center of gravity of the excited system).
The value is the average viscosity force between the particles and the medium in the energy phase space. The viscous force for a system of charged particles is the force of radiative friction [55]:
In the case of harmonic excitation with a frequency, the radiative friction force can be represented as a viscous friction force in the velocity space (energy space):
Here we introduced the coefficient of friction and the characteristic time , i.e., the time it takes the light to travel through the effective radius of an electron. In accordance with the equations of motion (13), positive feedback arises, and the coherent acceleration grows exponentially when the threshold is exceeded (determined by the dispersion in the acceleration space and the temperature of the chaotic component of the dynamics of the system of particles and the medium). The equations of motion obtained from the Vlasov kinetic equations agree with the relations for fractal media obtained in [34].
When comparing the equation of dynamics with allowance for radiative friction and the equation for the evolution of a system under the action of a body force, one can see that the forces of radiative friction manifest themselves as entropy forces, which are determined by a change in some structure.
Coherent acceleration of a system of particles leads to the anisotropy of the system—its properties and distribution functions are different in the direction of coherent acceleration and on surfaces orthogonal to acceleration and provide qualitatively different thermodynamic properties.
5. Conclusions
The paper presents the Vlasov kinetic equations and the corresponding dynamic transfer equations after averaging over higher accelerations, considering the change in the internal structure and, consequently, the inertia of the system. The obtained exact solutions of the Vlasov equation, which take into account the variation in the structure of the system, are given in the form of non-extensive Tsallis distribution functions and are consistent with the exact solutions of the kinetic equations describing quasi-homogeneous systems with flows in the phase space, and the thermodynamic distributions, which are obtained together with the corresponding expressions for the Lagrange coefficients—nonequilibrium temperature and number of states depending on the order parameter and nonequilibrium coefficient for coherently correlated states.
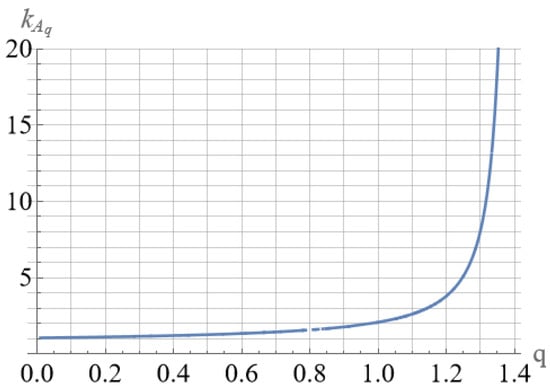
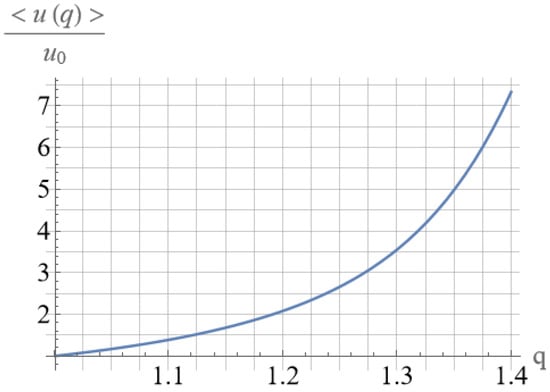
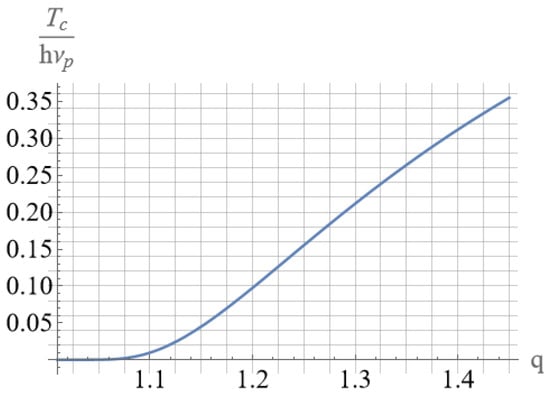
For the model distribution function, which reflects the order parameter in the system and its strong non-equilibrium, the phase transition temperature in the “jelly” model was estimated using V. Ginzburg’s functional relations. Using the thermodynamic relations obtained in the work, the dependence of the transition temperature on nonequilibrium parameters q is given, and it is shown that with an increase in the nonequilibrium parameter q, the phase transition temperature increases strongly and tends to the energy of the of electron plasma oscillations quantum under increasing at the nonequilibrium coherently correlated states.
Author Contributions
Conceptualization, S.P.K., R.I.E., V.E.N., A.M.O. and S.W.; methodology, S.P.K., R.I.E., V.E.N., A.M.O. and S.W.; software, S.P.K. and V.E.N. Novikov; validation, S.P.K., V.E.N. and A.M.O.; formal analysis, S.P.K., R.I.E., V.E.N., A.M.O. and S.W.; investigation, S.P.K., R.I.E., V.E.N., A.M.O. and S.W.; resources, S.P.K. and V.E.N.; data curation, S.P.K., V.E.N. and A.M.O.; writing—original draft preparation, S.P.K. and V.E.N.; writing-review and editing, S.P.K., R.I.E., V.E.N., A.M.O. and S.W.; visualization, S.P.K. and V.E.N.; supervision, S.P.K., V.E.N. and R.I.E.; project administration; S.P.K., R.I.E., V.E.N., A.M.O. and S.W.; funding acquisition, S.P.K., R.I.E., V.E.N., A.M.O. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
Calculations were performed using Latvian Super Cluster (LASC), located in the Center of Excellence at Institute of Solid State Physics, the University of Latvia, which is supported by European Union Horizon 2020 Framework Programme H2020-WIDESPREAD-01-2016-2017-Teaming. Phase two under Grant Agreement No. 739508, project CAMART.
Data Availability Statement
Not applicable.
Acknowledgments
S.P.K. acknowledges support by the National Academy of Sciences of Ukraine (Project No.0116U002067). S.P.K. thanks the Max-Planck-Institute for Chemical Physics of Solids (Dresden, Germany) for their support and hospitality during his visit.A.M.O. acknowledges Narodowe Centrum Nauki (NCN, Poland) Project No.2016/23/B/ST3/00839.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: Hoboken, NJ, USA, 1977. [Google Scholar]
- Liboff, R. Introduction to the Theory of Kinetic Equations; John Wiley & Sons: Hoboken, NJ, USA, 1969. [Google Scholar]
- Grad, H. Principles of the Kinetic Theory of Gases. In Handbuch der Physik XII; Flugge, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1958. [Google Scholar]
- Truesdell, C. Rational Thermodynamics; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fradkov, A. On the application of cybernetic methods in physics. Uspekhi Fiz. Nauk. 2005, 175, 113–138. [Google Scholar] [CrossRef]
- Binhi, V.N.; Savin, A.V. The effects of weak magnetic fields on biological systems: Physical aspects. Uspekhi Fiz. Nauk. 2003, 173, 265–300. [Google Scholar]
- Hide, R. A path of discovery in geo physical fluid dynamics. Astron. Geophys. 2010, 51, 4.16–4.23. [Google Scholar] [CrossRef][Green Version]
- Bogolubov, N.N. Problems of Dynamic Theory in Statistical Physics; Technical Information Service: Oak Ridge, TN, USA, 1960. [Google Scholar]
- Balescu, R. Equilibrium and Non-Equilibrium Statistical Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Cartan, E. La Methode du Repµere Mobile, la Theorie des Groupes Continus et les Espaces Generalizes; Esposes de Geometrie; Hermann: Paris, France, 1935; Volume 5. [Google Scholar]
- Sharpe, R.W. Differential Geometry, Cartan’s Generalization of Klein’s Erlangen Program; Springer: New York, NY, USA, 1997. [Google Scholar]
- Kobayashi, S.; Nomizu, K. Foundations of Differential Geometry; Wiley InterScience: Hoboken, NJ, USA, 1963; Volume 1. [Google Scholar]
- Penrose, R. The Road to Reality; Jonatan Cape: London, UK, 2004. [Google Scholar]
- Vlasov, A.A. The Theory of Many Particles; Gordon and Breach: New York, NY, USA, 1950. [Google Scholar]
- Vlasov, A.A. Statistical Distribution Functions; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Vlasov, A.A. Nonlocal Statistical Mechanics; Nauka: Moscow, Russia, 1978. [Google Scholar]
- Bell, J. Speakable and Unspeakable in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Maudlin, T. What Bell Did. J. Phys. A Math. Theor. 2014, 47, 424010. [Google Scholar]
- The Nobel Prize in Physics 4 October 2022. Available online: https://www.nobelprize.org/uploads/2022/10/press-physicsprize2022-2.pdf (accessed on 5 September 2023).
- Volterra, V. Theory of Functionals and of Integral and Integro-Differential Equations; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Samko, S.; Kilbas, A.A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Taylor & Francis: Abingdon-on-Thames, UK, 1993; ISBN 978-2-88124-864-1. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Adamenko, S.; Bogolubov, N.; Novikov, V.; Kruchinin, S. Self-organization and nonequilibrium structures in the phase space. Int. J. Mod. Phys. B 2008, 22, 2025–2045. [Google Scholar]
- Kats, A.V.; Kontorovich, V.M.; Moiseev, S.S.; Novikov, V.E. Power solutions of the Boltzmann kinetic equation describing the distribution of particles with flows over the spectrum. Pis’ma Zh. Eksp. Teor. Fiz. 1975, 21, 13–16. [Google Scholar]
- Karas, V.; Novikov, V.; Moiseev, S. Exact power solutions of kinetic equations in solid-state plasma. Zh. Eksp. Teor. Fiz. 1976, 71, 744. [Google Scholar]
- Kononenko, S.I.; Balebanov, V.; Zhurenko, V.; Kalantaryan, O.; Karas, V.I.; Muratov, V.; Kolesnic, V.; Novikov, V.E.; Potapenko, I.; Sagdeev, R.Z.; et al. Nonequilibrium distribution functions of electrons in the plasma of a semiconductor irradiated by fast ions. Plasma Phys. Rep. 2004, 30, 671–686. [Google Scholar] [CrossRef]
- Adamenko, S.; Selleri, F.; Merwe, A. Controlled Nucleosynthesis. Breakthroughs Experiment and Theory; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Adamenko, S.; Bolotov, V.; Novikov, V. Control of multiscale systems with constraints, Interdisciplinary Studies of Complex Systems. Basic principles of the concept of evolution of systems with varying constraints. Interdiscip. Stud. Complex Syst. Dragomanov Natl. Pedagog. Univ. 2012, 1, 33–77. [Google Scholar]
- Adamenko, S.; Bolotov, V.; Novikov, V. Control of multiscale systems with constraints. Geometrodynamics of the evolution of systems with varying constraints. Interdiscip. Stud. Complex Syst. 2013, 2, 60–125. [Google Scholar]
- Kruchinin, S.P.; Klepikov, V.F.; Novikov, V.E. Nonlinear current oscillations in the fractal Josephson junction. Mater. Sci. 2005, 23, 1003–1013. [Google Scholar]
- Klepikov, V.; Kruchinin, S.; Novikov, V.; Sotnikov, A. Composite materials with radioactive inclusions as artificial radio absorbing covering. Rev. Adv. Mater. Sci. 2006, 12, 127–132. [Google Scholar]
- Klepikov, V.; Novikov, V.; Kruchinin, S. Dynamics of charged particles in fractal media. Mod. Phys. Lett. B 2020, 34, 2040066. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive thermostatics: Brief review and comments. Phys. A Stat. Mech. Its Appl. 1995, 221, 277–290. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Abe, S.; Okamoto, Y. (Eds.) Nonextensive Statistical Mechanics and Its Application; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to Nonextensive Statistical Mechanics and Thermodynamics. arXiv 2003, arXiv:cond-mat/0309093. [Google Scholar]
- Misner, C.W.; Thorn, K.S.; Wheeler, J.A. Gravity; W. H. Freeman and Company: New York, NY, USA, 1973; Volume 1. [Google Scholar]
- Podosenov, S.A. The structure of the space-time and the fields of bound charges. Izv. Vuzov Ser. Fiz. 1997, 10, 63–74. [Google Scholar] [CrossRef]
- Podosenov, S.A.; Potapov, A.A.; Sokolov, A.A. Impulsive Electrodynamics of Wideband Radiosystems and the Fields of Bound Structures; Radiotekhnika: Moscow, Russia, 2003. [Google Scholar]
- Kinnersley, W. Field of an Arbitrary Accelerating Point Mass. Phys. Rev. 1969, 186, 1335. [Google Scholar] [CrossRef]
- Marakhtanov, M.K.; Okunev, V.S. Influence of mechanical collision macroobjects on nuclear-physical properties of components of their nuclides. Her. Bauman Mosc. State Tech. Univ. Nat. Sci. 2016, 1, 61–75. [Google Scholar] [CrossRef]
- Dodonov, V.; Man’ko, V. Generalizations of the uncertainty relation in quantum mechanics. Tr. FIAN 1987, 183, 5–70. [Google Scholar]
- Srodinger, E. About Heisenberg Uncertainty Relation. Ber. Kgl. Akad. Wiss. Berlin 1930, 24, 296. [Google Scholar]
- Robertson, H.P. A general formulation of the uncertainty principle and its classical interpretation. Phys. Rev. 1930, A35, 667. [Google Scholar]
- Jammer, M. The Conceptual Development of Quantum Mechanics; McGraw Hill: New York, NY, USA, 1966. [Google Scholar]
- Adamenko, S.V.; Vysotsky, V.I. Correlated states of interacting particles and the problem of transparency of the Coulomb barrier at low energy in nonstationary systems. Zh. Eksp. Teor. Fiz. 2010, 80, 23–31. [Google Scholar]
- Adamenko, S.; Vysotsky, V. Peculiarities of formation and application of correlated states in non.stationary systems at low energy of interacting particles. Zh. Eksp. Teor. Fiz. 2012, 141, 276–287. [Google Scholar]
- Kuchma, A.; Sverdlov, V. Quantum Acoustic Waves in Thin Semiconductor Films. FTP 1986, 20, 407–412. [Google Scholar]
- Karas, V.I.; Moiseyev, S.S.; Novikov, V.E.; Seminozhenko, V.P. The Role of Energy Locally Nonequilibrium Distributions of Electronic Excitations in Raising the Tc. Low Temp. Phys. 1977, 3, 695–704. [Google Scholar]
- Kruchinin, S. Modern aspect of superconductivity: Theory of superconductivity. World Sci. 2021, 52, 308. [Google Scholar]
- Ginzburg, V.L.; Kirzhnitsa, D.A. (Eds.) Problems of High-Temperature Superconductivity; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Starr, V. Physics of Negative Viscosity Phenomena; McGraw Hill: New York, NY, USA, 1968. [Google Scholar]
- Marchetti, M.; Ramaswamy, S.; Liverpool, T. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef]
- Rohrlich, F. The dynamics of a charged sphere and the electron. Am. J. Phys. 1997, 65, 1051–1056. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kirzhnits, D.A.; Lozovik, Y.E.; Shpatakovskaya, G.V. Statistical model of matter. Sov. Phys.-Usp. 1975, 18, 649–672. [Google Scholar] [CrossRef]
- Abramovits, M.; Stigan, I. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; National Bureau of Standards: Gaithersburg, MD, USA, 1964. [Google Scholar]
- Bateman, H. Higher Transcendental Functions; McGraw Hill: New York, NY, USA, 1953; Volume 1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).