Plane Cascade Aerodynamic Performance Prediction Based on Metric Learning for Multi-Output Gaussian Process Regression

Abstract

Multi-output Gaussian process regression measures the similarity between samples based on Euclidean distance and assigns the same weight to each feature. However, there are significant differences in the aerodynamic performance of plane cascades composed of symmetric and asymmetric blade shapes, and there are also significant differences between the geometry of the plane cascades formed by different blade shapes and the experimental working conditions. There are large differences in geometric and working condition parameters in the features, which makes it difficult to accurately measure the similarity between different samples when there are fewer samples. For this problem, a metric learning for the multi-output Gaussian process regression method (ML_MOGPR) for aerodynamic performance prediction of the plane cascade is proposed. It shares parameters between multiple output Gaussian distributions during training and measures the similarity between input samples in a new embedding space to reduce bias and improve overall prediction accuracy. For the analysis of ML_MOGPR prediction results, the overall prediction accuracy is significantly improved compared with multi-output Gaussian process regression (MOGPR), backpropagation neural network (BPNN), and multi-task learning neural network (MTLNN). The experimental results show that ML_MOGPR is effective in predicting the performance of the plane cascade, and it can quickly and accurately make a preliminary estimate of the aerodynamic performance and meet the performance parameter estimation accuracy requirements in the early stage.

1. Introduction

The blade shape in an aero-engine compressor is usually either symmetric or asymmetric, and the traditional symmetric blade shapes include the NACA series. As shown in Figure 1, the plane cascade consists of either a symmetrical shape or an asymmetrical blade shape. In order to obtain the advantages and disadvantages of symmetric or asymmetric blade shapes, plane cascades are usually used for testing. The aerodynamic coefficients of the plane cascade can reflect the pros and cons of symmetric and asymmetric blade shapes in a compressor, which in turn determines the performance of the compressor. As the core component of the aero-engine, the compressor can directly affect the aero-engine parameters, such as thrust-to-weight ratio, air flow rate, and efficiency. The geometry structure and test method of the plane cascade test piece determine the importance of the axial velocity density ratio (AVDR) parameter in determining the duality of the flow field and the validity of the data at the early stage of the test, and the value of AVDR is generally maintained at about 1 [1]. In subsonic and transonic tests, AVDR has a greater influence on the cascade loss coefficient (measurement of pressure, energy losses) and airflow turning angle [2].

The aerodynamic performance of traditional plane cascades can be obtained by theoretical analysis, computational fluid dynamics (CFD), and wind tunnel tests. Theoretical analysis is based on the laws of physics and deduced through the control equations, which will encounter great difficulties in dealing with complex problems, whereas wind tunnel tests have the problems of long test periods and high costs. CFD uses computer and the laws of physics to solve equations and has achieved excellent results in flow field prediction, control optimization, and turbulence modeling [3,4], but it consumes a lot of computing resources and takes a long time when performing complex calculations. In order to speed up the CFD time, machine learning and its combination have achieved good results in grid solving, geometric modeling, flow field prediction, and pressure distribution prediction [5,6,7,8,9]. However, limited by the computing resources required by CFD itself, the computing time and resource consumption of problems are still a major difficulty.

As artificial intelligence has matured, data-driven machine learning methods have been widely used in aerospace and other fields, such as target detection [10]. In research on aerodynamic performance prediction, commonly used machine learning methods include support vector regression (SVR) [11,12], Gaussian process regression (GPR) [13], Kriging [14,15], and neural networks [16,17,18,19,20,21,22]. For classical machine learning methods, Andrés-Pérez et al. [11] and Peng et al. [12] used SVR for airfoil and rocket aerodynamic performance prediction, respectively. Experimental results show that SVR has a stronger ability to fit nonlinear data. For GPR, the kernel has a decisive influence. Different kernels have different fitting abilities for data. Hu et al. [13] proposed a GPR based on automatic kernel construction, selecting different kernels according to the set construction rules and combining kernels, avoiding the empirical error caused by manual selection. Kriging, which is essentially similar to GPR, also has the same advantages in the task. Han et al. [14] and Zhao et al. [15] proposed a Kriging based on gradient and second-order forms, respectively.

The neural network methods studied in the field of aerodynamic coefficient prediction are BPNN [17,20,23], CNN [16,18,21,24,25,26], PINN, and MTLNN. BPNN is generally used for pure numerical data, and CNN is used for image data. Due to the multi-dimensional output characteristics of aerodynamic coefficients, Lin et al. [19] and Zhang et al. [27] utilized MTLNN to expand different aerodynamic coefficients and data forms into different tasks for the purpose of parameter sharing between different outputs and data forms and embedded physical knowledge to form PIMTLNN.

For the methods described above, the neural network and GPR have better prediction accuracy than the other methods, but the neural network model requires a large number of datasets to obtain excellent prediction results, and the plane cascade data collection has the problems of a long test period, high input cost, and low efficiency. GPR has great advantages over neural networks for small samples. However, the traditional single-output Gaussian process regression is limited by its own functional characteristics [28] and can only model each output dimension separately in the aerodynamic coefficient prediction task. For plane cascade data with the correlation between output dimensions, single-output Gaussian process regression not only takes a long time to model, but also cannot fit the correlation between multi-dimensional outputs. Multi-output Gaussian process regression can consider the correlation between multi-dimensional outputs, but there are two different types of input parameters in the plane cascade data, geometry and working conditions, and the traditional Euclidean distance-based sample similarity measure is difficult to improve the prediction accuracy and generalization performance of the model in the case of small samples.

For this problem, metric learning for multi-output Gaussian process regression is proposed. ML_MOGPR combines metric learning to learn a new embedding space of sample features, which can better distinguish different samples in the task of predicting the aerodynamic coefficients of plane cascade with fewer samples. In the new metric space, the input features corresponding to each output target can have better weight ratios.

The experimental results of the aerodynamic coefficient prediction of the plane cascade show that the multi-output model is better than the single-output model in overall prediction accuracy. ML_MOGPR further outperforms the rest of the multi-output models, backpropagation neural network (BPNN), multi-task neural network (MTLNN), and traditional MOGPR, in terms of overall prediction accuracy, which verifies the effectiveness of ML_MOGPR in the prediction of aerodynamic performance of a plane cascade, and it can provide an important reference for the preliminary estimation of aerodynamic coefficients of the plane cascade. The main symbols and abbreviations used in this paper are shown in

Table 1. Description of main variable symbols and abbreviations.

Symbol	Description	Symbol	Description
D	Training dataset	ℓ	Length-scale
${\epsilon }_i$	Noises	$\nu$	Kernel scale parameter
$k(x,x^{\prime })$	Covariance function	$\tau$	Distance calculation parameters
$B_q$	Positive semi-definite matrix	$a_{rq}^{(i,j)}$	Amplitude parameters
$X\in {\mathbf{R}}^{n\times d}$	Input features	${\phi }_q^{(i,j)}$	Displacement parameters
$Y\in {\mathbf{R}}^{n\times 1}$	Output targets	${\varphi }_q^{(i,j)}$	Delay parameters
$X_{*}\in {\mathbf{R}}^{n\times d}$	Test features	Q	Compunents
$A\in {\mathbf{R}}^{d\times d}$	Metrics matrix	$R_q$	Subcompoents
$\gamma$	Mounting angle/(${}^{\circ }$)	t	Raster distance/(mm)
$bax$	String length/(mm)	$Nob$	Number of blades
$\beta 1$	Inlet airflow angle/(${}^{\circ }$)	$Ma$	Mach number
$\alpha$	Angle attack/(${}^{\circ }$)	$\omega$	Loss coefficient
$\mathsf{\Omega }$	AVDR	${\sigma }_i^2$	Variance

.

2. Gaussian Process Regression (GPR)

2.1. Single-Output Gaussian Process Regression (SOGPR)

GPR is a non-parametric model that uses GP prior for regression analysis. According to the prior assumption and likelihood distribution, the posterior probability distribution of the predicted sample is obtained by the Bayesian rule.

Assuming a latent function $f\left(x\right)$ with a Gaussian prior, its mean $m\left(x\right)$ and covariance $k(x,x^{\prime })$ are as follows:

$$m\left(x\right)=E\left[f\right(x\left)\right]$$

(1)

$$k(x,x^{\prime })=E\left[(f\left(x\right)-m\left(x\right))(f\left(x^{\prime }\right)-m\left(x^{\prime }\right))\right]$$

(2)

The Gaussian process:

$$f\left(x\right)\sim GP(m\left(x\right),k(x,x^{\prime }))$$

(3)

In a regression task, suppose the training dataset $D=\{X,Y\}={\{x_i,y_i\}}_{i=1}^n$, $X\in {\mathbf{R}}^{n\times d}$ is the input matrix of $n\times d$, and $Y\in {\mathbf{R}}^{n\times 1}$ is the output vector of $n\times 1$; $x_i\in {\mathbf{R}}^d$ is the d-dimensional vector, and $y_i$ is the output scalar corresponding to $x_i$. There is generally noise in real datasets, i.e., $y_i=f\left(x_i\right)+{\epsilon }_i$, where ${\epsilon }_i$ is assumed to follow an independent and identically distributed Gaussian distribution with mean 0 and variance ${\sigma }_i^2$: ${\epsilon }_i\sim \mathcal{N}(0,{\sigma }_i^2)$. A GP is defined as a collection of random variables, for convenience of computation, assuming $m\left(x\right)=0$, then $Y\sim \mathcal{N}(0,K(X,X)+{\sigma }_n^{2}I)$, where I is the unit matrix, $K(X,X)$ is the covariance matrix of $N\times N$ with $K_{ij}=k(x_i,x_j)$. If the test set input is $X_{*}\in {\mathbf{R}}^{n\times d}$, the expected prediction value is $Y_{*}$, and since any finite number in a GP has a joint Gaussian distribution, the joint prior Gaussian distribution under the independent assumption is as follows:

$$\left[\begin{array}{c}Y\\ Y_{*}\end{array}\right]\sim \mathcal{N}\left(0,\left[\begin{array}{cc}K(X,X)+{\sigma }_n^{2}I& K(X,X_{*})\\ K(X_{*},X)& K(X_{*},K_{*})\end{array}\right]\right)$$

(4)

The joint posterior distribution can be obtained:

$$\begin{array}{c}{Y}_{*}|X_{*},Y,X\sim \mathcal{N}\left(\overline{Y_{*}},cov\left(Y_{*}\right)\right)\\ w.r.t\overline{Y_{*}}=K\left(X_{*},X\right){\left[K(X,X)+{\sigma }_n^{2}I\right]}^{-1}Y\\ cov\left(Y_{*}\right)=K(X_{*},X_{*})-K(X_{*},X){\left[K(X,X)+{\sigma }_n^{2}I\right]}^{-1}K(X,X_{*})\end{array}$$

(5)

The simplified expression $K(X,X)=K$, $K(X_{*},X_{*})=X_{*}$, where $\overline{Y_{*}}$ and $cov\left(Y_{*}\right)$ are the predicted value and covariance matrix of $Y_{*}$, respectively, and the covariance represents the uncertainty in the prediction results. If $x_{*}\in {\mathbf{R}}^{d\times 1}$ is a sample in test set $X_{*}$, then the predicted value $y_{*}={\sum }_{i=1}^n{\alpha }_{i}k(x_i,x_{*})$, $\mathit{\alpha }={\left(K+{\sigma }_n^2\right)}^{-1}Y$. As can be seen, GPR is mainly determined by the covariance, which is also called a kernel function. This kernel controls the covariance and similarity between any two samples.

Based on the SOGPR definition, the model itself is compatible with multiple inputs, but it is not capable of achieving multi-output target prediction, and it is not possible to jointly consider the aerodynamic performance coefficients of a multi-output plane cascade. The lack of correlation between the multiple output dimensions of the model affects the overall accuracy. Therefore, the multi-output Gaussian process regression model has advantages in this respect and can more accurately predict the aerodynamic performance coefficient of the multi-dimensional cascade.

2.2. Multi-Output Gaussian Process Regression (MOGPR)

The crucial aspect of Gaussian process regression is the kernel function selection and design. Earlier MOGPR considered each output individually as a Gaussian process with a Gaussian prior latent function and computed the covariance between different output dimensions by linearly combining the latent GP of each output dimension [29,30]. Assume $y\in {\mathbf{R}}^{1\times p}$ is a p-dimension output vector.

$$K=\sum _{q=1}^Q{B}_q\otimes k_q(x,x^{\prime })=\left[\begin{array}{ccc}{k}^{(1,1)}(x,x^{\prime })& \cdots & k^{(1,p)}(x,x^{\prime })\\ ⋮& \ddots & ⋮\\ k^{(p,1)}(x,x^{\prime })& \cdots & k^{(p,p)}(x,x^{\prime })\end{array}\right]$$

(6)

where Q is the number of components, and $B_q$ is a $p\times p$ positive semi-definite matrix of the multi-output kernel product, which represents the correlation between the outputs, also called the coregionalization matrix. The operator ⊗ is a Kronecker product, and $k^{(i,j)}$ represents the covariance of the ith and jth outputs.

The limited cross-covariance leads to a conflict with the ℓ of the SOGPR kernel, and there is no explanation for the correlation of multiple outputs. The kernel Fourier transform-based spectral mixture kernel (SM) [31] generates phase shifts through a linearly weighted combination of spectral Gaussian kernels (SG), which can give explicit covariance relations and solve the conflict problem.

$$k_{SG}\left(\tau \right)=exp\left(-\frac{\nu {\tau }^2}{2}\right)cos\left(\mu \tau \right)$$

(7)

$$k_{SM}\left(\tau \right)=\sum _{q=1}^Q{\omega }_q{k}_{SG}(\tau ;{\theta }_q)$$

(8)

where $\tau =\parallel x-x^{\prime }\parallel$, $\theta =\{\mu ,\nu \}$ is the kernel parameter, $\mu$ is the peak frequency, $\nu$ is the scale parameter, and ${\omega }_q$ is the relative contribution of each SG. The combination of SM and linear model of coregionalization (LMC) forms the basic spectral mixture multi-output model (SM_LMC), which can represent any combination of stationary kernels and better explain the relationship between different channels.

$$K_{SM\_LMC}(\tau ;\theta )=\sum _{q=1}^Q{B}_q{K}_{SG}(\tau ;{\theta }_q)$$

(9)

In addition, the SM-based extended multi-output kernels are cross-spectral mixture kernel (CSM) [32], multi-output spectral mixture kernel (MOSM) [33], and multi-output harmonizable spectral mixture (MOHSM) [34] proposed based on MOSM.

$$k_{CSM}\left(\tau \right)=\sum _{q=1}^Q\sum _{r=1}^{R_q}\sqrt{a_{rq}^{(i,j)}}exp\left(-\frac{{\nu }_q{\tau }^2}{2}\right)cos\left({\mu }_q+{\phi }_{rq}^{(i,j)}\right)$$

(10)

$$\begin{array}{cc}\hfill k_{MOSM}\left(\tau \right)& \hfill =\sum _{q=1}^Q{a}_q^{(i,j)}exp\left(-\frac{{\nu }_q^{(i,j)}{∥\tau +{\varphi }_q^{(i,j)}∥}^2}{2}\right)\times \hfill \\ \hfill & \hfill cos\left({\left(\tau +{\varphi }_q^{(i,j)}\right)}^T{\mu }_q+{\phi }_q^{(i,j)}\right)\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill k_{MOHSM}\left(\tau \right)& \hfill =\sum _{p=1}^P\sum _{q=1}^Q{a}_q^{(i,j)}exp\left(-\frac{{\nu }_q{∥\tau +{\varphi }_q^{(i,j)}∥}^2}{2}\right)\times \hfill \\ \hfill & \hfill cos\left({\left(\tau +{\varphi }_q^{(i,j)}\right)}^T{\mu }_q+{\phi }_q^{(i,j)}\right)\times \hfill \\ \hfill & \hfill exp\left(-\frac{l_p^{2(i,j)}{∥\overline{\tau }-x_p∥}^2}{2}\right)\hfill \end{array}$$

(12)

where $a_{rq}^{(i,j)}$ and ${\phi }_q^{(i,j)}$ are amplitude and displacement parameters; $R_q$ is the number of subcomponents; ${\varphi }_q^{(i,j)}$ are the delay parameters; $\overline{\tau }=\parallel x+x^{\prime }\parallel$, P is the input displacement number, $x_p$ is the input component, and l represents the length scale parameter. The SM extension-based method makes MOGPR smoother and is able to do joint consideration of the multidimensional aerodynamic coefficients of the plane cascade, which makes the model more generalizable.

3. Metric Learning for MOGPR

Metric learning has been shown to have significant benefits in areas such as image classification [35,36,37] and regression prediction, as it is able to measure sample similarity from different perspectives in a new embedding space and shows great benefits with fewer samples. In the traditional multi-output Gaussian process regression, the sample similarity calculation form is $\parallel x-x^{\prime }\parallel$, which gives the same weight to the input features. The input features of plane cascade data include two different types of parameters, geometry and working conditions, and the degree of influence on the aerodynamic coefficient has non-point-to-point characteristics.

As shown in Figure 2, the correlation strength between the plane cascade data features and coefficients is different. For example, the correlation between the geometrical parameter raster distance (t) and the aerodynamic coefficient $\mathsf{\Omega }$ is −0.07, whereas the correlation between the working condition parameter inlet airflow angle ($\beta 1$) and $\mathsf{\Omega }$ is −0.85. It is evident that there is a large difference between the influence of geometric and working condition parameters on the aerodynamic coefficients.

In the case of small samples, the generalization ability of the model will be reduced. Inspired by [38,39], the input features are embedded into a new space, denoted as: $x⟶Ax$, where $x\in {\mathbf{R}}^{d\times 1}$, then $A\in {\mathbf{R}}^{d\times d}$. The new distance metric formula is as follows:

$$d(x-x^{\prime })={∥A(x-x^{\prime })∥}^2$$

(13)

The model learns this new matrix by which to linearly project the original sample space. This new matrix is able to assign different weight ratios to the sample features based on the output coefficients, reducing the influence of uncorrelated features on the resulting predicted coefficients. In addition, different output coefficients have different focused features (i.e., the same input features of different output coefficients have different weights in single output modeling) in order to maintain different ratios of feature weights while further fitting the correlation between multiple output coefficients. Reference [40] has an embedding matrix A with the following form in the multi-output Gaussian kernel:

$$A^{i,j}=A^i·A^j$$

(14)

where $(·)$ is the matrix matmul product, and $i,j$ denote the output dimensions. Equivalent to $A^i,A^j$ is the subembedding matrix about the ith and jth dimensional output coefficients, and $A^{(i,j)}$ is the joint matrix.

As MOSM and MOHSM are the better multi-output Gaussian kernel functions in the current study, these two kernel functions are explored in this paper, and their functional forms based on metric learning are as follows:

$$\begin{array}{ll}{k}_{ML\_MOSM}(x,x^{\prime })\hfill & =\sum _{q=1}^Q{a}_q^{(i,j)}exp\left(-\frac{{\nu }_q^{(i,j)}{∥\beta ∥}^2}{2}\right)\times \hfill \\ \hfill & cos\left({\beta }^T{\mu }_q+{\phi }_q^{(i,j)}\right)\hfill \end{array}$$

(15)

$$\begin{array}{ll}{k}_{ML\_MOHSM}(x,x^{\prime })\hfill & =\sum _{p=1}^P\sum _{q=1}^{Q_p}{a}_q^{(i,j)}exp\left(-\frac{{\nu }_q^{(i,j)}{∥\beta ∥}^2}{2}\right)\times \hfill \\ \hfill & cos\left({\beta }^T{\mu }_q+{\phi }_q^{(i,j)}\right)\times \hfill \\ \hfill & exp\left(-\frac{l_p^{2(i,j)}{∥\overline{\tau }-x_p∥}^2}{2}\right)\hfill \end{array}$$

(16)

where $\beta =A_q^{(i,j)}(x-x^{\prime })+{\varphi }_q^{(i,j)}$. ML_MOSM and ML_MOHSM introduce new embedding matrices and learn new feature weight ratios while inheriting the multi-output form of the original kernel function. They not only consider the differences between the output targets, but also make the parameters of the measurement matrices of different output targets shared, which make them more generalizable. In plane cascade data with smaller samples, the model can be enhanced to assign weights to parameters with large differences, and similarity measures between different samples can be implemented in a more reasonable space.

4. Experiments and Analysis

The plane cascade test data used were obtained from real wind tunnel test data from a research institute. The data included plane cascades with symmetric and asymmetric blade compositions, which have varying degrees of difficulty in predicting aerodynamic coefficients. In addition, the complexity and high cost of the experimental process resulted in a complex and sparse dataset. Finally, after data cleaning, five groups of plane cascades totaling 310 samples were selected for the experiment. The input features include four geometric and three working condition parameters, and the output coefficients are cascade loss coefficient ($\omega$) and AVDR ($\mathsf{\Omega }$). The main geometric differences between the five datasets are shown in

Table 2. Differences of geometric parameters of five sets.

Num	Mounting Angle/(°)	Raster Distance/mm	Number of Blades	String Length/mm
1	63.2	43.35	9	70.32
2	58.29	48	8	79.18
3	40.86	50	10	64
4	76.67	48.05	6	51.08
5	76.9	35.44	11	78.11

.

To explore the performance of ML_MOGPR compared with other models in the case of small plane cascade samples, 200, 250, and 300 samples were randomly selected for the experiment. In addition, to make up for the differences caused by the random division of data and ensure the stability of the model as much as possible, each model performs ten experiments in each set of data to take the average value. The training, verification, and test set are randomly divided into 8:1:1. The regression evaluation metrics are RMSE and MAE, and the optimal values are marked in bold black.

$$\begin{array}{c}\hfill RMSE=\frac{1}{n}\sum _{i=1}^n\sqrt{{\left(e(x_i;\theta )-y_i\right)}^2}\end{array}$$

(17)

$$\begin{array}{c}\hfill MAE=\frac{1}{n}\sum _{i=1}^n\left|e(x_i;\theta )-y_i\right|\end{array}$$

(18)

Since ML_MOGPR is an innovation based on MOSM and MOHSM, in the field of data-driven prediction of aerodynamic coefficients, the neural networks mainly used for pure numerical data are backpropagation neural network (BPNN) and multi-task learning neural network (MTLNN), and the other single-output models are mainly SOGPR and SVR. Therefore, the comparative models are MOSM, MOHSM, BPNN, MTLNN, SOGPR, and SVR.

Neural networks have different network structures based on the data and loss function. Specific neural networks are described below:

(1) The form of the data in this paper is similar to [19]. The MTLNN model adopts its network structure, but the physical knowledge of the plane cascade data is implicit, the embedded physical knowledge module is not used, and only the multi-task network part is used. The task layer is changed to two layers according to the two-dimensional output characteristics of the data in this paper.

(2) BPNN has different numbers of network layers and nodes according to the amount of data. In order to ensure the relative fairness of the comparison results, the BPNN network structure will be explored under three sets of data.

(3) Since the prediction of the aerodynamic coefficient of the plane cascade is a regression task, BPNN and MTLNN train the network under the two loss functions of mean square error (MSE) and mean square absolute error (MAE). Each neural network is trained with a mini_batch size of 30 and a network output dimension of 2.

The neural network uses the pytorch, and MOGPR, ML_MOGPR uses the MOGPTK [41]. The experiments were performed on a computer configured with an Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz, 3.19 GHz.

4.1. Neural Network Structure and Loss Function Exploration

4.1.1. BPNN Experiments

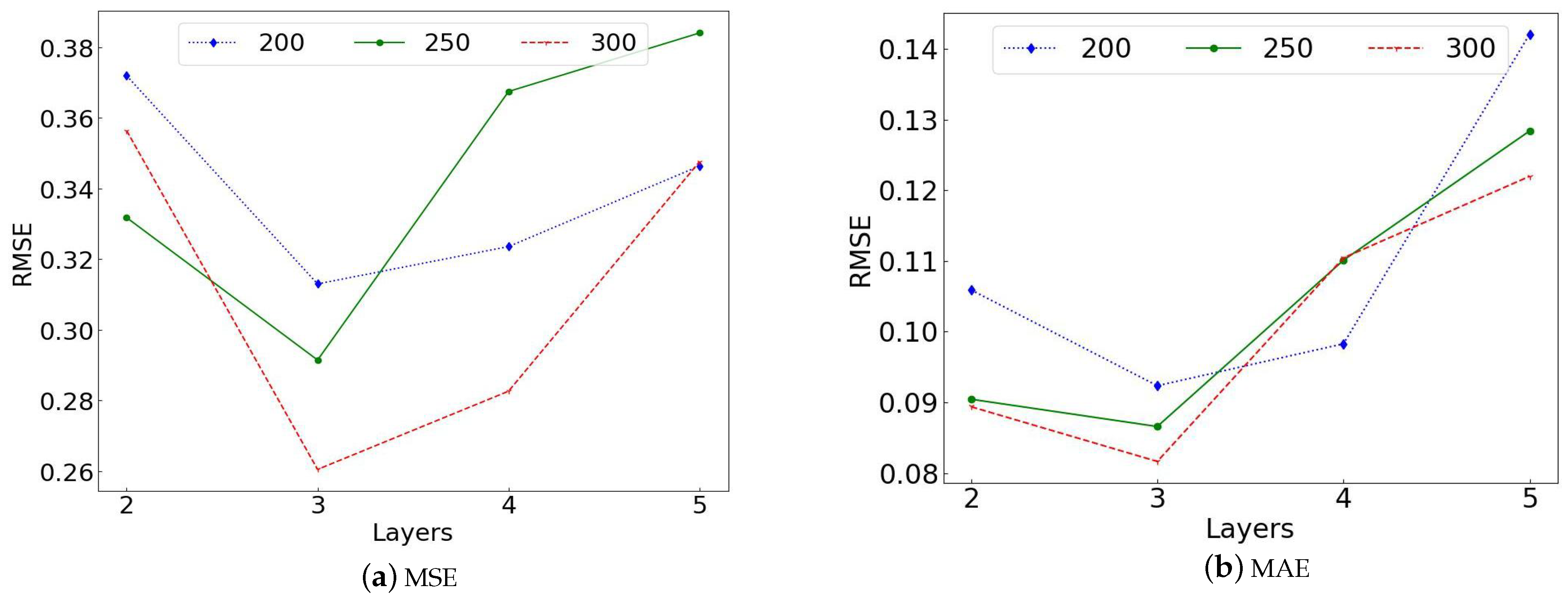
For the network structure exploration of BPNN, due to the small plane cascade data, in order to avoid network overfitting and underfitting, we first start with a network structure with two hidden layers and the number of nodes (8,4). Then, the number of network layers and the number of nodes in each layer are increased sequentially, and the loss functions are, respectively, chosen as MSE and MAE. Specific experiments were performed with MSE loss function and MAE loss function and sample sizes of 200, 250, and 300.

The experimental results shown in Figure 3 and Figure 4a,b represent the experimental results of BPNN trained under the MSE and MAE loss functions, respectively. The vertical coordinates in Figure 3 and Figure 4 indicate the RMSE prediction value, and the horizontal coordinates in Figure 3 denote the number of network layers (e.g., 2 indicates 2 hidden layers (8,4), 3 indicates 3 hidden layers (16,8,4), and incremented accordingly). 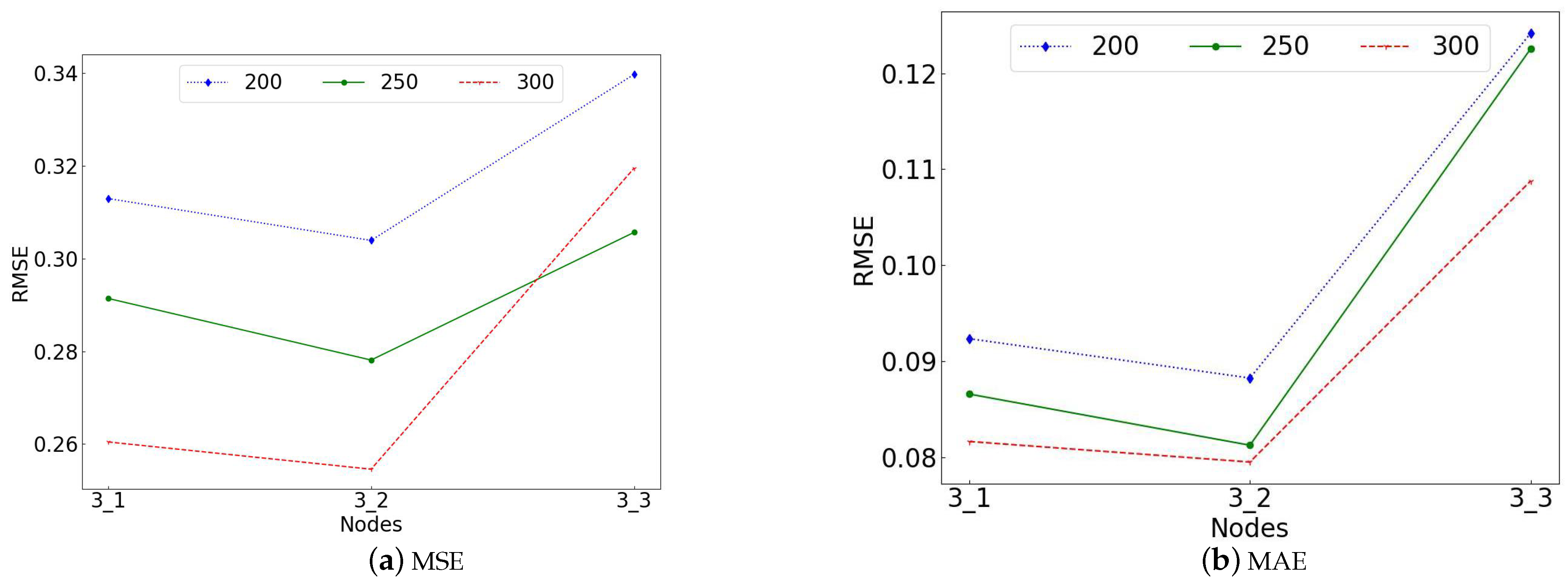The horizontal coordinates in Figure 4 indicate the number of nodes compared to the product of the initial three-layer nodes (16,8,4) in the three-layer hidden layer (e.g., 3_1 means (16,8,4) is the initial three-layer node number, 3_2 means multiplying the number of nodes in 1 by 2, and the number of nodes is (32,16,8)).

It can be seen from Figure 3 that, under the MSE and MAE, the number of hidden layers of the optimal BPNN network for the three groups of training samples is three and the network structure is (16,8,4); as shown in Figure 4, the optimal number of network nodes is (32,16,8). Refer to

Table 3. BPNN network structure and loss function exploration.

Loss Function	Number of Samples	Network Structure	RMSE
MSE	200	(8,4)	0.37188
		(16,8,4)	0.31296
		(32,16,8,4)	0.32353
		(64,32,16,8,4)	0.34634
		(32,16,8)	0.30392
		(64,32,16)	0.33974
	250	(8,4)	0.33172
		(16,8,4)	0.29141
		(32,16,8,4)	0.36742
		(64,32,16,8,4)	0.38399
		(32,16,8)	0.27811
		(64,32,16)	0.30556
	300	(8,4)	0.35633
		(16,8,4)	0.26045
		(32,16,8,4)	0.28259
		(64,32,16,8,4)	0.34756
		(32,16,8)	0.25457
		(64,32,16)	0.31949
MAE	200	(8,4)	0.10589
		(16,8,4)	0.09234
		(32,16,8,4)	0.09827
		(64,32,16,8,4)	0.14207
		(32,16,8)	0.08824
		(64,32,16)	0.12416
	250	(8,4)	0.09043
		(16,8,4)	0.08657
		(32,16,8,4)	0.11009
		(64,32,16,8,4)	0.12838
		(32,16,8)	0.08124
		(64,32,16)	0.12254
	300	(8,4)	0.08937
		(16,8,4)	0.08163
		(32,16,8,4)	0.11042
		(64,32,16,8,4)	0.12196
		(32,16,8)	0.07949
		(64,32,16)	0.10877

for the specific values in Figure 3 and Figure 4. It can be seen that, under the three sets of training data, the optimal values for the MSE are 0.30392, 0.27811, and 0.25457, respectively, and the optimal values for the MAE are 0.08824, 0.0814, and 0.07949. As the number of samples increases, the RMSE value is gradually decreasing regardless of the MSE or MAE. The overall prediction accuracy of MAE-guided BPNN training is far better than that of the MSE. Overall, for BPNN, the optimal network structure is (32,16,8) and the optimal loss function is MAE in the few-sample plane cascade dataset.

4.1.2. MTLNN Experiments

The output aerodynamic coefficients of the plane cascade data have a dimension of two and do not fit into the four task layers of the MTLNN network in [19]. The shared layer of the network structure remains unchanged, and the number of task layers is changed to two. The specific MTLNN process structure is shown in Figure 5, and the detailed number of network nodes is referred to in [19]. The experimental results under the MAE and MSE loss functions are shown in

Table 4. MTLNN loss function exploration.

Loss Function	Number of Samples	RMSE
MSE	200	0.63451
	250	0.51326
	300	0.40387
MAE	200	0.16859
	250	0.14789
	300	0.12659

. Under MSE and MAE, the RMSE value gradually decreases as the number of samples increases, and the prediction value of MAE training MTLNN is better than MSE.

From the training results of BPNN and MTLNN guided by MAE and MSE loss functions, the three training datasets show that for the plane cascade dataset, the MAE loss function outperforms the MSE loss function with a fewer number of samples. The reason may be that the loss coefficient of the cascade is small, usually around 0.05, while the value of the axial velocity density ratio is usually large, around 1. MSE will square the overall calculation, widening the gap between the two outputs, whereas MAE takes the absolute value directly, so under the MSE loss function, the training results of BPNN and MTLNN are inferior to the results from the MAE loss function.

4.2. Analysis of MOGPR Parameters

MOSM and MOHSM kernels have component combinations (Equations (11) and (12)), and different numbers of component combinations will affect the final prediction results. According to the properties of MOSM and MOHSM kernel functions and their corresponding literature, it can be known that the number of components and the output dimension are generally consistent with better experimental results.

Because the number of components Q determines the count of kernels and hyperparameters, the higher the number of parameters, the more difficult it is to optimize. From [33], Q is also called the rank of the decomposition, and the number of Q is usually less than or equal to the number of output dimensions, so the value of Q cannot be large. In this paper, the data output dimension is 2, and the number of components Q may be around 2 to make the model have an optimal value. The following will explore the specific influence of the number of components on the experimental results. The number of core components is selected as $Q=1,2,3,4,5$. The P parameter (Equation (16)) in MOHSM refers to [34], which has little influence on the final result and is fixed as $P=1$.

The experimental results of the specific number of MOGPR components are shown in Figure 6, where (a–d) represent the MOSM, MOHSM, ML_MOSM, and ML_MOHSM models, respectively, the ordinate represents the RMSE value, and the abscissa represents the number of components Q. Under the three groups of sample numbers, it can be seen from the subgraphs (a) and (c) that, for the MOSM and ML_MOSM models, the overall prediction progress shows an upward trend with the increase of Q, and the optimal value is around Q = 2. It can be seen from the sub-figures (b) and (d) that for the MOHSM and ML_MOHSM models, with the increase of Q, the overall RMSE value shows a downward trend. The optimal value of MOHSM is around Q = 4, and the value of ML_MOHSM is around Q = 3. ML_MOGPR has some volatility with Q on the MOHSM model, but the Q of ML_MOHSM is smaller, indicating that it has fewer parameters and is easier to optimize compared to the original MOHSM model. The specific experimental results of Figure 6 are shown in

Table 5. MOGPR component number analysis.

Number of Samples	Model	Components
		$\mathit{Q}\mathbf{=}\mathbf{1}$	$\mathit{Q}\mathbf{=}\mathbf{2}$	$\mathit{Q}\mathbf{=}\mathbf{3}$	$\mathit{Q}\mathbf{=}\mathbf{4}$	$\mathit{Q}\mathbf{=}\mathbf{5}$
200	MOSM	0.09031	0.09326	0.08927	0.09372	0.09688
	MOHSM	0.13041	0.28731	0.16916	0.12024	0.09843
	ML_MOSM	0.08766	0.08711	0.09436	0.08838	0.09224
	ML_MOHSM	0.09469	0.11852	0.08281	0.10147	0.08331
250	MOSM	0.09026	0.08724	0.09125	0.09081	0.09422
	MOHSM	0.09732	0.08811	0.12228	0.08904	0.08612
	ML_MOSM	0.08492	0.08081	0.08425	0.08932	0.08716
	ML_MOHSM	0.08721	0.09859	0.07804	0.08115	0.08103
300	MOSM	0.08519	0.08698	0.08959	0.09309	0.09124
	MOHSM	0.09401	0.08361	0.08665	0.07821	0.09062
	ML_MOSM	0.08356	0.07579	0.08394	0.09046	0.09662
	ML_MOHSM	0.08232	0.08362	0.07653	0.07729	0.07649

.

From Table 5, it can be seen that the experimental results of ML_MOSM and ML_MOHSM are better than their respective original models. The experimental results also illustrate that multi-output Gaussian process regression based on metric learning can learn a metric matrix that is more suitable for the input features of plane cascade data, avoiding the effect of large differences (As shown in Figure 2) in the features.

4.3. Analysis of Results

In the above Section 4.1 and Section 4.2, BPNN, MTLNN, and MOGPR have been analyzed under the RMSE evaluation metrics, respectively. For the prediction of the aerodynamic coefficient of the plane cascade, the optimal guidance function of BPNN and MTLNN networks is MAE, and the optimal network structure of BPNN is (32,16,8).

In the final comparison experiment, under three groups of sample sizes, MAE is used for the training loss function of BPNN and MTLNN, and (32,16,8) is used for the BPNN network structure. The number of MOSM, ML_MOSM, MOHSM, and ML_MOHSM components are, respectively, set to the component counts corresponding to the optimal RMSE values in Table 5.

Table 6. Comparison of RMSE values of different models.

Samples	SOGPR	SVR	BPNN	MTLNN	MOSM	MOHSM	ML_MOSM	ML_MOHSM
200	0.8676	5.2402	0.08824	0.16859	0.08927	0.09843	0.08711	0.08281
250	0.8289	4.6859	0.08124	0.14789	0.08724	0.08612	0.08081	0.07804
300	0.6487	4.2881	0.07949	0.12659	0.08519	0.07821	0.07579	0.07649

and

Table 7. Comparison of MAE values of different models.

Samples	SOGPR	SVR	BPNN	MTLNN	MOSM	MOHSM	ML_MOSM	ML_MOHSM
200	0.6241	0.8801	0.08976	0.12591	0.087561	0.06565	0.07405	0.04776
250	0.6101	0.7095	0.08876	0.10143	0.07246	0.05216	0.07126	0.04671
300	0.5736	0.6028	0.08347	0.09629	0.06635	0.05024	0.06284	0.04452

show the comparison of the best RMSE and MAE values of SOGPR (SOGPR uses a radial basis function kernel (RBF)), SVR, BPNN, MTLNN, MOSM, ML_MOSM, MOHSM, and ML_MOHSM, respectively.

As can be seen from Table 6 and Table 7, the multi-output model outperforms the single-output prediction of SOGPR and SVR in overall prediction, with SVR showing an overall higher RMSE value. The probable reason for this is that SVR’s prediction of nonlinear data has extremely noisy points and it is poorly adapted to the plane cascade data. In addition, RMSE is the root mean square error, which goes through the sum of squares, so it exhibits a larger RMSE value. It is known that the single-output model does not fit the relationship between the output dimensions well in multi-output tasks. As can be seen in Figure 2, there is some correlation between features and outputs. The single-output model lacks some ability to fit this multi-output regression prediction of aerodynamic coefficients.

In the case of fewer samples, MTLNN performs worse and BPNN predicts better. Traditional MOSM and MOHSM have slightly worse RMSE values than BPNN with fewer samples, but better MAE values than BPNN. ML_MOSM and ML_MOHSM are better than BPNN in terms of RMSE value and MAE value. The shortcomings of traditional multi-output Gaussian process regression based on the Euclidean distance measure of sample similarity make it difficult to accurately measure the relationship between different samples when there are large differences in the input features of plane cascade data.

Multi-output Gaussian process regression based on metric learning should learn a new sample embedding space. In addition, according to different output dimensions with joint embedding, ML_MOGPR is able to combine multi-dimensional embedding space based on the joint consideration of the relationship between multi-output coefficients and to assign different weights to each feature according to the relationship between the outputs, thus improving the generalization ability of the model under smaller samples. In addition, ML_MOGPR performs better in the task of predicting the aerodynamic coefficients of symmetric and asymmetric blades of plane cascade in the case of small samples compared to other models.

5. Conclusions

For the shortcomings of multi-output Gaussian process regression based on the Euclidean distance measure of sample similarity in the task of predicting the aerodynamic coefficients of the small-sample plane cascade, metric learning for multi-output Gaussian process regression is proposed.

There are experimental results that show that the single-output model is worse than the multi-output model. When ML_MOGPR is compared with its original MOSM and MOHSM models, ML_MOGPR experimental results are better. This indicates that ML_MOGPR should learn a new metric space in which to distinguish large difference features and assign different weight ratios and effectively improve the accuracy of MOGPR. Additionally, ML_MOGPR outperforms BPNN and MTLNN, which shows that the proposed method can be used for a few samples of plane cascade data.

ML_MOGPR can be applied to the preliminary estimation of plane cascade coefficients, provide a reference for the design of plane cascades, and speed up its design and test process. Further work in the future will incorporate more input features and output coefficients.