Impact of Delay on Stochastic Predator–Prey Models
Abstract
1. Introduction
A population is like a billiard ball: you get a lot of variability, but the variability is random, in all directions. Stephen Jay Gould: The Pattern of Life’s History. In [1].
2. The Prey–Predator Deterministic Model
- The trivial equilibrium: .
- The semi-trivial equilibrium:.
- The interior equilibrium: with
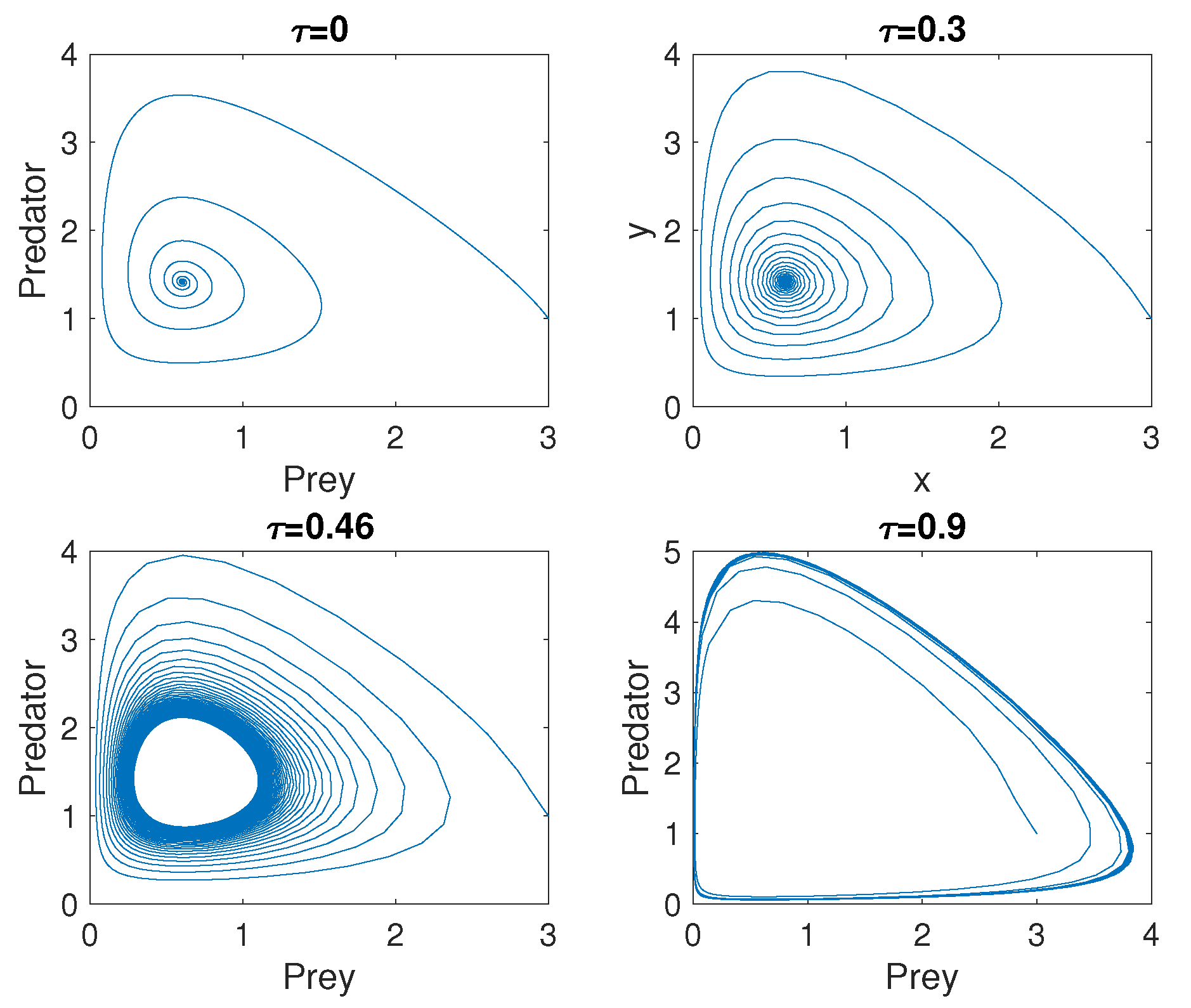
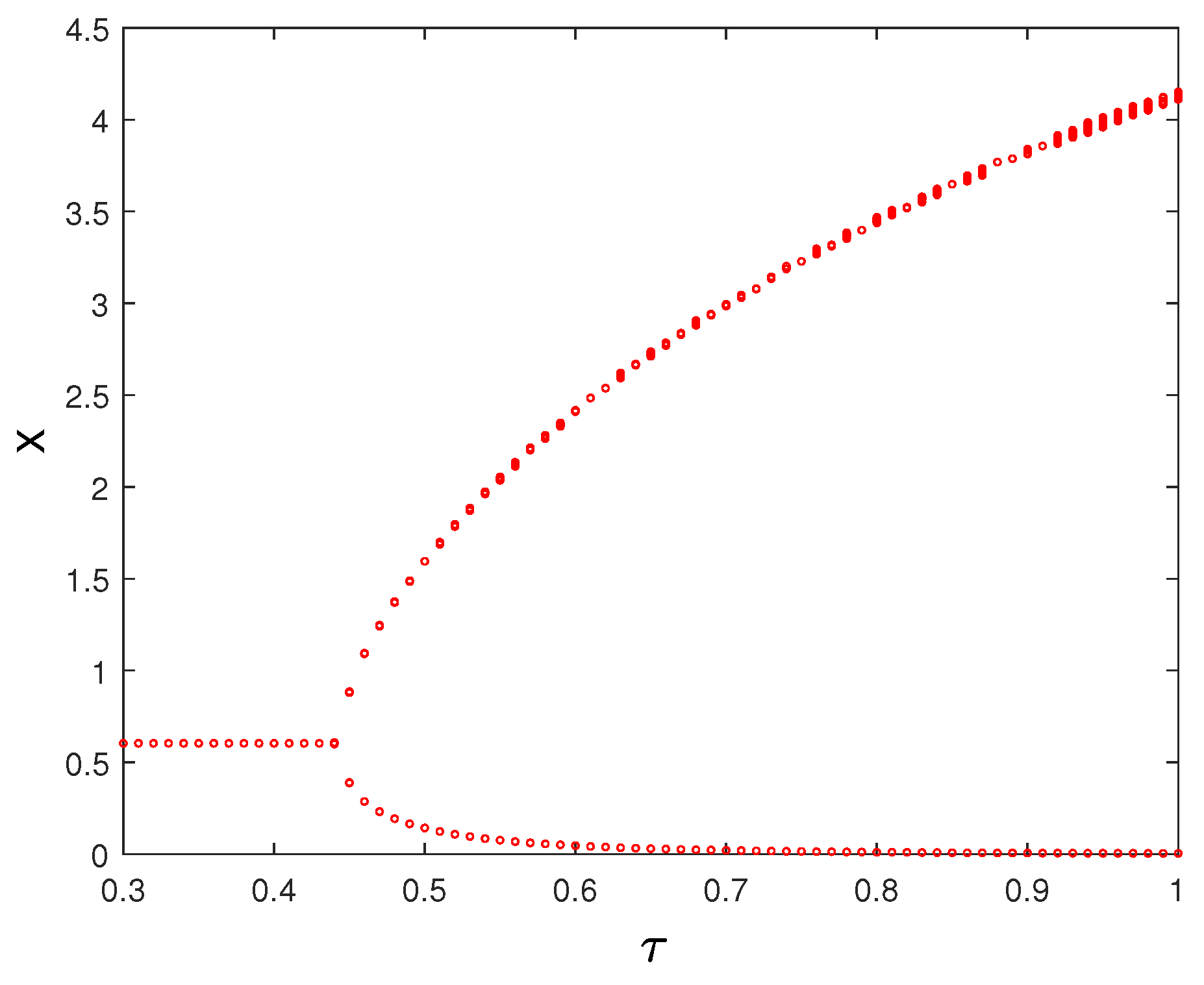
- Locally asymptotically stable when .
- If , there exist such that and the equilibrium is asymptotically stable, and unstable when .
3. Two Stochastic Models
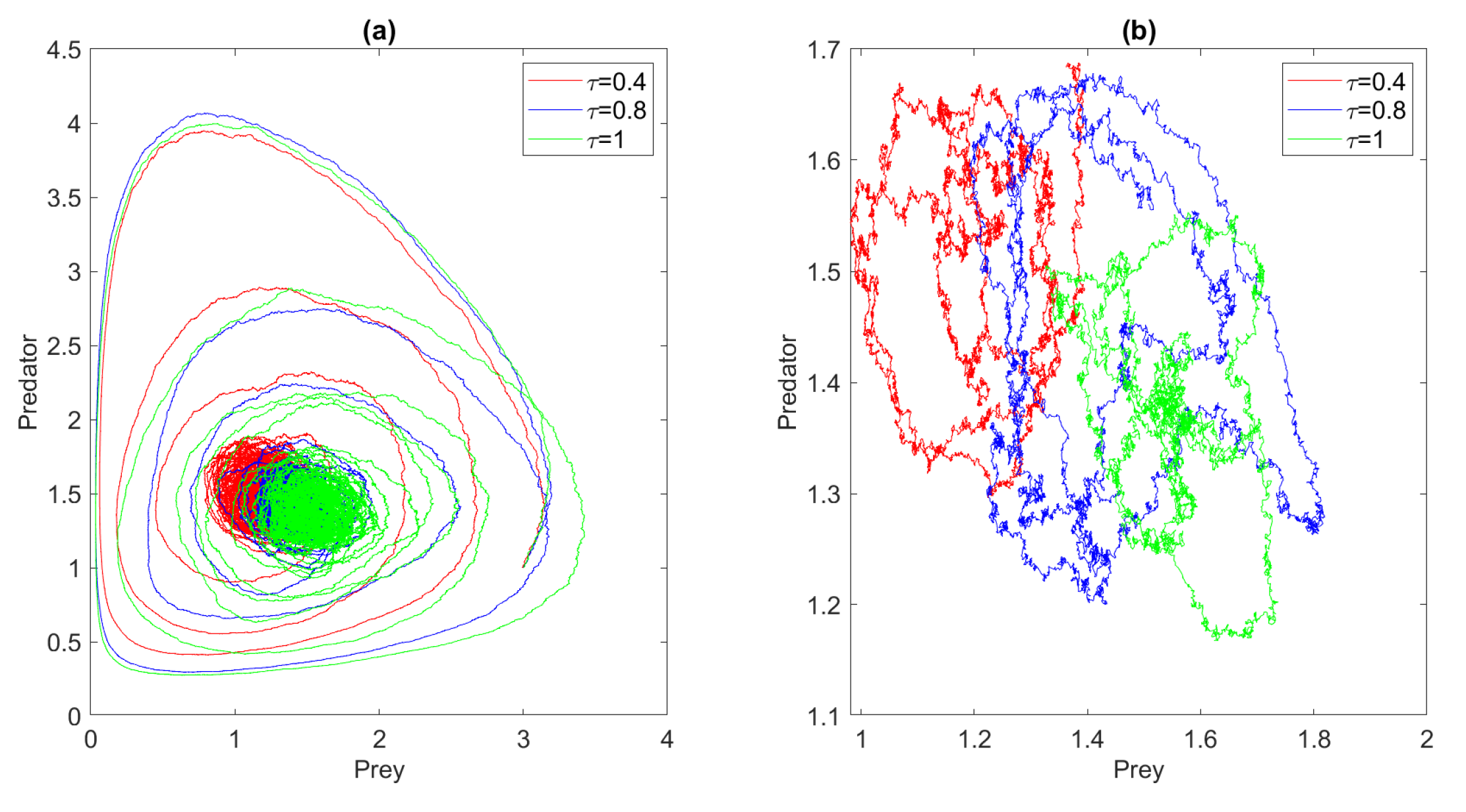
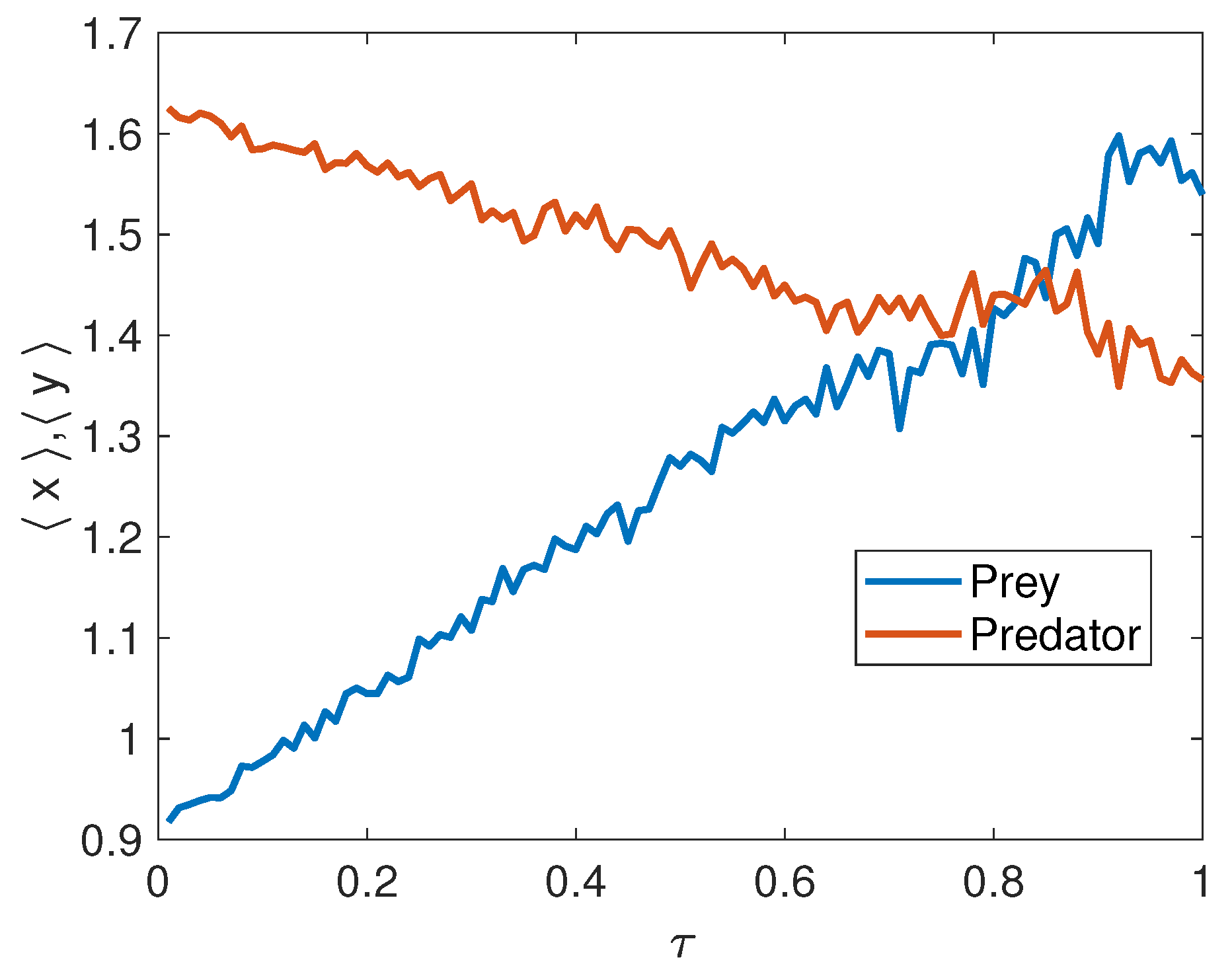
3.1. The First Stochastic Model (Model 1)
3.2. The Second Stochastic Model (Model 2)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brockman, J. The Third Culture: Beyond the Scientific Revolution; Simon and Shuster: New York, NY, USA, 1995. [Google Scholar]
- May, R. Stability and Complexity in Model Ecosystems; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Murray, J. Mathematical Biology I: An Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Simmons, G. Differential Equations with Applications and Historical Notes; McGraw-Hill International Editions: New York, NY, USA, 1972. [Google Scholar]
- Boyce, W.; Diprima, R. Elementary Differential Equations and Boundary Value Problems, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- de Vries, G.; Hillen, T.; Lewis, M.; Müller, J.; Schönfisch, B. A Course in Mathematical Biology; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Neal, D. Introduction to Population Biology; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sharin, M. Exploration of Methematical Modles in Biology with MATLAB; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Chou, C.; Friedman, A. Introduction to Mathematical Biology. Modeling, Analysis, and Simulations; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Allen, L. An Introduction to Stochastic Processes with Applications to Biology; Person Prentice Hall: London, UK, 2003. [Google Scholar]
- Allen, E. Modeling with Itô Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Chasnov, J. Mathematical Biolgy; The Hong Kong Univeristy of Science and Technology: Hong Kong, China, 2009. [Google Scholar]
- Pardoux, E. Probabilistic Models of Population Evolution Scaling Limits, Genealogies and Interactions; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Rihan, F. Delay Differential Equaitons and Applications to Biology; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Jeevan Kafle, I.M.; Jarad, F. Numerical Analysis of the Fractional-Order Nonlinear System of Volterra Integro-Differential Equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Freedman, H.I. Deterministic mathematical models in population ecology. Can. J. Stat. 1980, 10, 315. [Google Scholar]
- Shampine, L.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Hofmann, N.; Müller-Gronbach, T. A modified Milstein scheme for approximation of stochastic delay differential equations with constant time lag. J. Comput. Appl. Mathet. 2006, 197, 89–121. [Google Scholar] [CrossRef]
- Higham, D. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Kloeden, P.; Platen, E. Numerical Solution of Stochastic Differential Equations; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Higham, D.; Kloeden, E. An Introduction to the Numerical Simulation of Stochastic Differential Equations; SIAM: Philadelphia, PA, USA, 2021. [Google Scholar]
- de la Hoz, F.; Vadillo, F. A mean extinction-time estimate for a stochastic Lotka-Volterra predator-prey model. Appl. Math. Comput. 2012, 219, 170–179. [Google Scholar] [CrossRef]
- Vadillo, F. Comparing stochastic Lotka-Volterra predator-prey models. Appl. Math. Comput. 2019, 360, 181–189. [Google Scholar] [CrossRef]
- de la Hoz, F.; Doubova, A.; Vadillo, F. Persistence-time Estimation for some Stochastic SIS Epidemic Models. Discret. Countinous Dyn. Syst. Ser. B 2015, 20, 2933–2947. [Google Scholar] [CrossRef]
- Moujahid, A.; Vadillo, F. Modeling and Calibration for Stochastic Differential Models. Fractal Fract. 2022, 6, 707. [Google Scholar] [CrossRef]
- Engen, S.; Saether, B.E.; Moller, A.P. Stochastic Population Dynamics and Time to Extinction of a Declining Population of Barn Swallows. J. Anim. Ecol. 2001, 70, 789–797. [Google Scholar] [CrossRef]
| Change | Probability |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moujahid, A.; Vadillo, F. Impact of Delay on Stochastic Predator–Prey Models. Symmetry 2023, 15, 1244. https://doi.org/10.3390/sym15061244
Moujahid A, Vadillo F. Impact of Delay on Stochastic Predator–Prey Models. Symmetry. 2023; 15(6):1244. https://doi.org/10.3390/sym15061244
Chicago/Turabian StyleMoujahid, Abdelmalik, and Fernando Vadillo. 2023. "Impact of Delay on Stochastic Predator–Prey Models" Symmetry 15, no. 6: 1244. https://doi.org/10.3390/sym15061244
APA StyleMoujahid, A., & Vadillo, F. (2023). Impact of Delay on Stochastic Predator–Prey Models. Symmetry, 15(6), 1244. https://doi.org/10.3390/sym15061244





