Abstract
The simple leaves of deciduous forest trees in temperate zones have more irregular and asymmetric shapes than comparable non-deciduous leaves of trees in the tropics and subtropics. These shapes manifest as the irregular lobes and sinuses of temperate species of Quercus and Acer, as well as the greater bilateral asymmetry of Ulmaceae and Betulaceae, the serrated margins of many species, and the greater frequency of compound leaves generally (Fraxinus and Carya). These modifications may contribute to an early transition from laminar to turbulent flow, thus reducing the lateral movement of leaves when they drop during the onset of either winter or the dry season, or when they are simply shed for replacement. Such leaves are more likely to drop over the critical root zone than large, thin, broadly elliptic, and symmetric leaves. Here, we evaluate evidence for and against self-mulching as an explanation for differences in leaf shape between temperate and tropical forests. We suggest that the main evolutionary trade-offs are between competition for (1) light among tropical trees and temperate subcanopy trees, and (2) competition for water and soil nutrients among temperate canopy trees.
1. Introduction
The diversity of leaf shapes in forest angiosperms is poorly understood [1]. Photosynthetic efficiency is surely an important contributor [2], as is loss of water via evapotranspiration, but beyond that we know little. For example, what accounts for the deeply lobed leaves of temperate white and red oak (Quercus alba L. and Q. rubra L.)? Their tropical and subtropical counterparts (Q. copeyensis C. H. Mull and Q. elliptica Née) often have entire margins (smooth and without lobes) and elliptical shapes.
Bailey and Sinnott (p. 26, [3]) observed that among “woody plants, leaves and leaflets with entire margins are overwhelmingly predominant in tropical and subtropical environments … In cold-temperate regions, on the other hand, trees with entire leaves and leaflets are extremely infrequent.” They supported this observation with data on 24 tropical and subtropical floras and 20 temperate floras. In the tropics and subtropics, 81% of the tree species had entire leaves, while in the temperate zone the percentage of trees with entire leaves ranged from 2% in more northern floras to 34% in more southern floras. On the 26,000-acre campus of Berry College, where we have both worked, most temperate forest trees have lobed, composite, or serrated leaves, rather than entire leaves.
Bailey and Sinnott [3] suggested that there must be an adaptive environmental cause for the differences, but they provided few hypotheses. Leaf size and shape are thought to influence photosynthetic efficiency, water-use efficiency, transpirational cooling, heat dissipation, and water loss through transpiration [4]. Edwards et al. [5] suggested that winter bud-packing accounted for leaf shape differences. Givnish [6] and Givnish and Kriebel [7] examined a host of possible adaptations of leaf size and shape, including gas exchange, the economics of support and supply, hydraulics, vein geometry, leaf thickness, and rates of leaf expansion. Baker-Brosh and Peet [8] suggested that lobed and toothed leaves provided an early photosynthetic advantage.
In this paper, we suggest that leaf shape in temperate deciduous forests evolved in part to self-mulch the soil above the roots. Lobed leaves are hypothesized to drop over the critical root zone more often, preventing winter frost damage, retaining soil moisture during drought and seasonal dry spells, and nourishing co-adapted microbiota (mostly bacteria and fungi) that recycle lost nutrients back to the host tree through specialized mycorrhizae. We suggest that the difference between temperate and tropical and sub-tropical floras is driven largely by decomposition rates (greater in the tropics and subtropics [9,10,11]), as well as co-adapted soil bacteria, fungi, endophytes, and mycorrhizal fungi. The host specificity of mycorrhizae is greater in the temperate zone [12], and although mycorrhizae do not directly break down leaf litter, they thrive in soils conditioned by their host [13]. Moreover, arbuscular mycorrhizae provide carbon to saprophytes that decompose leaf litter [14]. Finally, this specialization may extend to soil fungi and bacteria that decompose leaves; the idea that leaves decompose more rapidly under their parent tree is called the Home-Field Advantage Hypothesis [15]. There are also situations, such as seasonal dry periods and fire, in which slow decomposition may be advantageous. These selection pressures should be stronger for trees in the canopy than for subcanopy trees, shrubs, and herbs, partly because the leaves have further to fall to the ground, but also because subcanopy plants compete more intensely for light than for water and nutrients.
Emarginate leaf shapes may influence where and how the leaves fall. Falling leaves that transition early from regimes of laminar to turbulent flow are more apt to fall over the critical root zone. To predict the behavior of various leaves, we estimate several parameters that influence the behaviors of falling objects in a fluid, including their aspect ratio, Froude number Fr, dimensionless moment of inertia I*, and Reynold’s number Re. We also examine the behaviors of falling leaves—lobed and unlobed, natural and artificial—in a controlled indoor environment.
1.1. Aerodynamics of Falling Leaves
The study of falling leaves, paper, and plates of various shapes has occupied physicists since James Clerk Maxwell [16]. These typically involve dropping a plate or card in a fluid (water, glycerol, or air) under controlled conditions. Early studies collapsed the fluid dynamics into two dimensions. Later studies expanded these to three dimensions.
According to Field [17], Belmonte et al. [18], and Andersen et al. [19,20], leaves or plates falling through a fluid flutter, tumble, gyrate, or fall in a chaotic fashion. Fluttering involves side-to-side oscillation with some lateral motion, while tumbling involves rotation around the long axis of the object, such as a leaf, and consequent sideways drift. Both motions can be collapsed into two dimensions, simplifying the analysis. In three dimensions, gyration can occur around a steep axis of descent, and a chaotic fall involves leaves falling end-over-end in steep descent, sometimes fluttering and sometimes tumbling or gyrating. Tumbling, as reported with falling plates, carries objects a longer distance from their drop point, and would be expected to do so with leaves [21]. In addition, we observed some leaves gliding in long, linear, gradual descent. Aeronautic gliders of human design are characterized by laminar flow over a wing surface. Andersen et al. [19,20] observed gliding at a low angle of attack, taking a plate a distance 15 times its width. In our initial observations, gliding carries leaves further than tumbling.
Of particular interest, Ishiguro and Miyaki [22] discovered that convex (elliptical) plates, similar to the entire, elliptical leaves of many trees, tended to drift further (lower angle of descent) than concave or rectangular plates. Their concave plates resembled the leaves of American holly (Ilex opaca) and some oaks. Like us, they also recognized that the shapes of leaves may cause leaves to drop over the root zone, being of some advantage to the tree.
Path instability is ubiquitous in nature, but can be minimized in a controlled laboratory setting with minimal air movement. For real leaves falling through air, there are several perturbations—wind, light breeze, and collision with other leaves or branches.
1.2. Hypothesized Advantages of Elliptical Leaves with Entire Margins
We argue that emarginate and lobed leaves provide an advantage in temperate forests, but we also need to explain why the entire leaf margins of elliptical leaves are dominant in the tropics and subtropics, as well as among subcanopy trees. Elliptical leaves may be more efficient photosynthetic structures, though there has been little research done to test this idea. A single circular leaf surface provides an efficient use of space and energy allotment when shading is not a problem. Circular leaves are found on floating leaves of aquatic macrophytes, such as members of the Nymphaeaceae. When shading becomes an issue in three-dimensional, above-ground space (or in a three-dimensional water column), elliptical leaves provide a compromise, providing an efficient photosynthetic surface while avoiding the shade of leaves higher in the canopy (or water column).
One advantage of elliptical leaves is that they minimize the shading of one another. This is a packing problem, a class of optimization problems. How many leaves can be packed into a three-dimensional space with minimal overlap? Ellipsoids with aspect ratios larger than δ = 1.732 can pack more densely than spheres [23,24,25]. By the same reasoning, ellipses in two dimensions with δ > 1.732 can pack more densely than a disk of δ = 1. An ellipse’s aspect ratio is the length of its main axis divided by the length of its minor axis. An ellipse with an aspect ratio of 1:1 (or 1.0) is a circle.
1.3. Testable Predictions
We list several testable predictions of our hypothesis. In this paper, we have been unable to critically test each prediction. Nevertheless, we try to address how these might be tested.
(1) Leaf lobes and serrated margins should influence how leaves fall. If this is not the case, then none of our other predictions matter. This can be tested by dropping both real leaves and artificial leaves and controlling, or accounting for, area and shape.
(2) Lobed leaves should fall closer to the source tree than leaves with entire margins.
(3) There should be a higher frequency of emarginate and lobed leaves in temperate forests than in tropical forests. This has already been studied by Baily and Sinnott [3], but the same has not been done for individual families or genera, or taking taxonomic contrasts into account.
(4) The taller species in a genus should have more deeply incised lobes and/or more asymmetric leaves than shorter species. Moreover, leaves near the top of the crown should be more deeply lobed than those lower in the crown (this has usually been ascribed to modulating transpiration rates and heat dissipation).
(5) The Reynold’s number, indicating transition from laminar to turbulent flow, should be higher for lobed leaves. This can be tested by analyzing the descent of falling leaves.
(6) Trees should drop most of their leaves over the critical root zone. This can be tested by estimating the density of leaves in concentric circles around trees that are isolated from other trees.
(7) Species in more arid (or seasonably dry) habitats should have either more deeply incised leaves or leaves with serrated margins, so as to build up a deeper layer of litter to retain soil moisture. This is testable by examining published floras.
(8) Riparian species should have more elliptical leaves. The reasoning here is that soil moisture is seldom limiting in these environments. Moreover, too much leaf litter may interfere with soil aeration. This is testable by examining published floras.
(9) Trees in humid climates should have more elliptical leaves. The reasoning here is that soil moisture is less of an issue when moisture is abundant.
(10) Because the distance from the leaf to the ground is so much shorter, and because competition for light overrides that for moisture and nutrients, subcanopy trees, shrubs, and herbs should have more elliptical leaves than canopy trees.
(11) Species that grow in monospecific groves (Populus tremuloides Michx. and Fagus grandifolia Ehrh. to some extent) should have more elliptical leaves. The reasoning here is that most neighboring trees are all of the same species, and may even be monoclonal.
(12) Thicker and heavier leaves, such as those of Magnolia grandiflora L. (southern magnolia), should be more likely to have entire margins. The density of such leaves makes it more likely that the leaves will fall within the root zone.
(13) Compound leaves should be the evolutionary endpoint of deep lobes. Among the maples, this includes Acer negundo L. (boxelder). Consequently, compound leaves (if dropped as a group) should fall within the root zone.
(14) Leaf lobes should increase the moment of inertia I* and Froude number Fr, promoting the transition from laminar to turbulent flow.
(15) Leaf shape should change in predictable ways along successional gradients, as competition for light becomes more pronounced, and the relative importance of competition for light, water, and soil nutrients changes.
2. Materials and Methods
2.1. Leaf Parameters
We measured leaf parameters on 16 species of temperate forest trees collected in Northwest Georgia and Southern New Jersey. We chose species on the basis of local availability; they do not represent a random sample. These parameters are relevant to the fluid dynamics of leaves falling in air. We note general characteristics of each species, such as number of lobes, leaf margin, pubescence, tree height, and crown shape. More specific leaf parameters include leaf length l (mm, parallel to the main vein and petiole, but excluding the petiole), leaf width w (mm, at right angles to the main vein and petiole), leaf thickness h (mm), leaf area α (mm2), and leaf mass m (mg, including the petiole). From these variables we can estimate leaf density (mg/mm3), as well as unitless values relevant to the behavior of a leaf falling through air [19,20]: aspect ratio (δ, length to width ratio), thickness to width ratio (β), dimensionless moment of inertia (I*), and Froude’s number (Fr). For elliptical leaves we use the maximum width w at right angles to the petiole; for lobed leaves we use the harmonic mean of the lobes and sinuses. So, for a lobed leaf having two lobes and two sinuses, we estimate leaf width as
where n is the number of lobes and sinuses, Li is the width across lobe i and Sj is the width across sinus j.
The Froude number (Fr) is a dimensionless number, the ratio of the flow inertia to the external gravitational field. The dimensionless moment of inertia I* is a measure of an object’s ability to resist angular acceleration. In estimating I* and Fr we make the following assumptions. The density (ρf) of the fluid (air) is assumed to be 1.225 kg/m3 (0.001225 mg/mm3) at sea level and 15 °C (International Standard Atmosphere) and its kinematic viscosity (υ) is 1.73 × 10−5 Newton-second/m2. The acceleration due to gravity (g) is 9.80665 m/s2. Following Andersen et al. [19], the dimensionless moment of inertia for an object of elliptic cross-section is then equal to
where is the density of the leaf (mg/mm3), is the density of air, h is the thickness (mm), and w is the width. The dimensionless moment of inertia can be thought of as the ratio of the moment of inertia of the object to a quantity proportional to the moment of inertia for a rigid sphere of fluid about its diameter [26].
According to Belmonte [18], the Froude’s number of falling paper is
One can also estimate the Froude’s number from the flow velocity (v), acceleration due to gravity (g), and the characteristic length (l),
all in units of cm/s, cm/s2, and cm. Using falling plates, Belmonte et al. [18] found that the critical Froude number for a transition from flutter to tumble was Frc = 0.67 ± 0.05.
2.2. Leaf Drops
How far do leaves fall, on average, from the point where they are dropped? To begin, we dropped leaves from several species of temperate trees, including Quercus shumardii Buckland (Shumard’s oak), Q. falcata Michx. (southern red oak), Q. nigra L. (water oak), Q. montana Willd. (chestnut oak), Q. marilandica Muenchh. (blackjack oak), Q. alba (white oak), Platanus occidentalis L. (American sycamore), and M. grandiflora. The species of Quercus can be arranged from most deeply incised to least deeply incised leaves: Q. alba, Q. shumardii, Q. falcata, Q. marilandica, Q. nigra, and Q. montana. Leaves of P. occidentalis have a greater leaf area than any of the Quercus species, but also have lobes (albeit broad ones). The Magnolia leaves are large, heavy, and elliptic; they are not deciduous, but are replaced seasonally by new leaves.
The leaves were dropped from a height (L) of 283.5 cm, and we measured how far each leaf drifted horizontally (D) from the drop point (the distance in cm from a plumb line to the nearest margin of the leaf, including the petiole). Leaves that bounced off a wall were not counted and were dropped again. Following Ishiguro and Miyaki [22], the average glide ratio λ is then λ = L/D, where L is the vertical distance from ceiling to floor and D is the lateral distance of the leaf from the plumb line point. Smaller values of the glide ratio indicate leaves drifting further from the drop point in our lab (or from their origin on a branch). Each leaf was dropped 10 times to estimate variance components (among species, among leaves within species, and among drops within leaves within species).
After the variance component analysis, we redesigned the leaf drops to increase the power of the species comparisons. We tried to drop at least 25 different leaves, twice for each leaf, from four species of oaks (Quercus), two magnolias (Magnolia), three hickories (Carya), catalpa (Catalpa speciosa (Warder) Warder ex Engelm.), American sycamore (P. occidentalis, both dry and pressed), and red maple (Acer rubrum L. mountain and swamp ecotypes). These leaves were of diverse origins. The oaks, magnolias, and one group of sycamore were collected from the forest floor after they had dropped. We did not know how long each leaf had been on the forest floor, but many leaves were dry and bent into three dimensions. In contrast, the hickories, catalpa, red maples, and one group of sycamore had been collected fresh and pressed in 2016. For comparing pressed and unpressed leaves we had both categories present for American sycamore.
Finally, we dropped the leaves of several species to categorize the behaviors of leaf-falling. We characterized each of the 25 drops as (1) steady descent, (2) fluttering, (3) tumbling, (4) gyration, (5) gliding, or (6) chaotic descent (a combination of any of the five in the same drop). These categories are based upon the ones used in the plate drop literature [17,18,19,20,27]. These leaves were dropped indoors, from a height of 273 cm, in a different room. We also measured the distance from the drop point (established by a plumb line) to the leaf (nearest point) for each of the 25 drops. We pooled the 25 drops for a rough estimate of their behavior.
2.3. Symmetrical and Asymmetrical Artificial Leaves
We also created artificial paper leaves to test the influence of leaf symmetry and asymmetry on the lateral distance traveled, D. We used photocopy paper (0.016 in = 0.4064 mm thickness), which is similar in thickness to the leaves of most forest trees [28]. The thickness to width ratio β of the artificial leaves is approximately 0.00456, which is also in the range of that for most leaves, and is relevant to behavior in an inviscid fluid.
The leaves were those used in a previous paper (Figures 4 and 10 in [29]). The leaves were from Q. velutina Lam. (black oak), A. rubrum, and Perilla frutescens (L.) Britton (shiso, an herb). The leaves (minus the petioles) were scanned and then symmetricized via the following approach: 200 landmarks were placed around the leaf margin and then a program created by Hagit Hel-Or (continuous symmetry measure, CSM) [29] was used to generate a perfectly symmetrical version of the leaf, having the same area as the original leaf. The leaf margins were printed on photocopy paper and trimmed with scissors. So, for each of the three species, we had a natural (asymmetrical) and a symmetrical version of each leaf.
For the artificial leaves, we characterized each of the 25 drops as steady descent, fluttering, tumbling, gyration, gliding, or chaotic descent (a combination of any of the five in the same drop). This is obviously a very small sample of artificial leaves, and does not take into account the variation in leaf shape within a species. Our goal was to explore this approach before pursuing it further with larger sample sizes.
2.4. Ginkgo biloba
Ginkgo biloba L. (ginkgo) is a widely-planted species, native to Asia, that has fan-shaped leaves. Leaves higher in the canopy tend to be more narrowly fan-shaped than leaves lower in the canopy. While this difference may be related to light intensity in different parts of the canopy, it may also be possible that narrowly fan-shaped leaves are more likely to drop over the root zone. We anecdotally observed that narrowly fan-shaped leaves tended to spiral down, petiole first, while widely fan-shaped leaves tended to tumble end-over-end at right angles to their petiole.
To test the hypothesis that leaf shape influences how a ginkgo leaf falls, we sampled 10 leaves from each of 5 individual ginkgo trees. For each leaf, we measured mass (m), basal angle (degrees), lamina area (cm2), and petiole length (cm). We dropped each leaf 10 times from a height of 283.5 cm and estimated the mean lateral distance D that the leaf drifted away from the drop point (cm).
In addition, we sampled leaves that had fallen from a single isolated individual of G. biloba on the Berry College campus. Using the point–center–quarter method, we sampled leaves from random angles and distances to estimate leaf density as a function of distance from the trunk.
Finally, we dropped leaves again in a different indoor setting (drop height was 273 cm) to see if there were differences in lateral distance D among wide, narrow, and bilobed leaves.
2.5. Reynold’s Number of Falling Leaves
The Reynold’s number (Re) is relevant to the behavior of objects falling in a fluid. It is the ratio of inertial forces to the viscous forces of a fluid—in this case air. We made videos of falling leaves against a scale taped to a wall and were able to estimate the Reynold’s number as Re = (μl)/ν, where µ is the terminal velocity (cm/s), l is the length (cm) of the leaf, and v is the kinematic viscosity (cm2/s) of air, v = 0.148. Re is a unitless number. The flow is laminar when Re is small, and the flow is turbulent when Re is large. Actual critical values of Re vary with the object and the fluid. Reynolds [30] estimated a critical Re ≈ 2300 for water in pipes. More recently, and for flat plates in air, Trinh et al. [31] estimated the transition from laminar to turbulent flow to be between Re ≈ 105 and 106 in the absence of perturbation. That critical value would be smaller in the presence of small to moderate disturbance, such as a light breeze.
We used the Tracker Video Analysis and Modeling Tool [32] to estimate the terminal velocity (µ) of falling leaves of several species, but focused on leaves of Q. alba and Ulmus americana L.
2.6. Packing Density in Elliptical Dogwood Leaves
Elliptical leaves with entire leaf margins are typical of tropical forest trees. The most likely advantage of such shapes is that they maximize packing density to minimize self-shading. These shapes are also common in understory trees of the temperate zone, presumably for the same reason.
We photographed an entire branch of elliptic dogwood (Benthamidia (Cornus) florida (L.) Spach.) leaves that were spaced and turned toward the sun. The goal was to make a crude estimate of the packing density (φ), taking leaf overlap into account. The packing density φ is the proportion of the two-dimensional space (area α) that is covered by nonoverlapping elliptical leaves, φ = (α − αopen)/α. Because the leaves do in fact overlap, we need to take that into account and introduce it as a penalty [33]. All else being equal, selection should favor leaves that generate the greatest packing density with minimal overlap. We define the packing density with overlap as φ′ = φ − φoverlap, where φoverlap is the proportion of the entire area α that consists of overlapping leaves φoverlap = (αtotal − (α − αopen))/α, where αtotal is the total area of all leaves in a group. The area of overlap, however, is difficult to measure because many leaves cannot be seen in their entirety. Consequently, we measured the following areas from the photograph and used an indirect estimate of the overlap area:
α = the entire area covered by all of the leaves (including interior open spaces and areas of overlap);
αmean = average area of the leaves that can be seen;
αopen = area not covered by leaves;
nl = number of leaves in the entire cluster.
Then, the estimate of the total area of all leaves αtotal = (αmean) nl and αoverlap = αtotal − (α − αopen). The nonoverlapping packing density is (α − αopen)/α and the overlapping packing density is φ′ = φ − φoverlap.
To generate areas, we saved the photograph as a tiff file, increased the contrast, increased the green saturation, and saved the file into ImageJ 1.53t [34]. We used ImageJ’s drawing tool to remove the background. We used the part of the photograph in which most of the leaves are directly facing the observer.
3. Results
3.1. Leaf Parameters
Various leaf parameters influence how leaves fall in air. The basic leaf and tree parameters are presented in Table 1 and Table 2, and the dimensionless moment of inertia (I*) and Froude number (Fr) are presented in Table 3.

Table 1.
General leaf and tree parameters for several species of trees.

Table 2.
Dimensional and nondimensional parameters of falling leaves and the fluid they fall through. The dimensional parameters are average length (l, parallel to the petiole and midrib if one is present), the average width (w) of a leaf, the average thickness (h) of a leaf, and the average density (ρs) of a leaf. The nondimensional parameters are aspect ratio (δ) and thickness to width ratio β = h/w. All values are means ± standard deviation.

Table 3.
Dimensionless moment of inertia I* and Froude number Fr, calculated from the dimensional parameters. The density (ρf) of the fluid (air) is assumed to be 1.225 kg/m3 at sea level and 15 °C (International Standard Atmosphere), and its kinematic viscosity (υ) is 1.73 × 10−5 Newton-second/m2. The acceleration due to gravity (g) is 9.80665 m/s2. All values are means ± standard deviation. Numbered species (1 and 2) are leaves from two different trees.
The leaves of all 16 species for which we estimated leaf parameters had Froude numbers (Fr) greater than Belmonte et al.’s [18] critical value of Frc = 0.67 for transitioning from flutter to tumble. Aspect ratios varied from δ < 1 (wide Ginkgo leaves and most P. occidentalis leaves) to δ > 5 (Q. phellos). Despite the diversity of leaf shapes (Figure 1), the estimated Froude numbers were independent of aspect ratio (r = 0.1202, n = 20, p = 0.6137).
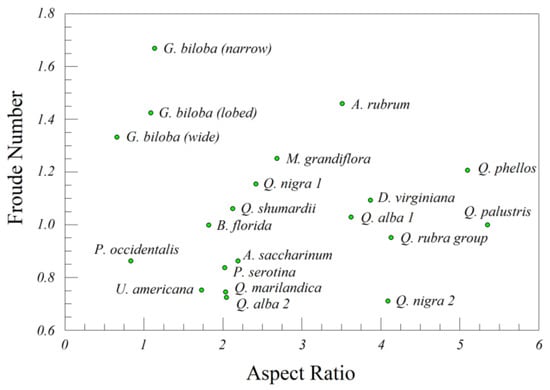
Figure 1.
Froude number (Fr) versus aspect ratio (δ) for a sample of the leaves of temperate forest trees.
3.2. Leaf Drops
3.2.1. Initial Leaf Drops
Of the nine species examined in the initial series of drops (Figure 2), more than 80% of the variation in distance D from the drop point was individual drops within leaves within species (Table 4). The variation among species only amounted to slightly more than 1% of the total variation, and was statistically insignificant (F8,68 = 1.3530, p = 0.2331). There was also considerable variation (18.7%) among leaves within a species. Consequently, detecting differences among species requires a larger sample of leaves than we used in the initial series of drops.
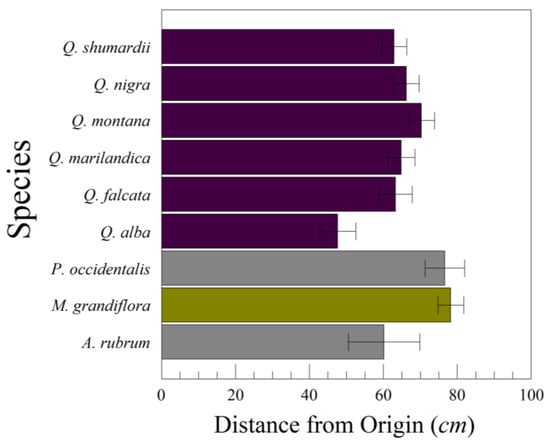
Figure 2.
Mean lateral distance traveled from a plumb line below the drop point to the leaf (±standard error). The species are six oaks (Quercus shumardii, Q. falcata, Q. nigra, Q. montana, Q. marilandica, Q. alba), American sycamore (Platanus occidentalis), a maple (Acer rubrum), and southern magnolia (Magnolia grandiflora).

Table 4.
Variance components for leaf drops of leaves from nine different species of trees on the Berry College Campus. The leaves are from just one tree of each species. The response variable is distance (cm) from the drop point.
3.2.2. Species Comparisons
In comparing several species, we used larger sample sizes, ideally 25 leaves and two drops for each leaf. There were some species for which we did not have 25 leaves. Moreover, some leaves were damaged during their first drop and were not used for a second drop. The reduced samples were Carya glabra Miller (n = 5), C. ovata (Mill.) K. Koch (n = 14), C. tomentosa Sarg. (n = 18), Catalpa speciosa (n = 8), M. virginiana (n = 20), P. occidentalis pressed (n = 10), and Q. rubra (n = 16).
As in the previous series of leaf drops, the variance among drops within a leaf within a species accounted for most of the total variation (75.34%). The variation among leaves within a species was 13.47%, and that among species was 11.19%. The differences among species (Figure 3) were statistically significant (F13,253 = 5.119, p = 0.00000005).
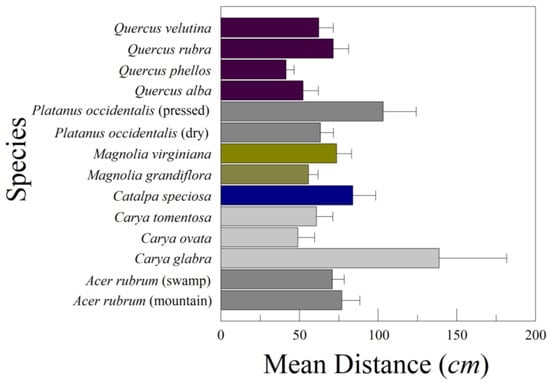
Figure 3.
Mean lateral distance traveled from a plumb line below the drop point to the leaf (±standard error). The species are four oaks, two magnolias, three hickories, catalpa, sycamore (dry and pressed), and red maple (mountain and swamp ecotypes).
The oaks (Quercus spp.) did not differ among one another (Table 5). The falls of Q. phellos were associated with both tumbling (rotation around the long axis of the leaf) and rotation around the trajectory of descent, thus doubling back on themselves. The other species of oak displayed chaotic falls and the occasional glide. The three species of hickory differed, with the small sample of C. glabra exhibiting long-distance linear glides, whereas C. ovata and C. tomentosa exhibited steady fall and flutter. The naturally dried and museum-pressed samples of P. occidentalis differed, with the pressed ones often gliding, while naturally dried leaves showed steady descent and flutter, often dropping like parachutes. The two ecotypes of A. rubrum (swamp and mountain) did not differ, despite being morphologically different. Magnolia virginiana leaves traveled further than those of M. grandiflora, but the differences were insignificant.

Table 5.
Significant Tukey contrasts following ANOVA of species comparisons. B is the parameter estimate and SE is the standard error. The significance codes are *** = p < 0.001, ** = p < 0.01, * = p < 0.05.
3.2.3. Categories of Fall
Figure 4 and Figure 5 show the percent of leaf drops that could be categorized as steady fall and flutter (both categories pooled), tumble, gyrate, glide, and chaos. The percentage of chaotic drops is represented by the size of the point.
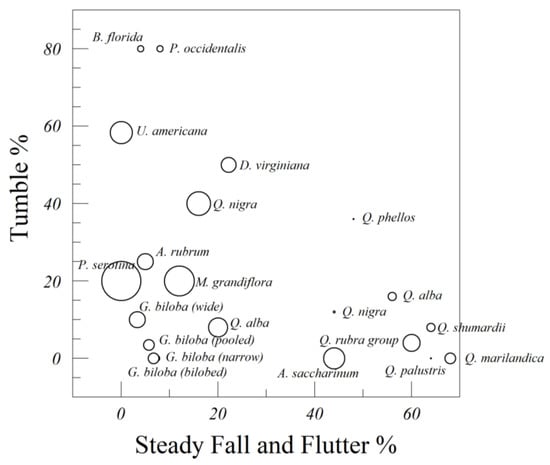
Figure 4.
Leaves from 16 species of trees, categorized by their mode of fall (steady fall and flutter, tumble, and chaos). Chaotic descents are represented by the size of the point.
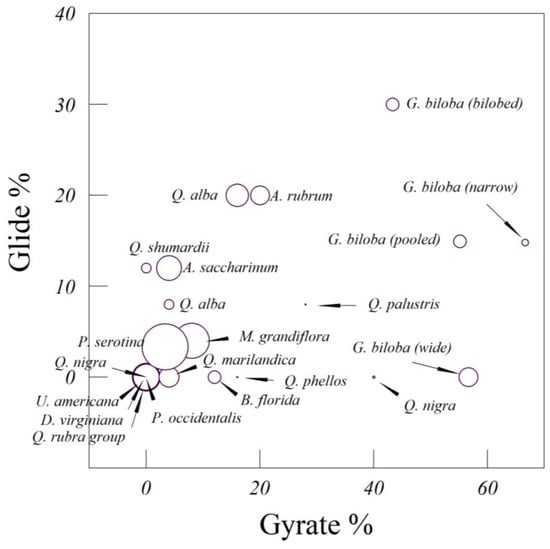
Figure 5.
Leaves from 16 species of trees, categorized by their mode of fall (gyration, glide, and chaos). Chaotic descents are represented by the size of the point.
The greatest lateral distances traveled by falling leaves are associated with tumbling and gliding, and especially gliding, unless it involved a secondary axis of rotation. The two species whose leaves were most likely to tumble were dogwood (B. florida) and American sycamore (P. occidentalis), followed by American elm (U. americana) and persimmon (D. virginiana). Gliding was rare for most leaves, but was notable in the bilobed ginkgo leaves. Gliding was shown by individual leaves that were more symmetrical than average. The smallest lateral distances recorded are associated with steady falling, flutter, gyration, and chaos.
3.2.4. Artificial Leaves
The symmetric members of the matched pairs of Q. velutina and P. frutescens transitioned quickly from fluttering to tumbling. Only 28% and 44% progressed to chaos, in a sequence from flutter to tumble to chaos. The asymmetrical leaves of these two species transitioned more often from flutter to chaos (Table 6 and Figure 6). Fluttering all the way to the floor only occurred once in 150 drops.

Table 6.
Artificial paper leaves dropped from 273 cm. Each drop is classified by treatment (original asymmetric or symmetric), species, and the description of descent (flutter, tumble, or chaos). Values are percentages, across species and treatment. Each treatment (species by symmetry) is n = 25.
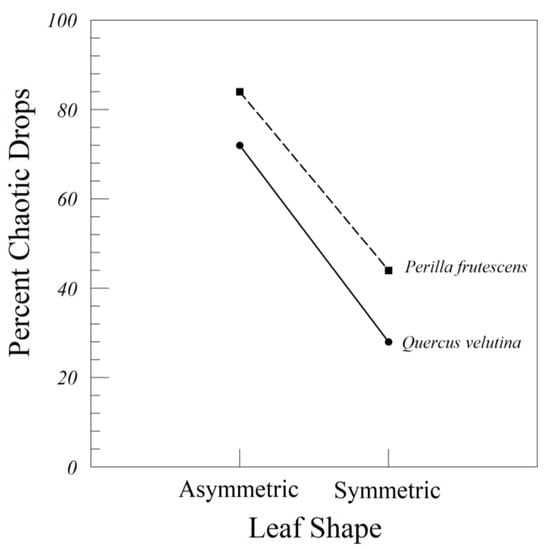
Figure 6.
Interaction plot of the percent of chaotic drops of artificial leaves by leaf shape (asymmetric or symmetric) and species (Q. velutina and P. frutescens). The symmetric leaves are symmetricized versions of the original asymmetric leaves, standardized by area and weight.
The leaves of A. rubrum were nearly symmetric to begin with, and symmetricized versions of the leaves were difficult to tell apart from the original asymmetric ones. In total, 92% of the drops of both symmetric and asymmetric A. rubrum leaves tumbled all the way down. Consequently, we eliminated A. rubrum from the generalized linear model in order to focus on the initially more asymmetric leaves of Q. velutina and P. frutescens.
The saturated generalized linear model (dispersion parameter taken from a Poisson distribution, with a log link function) suggests that the three-way interactions might be eliminated along with the effect of species (Table 7). We also eliminated flutter as a level in the analysis, combining it with tumble; it only appeared once out of 100 leaf drops of Q. velutina and P. frutescens.

Table 7.
Saturated model for drops of artificial leaves. Null deviance = 23.054, 7 df. Residual deviance = −8.8818 × 10−16, 0 df. AIC = 49.986. The reference categories are Perilla, asymmetric, and chaos. Exp(b) is the exponentiated value of the parameter estimate. The significance codes are *** = p < 0.001, ** = p < 0.01.
The reduced model containing both two-way interactions, and with flutter combined with tumble, gave a suitable fit (AIC = 44.176). The two-way interaction between symmetry class and drop class (flutter and tumble) was highly significant (Figure 6 and Table 8); the effect of symmetry class varied between tumble and chaos. Symmetricized leaves of both Q. velutina and P. frutescens were more likely to tumble than their original asymmetric counterparts, which quickly transitioned to chaos.

Table 8.
Estimated coefficients for the most parsimonious generalized linear model of number of artificial leaves observed to glide, gyrate, or fall in other ways (steady fall, flutter and tumble). Chaotic falls was the reference category. Residual deviance: 2.2468 on 4 degrees of freedom. AIC: 44.176. The reference categories are Perilla, asymmetric, and chaos. Exp(b) is the exponentiated value of the parameter estimate. The significance codes are *** = p < 0.001, ** = p < 0.01.
In separate drops to measure distances, there were highly significant differences in drop distances among species (Figure 7), with most of the difference being the longer distances traveled by the leaves of A. rubrum (Table 9). Although there were no significant differences between the asymmetric and symmetric versions of the leaves, there was a nearly significant interaction between species and treatment. Consequently, we selected A. rubrum in isolation for further analysis.
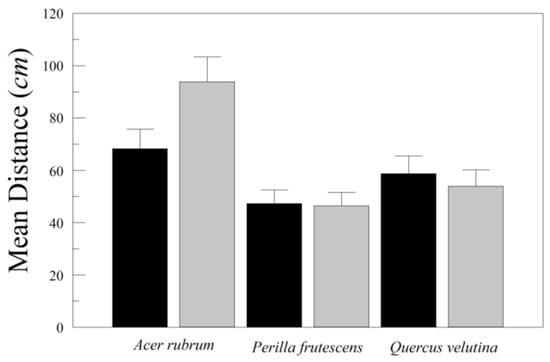
Figure 7.
Mean distance from drop point for artificial leaves of Acer rubrum, Perilla frutescens, and Quercus velutina, both asymmetric (black) and symmetricized (gray). Error bars are standard errors (n = 25).

Table 9.
Two-way ANOVA for the effects of species and treatment (asymmetric original, symmetric version) on distance (cm) from the drop point in a 273 cm drop from ceiling to floor. The significance codes are *** = p < 0.001, ns = not significant.
The symmetricized leaf of A. rubrum traveled further from the drop point than the original asymmetric version (F1,48 = 4.477, p = 0.0396, Hedge’s g = 0.59). While both leaves tended to tumble, the asymmetric version tended to double back on itself while tumbling. The longest distances traveled by A. rubrum leaves of both kinds involved unidirectional tumbling.
3.3. Reynold’s Number of Falling Leaves
Our estimates of the Reynold’s number (Re) were made with a single leaf each from just two species. Our estimates of Re were 26,527 for Q. alba (Figure 8) and 6376 for U. americana. For both species, the descents were chaotic, with periods of acceleration, stalling, and then reacceleration. For Q. alba, the leaf stalled at about 0.5 s and 1.5 s after accelerating to about 270 cm/s.
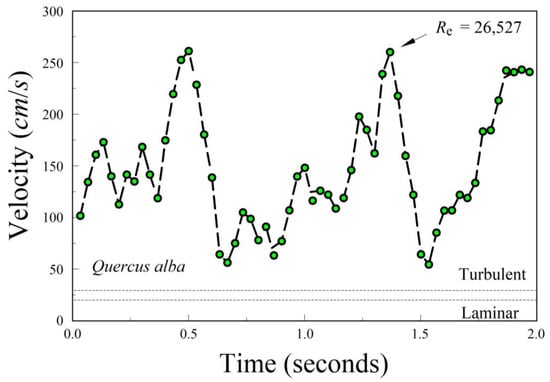
Figure 8.
Relationship between velocity (cm/s) and time during a descent for an individual leaf of Quercus alba. The Reynolds number Re was calculated using the peaks as the best estimates of the terminal velocity μ. The drop here was chaotic, with a combination of flutter and tumble.
3.4. Ginkgo biloba
Leaves of Ginkgo biloba range in shape from narrow to broadly fan-shaped, and without lobes or with two lobes. The more narrowly fan-shaped leaves are more abundant towards the top of the crown. Is this an adaptation to adjust photosynthetic efficiency and transpiration in leaves exposed to intense sunlight, or do these narrow leaves from high in the crown fall closer to the root zone? In other words, do these narrower leaves have a larger glide ratio than the more broadly fan-shaped leaves?
For the single individual ginkgo, isolated in a field, at least one leaf was 11 m from the base of the tree, while the majority of leaves fell within 2 m of the trunk, and over the presumed root zone (Figure 9).
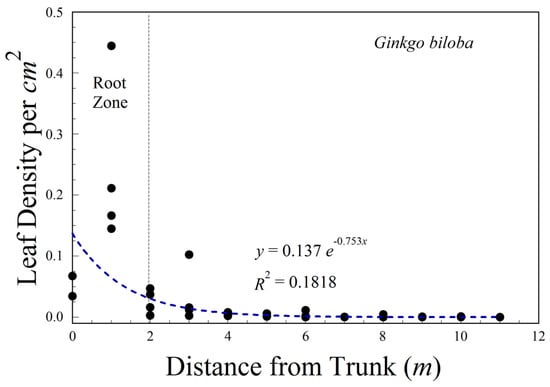
Figure 9.
Distribution of leaves about the base of a small Ginkgo tree. The root zone is the diameter of the drip line. The dashed line is a best fit exponential regression.
In a series of independent leaf drops, we examined the relationships between basal angle, leaf area, mass, petiole length, and distance from the drop point (Table 10). The relationships among the leaf parameters and the mean distance were nonlinear, and only mass was significantly correlated with mean distance. Figure 10 shows the nonlinear relationships. The other significant correlations were that basal angle, leaf area, and biomass were all positively correlated, representing leaf size, and that petiole length was negatively correlated with basal angle.

Table 10.
Spearman product–moment correlations between leaf variables of Ginkgo biloba (n = 50). Correlations are above the diagonal. Alpha probabilities are below the diagonal. Numbers in bold are statistically significant at p < 0.05.
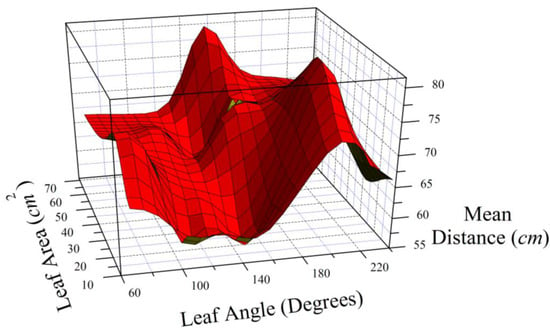
Figure 10.
Mean distance from the drop point for ginkgo leaves of varying lamina areas and basal angles.
Mean distance from the drop point showed two peaks (Figure 10). One peak was for leaves with low to moderate leaf area but with a basal angle wider than 190 degrees, and the other was leaves of large areas and basal angles of about 160 degrees. The leaves descending the shortest distance were small leaves with about 100–155-degree basal angles.
The glide ratio of Ginkgo leaves ranged from 0.65 to 2.65 (mean of 1.193). For a large tree of 35 m, the average lateral distance for a leaf dropped from 35 m would be D = L/λ = 35/1.193 = 29.34 m (range of 13.21 to 53.84 m).
There were no significant interactions between leaf shape (wide, narrow, and bilobed) and category of fall (gyration, glide, chaos, and other) (Table 11). We considered four models: (1) with all main effects and interactions, (2) with both main effects but without the two-way interactions, (3) with leaf shape as the only main effect, and (4) with the category of fall as the only main effect. An Analysis of Deviance has suggested that the simplest model capturing the relationships was the last one, with leaf shape as the only main effect. The frequencies of the categories of fall differed, with gyration > chaos = glide > other. Based on the exponentiated value of b, leaves were more than 2.5 times more likely to gyrate than fall chaotically during their descent (Table 12).

Table 11.
Contingency table for ginkgo leaves classified by shape (wide, narrow, and bilobed) and category of descent. The values are the percentages of each leaf shape category.

Table 12.
Estimated coefficients for the most parsimonious generalized linear model of number of ginkgo leaves observed to glide, gyrate, or fall in other ways (steady fall, flutter, tumble). Chaotic falls were the reference category. The significance codes are *** = p < 0.001, * = p < 0.05, ns = not significant.
3.5. Leaf Packing in Elliptical Dogwood Leaves
Flowering dogwood leaves are elliptical with a finely toothed margin. They are an important understory tree in the Eastern Deciduous Forest. Five leaves sampled from the tree in Figure 11 have a mean aspect ratio of δ = 1.818 ± 0.138 (std dev) and a mean area α = 2911.045 ± 839.74 mm2. The approximate packing density with overlap φ′ is 0.7826.

Figure 11.
Leaf packing on a single branch of flowering dogwood (Benthamidia (Cornus) florida L.). The estimated packing index φ is 0.9120 (ignoring overlaps), and φ′ = 0.7826 taking overlaps into account. The plant in the background is Magnolia grandiflora. The image has been modified to increase contrast and green saturation.
4. Discussion
Our experiments and observations demonstrate that leaf shape influences the behavior of leaves when they fall. The results, however, are far more complex than we imagined, and come with surprising observations.
4.1. Leaf and Tree Parameters
The leaves we examined originated from trees ranging in size from tall (U. americana) to medium-sized (Q. marilandica) canopy and small subcanopy (B. florida and D. virginiana) species. Leaf shape varied from elliptical (B. florida) to deeply lobed (Quercus alba). Numbers of lobes varied from none to nine (Q. shumardii). Leaf margins varied from entire (D. virginiana) to finely serrated (B. florida) and doubly serrated (U. americana). Leaf vestiture varied from glabrous (D. virginiana) to densely pubescent (some A. rubrum).
All of the leaves we examined had estimated values of I* and Fr beyond the threshold values for transition from laminar to turbulent flow (flutter to tumble to chaos) in air [18,19].
4.2. The Critical Root Zone
The size and lateral distribution of the critical root zone is essential to our hypothesis. Leaves must fall over this zone for self-mulching to make any sense. For practical purposes related to sylva-culture, the critical root zone is generally estimated from a tree’s circumference at breast height [35]. The radius of the critical root zone is then Rcrz = (circumference in inches at breast height/π) × 18 inches. For example, a typical large oak tree of 100 cm diameter at breast height and 33 m total height will have a critical root zone of approximately 18 m radius (36 m diameter). Consequently, a leaf dropped from the center of the very top of a 33 m tree would require a glide ratio λ of at least 1.833 to land within the critical root zone. Because λ = L/D, larger ratios imply steeper descents. For a leaf half-way up the trunk, in the densest part of the crown, falling over the critical root zone would imply a λ of 0.9167 or larger. This is well within the range of λ = 3.54 to 5.15 for a Ginkgo biloba leaf. Moreover, average glide ratios for the first nine species we examined fall in the range of 3.54 for Magnolia grandiflora to 6.3 for white oak—steep enough for a large tree of 33 m height. For the artificial leaves, the average glide ratios were all larger than 2.9, which was the glide ratio for the symmetricized A. rubrum leaf. These estimates suggest that even for very large trees, most leaves will fall over the critical root zone.
We should make clear that it is not necessary for all leaves to fall over the critical root zone—just enough to provide optimal mulch cover. At this time, we have no idea how much mulch is optimal, and too much can certainly have adverse effects [36]. Moreover, the crown itself is three-dimensional, and leaves can drop from anywhere within the crown, falling within a 360-degree radius around the trunk. Those leaves on the periphery can fall away from the tree or into it. Finally, leaves are apt to collide with branches and leaves not yet shed.
4.3. Leaf Shape of Temperate Forest Trees
We looked closely at the leaf shapes of several tree species that we had immediate access to. Lawrence [37] categorized leaves into several categories: structure (simple or compound), form or outline (ovate, elliptical, etc.), apex (acuminate, acute, etc.), base (oblique, truncate, etc.), margin (entire or emarginate), and arrangement (opposite, alternate, whorled). Leaf shape could be categorized into combinations of these categories: (1) entire, elliptical, (2) deeply lobed and elliptical, (3) elliptical with serrate, crenate or dentate margins, (4) elliptical and asymmetric (oblique base) with serrate, crenate, or dentate margins, (5) cordate (heart shaped), (6) pandurate (resembling a fiddle), (7) flabellate (fan-shaped), (7) spatulate (spoon shaped), (7) ovate (egg shaped), and (8) other.
The main species in our area with entire (or nearly entire in dogwood) and elliptical leaves were three magnolias (M. grandiflora, M. virginiana L., M. tripetala (L.) L.), black gum (Nyssa sylvatica Marshall), flowering dogwood (B. florida), and persimmon (D. virginiana). Of these, M. grandiflora and M. virginiana are lowland canopy trees. Magnolia grandiflora’s leaves are large, heavy, evergreen, and the margins are often curled towards the underside of the leaf, especially when the leaf is shed. Sweetbay magnolia (M. virginiana) has smaller leaves that can be either deciduous or evergreen. Umbrella magnolia (M. tripetala) is an upland understory tree, with deciduous leaves. Both dogwood and persimmon are understory trees, while black gum is mostly a lowland canopy tree, often found in the same communities as M. grandiflora and M. virginiana, but also occurring in low densities in mesic upland forests [38].
Of the widely distributed canopy trees, black cherry (P. serotina var. serotina) is the only one we examined, besides M. grandiflora and M. virginiana, that had symmetrical and elliptical leaves. However, black cherry leaves are not entire; they have fine serrations on most leaves. Black cherry occurs in a wide range of habitats, preferring rich soils. The leaves we collected were from the coastal plain of southern New Jersey in an area with a shallow water-table. The escarpment black cherry (P. serotina var. eximia), which occurs on the more arid Edward’s Plateau of Texas, has stronger serrations than var. serotina [39].
Several species of trees in northwest Georgia have asymmetrical leaves (oblique base in most cases). These include the elms (Ulmus alata Michx., U. americana, and U. rubra Muhl.), the basswoods (Tilia americana L.), the mulberries (Morus alba L. and M. rubra L.), witch hazel (Hamamelis virginiana L.), and the birch family (Alnus serrulata (Ait.) Willd., Carpinus caroliniana Walt., and Ostrya virginiana (P. Mill.) K. Koch). Of the elms, U. alata has the least asymmetrical leaves; it is also the shortest (13.1 m) of the three elms. Ulmus americana, in contrast, with more asymmetrical bases, can reach 30.5 to 42.6 m, while U. rubra can reach 12 to 19 m. The leaves of all three species have strongly serrated margins [39].
The shape of oak leaves is extremely variable, from the elliptical leaves of live oak, willow oak, and subtropical species, to the spatulate and deeply lobed leaves of species in the red oak and white oak groups. Some of the leaves of oak are hard to describe in words, and tree-to-tree and within-tree variation can be significant. In addition, widespread hybridization among species of oaks occurs throughout their range, further complicating leaf shape. Most of the upland species of oak (Q. alba, Q. rubra, Q. shumardii. Q. velutina) have lobed leaves. Pin oak, Q. palustris, is an exception; it is a species with deeply lobed leaves that is found primarily in northern wetlands, but is replaced by more shade-tolerant species, such as A. rubrum, C. ovata, Fraxinus pennsylvanica Marshall (green ash), and N. sylvatica [40]. Braun [38] also described Q. palustris as an early successional species. Blackjack oak, Q. marilandica, typically found on rocky or sandy soils, has three-lobed leaves. Water oak, Q. nigra, a southern semi-deciduous wetland species, has spatulate leaves with three very shallow lobes. Willow oak, Q. phellos, is a mostly wetland species with elliptical leaves of high aspect ratio.
Like oaks, maples are a genus that exhibits wide variation in leaf shape, from entire, elliptical leaves (A. fabri Hance 1884, A. oblongum Wall. ex DC. 1824, and A. coriaceifolium (cinnimomifolium) H. Lév. 1912), to deeply lobed leaves (A. saccharinum and A. palmatum Thunb. 1784 not Raf. 1836) and compound leaves (A. negundo L. and A. griseum (Franch.) Pax 1902). Maples with entire leaves are consistently found in cool, moist forests. Acer fabri is an evergreen shrub, A. oblongum is an evergreen to semi-deciduous tree, and A. coriaeifolium is a small evergreen shrub or tree. These characteristics are in agreement with our expectations for shade-tolerant species competing for light rather than water and nutrients. Boxelder (A. negundo), a species with compound leaves, is a short-lived, fast-growing species found along stream corridors in moist soils [41]. It can be considered an early successional species. Unlike most oaks, maples are not fire-resistant. Silver maple (A. saccharinum), for example, a species with deeply lobed leaves, is the least fire-resistant tree in a community of central hardwood species [42]. Nevertheless, a reappraisal of sugar maple (A. saccharum Marshall) suggests some fire resistance over a thousand years of recurrent fires in eastern Canada [43].
Individual species of maple are as variable as oaks. Red maple (A. rubrum) alone has upland and lowland ecotypes that have sometimes been classified as distinct species. Some lowland individuals have sinuses and lobes so reduced that the aspect ratio of the leaf approaches 1 (a disc). Some upland individuals have deeply lobed margins close to those of silver maple. Again, this is in agreement with our prediction that competition for light overrides competition for water and nutrients in lowland ecotypes.
Ginkgo has fan-shaped leaves of extreme variability. At one extreme, leaves lower in the canopy are widely fan-shaped, while those further up are narrowly fan-shaped. Some of the narrowly fan-shaped leaves have two lobes, hence the name G. biloba. The aspect ratio of ginkgo leaves ranges from a mean of 0.66 in widely fan-shaped leaves to 1.13 for narrowly fan-shaped leaves. Ginkgo leaves also have petioles that vary in length. Some petioles can be longer than the lamina, especially in leaves having narrow basal angles.
The leaves of American sycamore (P. occidentalis) are unusual in that their mean aspect ratio is less than one. They are lobed and dentate at the same time, and the leaves usually begin to dry before they are shed, assuming a more three-dimensional aspect.
Several of the species we observed (Juglans nigra L., Carya spp., Fraxinus americana L.) had compound leaves. While C. ovata tended to drop its compound leaves as an entire unit, J. nigra mostly dropped leaflets and the occasional entire leaf, while F. americana dropped all of its leaflets before dropping its main petiole [44,45].
We also observed that some trees shed their leaves while they were still green and flexible, while others dropped them when they were dried and brittle. Most of this realization came after we had already prepared leaves for being dropped. Some oaks hold on to their leaves for some time before shedding them. Further study is necessary. As we showed in some of our drops, the state of the leaf at the time it is shed influences the glide ratio.
4.4. Fluid Dynamics of Falling Leaves
Does leaf shape influence the way leaves fall? Most of our initial analysis is based on the published behavior of plates and cards falling through various fluids. To our knowledge, there are no papers on the actual behavior of leaves in a fluid (air). Emelianova [46] refers to falling cards as leaves in her paper, ‘A study of dynamics of a falling leaf based on a two-dimensional model’, but her leaves are not plant leaves, just thin sheets of paper. The tremendous variation in the shape of plant leaves is certainly an impediment to tightly controlled experiments in the lab.
We identified two categories of laminar flow associated with falling leaves, simple perpendicular fall [47] and gliding. Simple perpendicular fall is with a steep glide ratio, while gliding is associated with the shallowest glide ratios. Gliding was uncommon, but when it occurred it often took the leaves furthest away from their drop point, unless there was secondary rotation taking the glide back in the direction of its origin.
Higher Reynold’s and Froude’s numbers are associated with early transitions from laminar to turbulent flow. The main categories of leaf descent associated with turbulent flow were flutter, tumble, gyration, and chaotic descent. Of those four categories, tumbling is associated with a shallow glide ratio, again unless there is secondary rotation that takes it back towards the origin. Flutter, gyration, and chaotic descent have steep glide ratios. The most common transitions to a steep chaotic fall were from flutter to tumble to chaos. Willmarth [26] observed a turbulent motion and tumbling of rigid discs when the Reynolds numbers were greater than Re = 100. Trinh et al. [31] placed the transitional range between Re = 105 and 106 in the absence of perturbation. We estimated Re values of more than 26,000 for a falling leaf of Q. alba, which clearly demonstrated a chaotic descent.
Estimates of the dimensionless moment of inertia (I*), based on leaf thickness, width, and density, were generally less than 3.0, except for Q. phellos and G. biloba (narrow). These compare well with the estimates by Andersen et al. [19,20] for their plates and cards, which were generally between 0.17 and 6, varying with the equation used to estimate I* (cylinder, rectangular cross-section, or elliptical cross-section). Andersen et al. [19,20], however, used water as their fluid medium. We used Andersen et al.’s equation for an elliptical cross-section, as a better model for our leaves. Some of our leaves were elliptical and others not so much.
The glide ratios that we observed generally agreed with those estimated by Ishiguro and Miyaki [22] for rigid objects dropped in a fluid. The glide ratio for elliptical leaves of M. grandiflora was 3.54; it was 6.3 for the deeply incised leaves of Q. alba.
In a series of numerical simulations, Andersen et al. [19] found that the thickness to width ratio β influenced the transition from fluttering to tumbling of plates dropping through a theoretical fluid. The density ratio in their simulations was . Fluttering occurred at β ≤ 0.056. The plates began transitioning between β = 0.077 and 0.091; by β = 0.125, the plates were tumbling (and with a shallower glide ratio). Consequently, the thick, elliptical leaves of M. grandiflora ( in air) should transition more quickly from fluttering to tumbling than thinner leaves of the same size (width in Andersen et al.’s terminology). Though M. grandiflora had the thickest leaves in our study, they did not have the largest thickness to width ratio. The two species with the greatest thickness to width ratios, B. florida and Q. phellos, were also likely to tumble when dropped.
With asymmetric leaves, the torque relative to the center of mass is larger than for a symmetrical leaf. Torque is a twisting force that produces rotation. It is produced by air drag and lift forces. Gravity produces no net torque about the center of mass. Because the leaf is moving through air, the drag and lift forces can produce a net torque and cause the leaf to rotate. For a symmetrical leaf, the center of mass will coincide with its geometric center. A mostly symmetrical leaf will rotate (tumble) about its center of mass. A more asymmetric leaf of the same general shape should generate more torque, causing the leaf to rotate more forcibly about a center of mass that does not coincide with its main vein and petiole. We have observed leaves rotating about their midrib (the very definition of tumbling), and also about their trajectory of descent. Rotation about the trajectory of descent can return a tumbling leaf closer to its origin.
When falling, the torque should theoretically break the tumbling motion that would carry a leaf some distance from the drop point. Hence, asymmetric leaves should fall closer to the root zone. This was true for our artificial A. rubrum leaf, but not for Q. velutina or Perilla frutescens. Ulmus americana was the species with an asymmetric base, but many of the species, especially Acer and Quercus, had more or less asymmetric leaves. More study is clearly necessary.
Steadily falling would be ideal for dropping a leaf over the critical root zone, but the Reynold’s numbers of leaves, plates, or cards falling in a fluid are rarely small enough for this to occur. Fascicles of pine needles have very small β and drop straight down, but we only observed the occasional leaf of an angiosperm seeming to drop straight down without flutter. Fluttering objects swing from side to side, shedding turbulence. Fluttering prevails when I*, Fr, or β is small (but larger than some threshold value); when I*, Fr, or β is larger, tumbling prevails [19,20]. Tumbling, though, is likely to carry a leaf far from its origin. As I*, Fr, or β continue to increase, however, tumbling transitions to chaotic fall, though some mixture of flutter and tumble can occur in the transition region between flutter and tumble [19].
We are still unsure how gliding figures into this sequence of transitions from laminar to turbulent flow. Most papers in the falling plate/card literature do not mention a purely gliding motion, though it is important in the aeronautics literature. The most efficient gliders of human design try to minimize turbulent flow. Our anecdotal observations of leaves that were more likely to glide were that they were more symmetrical than average. They also had leaf shapes that were cuneate (wedge shaped) or flabellate, like a child’s paper glider. Some very symmetrical leaves of Q. alba were surprisingly likely to glide long distances. Other asymmetrical leaves of Q. alba quickly transitioned to flutter or chaos.
Do petioles increase the stability of a falling leaf, consequently influencing glide ratios? According to Brower [48], long-tailed pterosaurs had long tails that conveyed stability at the cost of maneuverability. Our observations suggested that long petioles in ginkgo may do just that. Many of the narrow fan-shaped leaves that glided some distance from the drop point had long petioles. This will require more study and manipulation of leaves to confirm.
Deep sinuses decrease r (half of w), the distance to the axis of rotation, thus decreasing the dimensionless moment of inertia I*. As an estimate for deeply lobed leaves, we assumed that half the leaf width r = the harmonic mean of the lobes and sinuses. As r decreases, I* increases. In simulated dynamics of falling plates, Andersen et al. [19] found that at I* = 1.1, plates exhibit periodic fluttering; at I* = 1.4 and 1.45 they exhibit tumbling; at I* = 1.6 they observed a mixture of fluttering and tumbling; at I* = 2.2 there were chaotic dynamics; at I* = 3.0 they observed small amplitude broadside on fluttering. Values of I* between 1.4 and 1.45 take the plates furthest from the drop point.
We have not yet mentioned serrated leaf margins. They are non-existent in the falling plate literature, but they beg the question, do teeth on leaf margins function as vortex-generators, making an early transition from laminar to turbulent flow more likely? There is, however, an alternate hypothesis for serrated margins—vortex generators can enhance heat transfer from a surface, cooling a leaf. However, if this was the main function of serrated margins in tree leaves, one might expect them to be common in tropical and subtropical tree species.
We only video-taped two leaves to estimate Reynold’s number, but both estimates were much higher than the published thresholds necessary for a transition from laminar to turbulent flow. These published thresholds vary greatly, depending on minor details of the falling objects and perturbations in the environment. Unsurprisingly, both videotaped drops were characterized by a chaotic descent.
4.5. Falling Leaves of Temperate Forest Trees
Our leaf drops demonstrated that most of the variation in lateral distance D traveled from the drop point (and glide ratio) is among leaf drops within individual leaves within a species. This accounts for 75–80% of the total variation in D. Any given leaf might fall directly over the critical root zone or at some distance from it. There is also considerable leaf-to-leaf variation within a species. Leaf shape within a single tree can vary greatly. Among-leaf variation within a species represents anywhere from 13 to 19% of the total variation in D. The least amount of variation was between species, but this still represented 1–11% of the total variation.
One surprising observation was how much the way leaves were collected and treated mattered. Some of the leaves we dropped were collected fresh and pressed prior to dropping them. Others were collected off the ground and had been lying on the ground for an unknown length of time. The pressed leaves were flattened into two dimensions, stiff and brittle, while those on the ground were dried, brittle, and distorted into three dimensions to some extent. With American sycamore leaves (P. occidentalis), the pressed leaves tended to glide and tumble a greater distance away from the drop point than those leaves we collected on the forest floor. The leaves from the forest floor tended to either drop straight down or flutter. Anecdotal observations of falling sycamore leaves in Great Smoky Mountains National Park on a breezy day in October 2022 suggest that most leaves fluttered down unless they were picked up in a strong gust. We observed that the sycamore leaves falling in the Smoky Mountains were dried and bent to some extent before the tree shed them. Other trees, such as Q. alba, tended to shed leaves that were still green and flexible.
All of the leaves we examined (16 species) for lamina length, width, and thickness had estimated Froude numbers greater than the critical value (Frc = 0.67 ± 0.05) necessary for a transition from flutter to tumble [18]. Moments of inertia (I*) were also in the range reported by Andersen et al. [19,20], and although we only estimated the Reynold’s number Re for the leaves of two species, it was very high as well. The combination of high I* and Re is associated with chaotic descent [17], which we observed in many of the leaf drops of both real and artificial leaves.
We only examined the compound leaves of three species of Carya—C. glabra, C. ovata, and C. tomentosa. As we had anticipated, the leaves of C. ovata and C. tomentosa tended to drop close to the drop point. However, the small sample (n = 5) of pressed C. glabra leaves behaved quite differently, gliding a distance from the drop point. The small sample size may have contributed to the differences, as well as the fact of all three groups of leaves being pressed flat before being dropped. In the field, we observed C. ovata dropping entire compound leaves when they were already dry, brittle, and distorted into three dimensions. Unlike our pressed leaves, these compound leaves fell straight down, rather than fluttering or gliding. Consequently, the behavior of C. glabra in our leaf drops may not be characteristic of actual falling leaves. On the other hand, C. glabra has much larger terminal leaflets than either C. ovata or C. tomentosa, which may contribute to the differences.
Additional observations on campus and in the Great Smoky Mountains revealed that species with compound leaves do not always drop the entire compound leaf. In many species, the leaflets also have abscission layers [44,45]. An American ash immediately adjacent to the shagbark hickory mentioned in the previous paragraph was observed dropping leaflets, not entire leaves. The leaflets of the ash were elliptical and nearly all of them tumbled a distance from the trunk. In the Great Smoky Mountains, a black walnut (Juglans nigra) was observed dropping both leaflets and entire leaves, but the vast majority shed were individual leaflets.
The leaves of elms (Ulmaceae) are roughly elliptical, but strongly asymmetric and strongly toothed at the same time. The tallest elms, such as Ulmus americana var. americana and U. rubra, have more asymmetrical leaves (strongly oblique) than shorter members of the genus, such as U. alata and U. crassifolia [39]. Our research suggests that asymmetric leaves may transition to chaotic descent more rapidly than symmetric leaves.
Among the oaks, Q. montana (prinus in some of the older literature) has elliptical leaves with a wavy margin. This species tends to be present on crestlines and moderately dry middle slopes in the Appalachian and Smoky Mountains [49,50], and well-drained sandy soils of the New Jersey Pinelands [51]. In the Pinelands, Q. montana was associated with deep litter and high ground cover.
4.6. Ginkgo biloba
We treated the leaves of ginkgo in separate analyses because of the extreme diversity in leaf shape, even on a single tree. In addition, ginkgo is taxonomically distinct from the other trees in this study, which were all Angiosperms, while ginkgo is a Gymnosperm.
Ginkgo has a diversity of leaf shapes and sizes. Those with smaller areas and narrower basal angles tend to be high up, while those with larger lamina areas and broader basal angles are generally from lower on the trunk. The petioles of ginkgo also tend to be longer than those of many species; consequently, those leaves with longer petioles tend to drop, or glide, petiole first.
The distribution of distances that ginkgo leaves fell was polymodal. Many of the smaller leaves with narrow angles, as well as the bilobed leaves, glided down, falling a great distance from their drop point. On the other hand, most leaves of all three shape categories spiraled (gyrated) straight down, petiole first. This distinction was specific to individual leaves. Those falling the closest to the drop point had basal angles of about 140 degrees, and a small area. An anecdotal observation was that the leaves most likely to glide were the more symmetrical ones, which we plan to test in the future.
We examined the effects of petiole length in relation to ginkgo. It was negatively correlated with basal angle. Leaves with narrow basal angles had the longest petioles. These leaves were most likely to spiral down with a very steep glide ratio, but given the great variation (some of the wide-basal angle leaves had long petioles too), the relationships are complex and deserve further study.
Although the interactions between leaves and categories of descent were insignificant, none of the leaves with a wide base were seen gliding, whereas many of those with either a narrow base or those with two lobes were seen to glide a distance from the drop point, often hitting a wall in the room we used. These glides probably reflect the two peaks in our analysis of basal angle, area, and distance. Most ginkgo leaves displayed gyrational or chaotic descents.
We examined the distribution of leaves around the base of a small, isolated ginkgo tree. The majority of leaves were on the ground within the 2 m radius drip line of the crown.
4.7. Artificial Leaves
The artificial leaves of Q. velutina, P. frutescens, and A. rubrum were all different in their behavior. Asymmetrical versions of Q. velutina and P. frutescens were more likely to fall chaotically than their symmetricized versions. Surprisingly, there were no differences in the distance D traveled by those same symmetrical and asymmetrical leaves. In contrast, the symmetrical leaf of A. rubrum drifted further from the drop point than the original asymmetric leaf, and all A. rubrum leaves drifted further than those of Q. velutina and P. frutescens. This result should be interpreted cautiously, because we only worked with one artificial leaf from each species. Our two variance components’ ANOVAs (including A. rubrum and Q. velutina) indicated that leaf-to-leaf variation within species accounts for 13% to 19% of the total variation in distance traveled from the drop point. A follow-up to this experiment should involve multiple symmetric and asymmetric artificial leaves of several species, standardized by size, and with added petioles.
The differences between symmetrical and asymmetrical leaves of A. rubrum were also interesting because the drops of both treatments were characterized by tumbling, and yet the asymmetrical leaves were more likely to involve autorotation in addition to tumbling. Tumbling involves rotation around the leaf’s long axis parallel to the mid-rib. The autorotation that we observed in the asymmetrical leaf occurred around the trajectory of descent, such that the leaf often doubled back on itself, drifting away from the drop point and then returning back towards the drop point. This is all the more remarkable given the subtle differences between the original and symmetricized versions of the A. rubrum leaf, compared to the dramatic differences between the original and symmetricized leaves of Q. velutina and P. frutescens.
4.8. Ellipse Packing of Temperate and Tropical Forest Leaves
Most forest trees in the tropics have entire leaves, which are elliptical in shape [3]. The likely explanation for elliptical leaves is that they provide minimal overlap in a three-dimensional environment where shading is a problem and leaves are approximately the same size. In theory, polyhedrons (including cubes) can be packed more efficiently in three-dimensional space, but only so long as all objects are the same size and placed purposefully. Therefore, shipping containers are generally polyhedrons of uniform dimension, but polyhedrons do not pack well if they are thrown together at random. In two dimensions, the corresponding shapes would be squares, rectangles, and triangles—again, all the same size. This is impractical for leaves, which are two-dimensional objects of variable sizes in a three-dimensional space, with an element of randomness applied.
Packing problems have focused on the packing of spheres, ellipsoids, cones, cubes, and tetrahedrons in three dimensions, and disks, ellipses, and triangles in two dimensions. Leaves can be thought of as two-dimensional objects in three-dimensional space. Most packing problems deal with situations in which there is no overlap of objects. For leaves, however, overlap is inevitable, but this overlap needs to be minimized to avoid self-shading.
Three categories of ellipsoids are in common commercial use, in part because they can pack efficiently. Many vitamin capsules, for example, are prolate ellipsoids, while M&M candies are oblate ellipsoids [23]. Many lenses are aspherical ellipsoids, to eliminate spherical aberration. Many leaves, on the other hand, are two-dimensional sections of either a cone or an ellipsoid, but deeply lobed, emarginate leaves are often not ellipses at all, and have shapes that can only be described mathematically as ellipses with super-imposed Fourier or polynomial transforms of the curved margins.
A review of the literature on packing suggests that elliptical leaves are by far the best at minimizing overlap. Ellipsoids having aspect ratios greater than = 1.7321 pack more densely than spheres, which have an aspect ratio = 1 [23,24]. A maximal packing index of 0.74 is to be expected. As we have seen with the leaves of trees in tropical forests, many have aspect ratios greater than 1.731. The aspect ratio of flowering dogwood, an understory tree with entire, finely serrated, elliptical leaves, was 1.818 ± 0.138, and the packing index φ’ (taking overlap as a penalty) was 0.7826. Water lilies have aspect ratios approaching δ = 1, but can still pack densely if their leaves vary greatly in size to fill the interstitial spaces, as they do with Victoria amazonica (Poepp.) J.C. Sowerby, a species in which overlap is inhibited by tall leaf margins that prevent overgrowth of neighboring leaves. The submerged leaves of other aquatic macrophytes tend to be elliptical, elongated, or linear in a three-dimensional space [52]. The average contact number increases above α ≈ 1.5 and then stabilizes at about 5.9 contacts per object [25].
The aspect ratios of the leaves we examined ranged from α < 1 for P. occidentalis to α > 5 for Q. phellos. Interestingly, P. occidentalis exhibits much greater variation in overall leaf size than all of the other species we examined; the coefficient of variation for leaf length was 0.2549. All other angiosperm leaves had coefficients of variation less than 0.1750. Wide ginkgo leaves have coefficients of variation slightly less than sycamore. This parallels observations on floating leaves of V. amazonica. As with V. amazonica, does this variation allow these leaves to minimize self-shading, despite aspect ratios that overlap those of a circular disc? These observations require considerably more research.
The aspect ratios we used for deeply lobed leaves such as Q. palustris (pin oak) involve our taking the harmonic mean of the sinuses and lobes. This is based on our untested assumption that the sinus diameters are likely more important than the lobe diameters in influencing behavior in a fluid. This assumption requires further attention, and it is likely that the aspect ratios of elliptical and lobed leaves cannot be compared.
Although there have been no studies on the packing of objects shaped like the leaves of white oak, silver maple, or American sycamore, it seems unlikely that these leaves would pack into a space without significant overlap. In contrast to the simple leaves of oaks and maples, the compound leaves of walnut, hickory, and ash may provide an efficient way to pack leaves in these species, by controlling the relative spatial positions of the leaflets. This is a project for future research.
4.9. Mulching and Litter Decomposition
One of the main arguments against our hypothesis is that in a temperate deciduous forest, trees of various species can supply their leaves as mulch for neighboring trees. Is there any advantage to self-mulching in a forest?
Mulching involves the human application of organic or inorganic materials to a soil surface for the purpose of stimulating plant growth or inhibiting that of weeds. The organic material can be leaves, grass, twigs, or woody material, while inorganic material can include plastic sheets, gravel, or cobbles. In this paper, we use the term ‘mulch’ to also mean the application of leaf litter by the plants themselves.
Mulching by leaf litter can have several advantages for trees. There is a large body of research on its beneficial aspects [36,53], such as the protection of roots from freezing, maintaining soil moisture, improving soil structure, and the recycling of nutrients lost during leaf fall. Mulching often increases plant growth, and presumably fitness, but can occasionally inhibit growth [53].
Too many leaves covering an already moist soil can inhibit aeration [36,53], and can sometimes promote the growth of disease-causing bacteria, water molds, and fungi, such as Phytophthora. This is likely to be a problem in swamps, bottomlands, and along stream corridors. We expect that leaves of trees in these habitats are less likely to have the characteristics we have focused on—deep sinuses, serrations, and asymmetry, unless they are early successional species for which competition for light is less important than competition for soil nutrients other than water.
Many temperate species with simple entire and elliptical leaves can be found in these bottomlands [54]. Black gum (Nyssa sylvatica Marshall) is the most common and notable species. Swamp Chestnut Oak (Quercus michauxii Nutt.) and Water Tupelo (Nyssa aquatica L.) are bottomland species that have elliptical leaves that may have shallow, rather than deep, serrations. Willow oak (Q. phellos L.) and laurel oak (Q. laurifolia Michx.) are species with large aspect ratios, conducive to tumbling falls and shallow glide angles. Water oak (Q. nigra L.) has spatulate leaves that resemble gliders. In some of our leaf drops, Q. nigra leaves were indeed prone to gliding if the leaves were dropped fresh.
Exceptions to this pattern of bottomland trees include red maple (Acer rubrum L.), swamp white oak (Q. bicolor Willd.), and sweetgum (Liquidambar styraciflua L.). However, even these exceptions prove the rule. Red maple exists in upland and lowland phenotypes. The lowland forms have less extreme sinuses and some leaves approach being entire. Swamp white oak has shallow serrations, compared to the closely related white oak, a mostly upland species. Sweetgum shows similar leaf shape variation [55,56], with var. rotundiloba being the variant with less extreme lobes and sinuses. These differences, and differences in leaf shape between upland and lowland trees, require further study.
In general, tropical forests have more leaf litter than temperate forests. There is a gradient in litter deposition from the boreal zone to the equator. According to Chakravarti [10], much of the gradient is due to the length of the growing season. Moreover, decomposition rates double (Q10 = 2) with each 10 °C increase in temperature [57]. Decomposition rates also increase with increasing humidity and moisture. Surprisingly, tropical forests also have little or no humus layer, because nutrients get recycled efficiently.
4.10. Home-Field Advantage Hypothesis and Ectomycorrhizal Fungi
The Home-Field Advantage Hypothesis posits that leaves decompose more rapidly under their parent tree [15]. The hypothesis is controversial, and there is contradictory evidence for different species and communities. To explain the discrepancies in the data, at least three alternative hypotheses have been proposed. Freschet et al. [58], for example, suggest that the Home-Field Advantage Hypothesis is a sub-category of an interaction between litter substrate quality (low, intermediate, high) and matrix quality (mass ratio of each leaf litter type), and that this can explain more of the discrepancies in the data. A second alternative is the Functional Breadth Hypothesis [59,60], which suggests that the ability of the soil biota to decompose a complex stew of litter components depends on the functional breadth of the microorganisms. Finally, Fanin et al. [61] argue that previous studies have ignored the microorganisms already present on the total above-ground surface of plants, the phyllosphere. Many previous studies have sterilized the leaves before placing them in either home or guest environments. When the leaves or litter are not sterilized before being placed in litter bags, the Home-Field Advantage Hypothesis is more easily demonstrated. Regardless of which hypothesis provides the best explanation for the observed data, the soil biota, and probably the phyllosphere as well, are now thought to be equivalent to climate and litter quality in determining decomposition rates [62].
It is an open question whether endophytes present within plant leaves contribute to the decomposition of a host-plant’s leaves [63]. Most studies of endophyte saprophytic capacity have involved grasses and aquatic decomposers rather than forest litter. Davis [64,65] has shown that endophytes associated with Quercus gambelii Nutt. (Gambel’s oak) can function as saprophytes within the litter. For tropical forests, endophyte diversity decreases linearly with increasing temperature seasonality, and curvilinearly with moisture seasonality [66].
As an example of the conflicting results, many species of oaks produce tannins, which deter herbivores and infective fungi, and have allelopathic properties. Tannins are allelopathic to seedlings, and are also toxic to many species of soil microbes [67]. Oaks also have high amounts of lignins, complex organic polymers. Both tannins and lignins render oak leaves resistant to decomposition. Such litter material has been termed recalcitrant litter [62]. Indeed, there is some evidence that oak leaves decompose more quickly under an oak canopies [68,69], but Ayers [15] sterilized the litter, thus excluding the phyllosphere; see also the work of Midgely [70]. Basidiomycota, common soil fungi, are efficient decomposers of lignin and other recalcitrant organic polymers [71].
In addition to soil fungi, mycorrhizal fungi, in particular arbuscular mycorrhizae (AM), may contribute to Home-Field Advantage for some species [14]. Midgely [70], for example, found that leaves from AM species (A. rubrum, Liriodendron tulipifera L., P. serotina) decomposed more rapidly within high-quality AM litter, and that AM species produced higher-quality litter than ectomycorrhizal (ECM) species of Quercus, Carya, and Fagus. Their experiments, however, did not support the predictions of the Home-Field Hypothesis. The leaves of the oaks in their study (Q. rubra, Q. prinus (montana) and Q. velutina) decomposed at the same slow rate under all treatments (AM litter vs. ECM litter, fertilized vs. unfertilized plots).
Arbuscular mycorrhizae dominate in the tropics, while ectomycorrhizae dominate in the temperate zone [12]. Ectomycorrhizal fungi are capable of decomposing litter in some rare circumstances [72]. Arbuscular mycorrhizal fungi, in contrast, are not known to decompose leaf litter directly. Nevertheless, nutrient recycling is more rapid in AM-dominated forests [71]. According to Bunn et al. [72], the AM fungi are able to acquire nutrients through other microorganisms. In addition, mycorrhizal fungal connections between neighboring trees may enhance the conspecific seedling growth of ECM trees; this is an example of positive plant–soil feedback [73,74]. This effect on seedling growth and survival has not been observed in AM trees, in part because of soil pathogens in the roots of AM trees [73].
The main microorganisms decomposing the leaf litter are saprophytic fungi and bacteria, but even if mycorrhizae are not directly involved in breaking down leaf litter, they are adapted to particular plant species and the soils those species create and inhabit. If oak leaves, for example, create a soil environment rich in tannins and lignins, those specialist mycorrhizae might benefit from those leaves if they inhibit competing fungi [75]. This suggests feedback between the tree and its mycorrhizae. The tree cultivates a soil beneficial to its mycorrhizae. This is quite independent of the Home-Field Advantage Hypothesis, which involves non-mycorrhizal fungi (as well as bacteria). Consequently, there is potential for the oak leachate to control the microbial community in its vicinity, perhaps even slowing decomposition. Plant–soil feedback is dauntingly complex [74,76].
Bagchega et al. [77] have argued that Home-Field Advantage is not to be expected in communities of predominantly generalist decomposers. They were unable to find any evidence of Home-Field Advantage for Eucalyptus and Acacia in a tropical ecosystem. We know that ectomycorrhizal fungi of the temperate zone tend to be specialists with respect to the genera and family of plants, whereas arbuscular mycorrhizal fungi in the tropics tend to be generalists [12]. Arbuscular mycorrhizae can form associations with almost any vascular plant that forms mycorrhizal associations [12]. Do these differences between mycorrhizae indirectly drive the observed examples of Home-Field Advantage? In other words, do species-specific microorganisms, including fungi, decompose host leaves faster than non-host leaves? This remains to be established.
Another possibility is that some litter and soil combinations may function to slow decomposition, especially if retaining soil moisture outweighs nutrient acquisition in drier habitats. A deeper litter layer will presumably maintain soil moisture. Midgley et al. [70] found that litter from several ECM oak species (Q. prinus (montana), Q. rubra, Q. velutina) decomposed more slowly than that of AM species (A. rubrum, Liriodendron tulipifera L., P. serotina), even when under an ECM canopy and when the soil was enriched with nitrogen. As a practical example, Collins and Good [51] observed deeper litter under oaks in the New Jersey Pinelands. This may also explain why many oaks hold on to their leaves longer before dropping them. Do some oaks drop their leaves later to slow decomposition?
4.11. The Role of Allelopathy
Allelopathy involves the chemical interactions, both negative and positive, among plants [78] and among plants and soil microbes [79]. Most research has focused on the negative interactions, but there are positive interactions as well. Moreover, there has been controversy regarding how important allelopathy is for plant communities, with some authors suggesting that it is unimportant for communities of co-evolved species. Several of the species we have examined, or those in our temperate forest communities, have been reported to have allelopathic properties. For our analysis, we are particularly interested in allelopathic leaves rather than roots.
Coder [80] ranked a variety of temperate forest species into categories of allelopathy: strongest, moderate, and slight effect. He also included information on the source of allelopathy—roots, leaves, fruit, or stems. Those species in our area with the greatest allelopathic effect of leaves include butternut (Juglans cinerea L.), black walnut (J. nigra L.), Prunus serotina, Q. falcata, Q. marilandica, Q. rubra, post oak (Q. stellata Wangenh.), sassafras (Sassafras albidum (Nutt.) Nees), and U. americana. Those of moderate effect include Q. alba, swamp chestnut oak (Q. michauxii Nutt.), and Q. shumardii. In addition, Quercus rubra and Fraxinus spp. have allelopathic leaves of slight effect. Note that Coder [80] includes Q. rubra in both the strongest and slight effect categories, based on conflicting papers; this observation underlines the extent of variation among studies of allelopathy. Nevertheless, it is apparent that many of the species we have examined or observed have allelopathic leaves. How does this figure into our argument?
Should an allelopathic tree drop its leaves over its critical root zone, or should it drop them beyond it? Does it matter? The potential for autotoxicity of allelopathic chemicals is always present. Does a tree benefit from allelopathic leaves if it drops them at a distance from its trunk and root zone?
Black walnut is one of the most allelopathic of temperate trees. Hydrojuglone, the main allelopathic chemical, is found in roots, leaves, fruit hulls, and inner bark [81,82]. When oxidized in the environment, hydrojuglone is converted to toxic juglone. According to Appleton et al. [82], the toxic effects of juglone can extend beyond the drip line. This may be due, in part, to the extent of the root zone. However, leaves dropped during the onset of winter may also play a role. The compound leaves of black walnut have as many as 19–23 leaflets. If the entire compound leaf falls as a unit, it does so close to the trunk, but black walnut also has abscission layers at the base of the leaflets, and these can fall independently of the entire compound leaf. Our observations of black walnut in Great Smoky Mountains National Park suggest that it is mainly independent leaflets that fall, and that these can tumble a distance from the trunk. In addition to black walnut, English walnut, shagbark hickory (C. ovata), and pecan also produce juglone [81]. Our observation of shagbark hickory is that the compound leaves drop as a unit in steady descent, and they do so when the leaves are thoroughly dried.
Oaks and other members of the Fagaceae produce allelopathic tannins [83]. According to Mole [84], 73% of Quercus species contain tannin. It will be interesting to compare tannin levels in oak leaves with different shapes. Water oak (Q. nigra L.), for example, has spatulate leaves that seem designed to glide far from the parent tree.
In addition to its impacts on potentially competing plants, allelopathy’s main target may be soil microorganisms [79]. Trees may use allelopathic chemicals to modify the soil microbiota in their favor, favoring co-adapted microorganisms. This seems likely for species of Quercus, favoring microorganisms that either (1) decompose oak leaves more quickly if nutrient cycling is important or (2) decompose oak leaves more slowly if retaining soil moisture is important.
4.12. Fire and Leaf Shape
Fire likely factors into the evolution of leaves with prominent lobes, deep sinuses, asymmetries, and serrated margins. Fire burns off litter and duff, releasing nutrients to both the soil and atmosphere [85]. Soils whose litter has burned off are likely to lose moisture. Consequently, it is important for trees to replenish litter over their roots, at least within reason. Leaf litter that is too heavy can kill a tree if the burning fuel transmits enough heat to shallow roots [86]. Fire frequency underscores another difference between temperate and tropical forests. Although fire frequency varies by forest type, tropical rain forests are, on average, more resistant to fire [87,88]. Some tropical forests have never burned.
Leaf shape may be important to re-establishing a layer of litter following fire in ecosystems having a high frequency of fire. Most fire-adapted oaks (pyrophytes), for example, in the southeastern United States, have leaves with deep lobes and sinuses. These include turkey oak (Q. laevis Walter), sand post oak (Q. margarettae (Ashe) Small), and southern red oak (Q. falcata) [89]. The exception here is bluejack oak (Q. incana Bartram, a pyrophytic sub-canopy species rarely exceeding 10 m in height. Two of the three species with incised leaves (Q. laevis and Q. falcata) are canopy species, growing to 28 m and 44 m, respectively. Quercus margarettae, also with broadly incised leaves, is usually a subcanopy tree rarely exceeding 12 m. Both fire-avoiding species, southern live oak (Q. virginiana Mill.) and sand live oak (Q. geminata Small) have entire leaves; they reach heights of 20 m and 15 m, respectively. Sand laurel oak (Quercus hemisphaerica Bartram ex Willd.) is a mesophyte with mostly entire leaves that reaches 18–35 m. Quercus nigra, another mesophyte, has spatulate leaves with very shallow sinuses; it reaches 30 m.
As with other aspects of our paper, leaf shape and fire frequency deserve a more in-depth analysis. This may be possible by examining the floras of both temperate and tropical forests with known fire frequencies, judged from fire scars on the trunks of cored trees.
4.13. Caveats
Not all leaves originate directly above the trunk. Most leaves are displayed around the periphery of the crown, so as not to shade one another. Consequently, crown architecture is likely to influence leaf fall. In addition, leaves near the center of the crown are apt to collide with leaves and branches while falling. This is especially true of southern magnolia, which has a tall pyramidal crown. For this species, most leaves accumulate 2–3 deep within the drip-line.
We have not examined the influence of pubescence and leaf hairs on how leaves fall in air. In general, we suspect that surface hairs are short enough to lay within a boundary layer of laminar flow. This should be examined in an experimental situation, using artificial and real leaves ranging from glabrous to densely pubescent, in a wind tunnel. For some leaves, the pubescent layer can be gently removed before dropping the leaves.
An alternative explanation for the aerodynamics of leaves is that they evolved to reduce drag and mechanical damage to tall trees during intense windstorms [90]. This hypothesis, however, does not explain the difference between temperate and tropical leaf shape. Intense storms (cyclones, hurricanes, etc.) are certainly not restricted to the temperate zone [91,92].
The key to future research on the topic of self-mulching is the use of artificial leaves of various shapes and sizes. Our artificial leaves only included the lamina. Future experiments should evaluate the role of the petiole (including petiole length), which clearly plays an important role in shifting the center of mass towards the base of the lamina. Moreover, we only used one artificial leaf of each of the three species, and Perilla frutescens is a herb, not a tree. Tree leaves of many species exhibit extreme variation among trees, and even within a single tree. Some of the within-tree variation is associated with location within the crown. This variation needs to be accounted for with artificial leaves.
We did not use the needle-like leaves of conifers in any of our comparisons. Nevertheless, we observed thousands of eastern white pine (Pinus stobus L.) needles (entire fascicles) being shed during a windy October day in the Great Smoky Mountains. Clumps of needles drop straight down, with steep glide ratios, much steeper indeed than any of the broadleaf trees we examined. Such behavior is to be expected given the very small thickness to width ratios β of pine needles.
5. Conclusions
In our view, the evolution of leaf shape entails trade-offs between light acquisition by leaves and water and nutrient acquisition by roots and mycorrhizae. Elliptical leaves with entire margins minimize self-shading, while emarginate leaves of various kinds contribute to the leaf litter over the critical root zone, maintaining moisture, nutrients, and a co-adapted community of fungi, bacteria, and protists. Elliptical leaves with aspect ratios of 1.7 or more can be more efficiently packed than most other shapes, thus avoiding self-shading. This strategy should apply to most tropical species, understory trees in temperate forests, and dominant lowland species not needing to conserve soil moisture. Emarginate leaves of temperate species sacrifice light acquisition for root health and increased feedback between the tree and its microbial community. Some trees, such as elms and birches, may hedge their bets by having elliptical leaves with serrated margins or asymmetric bases.
For subcanopy trees such as dogwood and persimmon, competition for sunlight is apt to be more critical than competition for water and nutrients. The same can be said for undisturbed tropical forests, where competition for light is fierce [93,94,95]. In addition, tropical and temperate forests differ in how strata develop during succession. Tropical forests have more layers of vegetation than temperate forests [96]. Moreover, tropical forests develop more rapidly than temperate forests following disturbances. Consequently, light attenuation occurs sooner.
There has been little research on leaf shape in successional sequences in tropical forests. One notable pioneer species, Macaranga gigantea (Reichb.f. and Zoll.) Müll. Arg., a euphorb from southeast Asia, has emarginate leaves [97], reminiscent of some temperate maples. Yamada et al. [98] concluded that the orientations of the leaves of this species were adapted to minimize self-shading, though it seems more likely that entire, elliptical leaves would do a better job.
In this paper, we have used aspect ratio to describe variation in the shape of elliptic leaves. The literature on the packing of ellipsoid objects uses aspect ratios. Nevertheless, other descriptors of elliptic leaf shape are available [99,100].
Given that leaf asymmetry may be adaptive in a variety of plant species, it makes little sense to use it as a measure of fluctuating asymmetry. Indeed, self-mulching by species having asymmetrical leaves “designed” to maximize torque may partly explain why leaf asymmetry is such a poor indicator of stress for some species [101]. Other plant organs, such as flowers, may provide better tools for estimating stress.
Few of the various hypotheses that have been proposed to explain temperate and tropical differences in leaf shape are mutually exclusive. In addition to our proposed ideas, these include photosynthetic efficiency, water-use efficiency, transpirational cooling, heat dissipation, water loss through transpiration, winter bud-packing, gas exchange, support and supply, hydraulics, vein geometry, leaf thickness, and rates of leaf expansion. The complexity of the various hypotheses is daunting.
Author Contributions
Conceptualization, J.H.G.; methodology, J.H.G. and R.C.; validation, J.H.G. and R.C.; formal analysis, J.H.G. and R.C.; investigation, J.H.G. and R.C.; resources, J.H.G.; data curation, J.H.G.; writing—original draft preparation, J.H.G.; writing—review and editing, J.H.G. and R.C.; visualization, J.H.G.; supervision, J.H.G.; project administration, J.H.G.; funding acquisition, J.H.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was initially funded in part by Berry College.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to lack of funding.
Acknowledgments
We thank Todd Timberlake, Serena Kargbo, Jared Blake, and Shannon Whitney for their help. D. Carl Freeman, Todd Timberlake, Martin Cipollini, and Tom Givnish read early drafts of the manuscript. J.H.G.’s two mentors, Ralph Good and Ted Stiles, provided the inspiration to ask evolutionary questions regarding plant community ecology and adaptive design. This project had its origins in a field lab taught by J.H.G. at Berry College; that lab was based on one taught by Ted Stiles. J.H.G.’s late wife, Catherine Chamberlin-Graham, helped during the early stages of this project, and this paper is dedicated to her.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicotra, A.B.; Leigh, A.; Boyce, C.K.; Jones, C.S.; Niklas, K.J.; Royer, D.L.; Tsukaya, H. The evolution and functional significance of leaf shape in the angiosperms. Funct. Plant Biol. 2011, 38, 535–552. [Google Scholar] [CrossRef]
- Chitwood, D.H.; Sinha, N.R. Evolutionary and environmental forces sculpting leaf development. Curr. Biol. 2016, 26, R297–R306. [Google Scholar] [CrossRef]
- Bailey, I.W.; Sinnott, E.W. The climatic distribution of certain types of angiosperm leaves. Am. J. Bot. 1916, 3, 24–39. [Google Scholar] [CrossRef]
- Parkhurst, D.F.; Loucks, O.L. Optimal leaf size in relation to environment. J. Ecol. 1972, 60, 505–537. [Google Scholar] [CrossRef]
- Edwards, E.J.; Spriggs, E.L.; Chatelet, D.S.; Donoghue, M.J. Unpacking a century-old mystery: Winter buds and the latitudinal gradient in leaf form. Am. J. Bot. 2016, 103, 975–978. [Google Scholar] [CrossRef]
- Givnish, T. On the Adaptive Significance of Leaf Form. In Topics in Plant Population Biology; Solbrig, O.T., Jain, S., Johnson, G.B., Raven, P.H., Eds.; Columbia University Press: New York, NY, USA, 1979; pp. 375–407. [Google Scholar]
- Givnish, T.J.; Kriebel, R. Causes of ecological gradients in leaf margin entirety: Evaluating the roles of biomechanics, hydraulics, vein geometry, and bud packing. Am. J. Botany 2017, 104, 354–366. [Google Scholar] [CrossRef]
- Baker-Brosh, K.F.; Peet, R.K. The ecological significance of lobed and toothed leaves in temperate forest trees. Ecology 1997, 78, 1250–1255. [Google Scholar] [CrossRef]
- Aerts, R. Climate, leaf litter chemistry and leaf litter decomposition in terrestrial ecosystems: A triangular relationship. Oikos 1997, 79, 439–449. [Google Scholar] [CrossRef]
- Chakravarty, S.; Rai, P.; Vineeta, V.; Pala, N.A.; Shukla, G. Litter production and decomposition in tropical forest. In Handbook of Research on the Conservation and Restoration of Tropical Dry Forests; Gupta, N.C., Kuma, A., Soares de Araújo, F., Chandra, K.K., Singh, A.K., Srivastava, N., Eds.; IGI Global: Hershey, PA, USA, 2020; pp. 193–212. [Google Scholar]
- Meentemeyer, V. The geography of organic decomposition rates. Ann. Assoc. Am. Geogr. 1984, 74, 551–560. [Google Scholar] [CrossRef]
- Allen, E.B.; Allen, M.F.; Helm, D.J.; Trappe, J.M.; Molina, R.; Rincon, E. Patterns and regulation of mycorrhizal plant and fungal diversity. Plant Soil 1995, 170, 47–62. [Google Scholar] [CrossRef]
- Prescott, C.E.; Grayston, S.J. Tree species influence on microbial communities in litter and soil: Current knowledge and research needs. For. Ecol. Manag. 2013, 309, 19–27. [Google Scholar] [CrossRef]
- Frey, S.D. Mycorrhizal fungi as mediators of soil organic matter dynamics. Annu. Rev. Ecol. Evol. Syst. 2019, 50, 237–259. [Google Scholar] [CrossRef]
- Ayres, E.; Steltzer, H.; Simmons, B.L.; Simpson, R.T.; Steinweg, J.M.; Wallenstein, M.D.; Mellor, N.; Parton, W.J.; Moore, J.C.; Wall, D.H. Home-field advantage accelerates leaf litter decomposition in forests. Soil Biol. Biochem. 2009, 41, 606–610. [Google Scholar] [CrossRef]
- Maxwell, J.C. On a particular case of the descent of a heavy body in a resisting medium. Camb. Dublin Math. J. 1854, 9, 145–148. [Google Scholar]
- Field, S.B.; Klaus, M.; Moore, M.G.; Nori, F. Chaotic dynamics of falling disks. Nature 1997, 388, 252–254. [Google Scholar] [CrossRef]
- Belmonte, A.; Eisenberg, H.; Moses, E. From flutter to tumble: Inertial drag and Froude similarity in falling paper. Phys. Rev. Lett. 1998, 81, 345–348. [Google Scholar] [CrossRef]
- Andersen, A.; Pesavento, U.; Wang, Z.J. Analysis of transitions between fluttering, tumbling and steady descent of falling cards. J. Fluid Mech. 2005, 541, 91–104. [Google Scholar] [CrossRef]
- Andersen, A.; Pesavento, U.; Wang, Z.J. Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 2005, 541, 65–90. [Google Scholar] [CrossRef]
- Bose, C. Flow dynamics of a fluttering-tumbling plate using #OpenFOAM #opensource #CFD. YouTube, 19 February 2022. Available online: https://www.youtube.com/shorts/kAjyyD8-fNU (accessed on 30 May 2023).
- Ishiguro, M.; Miyake, Y. Experimental study on directional stability of tumbling plate. J. Inst. Ind. Appl. Eng. 2021, 9, 1–8. [Google Scholar] [CrossRef]
- Donev, A.; Cisse, I.; Sachs, D.; Variano, E.A.; Stillinger, F.H.; Connelly, R.; Torquato, S.; Chaikin, P.M. Improving the density of jammed disordered packings using ellipsoids. Science 2004, 303, 990–993. [Google Scholar] [CrossRef] [PubMed]
- Donev, A.; Stillinger, F.H.; Chaikin, P.M.; Torquato, S. Unusually dense crystal packings of ellipsoids. Phys. Rev. Lett. 2004, 92, 255506. [Google Scholar] [CrossRef]
- Donev, A.; Connelly, R.; Stillinger, F.H.; Torquato, S. Underconstrained jammed packings of nonspherical hard particles: Ellipses and ellipsoids. Phys. Rev. E 2007, 75, 051304. [Google Scholar] [CrossRef] [PubMed]
- Willmarth, W.W.; Hawk, N.E.; Harvey, R.L. Steady and unsteady motions and wakes of freely falling disks. Phys. Fluids 1964, 7, 197–208. [Google Scholar] [CrossRef]
- Lau, E.M.; Huang, W.-X. Variations of flight patterns for falling flexible plates. Phys. Fluids 2021, 33, 081904. [Google Scholar] [CrossRef]
- Prior, L.D.; Eamus, D.; Bowman, D.M.J.S. Leaf attributes in the seasonally dry tropics: A comparison of four habitats in northern Australia. Funct. Ecol. 2003, 17, 504–515. [Google Scholar] [CrossRef]
- Graham, J.H.; Whitesell, M.J.; Fleming, M., II; Hel-Or, H.; Nevo, E.; Raz, S. Fluctuating asymmetry of plant leaves: Batch processing with LAMINA and continuous symmetry measures. Symmetry 2015, 7, 255–268. [Google Scholar] [CrossRef]
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 1883, 35, 84–99. [Google Scholar]
- Trinh, K.T. On the critical Reynolds number for transition from laminar to turbulent flow. arXiv 2010, arXiv:1007.0810. [Google Scholar]
- Anonymous. Tracker Video Analysis and Modeling Tool. Available online: https://physlets.org/tracker/ (accessed on 9 January 2023).
- Uhler, C.; Wright, S.J. Packing ellipsoids with overlap. Siam Rev. 2013, 55, 671–706. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Clark, J.; Gilpin, R.; Hauer, R.; Lilly, S.; Matheny, N.; Smiley, E.T. Why definitions matter: The Tree Protection Zone and the Critical Root Zone. Arborist News 2021, 30, 26–30. [Google Scholar]
- Preece, J.E.; Read, P.E. The Biology of Horticulture: An Introductory Textbook; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lawrence, G.H.M. An Introduction to Plant Taxonomy; The Macmillan, Co.: New York, NY, USA, 1955; p. 179. [Google Scholar]
- Braun, E.L. Deciduous Forests of Eastern North America; Blakiston, Co.: Waterton Park, AB, Canada, 1950; p. 596. [Google Scholar]
- Weakley, A.S.; Southeastern Flora Team. Flora of the Southeastern States; University of North Carolina Herbarium, North Carolina Botanical Garden: Chapel Hill, NC, USA, 2022. [Google Scholar]
- Saladyga, T.; Vanderhorst, J.; Cline, J. Successional dynamics of an Appalachian pin oak (Quercus palustris Münchh.) swamp forest. J. Torrey Bot. Soc. 2020, 147, 22–37. [Google Scholar] [CrossRef]
- Maeglin, R.R.; Ohmann, L.F. Boxelder (Acer negundo): A review and commentary. Bull. Torrey Bot. Club 1973, 100, 357–363. [Google Scholar] [CrossRef]
- Hengst, G.E.; Dawson, J.O. Bark thermal properties of selected central hardwood species. In Proceedings of the 9th Central Hardwood Forest Conference, Purdue University, West Lafayette, IN, USA, 8–10 March 1993; Gillespie, A.R., Parker, P.E., Pope, P.E., Rink, G., Eds.; United States Department of Agriculture, Purdue University: West Lafayette, IN, USA, 1993; pp. 55–75. [Google Scholar]
- Payette, S.; Frégeau, M.; Couillard, P.-L.; Pilon, V.; Laflamme, J. Sugar maple (Acer saccharum) at its northeastern range limit: A fire-resilient tree species. Botany 2018, 96, 411–423. [Google Scholar] [CrossRef]
- Facey, V. Abscission of leaves in Fraxinus americana L. New Phytol. 1950, 49, 103–116. [Google Scholar] [CrossRef]
- Moline, H.E.; Bostrack, J.M. Abscission of leaves and leaflets in Acer negundo and Fraxinus americana. Am. J. Bot. 1972, 59, 83–88. [Google Scholar] [CrossRef]
- Emelianova, Y.P. A study of dynamics of a falling leaf based on a two-dimensional model. In Proceedings of the 4th International Conference: Geometry, Dynamics, Integrable Systems–GDIS 2013, Izhevsk, Russia, 10–14 June 2013. [Google Scholar]
- Tanabe, Y.; Kaneko, K. Behavior of a falling paper. Phys. Rev. Lett. 1994, 73, 1372–1375. [Google Scholar] [CrossRef] [PubMed]
- Brower, J.C.; Veinus, J. Allometry in pterosaurs. Univ. Kans. Paleontol. Contrib. 1981, 105, 1–32. [Google Scholar]
- Martin, W.H. The Lilley Cornett Woods: A stable mixed mesophytic forest in Kentucky. Bot. Gaz. 1975, 136, 171–183. [Google Scholar] [CrossRef]
- Whittaker, R.H.; Levin, S.A.; Root, R.B. Niche, habitat, and ecotope. Am. Nat. 1973, 107, 321–338. [Google Scholar] [CrossRef]
- Collins, S.L.; Good, R.E. The seedling regeneration niche: Habitat structure of tree seedlings in an oak-pine forest. Oikos 1987, 48, 89–98. [Google Scholar] [CrossRef]
- Prescott, G. How to Know the Aquatic Plants; Wm. C. Brown: Dubuque, IA, USA, 1969; p. 155. [Google Scholar]
- Chalker-Scott, L. Impact of mulches on landscape plants and the environment—A review. J. Environ. Hortic. 2007, 25, 239–249. [Google Scholar] [CrossRef]
- Turner, R.E.; Forsythe, S.W.; Craig, N.J. Bottomland hardwood forest land resources of the southeastern United States. In Wetlands of Bottomland Hardwood Forests; Clark, J.R., Benforado, J., Eds.; Elsevier Scientific Publishers: New York, NY, USA, 1981; Volume 11, pp. 13–28. [Google Scholar]
- Duncan, W.H. Leaf variation in Liquidambar styraciflua L. Castanea 1959, 24, 99–111. [Google Scholar]
- Smith, R.F. The leaf dimorphism of Liquidambar styraciflua L. Am. Midl. Nat. 1967, 77, 42–50. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Climate–carbon cycle feedback analysis: Results from the C4MIP model intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Freschet, G.T.; Aerts, R.; Cornelissen, J.H. Multiple mechanisms for trait effects on litter decomposition: Moving beyond home-field advantage with a new hypothesis. J. Ecol. 2012, 100, 619–630. [Google Scholar] [CrossRef]
- Keiser, A.D.; Strickland, M.S.; Fierer, N.; Bradford, M.A. The effect of resource history on the functioning of soil microbial communities is maintained across time. Biogeosciences 2011, 8, 1477–1486. [Google Scholar] [CrossRef]
- Keiser, A.D.; Keiser, D.A.; Strickland, M.S.; Bradford, M.A. Disentangling the mechanisms underlying functional differences among decomposer communities. J. Ecol. 2014, 102, 603–609. [Google Scholar] [CrossRef]
- Fanin, N.; Lin, D.; Freschet, G.T.; Keiser, A.D.; Augusto, L.; Wardle, D.A.; Veen, G.F. Home-field advantage of litter decomposition: From the phyllosphere to the soil. New Phytol. 2021, 231, 1353–1358. [Google Scholar] [CrossRef]
- Osburn, E.D.; Hoch, P.J.; Lucas, J.M.; McBride, S.G.; Strickland, M.S. Evaluating the roles of microbial functional breadth and home-field advantage in leaf litter decomposition. Funct. Ecol. 2022, 36, 1258–1267. [Google Scholar] [CrossRef]
- Wolfe, E.R.; Ballhorn, D.J. Do foliar endophytes matter in litter decomposition? Microorganisms 2020, 8, 446. [Google Scholar] [CrossRef] [PubMed]
- Davis, E.L. Saprotrophic Capacity of Endophytic Fungi; Brigham Young University: Provo, UT, USA, 2021. [Google Scholar]
- Davis, E.L.; Weatherhead, E.; Koide, R.T. The potential saprotrophic capacity of foliar endophytic fungi from Quercus gambelii. Fungal Ecol. 2023, 62, 101221. [Google Scholar] [CrossRef]
- Oita, S.; Ibáñez, A.; Lutzoni, F.; Miadlikowska, J.; Geml, J.; Lewis, L.A.; Hom, E.F.Y.; Carbone, I.; U’Ren, J.M.; Arnold, A.E. Climate and seasonality drive the richness and composition of tropical fungal endophytes at a landscape scale. Commun. Biol. 2021, 4, 313. [Google Scholar] [CrossRef]
- Bhat, T.K.; Singh, B.; Sharma, O.P. Microbial degradation of tannins–a current perspective. Biodegradation 1998, 9, 343–357. [Google Scholar] [CrossRef]
- Hansen, R.A. Red oak litter promotes a microarthropod functional group that accelerates its decomposition. Plant Soil 1999, 209, 37–45. [Google Scholar] [CrossRef]
- Gao, J.; Kang, F.; Han, H. Effect of litter quality on leaf-litter decomposition in the context of Home-Field Advantage and non-additive effects in temperate forests in China. Pol. J. Environ. Stud. 2016, 25, 1911–1920. [Google Scholar] [CrossRef] [PubMed]
- Midgley, M.G.; Brzostek, E.; Phillips, R.P. Decay rates of leaf litters from arbuscular mycorrhizal trees are more sensitive to soil effects than litters from ectomycorrhizal trees. J. Ecol. 2015, 103, 1454–1463. [Google Scholar] [CrossRef]
- Bahram, M.; Netherway, T.; Hildebrand, F.; Pritsch, K.; Drenkhan, R.; Loit, K.; Anslan, S.; Bork, P.; Tedersoo, L. Plant nutrient-acquisition strategies drive topsoil microbiome structure and function. New Phytol. 2020, 227, 1189–1199. [Google Scholar] [CrossRef]
- Bunn, R.A.; Simpson, D.T.; Bullington, L.S.; Lekberg, Y.; Janos, D.P. Revisiting the ‘direct mineral cycling’ hypothesis: Arbuscular mycorrhizal fungi colonize leaf litter, but why? ISME J. 2019, 13, 1891–1898. [Google Scholar] [CrossRef]
- Liang, M.; Johnson, D.; Burslem, D.F.; Yu, S.; Fang, M.; Taylor, J.D.; Taylor, A.F.; Helgason, T.; Liu, X. Soil fungal networks maintain local dominance of ectomycorrhizal trees. Nat. Commun. 2020, 11, 2636. [Google Scholar] [CrossRef]
- De Long, J.R.; Heinen, R.; Heinze, J.; Morriën, E.; Png, G.K.; Sapsford, S.J.; Teste, F.P.; Fry, E.L. Plant-soil feedback: Incorporating untested influential drivers and reconciling terminology. Plant Soil 2023, 485, 7–43. [Google Scholar] [CrossRef]
- Bennett, J.A.; Klironomos, J. Mechanisms of plant–soil feedback: Interactions among biotic and abiotic drivers. New Phytol. 2019, 222, 91–96. [Google Scholar] [CrossRef]
- Tedersoo, L.; Bahram, M.; Zobel, M. How mycorrhizal associations drive plant population and community biology. Science 2020, 367, eaba1223. [Google Scholar] [CrossRef]
- Bachega, L.R.; Bouillet, J.-P.; de Cássia Piccolo, M.; Saint-André, L.; Bouvet, J.-M.; Nouvellon, Y.; de Moraes Gonçalves, J.L.; Robin, A.; Laclau, J.-P. Decomposition of Eucalyptus grandis and Acacia mangium leaves and fine roots in tropical conditions did not meet the Home Field Advantage hypothesis. For. Ecol. Manag. 2016, 359, 33–43. [Google Scholar] [CrossRef]
- Hierro, J.L.; Callaway, R.M. The ecological importance of allelopathy. Annu. Rev. Ecol. Evol. Syst. 2021, 52, 25–45. [Google Scholar] [CrossRef]
- Cipollini, D.; Rigsby, C.M.; Barto, E.K. Microbes as targets and mediators of allelopathy in plants. J. Chem. Ecol. 2012, 38, 714–727. [Google Scholar] [CrossRef] [PubMed]
- Coder, K.D.; Daniel, B. Potential Allelopathy in Different Tree Species; University of Georgia, Cooperative Extension Service, Forest Resources: Athens, GA, USA, 1999. [Google Scholar]
- Soderquist, C.J. Juglone and allelopathy. J. Chem. Educ. 1973, 50, 782–783. [Google Scholar] [CrossRef] [PubMed]
- Appleton, B.L.; Berrier, R.; Harris, R.; Alleman, D.; Swanson, L. The Walnut Tree: Allelopathic Effects and Tolerant Plants; Virginia State University Cooperative Extension: Blacksburg, VA, USA, 2000; p. 4. [Google Scholar]
- Li, G.-D.; Jia, L.-M.; Li, X.-W. Research advances in allelopathy of Quercus L. For. Stud. China 2007, 9, 287–294. [Google Scholar] [CrossRef]
- Mole, S. The systematic distribution of tannins in the leaves of angiosperms: A tool for ecological studies. Biochem. Syst. Ecol. 1993, 21, 833–846. [Google Scholar] [CrossRef]
- Spurr, S.H.; Barnes, B.V. Forest Ecology, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980; p. 687. [Google Scholar]
- Hood, S.M.; Varner, J.M.; Van Mantgem, P.; Cansler, C.A. Fire and tree death: Understanding and improving modeling of fire-induced tree mortality. Environ. Res. Lett. 2018, 13, 113004. [Google Scholar] [CrossRef]
- Nepstad, D.; Moreira, A.; Veríssimo, A.; Lefebvre, P.; Schlesinger, P.; Potter, C.; Nobre, C.; Setzer, A.; Krug, T.; Barros, A.C. Forest fire prediction and prevention in the Brazilian Amazon. Conserv. Biol. 1998, 12, 951–953. [Google Scholar] [CrossRef]
- Roberts, S.J. Tropical fire ecology. Prog. Phys. Geogr. 2000, 24, 281–288. [Google Scholar] [CrossRef]
- Varner, J.M.; Kane, J.M.; Hiers, J.K.; Kreye, J.K.; Veldman, J.W. Suites of fire-adapted traits of oaks in the southeastern USA: Multiple strategies for persistence. Fire Ecol. 2016, 12, 48–64. [Google Scholar] [CrossRef]
- Ennos, A. The aerodynamics and hydrodynamics of plants. J. Exp. Biol. 1999, 202, 3281–3284. [Google Scholar] [CrossRef] [PubMed]
- Vandermeer, J.; Cerda, I.G.; Boucher, D.; Perfecto, I.; Ruiz, J. Hurricane disturbance and tropical tree species diversity. Science 2000, 290, 788–791. [Google Scholar] [CrossRef]
- Murphy, H.T.; Metcalfe, D.J. The perfect storm: Weed invasion and intense storms in tropical forests. Austral Ecol. 2016, 41, 864–874. [Google Scholar] [CrossRef]
- Armesto, J.J.; Mitchell, J.D.; Villagran, C. A comparison of spatial patterns of trees in some tropical and temperate forests. Biotropica 1986, 18, 1–11. [Google Scholar] [CrossRef]
- Farrior, C.E.; Bohlman, S.A.; Hubbell, S.; Pacala, S.W. Dominance of the suppressed: Power-law size structure in tropical forests. Science 2016, 351, 155–157. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; Kuzee, M.E.; Bongers, F. Disentangling above- and below-ground competition between lianas and trees in a tropical forest. J. Ecol. 2005, 93, 1115–1125. [Google Scholar] [CrossRef]
- Matsuo, T.; Martínez-Ramos, M.; Bongers, F.; van der Sande, M.T.; Poorter, L. Forest structure drives changes in light heterogeneity during tropical secondary forest succession. J. Ecol. 2021, 109, 2871–2884. [Google Scholar] [CrossRef]
- Williams, J.; Jackson, T.D.; Schönlieb, C.-B.; Swinfield, T.; Irawan, B.; Achmad, E.; Zudhi, M.; Habibi, H.; Gemita, E.; Coomes, D.A. Monitoring early-successional trees for tropical forest restoration using low-cost UAV-based species classification. Front. For. Glob. Chang. 2022, 5, 876448. [Google Scholar] [CrossRef]
- Yamada, T.; Okuda, T.; Abdullah, M.; Awang, M.; Furukawa, A. The leaf development process and its significance for reducing self-shading of a tropical pioneer tree species. Oecologia 2000, 125, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Quinn, B.K.; Niinemets, Ü.; Schrader, J.; Gielis, J.; Liu, M.; Shi, P. Ellipticalness index: A simple measure of the complexity of oval leaf shape. Pak. J. Botany 2022, 54, 2233–2240. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zheng, Y.; Ratkowsky, D.A.; Wei, H.; Shi, P. Application of an ovate leaf shape model to evaluate leaf bilateral asymmetry and calculate lamina centroid location. Front. Plant Science 2022, 12, 822907. [Google Scholar] [CrossRef]
- Gavrikov, D.E.; Zverev, V.; Rachenko, M.A.; Pristavka, A.A.; Kozlov, M.V. Experimental evidence questions the relationship between stress and fluctuating asymmetry in plants. Symmetry 2023, 15, 339. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).