Abstract
In this paper, we study spontaneous coherent undulator emission from a short dense electron bunch. A special “negative-mass” undulator ensuring stabilization of the axial size of the bunch is considered. We focus on the situation where the competition between two different transverse waveguide modes takes place, so that the undulator resonance is provided simultaneously for three waves placed on the dispersion diagram symmetrically with respect to electrons (namely, the group velocity of the higher waveguide mode coincides with the electron velocity, whereas two resonance frequencies of the lower transverse mode correspond to wave group velocities, one of which slightly exceeds the translational velocity of electrons, with the other being less than the electron velocity). We show that the higher waveguide mode can win this competition due to its proximity to group synchronization with the electron bunch.
1. Introduction
The generation of short ultra-broadband (several wave cycles) terahertz (THz) electromagnetic pulses with high peak fields is an important problem from the point of view of various applications of such pulses (see, e.g., [1,2,3,4,5,6,7,8,9]). A well-known way to produce powerful coherent radiation is the use of various (undulator, cyclotron, Smith–Purcell) types of emission from relativistic high-current electron beams together with the use of the Doppler up-conversion of the electron oscillation frequency to achieve sub-THz and THz frequency ranges. However, if the length of the operating electron beam is much longer than the wavelength of the operating wave, the emission process is ensured as a result of bunching of the electrons in the field of the radiated wave [10,11]. In order to provide the induced characteristic of the radiation process, one should use either a feedback system in auto-oscillator schemes of electron masers (see, e.g., [12,13,14,15,16,17,18,19,20,21]) or an initial (feeding) wave signal in amplifier schemes (see, e.g., [22,23,24,25]). However, when working in sub-THz and THz frequency ranges, the first method is hampered by a number of problems (for example, the selectivity of the feedback system in an oversized microwave system, the difficulty of achieving the stationary generation regime when using short-pulse high-current electron beams, the technical difficulties of providing feedback at high frequencies). As for the second method, the obvious problem, as a rule, is the lack of an available and sufficiently powerful input signal source at THz frequencies. In the case of sufficiently short operating electron beams (bunches), an elegant solution to the problem of ensuring the induced nature of radiation is the use of a super-radiance regime, which is realized when the group velocity of the emitted wave is close to the translational velocity of electrons [26,27,28]. In this case, the induced radiation is provided due to the fact that the radiated wave packet is propagated together with the radiator (the electron bunch). However, relatively long lengths are required to achieve the saturated stage of the electron–wave interaction.
Due to the development of photoinjectors, which allow the formation of ps and sub-ps bunches of ultra-relativistic electrons with comparatively high charges (total charge 0.1–1 nC) [29,30,31], the undulator emission of short wave pulses from such bunches in the sub-terahertz frequency range can be organized in the so-called spontaneous coherent regime [32,33]. This regime is realized when the bunch length is close to (or shorter than) the length of the radiated wave (Figure 1a) [34,35,36,37,38,39]. Such bunches are “ready” to radiate the wave without an additional process of electron bunching required in free-electron masers based on the induced emission from relatively long electron beams. The use of this approach together with the idea of the use of the group electron–wave synchronism mentioned above can be a way to realize free-electron radiation sources, where high efficiencies of the electron–wave interaction can be provided in relatively short radiation systems [38,39].
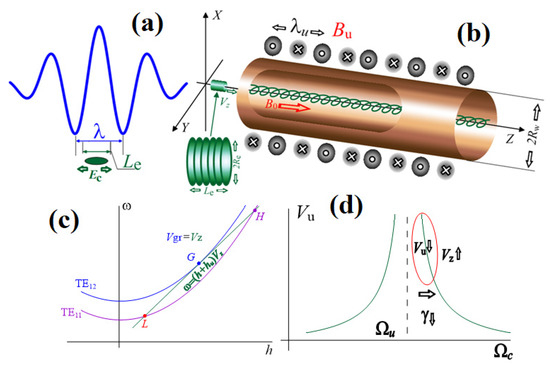
Figure 1.
(a) Spontaneous emission of a wave with a wavelength of 𝜆 from an electron bunch with a length of (b) Schematic of the model: electrons move in a cylindrical waveguide immersed in a periodic undulator field together with a guiding magnetic field The electron bunch is presented as a set of thin charged disks. (c) Dispersion characteristics of the two modes in a waveguide and electrons: “grazing” regime with TE12 mode and intersection with TE11 mode. (d) The dependence of the transverse velocity of an electron on its cyclotron frequency.
If the regime of the group synchronism is realized (when the group velocity of the wave is close to the bunch velocity), then the energy emitted from the electron bunch is concentrated within a short powerful wave pulse. The regime of the group synchronism (the super-radiation regime) is optimal from the point of view of radiation as the bunch is placed in the maximum of the radiated pulse. It provides the high efficiency of the electron–wave interaction. However, other factors related to particle dynamics strongly influence the spontaneous radiation process, and they can stop this process due to an increase in the effective length of the bunch. First, as the electrons are constantly in the region of a strong wave field during the radiation process, this field significantly affects the length of the electron bunch. In addition, the Coulomb repulsion of particles plays an important role in dense, short photo-injector bunches at relatively low particle energies (units of MeV) [38]. As a result, special methods for the stabilization of the effective axial size of the operating electron bunch (or even for axial compression of the bunch) can be required.
In this paper, we consider the situation when two methods of beam length stabilization based on the use of their electromagnetic fields of the bunch are used simultaneously. First, there exist the effects of the self-compression of the bunch by its super-radiative wave field [40]. This effect is realized in the regime of the exact group synchronism between the radiated wave and a short enough (shorter than the wavelength) electron bunch. In this case, the bunch is placed automatically in a “proper” wave phase so that the front of the bunch is decelerated by the radiated field, whereas the “tail” of the bunch is placed close to the “zero” of the wave field. Another effect occurs in spontaneous radiation in the undulator if there is a mismatch of the group synchronism when there are two resonance frequencies (the resonances H and L in Figure 1c). In this case, if the bunch length is close to the wavelength of the low-frequency radiated wave L, the compression of the bunch in the field of this wave results in a significant improvement of the micro-scale bunching concerning the high-frequency wave H [41].
The second considered approach to provide axial compression of an electron bunch is based on the use of the quasi-static Coulomb electric fields of the bunch. This is possible if the so-called “negative-mass” regime of the electron motion in the undulator field is provided [38,39]. The term “negative mass” denotes the fact that in the process of the motion of a particle in the undulator field, the changes in the energy of the particle and its axial velocity have opposite signs (for instance, an increase in the energy results in a decrease in the axial velocity). The negative-mass regime is implemented in an undulator with a guiding magnetic field (Figure 1b) [42]. The electrons perform forced bounce oscillations in the transverse periodic magnetic field of the undulator with wavenumber with frequency (where is the undulator period and is the axial electron velocity). If the frequency of free cyclotron oscillations in the guiding axial magnetic field slightly exceeds the bounce frequency , the change in the velocities and energies of the particles will have different signs. Thus, if a particle is accelerated, then its relativistic Lorentz-factor increases, and the corresponding cyclotron frequency becomes closer to the resonance with the bounce frequency (Figure 1d). As a result, an increase in the velocity of the transverse undulator oscillations, , leads to a decrease in the axial velocity .
In that way, we study the spontaneous coherent emission from a short, moderately relativistic (units of MeV) electron bunch moving in a waveguide placed inside a negative-mass undulator in the situation shown in Figure 1d, when the undulator electron–wave resonance is provided for three waves simultaneously. In our system, electrons perform undulator oscillations around the axis of the waveguide and, therefore, at the fundamental undulator resonance, they can interact only with transverse modes of the waveguide having the azimuthal index equal to 1.
The simplest (from the point of view of the mode competition problem) way to organize the group electron–wave synchronism regime is to use the lowest waveguide mode as the operating approach. However, in reality, such a solution may be hampered by limitations on the transverse size of the waveguide. In this paper, we study a situation in which the group synchronism regime is provided for higher waveguide modes. Namely, we suppose that the group synchronism (the regime of grazing of the dispersion characteristics of the wave and electrons in point G) is provided for the TE12 mode (Figure 1c). In this situation, for the lowest mode TE11, we have two intersections of the electron and the wave dispersion characteristics corresponding to low-frequency and high-frequency resonant frequencies (points L and H in Figure 1d, respectively). We study the competition between the pulse emitted in the group synchronism regime, when an electron bunch does not “slip” relative to the maximum of the pulse, and the pulse consisting of the wave components, the transverse structure of which accords to the lowest mode TE11.
2. Model and Equations
We consider the radiation of a short dense electron bunch moving in a waveguide placed in a negative-mass undulator with a guiding magnetic field (Figure 1b). For an electron moving in a circularly polarized undulator:
along the stationary trajectory, the transverse components of the normalized velocity are described as follows:
where the amplitude / of the undulator oscillations is determined by the undulator parameter and by the mismatch of the undulator-cyclotron synchronism [38,42].
As mentioned above, we are interested in the regime in which a wave with a transverse structure corresponding to the TE12 mode is excited in the regime of “grazing” of the dispersion characteristics (Figure 1c, point G). This “grazing” regime (the regime of the group synchronism ) corresponds to one resonant frequency,
where is the “axial” relativistic Lorentz factor and is the dimensionless axial velocity. In this situation, the pulse according to the lower transverse mode TE11 can also be emitted, and there are two resonance frequencies in the intersection of the dispersion characteristics regime:
Correspondingly, two frequency components form the radiated wave field corresponding to the mode TE11.
Note that these two waves have different advantages from the point of view of the spontaneous coherent emission from a short electron bunch [43,44]. As , the spontaneous coherent emission of the low-frequency wave L can be provided from a longer electron bunch. On the other hand, as the group velocity of the high-frequency wave H is higher, this wave is closer to the high-efficiency group synchronism with electrons due to a smaller slippage with respect to the moving electron bunch, .
Let us start with the equations describing the interaction for the system under consideration. For each of the electromagnetic pulses emitted by the bunch, we assume that the transverse structure is fixed, and for the evolution of the longitudinal structure, we use the space–time equations for vector potentials in projections to the transverse directions (similar for both):
where is the normalized time, is the normalized axial coordinate with respect to the “tail” of the electron bunch, and are the normalized components of the vector potential. is the normalized transverse wavenumber, is the norm of the corresponding mode (TE11 or TE12), and is the waveguide radius.
We consider the radiation of an electron bunch as the emission from a set of extended planar (pancake-like) macroparticles (Figure 1). Thus, we divide the space of the electron bunch into cells whose length is equal to the length of the macroparticle, and introduce as a function that determines the presence/absence of particles in the k-th cell (). At the beginning of the process, inside the electron bunch and outside the bunch.
The change in the dimensionless relativistic electron energy, , is the sum of three components:
where and are related to the electron–wave interaction with the TE11 and TE12 wave packets, respectively, whereas is caused by the Coulomb interaction inside the electron bunch:
In Equation (3), is the complex normalized transverse velocity of electrons, whereas and are the total complex transverse electric fields of the TE11 and TE12 wave packets, respectively. These complex fields are determined by the formula , where are found from the relation of a dimensionless electric field to a vector potential.
To describe the Coulomb interaction, we use the representation of an electron bunch in the form of a set of charged disks [45]. Naturally, this is a simple quasi-analytical model that does not take into account a number of important factors (for example, the inhomogeneity of the transverse distribution of the Coulomb field or the effect of the walls of the waveguide). At the same time, the adequacy of such a model was confirmed in papers [38,39,40], which also solved problems related to the spontaneous emission of dense short electron bunches with parameters close to our parameters. In particular, the results predicted by this model are well confirmed by calculations based on more complex multidimensional numerical codes. Within frameworks of this model, , where is the total bunch charge, is the cross-sectional area of the electron bunch, , , and is the normalized longitudinal coordinate of the l-th disk that coincides with the center coordinate of the corresponding macroparticle.
The equation of motion of electrons in the undulator field follows the equation for the normalized complex transverse moment:
where is the normalized transverse momentum and is the ratio of the frequency of cyclotron rotation to the frequency of undulatory bounce oscillations.
Equations (1)–(4) together with the following equation describing the evolution of the axial coordinate of the macroparticles:
form the complete system of equations describing the electron–wave interaction and the dynamics of the particles. In our simulations, we find the efficiencies and of the interaction between the electron ensemble and the TE11 and TE12 wave packets using the following formulas:
where <…> denotes averaging over all particles of the radiating electron bunch. Note that although the TE11 wave packet is formed mainly by waves at two different resonant frequencies and (Figure 1c), it is described by the dimensionless field common to all frequencies. Accordingly, within the framework of our approach, it is impossible to divide the electron efficiency corresponding to this wave packet into a low-frequency and a high-frequency component.
3. Simulations of the Mode Competition
In numerical simulations, we consider the emission from an electron bunch with the following parameters: the initial duration of the electron bunch is 0.6 ps, the total charge is 0.5 nC, the initial energy of the particles is 5 MeV (), the radius of the waveguide is 5 mm, the undulator period is 5 cm, the undulator factor is , and the amplitude of the guiding magnetic field is . The latter corresponds to the mismatch between the cyclotron and the bounce frequency in the negative-mass regime of the motion of an electron along the undulator.
The resonance frequencies GHz, THz, and THz. In this case, the bunch emits both wave packets in the spontaneous regime. In our simulations, our goal is to achieve the highest possible efficiency of the TE12 wave packet generation. According to simulations, this goal is achieved when the TE12 wave packet is emitted in the regime of the exact group synchronism, i.e., the bunch does not slip relative to the radiated pulse amplitude maximum. Note that the field of this mode in the waveguide axis is smaller as compared to the lowest TE11 mode. The components of the TE11 pulse will “run away” from the electron bunch, while the part of the radiation that runs forward will leave the electron bunch much slower (the group synchronism disorder in this case is much less). Even though the excitation factor of a wave with a transverse field structure corresponding to the TE11 mode is 4 times higher than the excitation factor of the TE12 mode, the spontaneous emission efficiencies of both pulses are approximately equal (6% and 8%, respectively; see Figure 2). This is because the TE12 mode is excited in the group synchronism regime, and for the TE11 mode, there is a group synchronism mismatch.
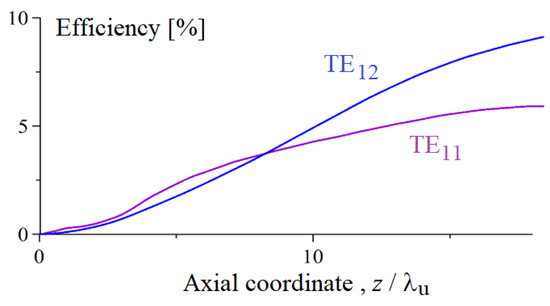
Figure 2.
Efficiency of radiation as a function of the axial coordinate normalized to the undulator period. The blue curve accords to the efficiency of electron–wave interaction with the TE12 mode, and the purple curve is the efficiency of electron–wave interaction with the TE11 mode in the case of the total bunch charge of 0.5 nC and the initial duration of 0.5 ps.
Figure 3 shows the results of the numerical simulation for the electric field of the radiated pulses and the dynamics of the linear charge density of the bunch (green fills) at different points in the interaction space. The blue curves correspond to the TE12 mode being close to the group synchronism with the electron bunch. In fact, the initial stage of emission of such a wave packet is the formation and subsequent amplification of a single wave cycle (Figure 3, Nu = 2–5) [44]. At the same time, diffraction of the wave pulse inside the waveguide leads to a gradual transformation of a short single-cycle wave pulse into a longer one, represented by several wave cycles. The electron bunch is located in the region of the maximum electric field of the emitted pulse, so that at the first stage of the electron–wave interaction process (Nu < 10), the amplitude of the “central” cycle increases due to the amplification of this cycle by electrons. However, at a distance corresponding to 10 undulator periods, the decrease in the amplitude due to the dispersion of waves in the waveguide by interaction begins to prevail over the increase in the amplitude of the central one due to the electron–wave interaction. A similar process (but in the approximation of one transverse waveguide mode) of formation and amplification of a short wave pulse, which is in group synchronism with electrons, is described in more detail in the work [44].
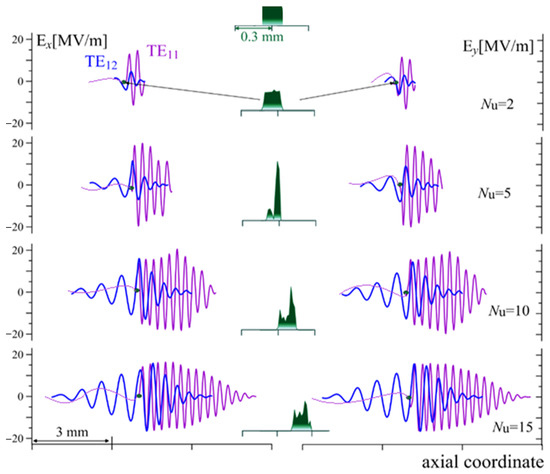
Figure 3.
Radiated electric field and charge distribution inside the electron bunch at various points of the electron–wave interaction region in the case of the bunch charge 0.5 nC and the initial duration of 0.5 ps.
In addition to the diffraction mechanism, another reason for the slow spread of the wave packet of the TE12 mode is that it is not excited exactly at the grazing point of the exact group synchronism (as shown in Figure 1c). Thus, analogously to the TE11 wave packet, TE12-type waves are excited at two frequencies, one of which slightly exceeds (and the corresponding group velocity slightly exceeds the electron velocity), with the other frequency being slightly less than (and the corresponding group velocity is slightly less than the electron velocity). This is clearly seen from the comparison of the characteristic wavelengths of the TE12 wave packet fields located in Figure 3 to the right and left of the electron bunch.
The radiation of the TE11 wave packet at a high frequency is constantly ahead of the electron bunch (see Figure 3, purple lines), as a result of which the maximum amplitude of the electric field of the emitted pulse increases during only the first 5 periods, while the part of the radiation “escaping” back from the bunch is not significant at all. Thus, two pulses are emitted; their durations amount to several tens of picoseconds, and their characteristic frequencies differ twice. The amplitudes of the fields of the emitted pulses are close to 20 MV/m. It should also be noted that the duration of the electron bunch is maintained within the initial range due to stabilization by both Coulomb fields and radiation fields at the same time.
Note that the efficiency of the interaction between the electron bunch and the TE11 wave packet shown in Figure 2 describes the electron–wave interaction for both components of the TE11 wave packet corresponding to the frequencies and . Within the approach used in this paper, it is difficult to decompose this efficiency into two components corresponding to two different frequency components of the wave packet. At the same time, it is clear from the analysis of Figure 3 that the contribution of the low-frequency component of the TE11 wave packet to the total efficiency of the electron–wave interaction is very small. This is explained by the large difference between the group velocity of the low-frequency component of the TE11 wave packet and the translational velocity of the particles, so the low-frequency component “runs away” from the electron bunch, not having time to effectively interact with it.
It should also be mentioned that in our calculations, we use an approximation of the simplest rectangular distribution of the charge density in the initial electron bunch (Figure 3). In this case, sharp edges of the bunch initiate the coherent radiation of the TE11 wave packet at frequencies close to at the beginning of the undulator. Evidently, this effect can be suppressed, for instance, in the case of the Gaussian distribution of the electron density inside the initial bunch. At the same time, this effect is important only at the beginning of the motion of the bunch through the undulator. This is due to the fact that under the influence of the own fields of the bunch (both radiation fields and the quasi-static Coulomb field, which, in the negative-mass undulator, does not lead to the repulsion of electrons, but to the compression of the electron bunch), the initial quasi-uniform distribution of the charge density inside the bunch rapidly evolves during the movement of the bunch, and it takes on much more complex forms (Figure 3).
Consider the radiation of an electron bunch with the same charge density, but with twice the length (a total charge of 1 nC, an initial duration of 1 ps). In this case, the radiation at a high frequency must be preceded by the compression of the electron bunch (the process of cascade radiation [46]). At the beginning of the interaction (approximately at a distance corresponding to 5 undulator periods), spontaneous radiation prevails at a frequency corresponding to group synchronism, and a little energy is spent on the low-frequency () spontaneous radiation of the TE11 wave (compare blue and purple curves in Figure 4 and Figure 5). As the initial length of the electron bunch is too long for the spontaneous high-frequency () radiation of the TE11 wave packet, at the initial stage of the process (), a relatively low-power wave pulse is radiated basically due to the effect of edges of the bunch. However, when the length of the electron bunch becomes sufficiently small (see the green filling in Figure 5, ) due to compression by the fields of radiation and Coulomb fields, the process of spontaneous high-frequency radiation of the TE11 wave packet becomes more effective. Because the effective high-frequency spontaneous radiation of the TE11 wave begins later (as compared to the TE12 wave) and is emitted by a denser compact bunch, the amplitude of the TE11-wave electric field is quite large, and the emitted pulse is several-cycles more compact compared to the duration of the pulse emitted in the group synchronism regime.
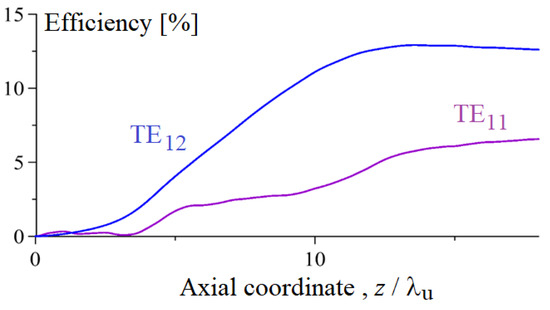
Figure 4.
The efficiency of radiation as a function of the axial coordinate normalized by the undulator period. The blue curve accords to the efficiency of electron–wave interaction with the TE12 mode, and the purple curve is the efficiency of electron–wave interaction with the TE11 mode in the case of the total bunch charge of 1 nC and the initial duration of 1 ps.
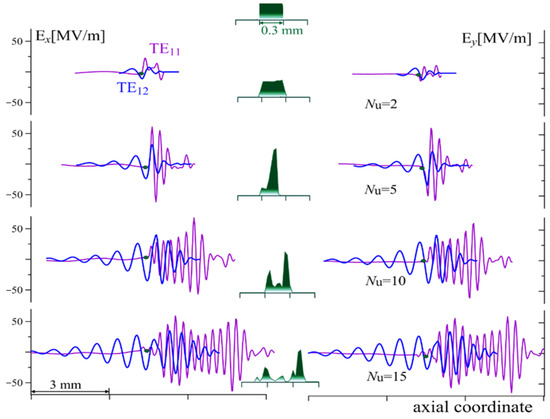
Figure 5.
Radiated electric field and charge distribution inside the electron bunch at various points of the electron–wave interaction region in the case of the bunch charge of 1 nC and the initial duration of 1 ps.
An increase in the length of the electron bunch with a fixed linear charge density by half (a total charge of 2 nC, an initial duration of 2 ps) leads to the suppression of the generation of a wave pulse consisting of waves, whose transverse structure corresponds to the TE11 mode (see Figure 6). In this case, the length of the bunch is approximately equal to the wavelength corresponding to the group synchronism and almost twice the length of the high-frequency wave; that is, the radiation of both pulses must be preceded by a grouping of particles as soon as the length of the electron bunch becomes small enough for spontaneous emission of the pulse in the group synchronism regime. The radiation of the bunch with this phase size does not stabilize but stretches the electron bunch. Approximately at a distance of 5 undulator periods, the particles are distributed in such a way that two bunches are formed in points of the “zero” wave phases (Figure 7); here, the “zero” phase corresponds to the zero change in electron energy in the wave field. The sizes of these bunches are stabilized due to the Coulomb attraction of particles moving in the negative-mass undulator. Note that in a traditional “positive-mass undulator”, where Coulomb fields lead to the repulsion of particles, low-frequency radiation, on the contrary, leads to an increase in the efficiency of high-frequency radiation due to the effect of compression of an electron bunch in its own radiation field [41].
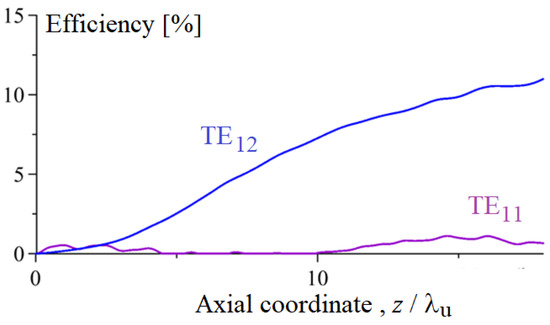
Figure 6.
Radiated electric field and charge distribution inside the electron bunch at various points of the electron–wave interaction region in the case of the bunch charge of 2 nC and the initial duration of 2 ps.
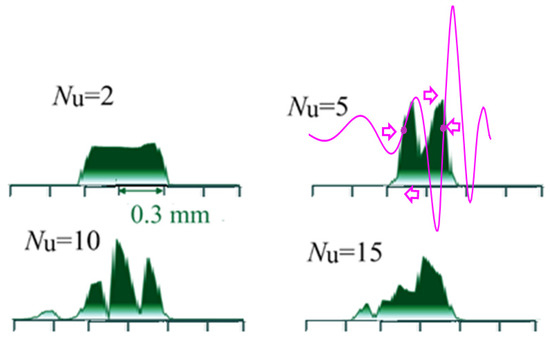
Figure 7.
Charge distribution inside the electron bunch at various points of the electron–wave interaction region in the case of the bunch charge of 2 nC and the initial duration of 2 ps. In the case of , the wave field profile is also shown; here, the arrows illustrate the accelerating–decelerating phases of the wave field and the dots show the “zero” phases of the wave.
4. Conclusions
In this paper, the competition between the lowest waveguide mode and a higher mode, which is in the group synchronism with a bunch, in the process of the spontaneous emission of these two waves from a short electron bunch is studied. Naturally, the particles’ dynamics affect the radiation process; in particular, the axial self-compression effects (by the radiated fields and by Coulomb fields inside a bunch) are especially important. It is shown that the generation conditions at each of the modes can be changed by varying the phase size of the electron bunch. At the same time, the competition processes have differences in the described regimes. Thus, if the length of the bunch is close to the wavelength according to the group-synchronism frequency, it is possible to provide the lowest mode suppression. We must note that this effect takes place in the negative-mass regime. In the normal positive-mass regime, the effect of micro-scale bunching [41] may make significant changes in the competition process. In particular, the generation at the highest frequency may predominate even in the cases of the “proper” bunch lengths. Paradoxical as it may seem, the additional axial stabilization, which must provide compression and as a consequent better condition for the high-frequency radiation, prevents particles from being in its decelerating phase.
The importance of these results is related to real problems arising in the process of the experimental realization of undulator sources of spontaneous coherent emission from short electron bunches. As it is mentioned above, generation in the group synchronism regime is attractive both from the point of view of achieving high efficiencies of electron–wave interaction and high peak powers of the high-frequency wave signal, and from the point of view of ensuring stability of the axial size of the operating electron bunch. At the same time, however, providing the group synchronism regime on the lowest waveguide mode may be difficult, for example, by natural restrictions on the transverse size of the operating waveguide. In this paper, we demonstrate that at definite conditions, such a regime can be provided at higher waveguide modes, without the problem of competition with resonances at lower modes that are far from the group synchronism regime.
Author Contributions
Conceptualization, Y.O. and A.S.; methodology, Y.O. and A.S.; software, Y.O.; formal analysis, Y.O. and A.S.; writing—original draft preparation, Y.O.; writing—review and editing, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation, grant no. 21-72-30027.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Blaga, C.I.; Catoire, F.; Colosimo, P.; Paulus, G.G.; Muller, H.G.; Agostini, P.; Dimauro, L.F. Strong-field photoionization revisited. Nat. Phys. 2009, 5, 335. [Google Scholar] [CrossRef]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-tometal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345. [Google Scholar] [CrossRef] [PubMed]
- Feorst, M.; Manzoni, C.; Kaiser, S.; Tomioka, Y.; Tokura, Y.; Merlin, R.; Cavalleri, A. Nonlinear phononics as an ultrafast route to lattice control. Nat. Phys. 2011, 7, 854–856. [Google Scholar] [CrossRef]
- Schubert, O.; Hohenleutner, M.; Langer, F.; Urbanek, B.; Lange, C.; Huttner, U.; Golde, D.; Meier, T.; Kira, M.; Koch, S.W.; et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photonics 2014, 8, 119–123. [Google Scholar] [CrossRef]
- Zhang, W.; Maldonado, P.; Jin, Z.; Seifert, T.S.; Arabski, J.; Schmerber, G.; Beaurepaire, E.; Bonn, M.; Kampfrath, T.; Oppeneer, P.M.; et al. Ultrafast terahertz magnetometry. Nat. Commun. 2020, 11, 4247. [Google Scholar] [CrossRef]
- Kubacka, T.; Johnson, J.A.; Hoffmann, M.C.; Vicario, C.; De Jong, S.; Beaud, P.; Gr€ubel, S.; Huang, S.-W.; Huber, L.; Patthey, L.; et al. Largeamplitude spin dynamics driven by a THz pulse in resonance with an electromagnon. Science 2014, 343, 1333. [Google Scholar] [CrossRef]
- Piccirillo, B.; Paparo, D.; Rubano, A.; Andreone, A.; Rossetti Conti, M.; Giove, D.; Vicuña-Hernández, V.; Koral, C.; Masullo, M.R.; Mettivier, G.; et al. Liquid Crystal-Based Geometric Phase-Enhanced Platform for Polarization and Wavefront Analysis Techniques with the Short-TeraHertz FEL Oscillator TerRa@BriXSinO. Symmetry 2023, 15, 103. [Google Scholar] [CrossRef]
- Zhu, X.; Bacon, D.R.; Madéo, J.; Dani, K.M. High Field Single- to Few-Cycle THz Generation with Lithium Niobate. Photonics 2021, 8, 183. [Google Scholar] [CrossRef]
- Novelli, F.; Ma, C.Y.; Adhlakha, N.; Adams, E.M.; Ockelmann, T.; Das Mahanta, D.; Di Pietro, P.; Perucchi, A.; Havenith, M. Nonlinear TeraHertz Transmission by Liquid Water at 1 THz. Appl. Sci. 2020, 10, 5290. [Google Scholar] [CrossRef]
- Colson, W.B.; Louisell, W.H.; Lam, J.F.; Cantrell, C.D. Classical evolution of a free electron laser oscillator. J. Opt. Soc. Am. 1978, 68, 1620. [Google Scholar]
- Bratman, V.L.; Ginzburg, N.S.; Petelin, M.I. Common properties of free electron lasers. Opt. Commun. 1979, 30, 409. [Google Scholar] [CrossRef]
- Bratman, V.L.; Denisov, G.G.; Ginzburg, N.S.; Petelin, M.I. FEL’s with Bragg reflection resonators: Cyclotron autoresonance masers versus ubitrons. IEEE J. Quantum Electron. 1983, 19, 282. [Google Scholar] [CrossRef]
- Alberti, S.; Danly, B.G.; Gulotta, G.; Giguet, E.; Kimura, T.; Menninger, W.L.; Rullier, J.L.; Temkin, R.J. Experimental Study of a 28 GHz High-Power Long-Pulse Cyclotron Autoresonance Maser Oscillator. Phys. Rev. Lett. 1993, 71, 2018. [Google Scholar] [CrossRef]
- Chu, T.S.; Hartemann, F.V.; Danly, B.G.; Temkin, R.J. Single-Mode Operation of a Bragg Free-Electron Maser Oscillator. Phys. Rev. Lett. 1994, 72, 2391. [Google Scholar] [CrossRef]
- Urbanus, W.H.; Bongers, W.A.; Van Der Geer, C.A.J.; Manintveld, P.; Plomp, J.; Pluygers, J.; Poelman, A.J.; Smeets, P.H.M.; Verhoeven, A.G.A.; Bratman, V.L.; et al. High-power electrostatic free-electron maser as a future source for fusion plasma heating: Experiments in the short-pulse regime. Phys. Rev. E 1999, 59, 6058. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Kaminsky, A.A.; Kaminsky, A.K.; Peskov, N.Y.; Sedykh, S.N.; Sergeev, A.P.; Sergeev, A.S. High-Efficiency Single-Mode Free-Electron Maser Oscillator Based on a Bragg Resonator with Step of Phase of Corrugation. Phys. Rev. Lett. 2000, 84, 3574. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Peskov, N.Y.; Sergeev, A.S.; Phelps, A.D.R.; Cross, A.W.; Konoplev, I.V. The use of a hybrid resonator consisting of one-dimensional and two-dimensional Bragg reflectors for generation of spatially coherent radiation in a coaxial free-electron laser. Phys. Plasmas 2002, 9, 2798. [Google Scholar] [CrossRef]
- Knyazev, B.A.; Kulipanov, G.N.; Vinokurov, N.A. Novosibirsk terahertz free electron laser: Instrumentation development and experimental achievements. Meas. Sci. Technol. 2010, 21, 54017. [Google Scholar] [CrossRef]
- Vinokurov, N.A. Free electron lasers as a high-power terahertz sources. J. Infrared Millim. THz Waves 2011, 32, 1123. [Google Scholar] [CrossRef]
- Ceccuzzi, S.; Doria, A.; Gallerano, G.P.; Ravera, G.L.; Spassovsky, I.; Ginzburg, N.S.; Glyavin, M.Y.; Peskov, N.Y.; Savilov, A.V. Traditional vs. advanced Bragg reflectors for oversized circular waveguide. Fusion Eng. Des. 2017, 123, 477. [Google Scholar] [CrossRef]
- Oparina, Y.S.; Peskov, N.Y.; Savilov, A.V. Electron rf Oscillator Based on Self-Excitation of a Talbot-Type Supermode in an Oversized Cavity. Phys. Rev. Appl. 2019, 12, 044070. [Google Scholar] [CrossRef]
- Orzechowski, T.; Anderson, B.; Fawley, W.M.; Prosnitz, D.; Scharlemann, E.T.; Yarema, S.; Hopkins, D.; Paul, A.C.; Sessler, A.M.; Wurtele, J. Microwave radiation from a high-gain free-electron laser amplifier. Phys. Rev. Lett. 1985, 54, 889. [Google Scholar] [CrossRef] [PubMed]
- Peskov, N.Y.; Bandurkin, I.V.; Donetc, D.E.; Kaminsky, A.K.; Perelstein, E.A.; Sedykh, S.N.; Zaslavsky, V.Y. Desktop megawatt superradiant freeelectron laser at terahertz frequencies. Appl. Phys. Lett. 2017, 110, 013501. [Google Scholar] [CrossRef]
- Snively, E.C.; Xiong, J.; Musumeci, P.; Gover, A. Broadband THz amplification and superradiant spontaneous emission in a guided FEL. Opt. Express 2019, 27, 20221. [Google Scholar] [CrossRef]
- Kaminsky, A.K.; Sedykh, S.N.; Bandurkin, I.V.; Golubev, I.I.; Golubykh, S.M.; Kozlov, A.P.; Peskov, N.Y.; Savilov, A.V.; Sidorov, A.I. Experimental demonstration of free electron maser operation in the regime of non-resonant trapping. Appl. Phys. Lett. 2019, 115, 163501. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Zotova, I.V.; Sergeev, A.S. Cyclotron superradiance of a moving electron swarm under group synchronization conditions. JETP Lett. 1994, 60, 513. [Google Scholar]
- Ginzburg, N.S.; Zotova, I.V.; Sergeev, A.S.; Konoplev, I.V.; Phelps, A.D.R.; Cross, A.W.; Cooke, S.J.; Shpak, V.G.; Yalandin, M.I.; Shunailov, S.A.; et al. Experimental observation of cyclotron superradiance under group synchronism conditions. Phys. Rev. Lett. 1997, 78, 2365. [Google Scholar] [CrossRef]
- Ginzburg, N.S.; Zotova, I.V.; Sergeev, A.S.; Rozental, R.M.; Phelps, A.D.R.; Cross, A.W.; Ronald, K. Theory of cyclotron super-radiance from a moving electron bunch under group synchronism condition. Phys. Plasmas 2003, 10, 4494. [Google Scholar] [CrossRef]
- Power, J.G. Overview of photoinjectors. AIP Conf. Proc. 2010, 1299, 20. [Google Scholar]
- Valloni, A.; Alesini, D.; Andonian, G.; Bernard, N.; Faillace, L.; Ficcadenti, L.; Fukusawa, A.; Hidding, B.; Migliorati, M.; Mostacci, A.; et al. Design and applications of an X-band hybrid photoinjector. Nucl. Instrum. Methods Phys. Res. Sect. A 2011, 657, 107. [Google Scholar]
- Gulliford, C.; Bartnik, A.; Bazarov, I.; Dunham, B.; Cultrera, L. Demonstration of cathode emittance dominated high bunch charge beams in a DC gun-based photoinjector. Appl. Phys. Lett. 2015, 106, 094101. [Google Scholar] [CrossRef]
- Ginzburg, V.L. On radiation of microradiowaves and their absorption in air. Akad. Nauk SSSR 1947, 11, 1651. [Google Scholar]
- Motz, H. Applications of the radiation from fast electron beams. J. Appl. Phys. 1951, 22, 527. [Google Scholar] [CrossRef]
- Doria, A.; Bartolini, R.; Feinstein, J.; Gallerano, G.P.; Pantell, R.H. Coherent emission and gain from a bunched electron beam. IEEE J. Quantum Electron. 1993, 29, 1428. [Google Scholar] [CrossRef]
- Gover, A.; Hartemann, F.V.; Le Sage, G.P.; Luhmann, N.C.; Zhang, R.S.; Pellegrini, C. Time and frequency domain analysis of superradiant coherent synchrotron radiation in a waveguide free-electron laser. Phys. Rev. Lett. 1994, 72, 1192. [Google Scholar] [CrossRef]
- Doria, A.; Gallerano, G.P.; Giovenale, E.; Messina, G.; Spassovsky, I. Enhanced coherent emission of terahertz radiation by energy-phase correlation in a bunched electron beam. Phys. Rev. Lett. 2004, 93, 264801. [Google Scholar] [CrossRef]
- Bratman, V.L.; Jaroszynsky, D.A.; Samsonov, S.V.; Savilov, A.V. Generation of ultrashort quasi-unipolar electromagnetic pulses from quasiplanar electron bunches. Nucl. Instrum. Methods Phys. Res. Sect. A 2001, 475, 436. [Google Scholar] [CrossRef]
- Balal, N.; Bandurkin, I.V.; Bratman, V.L.; Magory, E.; Savilov, A.V. Negative-mass mitigation of Coulomb repulsion for terahertz undulator radiation of electron bunches. Appl. Phys. Lett. 2015, 107, 163505. [Google Scholar] [CrossRef]
- Lurie, Y.; Bratman, V.L.; Savilov, A.V. Energy enhancement and spectrum narrowing in terahertz electron sources due to negative mass instability. Phys. Rev. Accel. Beams 2016, 19, 050704. [Google Scholar] [CrossRef]
- Bandurkin, I.V.; Oparina, Y.S.; Savilov, A.V. Super-radiative self-compression of photo-injector electron bunches. Appl. Phys. Lett. 2017, 110, 263508. [Google Scholar] [CrossRef]
- Bratman, V.L.; Oparina, Y.S.; Lurie, Y. Simultaneous High-Frequency Super-Radiance and Low-Frequency Coherent Spontaneous Radiation from Ultrarelativistic Electrons in a Waveguide. Nucl. Instr. Methods Phys. Res. Sect. A 2020, 976, 164268. [Google Scholar] [CrossRef]
- Freund, H.P. Principles of Free-Electron Lasers; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Oparina, Y.S.; Savilov, A.V. Spontaneous superradiant sub THz coherent cyclotron emission from a short dense electron bunch. Phys. Rev. AB 2019, 22, 030701. [Google Scholar] [CrossRef]
- Oparina, Y.S.; Savilov, A.V. Coherent Super-Radiative Undulator Emission of Ultra-Short THz Wave Pulses. Phys. Plasmas 2021, 28, 093302. [Google Scholar] [CrossRef]
- Bandurkin, I.V.; Kurakin, I.S.; Savilov, A.V. Compression of a photoinjector electron bunch in the negative-mass undulator. Phys. Rev. Accel. Beams 2017, 20, 020704. [Google Scholar] [CrossRef]
- Bandurkin, I.V.; Oparina, Y.S.; Osharin, I.V.; Savilov, A.V. Spontaneous super-radiative cascade undulator emission from short dense electron bunches. Phys. Plasmas 2019, 26, 113105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).