A Detailed Study of Mathematical Rings in q-Rung Orthopair Fuzzy Framework

Abstract

Symmetry-related problems can be addressed by means of group theory, and ring theory can be seen as an extension of additive group theory. Ring theory, a significant topic in abstract algebra, is currently active in a diverse range of study domains across the disciplines of mathematics, theoretical physics and coding theory. The study of ideals is vital to the theory of rings in a wide range of ways. The uncertainties present in the information are addressed well by the q-rung orthopair fuzzy set (q-ROFS). Considering the significance of ring theory and the q-ROFS, this article defines q-rung orthopair fuzzy ideals (q-ROFIs) in conventional rings and investigates its various algebraic features. We introduce the notion of q-rung orthopair fuzzy cosets (q-ROFCs) of a q-ROFI and demonstrate that, under certain binary operations, the collection of all q-ROFCs of a q-ROFI forms a ring. In addition, we provide a q-rung orthopair analog of the fundamental theorem of ring homomorphism. Furthermore, we present the notion of q-rung orthopair fuzzy semi-prime ideals (q-ROFSPIs) and provide a comprehensive explanation of their many algebraic properties. Finally, regular rings were characterized using q-ROFIs.

1. Introduction

Fuzzy sets (FSs), first introduced by Zadeh [1], have several uses in fields such as data mining, business, economics, etc. To represent a fuzzy subset $\varnothing$ on a universe $S$, we write $\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$, where ${\mu }_{\varnothing }$:$S\to \left[0,1\right]$ is membership function of $\varnothing$ and ${\mu }_{\varnothing }\left(\varsigma \right)$ represents the degree of membership of $\varsigma$ in $\varnothing$. As a natural extension of crisp set theory, fuzzy set theory is a useful tool in many contexts. The characteristic function of a classical set, which is equal to $1$ if $\varsigma$ is in the set $S$, and 0 otherwise, corresponds to the membership function of the set. To cope with ambiguity and uncertainty, several new ideas have emerged since the advent of fuzzy sets. There are a variety of theories that attempt to handle ambiguity and vagueness, some of them are extensions of fuzzy set theory. There are numerous types of data for which the membership value alone is insufficient. As a result, a component known as “non-membership value” is introduced to properly illustrate the information. In 1986, Atanassov [2] defined intuitionistic fuzzy sets (IFSs) and provided a generalization of FSs. An IFS $\varnothing$ of a crisp set $S$ is an object $\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$, where ${\mu }_{\varnothing }$:$S\to \left[0,1\right]$ and ${\nu }_{\varnothing }$:$S\to \left[0,1\right]$ are membership and non-membership functions satisfying ${\mu }_{\varnothing }\left(\varsigma \right)+{\nu }_{\varnothing }\left(\varsigma \right)$ $\le 1$ for all $s \in S$. In comparison to conventional FSs, the positive and negative membership functions of IFSs make it possible to effectively deal with uncertainty and ambiguity in physical problems, particularly in the decision-making domain [3,4,5,6]. Yager [7] generalized IFSs in 2013 by proposing the concept of a Pythagorean fuzzy set (PFS) $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$, where ${\mu }_{\varnothing }$:$S\to \left[0,1\right]$ and ${\nu }_{\varnothing }$:$S\to \left[0,1\right]$ are membership and non-membership functions satisfying ${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^2+{\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^2$ $\le 1$ for all $s \in S$. This concept aims to transform an uncertain and ambiguous environment into mathematics and to identify better solutions to tackle such problems in the physical realm [8,9,10,11]. Although PFSs solve many real-world problems, they still fail in many situations, requiring further development. Pythagorean fuzzy subsets cannot handle scenarios where a decision maker recommends positive and negative membership values of $0.90$ and $0.50$, respectively, because ${\left(0.90\right)}^2+{\left(0.50\right)}^2$ $>1$; therefore, Pythagorean fuzzy subsets cannot handle such situations. Yager [12] defines the concept of q-rung orthopair fuzzy set (q-ROFS), where q is a natural number, in order to discover a reasonable solution to situations of this type. The q-ROFS is represented by $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$, where ${\mu }_{\varnothing }$:$S\to \left[0,1\right]$ and ${\nu }_{\varnothing }$:$S\to \left[0,1\right]$ are membership and non-membership functions satisfying ${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q+{\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q$ $\le 1$ for all $s \in S$. We recommend reading [13,14,15] for more information on practical applications of q-ROFSs.

The theory of rough sets was first introduced by Zdzisław I. Pawlak, a Polish mathematician [16]. The application of rough sets and soft rough sets has proven to be a significant tool for managing uncertainty and vagueness in data, with widespread use in the medical and economic domains [17,18,19,20].

1.1. Background and Importance of Ring Theory

Ring theory is a branch of abstract algebra [21,22] concerned with the characteristics and behaviors of mathematical objects known as rings. Rings are collections of objects that fulfill a set of axioms known as the ring axioms and have two binary operations, often addition and multiplication. In the late 19th century, the German mathematician Richard Dedekind properly described the notion of a ring, and Emmy Noether made substantial contributions to the theory of rings and its applications to algebraic number theory and algebraic geometry.

In order to study rings, mathematicians devised many methods to divide rings into smaller, more manageable components, such as subrings, ideals and quotient rings. Ring theorists also distinguish between commutative and noncommutative rings by additional abstract features. Commutative rings play an important role in number theory and algebraic geometry. Complex number extension led to noncommutative ring theory. Commutative and non-commutative ring theories originated in the early 19th century and matured in the third decade of the twentieth century. Figure 1 is a schematic diagram summarizing the above comments. The examples come first, and the theorems come later.

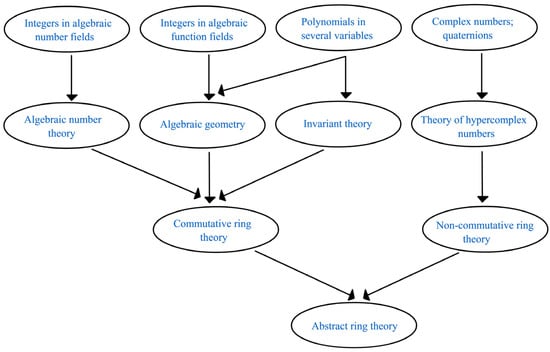
Figure 1. Evolution of theory of rings.

The link between ring theory and other fields of mathematics, such as number theory, algebraic geometry, and algebraic topology, is one of its most essential features. Moreover, ring theory has many applications in computer science, especially in the study of error-correcting codes and cryptography [23,24,25,26,27]. In these applications, the features of polynomial rings and finite fields are used to create algorithms for error detection and correction in digital communications. Its study continues to play an important role in mathematics and computer science, and it remains an active research field.

1.2. Literature Review

Fuzzy subrings and fuzzy ideals of rings were introduced by Liu [28] in 1982 as a generalization of the concept of subrings and ideals of rings. Several operations that can be performed between fuzzy ideals of a ring have been defined in [29]. Mukherjee and Sen [30] characterized Noetherian and regular rings with regard to fuzzy ideals and found all fuzzy prime ideals of $\mathbb{Z}$. An interesting paper [31] on L-fuzzy semilattices and their ideals appeared in 1987. In [32], notions of fuzzy prime ideal and fuzzy maximal ideal were defined. The authors found a necessary and sufficient condition for a prime (maximal) ideal of ring $S$ to be fuzzy prime (maximal) ideal of $S$. Yue [33] initiated the study on of a primary L-fuzzy ideal and a prime L-fuzzy ideal and proved several basic results related to these concepts. Malik [34] presented a seminal study on fuzzy ideals over Artinian rings. The authors discuss Artinian rings in terms of fuzzy ideals. A generalization of the correspondence theorem of ideals of a classical ring in fuzzy framework has been performed in [35]. Kumar discussed several basic results of fuzzy cosets of a fuzzy ideal [36]. Another important study on fuzzy cosets of a fuzzy ideal and fuzzy semiprime ideals has been conducted in [37]. If the readers are interested in finding more details about fuzzy subrings and ideals, we recommend studying [38,39,40,41]. Hur et al. [42] defined the notion of intuitionistic fuzzy ideals (IFIs) of a ring. In [43], an important study about lattice of IFIs was performed by Ahn et al. In [44], Jun et al. characterized IFIs by using intrinsic product of IFSs. Lee et al. [45] discussed the group action on IFIs. To read more studies about ideals of rings in different fuzzy forms, we refer the readers to [46,47,48,49,50].

1.3. Research Gap in the Existing Literature, Major Contributions and Innovative Aspects of the Study

Examining previous publications, we determine that some advances are achieved in the fields of classical, intuitionistic, and Pythagorean fuzzy ring theory. Moreover, several results are proven for $\left(\alpha ,\beta \right)$-PFSRs and bipolar PFSRs of a ring, but there are still many unsolved questions.

(1)

According to traditional ring theory, if $J$ and $I$ are a subring and an ideal, respectively, of a ring $S$, then the intersection of $J$ and $I$ is an ideal of $S.$ This raises the question of whether the intersection of a q-ROFSR and q-ROFI of a ring $S$ is a q-ROFI of $S$.

(2)

The existing research on classical, intuitionistic, and Pythagorean fuzzy subrings and ideals characterizes these notions in terms of classical, intuitionistic, and Pythagorean fuzzy level subrings and ideals. This categorization is essential for exploring the characteristics and connections of these mathematical concepts. Given that a q-ROFR theory generalizes the PFR theory, it becomes important to investigate the characterization of q-ROFSRs and q-ROFIs in terms of q-ROFLSRs and q-ROFLIs, respectively.

(3)

In classical ring theory, the concept of cosets of a subring or ideal of a ring $S$ is a crucial notion in the study of quotient rings. The set of all cosets of an ideal of $S$ forms a ring under a certain binary operation, called the quotient ring. In the context of q-ROFSs, a natural question arises as to whether the set of all q-ROFCs of a q-ROFI of $S$ also forms a ring under a specific binary operation.

(4)

The fundamental theorem of ring homomorphism is a widely regarded result in classical ring theory. This theorem demonstrates a key relationship between the features of a ring homomorphism and the ideal structure of the domain ring, and it has significant repercussions in a variety of mathematical disciplines, including algebra and number theory. Consequently, it is essential to study this significant theorem in the context of q-ROF systems. In the context of q-ROF environments, the fundamental theorem of ring homomorphism provides a basis for further investigation and comprehension of the interplay between ring theory and fuzzy mathematics.

(5)

The algebraic properties of fuzzy semi-prime ideals have been extensively studied in the academic literature. In addition, the relationship between regular rings and FIs has been examined. However, the analysis of these studies within a q-ROF perspective has yet to be investigated.

The ultimate goal of this study is to address the aforementioned open problems and to fill the existing knowledge gap in the literature. This has been achieved through a comprehensive and systematic examination presented in this article. These findings provide new insights into the study of q-ROFIs of crisp rings.

The Chinese remainder theorem, a fundamental concept in crisp ring theory, enables us to analyze the structure of a ring by examining its quotient rings. Its applications span a wide range of fields, including algebraic geometry, finite field construction, and secure message encryption. The present research establishes a foundation for formulating a q-ROF variant of the Chinese remainder theorem. Fuzzy ring homomorphisms are used in certain cryptographic systems, such as the fuzzy identity-based encryption (FIBE) scheme. These homomorphisms provide a method for mapping messages and keys between rings while ensuring system security. Since q-ROFS is a significant extension of FS, applying the concepts of q-ROF homomorphisms in image encryption and information security is expected to yield superior results compared to classical fuzzy homomorphisms.

2. Basic Definitions

The objective of this section is to introduce the essential terminology and concepts that form the basis of our main theorems. It aims to provide a contextual framework that enables readers to grasp the fundamental principles and definitions required for understanding our research.

Definition 1. 

[28] An FS $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$ of a ring $S$ is referred to as an FSR of $S$ if for any ${\varsigma }_1,{\varsigma }_2\in S$, the preceding conditions are met:

(i)

${\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\ge min\left\{{\mu }_{\varnothing }\left({\varsigma }_1\right),{\mu }_{\varnothing }\left({\varsigma }_2\right)\right\}$

(ii)

${\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\ge min\left\{{\mu }_{\varnothing }\left({\varsigma }_1\right),{\mu }_{\varnothing }\left({\varsigma }_2\right)\right\}$

The fuzzy ideal (FI) of $S$ is defined in the same way, except that in condition (ii), “min” is changed to “max”.

Definition 2. 

[42] An IFS $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S\} \right\}$ of $S$ is referred to as an IFSR of $S$ if for any ${\varsigma }_1,{\varsigma }_2\in S$, the preceding conditions are met:

(i)

${\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\ge min\left\{{\mu }_{\varnothing }\left({\varsigma }_1\right),{\mu }_{\varnothing }\left({\varsigma }_2\right)\right\}$ and ${\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\le max\left\{{\nu }_{\varnothing }\left({\varsigma }_1\right),{\nu }_{\varnothing }\left({\varsigma }_2\right)\right\}$

(ii)

${\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\ge min\left\{{\mu }_{\varnothing }\left({\varsigma }_1\right),{\mu }_{\varnothing }\left({\varsigma }_2\right)\right\}$ and ${\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\le max\left\{{\nu }_{\varnothing }\left({\varsigma }_1\right),{\nu }_{\varnothing }\left({\varsigma }_2\right)\right\}$

The IFI of $S$ is defined by replacing “min” and “max” in condition (ii) to “max” and “min”, respectively.

Definition 3. 

[50] A PFS $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S\} \right\}$ of $S$ is referred to as a PFSR of $\mathrm{S}$ if for any ${\mathsf{\varsigma }}_1,{\mathsf{\varsigma }}_2\in \mathrm{S}$, the preceding conditions are met:

(i)

${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^2\ge min\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^2,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^2\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^2\le max\left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^2,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^2\right\}$

(ii)

${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^2\ge min\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^2,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^2\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^2\le max\left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^2,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^2\right\}$

The PFI of $S$ is obtained by replacing “min” and “max” in condition (ii) to “max” and “min”, respectively.

We now give the definitions of q-ROSR and q-ROFIs of a ring $S$.

Definition 4. 

A q-ROFS $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S\} \right\}$ of $S$ is referred to as a q-ROFSR of $S$ if for any ${\varsigma }_1,{\varsigma }_2\in S$, the preceding conditions are met:

(i)

${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\ge min\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\le max\left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$

(ii)

${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\ge min\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\le max\left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$

The q-ROFS $\varnothing$ is known to be q-ROFI of $S$, if condition (ii) is replaced with ${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\ge max\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\le min\left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$.

Definition 5. 

Let $\varnothing =\left\{(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right):\varsigma \in S\right\}$ be a q-ROFSR/PFI of $S$ and $s,t\in \left[0,1\right]$. Then, the set ${\varnothing }_{\left(s,t\right)}=\left\{\varsigma \in S:{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q\ge s,{\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q\le t\right\}$ is known as q-rung orthopair fuzzy level set (q-ROFLS) of $\varnothing$.

Definition 6. 

Let $\varnothing$ and $\psi$ be two q-ROFSRs/q-ROFIs of $S$, then the product of $\varnothing$ and $\psi$ is denoted by $\varnothing \circ \psi$ such that

$$\varnothing \circ \psi =\left\{(\varsigma ,{\mu }_{\varnothing \circ \psi }\left(\varsigma \right),{\nu }_{\varnothing \circ \psi }\left(\varsigma \right):\varsigma \in S\right\}$$

where ${\left({\mu }_{\varnothing \circ \psi }\left(\varsigma \right)\right)}^q=\max \left\{\min \left({\left({\mu }_J\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_S\left({\varsigma }_2\right)\right)}^q\right):{\varsigma }_1,{\varsigma }_2\in S,{\varsigma }_1{\varsigma }_2=\varsigma \right\}$ and ${\left({\nu }_{\varnothing \circ \psi }\left(\varsigma \right)\right)}^q=\min \left\{\max \left({\left({\nu }_J\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_S\left({\varsigma }_2\right)\right)}^q\right):{\varsigma }_1,{\varsigma }_2\in S,{\varsigma }_1{\varsigma }_2=\varsigma \right\}$.

3. Fundamental Properties of q-Rung Orthopair Fuzzy Ideals

In this section, we investigate some basic algebraic characteristics of q-ROFIs. The following advancement have been made in this section.

(1)

By Definition 4, it is easy to see that a q-ROFI is a q-ROFSR as well. In the start of section, we show that a q-ROFSR need not to be a q-ROFI.

(2)

If $\varnothing$ is a q-ROFI of $S$, then the q^th power of the membership value of zero of $S$ cannot be less than the q^th power of the membership value of any element of $S$. Similarly, the q^th power of the non-membership value of zero of $S$ cannot be greater than the q^th power of the non-membership value of any element of $S$, that is, ${\left({\mu }_{\varnothing }\left(0\right)\right)}^q\ge {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(0\right)\right)}^q\le {\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q$ for all $\varsigma \in S.$

(3)

According to traditional ring theory, if $J$ and $I$ are a subring and an ideal, respectively, of a ring $S$, then the intersection of $J$ and $I$ is an ideal of $S.$ This raises the question of whether the intersection of a q-ROFSR and q-ROFI of a ring $S$ is a q-ROFI of $S$. We have answered this question.

(4)

The existing research on classical, intuitionistic, and Pythagorean fuzzy subrings and ideals characterizes these notions in terms of classical, intuitionistic, and Pythagorean fuzzy level subrings and ideals. This categorization is essential for exploring the characteristics and connections of these mathematical concepts. Given that a q-ROFR theory generalizes the PFR theory, it becomes important to investigate the characterization of q-ROFSRs and q-ROFIs in terms of q-ROFLSRs and q-ROFLIs, respectively. We have achieved this in this section by proving that a q-ROFS $\varnothing$ of $S$ is a q-ROFI of $S$ if and only if ${\varnothing }_{\left(s,t\right)}$ is an ideal of $S.$

(5)

We determine that in the case of a division ring $S,$ to form a q-ROFI of $S$ maximum, two distinct membership values can be assigned to all elements of $S$. The same is true while assigning non-membership values.

We start with following example, which shows that a q-ROFSR of $S$ is not a q-ROFI.

Example 1. 

Let us assume $S=\left\{1,2,3\right\}$; it is well known that $\left(2^S, \Delta ,\cap \right)$ is a classical ring. Next, we design a 3-ROFSR of $2^S$ as follows;

$$\varnothing =\left\{\begin{array}{c}\left(\left\{ \right\},0.85,0.70\right),\left(S,0.85,0.70\right),\left(\left\{1\right\},0.70,0.80\right),\left(\left\{2\right\},0.70,0.800\right),\\ \left(\left\{3\right\},0.85,0.70\right),\left(\left\{1,2\right\},0.85,0.70\right),\left(\left\{1,3\right\},0.70,0.80\right),\left(\left\{2,3\right\},0.70,0.80\right)\end{array}\right\}$$

Since ${\left({\mu }_{\varnothing }\left(\left\{1,2\right\}\cap \left\{1\right\}\right)\right)}^3={\left({\mu }_{\varnothing }\left(\left\{1\right\}\right)\right)}^3={\left(0.70\right)}^3$

and $max\left[{\left({\mu }_{\varnothing }\left(\left\{1,2\right\}\right)\right)}^3,{\left({\mu }_{\varnothing }\left(\left\{1\right\}\right)\right)}^3\right]={\left(0.85\right)}^3$.

Therefore,

$${\left({\mu }_{\varnothing }\left(\left\{1,2\right\}\cap \left\{1\right\}\right)\right)}^3\ne max\left[{\left({\mu }_{\varnothing }\left(\left\{1,2\right\}\right)\right)}^3,{\left({\mu }_{\varnothing }\left(\left\{1\right\}\right)\right)}^3\right]$$

Theorem 1. 

If $\varnothing$ be a q-ROFI of $S$, then ${\left({\mu }_{\varnothing }\left(0\right)\right)}^q\ge {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(0\right)\right)}^q\le {\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q$ for all $\varsigma \in S$.

Proof. 

Assume that $\varsigma \in S$, then ${\left({\mu }_{\varnothing }\left(0\right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma -\varsigma \right)\right)}^q\ge min\left\{{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q\right\}={\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$. Similarly, ${\left({\nu }_{\varnothing }\left(0\right)\right)}^q\le {\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q$ for all $\varsigma \in S$. □

Theorem 2. 

If ${\mu }_{\varnothing }\left({\varsigma }_1\right)\ne {\mu }_{\varnothing }\left({\varsigma }_2\right)$ and ${\nu }_{\varnothing }\left({\varsigma }_1\right)\ne {\nu }_{\varnothing }\left({\varsigma }_2\right)$ for some ${\varsigma }_1$, ${\varsigma }_2\in S$, then ${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_q\right)\right)}^q=min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q=max\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$.

Proof. 

Since ${\mu }_{\varnothing }\left({\varsigma }_1\right)>{\mu }_{\varnothing }\left({\varsigma }_2\right)$ therefore ${\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q>{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q$. □

Now,

$${\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left({\varsigma }_1-\left({\varsigma }_1-{\varsigma }_2\right)\right)\right)}^q$$

$$\ge min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\right]$$

(1)

If $min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\right]={\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q$, then ${\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\ge {\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q$ but ${\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q>{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q$. Therefore, $min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\right]={\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q$; thus, Equation (1) becomes

$${\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\ge {\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q$$

(2)

Furthermore,

$${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\ge min\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$$

$$={\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q$$

(3)

Equations (2) and (3) together imply that

$${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q=min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

In the fashion, we can prove that

$${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q=max\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

Theorem 3. 

The intersection of two q-ROFIs ${\varnothing }_1$ and ${\varnothing }_2$ of $S$ is a q-ROFI of $S$.

Proof. 

Assume that ${\varnothing }_1=\left\{\varsigma ,{\mu }_{{\varnothing }_1}\left(\varsigma \right),{\nu }_{{\varnothing }_1}\left(\varsigma \right)\right\}$ and ${\varnothing }_2=\left\{\varsigma ,{\mu }_{{\varnothing }_2}\left(\varsigma \right),{\nu }_{{\varnothing }_2}\left(\varsigma \right)\right\}$ are q-ROFIs of $S$. Then,

$$\begin{array}{cc}{\left({\mu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q& =min\left[{\left({\mu }_{{\varnothing }_1}\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\right]\hfill \\ & \ge min\left[min\left({\left({\mu }_{{\varnothing }_1}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_1}\left({\varsigma }_2\right)\right)}^q\right),min\left({\left({\mu }_{{\varnothing }_2}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right)\right]\hfill \\ & =min\left[min\left({\left({\mu }_{{\varnothing }_1}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_1\right)\right)}^q\right),min\left({\left({\mu }_{{\varnothing }_1}\left({\varsigma }_2\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right)\right]\hfill \\ & =min\left[{\left({\mu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right]\hfill \end{array}$$

Similarly,

$${\left({\nu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\le max\left[{\left({\nu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right]$$

Moreover,

$$\begin{array}{cc}{\left({\mu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1{\varsigma }_2\right)\right)}^q& =min\left[{\left({\mu }_{{\varnothing }_1}\left({\varsigma }_1{\varsigma }_2\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\right]\hfill \\ & \ge min\left[\mathit{max}\left({\left({\mu }_{{\varnothing }_1}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_1}\left({\varsigma }_2\right)\right)}^q\right),\mathit{max}\left({\left({\mu }_{{\varnothing }_2}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right)\right]\hfill \\ & \ge \mathit{max}\left[min\left({\left({\mu }_{{\varnothing }_1}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_1\right)\right)}^q\right),min\left({\left({\mu }_{{\varnothing }_1}\left({\varsigma }_q\right)\right)}^q,{\left({\mu }_{{\varnothing }_2}\left({\varsigma }_q\right)\right)}^q\right)\right]\hfill \\ & =\mathit{max}\left[{\left({\mu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right]\hfill \end{array}$$

In a similar way, we can obtain

$${\left({\nu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\le \mathit{min}\left[{\left({\nu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{{\varnothing }_1\cap {\varnothing }_2}\left({\varsigma }_2\right)\right)}^q\right]$$

Thus, ${\varnothing }_1\cap {\varnothing }_2$ is a q-ROFI of $S$. □

Theorem 4. 

Let $\varnothing =\left\{\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right) \right\}$ be a q-ROFI of $S$. Then,

(i)

${\varnothing }_{\ast +}=\left\{\varsigma \in S:{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q \right\}$ is an ideal of $S$.

(ii)

${\varnothing }_{\ast -}=\left\{\varsigma \in S:{\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q \right\}$ is an ideal of $S$

(iii)

${\varnothing }_{\ast }=\left\{\varsigma \in S:{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q \mathit{and} {\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q\right\}$ is an ideal of $S$.

Proof. 

(i) It is straightforward to show that ${\varnothing }_{\ast +}$ is non-empty subset of $S$. Next, suppose that ${\varsigma }_1,{\varsigma }_2\in {\varnothing }_{\ast +}$, then ${\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q={\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q$.

Consider

$${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\ge min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

$$=min\left[{\left({\mu }_{\varnothing }\left(0\right)\right)}^q,{\left({\mu }_{\varnothing }\left(0\right)\right)}^q\right]$$

$$={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$$

Using Theorem 1, we obtain ${\left({\mu }_{\varnothing }\left(0\right)\right)}^q\ge {\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q$; therefore, ${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$. Consequently, ${\varsigma }_1-{\varsigma }_2\in {\varnothing }_{\ast +}$.

Now, suppose that $\varsigma \in {\varnothing }_{\ast +}$ and $a\in S$. Then,

$${\left({\mu }_{\varnothing }\left(\varsigma a\right)\right)}^q\ge \mathit{max}\left[{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\mu }_{\varnothing }\left(a\right)\right)}^q\right]$$

$$={\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$$

$$={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$$

Moreover ${\left({\mu }_{\varnothing }\left(0\right)\right)}^q\ge {\left({\mu }_{\varnothing }\left(\varsigma a\right)\right)}^q$; thus, ${\left({\mu }_{\varnothing }\left(\varsigma a\right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q,$ which further implies that $\varsigma a\in {\varnothing }_{\ast +}$.

Thus, ${\varnothing }_{\ast +}$ is an ideal of $S.$

(ii) The proof of this part is analogous to that of (i).

(iii) Combining (i) and (ii), the proof is simple. □

Theorem 5. 

Assume that ${\rm X}$ and $\varnothing$ are q-ROFSR and q-ROFI of a ring $S$, respectively, then ${\rm X}\cap \varnothing$ is q-ROFI of ${\varnothing }_{\ast }$.

Proof. 

Let ${\varsigma }_1$, ${\varsigma }_2\in {\varnothing }_{\ast }$, then

$$\begin{array}{cc}{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q& =min\left[{\left({\mu }_{{\rm X}}\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\right]\hfill \\ & \ge min\left[min\left({\left({\mu }_{{\rm X}}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\rm X}}\left({\varsigma }_2\right)\right)}^q\right),min\left({\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right)\right]\hfill \\ & =min\left[min\left({\left({\mu }_{{\rm X}}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q\right),min\left({\left({\mu }_{{\rm X}}\left({\varsigma }_2\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right)\right]\hfill \\ & =min\left[{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_2\right)\right)}^q\right]\hfill \end{array}$$

Similarly, it can be shown that ${\left({\nu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\le max\left[{\left({\nu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{{\rm X}\cap \varnothing }\left({\varsigma }_2\right)\right)}^q\right]$.

Next,

$${\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q=min\left[{\left({\mu }_{{\rm X}}\left({\varsigma }_1{\varsigma }_2\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\right]$$

$$\ge min\left[min\left({\left({\mu }_{{\rm X}}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\rm X}}\left({\varsigma }_2\right)\right)}^q\right),max\left({\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right)\right]$$

$$=min\left[\begin{array}{c}max\left({\left({\mu }_{{\rm X}}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\rm X}}\left({\varsigma }_2\right)\right)}^q\right),\hfill \\ max\left({\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right)\hfill \end{array}\right],\mathrm{as}{\left({\mu }_{{\rm X}}\left({\varsigma }_1\right)\right)}^q=0={\left({\mu }_{{\rm X}}\left({\varsigma }_2\right)\right)}^q$$

$$\begin{gathered} \ge max\left[min\left({\left({\mu }_{{\rm X}}\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q\right),min\left({\left({\mu }_{{\rm X}}\left({\varsigma }_2\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right)\right] \\ =max\left[{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_2\right)\right)}^q\right] \end{gathered}$$

That is, ${\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\ge max\left[{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{{\rm X}\cap \varnothing }\left({\varsigma }_2\right)\right)}^q\right]$.

Using the same reasoning, it is easy to show that

$${\left({\nu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\le \min \left[{\left({\nu }_{{\rm X}\cap \varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{{\rm X}\cap \varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

Thus, ${\rm X}\cap \varnothing$ is a q-ROFI of $S$. □

Theorem 6. 

Let $s\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and $t\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$. Then, q-ROFS $\varnothing$ of a ring $S$ is a q-ROFI of $S$ if and only if ${\varnothing }_{\left(s,t\right)}$ is an ideal of $S$.

Proof 

Let $\varnothing =\left\{(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right):\varsigma \in S\right\}$ be a q-ROFI of $S$. We need to show that ${\varnothing }_{\left(s,t\right)}$ is an ideal of $S$ for all $s\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and $t\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$.

Since $s\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and $t\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$; therefore, $0\in {\varnothing }_{\left(s,t\right)}$ implying that ${\varnothing }_{\left(s,t\right)}\ne \varnothing$.

Assume that ${\varsigma }_1,{\varsigma }_2\in {\varnothing }_{\left(s,t\right)}$, then ${\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\ge s$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\le t$.

Consider

$${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\ge min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

$$\ge min\left[s,s\right]=s$$

and

$${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\le max\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

$$\le max\left[t,t\right]=t$$

$$\Rightarrow {\varsigma }_1-{\varsigma }_2\in {\varnothing }_{\left(s,t\right)}$$

Next, let $\varsigma \in {\varnothing }_{\left(s,t\right)}$ and $a\in S$

$${\left({\mu }_{\varnothing }\left(\varsigma a\right)\right)}^q\ge max\left[{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\mu }_{\varnothing }\left(a\right)\right)}^q\right]\ge max\left[s,{\left({\mu }_{\varnothing }\left(a\right)\right)}^q\right]\ge s$$

and

$${\left({\nu }_{\varnothing }\left(\varsigma a\right)\right)}^q\le max\left[{\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\nu }_{\varnothing }\left(a\right)\right)}^q\right]\le max\left[t,{\left({\nu }_{\varnothing }\left(a\right)\right)}^q\right]=\le$$

$$\Rightarrow \varsigma a\in {\varnothing }_{\left(s,t\right)}$$

Thus, ${\varnothing }_{\left(s,t\right)}$ is an ideal of $S$.

Conversely, assume that for all $s\in \left[0,{\left({\mu }_{\varnothing }\left(0\right)\right)}^q\right]$ and $t\in \left[{\left({\nu }_{\varnothing }\left(0\right)\right)}^q,1\right]$, ${\varnothing }_{\left(s,t\right)}$ is an ideal of $S$. To prove that $\varnothing$ is a q-ROFI of $S$, we let ${\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q=s_1,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q=s_2,{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q=t_1$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q=t_2$ for ${\varsigma }_1,{\varsigma }_2\in S$. Then,

i

${\varsigma }_1,{\varsigma }_2\in {\varnothing }_{\left(min\left(s_1,s_2\right),max\left(t_1,t_2\right)\right)}$, since ${\varnothing }_{\left(min\left(s_1,s_2\right),max\left(t_1,t_2\right)\right)}$ is an ideal of $S$; thus, ${\varsigma }_1-{\varsigma }_2\in {\varnothing }_{\left(min\left(s_1,s_2\right),max\left(t_1,t_2\right)\right)}$, which further implies that ${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\ge min\left(s_1,s_2\right)=min\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\le max\left(t_1,t_2\right)=max\left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$.

ii

either ${\varsigma }_1\in {\varnothing }_{\left(max\left(s_1,s_2\right),min\left(t_1,t_2\right)\right)}$ or ${\varsigma }_2\in {\varnothing }_{\left(max\left(s_1,s_2\right),min\left(t_1,t_2\right)\right)}$. Since ${\varnothing }_{\left(\mathit{max}\left(s_1,s_2\right),min\left(t_1,t_2\right)\right)}$ is an ideal of $S$; therefore, ${\varsigma }_1{\varsigma }_2\in {\varnothing }_{\left(max\left(s_1,s_2\right),min\left(t_1,t_2\right)\right)}$ in both cases. Then,

${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\ge \max \left(s_1,s_2\right)=max\left\{{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\le min\left(t_1,t_2\right)=\min \left\{{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right\}$. Thus, $\varnothing$ is a q-ROFI of $S$. □

Theorem 7. 

For a q-ROFS $\varnothing$ of a division ring $S$ to be a q-ROFI, it is necessary and sufficient that for all $\varsigma \in S-\left\{0\right\}$, the following conditions are obeyed.

(i)

${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(1\right)\right)}^q\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$

(ii)

${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(1\right)\right)}^q\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$

Proof 

Necessity. Assume that $\varnothing$ is a q-ROFI of $S$. Then,

$${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma .1\right)\right)}^q\ge max\left[{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\mu }_{\varnothing }\left(1\right)\right)}^q\right]$$

$$\ge {\left({\mu }_{\varnothing }\left(1\right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma {\varsigma }^{-1}\right)\right)}^q\ge max\left[{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }^{-1}\right)\right)}^q\right]$$

$$\ge {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$$

$$\Rightarrow {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(1\right)\right)}^q$$

In a similar manner, we obtain ${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(1\right)\right)}^q$. Lastly, using Theorem 1 yields the desired result.

Sufficiency. Let ${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(1\right)\right)}^q\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(1\right)\right)}^q\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$ for all $\varsigma \in S\backslash \left\{0\right\}$.

(i)

Suppose that ${\varsigma }_1,{\varsigma }_2\in S$.

If ${\varsigma }_1\ne {\varsigma }_2$, then

${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left(1\right)\right)}^q\ge min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\nu }_{\varnothing }\left(1\right)\right)}^q\le max\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$.

If ${\varsigma }_1={\varsigma }_2$, then

${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q\ge min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q\le max\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$.

(ii)

Let ${\varsigma }_1,{\varsigma }_2\in S$.

If ${\varsigma }_1=0$ or ${\varsigma }_2=0$, then

${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q=\mathit{max}\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q=\mathit{min}\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$.

If ${\varsigma }_1\ne 0$ and ${\varsigma }_2\ne 0$, then again

${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left(1\right)\right)}^q=\mathit{max}\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q={\left({\mu }_{\varnothing }\left(1\right)\right)}^q=\mathit{min}\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$. Thus, $\varnothing$ is a q-ROFI of $S$. □

4. q-Rung Orthopair Fuzzy Cosets of a q-Rung Orthopair Fuzzy Ideal

In classical ring theory, the concept of cosets of a subring or ideal of a ring $S$ is a crucial notion in the study of quotient rings. In this section, we have expanded this concept to q-ROF environment. The key findings of this section are:

(1)

The set of all cosets of an ideal of $S$ forms a ring under a certain binary operation, called the quotient ring. In this section, we extend the notion of quotient ring in q-ROF framework by proving that the set of all q-ROFCs of a q-ROFI of $S$ also forms a ring under a specific binary operation.

(2)

The fundamental theorem of ring homomorphism is a widely regarded result in classical ring theory. This theorem demonstrates a key relationship between the features of a ring homomorphism and the ideal structure of the domain ring, and it has significant repercussions in a variety of mathematical disciplines, including algebra and number theory. Consequently, it is essential to study this significant theorem in the context of q-ROF systems, as has been conducted in this section.

Definition 7. 

Let $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$ be a q-ROFI of a ring $S$. We know ${\varnothing }_{\ast }$ is an ideal of $S$ which give rise to the quotient ring $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.=\left\{\varsigma +{\varnothing }_{\ast }:\varsigma \in S\right\}$. In order to design a q-ROFS of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.,$ let us define two mapping ${\mu }_{{\aleph }_{\varnothing }}:\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.\to \left[0,1\right]$ and ${\nu }_{{\aleph }_{\varnothing }}$ : $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.\to \left[0,1\right]$ by ${\mu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right)={\mu }_{\varnothing }\left(\varsigma \right)$ and ${\nu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right)={\nu }_{\varnothing }\left(\varsigma \right)$, respectively. Then, obviously, ${\aleph }_{\varnothing }=\left\{\left(\varsigma +{\varnothing }_{\ast },{\mu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right),{\nu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right)\right):\varsigma +{\varnothing }_{\ast }\in \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.\right\}$ is a q-ROFS of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$.

The following theorem forms the basis for defining q-ROCs of a q-ROFI in S.

Theorem 8. 

Let $\varnothing =\left\{\left(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right)\right):\varsigma \in S \right\}$ be a q-ROFI of a ring $S$. Suppose that ${\mu }_{{\aleph }_{\varnothing }}:\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.\to \left[0,1\right]$ and ${\nu }_{{\aleph }_{\varnothing }}$: $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.\to \left[0,1\right]$ are defined by ${\mu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right)={\mu }_{\varnothing }\left(\varsigma \right)$ and ${\nu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right)={\nu }_{\varnothing }\left(\varsigma \right)$, respectively. Then, ${\aleph }_{\varnothing }=\left\{\left(\varsigma +{\varnothing }_{\ast },{\mu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right),{\nu }_{{\aleph }_{\varnothing }}\left(\varsigma +{\varnothing }_{\ast }\right)\right):\varsigma +{\varnothing }_{\ast }\in \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.\right\}$ is a q-ROFI of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$.

Proof 

Firstly, we prove that ${\mu }_{{\aleph }_{\varnothing }}$ and ${\nu }_{{\aleph }_{\varnothing }}$ are well-defined. For this, assume that ${\varsigma }_1,{\varsigma }_2\in S$ satisfying

$${\varsigma }_1+{\varnothing }_{\ast }={\varsigma }_2+{\varnothing }_{\ast }$$

$\Rightarrow {\varsigma }_1-{\varsigma }_2\in {\varnothing }_{\ast }\Rightarrow {\varsigma }_1,{\varsigma }_2\in {\varnothing }_{\ast }$ (Since ${\varnothing }_{\ast }$ is an ideal of $S)$

$\Rightarrow {\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q={\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q={\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q$

$\Rightarrow {\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1+{\varnothing }_{\ast }\right)\right)}^q={\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q$ and ${\left({\nu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1+{\varnothing }_{\ast }\right)\right)}^q={\left({\nu }_{{\aleph }_{\varnothing }}\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q$.

This means that ${\mu }_{{\aleph }_{\varnothing }}$ and ${\nu }_{{\aleph }_{\varnothing }}$ are well defined. It is simple to show that ${\aleph }_{\varnothing }$ is a q-ROFS of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right..$

Lastly, we prove that ${\aleph }_{\varnothing }$ is a q-ROFI of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$. Let ${\varsigma }_1+{\varnothing }_{\ast },{\varsigma }_2+{\varnothing }_{\ast }\in \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$, then

$${\left({\mu }_{{\aleph }_{\varnothing }}\left(\left({\varsigma }_1+{\varnothing }_{\ast }\right)-\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)\right)}^q={\left({\mu }_{{\aleph }_{\varnothing }}\left(\left({\varsigma }_1-{\varsigma }_2\right)+{\varnothing }_{\ast }\right)\right)}^q$$

$$={\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\ge min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

$$=min\left[{\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1+{\varnothing }_{\ast }\right)\right)}^q,{\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q\right]$$

Similarly,

$${\left({\nu }_{{\aleph }_{\varnothing }}\left(\left({\varsigma }_1+{\varnothing }_{\ast }\right)-\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)\right)}^q\le max\left[{\left({\nu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1+{\varnothing }_{\ast }\right)\right)}^q,{\left({\nu }_{{\aleph }_{\varnothing }}\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q\right]$$

Moreover,

$${\left({\mu }_{{\aleph }_{\varnothing }}\left(\left({\varsigma }_1+{\varnothing }_{\ast }\right)\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)\right)}^q={\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1{\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q$$

$$={\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\ge max\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

$$=max\left\{{\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1+{\varnothing }_{\ast }\right)\right)}^q,{\left({\mu }_{{\aleph }_{\varnothing }}\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q\right\}$$

The same reasoning can be used to obtain;

$${\left({\nu }_{{\aleph }_{\varnothing }}\left(\left({\varsigma }_1+{\varnothing }_{\ast }\right)\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)\right)}^q\le min\left[{\left({\nu }_{{\aleph }_{\varnothing }}\left({\varsigma }_1+{\varnothing }_{\ast }\right)\right)}^q,{\left({\nu }_{{\aleph }_{\varnothing }}\left({\varsigma }_2+{\varnothing }_{\ast }\right)\right)}^q\right]$$

Thus, we obtain the conclusion that ${\aleph }_{\varnothing }$ is a q-ROFI of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$. □

The following example explains the result established by Theorem 8.

Example 2. 

Let us design a 3-ROFI $\varnothing$ of a ring ${\mathbb{Z}}_{12}$ of integer modulo 12 as

$$\varnothing =\left\{\begin{array}{c}\left(0,0.90,0.60\right),\left(1,0.75,0.75\right),\left(2,0.85,0.70\right),\left(3,0.75,0.75\right),\left(4,0.90,0.60\right),\left(5,0.75,0.75\right)\\ \left(6,0.85,0.70\right),\left(7,0.75,0.75\right),\left(8,0.90,0.60\right),\left(9,0.75,0.75\right),\left(10,0.85,0.70\right),\left(11,0.75,0.75\right)\end{array}\right\}$$

Then, we find ${\varnothing }_{\ast }=\left\{0,4,8\right\}$ and $\raisebox{1ex}{${\mathbb{Z}}_{12}$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.=\left\{\left\{0,4,8\right\},\left\{1,5,9\right\},\left\{2,6,10\right\},\left\{3,7,11\right\}\right\}$. We now generate a 3-ROFS ${\aleph }_{\varnothing }$ of $\raisebox{1ex}{${\mathbb{Z}}_{12}$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$ using the approach mentioned in Theorem 8, that is,

$${\aleph }_{\varnothing }=\left\{\left(\left\{0,4,8\right\},0.90,0.60\right),\left(\left\{1,5,9\right\},0.75,0.75\right),\left(\left\{2,6,10\right\},0.85,0.70\right),\left(\left\{3,7,11\right\},0.75,0.75\right)\right\}$$

As can be seen, the constructed q-ROFS ${\aleph }_{\varnothing }$ is a q-ROFI of $\raisebox{1ex}{${\mathbb{Z}}_{12}$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$.

Theorem 9. 

Assume that $J$ is an ideal of a ring $S$ and $\theta$ is a q-ROFI of $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$J$}\right.$. Then, ${\mu }_{\theta }\left(\varsigma +J\right)={\mu }_{\theta }\left(J\right)$ and ${\nu }_{\theta }\left(\varsigma +J\right)={\nu }_{\theta }\left(J\right)$ if and only if $\varsigma \in J$ implies there exists a q-ROFI $\varnothing$ of $S$ such that ${\varnothing }_{\ast }=J$.

Proof 

Let us define a q-ROFS $\varnothing$ of $S$ as follows;

${\mu }_{\varnothing }\left(\varsigma \right)={\mu }_{\theta }\left(\varsigma +J\right)$ and ${\nu }_{\varnothing }\left(\varsigma \right)={\nu }_{\theta }\left(\varsigma +J\right)$, for all $\varsigma \in S$

$${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q={\left({\mu }_{\theta }\left(\left({\varsigma }_1-{\varsigma }_2\right)+J\right)\right)}^q$$

$$\begin{gathered} ={\left({\mu }_{\theta }\left(\left({\varsigma }_1+J\right)-\left({\varsigma }_1+J\right)\right)\right)}^q\ge min\left[{\left({\mu }_{\theta }\left({\varsigma }_1+J\right)\right)}^q,{\left({\mu }_{\theta }\left({\varsigma }_2+J\right)\right)}^q\right] \\ =min\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right] \end{gathered}$$

Similarly,

$${\left({\mu }_{\varnothing }\left({\varsigma }_1-{\varsigma }_2\right)\right)}^q\le max\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

Moreover,

$${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q={\left({\mu }_{\theta }\left({\varsigma }_1{\varsigma }_2+J\right)\right)}^q$$

$$={\left({\mu }_{\theta }\left(\left({\varsigma }_1+J\right)\left({\varsigma }_1+J\right)\right)\right)}^q\ge max\left[{\left({\mu }_{\theta }\left({\varsigma }_1+J\right)\right)}^q,{\left({\mu }_{\theta }\left({\varsigma }_2+J\right)\right)}^q\right]$$

$$=max\left[{\left({\mu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

Similarly,

$${\left({\mu }_{\varnothing }\left({\varsigma }_1{\varsigma }_2\right)\right)}^q\le min\left[{\left({\nu }_{\varnothing }\left({\varsigma }_1\right)\right)}^q,{\left({\nu }_{\varnothing }\left({\varsigma }_2\right)\right)}^q\right]$$

This shows that $\varnothing$ is a q-ROFI of $S$.

Now,

$\varsigma \in {\varnothing }_{\ast }\iff {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q$

$\iff {\left({\mu }_{\theta }\left(\varsigma +J\right)\right)}^q={\left({\mu }_{\varnothing }\left({\mu }_{\theta }\left(J\right)\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left({\mu }_{\theta }\left(\varsigma +J\right)\right)\right)}^q={\left({\nu }_{\varnothing }\left({\mu }_{\theta }\left(J\right)\right)\right)}^q\iff \varsigma \in J$.

Thus, ${\varnothing }_{\ast }=J.$ □

In the example below, we validate the result given in Theorem 9.

Example 3. 

Let us assume an ideal $⟨6⟩$ of $\mathbb{Z}$. Then,

$$\raisebox{1ex}{$\mathbb{Z}$}\!\left/ \!\raisebox{-1ex}{$⟨6⟩$}\right.=\left\{⟨6⟩,1+⟨6⟩,2+⟨6⟩,3+⟨6⟩,4+⟨6⟩,5+⟨6⟩\right\}$$

Now, taking into account the criterion mentioned in the Theorem 9, we form a 3-ROFI $\theta$ of $\raisebox{1ex}{$\mathbb{Z}$}\!\left/ \!\raisebox{-1ex}{$⟨6⟩$}\right.$ as follows,

$$\theta =\left\{\begin{array}{c}\begin{array}{c}\left(⟨6⟩,0.95,0.30\right),\left(1+⟨6⟩,0.70,0.40\right),\left(2+⟨6⟩,0.85,0.35\right),\end{array}\\ \left(3+⟨6⟩,0.70,0.40\right),\left(4+⟨6⟩,0.85,0.35\right),\left(5+⟨6⟩,0.70,0.40\right)\end{array}\right\}$$

Then, as per the rule defined in Theorem 9, we design 3-ROFI $\varnothing$ of $\mathbb{Z}$ as;

$\varnothing =\left\{\begin{array}{c}m,{\mu }_{\varnothing }\left(m\right),{\nu }_{\varnothing }\left(m\right):m\in Z\end{array}\right\}$, where

${\mu }_{\varnothing }\left(m\right)=\left\{\begin{array}{c}0.90 if m\in ⟨6⟩ \\ 0.85 if m\in 2+⟨6⟩\\ 0.85 if m\in 4+⟨6⟩\\ 0.70 otherwise\end{array}\right.$ and ${\nu }_{\varnothing }\left(m\right)=\left\{\begin{array}{c}0.30 if m\in ⟨6⟩ \\ 0.35 if m\in 2+⟨6⟩\\ 0.35 if m\in 4+⟨6⟩\\ 0.40 otherwise\end{array}\right.$.

It is simple to compute ${\varnothing }_{\ast }=⟨6⟩$, which validates Theorem 9.

Definition 8. 

Assume that $\varnothing$ is a q-ROFI of $S$ and $\lambda \in S$. Then, the q-ROFS ${\varnothing }_{\lambda }=\left\{(\varsigma ,{\mu }_{{\varnothing }_{\lambda }}\left(\varsigma \right),{\nu }_{{\varnothing }_{\lambda }}\left(\varsigma \right):\varsigma \in S \right\}$ of $S$, where ${\left({\mu }_{{\varnothing }_{\lambda }}\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma -\lambda \right)\right)}^q$ and ${\left({\nu }_{{\varnothing }_{\lambda }}\left(\varsigma \right)\right)}^q={\left({\nu }_{\varnothing }\left(\varsigma -\lambda \right)\right)}^q$ is called a q-ROFC of q-ROFI $\varnothing$ in $S$ related to $\lambda .$

The following example explains the notion of q-ROFC of q-ROFI $\varnothing$ in $S$.

Example 4. 

Let us design a 3-ROFI $\varnothing$ of a ring ${\mathbb{Z}}_6$ in the following way;

$$\begin{gathered} \varnothing =\left\{\begin{array}{c}\left(0,0.95,0.65\right),\left(1,0.90,0.75\right),\left(2,0.90,0.75\right),\\ \left(3,0.95,0.65\right),\left(4,0.90,0.75\right),\left(5,0.90,0.75\right) \end{array}\right\} \\ \mathrm{Next}, \mathrm{we}\mathrm{compute} \mathrm{all} \text{3-ROFC} \mathrm{of} \varnothing \mathrm{related}\mathrm{all}\mathrm{elements}\mathrm{of}{\mathbb{Z}}_6. \end{gathered}$$

(i)

The 3-ROFC of $\varnothing$ related to 0 is

$${\varnothing }_0=\left\{\begin{array}{c}\left(0,{\mu }_{\varnothing }\left(0\right),{\nu }_{\varnothing }\left(0\right)\right),\left(1,{\mu }_{\varnothing }\left(1\right),{\nu }_{\varnothing }\left(1\right)\right),\left(2,{\mu }_{\varnothing }\left(2\right),{\nu }_{\varnothing }\left(2\right)\right),\\ \left(3,{\mu }_{\varnothing }\left(3\right),{\nu }_{\varnothing }\left(3\right)\right),\left(4,{\mu }_{\varnothing }\left(4\right),{\nu }_{\varnothing }\left(4\right)\right),\left(5,{\mu }_{\varnothing }\left(5\right),{\nu }_{\varnothing }\left(5\right)\right) \end{array}\right\}$$

$$=\left\{\begin{array}{c}\left(0,0.95,0.65\right),\left(1,0.90,0.75\right),\left(2,0.90,0.75\right),\\ \left(3,0.95,0.65\right),\left(4,0.90,0.75\right),\left(5,0.90,0.75\right) \end{array}\right\}$$

(ii)

The 3-ROFC of $\varnothing$ related to 1 is

$${\varnothing }_1=\left\{\begin{array}{c}\left(0,{\mu }_{\varnothing }\left(5\right),{\nu }_{\varnothing }\left(5\right)\right),\left(1,{\mu }_{\varnothing }\left(0\right),{\nu }_{\varnothing }\left(0\right)\right),\left(2,{\mu }_{\varnothing }\left(1\right),{\nu }_{\varnothing }\left(1\right)\right),\\ \left(3,{\mu }_{\varnothing }\left(2\right),{\nu }_{\varnothing }\left(2\right)\right),\left(4,{\mu }_{\varnothing }\left(3\right),{\nu }_{\varnothing }\left(3\right)\right),\left(5,{\mu }_{\varnothing }\left(4\right),{\nu }_{\varnothing }\left(4\right)\right) \end{array}\right\}$$

$$=\left\{\begin{array}{c}\left(0,0.90,0.75\right),\left(1,0.95,0.65\right),\left(2,0.90,0.75\right),\\ \left(3,0.90,0.75\right),\left(4,0.95,0.65\right),\left(5,0.90,0.75\right) \end{array}\right\}$$

(iii)

The 3-ROFC of $\varnothing$ related to 2 is

$${\varnothing }_2=\left\{\begin{array}{c}\left(0,{\mu }_{\varnothing }\left(4\right),{\nu }_{\varnothing }\left(4\right)\right),\left(1,{\mu }_{\varnothing }\left(5\right),{\nu }_{\varnothing }\left(5\right)\right),\left(2,{\mu }_{\varnothing }\left(0\right),{\nu }_{\varnothing }\left(0\right)\right),\\ \left(3,{\mu }_{\varnothing }\left(1\right),{\nu }_{\varnothing }\left(1\right)\right),\left(4,{\mu }_{\varnothing }\left(2\right),{\nu }_{\varnothing }\left(2\right)\right),\left(5,{\mu }_{\varnothing }\left(3\right),{\nu }_{\varnothing }\left(3\right)\right) \end{array}\right\}$$

$$=\left\{\begin{array}{c}\left(0,0.90,0.75\right),\left(1,0.90,0.75\right),\left(2,0.95,0.65\right),\\ \left(3,0.90,0.75\right),\left(4,0.90,0.75\right),\left(5,0.95,0.65\right) \end{array}\right\}$$

(iv)

The 3-ROFC of $\varnothing$ related to 3 is

$${\varnothing }_3=\left\{\begin{array}{c}\left(0,{\mu }_{\varnothing }\left(3\right),{\nu }_{\varnothing }\left(3\right)\right),\left(1,{\mu }_{\varnothing }\left(4\right),{\nu }_{\varnothing }\left(4\right)\right),\left(2,{\mu }_{\varnothing }\left(5\right),{\nu }_{\varnothing }\left(5\right)\right),\\ \left(3,{\mu }_{\varnothing }\left(0\right),{\nu }_{\varnothing }\left(0\right)\right),\left(4,{\mu }_{\varnothing }\left(1\right),{\nu }_{\varnothing }\left(1\right)\right),\left(5,{\mu }_{\varnothing }\left(2\right),{\nu }_{\varnothing }\left(2\right)\right) \end{array}\right\}$$

$$=\left\{\begin{array}{c}\left(0,0.95,0.65\right),\left(1,0.90,0.75\right),\left(2,0.90,0.75\right),\\ \left(3,0.95,0.65\right),\left(4,0.90,0.75\right),\left(5,0.90,0.75\right) \end{array}\right\}$$

(v)

The 3-ROFC of $\varnothing$ with respect to 4 is

$${\varnothing }_4=\left\{\begin{array}{c}\left(0,{\mu }_{\varnothing }\left(2\right),{\nu }_{\varnothing }\left(2\right)\right),\left(1,{\mu }_{\varnothing }\left(3\right),{\nu }_{\varnothing }\left(3\right)\right),\left(2,{\mu }_{\varnothing }\left(4\right),{\nu }_{\varnothing }\left(4\right)\right),\\ \left(3,{\mu }_{\varnothing }\left(5\right),{\nu }_{\varnothing }\left(5\right)\right),\left(4,{\mu }_{\varnothing }\left(0\right),{\nu }_{\varnothing }\left(0\right)\right),\left(5,{\mu }_{\varnothing }\left(1\right),{\nu }_{\varnothing }\left(1\right)\right) \end{array}\right\}$$

$$=\left\{\begin{array}{c}\left(0,0.90,0.75\right),\left(1,0.95,0.65\right),\left(2,0.90,0.75\right),\\ \left(3,0.90,0.75\right),\left(4,0.95,0.65\right),\left(5,0.90,0.75\right) \end{array}\right\}$$

(vi)

The 3-ROFC of $\varnothing$ related to 5 is

$${\varnothing }_5=\left\{\begin{array}{c}\left(0,{\mu }_{\varnothing }\left(1\right),{\nu }_{\varnothing }\left(1\right)\right),\left(1,{\mu }_{\varnothing }\left(2\right),{\nu }_{\varnothing }\left(2\right)\right),\left(2,{\mu }_{\varnothing }\left(3\right),{\nu }_{\varnothing }\left(3\right)\right),\\ \left(3,{\mu }_{\varnothing }\left(4\right),{\nu }_{\varnothing }\left(4\right)\right),\left(4,{\mu }_{\varnothing }\left(5\right),{\nu }_{\varnothing }\left(5\right)\right),\left(5,{\mu }_{\varnothing }\left(0\right),{\nu }_{\varnothing }\left(0\right)\right) \end{array}\right\}$$

$$=\left\{\begin{array}{c}\left(0,0.90,0.75\right),\left(1,0.90,0.75\right),\left(2,0.95,0.65\right),\\ \left(3,0.90,0.75\right),\left(4,0.90,0.75\right),\left(5,0.95,0.65\right) \end{array}\right\}$$

Thus, in terms of all elements of ${\mathbb{Z}}_6$, there are $3$ different 3-ROFCs of $\varnothing$, namely

${\varnothing }_0={\varnothing }_3$, ${\varnothing }_1={\varnothing }_4$ and ${\varnothing }_2={\varnothing }_5$.

Remark 1. 

Let us denote the set of all q-ROFCs of q-ROFI $\varnothing$ in $S$ by ${\mathcal{F}}_{\varnothing }$.

Theorem 10. 

Let $\varnothing$ be a q-ROFI of $S$. Then, ${\mathcal{F}}_{\varnothing }$ forms a ring with respect to the following

binary operations,

${\varnothing }_{{\zeta }_1}+{\varnothing }_{{\zeta }_2}={\varnothing }_{{\zeta }_1+{\zeta }_2}$ and ${\varnothing }_{{\zeta }_1}.{\varnothing }_{{\zeta }_2}={\varnothing }_{{\zeta }_1{\zeta }_2}$ for all ${\zeta }_1,{\zeta }_2\in S$.

Proof. 

In the first phase, we prove that binary operations “+” and “.” defined on ${\mathcal{F}}_{\varnothing }$ are well defined.

Suppose that ${\zeta }_1,{\zeta }_2,{\zeta }_1^{\prime },{\zeta }_2^{\prime }\in S$ and ${\varnothing }_{{\zeta }_1}={\varnothing }_{{\zeta }_1^{\prime }}$ and ${\varnothing }_{{\zeta }_2}={\varnothing }_{{\zeta }_2^{\prime }}$. Then, for all $\varsigma \in S$.

$${\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)={\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)\mathrm{and}{\nu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)={\nu }_{{\zeta }_1^{\text{'}}}\left(\varsigma \right)$$

(4)

$${\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)={\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)\mathrm{and}{\nu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)={\nu }_{{\zeta }_2^{\text{'}}}\left(\varsigma \right)$$

(5)

Thus,

$${\mu }_{\varnothing }\left(\varsigma -{\zeta }_1\right)={\mu }_{\varnothing }\left(\varsigma -{\zeta }_1^{\text{'}}\right)\mathrm{and}{\nu }_{\varnothing }\left(\varsigma -{\zeta }_1\right)={\nu }_{\varnothing }\left(\varsigma -{\zeta }_1^{\text{'}}\right)$$

(6)

$${\mu }_{\varnothing }\left(\varsigma -{\zeta }_2\right)={\mu }_{\varnothing }\left(\varsigma -{\zeta }_2^{\text{'}}\right)\mathrm{and}{\nu }_{\varnothing }\left(\varsigma -{\zeta }_2\right)={\nu }_{\varnothing }\left(\varsigma -{\zeta }_2^{\text{'}}\right)$$

(7)

Putting $\varsigma ={\zeta }_1+{\zeta }_2-{\zeta }_2^{\text{'}}$ in (6) $\varsigma ={\zeta }_2$ in (7) and $\varsigma ={\zeta }_1$ in (6), we have

$${\mu }_{\varnothing }\left({\zeta }_2-{\zeta }_2^{\text{'}}\right)={\mu }_{\varnothing }\left({\zeta }_1+{\zeta }_2-{\zeta }_2^{\text{'}}-{\zeta }_1^{\text{'}}\right)\mathrm{and}{\nu }_{\varnothing }\left({\zeta }_2-{\zeta }_2^{\text{'}}\right)={\nu }_{\varnothing }\left({\zeta }_1+{\zeta }_2-{\zeta }_2^{\text{'}}-{\zeta }_1^{\text{'}}\right)$$

(8)

$${\mu }_{\varnothing }\left(0\right)={\mu }_{\varnothing }\left({\zeta }_2-{\zeta }_2^{\text{'}}\right)\mathrm{and}{\nu }_{\varnothing }\left(0\right)={\nu }_{\varnothing }\left({\zeta }_2-{\zeta }_2^{\text{'}}\right)$$

(9)

$${\mu }_{\varnothing }\left(0\right)={\mu }_{\varnothing }\left({\zeta }_1-{\zeta }_1^{\text{'}}\right)\mathrm{and}{\nu }_{\varnothing }\left(0\right)={\nu }_{\varnothing }\left({\zeta }_1-{\zeta }_1^{\text{'}}\right)$$

(10)

Now,

$$\begin{array}{cc}{\left({\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)\right)}^q& ={\left({\mu }_{{\varnothing }_{{\zeta }_1+{\zeta }_2}}\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma -{\zeta }_1-{\zeta }_2\right)\right)}^q\hfill \\ & ={\left({\mu }_{\varnothing }\left(\left(\varsigma -{\zeta }_1^{\text{'}}-{\zeta }_2^{\text{'}}\right)-\left({\zeta }_1-{\zeta }_1^{\text{'}}+{\zeta }_2-{\zeta }_2^{\text{'}}\right)\right)\right)}^q\hfill \\ & \ge min\left[{\left({\mu }_{\varnothing }\left(\varsigma -\left({\zeta }_1^{\text{'}}+{\zeta }_2^{\text{'}}\right)\right)\right)}^q,{\left({\mu }_{\varnothing }\left({\zeta }_1-{\zeta }_1^{\text{'}}+{\zeta }_2-{\zeta }_2^{\text{'}}\right)\right)}^q\right]\hfill \end{array}$$

$\ge min\left[{\left({\mu }_{\varnothing }\left(\varsigma -\left({\zeta }_1^{\prime }+{\zeta }_2^{\prime }\right)\right)\right)}^q,{\left({\mu }_{\varnothing }\left(0\right)\right)}^q\right]$ (by using (9) and (10)

$$={\left({\mu }_{\varnothing }\left(\varsigma -\left({\zeta }_1^{\text{'}}+{\zeta }_2^{\text{'}}\right)\right)\right)}^q={\left({\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}+{\zeta }_2^{\text{'}}}}\left(\varsigma \right)\right)}^q={\left({\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)\right)}^q$$

Thus,

$${\left({\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)\right)}^q\ge {\left({\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)\right)}^q$$

(11)

The same reasoning leads to

$${\left({\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)\right)}^q\ge {\left({\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)\right)}^q$$

(12)

The inequalities (11) and (12) yields

$${\left({\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)\right)}^q={\left({\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)\right)}^q+{\left({\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)\right)}^q$$

(13)

Then, by using (4) and (5), we obtain

$${\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)+{\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)={\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)+{\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)$$

(14)

Similarly,

$${\nu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right)+{\nu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)={\nu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right)+{\nu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)$$

(15)

Using the same technique again, we can obtain

$${\mu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right){\mu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)={\mu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right){\mu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)$$

(16)

and

$${\nu }_{{\varnothing }_{{\zeta }_1}}\left(\varsigma \right){\nu }_{{\varnothing }_{{\zeta }_2}}\left(\varsigma \right)={\nu }_{{\varnothing }_{{\zeta }_1^{\text{'}}}}\left(\varsigma \right){\nu }_{{\varnothing }_{{\zeta }_2^{\text{'}}}}\left(\varsigma \right)$$

(17)

Equations (14) to (17) give

$${\varnothing }_{{\zeta }_1}+{\varnothing }_{{\zeta }_2}={\varnothing }_{{\zeta }_1^{\prime }}+{\varnothing }_{{\zeta }_2^{\prime }}\mathrm{and}{\varnothing }_{{\zeta }_1}{\varnothing }_{{\zeta }_2}={\varnothing }_{{\zeta }_1^{\prime }}{\varnothing }_{{\zeta }_2^{\prime }}.$$

Thus, “+” and “.” defined on ${\mathcal{F}}_{\varnothing }$ are well-defined.

Furthermore, ${\varnothing }_0=\varnothing$ is zero of ${\mathcal{F}}_{\varnothing }$ and for all ${\varnothing }_{\zeta }\in {\mathcal{F}}_{\varnothing }$ there is a ${\varnothing }_{-\zeta }\in {\mathcal{F}}_{\varnothing }$ so that

${\varnothing }_{\zeta }+{\varnothing }_{-\zeta }={\varnothing }_0={\varnothing }_{-\zeta }+{\varnothing }_{\zeta }$. The proof of the remaining properties is simple. □

Remark 2. 

If $\varnothing =\left\{(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right):\varsigma \in S \right\}$ is a q-ROFI of $S$ such that ${\mu }_{\varnothing }$ and ${\nu }_{\varnothing }$ are

constant mappings, then ${\mathcal{F}}_{\varnothing }=\left\{{\varnothing }_0\right\}$.

Definition 9. 

Let $\varnothing$ be a q-ROFI of $S$, then the q-ROFI ${\varnothing }^{\prime }$ of ${\mathcal{F}}_{\varnothing }$ defined by

${\mu }_{{\varnothing }^{\prime }}\left({\varnothing }_{\zeta }\right)={\mu }_{\varnothing }\left(\zeta \right)$ and ${\nu }_{{\varnothing }^{\prime }}\left({\varnothing }_{\zeta }\right)={\nu }_{\varnothing }\left(\zeta \right)$, for all $\zeta \in S$, is referred to as a q-rung orthopair fuzzy quotient ideal (q-ROFQI) with respect to $\varnothing$.

Next, we present an analogue of the fundamental theorem of homomorphism.

Theorem 11. 

Suppose that $\varnothing =\left\{(\varsigma ,{\mu }_{\varnothing }\left(\varsigma \right),{\nu }_{\varnothing }\left(\varsigma \right):\varsigma \in S \right\}$ is a q-ROFI of a ring $S$, then

$h:S\to {\mathcal{F}}_{\varnothing }$ defined by $h\left(\zeta \right)={\varnothing }_{\zeta }$ for all $\zeta \in S$ is a ring homomorphism and Ker$\left(h\right)$ ${\varnothing }_{\ast }$.

Proof 

Let ${\zeta }_1,{\zeta }_2\in S$, then

$$h\left({\zeta }_1+{\zeta }_2\right)={\varnothing }_{{\zeta }_1+{\zeta }_2}$$

$$={\varnothing }_{{\zeta }_1}+{\varnothing }_{{\zeta }_2}$$

$$=h\left({\zeta }_1\right)+h\left({\zeta }_2\right)$$

and

$$h\left({\zeta }_1{\zeta }_2\right)={\varnothing }_{{\zeta }_1{\zeta }_2}$$

$$={\varnothing }_{{\zeta }_1}{\varnothing }_{{\zeta }_2}$$

$$=h\left({\zeta }_1\right)h\left({\zeta }_2\right).$$

Now, we demonstrate that for all $\zeta \in S$,

$${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q\mathrm{and}{\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q\iff {\varnothing }_{\zeta }={\varnothing }_0.$$

For this, let ${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q$. Then, for all $\varsigma \in S$, we obtain ${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q\le {\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q\ge {\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q$. If ${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q<{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q$, then the application of Theorem 2 gives ${\left({\mu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$. On the other hand, ${\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\Rightarrow \varsigma ,\zeta \in \left\{\gamma \in S:{\left({\mu }_{\varnothing }\left(\gamma \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q\right\}\Rightarrow {\left({\mu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$.

Thus,

$${\left({\mu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q\mathrm{for}\mathrm{all}\varsigma \in S.$$

The same reasoning yields;

$${\left({\nu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q\mathrm{for}\mathrm{all}\varsigma \in S.$$

Thus, ${\varnothing }_{\zeta }={\varnothing }_0$.

Conversely, assume that ${\varnothing }_{\zeta }={\varnothing }_0$. Then, for all $\varsigma \in S$, ${\left({\mu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma -0\right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(\varsigma -0\right)\right)}^q$.

Now,

$${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(\varsigma -\left(\varsigma -\zeta \right)\right)\right)}^q\ge min\left\{{\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q,{\left({\mu }_{\varnothing }\left(\varsigma -\zeta \right)\right)}^q\right\}={\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$$

This mean that ${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\ge {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q$ for all $\varsigma \in S$, thus ${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$.

The same reasoning leads to ${\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q$.

Consider,

$$\mathrm{Ker}h=\left\{\zeta \in S:h\left(\zeta \right)={\varnothing }_0\right\}=\left\{\zeta \in S:{\varnothing }_{\zeta }={\varnothing }_0\right\}$$

$$=\left\{\zeta \in S:{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(0\right)\right)}^q \mathrm{and} {\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left(0\right)\right)}^q\right\}={\varnothing }_{\ast }.$$

The result established in Theorem 11 is explained by the subsequent example. □

Example 5. 

In Example 4, we computed ${\mathcal{F}}_{\varnothing }=\left\{{\varnothing }_0,{\varnothing }_1,{\varnothing }_2\right\}$ for 4-ROFI

$$\varnothing =\left\{\begin{array}{c}\left(0,0.95,0.65\right),\left(1,0.90,0.75\right),\left(2,0.90,0.75\right),\\ \left(3,0.95,0.65\right),\left(4,0.90,0.75\right),\left(5,0.90,0.75\right) \end{array}\right\}\mathrm{of}{\mathbb{Z}}_6.$$

The method described in Theorem 11 enables us to establish a mapping $h:{\mathbb{Z}}_6\to {\mathcal{F}}_{\varnothing }$ defined by,

$$h\left(0\right)=h\left(3\right)={\varnothing }_0,h\left(1\right)=h\left(4\right)={\varnothing }_1\mathrm{and}h\left(2\right)=h\left(5\right)={\varnothing }_2.$$

Now, $h\left(1+2\right)=h\left(3\right)={\varnothing }_0$ and $h\left(1\right)+h\left(2\right)={\varnothing }_1+{\varnothing }_2={\varnothing }_3={\varnothing }_0$ show that $h\left(1+2\right)=h\left(1\right)+h\left(2\right)$.

Furthermore, $h\left(\left(1\right)\left(2\right)\right)=h\left(2\right)={\varnothing }_2$ and $h\left(1\right)h\left(2\right)={\varnothing }_1{\varnothing }_2={\varnothing }_2$ together imply that $h\left(\left(1\right)\left(2\right)\right)=h\left(1\right).h\left(2\right)$. In the same way, it is simple to find that $h\left({\lambda }_1+{\lambda }_2\right)=h\left({\lambda }_1\right)+h\left({\lambda }_2\right)$ and $h\left({\lambda }_1{\lambda }_2\right)=h\left({\lambda }_1\right).h\left({\lambda }_2\right)$ for all ${\lambda }_1,{\lambda }_2\in {\mathbb{Z}}_6$. Thus, we conclude that $h$ is a ring homomorphism. Furthermore, $0,3\in {\mathbb{Z}}_6$ maps onto ${\varnothing }_0$ zero of ${\mathcal{F}}_{\varnothing }$ and ${\varnothing }_{\ast }=\left\{0,3\right\}$. Thus, Ker $\left(h\right)={\varnothing }_{\ast }$ validating Theorem 11.

5. q-Rung Orthopair Fuzzy Semi-Prime Ideals and Regular Rings

The algebraic properties of FSPIs have been extensively studied in the academic literature. In addition, the relationship between regular rings and FIs has been examined. However, the analysis of these studies within a q-ROF perspective has yet to be investigated. The ultimate goal of this section is to fill the aforementioned existing knowledge gap. The following new results and notions have been developed in this section:

(1)

We have extended the notion of fuzzy semi-prime ideals by defining q-ROFSPIs.

(2)

A necessary and sufficient condition for a q-ROFI to be a q-ROFSPI is presented.

(3)

We have pointed out an interesting characteristic of the ring of all q-ROFCs of q-ROFSPI $\varnothing$ in $S$, which it is free from nonzero nilpotent elements.

(4)

If $\varnothing$ is a q-ROFSPI of $S$, then ${\mathcal{F}}_{\varnothing }$, the ring of all q-ROFCs of $\varnothing$ in $S$, is free

(5)

from nonzero nilpotent elements.

(6)

We characterized regular rings via q-ROFI.

Definition 10. 

A q-ROFI $\varnothing$ of a ring $S$ is called q-ROFSPI if for all q-ROFI $\psi$ of $S$, the condition ${\psi }^n\subseteq \varnothing$ implies that $\psi \subseteq \varnothing$, where all $n\in {\mathbb{Z}}^{+}$.

Theorem 12. 

For a q-ROFI $\varnothing$ of a ring $S$ to be a q-ROFSPI it is necessary and sufficient that ${\varnothing }_{\left(s,t\right)}$ is a semi-prime for all $s\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and $t\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$.

Proof 

Necessity. Let $\varnothing$ be a q-ROFSPI of $S$ and $\zeta \in S$ such that ${\zeta }^n\in {\varnothing }_{\left(s,t\right)}$. Consider a q-ROFI $\psi$ of $S$ defined by;

$${\left({\mu }_{\psi }\left(\varsigma \right)\right)}^q=\left\{\begin{array}{c}s, if \varsigma \in ⟨\zeta ⟩\hfill \\ 0, otherwise\hfill \end{array}\right.\mathrm{and}{\left({\nu }_{\psi }\left(\varsigma \right)\right)}^q=\left\{\begin{array}{c}t, if \varsigma \in ⟨\zeta ⟩\hfill \\ 1, otherwise\hfill \end{array}\right..$$

Assume that ${\left({\mu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q\ne 0$, then $\varsigma ={\varsigma }_1{\varsigma }_2,\dots ,{\varsigma }_n$ such that ${\left({\mu }_{\psi }\left({\varsigma }_j\right)\right)}^q\ne 0$, for all

$j=1,2,\dots ,n$; otherwise, in each representation of $\varsigma$ as $\varsigma ={\varsigma }_1{\varsigma }_2,\dots ,{\varsigma }_n$, there exists

$i\in \left\{1,2,\dots ,n\right\}$ such that ${\left({\mu }_{\psi }\left({\varsigma }_i\right)\right)}^q=0$, therefore,

$${\left({\mu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q={\left({\mu }_{\psi }{\mu }_{}{}_{\psi }^{n-1}\left({\varsigma }_i{\varsigma }_1{\varsigma }_2,\dots ,{\varsigma }_{j-1}{\varsigma }_{j+1},{\varsigma }_{j+2},\dots ,{\varsigma }_n\right)\right)}^q$$

$=0$, since ${\left({\mu }_{\psi }\left({\varsigma }_i\right)\right)}^q=0$.

which is a contradiction.

The same reasoning yields that if ${\left({\nu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q\ne 1$ then $\varsigma ={\varsigma }_1{\varsigma }_2,\dots ,{\varsigma }_n$ such that

$${\left({\nu }_{\psi }\left({\varsigma }_j\right)\right)}^q\ne 1,\mathrm{for}\mathrm{all}j=1,2,\dots ,n.$$

Thus, by definition of $\psi$, we obtain ${\left({\mu }_{\psi }\left({\varsigma }_j\right)\right)}^q=s={\left({\mu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q$ and ${\left({\nu }_{\psi }\left({\varsigma }_j\right)\right)}^q=t={\left({\nu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q$ for all $j=1,2,\dots ,n$. In addition, the definition of $\psi$ gives us

${\varsigma }_j\in ⟨\zeta ⟩\Rightarrow \varsigma ={\varsigma }_1{\varsigma }_2,\dots ,{\varsigma }_n\in ⟨{\zeta }^n⟩\subseteq {\varnothing }_{\left(s,t\right)}$, since ${\zeta }^n\in {\varnothing }_{\left(s,t\right)}$

$\Rightarrow \varsigma \in {\varnothing }_{\left(s,t\right)}\Rightarrow {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q\ge s$ and ${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q\le t$

$\Rightarrow {\left({\mu }_{\varnothing }\left(\varsigma \right)\right)}^q\ge {\left({\mu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q$ and ${\left({\nu }_{\varnothing }\left(\varsigma \right)\right)}^q\le {\left({\nu }_{}{}_{\psi }^n\left(\varsigma \right)\right)}^q$

$\Rightarrow {\psi }^n\subseteq \varnothing$

$\Rightarrow \psi \subseteq \varnothing$, since $\varnothing$ is a q-ROFSPI of $S$

$\Rightarrow {\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\ge {\left({\mu }_{\psi }\left(\zeta \right)\right)}^q=s$ and ${\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q\le {\left({\nu }_{\psi }\left(\zeta \right)\right)}^q=t\Rightarrow \zeta \in {\varnothing }_{\left(s,t\right)}$

Hence, ${\varnothing }_{\left(s,t\right)}$ is a semi-prime ideal of $S$.

Sufficiency. Let ${\varnothing }_{\left(s,t\right)}$ be a semi-prime ideal of $S$, where $s\le {\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and $t\ge {\left({\nu }_{\varnothing }\left(0\right)\right)}^q$.

Assume that $\varnothing$ is not a q-ROFSPI of $S$; thus, there exists a q-ROFI $\psi$ of $S$ such that for some

$n\in {\mathbb{Z}}^{+}$, ${\psi }^n\subseteq \varnothing$ but $\psi ⊈\varnothing$. Therefore,

$${\left({\mu }_{\psi }\left(\zeta \right)\right)}^q>{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\mathrm{or}{\left({\mu }_{\psi }\left(\zeta \right)\right)}^q<{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\mathrm{for}\mathrm{some}\zeta \in S$$

(18)

Let ${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q=s$ and ${\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q=t$, then $\zeta \in {\varnothing }_{\left(s,t\right)}$ but $\zeta \notin {\varnothing }_{\left(s^{\prime },t^{\prime }\right)}$ if $s^{\prime }>s$ and $t^{\prime }<t$.

Therefore, ${\zeta }^n\notin {\varnothing }_{\left(s^{\prime },t^{\prime }\right)}$ if $s^{\prime }>s$ and $t^{\prime }<t$, since ${\varnothing }_{\left(s^{\prime },t^{\prime }\right)}$ is a semi-prime ideal of $S$.

Furthermore, ${\zeta }^n\in {\varnothing }_{\left(s,t\right)}$ implies that ${\left({\mu }_{\varnothing }\left({\zeta }^n\right)\right)}^q=s$ and ${\left({\nu }_{\varnothing }\left({\zeta }^n\right)\right)}^q=t$. Therefore,

$${\left({\mu }_{\varnothing }\left({\zeta }^n\right)\right)}^q={\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\mathrm{and}{\left({\nu }_{\varnothing }\left({\zeta }^n\right)\right)}^q={\left({\nu }_{\varnothing }\left(\zeta \right)\right)}^q$$

(19)

It is easy to prove that

$${\left({\mu }_{}{}_{\psi }^n\left(\zeta \right)\right)}^q\ge {\left({\mu }_{\psi }\left(\zeta \right)\right)}^q\mathrm{and}{\left({\nu }_{}{}_{\psi }^n\left(\zeta \right)\right)}^q\le {\left({\nu }_{\psi }\left(\zeta \right)\right)}^q$$

(20)

Then, the application of Equation (18) to (20) gives us

${\left({\mu }_{}{}_{\psi }^n\left(\zeta \right)\right)}^q\ge {\left({\mu }_{\psi }\left(\zeta \right)\right)}^q>{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left({\zeta }^n\right)\right)}^q$ or ${\left({\nu }_{}{}_{\psi }^n\left(\zeta \right)\right)}^q\le {\left({\nu }_{\psi }\left(\zeta \right)\right)}^q<{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\nu }_{\varnothing }\left({\zeta }^n\right)\right)}^q$. Therefore, ${\psi }^n⊈\varnothing$; thus, a contradiction is achieved. □

Theorem 13. 

If $\varnothing$ is a q-ROFSPI of $S$, then ${\mathcal{F}}_{\varnothing }$, the ring of all q-ROFCs of $\varnothing$ in $S$, is free

from nonzero nilpotent elements.

Proof. 

Let $\varnothing$ be a q-ROFSPI of $S$, then from Theorem 12, we have ${\varnothing }_{\ast }$ is a semi-prime ideal

of $S$, for all $s={\left({\mu }_{\varnothing }\left(0\right)\right)}^q$ and $t={\left({\nu }_{\varnothing }\left(0\right)\right)}^q$. Furthermore, Theorem 11 yields that

${\mathcal{F}}_{\varnothing }\cong \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$.

Now, suppose that ${\varnothing }_{\ast }\ne \varsigma +{\varnothing }_{\ast }\in \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$ is a nilpotent element. Then,

$${\left(\varsigma +{\varnothing }_{\ast }\right)}^n={\varnothing }_{\ast }$$

$$\Rightarrow {\varsigma }^n+{\varnothing }_{\ast }={\varnothing }_{\ast }$$

$$\Rightarrow {\varsigma }^n\in {\varnothing }_{\ast }$$

$$\Rightarrow \varsigma \in {\varnothing }_{\ast }$$

$$\Rightarrow \varsigma +{\varnothing }_{\ast }={\varnothing }_{\ast }$$

which is a contradiction; thus, $\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$ is free from non-zero nilpotent element. Thus, the required result is obtained because ${\mathcal{F}}_{\varnothing }\cong \raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{${\varnothing }_{\ast }$}\right.$. □

Definition 11. 

Assume that $K$ is a subset of a ring $S$. Let us define ${\chi }_K:S\to \left[0,1\right]$ and ${\chi }_K{}^c:S\to \left[0,1\right]$ by

${\chi }_K\left(\varsigma \right)=\left\{\begin{array}{c}1, if \varsigma \in K \\ 0, if \varsigma \notin K\end{array}\right.$ and ${\chi }_K{}^c\left(\varsigma \right)=\left\{\begin{array}{c}0, if \varsigma \in K \\ 1, if \varsigma \notin K\end{array}\right.$. Then, $\Gamma \left(K\right)=\left\{\left(\varsigma ,{\chi }_K\left(\varsigma \right),{\chi }_K{}^c\left(\varsigma \right)\right):\varsigma \in S\right\}$

is a q-ROFS of $S$.

Lemma 1. 

$\Gamma \left(K\right)$ is q-ROFI of $S$ if $K$ is an ideal of $S$.

The proof is easy.

Theorem 14. 

Let $\varnothing$ and $\psi$ be q-ROFIs of a ring $S$, then $\varnothing \circ \psi =\varnothing \cap \psi$ if and only if $S$ is regular.

Proof 

Assume that $S$ is a regular ring. We need to prove that $\varnothing \circ \psi =\varnothing \cap \psi$. It is simple to prove that $\varnothing \circ \psi \subseteq \varnothing \cap \psi$. Let $\zeta \in S$, the regularity of $S$ implies that there exists ${\zeta }_1$ and ${\zeta }_2$ in $S$ such that $\zeta ={\zeta }_1{\zeta }_2.$ Now,

$${\left({\mu }_{\varnothing \circ \psi }\left(\zeta \right)\right)}^q=max\left\{min\left({\left({\mu }_{\varnothing }\left({\zeta }_1\right)\right)}^q,{\left({\mu }_{\psi }\left({\zeta }_2\right)\right)}^q\right)\right\}$$

Since $\zeta =\zeta \gamma \zeta$ for some $\gamma \in S$. Then,

$${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q={\left({\mu }_{\varnothing }\left(\zeta \gamma \zeta \right)\right)}^q\ge max\left\{{\left({\mu }_{\varnothing }\left(\zeta \gamma \right)\right)}^q,{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\right\}$$

$$\ge {\left({\mu }_{\varnothing }\left(\zeta \gamma \right)\right)}^q\ge max\left\{{\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q,{\left({\mu }_{\varnothing }\left(\gamma \right)\right)}^q\right\}\ge {\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q$$

In short, ${\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q\ge {\left({\mu }_{\varnothing }\left(\zeta \gamma \right)\right)}^q\ge {\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q$; therefore, ${\left({\mu }_{\varnothing }\left(\zeta \gamma \right)\right)}^q={\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q$. Then,

$${\left({\mu }_{\varnothing \circ \psi }\left(\zeta \right)\right)}^q=max\left\{min\left({\left({\mu }_{\varnothing }\left({\zeta }_1\right)\right)}^q,{\left({\mu }_{\psi }\left({\zeta }_2\right)\right)}^q\right)\right\}$$

$\ge min\left({\left({\mu }_{\varnothing }\left(\zeta \gamma \right)\right)}^q,{\left({\mu }_{\psi }\left(\zeta \right)\right)}^q\right)$, taking ${\zeta }_1=\zeta \gamma$ and ${\zeta }_2=\zeta$

$$=min\left({\left({\mu }_{\varnothing }\left(\zeta \right)\right)}^q,{\left({\mu }_{\psi }\left(\zeta \right)\right)}^q\right)={\left({\mu }_{\varnothing \cap \psi }\left(\zeta \right)\right)}^q$$

Similarly, we obtain ${\left({\eta }_{\varnothing \circ \psi }\left(\zeta \right)\right)}^q\le {\left({\eta }_{\varnothing \cap \psi }\left(\zeta \right)\right)}^q,$ which gives $\varnothing \cap \psi \subseteq \varnothing \circ \psi$.

Conversely, suppose that $\varnothing \circ \psi =\varnothing \cap \psi$. Let $K$ and $U$ be two ideals of $S$. In view of

Lemma 1, $\Gamma \left(K\right)=\left\{\left(\varsigma ,{\chi }_K\left(\varsigma \right),{\chi }_K{}^c\left(\varsigma \right)\right):\varsigma \in S\right\}$ and $\Gamma \left(U\right)=\left\{\left(\varsigma ,{\chi }_U\left(\varsigma \right),{\chi }_U{}^c\left(\varsigma \right)\right):\varsigma \in S\right\}$ are q-

ROFIs of $S$. Assume that $\zeta \in K\cap U$, then ${\left({\chi }_K\left(\zeta \right)\right)}^q\cap {\left({\chi }_{\varsigma }\left(\zeta \right)\right)}^q=1$ and ${\left({\chi }_K{}^c\left(\zeta \right)\right)}^q\cap$

${\left({\chi }_U{}^c\left(\zeta \right)\right)}^q=0$. Since $\Gamma \left(K\right)\cap \Gamma \left(U\right)=\Gamma \left(U\right)\circ \Gamma \left(U\right)$; therefore,

${\left({\chi }_K\left(\zeta \right)\right)}^q\cap {\left({\chi }_{\varsigma }\left(\zeta \right)\right)}^q={\left({\chi }_K\left(\zeta \right)\right)}^q\circ {\left({\chi }_{\varsigma }\left(\zeta \right)\right)}^q=1$ and ${\left({\chi }_K{}^c\left(\zeta \right)\right)}^q\cap {\left({\chi }_U{}^c\left(\zeta \right)\right)}^q={\left({\chi }_K{}^c\left(\zeta \right)\right)}^q\circ$

${\left({\chi }_U{}^c\left(\zeta \right)\right)}^q=0$ implying that

$max\left\{min\left({\left({\chi }_K\left({\zeta }_1\right)\right)}^q,{\left({\chi }_{\varsigma }\left({\zeta }_2\right)\right)}^q\right):{\zeta }_1{\zeta }_2=\zeta ,{\zeta }_1,{\zeta }_2\in S\right\}=1$ and

$min\left\{max\left({\left({\chi }_K{}^c\left({\zeta }_1\right)\right)}^q,{\left({\chi }_U{}^c\left({\zeta }_2\right)\right)}^q\right):{\zeta }_1{\zeta }_2=\zeta ,{\zeta }_1,{\zeta }_2\in S\right\}=0$.

It means that there exists ${\gamma }_1,{\gamma }_2\in S$ such that ${\left({\chi }_K\left({\gamma }_1\right)\right)}^q=1={\left({\chi }_U\left({\gamma }_2\right)\right)}^q$ and ${\left({\chi }_K{}^c\left({\gamma }_1\right)\right)}^q=$

$0={\left({\chi }_U{}^c\left({\gamma }_2\right)\right)}^q$ with $\zeta ={\gamma }_1{\gamma }_2$. Thus, $\zeta ={\gamma }_1{\gamma }_2\in KU$, which gives $K\cap U\subseteq K.U$.

Furthermore, $K.U\subseteq K\cap U$ is obvious. Thus, $K\cap U=K.U$; then, the regularity of $S$ is

directly followed by using Theorem on page 184 of [51]. □

Theorem 15. 

A ring $S$ is regular if and only if every q-ROFI of $S$ is idempotent.

Proof. 

Let $\varnothing$ be a q-ROFI of a regular ring $S$. Then, in view of Theorem 14, it is

straightforward to show that ${\varnothing }^2=\varnothing$.

Conversely, let every q-ROFI of $S$ be idempotent. Suppose that $\varnothing$ and $\psi$ are q-ROFIs of

$S$. In view of Theorem 14, we require $\varnothing \circ \psi =\varnothing \cap \psi$ to prove the regularity of $S$. For this,

we proceed as follows,

$${\left({\mu }_{\varnothing \cap \psi }\left(\zeta \right)\right)}^q={\left({\mu }_{\left(\varnothing \cap \psi \right)\circ \left(\varnothing \cap \psi \right)}\left(\zeta \right)\right)}^q$$

$$=max\left\{min\left({\left({\mu }_{\varnothing \cap \psi }\left({\zeta }_1\right)\right)}^q,{\left({\mu }_{\varnothing \cap \psi }\left({\zeta }_2\right)\right)}^q\right):\zeta ={\zeta }_1{\zeta }_2\right\}$$

$$\le max\left\{min\left({\left({\mu }_{\varnothing }\left({\zeta }_1\right)\right)}^q,{\left({\mu }_{\psi }\left({\zeta }_2\right)\right)}^q\right):\zeta ={\zeta }_1{\zeta }_2\right\}={\left({\mu }_{\varnothing \circ \psi }\left(\zeta \right)\right)}^q$$

The same reasoning leads us to ${\left({\nu }_{\varnothing \cap \psi }\left(\zeta \right)\right)}^q\ge {\left({\nu }_{\varnothing \circ \psi }\left(\zeta \right)\right)}^q$. So, $\varnothing \cap \psi \subseteq \varnothing \circ \psi$. Furthermore, $\varnothing \circ \psi \subseteq \varnothing \cap \psi$ is obvious. Thus, $\varnothing \circ \psi =\varnothing \cap \psi$. □

Lemma 2. 

${\left(\Gamma (⟨\zeta ⟩)\right)}^2=\Gamma \left(⟨{\zeta }^2⟩\right)$ for all $\zeta \in S$

The proof only requires some basic computations.

Theorem 16. 

For a commutative ring $S$ to be regular, it is necessary and sufficient that every q-ROFI of $S$ is a q-ROFSP.

Proof 

Necessity. Consider $S$ to be regular ring and $\varnothing$ to be a q-ROFI of $S$. Let $\psi$ represent any q-ROFI of $S$ satisfying the condition ${\psi }^n\subseteq \varnothing$. Since $S$ is regular, we can derive ${\psi }^n=\psi$ from Theorem 15. Therefore, $\psi \subseteq \varnothing ,$ and consequently, we obtain $\varnothing$ as a q-ROFSPI of $S$.

Sufficiency, suppose that every q-ROFI of $S$ is q-ROFSP. Lemma 2 implies ${\left(\Gamma (⟨\zeta ⟩)\right)}^2=\Gamma \left(⟨{\zeta }^2⟩\right)$ for all $\zeta \in S$. Since $\Gamma \left(⟨{\zeta }^2⟩\right)$ is q-ROFSPI of $S$; therefore, $\Gamma (⟨\zeta ⟩)\subseteq \Gamma \left(⟨{\zeta }^2⟩\right)$. In addition, $\Gamma \left(⟨{\zeta }^2⟩\right)\subseteq \Gamma (⟨\zeta ⟩)$ is obvious. Hence $\Gamma (⟨\zeta ⟩)=\Gamma \left(⟨{\zeta }^2⟩\right)$. It means that $\zeta \in \Gamma \left(⟨{\zeta }^2⟩\right)$; therefore, $\zeta =\varsigma {\zeta }^2=\zeta \varsigma \zeta$ for some $\varsigma \in S$. Thus, $S$ is a regular ring. □

6. Discussion

After surveying the prior literature, it has been established that certain progress has been made in the domains of classical, intuitionistic, and Pythagorean fuzzy ring theory. In addition, despite achieving several results for (α, β)-PFSRs and bipolar PFSRs of a ring, there are numerous unresolved questions that require further exploration. This study has made significant contributions to the field by filling numerous research gaps and providing solutions to several open problems.

(1)

Within the context of crisp ring theory, a subring of a ring $S$ is not necessarily an ideal of $S$. Moreover, the intersection of a subring $J$ and an ideal $I$ of $S$ is an ideal of $S$. In the present study, the implications of these significant findings within the field of ring theory are examined with respect to q-ROFS.

(2)

The article characterizes q-ROFIs in terms of q-ROFLIs, by demonstrating that a q-ROFS $\varnothing$ of $S$ is a q-ROFI of $S$ if and only if ${\varnothing }_{\left(s,t\right)}$ is an ideal of $S.$ This categorization is essential for exploring the characteristics and connections of these mathematical concepts.

(3)

Based on the findings of this research, it has been found that, in the case of a division ring S, no more than two distinct membership values can be assigned to the elements of $S$ in order to design a q-ROFI. This holds true when assigning non-membership values as well.

(4)

The concept of cosets is a fundamental building block in the study of rings and their ideals, and it has many important applications in algebraic geometry, number theory, and other fields of mathematics. It provides a way to study the structure of rings and their ideals. Cosets help us understand the relationship between rings and their ideals. By partitioning a ring into cosets of an ideal, we can better understand how the elements of the ring interact with the ideal. This provides a way to study the relationship between a ring and its ideals and helps us prove important theorems about rings. The present paper expands the concept of cosets of ideals in classical rings in the framework of q-ROFSs. Moreover, it has been proven that the set of all q-ROFCs of a q-ROFI of $S$ forms a ring under a specific binary operation.

(5)

The fundamental theorem of ring homomorphism is widely recognized as a vital result in classical ring theory. It establishes a fundamental link between the properties of a ring homomorphism and the ideal configuration of the domain ring. It has significant implications across various mathematical domains, such as algebra and number theory. Thus, the present study provides a comprehensive examination of this significant theorem in the context of q-ROF systems.

(6)

The algebraic properties of fuzzy semi-prime ideals have been extensively studied in the academic literature. In addition, the relationship between regular rings and FIs has been examined. However, the analysis of these studies from a q-ROF perspective has yet to be investigated. This research extends the notion of fuzzy semi-prime ideals by defining q-ROFSPIs. A necessary and sufficient condition for a q-ROFI to be a q-ROFSPI is presented, and characterization of regular rings with respect to q-ROFI is performed.

Overall, this article provides a comprehensive study of the algebraic properties of q-ROFS in the context of ring theory. The article introduces essential concepts and terminology and investigates the important algebraic characteristics of q-ROFIs. Consequently, this study has substantially enhanced the understanding of fuzzy ring theory and has opened up new directions for future research.

7. Conclusions

The primary objective of this study is to explore the notion of q-ROFI of a crisp ring in a q-rung orthopair fuzzy context. This is achieved by converting a variety of concepts from ring theory into the q-rung orthopair fuzzy framework, including cosets of an ideal, quotient ideals, and semiprime ideals. We establish that the intersection of two q-ROFIs of ring $S$ is a q-ROFI. Additionally, the paper introduces the concept of q-ROFCs of a q-ROFI and shows that, under certain binary operations, the collection of all q-ROFCs forms a ring. An analogue of the fundamental theorem of ring homomorphism is also presented in terms of q-ROFSs. The study also introduces the concept of q-ROFSPIs and provides a comprehensive examination of their algebraic properties. Finally, q-ROFIs are utilized to characterize regular rings.

In crisp case, the ideals of rings provide a framework for the study of prime, maximal, and irreducible ideals, which are important in commutative algebra, algebraic geometry, and number theory. Based on the results regarding q-ROF ideals presented in this study, we want to further explore the q-ROF context of prime, maximal, and irreducible ideals and their algebraic features. In crisp ring theory, the Chinese remainder theorem provides a way to understand the structure of a ring by studying its quotient rings. It can be used to study the geometry of algebraic curves and surfaces, to construct finite fields, and to encrypt messages securely. The present study provides a base to develop q-ROF version of Chinese remainder theorem. Fuzzy ring homomorphisms are used in certain cryptographic systems, such as the fuzzy identity-based encryption (FIBE) scheme. Fuzzy ring homomorphisms provide a way to map messages and keys from one ring to another, while preserving the security of the system. Since q-ROFS is one of the prime generalizations of FS, the application of the concepts of q-ROF homomorphisms in image encryption and information security will thus produce better results as compared to classical fuzzy homomorphisms.

In addition, future work will extend the developed concepts under other fuzzy set extensions, such as bipolar fuzzy sets, picture fuzzy sets, fuzzy soft set, fuzzy hypersoft set, etc.