Abstract
The role of spin and orbital rotational symmetry on the laser-induced magnetization dynamics of itinerant-electron ferromagnets was theoretically investigated. The ultrafast demagnetization of transition metals is shown to be the direct consequence of the fundamental breaking of these conservation laws in the electronic system, an effect that is inherent to the nature of spin-orbit and electron-lattice interactions. A comprehensive symmetry analysis is complemented by exact numerical calculations of the time evolution of optically excited ferromagnetic ground states in the framework of a many-body electronic Hamiltonian. Thus, quantitative relations are established between the strength of the interactions that break the rotational symmetries and the time scales that are relevant for the magnetization dynamics.
1. Introduction
Symmetry and the absence thereof are known to play a central role in a wide variety of physical phenomena, most decisively when these have a quantum mechanical origin. Condensed-matter magnetism, as a profoundly quantum mechanical effect, is one of its most remarkable demonstrations. Indeed, the pseudovector character of the spin and orbital contributions to the average magnetization renders geometry and symmetry arguments particularly appealing. Let us mention, for example, the Mermin–Wagner theorem, which establishes the absence of finite-temperature long-range magnetic order in two-dimensional systems with a continuous symmetry [1], the spontaneous symmetry breaking at the origin of long-range magnetic-order below the Curie and Néel temperatures, or the breaking of spin-rotational symmetry through spin-orbit interaction, which explains the stability of the magnetization direction with respect to the lattice structure. Whenever the magnetic behavior is conditioned by symmetry arguments, it is clear that the presence of any interaction or external field lifting the underlying symmetry results in dramatic effects. For instance, in the context of the Mermin–Wagner theorem, breaking the spin-rotational symmetry triggers the appearance of an easy magnetization axis, which stabilizes the long-range order and the magnetization direction at finite temperatures. Therefore, characterizing the symmetries underlying a given physical problem and identifying the possible sources of their absence are crucial for the theoretical description of magnetic materials.
Symmetry considerations are also very helpful for understanding time-dependent quantum phenomena, not least as the justification for absorption selection rules and for any conservation laws relevant to the subsequent time evolution. And yet, in the particular case of the laser-induced magnetization dynamics of ferromagnetic metals, a straightforward analysis of the selection rules and conservation laws seems quite puzzling at first, to the point that it actually reveals the fundamental interest of the phenomenon. The basic experimental observation is the following. When a ferromagnetic material, such as a Ni film, is optically excited with a very short intense laser pulse having a wavelength 600–800 nm, a very rapid decrease of the sample magnetization is observed within times of the order of a few hundreds of femtoseconds [2,3,4,5,6]. These experimental findings are fascinating for several reasons: (i) The time scale is far too short to justify the validity of the hypothesis of equilibrium statistical mechanics, which would allow explaining the demagnetization simply as the result of thermalization. A microscopic understanding requires, therefore, taking explicitly into account the nonadiabatic dynamics of the ferromagnetic solid as a correlated many-body system. (ii) The laser excitation cannot be directly responsible for the observed significant magnetization change, because the total spin of the system is conserved to an extremely high degree in optical absorptions and because experiments with very short pulses show that the demagnetization takes place even well after the exciting pulse is over [7,8,9]. Furthermore, similar ultrafast demagnetizations have been observed by using indirect non-optical sources of excitation [10,11,12]. One concludes that the observed ultrafast demagnetization (UFD) reflects the non-conservation of the electronic spin polarization of the solid. (iii) The fundamental interaction coupling the electron spin with other degrees of freedom, thus allowing for the non-conservation of the total spin polarization, is the spin-orbit coupling. Since this interaction preserves the total spin-plus-orbital angular momentum, as rooted in the isotropy of space, one has experimentally looked for signs of an enhancement of the orbital magnetic moments along the demagnetization process. However, time-resolved X-ray magnetic circular dichroism (XMCD) experiments clearly show that the orbital moments at the d-shell of the magnetic transition-metal atoms are not enhanced in any significant way as the system demagnetizes [4,5,6]. Elucidating the microscopic mechanisms behind the non-conservation of the spin angular momentum represents, therefore, a fundamental theoretical challenge.
In past years, the UFD effect has been the subject of a considerable theoretical and experimental research activity. Several theoretical explanations have been proposed, some of them based on a purely electronic description of the problem [13,14,15,16,17,18] and others that do not require respecting electronic angular momentum conservation, such as temperature models [2,19,20], superdiffusive transport [21,22], and spin-to-lattice angular momentum transfer [23,24,25]. These interpretations are not all necessarily mutually exclusive. The possibility that more than one type of process contributes to the UFD effect cannot be ruled out a priori. It is the purpose of this paper to review and analyze a previously formulated many-body electronic theory of the magnetization dynamics of laser-excited transition metals from the perspective of symmetry [15,18]. In this way, it is shown how the experimentally observed UFD of itinerant-electron ferromagnets can be understood as the consequence of breaking two fundamental rotational symmetries, namely, the spin-rotational symmetry, due to spin-orbit interactions, and the orbital rotational symmetry, due to the interaction of the electrons with the lattice.
The remainder of the paper is organized as follows. In Section 2, the theoretical background is recalled. The fundamental symmetries behind the problem, the different interactions which may break them, and the consequences that this would have on the laser-induced magnetization dynamics are pointed out. These qualitative considerations are complemented in Section 3, where the results of exact numerical calculations of the many-electron dynamics triggered by short-pulse optical excitations are presented. The time evolutions of the spin and orbital average magnetizations are analyzed. The corresponding demagnetization times are derived together with the degrees of demagnetization reached at long times. Thus, quantitative relations between the ultrafast demagnetization effect and the interactions responsible for the rotational symmetry breakings are revealed. Finally, Section 4 summarizes our conclusions.
2. Theory
Symmetries are not obvious a priori since most real situations we are confronted with are asymmetric. Therefore, in order to analyze the UFD effect from the perspective of symmetries, it is useful to start from an idealized situation in which the sources of asymmetry are absent. If the electronic spin and translational degrees of freedom were decoupled, and in the absence of external magnetic fields, the Hamiltonian of the system would commute with the spin operator . The total spin of the system would be then conserved, even in the presence of a laser field, once the highly improbable direct coupling to the magnetic field is ruled out. Consequently, no demagnetization effect would be possible. One concludes that breaking spin-rotational symmetry through the spin-orbit interaction is central to a microscopic understanding of the problem. Furthermore, if the lattice potential acting on the electrons were absent or rotationally invariant, the total angular momentum would be conserved, even in the presence of spin-orbit coupling (SOC). Thus, any decrease of would be compensated by an enhancement of the orbital angular momentum , again in contrast to the experimental observations. One concludes that breaking the orbital rotational symmetry, a natural consequence of the lattice potential of the solid, is equally important for the theoretical description of the UFD effect. As is often the case with symmetry arguments, the previous line of reasoning provides no information about the actual quantitative consequences of these symmetry breakings on any specific system under study. Indeed, the strength and effectiveness of the SOC depend strongly on the considered element and its electronic structure, and the influence of the lattice potential on the magnetically relevant d or f orbitals is sensitive to the spatial extent of the corresponding wave functions. Nevertheless, the above symmetry considerations are very useful since they define the minimum requirements to be fulfilled by a quantum theory of the laser-induced magnetization dynamics.
In order to analyze the consequences of spin and orbital rotational symmetry on the laser-induced magnetization dynamics, we considered an electronic model Hamiltonian that focuses on the itinerant electrons responsible for transition-metal (TM) magnetism [15]. The many-body Hamiltonian is given by
The first term:
describes the single-particle band structure of the most relevant valence bands and is responsible for electron delocalization, band formation, and metallic behavior. In the usual notation , , and stand for the creation, annihilation, and number operators of a spin- electron at atom i having the radial and orbital quantum numbers . For simplicity, only the and valence orbitals are taken into account explicitly in the calculations, since they determine the magnetic properties and the optical absorption. Thus, represents the energy of the atomic-like or orbitals, which are assumed to be independent of the magnetic quantum number m, and denotes the corresponding hopping integrals between atoms i and j. The second term:
describes the dominant intra-atomic Coulomb interaction among the electrons, where and refer, respectively, to the total number and spin operators at atom i. is characterized by the average direct Coulomb integral U and exchange integral J, as derived, for example, in [18,26]. The interplay between the strength of the local Coulomb interactions U and J and the kinetic energy gain resulting from electron delocalization, as measured by the electron hoppings and the d band width, defines the ground-state magnetic order and the stability of magnetism at finite temperatures [27,28,29,30]. The third term in Equation (1) takes into account the spin-orbit interaction among the electrons. It is given by
where is the SOC constant and denotes the intra-atomic matrix elements of the scalar product between the orbital and spin angular momenta at atom i. Finally, the last term:
describes the interaction with the external laser field in the intra-atomic dipole approximation, where denotes a dimensionless normalized polarization vector and is the electron charge. Notice that the dipole matrix elements satisfy the atomic selection rule unless , so that the optical excitation involves only - transitions.
Before closing this section, it is worth underlining the most important symmetries of the problem, together with the main interactions that could break them, which are common to both the present model description and the complete first-principles Hamiltonian. The single-particle kinetic and potential energy operator , the electron-electron interaction , and the interaction with the laser field conserve the total spin of the electronic system, since . Consequently, in the absence of SOC, the Hamiltonian would conserve . In fact, it is the spin-orbit operator that breaks the spin-rotational symmetry of by coupling the spin and orbital degrees of freedom (). Furthermore, the electronic transitions induced by involve angular momentum transfers between and , keeping unchanged since for all i. The invariance of the total angular momentum under follows. Moreover, the conservation of is also respected by the Coulomb interactions, which are invariant upon spin and orbital rotations, thus preserving , , and . However, it is important to notice that the interatomic hybridizations in , though total-spin conserving, do not preserve the orbital angular momentum . Indeed, the interatomic hoppings are the consequence of the interaction of the electrons with the lattice potential, which is obviously not invariant upon rotations of the electronic coordinates. As a result, and . The conservation of the total angular momentum is broken. The origin of the non-conservation of lies, as already mentioned, in the lack of rotational symmetry of the lattice potential, which leads to non-vanishing hopping integrals between orbitals and having different magnetic quantum numbers m at neighboring atoms. In this context, it is useful to recall that in the present electronic model [Equations (1)–(5)] the ionic degrees of freedom and the lattice potential are regarded as static. Therefore, electronic transitions involving angular momentum transfer due to dynamical electron-phonon processes, which are also a consequence of breaking the orbital rotational symmetry of the electronic system, were not taken into account. Finally, notice that the previous symmetry considerations apply not only to the model Hamiltonian given by Equations (1)–(5), but also to the complete first-principles electronic Hamiltonian. Indeed, from an ab initio perspective, the orbital rotational symmetry and the conservation of are broken by the electrostatic potential generated by the ions in the solid, while the spin-rotational invariance and the conservation of , in the absence of magnetic fields, are broken by the SOC. In the following section, the consequences of these main symmetry breakings on the ultrafast magnetization dynamics of transition metals are quantified by calculating the exact time evolution of the laser-excited ferromagnetic ground states in the framework of the proposed many-body model.
3. Results and Discussion
For the calculations we used a tetrahedral cluster model, which corresponds to the local structure of a face-centered cubic crystal such as Ni, with parameters appropriate for TM ferromagnets: the SOC constant meV, which was taken from calculations on TM atoms [31], a direct Coulomb integral eV and an exchange integral eV, estimated from experimental photoemission spectra and theoretical calculations of the Ni density of electronic states [32,33,34,35], and a - promotion energy eV, estimated from band structure calculations [36]. The hopping integrals were determined by applying the two-center approximation [37] with the nearest-neighbor (NN) Slater–Koster integrals eV, eV, eV, and eV. These values are similar to those obtained in [36] by fitting the band structure of bulk Ni. For simplicity, the orbital degeneracy was reduced by considering only the orbitals having and the orbital having . In this way, one obtains, for example for electrons, a ground state showing an almost saturated spin polarization per atom, a strongly quenched orbital angular momentum per atom, and a small but non-negligible band occupation per atom. Notice that the quantization z axis coincides with the easy magnetization axis.
The laser excitation triggering the magnetization dynamics is given by a time-dependent electric laser field with wavelength nm and a Gaussian envelope having a pulse width fs. The fluence of the pulse was chosen so that the absorbed energy amounts to meV per atom, which is not far from the typical absorbed energies estimated in experiment (e.g., meV in. [3]). The dynamics following the laser excitation of the ground state has been calculated exactly by using the short-time iterative Lanczos method [38]. In this way, any mean-field approximation to the many-body Coulomb interaction , which would introduce artificial symmetry breakings, is avoided. The full correlated nature of the dynamics of the many-electron system and, in particular, its fundamental conservation laws are thereby preserved.
From a physical perspective, the model respects the semilocal nature of the microscopic mechanisms of angular momentum transfer behind the UFD effect, as discussed in [15,18]. Furthermore, by varying the strength of the spin-orbit coupling and hopping integrals , it is possible to quantify the effects of spin-rotational and orbital-rotational symmetry breakings on the magnetization dynamics. To this aim, it is meaningful to always consider the same initial laser-excited state corresponding to the above-given realistic SOC strength and hopping integrals , since, otherwise, changes in and would alter the absorption spectra and the absorbed energy, which are known to have a strong effect on the subsequent dynamics [18]. In this way, the different time evolutions can be directly related to the symmetry-breaking interactions without any spurious effects due to changes in the initial excitation. Thus, the focus is set on the role played by the spin-orbit interaction and the electron delocalization on the electronic dynamics.
3.1. Breaking Spin-Rotational Symmetry
The role of spin-rotational symmetry on the laser-induced magnetization dynamics has been investigated by comparing the time evolutions for different spin-orbit coupling strengths . Since the spin-orbit interaction is the only term in the Hamiltonian that precludes total spin conservation, one may regard as a measure of the importance of this symmetry breaking. Figure 1 shows the time dependence of the average spin-component along the favored magnetization direction for representative values of in the range meV. The averages of the perpendicular components and are nearly zero for the tetrahedral geometry. For the sake of comparison, the same initial state has been considered in all cases, which corresponds to meV at fs. As expected, no demagnetization takes place for , since the total spin is conserved. In contrast, already the smallest considered meV is sufficient for an appreciable, albeit modest demagnetization to set in. The mechanism by which the laser excitation triggers the magnetization dynamics can be qualitatively understood by noting that the laser absorption changes the single-particle electronic occupations, by exciting majority-spin electrons to energies where empty minority-spin states are available and by creating holes in the minority levels at energies comparable to those of occupied majority-spin states. This allows for efficient spin-orbit-induced spin-flip transitions, which set in motion the spin-to-orbital angular momentum transfer at the origin of the ultrafast demagnetization. The results for different clearly demonstrate that the SOC strength plays a central role in the demagnetization process, by affecting both the demagnetization rate and the degree of demagnetization at long times after the excitation. This is noteworthy taking into account that all the time propagations shown in Figure 1 were obtained starting from the same excited state with the same absorbed energy and number of photons [18].
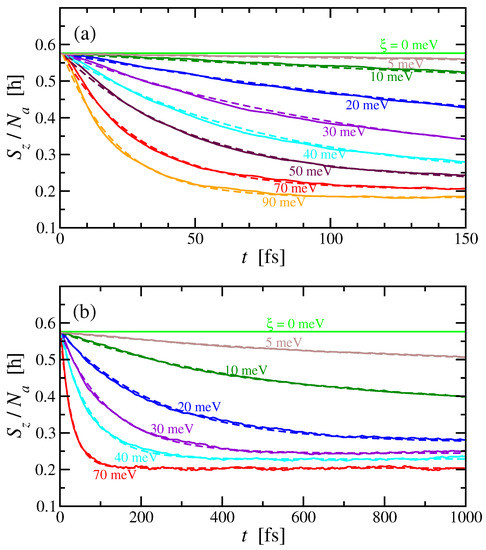
Figure 1.
Time dependence of the total spin per atom for different SOC strengths following an optical excitation with a 1 fs laser pulse. The full curves were obtained from exact time propagations, while the dashed curves show the corresponding fits to the exact results using the exponential law . The subfigures (a,b) highlight the behavior for shorter and longer times, respectively.
The calculated time dependence of for different can be characterized by two main parameters, namely, the spin demagnetization time and the degree of spin demagnetization at long times. Indeed, as shown by the dashed curves in Figure 1, can be reasonably well fitted by a function of the form . The results for and derived from the exponential fits to the exact are given in Figure 2 as a function of . One observes that decreases monotonously with increasing . In particular, for meV the demagnetization time is fs, whereas for meV it is only fs. The dependence of on can be approximated by an inverse power-law of the form with , which lies in between , as estimated from the energy-time uncertainty relation, and , which would follow from Fermi’s golden rule. The importance of the strength of the interaction breaking spin-rotational symmetry is thus quantified, as it determines the time scale of the demagnetization effect [15].
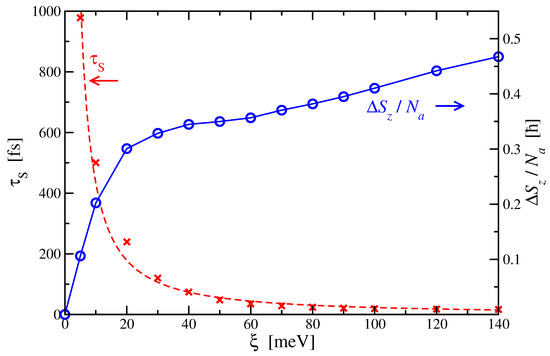
Figure 2.
Spin demagnetization time (red crosses) and long-time degree of demagnetization (blue circles) as a function of the SOC strength . The results were derived from the exponential fits to the exact time dependence given in Figure 1. The dashed red curve shows the fitted inverse power-law with . The blue lines connecting the circles are a guide to the eye.
A further important result concerning the role of spin-orbit interactions is that also conditions the long-time degree of demagnetization , where denotes the spin projection in the initial state and its value in the limit of . In Figure 2, results are given for as a function of , which were derived from the exponential fits to the exact of Figure 1. Starting from , where the absence of SOC implies , and increasing , one observes that grows relatively fast for small up to meV. This is followed by a much slower linear increase of in the range 30 meV meV. Note that we are unable to properly assess numerically the limit of for , where itself diverges. Thus, the question whether an arbitrary small symmetry breaking (i.e., ) might yield a finite for cannot be addressed in the present theoretical framework. Nevertheless, for reasonably long finite times (e.g., 1–2 ps), the calculations clearly show that the degree of demagnetization vanishes as . In fact, a continuous decrease in the limit can be qualitatively understood by recalling that the SOC-induced spin flips leading to demagnetization necessarily involve finite changes in the local exchange energy as well as changes in the relative orientations between neighboring spins [see Equation (3)]. Since these energy differences remain finite independently of the value of , the spin fluctuations induced by the SOC should be progressively inhibited as the coupling constant vanishes.
The results presented in the following section show that the ultrafast demagnetization effect is as indissociable from breaking the spin-rotational symmetry as it is indissociable from the absence of orbital rotational symmetry caused by the lattice potential. In fact, all the above results were obtained by taking full account of the interactions of the electrons with the lattice, as given by the corresponding realistic values of the hopping integrals and d band width. Still, before quantifying the role of orbital rotational symmetry, it is meaningful to turn our attention to the dynamics of the orbital angular momentum , which is triggered by the laser excitation. Figure 3 shows the time dependence of the spin, orbital, and total angular momenta per atom , , and for realistic values of both and . One observes that in the ground state, before the excitation, is already strongly quenched, since almost any residue of the atomic second Hund rule is washed away by the interatomic hybridizations responsible for band formation and electron delocalization. This trend is in good agreement with the behavior found in transition metals [39]. After the excitation, shows some oscillations in the range , remaining essentially quenched, while decreases most significantly from in the ground state to in the long-time limit. The total electronic angular momentum decreases accordingly (see Figure 3). These results show that the orbital is no reservoir for the decreasing spin , in agreement with time-resolved XMCD experiments [4,5,6]. Physically, the fact that remains quenched for all times and that is not conserved during the demagnetization process reflects the transfer of angular momentum from the electronic to the lattice degrees of freedom. It is the goal of the following section to show that the non-conservation of is the consequence of the absence of orbital rotational symmetry.
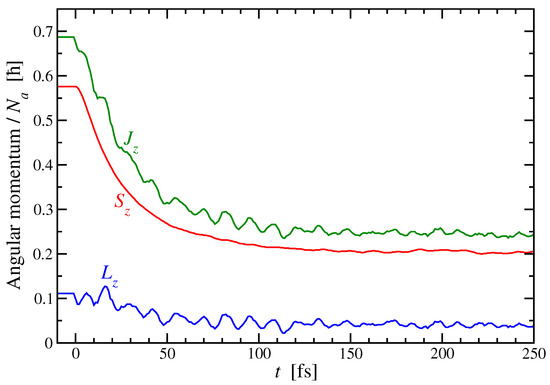
Figure 3.
Time dependence of the spin , orbital , and total electronic angular momenta per atom following a 1 fs laser-pulse excitation for SOC strength meV.
3.2. Breaking Orbital Rotational Symmetry
The orbital rotational symmetry is broken in a solid by the deviations of the lattice potential from atomic-like spherical symmetry. In the tight-binding method considered in this paper it is precisely that defines the interatomic hoppings for [40] once the local orbitals have been chosen [see Equations (1)–(5)]. Therefore, the interatomic hybridizations at the origin of electron delocalization and metallic behavior give a direct measure of the quantitative importance of this symmetry breaking. Formally, one may consider that the atomic spherically symmetric limit is progressively achieved by increasing the distance between NN atoms i and j up to infinity or, equivalently, by reducing the absolute value of the hopping integrals down to zero. In order to understand and quantify the importance of breaking orbital rotational symmetry on the laser-induced dynamics of TMs, we took advantage of our model approach and varied the strength of the hybridizations systematically by scaling the interatomic hoppings for as , where and stands for the hopping matrix in the considered solid.
In Figure 4, results are given for the time dependence of the spin, orbital, and total angular momenta per atom , , and after the laser excitation for representative values of the hopping scaling keeping the SOC constant meV. For the sake of comparison, the same initial state has been considered in all cases, which corresponds to at fs, as in Section 3.1. In the absence of symmetry breaking, i.e., for , the total angular momentum is conserved and no demagnetization takes place. However, both and depend strongly on time, showing strong oscillations with an amplitude – per atom and a period fs. The amplitude of the oscillations corresponds approximately to one or transition, whereas the oscillation period is of the order of the SOC timescale fs. Clearly, these oscillations reflect the exchange between spin and orbital angular momenta within the many-electron system, which is decoupled from the lattice for .
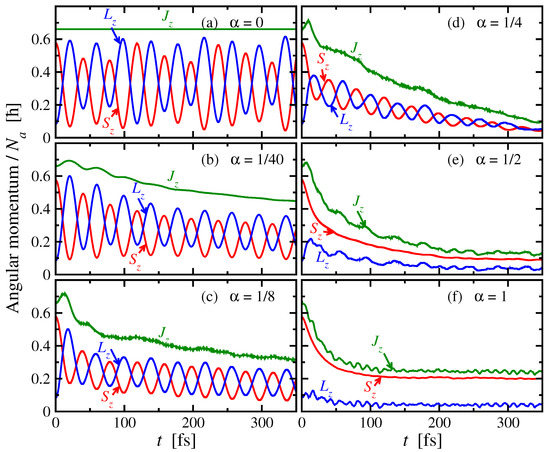
Figure 4.
Time dependence of the average spin, orbital, and total angular momenta , , and after a 1 fs laser-pulse excitation for representative scalings of the electronic hopping integrals , where corresponds to the Ni d band width. The SOC strength is meV.
For nonvanishing hopping integrals () different regimes need to be distinguished. For very small (e.g., as in Figure 4b) the hopping time scale , i.e., the time that an electron typically spends on the same atom, is much longer than the time involved in intra-atomic spin-orbit transitions. Therefore, the oscillations are strong and very weakly damped. In this hypothetical situation where the importance of orbital symmetry breaking is quantitatively weak () it is not the SOC but the hoppings what control the demagnetization rate, since the transfer of the angular momentum to the lattice, or equivalently the quenching of , is the slowest quantum mechanical process. Of course, this limit does not apply to TMs, where the SOC strength is about two orders of magnitude smaller than the d band width. However, one could imagine possibilities of realizing this situation in some artificially made material, for example, in an optical lattice or with magnetic impurities at low concentrations.
As the scaling factor is increased and the hopping and SOC times start to become comparable (e.g., or as in Figure 4c,d) the quenching of is no longer the bottleneck. The oscillations of and are still present, keeping essentially the same period as for small . However, their amplitude is strongly reduced, not just at short times but more and more as the system evolves in time. Furthermore, the demagnetization effect, as measured by the importance and speed of the decay of and , becomes increasingly important as increases. Finally, for realistic values of the hopping integrals (e.g., and as in Figure 4e,f) the hopping time is of the order of 1 fs, which is much shorter than the time involved in spin-orbit transitions. The rate by which the orbital angular momentum is quenched and transferred to the lattice is much stronger than the rate by which spin polarization is transferred to the orbital angular momentum by the SOC, so that all oscillations between and disappear (see Figure 4e,f). In this regime, the demagnetization time is controlled by the SOC strength , as discussed in the previous section and in [15]. The central importance of breaking orbital rotational symmetry to the ultrafast demagnetization of TMs is hereby demonstrated.
The characteristic time scale for the quenching of orbital angular momentum and the transfer of electronic angular momentum to the lattice can be estimated by fitting the exact calculated time dependence of with an exponential function. Notice, however, that does not follow a simple exponential behavior very closely, since it shows some oscillations superimposed on the overall decay as a function of t. The thus obtained decay time and long-time angular momentum transfer are shown in Figure 5 as a function of the hopping-scaling parameter . For , which corresponds to typical values of the d band width in transition metals, fs is in qualitative agreement with the experimental observations [2,3,4,5,6]. As the hopping integrals are reduced (), one observes that increases monotonously with decreasing , tending to diverge in the limit of , where the orbital rotational symmetry is restored. The increase of is rather weak at first, for , as long as the hopping integrals are not far from the realistic values, then becoming quite strong as starts to approach values comparable with the SOC strength , and finally diverging. However, note that the enhancement of is significant even if the hopping integrals and d band width are much larger than the SOC strength . For example, for , is about twice as large as for . Therefore, the hopping integrals are important, together with the dominant , for defining the actual value of the demagnetization rate. When is further reduced, starts to approach values comparable to the SOC strength and the hopping time becomes comparable to . Then, a much more rapid increase of is observed, which reflects a strong reduction of the quenching rate of (). In this regime, the rate of the angular momentum transfer into the lattice is governed by the strength of the hopping integrals. They give a measure of the importance of the interaction between the electrons and the lattice and, thus, quantify the deviations from perfect rotational symmetry.
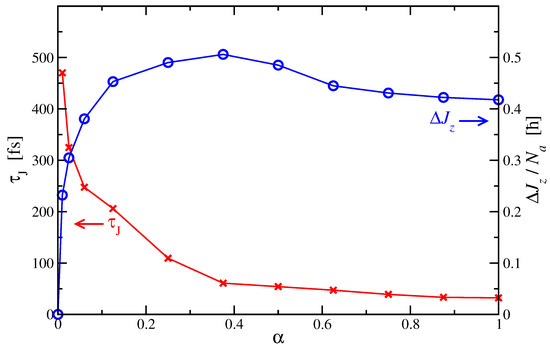
Figure 5.
Decay time (red crosses) and long-time transfer (blue circles) of the total electronic angular momentum as a function of the strength of the interatomic hopping integrals (). The results were derived by fitting the function to the exact time dependencies of shown in Figure 4. The lines connecting the points are a guide to the eye. For , the total angular momentum is strictly conserved, and thus, and .
The change of the total electronic angular momentum at long times depends rather weakly on the strength of the hopping integrals for , where it amounts to – (see Figure 5). One concludes that the quenching of in the limit of is quite effective, as soon as the hopping integrals and d band width are comparable or larger than the spin-orbit interactions. The electron delocalization throughout the lattice due to the interatomic hoppings represents, therefore, a most effective dissipation channel of angular momentum into the lattice.
4. Conclusions
The laser-induced ultrafast demagnetization of transition metals has been investigated from the perspective of rotational symmetry. General considerations clearly demonstrate that breaking both the spin and orbital rotational symmetries of a ferromagnetic material is crucial in order to explain the experimentally observed time dependence of the spin and orbital moments following a strong laser excitation. However, the absence of these symmetries alone provides no information on the actual extent of the effects that the sources of these symmetry breakings —the spin-orbit interactions and the interatomic hybridizations— have on the magnetization dynamics under realistic conditions. Therefore, the qualitative symmetry analysis has been complemented by performing exact numerical calculations of the time evolution following a laser excitation in the framework of a many-body electronic Hamiltonian. The results obtained as a function of the most relevant interaction parameters allowed us to quantify the consequences of spin and orbital symmetry breaking on the time-dependent properties observed in the experiment. In particular, one observes that the characteristic demagnetization time is controlled by the spin-orbit coupling strength, which is the smallest energy scale, whereas the quenching of the orbital angular momentum resulting from the motion of the electrons in the lattice is controlled by the much stronger electronic hoppings. For this reason, the latter takes place at a much shorter time scale of the order of 1 fs.
The present investigations addressed the problem of laser-induced magnetization dynamics from the perspective of the electronic system by regarding the ionic lattice as a static framework, whose degrees of freedom are classical and independent of time. While this is a sound approximation taking into account the large differences in mass and time scales between lattice and electronic degrees of freedom, it certainly does not cover all theoretically relevant aspects of the problem. It is therefore meaningful to extend the present investigations by incorporating the lattice degrees of freedom explicitly in order to elucidate the consequences of the transfer of angular momentum on the lattice dynamics. A quantum mechanical treatment of the lattice vibrations in such an extended electron-lattice many-body model would allow one to quantify the importance of the electron-phonon coupling in the ultrafast demagnetization relative to the static effects of the lattice potential considered in this work. Research in this direction is currently in progress and will be reported elsewhere.
Author Contributions
W.T., G.S. and G.M.P. have contributed equally to all parts of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Computer resources provided by the IT Service Center of the University of Kassel and by the Center for Scientific Computing of the University of Frankfurt are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Beaurepaire, E.; Merle, J.C.; Daunois, A.; Bigot, J.Y. Ultrafast Spin Dynamics in Ferromagnetic Nickel. Phys. Rev. Lett. 1996, 76, 4250–4253. [Google Scholar] [CrossRef]
- Rhie, H.S.; Dürr, H.A.; Eberhardt, W. Femtosecond Electron and Spin Dynamics in Ni/W(110) Films. Phys. Rev. Lett. 2003, 90, 247201. [Google Scholar] [CrossRef]
- Stamm, C.; Kachel, T.; Pontius, N.; Mitzner, R.; Quast, T.; Holldack, K.; Khan, S.; Lupulescu, C.; Aziz, E.F.; Wietstruk, M.; et al. Femtosecond modification of electron localization and transfer of angular momentum in nickel. Nat. Mater. 2007, 6, 740. [Google Scholar] [CrossRef]
- Stamm, C.; Pontius, N.; Kachel, T.; Wietstruk, M.; Dürr, H.A. Femtosecond X-ray absorption spectroscopy of spin and orbital angular momentum in photoexcited Ni films during ultrafast demagnetization. Phys. Rev. B 2010, 81, 104425. [Google Scholar] [CrossRef]
- Boeglin, C.; Beaurepaire, E.; Halté, V.; López-Flores, V.; Stamm, C.; Pontius, N.; Dürr, H.A.; Bigot, J.Y. Distinguishing the ultrafast dynamics of spin and orbital moments in solids. Nature 2010, 465, 458. [Google Scholar] [CrossRef]
- Turgut, E.; Zusin, D.; Legut, D.; Carva, K.; Knut, R.; Shaw, J.M.; Chen, C.; Tao, Z.; Nembach, H.T.; Silva, T.J.; et al. Stoner versus Heisenberg: Ultrafast exchange reduction and magnon generation during laser-induced demagnetization. Phys. Rev. B 2016, 94, 220408. [Google Scholar] [CrossRef]
- You, W.; Tengdin, P.; Chen, C.; Shi, X.; Zusin, D.; Zhang, Y.; Gentry, C.; Blonsky, A.; Keller, M.; Oppeneer, P.M.; et al. Revealing the Nature of the Ultrafast Magnetic Phase Transition in Ni by Correlating Extreme Ultraviolet Magneto-Optic and Photoemission Spectroscopies. Phys. Rev. Lett. 2018, 121, 077204. [Google Scholar] [CrossRef]
- Tengdin, P.; You, W.; Chen, C.; Shi, X.; Zusin, D.; Zhang, Y.; Gentry, C.; Blonsky, A.; Keller, M.; Oppeneer, P.M.; et al. Critical behavior within 20 fs drives the out-of-equilibrium laser-induced magnetic phase transition in nickel. Sci. Adv. 2018, 4, eaap9744. [Google Scholar] [CrossRef]
- Eschenlohr, A.; Battiato, M.; Maldonado, P.; Pontius, N.; Kachel, T.; Holldack, K.; Mitzner, R.; Föhlisch, A.; Oppeneer, P.M.; Stamm, C. Ultrafast spin transport as key to femtosecond demagnetization. Nat. Mater. 2013, 12, 332. [Google Scholar] [CrossRef]
- Vodungbo, B.; Tudu, B.; Perron, J.; Delaunay, R.; Müller, L.; Berntsen, M.H.; Grübel, G.; Malinowski, G.; Weier, C.; Gautier, J.; et al. Indirect excitation of ultrafast demagnetization. Sci. Rep. 2016, 6, 18970. [Google Scholar] [CrossRef]
- Bergeard, N.; Hehn, M.; Mangin, S.; Lengaigne, G.; Montaigne, F.; Lalieu, M.L.M.; Koopmans, B.; Malinowski, G. Hot-Electron-Induced Ultrafast Demagnetization in Co/Pt Multilayers. Phys. Rev. Lett. 2016, 117, 147203. [Google Scholar] [CrossRef]
- Krauß, M.; Roth, T.; Alebrand, S.; Steil, D.; Cinchetti, M.; Aeschlimann, M.; Schneider, H.C. Ultrafast demagnetization of ferromagnetic transition metals: The role of the Coulomb interaction. Phys. Rev. B 2009, 80, 180407. [Google Scholar] [CrossRef]
- Krieger, K.; Dewhurst, J.K.; Elliott, P.; Sharma, S.; Gross, E.K.U. Laser-Induced Demagnetization at Ultrashort Time Scales: Predictions of TDDFT. J. Chem. Theory Comput. 2015, 11, 4870–4874. [Google Scholar] [CrossRef]
- Töws, W.; Pastor, G.M. Many-Body Theory of Ultrafast Demagnetization and Angular Momentum Transfer in Ferromagnetic Transition Metals. Phys. Rev. Lett. 2015, 115, 217204. [Google Scholar] [CrossRef]
- Shokeen, V.; Sanchez Piaia, M.; Bigot, J.Y.; Müller, T.; Elliott, P.; Dewhurst, J.K.; Sharma, S.; Gross, E.K.U. Spin Flips versus Spin Transport in Nonthermal Electrons Excited by Ultrashort Optical Pulses in Transition Metals. Phys. Rev. Lett. 2017, 119, 107203. [Google Scholar] [CrossRef]
- Dewhurst, J.K.; Elliott, P.; Shallcross, S.; Gross, E.K.U.; Sharma, S. Laser-Induced Intersite Spin Transfer. Nano Lett. 2018, 18, 1842–1848. [Google Scholar] [CrossRef]
- Töws, W.; Pastor, G.M. Tuning the laser-induced ultrafast demagnetization of transition metals. Phys. Rev. B 2019, 100, 024402. [Google Scholar] [CrossRef]
- Koopmans, B.; Kicken, H.; van Kampen, M.; de Jonge, W. Microscopic model for femtosecond magnetization dynamics. J. Magn. Magn. Mater. 2005, 286, 271–275. [Google Scholar] [CrossRef]
- Koopmans, B.; Malinowski, G.; Dalla Longa, F.; Steiauf, D.; Fähnle, M.; Roth, T.; Cinchetti, M.; Aeschlimann, M. Explaining the paradoxical diversity of ultrafast laser-induced demagnetization. Nat. Mater. 2010, 9, 259. [Google Scholar] [CrossRef]
- Battiato, M.; Carva, K.; Oppeneer, P.M. Superdiffusive Spin Transport as a Mechanism of Ultrafast Demagnetization. Phys. Rev. Lett. 2010, 105, 027203. [Google Scholar] [CrossRef]
- Battiato, M.; Carva, K.; Oppeneer, P.M. Theory of laser-induced ultrafast superdiffusive spin transport in layered heterostructures. Phys. Rev. B 2012, 86, 024404. [Google Scholar] [CrossRef]
- Steiauf, D.; Illg, C.; Fähnle, M. Extension of Yafet’s theory of spin relaxation to ferromagnets. J. Magn. Magn. Mater. 2010, 322, L5–L7. [Google Scholar] [CrossRef]
- Fähnle, M.; Illg, C. Electron theory of fast and ultrafast dissipative magnetization dynamics. J. Phys. Condens. Matter 2011, 23, 493201. [Google Scholar] [CrossRef]
- Carva, K.; Battiato, M.; Oppeneer, P.M. Ab Initio Investigation of the Elliott-Yafet Electron-Phonon Mechanism in Laser-Induced Ultrafast Demagnetization. Phys. Rev. Lett. 2011, 107, 207201. [Google Scholar] [CrossRef]
- Garibay-Alonso, R.; Dorantes-Dávila, J.; Pastor, G.M. Noncollinear spin-fluctuation theory of transition-metal magnetism: Role of transverse spin fluctuations in Fe. Phys. Rev. B 2015, 91, 184408. [Google Scholar] [CrossRef]
- Hubbard, J. The magnetism of iron. Phys. Rev. B 1979, 19, 2626–2636. [Google Scholar] [CrossRef]
- Hubbard, J. Magnetism of iron. II. Phys. Rev. B 1979, 20, 4584–4595. [Google Scholar] [CrossRef]
- Hasegawa, H. Single-Siet Spin Fluctuation Theory of Itinerant-Electron Systems with Narrow Bands. J. Phys. Soc. Jpn. 1980, 49, 178–188. [Google Scholar] [CrossRef]
- Hasegawa, H. Single-Site Spin Fluctuation Theory of Itinerant-Electron Systems with Narrow Bands. II. Iron and Nickel. J. Phys. Soc. Jpn. 1980, 49, 963–971. [Google Scholar] [CrossRef]
- Bruno, P. Physical origins and theoretical models of magnetic anisotropy. In Magnetismus von Festkörpern und Grenzflächen; Forschungszentrum Jülich: Jülich, Germany, 1993; Chapter 24. [Google Scholar]
- Victora, R.H.; Falicov, L.M. Exact Solution of a Four-Site d-Electron Problem: The Nickel-Metal Photoemission Spectrum. Phys. Rev. Lett. 1985, 55, 1140–1143. [Google Scholar] [CrossRef]
- Hüfner, S.; Wertheim, G. Multielectron effects in the XPS spectra of nickel. Phys. Lett. A 1975, 51, 299–300. [Google Scholar] [CrossRef]
- Eberhardt, W.; Plummer, E.W. Angle-resolved photoemission determination of the band structure and multielectron excitations in Ni. Phys. Rev. B 1980, 21, 3245–3255. [Google Scholar] [CrossRef]
- Feldkamp, L.A.; Davis, L.C. X-ray photoemission spectra of core levels in Ni metal. Phys. Rev. B 1980, 22, 3644–3653. [Google Scholar] [CrossRef]
- Papaconstantopoulos, D.A. Handbook of the Band Structure of Elemental Solids; Plenum Press: New York, NY, USA, 1986. [Google Scholar]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Tannor, D.J. Introduction to Quantum Mechanics: A time-Dependent Perspective; University Science Books: Sausalito, CA, USA, 2007. [Google Scholar]
- Guirado-López, R.A.; Dorantes-Dávila, J.; Pastor, G.M. Orbital Magnetism in Transition-Metal Clusters: From Hund’s Rules to Bulk Quenching. Phys. Rev. Lett. 2003, 90, 226402. [Google Scholar] [CrossRef]
- Ashcroft, N.; Mermin, N. Solid State Physics; Thomson Learning: London, UK, 1976. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).