Abstract
In this study, we present a new approach with semi-analytical and numerical findings for solving equations of motion of small orbiter m, which is moving under the combined gravitational attraction of three primaries, , , and , in case of the bi-elliptic restricted problem of four bodies (BiER4BP), where three such primaries, , , and , are moving on elliptic orbits with hierarchical configuration << << within one plane as follows: third primary body is moving on elliptical orbit around second , and second primary is moving on elliptical orbit around first . Our aim for constructing the aforementioned quasi-planar motion of planetoid m is obtaining its coordinates supporting its orbit in a regime of close motion to the plane of orbiting the main bodies , , and . Meanwhile, the system of equations of motion was successfully numerically explored with respect to the existence and stable positioning of approximate solution for a Dyson sphere. As a result, the concept of the Dyson sphere for possible orbiting variety of solar energy absorbers was transformed to the elongated Dyson space net with respect to their trajectories for the successful process of absorbing the energy from the Sun; this can be recognized as symmetry reduction. We obtain the following: (1) the solution for coordinates {x, y} is described by the simplified system of two nonlinear ordinary differential equations of second order, depending on true anomaly f; (2) the expression for coordinate z is given by an equation of Riccati-type where small orbiter that quasi-oscillates close to the fixed plane .
1. Introduction
It is a well-established fact in celestial mechanics that equations of the restricted three-body problem [1,2,3,4,5], hereafter referred to as R3BP, are nonintegrable (where we consider orbiting of infinitesimal planetoid gravitationally influenced by a duet of two primaries (Sun) and (planet), both orbiting in Kepler-type dynamics, and is assumed to be less than ); we should note that the hypothesis that one of the primaries has a bigger mass than the other is basically extraneous to the problem: it enters the game later, when the researcher’s attention is focused on practical applications. This is a classical well-known problem: two primaries revolve on Keplerian orbits around the barycenter, and a third body, named planetoid, moves under the gravitational attraction of the primaries, without affecting their motion. If the motion of the primaries is circular, then one obtains the classical R3BP. It is worth noting a valuable contribution of famous participants of the celestial mechanics community regarding analytical methods and the obtained results in R4BP [6,7,8,9], stability of solutions in R3BP [10,11,12], input of such findings to investigation of influence of tidal phenomena on dynamics of fluidic envelope of fluid-type planets and their rotational dynamics along with their satellites [13], variety of partial formulations [14,15,16,17,18] and applications in celestial mechanics (including of those of nongravitational nature [19]), investigations of stability of the solutions (including of those in the vicinity of libration points), and partially applying the aforedescribed findings in investigations of various nonlinear perturbing effects and phenomena, e.g., in investigations of the escape and collision dynamics as well. Especially, let us mention a case of an elliptic restricted three-body problem [12,13,14,15,16] (ER3BP, where primaries are orbiting not far from their center of masses on elliptic orbits) and, also, of BiER4BP (bi-elliptic restricted four-body problem) [7].
The problem investigated here may be enunciated as follows: let us suppose that three primaries move on elliptic orbits located preferably within one plane (which is the plane of orbital motion of two main primaries) orbiting there in a hierarchical configuration: the third primary body is moving on an elliptical orbit around the second primary (whereas mass of first, second, and third primary are supposed to be arranged hierarchically; the first primary has the mass which is much more massive than the combined mass of the second and third primaries, while the third primary has a mass much less than the second primary); let us study the dynamics of a fourth body, the planetoid, subjected to the attraction of the primaries without affecting their orbits. The existence of the motions in such a problem was considered in [20], but they neglected the terms in basic equations of motion depending on the elliptical motion of the third primary body around the second primary. The idea exploited in this paper is as follows: using the same model formulated in [20] as a basis, let us explore solutions taking into account the terms depending on elliptical motion of the third primary body around the second primary, including those depending on the true anomaly of such secondary motion (i.e., depending on the second true anomaly, where the first true anomaly corresponds to the angular motion of the second primary in its elliptical motion around the first primary body).
As an obvious practical application, we refer to the idea of the Dyson sphere [21], for which Freeman J. Dyson himself stated, regarding the idea of the Dyson sphere, that (1) “he had not envisioned a monolithic shell or ring which he wrote would be mechanically impossible”, (2) “but rather a loose collection or swarm of objects traveling on independent orbits around the star”. Thus, we will consider the Dyson sphere in a form (2) above, i.e., as a “swarm of objects traveling on independent orbits around the star”.
Therefore, it is a quite intriguing question to illuminate whether such stable orbits do exist within formulation of the aforementioned BiER4BP (bi-elliptic restricted four-body problem), because, if even one shell of such swarm has no stable orbit, the idea of the Dyson sphere is merely a fantastic dream.
Let us note that we schematically imagine in Figure 1 the motions of multiple swarms of planetoids (on their stable orbits around the Sun, between the system “Moon–Earth” and Sun) absorbing the light power from the Sun, which will be then afterwards converting such power to other types of energy (EM energy), further transferring to the Earth as, e.g., a laser beam or via microwave-length radiation.
Figure 1.
Dyson sphere (as a swarm of objects traveling on orbits around the star).
2. Description of the Model, Equations of Motion
Let us present in the current investigation a novel method for resolving equations of a quasi-planar orbiting of infinitesimal planetoid m close to the plane of mutual orbitings of the main primaries around each other (in the case of a special type of BiER4BP), illuminating the results by numerical findings.
We consider three primaries, , , and , which are orbiting on elliptical orbits within one plane (which is a plane of orbital motion of two main primaries, and ) orbiting there with hierarchical configuration as follows: the third primary body, , is moving on an elliptical orbit around the second primary, (whereas masses of the first, second, and third primaries are supposed to be arranged hierarchically: the first primary is much more massive than the combined mass of the second and third primary bodies {, }, while the third primary, , has a mass much less than the second primary ). Our aim for constructing the aforementioned quasi-planar motion is to obtain coordinates of an infinitesimal planetoid m which maintains its orbit located close to the plane of orbiting primaries , , and .
According to the approach in [20], equations of BiER4BP for a small orbiter can be presented in the synodic constantly rotating cartesian coordinates = {x, y, z} in nondimensional scaling type (for given initial conditions):
where ′ denotes (d/d f) in (1), and is scalar function.
and μi = (/) (i = 1, 2, 3), is the nondimensional distance between orbiter m and i-th primary [20], which are to be determined as follows:
where, r is the relative distance from primary to ; in the meantime, θ denotes angle between radius-vector from center of mass of {, } to and Ox axis (M is the combined sum of masses of primaries, the unit of time is chosen so [20] that constant G equals 1, where G is the Gaussian constant of gravitation law). The expression for r can be written as
where a1 is the semimajor axis of the binary system {, }, << ; e1 is the eccentricity of elliptic orbit of the rotating primary around primary , f is the true anomaly for this orbital primary motion; a2 is the semimajor axis of the binary system {, }, << ; e2 is the eccentricity of elliptic orbit of the rotating primary around the barycenter of primaries {, }, and f2 is the true anomaly for this orbital secondary motion. The parameter θ is determined as in the work [20] by
where θ0 is initial value of θ. Meanwhile, from (4) and (5), we obtain
Let us note that with regard to the orbiter’s motion, we will consider the Cauchy problem in the whole space, here and below.
Then, further, with help of (2)–(6), system (1) can be transformed as follows:
where (by three primaries, we mean “Sun–Earth–Moon” in BiER4BP):
3. Semi-Analytical Approximate Solution to the System of Equation (7)
Assuming that the orbiter m is moving around and close to the primary , we can conclude that in Equation (7).
Such approximation yields, from (7) with the help of (8),
Let us recall our valid (realistic) assumptions which were made previously in [20]: μ3 << μ2 ⇒ (μ3 · μ2)/(μ3 + μ2) ≅ μ3.
In addition, we assumed that z belongs to the subclass of trapped motions where condition z << 1 should be valid in (9). This means that orbiter m is supposed to be in quasi-oscillating regime close to the fixed plane .
Thus, let us neglect all terms such as and less in Equation (9). We will obtain from the third equation of (9) (taking into account (6)):
where Equation (10) can be classified as Riccati ODE [15].
Thus, we obtain from the first and second equations in Equation (9) (taking into account also that , μ3 << μ2, e2 << 1, and by three primaries, we mean “Sun–Earth–Moon” in BiER4BP):
Equation (11) above is the system of two nonlinear differential equations of second order, which depends on true anomaly f (independent variable); general solution of equations of this such type is unknown.
4. Families of Quasi-Stable Plane Orbits of System (7) and Equation (11), Their Graphical and Numerical Solutions
Let us present furthermore the schematic plots for numerical solutions of Equation (7) and (11) (see Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7), where we use approximation (11) if assumption is valid for initial conditions (initial data) when constructing the numerical solutions.
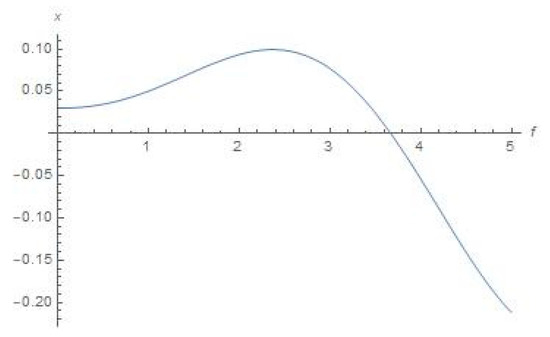
Figure 2.
Schematic plot for x(f) with the help of Equation (11) (true anomaly f is depicted as abscissa).
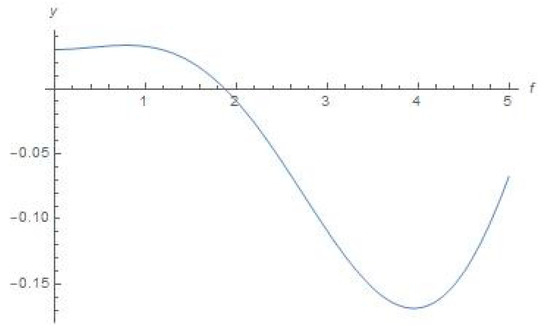
Figure 3.
Schematic plot for y(f) with the help of Equation (11) (true anomaly f is depicted as abscissa).
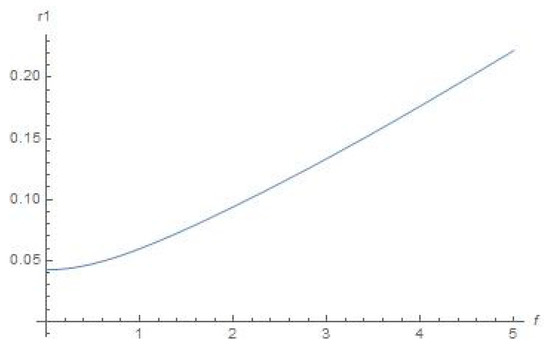
Figure 4.
Schematic plot for distance r1 (f) with the help of Equation (11) (true anomaly f is depicted as abscissa), .
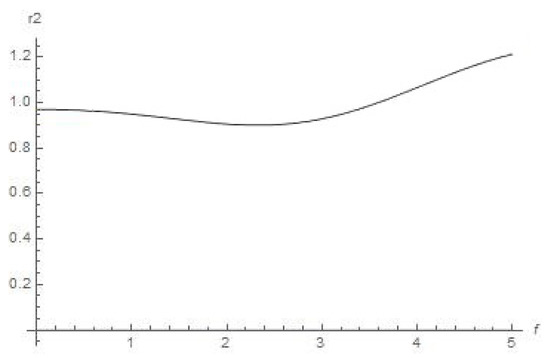
Figure 5.
Schematic plot for distance r2 (f) from Earth with the help of Equation (11) (true anomaly f is depicted as abscissa), .
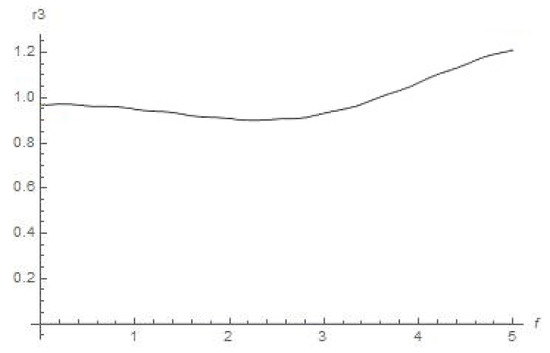
Figure 6.
Schematic plot for distance r3 (f) from Moon with the help of Equation (11) (true anomaly f is depicted as abscissa), .
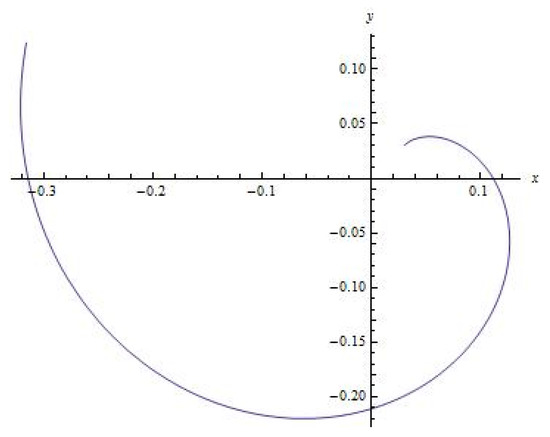
Figure 7.
Numerically obtained solution of Equation (11) for dependence y(x) (which means the actual trajectory of the small orbiter starting from initial conditions in a plane {x, y, 0}).
Regarding the initial data, we have chosen the following:
In a series of graphical solutions obtained numerically in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 we used the Runge–Kutta fourth-order method (step 0.001 with launching algorithm from initial data).
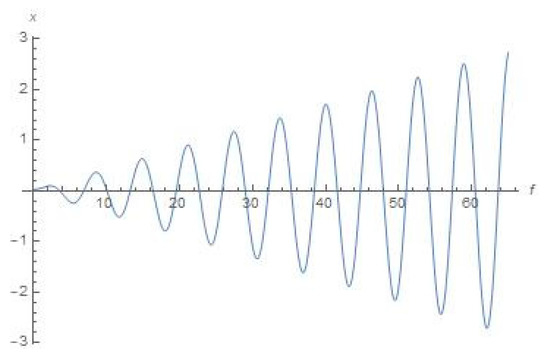
Figure 8.
Schematic plot for x(f) with the help of Equation (11) (true anomaly f is depicted as abscissa).
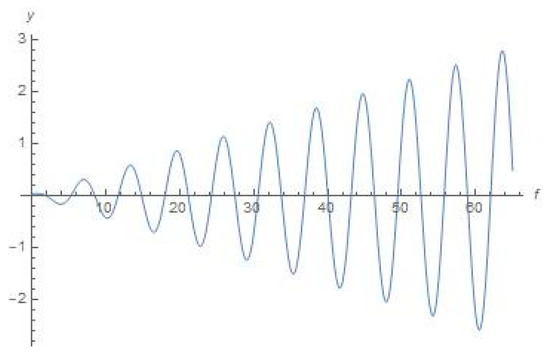
Figure 9.
Schematic plot for y(f) with the help of Equation (11) (true anomaly f is depicted as abscissa).
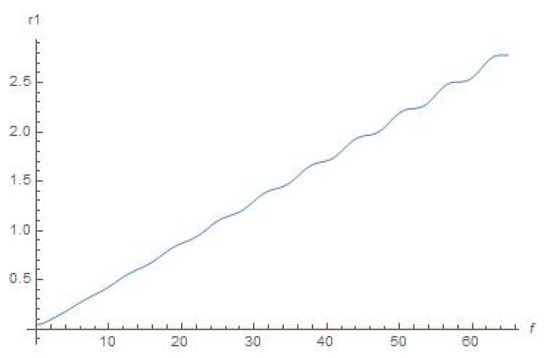
Figure 10.
Schematic plot for distance r1 (f) with the help of Equation (11) (true anomaly f is depicted as abscissa), .
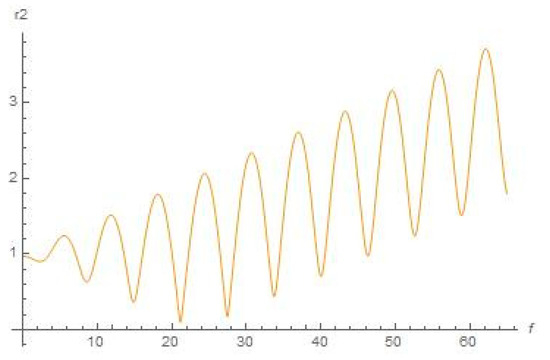
Figure 11.
Schematic plot for distance r2 (f) from Earth with the help of Equation (11) (true anomaly f is depicted as abscissa), .
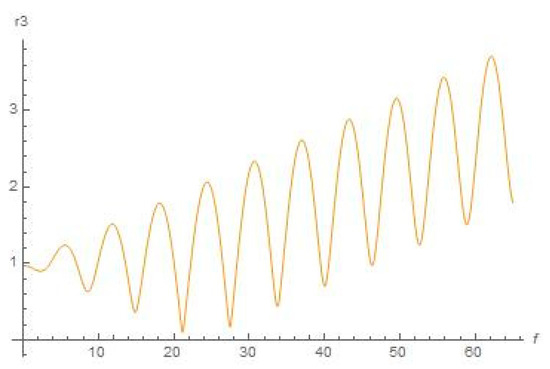
Figure 12.
Schematic plot for distance r3 (f) from Moon with the help of Equation (11) (true anomaly f is depicted as abscissa), .
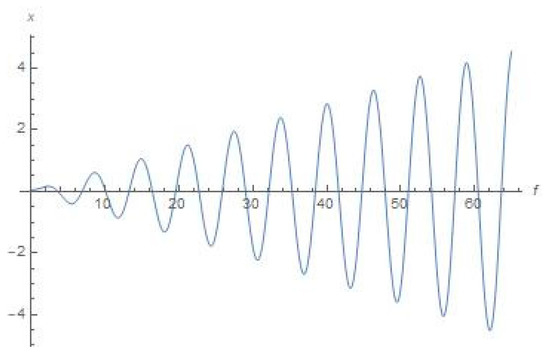
Figure 13.
Schematic plot for x(f) with the help of Equation (11) (true anomaly f is depicted as abscissa).
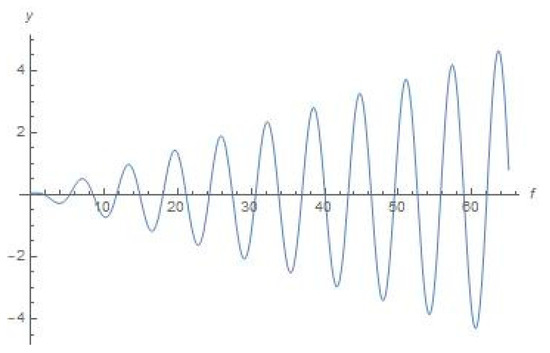
Figure 14.
Schematic plot for y(f) with the help of Equation (11) (true anomaly f is depicted as abscissa).
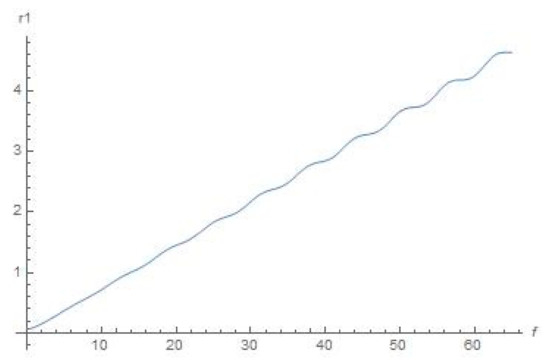
Figure 15.
Schematic plot for distance r1 (f) with the help of Equation (11) (true anomaly f is depicted as abscissa), .
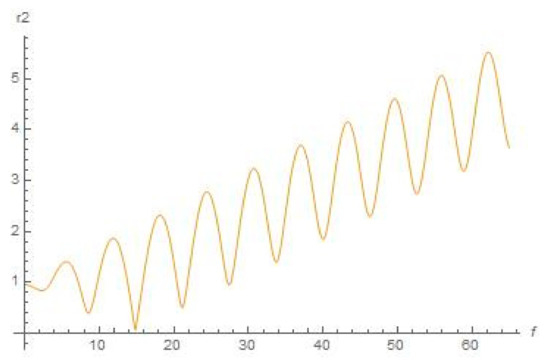
Figure 16.
Schematic plot for distance r2 (f) from Earth with the help of Equation (11) (true anomaly f is depicted as abscissa), .
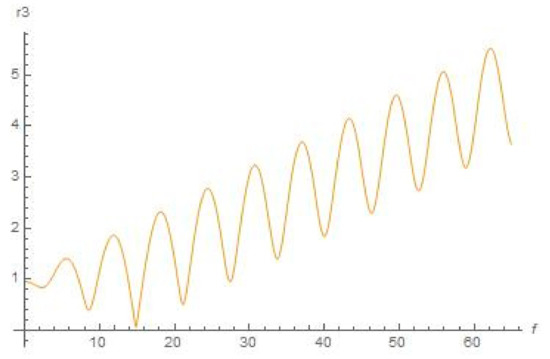
Figure 17.
Schematic plot for distance r3 (f) from Moon with the help of Equation (11) (true anomaly f is depicted as abscissa), .
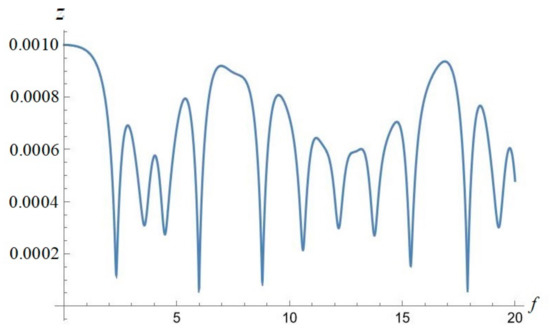
Figure 18.
Numerical solution for coordinate z(f) using Equation (10) (depending on true anomaly f, depicted on abscissa axis).
We can conclude from Figure 4 that the orbiter will be leaving outside the sphere of strong influence of the Sun. The abovementioned regime of the orbiter’s space drift in an outward direction from the Sun stems, as we guess, from accelerating by centrifugal force from Sun (since we consider this motion in the synodic constantly rotating Cartesian system) at its motion in ER4PB (case “Moon–Earth–Sun” for system “small orbiter–Sun–Earth–Moon”). Regarding similarity of graphical plots in Figure 5 and Figure 6, it is quite obvious for the chosen case of the three primaries “Moon–Earth–Sun”, where the distance from the Moon to Earth is permanently negligible with respect to the distance from Earth to the Sun. Therefore, the distance from the Moon to the Sun is circa the same as the distance from Earth to the Sun for all the range of true anomaly f (which determines the angular motion of Earth on orbit around the Sun).
5. Discussion
We consider in the current study the plane approximation for BiER4BP (bi-elliptic restricted four-body problem) formulated in (1)–(11). In the meantime, coordinate z should quasi-periodically oscillate nearby the plane .
However, even without approximation (11), we tested a lot of initial data for the numerical solutions of system (7); the most successful case is presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. Others exhibit very fast movement in an outward direction from the Sun, which stems, as we guess, from accelerating by centrifugal force from the Sun (in the synodic constantly rotating cartesian coordinates).
We wish also to clearly outline the simplifying assumptions made above with respect to the solution with the aim of further numerical solving:
- We consider in (11) two primaries of masses {, }, μ3 << μ2, rotating on elliptic orbits, whereas their barycenter is Kepler-rotating around the main primary M1, μ2 << μ1.
- The motions of the primaries are preferably coplanar (while it is a well-known fact that the orbit of the Moon is inclined on circa 5 degrees with respect to the invariable plane of rotation of Earth around the Sun).
- Eccentricity e2 of orbit around is negligible, e2 << 1.
- Orbiter m is moving outside the Hill sphere [15] of second primary with radius (minimal distance) ~ 0.101 AU for the system “Sun–Earth”.
- Small orbiter m is assumed to oscillate nearby plane .
- Masses of all primaries are constant.
Meanwhile, the aforepresented list of simplifications demonstrates that the formulated problem discussed hereby is far from realistic conditions. Indeed, while we can exclude the influence of Mercury (due to its thin Hill sphere [15] ~0.015 AU), the attraction of Venus can be ignored insofar as only if it is remaining sufficiently distant from the small orbiter on its current orbit in the aforeformulated kind of BiER4BP.
Let us also present other distinguished cases for the aforeinvestigated motion of small satellite or orbiter inside the spheres of influences by participants of duet “second primary body + third primary body” (here, “Earth + Moon”).
First, as previously, we choose initial conditions = 0.03, = 0; = 0.03, = 0 for plots depicted in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 (but we chose the larger range of true anomaly, up to f = 65).
Secondly, let us choose the initial conditions to be = 0.05, = 0; = 0.05, = 0 for plots numerically depicted in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 (where we also chose the range of true anomaly up to f = 65).
As we can see from Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, the dynamical character of the resulted numerical graphical solutions was typically the same for all range of initial data that we used in our numerical experiments. Namely, there are growing oscillations to the solutions for x(f), y(f), r2 (f), and r3 (f) shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, and graphical solutions for r1 (f) demonstrate to us that the orbiter will move outside the most active sphere of influence by the Sun and Earth. However, this does not mean there will be a divergence for the solution (as soon as true anomaly moves to infinity), or this does not relate with respect to a correction to the position, or any numerical error associated with the solution to the equations. This means that there are not any stable orbits (which were supposed to be existing in the concept of Dyson sphere), or at least quasi-stable orbits, within formulation of the aforementioned bi-elliptic restricted four-body problem.
To finalize the discussion, it is worth noting the demonstration of stable character of coordinate z(f) on Figure 18, obtained numerically for solutions illuminated in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17; we chose the initial data as follows: = 0.001, = 0 (where we also chose the range of true anomaly up to f = 20, which can be surely prolongated further, up to f = 65 as in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17).
6. Conclusions
In this study, we presented a novel algorithm with semi-analytical and numerical findings for motion of a small orbiter m, governed by the combined Newtonian attraction of three primaries, , , and M3, in the case of a bi-elliptic restricted four-body problem, where three primaries, , M2, and M3, are Kepler-moving on their orbits (M3 << << ) in one plane as follows: the third primary body, , is moving on an elliptical orbit around the second, , the second primary, , is moving on an elliptical orbit around the first, . Our aim for constructing the aforementioned quasi-planar motion of a planetoid or an orbiter m is to obtain its coordinates supporting its orbit in a regime of close motion to the plane of orbiting the main bodies , , and . We considered stable positioning of approximate solution for elements of the Dyson sphere (Dyson swarm) for the aforeformulated problem from the point of view of equations of motion in celestial mechanics formulated in the case of BiER4BP.
Our findings are the following: (1) the pair {x, y} of orbiter’s coordinates is described by the simplified system of two nonlinear ODEs of second order (in dependence on true anomaly f); (2) vertical coordinate z is described by an equation of Riccati-type where small orbiter is supposed to be in quasi-oscillating regime close to the fixed plane .
As the main conclusion with respect to exploring the stable positioning of the elements of a Dyson sphere (considered here as a swarm of small planetoids orbiting around the primary star), we should illuminate and definitely clarify that we have not found any stable orbits for the aforesupposed Dyson sphere even for one shell of such swarm surrounding the Sun with various initial data of their positioning, nearby and far away.
Nevertheless, we can see from Figure 11, Figure 12, Figure 16 and Figure 17 that the small orbiter will return close to Earth approximately at the meaning of true anomaly f ≅ 21 (which corresponds to more than three revolutions of Earth around the Sun or to more than three years); at this moment, the shell may transfer the absorbed energy to Earth or to the International Space Station by means of laser beam. Thus, we can conclude that the Dyson sphere appears to be transformed to the phenomenon of a dynamical Dyson space net, shells of which are allocated at a distance of circa 2 AU from the Sun and forming a space net of shells absorbing energy from the Sun.
Apparently, such a clearly formulated transformation of conception of a sphere in three dimensions for possible orbiting variety of solar energy absorbers (here, Dyson sphere) to the elongated quasi-ellipse preferably in two dimensions (presented above as Dyson space net), with respect to their trajectories for the successful process of absorbing energy from the Sun, can be recognized as symmetry reduction.
It is worth noting that the best initial conditions we tested were located from (, ) = (0.03, 0.03) (corresponds to equals circa 0.042 AU) to (, ) = (0.08, 0.08) (corresponds to equals circa 0.113 AU) with various starting velocities: the dynamical character of the resulted numerical solutions (graphical plots) was typically the same as for those presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.
For optimizing the governing of maneuvering between elements of the abovementioned Dyson space net, we can use (with the aim of choosing the optimal set of initial data) the analogue of continuity equation for spatial spreading of velocities of such discrete shells to form a large-scale coherent structure [22] from them located close one to another in space. Such an analogue of continuity equation should be determined by condition (12) for compactness of a Dyson space net as follows:
where n is the number of shell, is the vector of velocity of the n-th small orbiter (shell), and is the well-known Hamilton operator. It is worth noting that ultimate restricting condition (12) should be tested additionally in numerical experiments for adjusting of configuration of a Dyson space net for the sets of realistic initial conditions chosen for its elements (shells).
Thus, we illuminated and outlined the main features determining the stable drift dynamics of approximate solutions for an analogue of a Dyson sphere considered in the current research as a swarm of small artificial satellites (on their orbits around the Sun, between system “Moon–Earth” and Sun), which are absorbing the light power from the Sun, then afterwards converting such power to other types of energy (EM energy) and further transferring to the Earth as, e.g., a laser beam or via microwave-length radiation.
Furthermore, an additional list of related articles should be mentioned which may be important for understanding aspects of the problem under consideration [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] (where review [28] tackles the theme of orbital resonances in the solar system, whereas works [29,30] describe external or internal (tidal) effects influencing on orbits of planetoids; influencing tidal effects [30], and losses of angular momentum via tidal interactions on the dynamics of celestial bodies are tackled in [42]).
In addition, we should especially remark that we restricted ourselves in exploring the case of the orbiter’s motion close to invariable plane z = 0 (while Equation (9) or (11) for modelling of approximate motion can be easily updated for any fixed, sufficiently small value of coordinate z in the vicinity of which oscillating motion of an orbiter takes place).
Meanwhile, in the section “Energy Capturing Megastructure Dyson Spheres?” of article [33], the author presents a brief review of possible existence and discovery of megastructures surrounding host stars in a space which reduces their natural radiation flux (which are thus supposed to be acting in a manner similar to Dyson spheres around their host stars).
It is worthwhile to clearly state the conclusions, impacts, applications, and the “main points”:
- Elegant ansatz is developed for analysis of motion of a small mass in BiER4BP.
- Three primaries rotate around a barycenter on bi-elliptic orbits: << , << .
- Coordinate z is considered to be stable in oscillating close to fixed plane {x, y, 0}.
- The planar bi-elliptic restricted four-body problem (BiER4BP) is investigated well.
- Stable drift dynamics of solutions for analogue of a Dyson sphere are analyzed.
- No stable solutions for a Dyson swarm were found, but an orbiter will flyby near Earth.
Author Contributions
Conceptualization, S.E.; methodology, S.E.; software, E.Y.P.; validation, S.E., D.L. and E.Y.P.; formal analysis, S.E.; investigation, S.E.; data curation, E.Y.P.; writing: original draft, S.E.; writing: review and editing, S.E.; visualization, S.E. and E.Y.P.; supervision, S.E. and D.L.; project administration, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data associated with the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Celletti, A. Stability and Chaos in Celestial Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wintner, A. The Analytical Foundations of Celestial Mechanics; Princeton University Press: Princeton, NJ, USA, 1941. [Google Scholar]
- Szebehely, V. Theory of Orbits. The Restricted Problem of Three Bodies; Yale University: New Haven, CT, USA; Academic Press: New York, NY, USA; London, UK, 1967. [Google Scholar]
- Siegel, C.L.; Moser, J. Lectures on Celestial Mechanics; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Marchal, C. The Three-Body Problem; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Chakraborty, A.; Narayan, A. A new version of restricted four body problem. New Astron. 2019, 70, 43–50. [Google Scholar] [CrossRef]
- Chakraborty, A.; Narayan, A. BiElliptic Restricted Four Body Problem. Few Body Syst. 2019, 60, 7. [Google Scholar] [CrossRef]
- Dewangan, R.R.; Chakraborty, A.; Narayan, A. Stability of generalized elliptic restricted four body problem with radiation and oblateness effects. New Astron. 2020, 78, 101358. [Google Scholar] [CrossRef]
- Ansari, A.A.; Prasad, S.N. Generalized elliptic restricted four-body problem with variable mass. Astron. Lett. 2020, 46, 275–288. [Google Scholar] [CrossRef]
- Singh, J.; Leke, O. Stability of the photogravitational restricted three-body problem with variable masses. Astrophys. Space Sci. 2010, 326, 305–314. [Google Scholar] [CrossRef]
- Kushvah, B.S.; Sharma, J.P.; Ishwar, B. Nonlinear stability in the generalised photogravitational restricted three body problem with Poynting-Robertson drag. Astrophys. Space Sci. 2007, 312, 279–293. [Google Scholar] [CrossRef]
- Ershkov, S.; Abouelmagd, E.I.; Rachinskaya, A. A novel type of ER3BP introduced for hierarchical configuration with variable angular momentum of secondary planet. Arch. Appl. Mech. 2021, 91, 4599–4607. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Abouelmagd, E. About influence of differential rotation in convection zone of gaseous or fluid giant planet (Uranus) onto the parameters of orbits of satellites. Eur. Phys. J. Plus 2021, 136, 387. [Google Scholar] [CrossRef]
- Llibre, J.; Conxita, P. On the elliptic restricted three-body problem. Celest. Mech. Dyn. Astron. 1990, 48, 319–345. [Google Scholar] [CrossRef]
- Ershkov, S.; Rachinskaya, A. Semi-analytical solution for the trapped orbits of satellite near the planet in ER3BP. Arch. Appl. Mech. 2021, 91, 1407–1422. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Ledkov, A.S. Swing principle in tether-assisted return mission from an elliptical orbit. Aerosp. Sci. Technol. 2017, 71, 156–162. [Google Scholar] [CrossRef]
- Ansari, A.A.; Singh, J.; Alhussain, Z.A.; Belmabrouk, H. Perturbed Robe’s CR3BP with viscous force. Astrophys. Space Sci. 2019, 364, 95. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Leshchenko, D. Solving procedure for 3D motions near libration points in CR3BP. Astrophys. Space Sci. 2019, 364, 207. [Google Scholar] [CrossRef]
- Ershkov, S.V. The Yarkovsky effect in generalized photogravitational 3-body problem. Planet. Space Sci. 2012, 73, 221–223. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Leshchenko, D.; Rachinskaya, A. Solving procedure for the motion of infinitesimal mass in BiER4BP. Eur. Phys. J. Plus 2020, 135, 603. [Google Scholar] [CrossRef]
- Wright, J.T. Dyson spheres. Serb. Astron. J. 2020, 200, 1–18. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Rachinskaya, A.; Prosviryakov, E.Y.; Shamin, R.V. On the semi-analytical solutions in hydrodynamics of ideal fluid flows governed by large-scale coherent structures of spiral-type. Symmetry 2021, 13, 2307. [Google Scholar] [CrossRef]
- Shen, H.-X.; Luo Y-Zh Zhu, Y.-H.; Huang, A.-Y. Dyson sphere building: On the design of the GTOC11 problem and summary of the results. Acta Astronaut. 2022; in press. [Google Scholar] [CrossRef]
- Absil, C.O.; Serra, R.; Martinez, I.S.; Charpigny, N.; Labroquère, J.; Morales, V.M.; Olympio, J.; Rodriguez-Fernandez, V. Design of impulsive asteroid flybys and scheduling of time-minimal optimal control arcs for the construction of a Dyson ring (GTOC 11). Acta Astronaut. 2022, 201, 94–110. [Google Scholar] [CrossRef]
- Huston, M.; Wright, J. Evolutionary and Observational Consequences of Dyson Sphere Feedback—IOPscience. Astrophys. J. 2022, 924, 78. [Google Scholar] [CrossRef]
- Suazo, M.; Zackrisson, E.; Wright, J.; Korn, A.J.; Huston, M. Project Hephaistos—I. Upper limits on partial Dyson spheres in the Milky Way. Mon. Not. R. Astron. Soc. 2022, 512, 2988–3000. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Ansari, A.A. The motion properties of the infinitesimal body in the framework of bicircular Sun perturbed Earth–Moon system. New Astron. 2019, 73, 101282. [Google Scholar] [CrossRef]
- Peale, S.J. Orbital Resonances In The Solar System. Annu. Rev. Astron. Astrophys. 1976, 14, 215–246. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Leshchenko, D. Revisiting Apophis 2029 approach to Earth (staying on shoulders of NASA’s experts) or Can we be sure in almost ricocheting fly-by of Apophis on 13 of April 2029 near the Earth? J. Space Saf. Eng. 2022, 9, 363–1374. [Google Scholar] [CrossRef]
- Ershkov, S.V. About tidal evolution of quasi-periodic orbits of satellites. Earth Moon Planets 2017, 120, 15–30. [Google Scholar] [CrossRef]
- Smith, J. Review and viability of a Dyson Swarm as a form of Dyson Sphere. Phys. Scr. 2022, 97, 122001. [Google Scholar] [CrossRef]
- Liu, C.; Gong, S. Hill stability of the satellite in the elliptic restricted four-body problem. Astrophys. Space Sci. 2018, 363, 162. [Google Scholar] [CrossRef]
- Veysi, H. Technological Evolution of Extraterrestrial Civilizations: Dyson Spheres, Warp Drives, Energy Capturing Conquerors. J. Astrobiol. 2022, 13, 14–25. [Google Scholar]
- Meena, P.; Kishor, R. First order stability test of equilibrium points in the planar elliptic restricted four body problem with radiating primaries. Chaos Solitons Fractals 2021, 150, 111138. [Google Scholar] [CrossRef]
- Dyson, F.J. Search for artificial stellar sources of infrared radiation. Science 1960, 131, 1667–1668. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, N.; Guo, X.; Wu, D.; Xie, X.; Li, J.; Yang, J.; Chen Sh Jiang, F.; Baoyin, H. GTOC 11: Results from Tsinghua University and Shanghai Institute of Satellite Engineering. Acta Astronaut. 2022; in press. [Google Scholar] [CrossRef]
- Umar, A.; Jagadish, S. Semi-analytic solutions for the triangular points of double white dwarfs in the ER3BP: Impact of the body’s oblateness and the orbital eccentricity. Adv. Space Res. 2015, 55, 2584–2591. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Rachinskaya, A. Revisiting the dynamics of finite-sized satellite near the planet in ER3BP. Arch. Appl. Mech. 2022, 92, 2397–2407. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Rachinskaya, A. Capture in regime of a trapped motion with further inelastic collision for finite-sized asteroid in ER3BP. Symmetry 2022, 14, 1548. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Rachinskaya, A. Semi-analytical findings for rotational trapped motion of satellite in the vicinity of collinear points {L1, L2} in planar ER3BP. Arch. Appl. Mech. 2022, 92, 3005–3012. [Google Scholar] [CrossRef]
- Dziobek, O. Ueber einen merkwürdigen Fall des Vielkörperproblems. Astron. Nachr. 1900, 152, 33–46. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D. Estimation of the size of the solar system and its spatial dynamics using Sundman inequality. Pramana J. Phys. 2022, 96, 158. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Prosviryakov, E.Y. A novel type of ER3BP introducing Milankovitch cycles or seasonal irradiation processes influencing onto orbit of planet. Arch. Appl. Mech. 2022; in press. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D. Analysis of the size of Solar system close to the state with zero total angular momentum via Sundman’s inequality. An. Acad. Bras. Ciências 2021, 93 (Suppl. S3), e20200269. [Google Scholar] [CrossRef]
- Zotos, E.E.; Chen, W.; Abouelmagd, E.I.; Han, H. Basins of convergence of equilibrium points in the restricted three-body problem with modified gravitational potential. Chaos Solitons Fractals 2020, 134, 109704. [Google Scholar] [CrossRef]
- Alshaery, A.A.; Abouelmagd, E.I. Analysis of the spatial quantized three-body problem. Results Phys. 2020, 17, 103067. [Google Scholar] [CrossRef]
- Abozaid, A.A.; Selim, H.H.; Gadallah, K.A.; Hassan, I.A.; Abouelmagd, E.I. Periodic orbit in the frame work of restricted three bodies under the asteroids belt effect. Appl. Math. Nonlinear Sci. 2020, 5, 157–176. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Mostafa, A.; Guirao, J.L.G. A first order automated Lie transform. Int. J. Bifurc. Chaos 2015, 25, 1540026. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Pal, A.K.; Guirao, J.L. Analysis of nominal halo orbits in the Sun–Earth system. Arch. Appl. Mech. 2021, 91, 4751–4763. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Leshchenko, D. Revisiting dynamics of Sun center relative to barycenter of Solar system or Can we move towards stars using Solar self-resulting photo-gravitational force? J. Space Saf. Eng. 2022, 9, 160–164. [Google Scholar]
- Abouelmagd, E.I.; Ansari, A.A.; Ullah, M.S.; García Guirao, J.L. A planar five-body problem in a framework of heterogeneous and mass variation effects. Astron. J. 2020, 160, 216. [Google Scholar] [CrossRef]
- Mia, R.; Prasadu, B.R.; Abouelmagd, E.I. Analysis of stability of non-collinear equilibrium points: Application to Sun–Mars and Proxima Centauri systems. Acta Astronaut. 2023, 204, 199–206. [Google Scholar] [CrossRef]
- Idrisi, M.J.; Ullah, M.S. A Study of Albedo Effects on Libration Points in the Elliptic Restricted Three-Body Problem. J. Astronaut. Sci. 2020, 67, 863–879. [Google Scholar] [CrossRef]
- Younis, S.H.; Ismail, M.N.; Mohamdien, G.H.F.; Ibrahiem, A.H. Effects of Radiation Pressure on the Elliptic Restricted Four-Body Problem. J. Appl. Math. 2021, 2021, 5842193. [Google Scholar] [CrossRef]
- Vincent, A.E.; Perdiou, A.E.; Perdios, E.A. Existence and Stability of Equilibrium Points in the R3BP With Triaxial-Radiating Primaries and an Oblate Massless Body Under the Effect of the Circumbinary Disc. Front. Astron. Space Sci. 2022, 9, 877459. [Google Scholar] [CrossRef]
- Cheng, H.; Gao, F. Periodic Orbits of the Restricted Three-Body Problem Based on the Mass Distribution of Saturn’s Regular Moons. Universe 2022, 8, 63. [Google Scholar] [CrossRef]
- Arif, M.; Ullah, M.S.; Kant, L. Photogravitational magnetic-binary problem with oblateness and belt of material points. New Astron. 2022, 97, 101877. [Google Scholar] [CrossRef]
- Ansari, A.A. Kind of Robe’s restricted problem with heterogeneous irregular primary of N-layers when outer most layer has viscous fluid. New Astron. 2010, 83, 101496. [Google Scholar] [CrossRef]
- Ansari, A.A.; Singh, J.; Alhussain, Z.A.; Belmabrouk, H. Effect of oblateness and viscous force in the Robe’s circular restricted three-body problem. New Astron. 2019, 73, 101280. [Google Scholar] [CrossRef]
- Umar, A.; Hussain, A.A. Motion in the ER3BP with an oblate primary and a triaxial stellar companion. Astrophys. Space Sci. 2016, 361, 344. [Google Scholar] [CrossRef]
- Singh, J.; Umar, A. Effect of Oblateness of an Artificial Satellite on the Orbits Around the Triangular Points of the Earth–Moon System in the Axisymmetric ER3BP. Differ. Equ. Dyn. Syst. 2017, 25, 11–27. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).