Abstract
This study investigates magnetohydrodynamic (MHD) nanofluid flow through a stretching vertical surface influenced by Joule heating, chemical reaction, viscosity dissipation, thermal radiation, and activation energy. Such physical problems have significance in applied mathematics, engineering, and physics, and they are frequently found in symmetrical scenarios. A transformation of the similarity technique is used to reduce the difficulty of the boundary layer equations for nonlinear motion, energy, solute, and nanoparticle concentration. To identify these variations with local similarity, we employ symmetry analysis. The altered equations were solved using the shooting technique with Matlab bvp4c. It was found that raising the Schmidt number increases the impact of temperature and concentration profiles. As the Biot number and thermal radiation rise, the local Nusselt number, local Sherwood number, and skin friction increase as well. The comparative table shows good agreement with the current results.
1. Introduction
The dynamics of nonzero electrically conductive fluids interacting with a magnetic field are the focus of MHD. Applications for MHD include fusion research, MHD accelerators, and power plants. Jabeen et al. [1] examined how chemical reactions and activation energy affect mixed convection fluid flow on a stretching foil. The activation energy parameter was increased along with the fluid concentration. The impact of chemical processes in MHD mixed convection flow across a plate in a porous media was examined by Niranjan et al. [2]. They found that the chemical reaction parameter increases in the case of generation but decreases in the case of destruction. Hayat et al. [3] and Lakshmi Devi et al. [4] investigated over a strecting sheet in an MHD flow with the effects of chemical reaction and radiation in a porus medium near a stagnation point.
Heat transmission has numerous applications in heat transfer rate, which is influenced by thermal conduction in moving liquids; one can determine the heat requirements of processes and equipment. Nanofluids, which contain nanoparticles, greatly improve the properties of basic fluids. These effects of thermal, radiation, Brownian motion, and thermophoresis over a sheet were studied by Asha et al. [5], Kumaran et al. [6], and Kodi et al. [7].
Swain et al. [8] and Ramesh et al. [9] examined the effect of aiding force and chemical reaction in Casson fluid over a stretching sheet and parallel plates. Chemical reactions occur in diffusive processes and are crucial to many chemical engineering activities, including food processing, yield destruction, air and water pollution, and the design of chemical instruments. Heat and mass are transferred through chemical processes. Ahmad et al. [10] and Abbas et al. [11] explored Williamson’s nanoliquid flow on an exponentially porous stretched surface while considering heat transfer. The effects of chemical reaction and thermal radiation from an incompressible flow of Darcy were investigated by Rasool et al. [12] and Sharma et al. [13]. They found that the concentrattion distribution significantly increases as the Soret parameter is raised.
Williamson fluid flow through an exponentially stretched sheet interacts with Brownian motion; thermophoresis diffusion was studied by Asjad et al. [14]. The impact of buoyancy and radiation parameters over a magnetohydrodynamic (MHD) nanofluid flow was studied by Rehman et al. [15]. The MHD boundary layer flow past a flat plate with radiation, joule heating, and viscous dissipation effects were studied by refs. [16,17,18,19]. Chemical industry, physics, and engineering applications of thermal radiation include space technology, nuclear reactors, glass making, polymer processing, etc.
The combined effects of activation energy and chemical reaction on induced MHD fluid flow over a vertical strecthing surface were addressed by Lakshmi et al. [20] and Patel et al. [21]. The MHD stagnation point flow of a Casson fluid across a stretching sheet in the presence of a heat source, joule heating, and chemical reaction with slip boundary conditions were examined by Ramana et al. [22] and Kotnurkar et al. [23]. Khan et al. [24] examined the irreversibility analysis in Reiner–Rivlin nanoliquid hydromagnetic flow caused by a revolving disk that is stretched. Thammanna et al. [25] and Mahanthesh et al. [26] analyzed numerically the three-dimensional flow of a nanofluid along a bidirectional strecthing surface.
Zhang et al. [27] and Khan et al. [28] evaluated convection and joule heating characteristics over a two-dimensional stagnation point flow of a nanoliquid in a curved stretching/shrinking surface. In 1889, Svante Arrhenius used the word activation energy for the first time. He described activation energy as energy that can be recovered for survival from a chemical reaction. It also shows how little energy is needed to initiate a chemical reaction. Applications of activation energy include the use of heat pharmaceuticals and oil-and-water emulsions. Bestman et al. [29] and Ram Reddy et al. [30] examined how the Soret effect affects mixed convection heat and mass transport in a semi-infinite nanofluid over a vertical flat plate. Hussain et al. [31] focused at the movement of gyrotactic swimming microorganisms in the generalized slip flow of MHD nanoliquid past a stretching cylinder. Nield conditions and convective heat transfer are assumed to exist at the boundary. Researchers Qayyum et al. [32] and Kumbhakar et al. [33] focused on how a material’s thermal conductivity could increase heat transfer effectiveness.
Praveen et al. [34] and Hayat et al. [35] statistically analyzed peristaltic mechanism for nanofluid flow through an asymmetric channel. Using nonmagnetic chemotactic bacteria increases the stability of nanofluids. Mustafa et al. [36] carried out numerical investigation on the convective flow of the magnetic nanofluid under the influence of chemical reaction and activation energy. Gurdal et al. [37] and Tekir et al. [38] numerically studied the effect of hybrid nanofluid flow in a dimpled-tube-implemented constant magnetic field to determine the heat transfer rate. Nanoparticles are applied due to their detailed information phenomenon, such as exceptional thermal conductivity, which is crucial in current nanotechnology and electronics, as examined by Akbar et al. [39] and Khan et al. [40].
This article’s main objective is to examine how thermal radiation, viscous dissipation, and joule heating impact the MHD nanofluid flow on a vertical stretching surface. A similarity transformation is used to convert the governing equations into ordinary differential equations. The resulting equations were numerically solved using matlab 4c. In order to investigate how different dimensionless parameters affect velocity, temperature, solute concentration, nanoparticle concentration, skin friction, the local Nusselt number, and the Sherwood number graphs are deployed. The numerical outcomes are compared with Devi et al. [20] and Mustafa et al. [36].
2. Mathematical Formulation
There is steady, incompressible laminar MHD two-dimensional flow of an electrically conducting nanofluid in a stretching sheet, when it is parallel to the ground. In this problem, the combined effects of chemical reaction and activation energy are taken into account. The velocity components u and v are expressed by the x and y directions, respectively, where the y-axis extended along the surface’s normal and the x-axis along the surface (Figure 1).
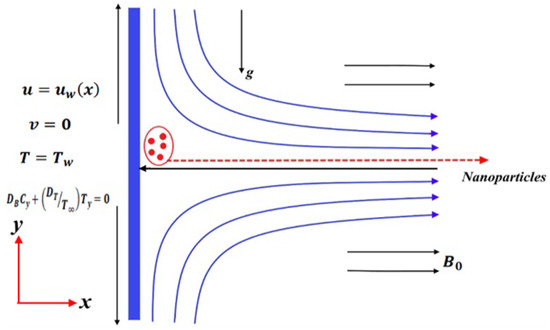
Figure 1.
Schemetic diagram of the problem.
Assume that the sheet surface is stretched vertically by the linear velocity , with . Let the surface temperature be higher than the fluid temperature at the ambient condition. These are the governing equations
where and
Subject to the boundary conditions are:
The radiative heat flux is given by
Using Taylor’s series expansion about and ignoring higher-order terms, i.e., , then:
.
Finally, we obtain
The Stream function is defined as
Equations (8)–(10) are used to convert the governing Equations (1)–(5) into ordinary differential equations.
The corresponding boundary conditions, Equation (6), are
The following dimensionless quantities are now introduced.
The local Nusselt number, Sherwood number, and the local nanoparticle Sherwood number are few physical quantities that describe skin friction.
where
In Equation (9), the similarity variable and nondimensional functions are used to produce
3. Numerical Method
For the purpose of solving nonlinear governing ordinary differential Equations (11)–(14) with boundary conditions (15), the shooting technique is combined with MATLAB bvp4c. First, we converted the nonlinear governing ordinary differential equations into ordinary differential equations. For this, we take into account;
Equations (11)–(15) are used to convert the nonlinear governing ODE into first-order differential Equation (19).
Subject to the boundary conditions
In order to examine the variation of variables on succeeding profiles, the Matlab bvp4c software uses these simplified equations.
4. Results and Discussion
This article examines how the nanofluid flow of MHD on a vertical stretching surface is impacted by thermal radiation, viscous dissipation, and joule heating. The governing equations are solved through the matlab bvp4c by applying boundary conditions. Graphs are used to analyze the effects of multiple dimensionless parameters on velocity, temperature, solute concentration, nanoparticle concentration, skin friction, local Nusselt, and Sherwood numbers.
The current numerical results are compared against the Devi [20] and Mustafa [36] results presented in Table 1. Tabulated results show the impact of the mixed convection parameter (, the local Nusselt number (), and the thermophoresis parameter (Nt). It can be observed that the Prandtl number increases as the Nusselt number increases. The thermophoresis parameter increases as the local Nusselt number decreases.

Table 1.
Comparison of wall slope of temperature values with Mustafa et al. [36] and Devi et al. [20] for M = 0.5 = Nr, Sc = 5 and = 1.
The velocity differences between various magnetic field values are shown in Figure 2. It was found that a decrease in the flow velocity field and an increase in magnetic characteristics are correlated. The magnetic field of the Lorentz force, which is increasing in magnitude, opposes the flow of fluid. Figure 3 depicts the effect of a magnetic field on temperature profiles. The establishment of a magnetic field on the temperature profile is shown in Figure 3. The Lorentz force and this magnetic field are related; the temperature is increased because the Lorentz force affects this most expensive magnet field’s parameter.
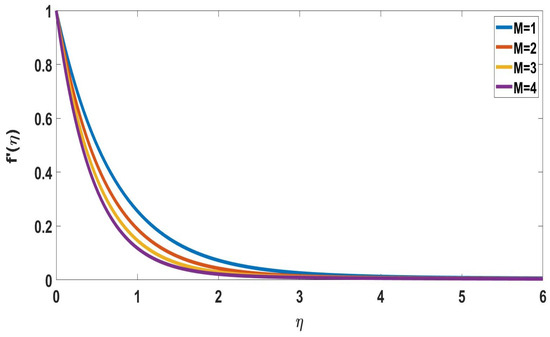
Figure 2.
Profile of velocity for different M, when E = 2, Nb = Nt = 0.5, Sc = 0.22, = Pr = Nc = Rd = Nr = Bi = 0.1 = n = Ec.
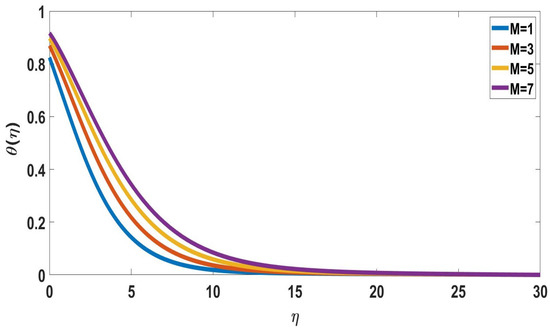
Figure 3.
Profile of temperature for different M, when = 5, Nc = Pr = Nb = Nt = Sc = Nr = Rd = n = 0.1, Bi = 1, = 0.1, E = 2, Ec = 0.1.
Figure 4 depicts the solute concentration profile for various magnetic parameter values. It indicates the solute concentration increases and the boundary layer thickness gradually decreases as the magnetic parameter values increase. In Figure 5, the temperature profile variations of the Eckert number are illustrated. It was discovered that the temperature profile is important for magnifying Eckert number values. Because friction generates more heat, the temperature profile rises as the Eckert number increases. The effect of the Eckert number on the nanoparticle concentration profile is depicted in Figure 6. The concentration of the fluid increases as the Eckert number increases, and the thickness of the boundary layer gradually decreases.
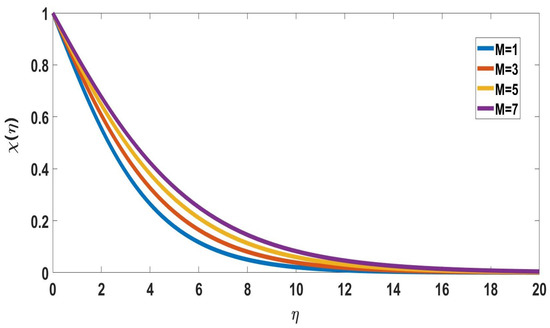
Figure 4.
Profile of solute concentration for different M, when = 5, Nc = Pr = Nb = Nt = Sc = Nr = Rd = n = 0.1, Bi = 1, = 0.1, E = 2, Ec = 0.1.
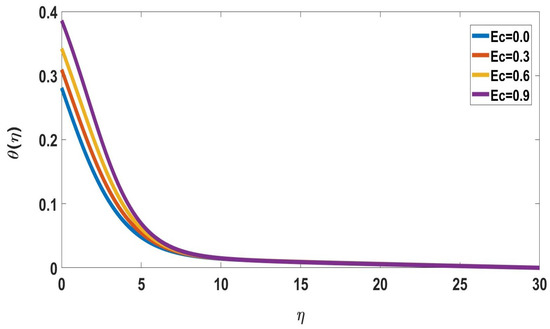
Figure 5.
Profile of temperature for different Ec, when = 5, Nc = 0.2, M = Pr = 0.1, Nb = Nt = 0.5, Sc = 1, Nr = 0.1, Rd = 0.5, Bi = 0.1 = , E = 2.
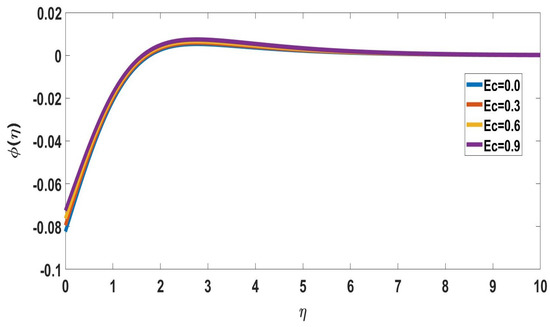
Figure 6.
Profile of nanoparticle concentration for different Ec, when = 5, Nc = 0.2, M = 0.1 = Pr, Nb = Nt = 0.5, Sc = 1, Rd = 0.5, n = Bi = Nr = = 0.1, E = 2.
Figure 7 shows the solute concentration profile with various Eckert number values. It reveals that while the thickness of the boundary layer steadily decreases, the solute concentration increases with the Eckert number. The effects of Schmidt number on concentration profiles are displayed in Figure 8 and Figure 9. The profile of nanoparticle concentration changes in response to a rise in the Schmidt number. It is shown that the Schmidt number rises as the Solute concentration drops.
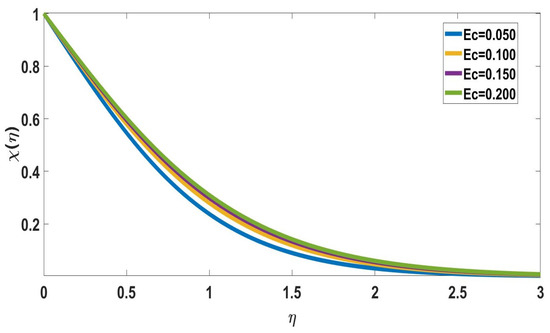
Figure 7.
Profile of solute concentration for different Ec, when = 5, Nc = 0.2, Pr = 7, Nb = Nt = 0.5, Sc = 1, Rd = 0.5, M = Nr = n = Bi = = 0.1, E = 2.
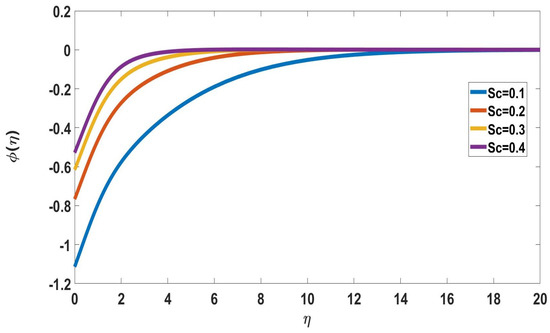
Figure 8.
Profile of nanoparticle concentration for different Sc, when Nr = M = 0.5, Rd = 0.3, E = 2, = Pr = n = Bi = 1,Nc = Nb = Nt = 0.1 = Ec, = 1.
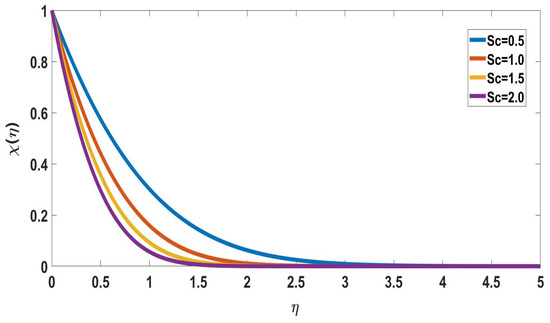
Figure 9.
Profile of solute concentration for different Sc, when Nc = 0.1 = Nb = Nt = Pr, M = 0.5, Rd = 0.3, = 5, Nr = 0.5, n = 1 = Bi = = E, Ec = 0.1.
The behavior of activation energy (E) on concentration profiles is depicted in Figure 10 and Figure 11. In Figure 10, the solute concentration increased while the nanoparticle concentration profile decreased with activation energy. The fluid velocity decreases as the concentration of solutes increases. Therefore, higher activation energy values diminish the fluid velocity. Figure 12 and Figure 13 exhibit radiation (Rd) behavior on concentration profiles. The radiation-induced elevation in solute concentration is shown in Figure 12. The transport rate increased upon increasing the thermal radiation. In Figure 13, the nanoparticle concentration profile decreases upon increasing the radiation parameter.
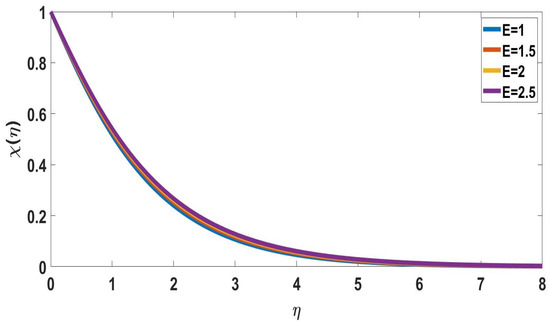
Figure 10.
Profile of solute concentration for different E, when Nc = 0.2, Pr = M = Sc = 1, Rd = n = Nb = Nt = 0.5, = Nr = 0.1 = = Bi = Ec = 0.1.
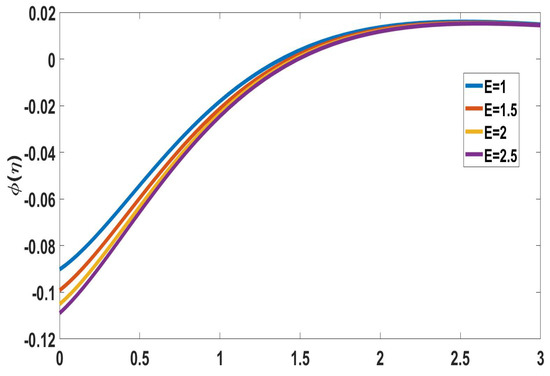
Figure 11.
Profile of nanoparticle concentration for different E, when Nc = 0.2, Pr = M = Sc = 1, = Nr = 0.1, Rd = Nb = Nt = n = 0.5, = Bi = Ec = 1.
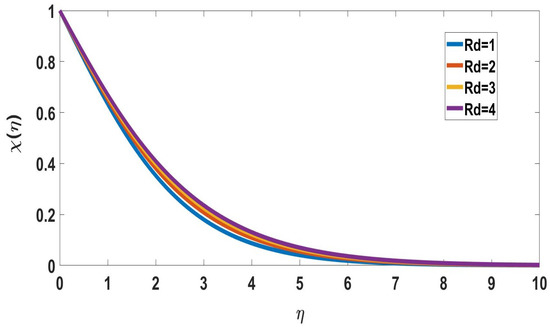
Figure 12.
Profile of solute concentration for different Rd, when Nc = Pr = Nb = Nt = Nr = n = Ec = 0.1, E = 2, = 5, M = 0.01, = 0.1, Bi = 1, Sc = 0.22.
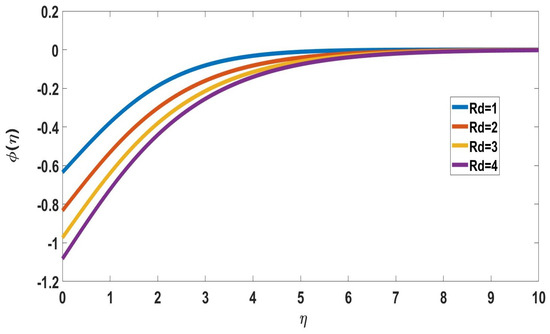
Figure 13.
Profile of nanoparticle concentration for different Rd, when Nc = 0.1 = Pr = Nb = Nt = Nr = n, Sc = 0.22, M = 0.01, E = 2, = 5, = Ec = 0.1, Bi = 1.
The effects of Prandtl number on concentration profiles are depicted in Figure 14 and Figure 15. It represents that as the Pandtl number increases, both concentration profiles of solute and nanoparticle concentrations decrease. Figure 16 and Figure 17 depict the effects of mixed convection parameters on concentration profiles. The mixed convection parameter is used to reduce the concentration of the boundary layer.
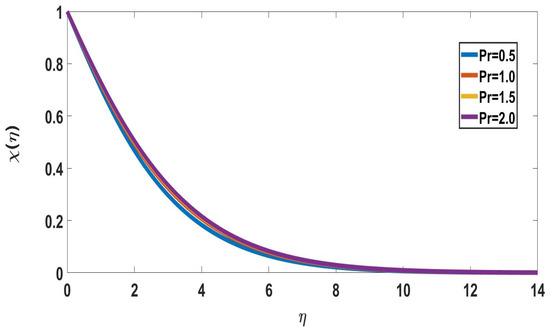
Figure 14.
Profile of solute concentration for different Pr values, when = 5, Nc = 0.2, M = 1, Nb = Nt = 0.5, Sc = 0.22, Rd = 0.5, Bi = 1, = Ec = 0.1 = n = Nr, E = 2.
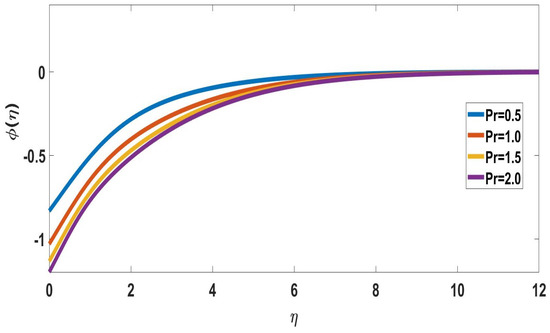
Figure 15.
Profile of nanoparticle concentration for different Pr, when = 5, Nc = 0.2, M = 1, Nb = Nt = n = 0.5, Sc = 0.22, Rd = 0.5, Bi = 1, n = Nr = = 0.1 = Ec, E = 2.
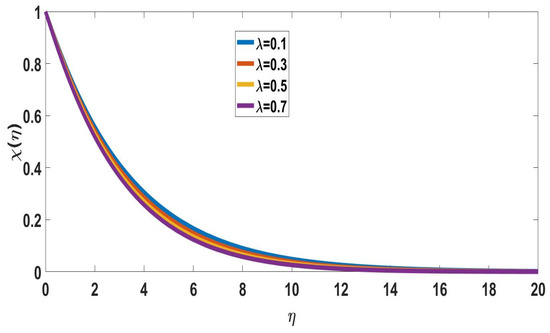
Figure 16.
Profile of solute concentration for different , when Nc = 0.1, M = 4, Pr = 7, b = Nt = n = 0.1, Sc = 0.5, Rd = Nr = = 0.1, E = 1, Ec = 0.2.
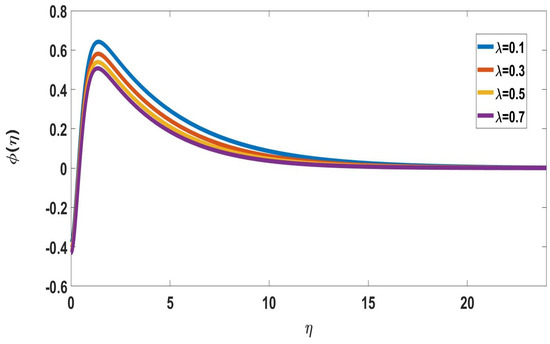
Figure 17.
Profile of nanoparticle concentration for different , when Nc = 0.1, M = 4, Pr = 7, Rd = 0.3, Nb = Nt = 0.5, Sc = 0.5, Nr = 0.1 = Rd = n = Bi = E = 1, Ec = 0.2.
The skin friction increases upon increasing the Eckert and Biot numbers, but the boundary layer thickness decreases, as shown in Figure 18. As the Eckert number increases, the local Sherwood number increases, but the Biot number decreases, as shown in Figure 19. As the Eckert and Biot numbers increase, the local nanoparticle Sherwood number and layer thickness increase, as shown in Figure 20. Figure 21 depicts skin friction with thermal radiation and Biot number. Vertical surface friction increases with Biot number, but boundary layer thickness decreases as radiation decreases. Figure 22 shows the increase in radiation and Biot number, as well as the local Nusselt number and boundary layer thickness. Figure 23 illustrates the local Sherwood number increases, and the thermal radiation parameter increases as the Biot number increases. Figure 24 shows the Sherwood number of local nanoparticles decreases as the biot number and the thermal radiation parameter increase.
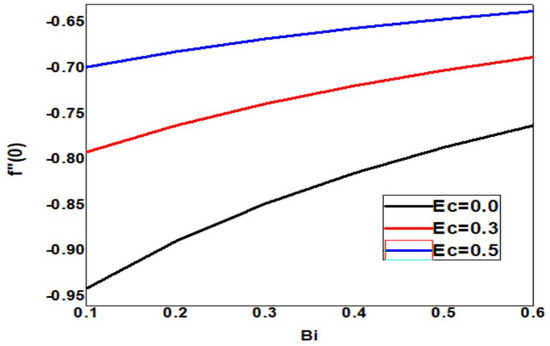
Figure 18.
Skin friction for various values of Bi and Ec when = 1, Nc = 0.1, Pr = 1, Nb = 0.1 = Nt, Sc = 0.4, Rd = 0.3, n = 1, = 01, E = 02, M = Nr = Ec = 0.5.
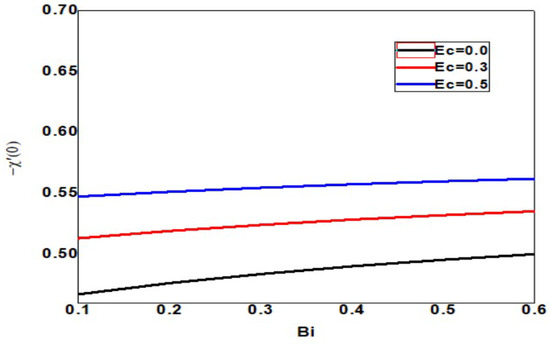
Figure 19.
Local Sherwood number for different values of Bi and Ec when = 1, Nc = 0.1, Pr = 1, Nb = 0.1 = Nt, Sc = 0.4, Rd = 0.3, n = 1, = 01, E = 02, M = Nr = Ec = 0.5.
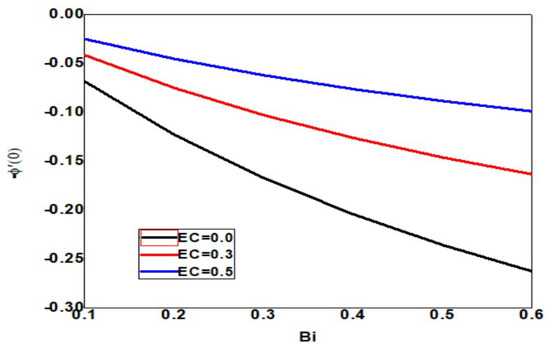
Figure 20.
Local nanoparticle Sherwood number for different values of Bi and Ec when = 1, Nc = 0.1, Pr = 1, Nb = 0.1 = Nt, Sc = 0.4, Rd = 0.3, n = 1, = 01, E = 02, M = Nr = 0.5.
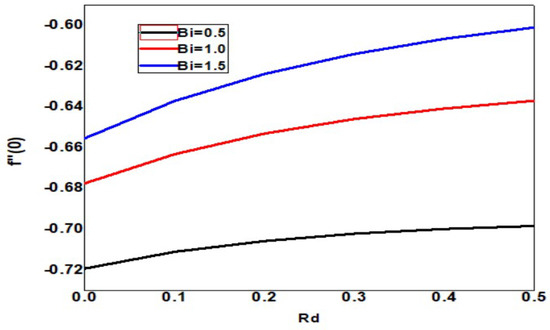
Figure 21.
Skin friction for different values of Bi and Rd when = Pr = n = 1, Nb = 0.1 = Nc = Nt, Sc = 0.4, = 01, E = 02, M = Nr = 0.5, Ec = 0.3.
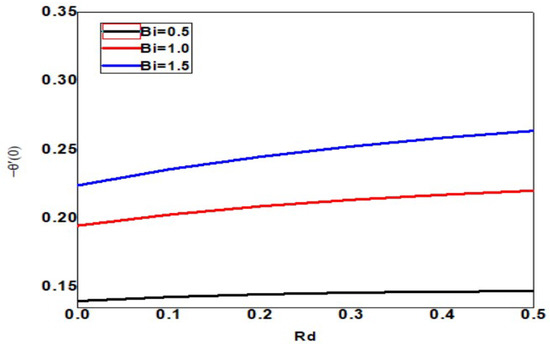
Figure 22.
Local Nusselt number for different values of Bi and Rd when = Pr = n = 1, Sc = 0.4, Nb = 0.1 = Nc = Nt, = 01, E = 02, M = Nr = 0.5, Ec = 0.3.
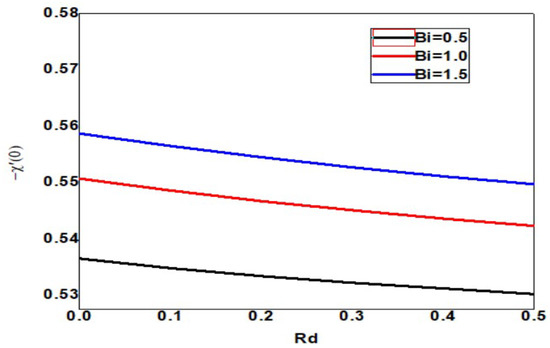
Figure 23.
Local Sherwood number for various values of Bi and Rd when = Pr = n = 1, Nb = 0.1 = Nc = Nt, Sc = 0.4, = 01, E = 02, M = Nr = 0.5, Ec = 0.3.
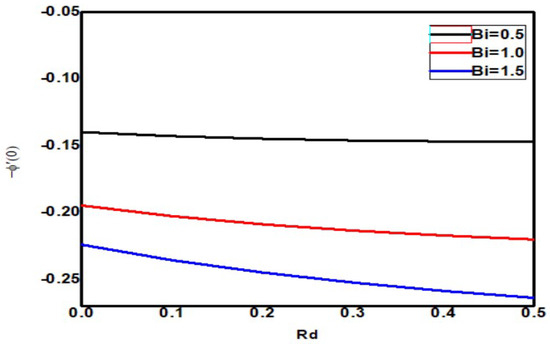
Figure 24.
Local nanoparticle Sherwood number for different values of Bi and Rd when = Pr = n = 1, Nb = 0.1 = Nc = Nt, Sc = 0.4, = 01, E = 02, M = Nr = 0.5, Ec = 0.3.
The skin friction decreases as the Schmidt number and dimensionless reaction rate increase, but the layer thickness decreases as the dimensionless reaction rate decreases, as shown in Figure 25. The local Nusselt number increases as Schmidt number and dimensionless reaction rate increase but decreases as dimensionless reaction rate and boundary layer thickness increase (See Figure 26). In Figure 27, the Schmidt number and dimensionless reaction rate values, as well as the thickness of the boundary layer, increase as the value of the local Sherwood number increases. Figure 28 clearly shows that increasing the local Sherwood number for varying values of Schmidt number and dimensionless reaction rate increases the layer thickness.
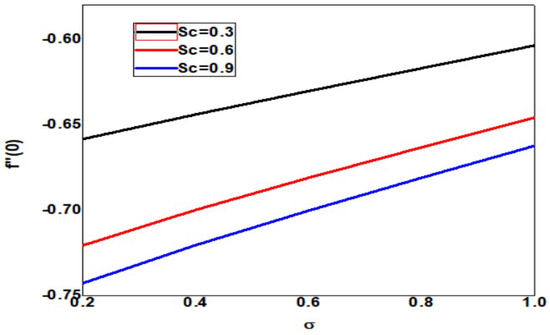
Figure 25.
Skin friction for different values of Sc and when = Pr = n = 1, Nb = 0.1 = Nc = Nt, = 01, Rd = 0.2, Bi = 1.5, E = 02, M = Nr = 0.5, Ec = 0.3.
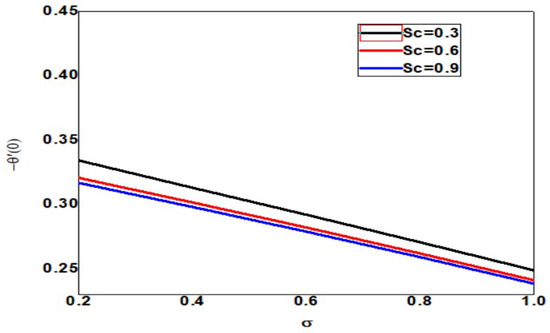
Figure 26.
Local Nusselt number for different values of Sc and when = Pr = n = 1, = 01, Nb = 0.1 = Nc = Nt, Rd = 0.2, Bi = 1.5, E = 02, M = Nr = 0.5, Ec = 0.3.
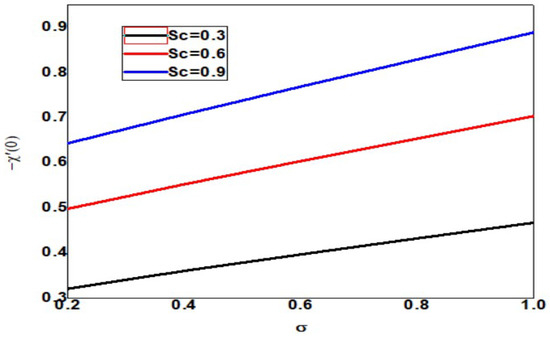
Figure 27.
Local Sherwood number for different values of Sc and when = Pr = n = 1, = 01, Nb = 0.1 = Nc = Nt, Rd = 0.2, Bi = 1.5, E = 02, M = Nr = 0.5, Ec = 0.3.
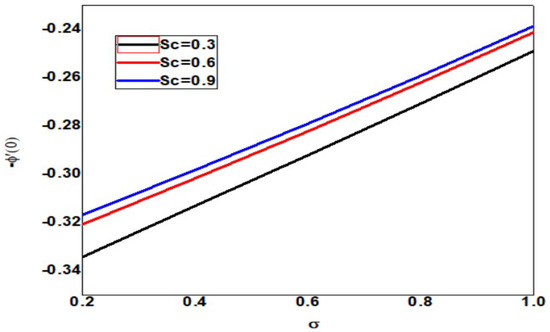
Figure 28.
Local nanoparticle Sherwood number for different values of Sc and when = Pr = n = 1, Nb = 0.1 = Nc = Nt, = 01, Rd = 0.2, Bi = 1.5, E = 02, M = Nr = 0.5, Ec = 0.3.
5. Conclusions
The combined effects of joule heating, viscous dissipation, thermal radiation, activation energy, and chemical reaction of magnetohydrodynamic nanofluid flow over a stretching vertical surface were presented. The findings of our investigation are as follows:
- As the magnetic parameter increases, the velocity profile over the vertical surface decreases.
- The temperature of the fluid rises as the magnetic parameters and Eckert number increases.
- The magnetic parameter, Eckert number, activation energy, Schmidt number, thermal radiation, and Prandtl number all rise as the solute concentration profile rises.
- When the Schmidt number, activation energy, radiation parameter, Prandtl number, and Eckert number increases, the fluid’s nanoparticle concentration decreases.
- Skin friction, local Sherwood number increase the Eckert number values as the Biot number increases.
- As Bi and Rd are increased, skin friction and the local Nusselt number increased.
- Skin friction and Nusselt number decrease upon increasing , Sc; nanoparticle Sherwood number increases as Sc increases.
Author Contributions
S.J. investigation; data collection and visualization. H.N. contributed by reading, write-up reviewing, editing, overviewing and supervising the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable for to this article.
Acknowledgments
The authors extend their appreciation to their leadership of the Scientific Research at VIT deemed University in this section.
Conflicts of Interest
The authors declared no complicit of interest.
Nomenclature
| Strength of magnetic field (kgsm) | |
| C | Concentration |
| Local Reynolds number | |
| Schmidt number | |
| Thermal radiation parameter | |
| T | Temperature(K) |
| Radiative heat flux | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient (ms) | |
| Prandtl number of base fluid | |
| E | Nondimensional activation energy |
| n | Fitted rate constant |
| Activation energy | |
| Dimensionless velocity | |
| Thermophoresis parameter | |
| Local Grashof number | |
| Buoyancy ratio parameter | |
| g | Gravitational acceleration (ms) |
| K | Boltzmann constant |
| Regular buoyancy parameter | |
| K’ | Mean absorption coefficient |
| k | Thermal conductivity (mkgsK) |
| Reaction rate | |
| M | Magnetic field parameter |
| Brownian diffusion parameter |
Greek Symbols
| Mixed convection parameter | |
| Dimensionless reaction rate | |
| Dimensionless solute concentration | |
| Temperature difference parameter | |
| Dimensionless temperature | |
| Kinematic viscosity (ms) | |
| Effective heat capacity of the nanoparticle material | |
| Heat capacity of the base fluid | |
| Electrical conductivity | |
| T | Ratio of the effective heat capacity of the fluid and the heat capacity of |
| the nanoparticle material | |
| Stefan–Boltzmann constant (WmK) | |
| Thermal diffusivity of the base fluid (ms) | |
| Density of the fluid (kgm) | |
| Coefficient of thermal expansion (K) | |
| Nanoparticle density | |
| Dimensionless nanoparticle concentration |
Subscripts
| w | Condition at a wall |
| ∞ | Condition at free stream |
References
- Jabeen, S.; Hayat, T.; Alsaedi, A.; Alhodaly, M.S. Consequences of activation energy and chemical reaction in radiative flow of tangent hyperbolic nanoliquid. Sci. Iran. 2019, 26, 3928–3937. [Google Scholar] [CrossRef]
- Niranjan, H.; Sivasankaran, S.; Bhuvaneswari, M. Chemical reaction, Soret and Dufour effects on MHD mixed convection stagnation point flow with radiation and slip condition. Sci. Iran. 2017, 24, 698–706. [Google Scholar] [CrossRef]
- Hayat, T.; Ullah, I.; Alsaedi, A.; Asghar, S. Flow of magneto Williamson nanoliquid towards stretching sheet with variable thickness and double stratification. Radiat. Phys. Chem. 2018, 152, 151–157. [Google Scholar] [CrossRef]
- Lakshmi Devi, G.; Niranjan, H. The Novelty of Thermo-Diffusion and Diffusion-Thermo, Slip, Temperature and Concentration Boundary Conditions on Magneto–Chemically Reactive Fluid Flow Past a Vertical Plate with Radiation. Symmetry 2022, 14, 1496. [Google Scholar] [CrossRef]
- Asha, S.K.; Sunitha, G. Thermal radiation and Hall effects on peristaltic blood flow with double diffusion in the presence of nanoparticles. Case Stud. Therm. Eng. 2020, 17, 100560. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N.; Ali, M.E. Computational analysis of magnetohydrodynamic Casson and Maxwell flows over a stretching sheet with cross diffusion. Results Phys. 2017, 7, 147–155. [Google Scholar] [CrossRef]
- Kodi, R.; Mopuri, O. Unsteady MHD oscillatory Casson fluid flow past an inclined vertical porous plate in the presence of chemical reaction with heat absorption and Soret effects. Heat Transf. 2022, 51, 733–752. [Google Scholar] [CrossRef]
- Swain, B.K.; Parida, B.C.; Kar, S.; Senapati, N. Viscous dissipation and joule heating effect on MHD flow and heat transfer past a stretching sheet embedded in a porous medium. Heliyon 2020, 6, e05338. [Google Scholar] [CrossRef]
- Ramesh, K.; Riaz, A.; Dar, Z.A. Simultaneous effects of MHD and Joule heating on the fundamental flows of a Casson liquid with slip boundaries. Propuls. Power Res. 2021, 10, 118–129. [Google Scholar] [CrossRef]
- Ahmed, K.; Akbar, T. Numerical investigation of magnetohydrodynamics Williamson nanofluid flow over an exponentially stretching surface. Adv. Mech. Eng. 2021, 13, 16878140211019875. [Google Scholar] [CrossRef]
- Abbas, A.; Shafqat, R.; Jeelani, M.B.; Alharthi, N.H. Significance of Chemical Reaction and Lorentz Force on Third-Grade Fluid Flow and Heat Transfer with Darcy–Forchheimer Law over an Inclined Exponentially Stretching Sheet Embedded in a Porous Medium. Symmetry 2022, 14, 779. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Baleanu, D. Consequences of Soret–Dufour effects, thermal radiation, and binary chemical reaction on Darcy Forchheimer flow of nanofluids. Symmetry 2020, 12, 1421. [Google Scholar] [CrossRef]
- Sharma, B.K.; Gandhi, R.; Bhatti, M.M. Entropy analysis of thermally radiating MHD slip flow of hybrid nanoparticles (Au-Al2O3/Blood) through a tapered multi-stenosed artery. Chem. Phys. Lett. 2022, 790, 139348. [Google Scholar] [CrossRef]
- Asjad, M.I.; Zahid, M.; Inc, M.; Baleanu, D.; Almohsen, B. Impact of activation energy and MHD on Williamson fluid flow in the presence of bioconvection. Alex. Eng. J. 2022, 61, 8715–8727. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Naseem, T.; Fatima, U.; Munir, M.; Shahzad, A.; Kausar, N.; Nisar, K.S.; Saleel, C.A.; Abbas, M. Joule heating and viscous dissipation effects in hydromagnetized boundary layer flow with variable temperature. Case Stud. Therm. Eng. 2022, 35, 102083. [Google Scholar] [CrossRef]
- Biswas, R.; Hossain, M.S.; Islam, R.; Ahmmed, S.F.; Mishra, S.R.; Afikuzzaman, M. Computational treatment of MHD Maxwell nanofluid flow across a stretching sheet considering higher-order chemical reaction and thermal radiation. J. Comput. Math. Data Sci. 2022, 4, 100048. [Google Scholar] [CrossRef]
- Bejawada, S.G.; Reddy, Y.D.; Jamshed, W.; Nisar, K.S.; Alharbi, A.N.; Chouikh, R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alex. Eng. J. 2022, 61, 8207–8220. [Google Scholar] [CrossRef]
- Gopal, D.; Jagadha, S.; Sreehari, P.; Kishan, N.; Mahendar, D. A numerical study of viscous dissipation with first order chemical reaction and ohmic effects on MHD nanofluid flow through an exponential stretching sheet. Mater. Today Proc. 2022, 59, 1028–1033. [Google Scholar] [CrossRef]
- Lakshmi Devi, G.; Niranjan, H.; Sivasankaran, S. Effects of chemical reactions, radiation, and activation energy on MHD buoyancy induced nano fluidflow past a vertical surface. Sci. Iran. 2022, 29, 90–100. [Google Scholar]
- Patel, H.R.; Singh, R. Thermophoresis, Brownian motion and non-linear thermal radiation effects on mixed convection MHD micropolar fluid flow due to nonlinear stretched sheet in porous medium with viscous dissipation, joule heating and convective boundary condition. Int. Commun. Heat Mass Transf. 2019, 107, 68–92. [Google Scholar] [CrossRef]
- Ramana, R.M.; Raju, K.V.; Kumar, J.G. Multiple slips and heat source effects on MHD stagnation point flow of casson fluid over a stretching sheet in the presence of chemical reaction. Mater. Today Proc. 2022, 49, 2306–2315. [Google Scholar] [CrossRef]
- Kotnurkar, A.S.; Talawar, V.T. Impact of electroosmosis and joule heating effects on peristaltic transport with thermal radiation of hyperbolic tangent fluid through a porous media in an endoscope. Partial. Differ. Equations Appl. Math. 2022, 5, 100340. [Google Scholar] [CrossRef]
- Khan, S.A.; Hayat, T.; Alsaedi, A. Irreversibility analysis in hydromagnetic Reiner-Rivlin nanofluid with quartic autocatalytic chemical reactions. Int. Commun. Heat Mass Transf. 2022, 130, 105797. [Google Scholar] [CrossRef]
- Thammanna, G.T.; Gireesha, B.J.; Mahanthesh, B. Partial slip and Joule heating on magnetohydrodynamic radiated flow of nanoliquid with dissipation and convective condition. Results Phys. 2017, 7, 2728–2735. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Gorla, R.S. Unsteady three-dimensional MHD flow of a nano Eyring-Powell fluid past a convectively heated stretching sheet in the presence of thermal radiation, viscous dissipation and Joule heating. J. Assoc. Arab. Univ. Basic Appl. Sci. 2017, 23, 75–84. [Google Scholar] [CrossRef]
- Zhang, X.H.; Abidi, A.; Ahmed, A.E.; Khan, M.R.; El-Shorbagy, M.A.; Shutaywi, M.; Issakhov, A.; Galal, A.M. MHD stagnation point flow of nanofluid over a curved stretching/shrinking surface subject to the influence of Joule heating and convective condition. Case Stud. Therm. Eng. 2021, 26, 101184. [Google Scholar] [CrossRef]
- Khan, W.A.; Makinde, O.D.; Khan, Z.H. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. Int. J. Heat Mass Transf. 2014, 74, 285–291. [Google Scholar] [CrossRef]
- Bestman, A.R. Natural convection boundary layer with suction and mass transfer in a porous medium. Int. J. Energy Res. 1990, 14, 389–396. [Google Scholar] [CrossRef]
- RamReddy, C.; Murthy, P.V.; Chamkha, A.J.; Rashad, A.M. Soret effect on mixed convection flow in a nanofluid under convective boundary condition. Int. J. Heat Mass Transf. 2013, 64, 384–392. [Google Scholar] [CrossRef]
- Hussain, A.; Malik, M.Y. MHD nanofluid flow over stretching cylinder with convective boundary conditions and Nield conditions in the presence of gyrotactic swimming microorganism: A biomathematical model. Int. Commun. Heat Mass Transf. 2021, 126, 105425. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Kanwal, M.; Alsaedi, A.; Khan, M.I. Transportation of entropy optimization in radiated chemically dissipative flow of Prandtl–Eyring nanofluid with activation energy. Comput. Methods Programs Biomed. 2020, 184, 105130. [Google Scholar] [CrossRef]
- Kumbhakar, B.; Nandi, S.; Chamkha, A.J. Unsteady hybrid nanofluid flow over a convectively heated cylinder with inclined magnetic field and viscous dissipation: A multiple regression analysis. Chin. J. Phys. 2022, 79, 38–56. [Google Scholar] [CrossRef]
- Parveen, N.; Awais, M.; Awan, S.E.; Shah, S.A.; Yuan, A.; Nawaz, M.; Akhtar, R.; Malik, M.Y. Thermophysical properties of chemotactic microorganisms in bio-convective peristaltic rheology of nano-liquid with slippage, Joule heating and viscous dissipation. Case Stud. Therm. Eng. 2021, 27, 101285. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Melting heat transfer in the MHD flow of Cu–water nanofluid with viscous dissipation and Joule heating. Adv. Powder Technol. 2016, 27, 1301–1308. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Buoyancy effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy. Int. J. Heat Mass Transf. 2017, 108, 1340–1346. [Google Scholar] [CrossRef]
- Gürdal, M.; Pazarlıoğlu, H.K.; Tekir, M.; Arslan, K.; Gedik, E. Numerical investigation on turbulent flow and heat transfer characteristics of ferro-nanofluid flowing in dimpled tube under magnetic field effect. Appl. Therm. Eng. 2022, 200, 117655. [Google Scholar] [CrossRef]
- Tekir, M.; Gedik, E.; Arslan, K.; Pazarlıoğlu, H.K.; Aksu, B.; Taskesen, E. Hydrothermal behavior of hybrid magnetite nanofluid flowing in a pipe under bi-directional magnetic field with different wave types. Therm. Sci. Eng. Progress. 2022, 34, 101399. [Google Scholar] [CrossRef]
- Akbar, A.A.; Ahammad, N.A.; Awan, A.U.; Hussein, A.K.; Gamaoun, F.; Tag-ElDin, E.M.; Ali, B. Insight into the role of nanoparticles shape factors and diameter on the dynamics of rotating water-based fluid. Nanomaterials 2022, 12, 2801. [Google Scholar] [CrossRef]
- Khan, I.; Saeed, K.; Khan, I. Nanoparticles: Properties, applications and toxicities. Arab. J. Chem. 2019, 12, 908–931. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).