Abstract
The role of experts in decision-making is highly significant. The soft expert set (SES) is yet another milestone, as it plays a vital role in generalizing soft set theory. Soft expert set is creative and original because it involves more than one expert. This served as a driving force behind the creation of the current work. The present paper generalizes the framework of soft experts set to the inverse soft setting, namely the inverse soft expert set (ISES). Some captivating characteristic features of the soft expert set (SES) are established. On the inverse soft expert sets, numerous striking characteristics of symmetric matrices are presented. The ground-breaking idea of symmetric matrices on inverse soft expert sets (SMISES) is introduced. A MCDM problem for SMISES is described with an algorithm and interesting comparative analysis.
1. Introduction
Situations of uncertainty are dealt with by several researchers in an excellent manner. Fuzzy sets (Zadeh [1]), rough sets (Pawlak [2]) and the same kinds of math tools have found widespread use in many domains because of the need to work with uncertain data. In 1999, Molodtsov presented a new method, namely soft set theory, and used it to exemplify the fact that all soft sets are fuzzy sets.
Researchers’ standard practice is to evaluate both the importance of a newly proposed uncertainty theory as well as the characteristics of the theory. Molodtsov [3] is one such researcher who listed out the difficulties that prevailed while implementing the existing uncertainty theories, including rough sets, and gave an alternative, namely soft set theory. It is a function between the power set of the universe set and the parameter set. Soft set theory includes uncertainty in terms of its parameters and is particularly novel for being the first theory to address uncertainty through parameter. Maji and Roy [4] established the AHP technique for applying soft set theory to decision-making scenarios. Çağman [5] utilized soft sets to develop the novel concept of soft matrices. Vijayabalaji et al. [6,7] created and applied multiple types of soft sets for multi-criteria decision-making (MCDM) situations.
Different kinds of soft matrices were established by Mitra Basu et al. [8] and they provided some operations with them. They also introduced the idea of a choice matrix, which depicts the decision-maker’s selection criteria. In order to handle soft set-based decision-making problems, they ultimately suggested a new technique employing various soft matrix operations and emphasising choice matrices. This novel strategy’s distinctive benefit is that it can quickly and simply resolve any soft set-based decision-making problem that incorporates a significant number of decision-makers and, in comparison to the method for performing computations, is further simplified.
Sun et al. [9] presented the parallel fuzzy relationship matrix (FRM) of the MIMO fuzzy system and they constructed an algebraic description of MIMO fuzzy system. According to Feng et al. [10], coupled fuzzy controls, such as coupled fuzzification and coupled defuzzification, are made using their research on the fuzzy relation of multiple fuzzy technique. Additionally, they use coupled fuzzy controls designed using group-to-group fuzzy inference. New operations on the modified soft rough sets were proposed by Zhan et al. [11], and these researchers also looked into various characterizations of soft rough hemirings. They ended up settling on a method for solving decision-making issues owing to soft rough sets. Alkhazaleh and Salleh [12] opened up a brand new avenue of through the implementation of soft expert sets (SESs). It has a distinct benefit over earlier models in that they can readily take into account several expert viewpoints. Those authors looked at the implementation of SESs in decision-making. Then, in 2014, Alkhazaleh and Salleh [13] created fuzzy SESs, a hybrid structure. The development of SESs has led to the presentation of numerous innovative hybrid models by various researchers. One of the drawbacks of using soft sets is that it deals with only one expert [12]. A single expert finding solutions to problems requiring several contexts for making decisions is certainly difficult. By using soft expert sets, they were able to address this problem. This mapping applies from the sum of three sets to the universe set’s power set. The three sets are the expert set, the parameter set and the expert opinion (especially the two opinions 0 and 1). Experts are essential in a variety of MCDM contexts.
Several experts offered their opinions on a range of sporting events happening all over the world. There are many professional perspectives that are quite astonishing, even in medical diagnosis. Recent developments in soft expert sets across a range of areas are documented in the papers on fuzzy soft expert sets and m-polar fuzzy soft expert sets [14].
The soft expert set is capable of handling MCGDM circumstances in an effortless manner. The examples of the extension of soft expertise can be viewed in [12]. An inverse fuzzy soft set alongside it’s own characteristics, operations and features was introduced by Khalil et al. [15]. An algorithm is developed and it is used to apply an inverse fuzzy soft set to a problem involving decision-making. We use soft expert sets to broaden the idea in inverse soft expert setting based on the aforementioned concepts. The framework of SES is being extended to ISES. The definition of symmetric matrices on the inverse soft expert set (SMISES) yields fascinating results. The remainder of this article’s sections are outlined as follows. The idea of symmetric matrices on inverse soft expert sets are proposed in Section 3 along with pertinent illustrations and interesting findings. An SMSES algorithm is exemplified in Section 4. Further, Section 5 includes two comparative analyses with extensive research.
2. Preliminaries
We discuss several well-known concepts that have significant influenced the development of this work.
Definition 1
([3]). For a given universe set U with parameter Υ, a soft set is mapping from S to , where .
Definition 2
([12]). The mapping from set to the power set of set U constitutes a soft expert set, where , , Υ is a set of parameters, is a set of experts and Θ is the set of opinions.
Definition 3
([15]). Let be the set of all subsets of parameter set Υ. A pair is called an inverse soft set over Υ, where F is a mapping given by .
Definition 4
([7]). Given two parameter-based soft seta (PBSS), namely and , their distance is defined as
.
3. Symmetric Matrices on Inverse Soft Expert Sets
Accordingly, we emphasise that the concept of an ISES is analogous to the inverse soft set.
Definition 5.
Consider a mapping , where U denotes the universe set and Υ denotes the set of parameters. Then the pair is defined as inverse soft expert sets, where , , Υ is a set of parameters, is a set of experts and Θ is the set of opinions.
Example 1.
Reviewing data in medical diagnosis can be crucial for collaborative decision-making with the patient at the centre of the conversation. This example demonstrates the value of utilizing specificity when diagnosing patients and billing visit encounters via Practice Fusion, which enables us to generate and examine such data to discover much about patients’ requirements, to achieve optimal high quality care, and to deliver quality measures for improvement that are crucial to patients.
Let , be the list of hospitals, and the parameters , -treatment cost, -recovery time and -quality of the service provided to the patients. The evaluators (experts) of the project are , and the opinion . Then the pair is defined as inverse soft expert sets.
The ISES data have been tabulated and are presented in the following Table 1.

Table 1.
Inverse soft expert sets.
Definition 6.
The collection of all inverse soft expert sets (ISES) agreeing with expert opinion ‘1’ from the ISES is said to agree with the inverse soft expert sets (AISES); likewise, the collection of all ISES agreeing with expert opinion ‘0’ from the ISES is said to disagree with the inverse soft expert sets (DISES).
Example 2.
Consider Example 1.
Definition 7.
The distance between and is defined as
Remark 1.
Note that,
- iff
- The distance between ISES obeys the symmetric property that is,.
Example 3.
Consider the Example 2.
Now, . Then, .
The distance between and is
Similarly, we can find the other AISES distances and the distances between DISES.
Remark 2.
By applying the operation of union (also known as maximum), we are able to obtain the distance of soft expert sets. This is achieved by combining the AISES distance and DISES distance.
Definition 8.
Let be inverse soft expert sets. The SMISES is defined as
Example 4.
Let us consider the Example 1. The SMISES is
4. MCDM Problem Using Symmetric Matrix on Inverse Soft Expert Sets
In this section, we focus on providing a SMISES method for addressing the MCDM problem. The algorithm is described below.
4.1. Algorithm
- Input: The ISES
- Output: Ranking the alternatives.
- 1: Construct the ISES
- 2: Determine the distances between the two ISES.
- 3: Construct the SMISES.
- 4: Find , i=1,2,3…,n.
- 5: Find .
- 6: Calculate .
- 7: The alternatives are ranked in order of preference.
- 8: Conclusion.
Figure 1 displays the fundamental steps of the suggested paradigm.
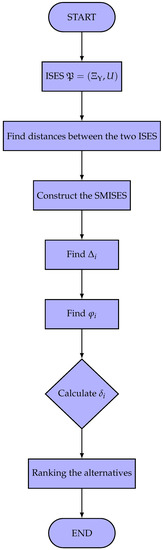
Figure 1.
Flowchart of the algorithm presented in Section 4.1.
4.2. Pseudocode
READ
COMPUTE distance between two
COMPUTE
CALCULATE
CALCULATE
PRINT
DETERMINE rank
SHOW
4.3. Illustrative Example’s Problem Statement
Assume that a person wishes to build a house to their specifications. They approach five construction companies and want to select the best one. They require expert advice in this regard. Let be the construction companies and let the parameters be , with representing the cost of the house, = the construction period and = the quality of the materials used for the house. Let the evaluators (experts) of the project be and the opinion be .
Step 1: Construct the ISES.
The ISES data have been tabulated and are presented in the following Table 2.

Table 2.
Inverse soft expert sets.
Now, we write AISES and DISES using Table 2.
Step 2: We can find the distance measures on all the alternatives.
The AISES distances of and are
Similarly, we can find the other AISES distances.
Next, we find the DISES distances of and as follows.
In a similar fashion, we are able to determine the various DISES distances.
Step 3: The SMISES is
Step 4:
Step 5: Find .
Similarly, we can find
Step 6: Calculate .
Similarly, we can find
Step 7: Compute min
The minimum of is and .
Step 8: The expert may choose any of the for the construction company.
5. Comparative Analysis
5.1. Comparative Analysis 1’s Problem Statement
We use the problem outlined by Mitra Basu et al. [8] to validate our approach. He came up with the following problem formulation. Consider a situation where there are three friends and they all have a friend in common. They all want to get a dress for their mutual friend. Let be the collection of four dresses. Let be the parameter set. According to our algorithm, let the experts be and the opinion be .
Step 1: Construct the ISES.
The ISES data have been tabulated and are presented in the following Table 3.

Table 3.
Inverse soft expert sets.
Step 2: We can find distance measures on all the alternatives.
Step 3: The SMISES is
Step 4: .
Step 5: Find .
Similarly, we can find
Step 6: Calculate .
Similarly, we can find
Step 7: Compute min
The minimum of is .
Step 8: As per the expert opinion, the three friends will jointly buy the dress .
From the above-mentioned steps and also Table 4, we strongly claim that, in the existing literature, two alternatives were identified as the best alternatives, whereas in our proposed framework, only one has been identified. From this perspective, we have emphasised that our strategy is more effective than the existing strategy by a diagrammatic representation in Figure 2.

Table 4.
Comparative analysis of the differences between the two methods.
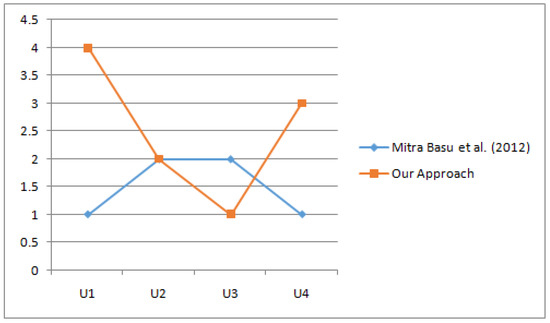
Figure 2.
Comparative analysis of our approach with Mitra Basu et al. [8].
5.2. Comparative Analysis 2’s Problem Statement
Make the assumption that a family wishes to purchase a car from the market, letting
and be the parameter set. According to our algorithm, let the experts be and the opinion be .
Step 1: Construct the ISES.
The ISES data have been tabulated and are presented in the following Table 5.

Table 5.
Inverse soft expert sets.
Now, we write the AISES and DISES using Table 5.
Step 2: We can find distance measures on all the alternatives.
Step 3: The SMISES is
Step 4: .
Step 5: Find .
Similarly, we can find
Step 6: Calculate .
Similarly, we can find
Step 7: Compute min
The minimum of is and .
Step 8: As per the expert opinion, the family may choose any car from and is shown in Table 6.

Table 6.
Comparative analysis of the differences between the two methods.
Our work is compared with [11]. In that paper, soft rough sets were transformed into fuzzy sets (low, middle and high confidence) and weighting vectors were also used. The range of the alternative was also modified if the weighting vectors varied. In other words, the alternative was not unique. However, our method of decision-making is unique and accurate which is clearly depicted in Figure 3.
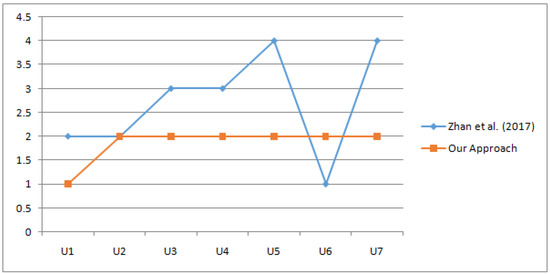
Figure 3.
Comparative analysis of our approach with Zhan et al. [11].
Even though our strategy yields a large number of possibilities, it is much simpler than the prior one. Consequently, our approach is more effective than the earlier approach.
5.3. Limitations and Complexity
During the evaluation of the developed framework, we identified the following limitation: the existence of huge data sets of alternatives, parameters and experts in a wide range of MCDM situations can negatively affect the computing speed, owing to the increase in information extracted. Moreover, the ranking order may change when current parameters (or objects) are deleted, or even when new parameters (or objects) are introduced into an MCDM situation. It happens due to the fact that the entities and parameters behave independently of one another.
Due to the fact that it has fewer nested loops, it is simpler to execute and has a low time complexity.
6. Conclusions
The notion of a soft expert set is developed further into an inverse soft expert set within its own scope of the current research. Several results on SMISES have been presented. In addition, the concept of symmetric matrices on inverse soft expert sets is explained alongside important illustrations and novel findings, and an SMSES algorithm is exhibited. Additionally, two comparative analyses are conducted. We have demonstrated that our approach yields distinct and superior results compared to the existing approach in the literature. To justify our results, visual representations are also provided.
We intend to expand on this concept in future research by applying it to the neutrosophic environment. We are particularly interested in creating various structures such as the inverse neutrosophic soft expert sets and the symmetric matrix on inverse neutrosophic soft expert sets.
Author Contributions
Methodology, N.S.; Validation, N.S. and J.C.R.A.; Formal analysis, N.S.; Investigation, S.V. and J.C.R.A.; Resources, S.V. and J.C.R.A.; Visualization, N.S.; Supervision, S.V. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like it made clear that the publication of this work did not receive any funding or other form of financial help.
Data Availability Statement
Not applicable.
Acknowledgments
The reviewers provocative comments and insightful suggestions have been greatly appreciated by the authors, who would like to extend their sincere gratitude.
Conflicts of Interest
The authors state firmly that they have no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets. Int. J. Inf. Comput. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft Set Theory First Results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R. A fuzzy soft set theoretic approach to decision making problems. J. Comput. Appl. Math. 2002, 44, 1077–1083. [Google Scholar] [CrossRef]
- Çağman, N.; Enginoglu, S. Soft matrix theory and its decision making. Comput. Math. Appl. 2010, 59, 3308–3314. [Google Scholar] [CrossRef]
- Vijayabalaji, S.; Balaji, P.; Ramesh, A. Sigmoid valued fuzzy soft set and its application to haze management. J. Intell. Fuzzy. Syst. 2020, 39, 7177–7187. [Google Scholar] [CrossRef]
- Vijayabalaji, S.; Balaji, P.; Ramesh, A. A New Distance and Similarity Measure on Soft Parameter Sets and Their Applications to MCDM Problem. In Fuzzy Mathematical Analysis and Advances in Computational Mathematics. Studies in Fuzziness and Soft Computing; Kannan, S.R., Last, M., Hong, T.P., Chen, C.H., Eds.; Springer: Singapore, 2022; Volume 419, pp. 127–136. [Google Scholar]
- Mitra Basu, T.; Mahapathra, K.N.; Mondal, S.K. Matrices in soft set theory and their applications in decision making problems. S. Asian J. Math. 2012, 2, 126–143. [Google Scholar]
- Sun, C.; Li, H. Parallel fuzzy relation matrix factorization towards algebraic formulation, universal approximation and interpretability of MIMO hierarchical fuzzy systems. Fuzzy Sets Syst. 2022, 450, 68–86. [Google Scholar] [CrossRef]
- Feng, J.; Li, H.; Cheng, D. Multiple Fuzzy Relation and Its Application to Coupled Fuzzy Control. Asian J. Control 2013, 15, 1313–1324. [Google Scholar] [CrossRef]
- Zhan, J.; Liua, Q.; Herawan, T. A novel soft rough set: Soft rough hemirings and correspondingmulticriteria group decision making. Appl. Soft Comput. 2017, 54, 393–402. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R. Soft Expert Sets. Adv. Decis. Sci. 2011, 15, 1–12. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R. Fuzzy soft Expert Set and its Application. Appl. Math. 2014, 5, 1349–1368. [Google Scholar] [CrossRef]
- Ali, G.; Akram, M.; Alcantud, J.C.R. Novel MCGDM analysis under m-polar fuzzy soft expert sets. Neural Comput. Appl. 2021, 33, 12051–12071. [Google Scholar]
- Khalil, A.M.; Hassan, N. Inverse fuzzy soft set and its application in decision making. Int. J. Inf. Decis. Sci. 2019, 11, 73–92. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).