Enumerating Subtrees of Flower and Sunflower Networks
Abstract
1. Introduction
2. Terminologies and Notations
- denotes the graph produced after excluding X from G, where X may be a vertex set or an edge set, or mixed set of vertices and edges).
- denotes the subtree set of G.
- denotes the subtree set containing X in G.
- : not containing ;
- : contains but not ;
- : contains , namely, the path connecting and of .
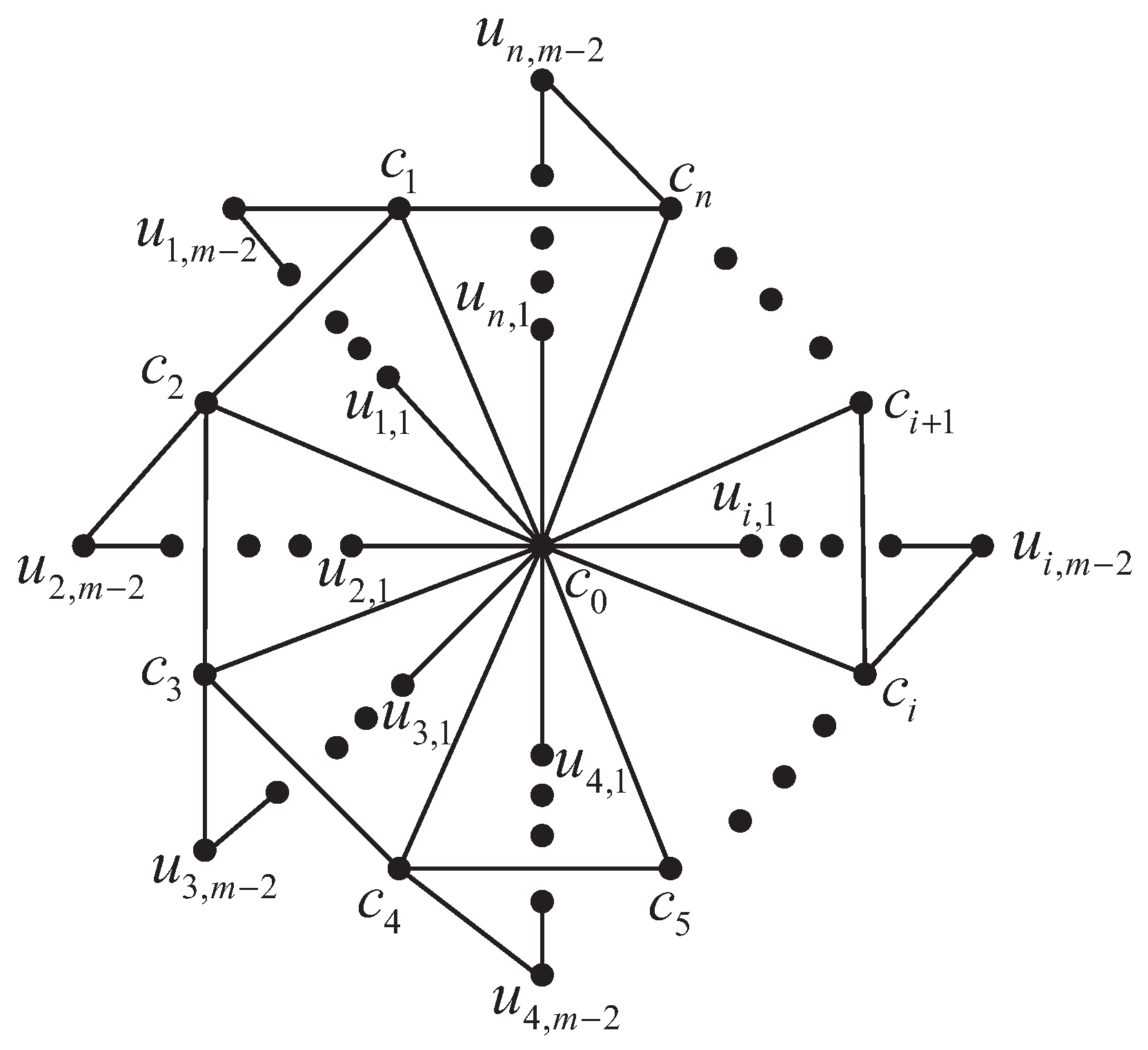
3. The Subtree Number of Flower Network
- : not containing ;
- : contains but not .
4. The Subtree Number of Sunflower Network
- For , is an unicyclic graph with length n;
- For , let be an unicyclic graph with length t, the vertex set be , and be derived from by replacing each existing edge in by two parallel paths of length a and b (see Figure 4).
- : not containing and ;
- : contains but not and ;
- : contains but not and ;
- : contains but not , .
- for ,where ;
- for ,where , , , , .
5. Results and Discussions
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, B.; Lippner, G.; Chen, Y.T.; Fotouhi, B.; Momeni, N.; Yau, S.T.; Nowak, M.A. Evolutionary dynamics on any population structure. Nature 2017, 544, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Park, H.J.; Friston, K. Structural and functional brain networks: From connections to cognition. Science 2013, 342, 1238411. [Google Scholar] [CrossRef]
- Débarre, F.; Hauert, C.; Doebeli, M. Social evolution in structured populations. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Hafeez, S.; Akhter, S.; Iqbal, Z.; Aslam, A. The Generalized Inverse Sum Indeg Index of Some Graph Operations. Symmetry 2022, 14, 2349. [Google Scholar] [CrossRef]
- Harry, W. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Ali, F.; Rather, B.A.; Fatima, N.; Sarfraz, M.; Ullah, A.; Alharbi, K.A.M.; Dad, R. On the Topological Indices of Commuting Graphs for Finite Non-Abelian Groups. Symmetry 2022, 14, 1266. [Google Scholar] [CrossRef]
- Khadikar, P.V.; Deshpande, N.V.; Kale, P.P.; Dobrynin, A.; Gutman, I.; Domotor, G. The Szeged index and an analogy with the Wiener index. J. Chem. Inf. Comput. Sci. 1995, 35, 547–550. [Google Scholar] [CrossRef]
- Al-Fozan, T.; Manuel, P.; Rajasingh, I.; Rajan, R.S. Computing Szeged index of certain nanosheets using partition technique. Match Commun. Math. Comput. Chem. 2014, 72, 339–353. [Google Scholar]
- Székely, L.A.; Wang, H. On subtrees of trees. Adv. Appl. Math. 2005, 34, 138–155. [Google Scholar] [CrossRef]
- Yan, W.; Yeh, Y.N. Enumeration of subtrees of trees. Theor. Comput. Sci. 2006, 369, 256–268. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Jin, M.; Li, L.; Wang, H.; Zhang, X. Enumeration of subtrees and BC-subtrees with maximum degree no more than k in trees. Theor. Comput. Sci. 2021, 892, 258–278. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Zhang, X.D.; Chen, C.P. On enumerating algorithms of novel multiple leaf-distance granular regular α-subtrees of trees. Inf. Comput. 2022, 289, 104942. [Google Scholar] [CrossRef]
- Furtula, B.; Graovac, A.; Vukičević, D. Augmented zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Gutman, I. An exceptional property of first Zagreb index. Match Commun. Math. Comput. Chem. 2014, 72, 733–740. [Google Scholar]
- Kazemi, R. Note on the multiplicative Zagreb indices. Discret. Appl. Math. 2016, 198, 147–154. [Google Scholar] [CrossRef]
- Dong, L.; Zhao, H.; Lai, H.J. Entropy and Enumeration of Subtrees in a Cactus Network. Front. Phys. 2020, 8, 575648. [Google Scholar] [CrossRef]
- Knudsen, B. Optimal multiple parsimony alignment with affine gap cost using a phylogenetic tree. In Proceedings of the International Workshop on Algorithms in Bioinformatics, Budapest, Hungary, 15–20 September 2003; pp. 433–446. [Google Scholar]
- Wagner, S.G. Correlation of graph-theoretical indices. SIAM J. Discret. Math. 2007, 21, 33–46. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Gray, D.; Wang, H. The number of subtrees of trees with given degree sequence. J. Graph Theory 2013, 73, 280–295. [Google Scholar] [CrossRef]
- Andriantiana, E.O.D.; Wagner, S.; Wang, H. Greedy trees, subtrees and antichains. Electron. J. Comb. 2013, 20, P28. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Feng, S. On algorithms for enumerating BC-subtrees of unicyclic and edge-disjoint bicyclic graphs. Discret. Appl. Math. 2016, 203, 184–203. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, X.; Cao, J.; Wang, H.; Zhang, X. The expected subtree number index in random polyphenylene and spiro chains. Discret. Appl. Math. 2020, 285, 483–492. [Google Scholar] [CrossRef]
- Székely, L.A.; Wang, H. Binary trees with the largest number of subtrees. Discret. Appl. Math. 2007, 155, 374–385. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Gray, D.; Wang, H. Trees with the most subtrees—An algorithmic approach. J. Comb. 2012, 3, 207–223. [Google Scholar]
- Yang, Y.; Liu, H.; Wang, H.; Fu, H. Subtrees of spiro and polyphenyl hexagonal chains. Appl. Math. Comput. 2015, 268, 547–560. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Deng, A.; Magnant, C. On Algorithms for Enumerating Subtrees of Hexagonal and Phenylene Chains. Comput. J. 2017, 60, 690–710. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, B.; Zhang, G.; Li, Y.; Sun, D.; Liu, H. Algorithms based on path contraction carrying weights for enumerating subtrees of tricyclic graphs. Comput. J. 2022, 65, 554–572. [Google Scholar] [CrossRef]
- Chin, A.J.; Gordon, G.; MacPhee, K.J.; Vincent, C. Subtrees of graphs. J. Graph Theory 2018, 89, 413–438. [Google Scholar] [CrossRef]
- Poureidi, A. On computing the number of (BC-) subtrees, eccentric subtree number, and global and local means of trees. Inf. Process. Lett. 2022, 178, 106302. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y.; Han, X. Characterization of Symmetry of Complex Networks. Symmetry 2019, 11, 692. [Google Scholar] [CrossRef]
- MacArthur, B.D.; Sánchez-García, R.J.; Anderson, J.W. Symmetry in complex networks. Discret. Appl. Math. 2008, 156, 3525–3531. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Wu, W.T.; Wang, H.; Xiong, M.; Wang, W. Symmetry-based structure entropy of complex networks. Phys. A Stat. Mech. Its Appl. 2008, 387, 2611–2619. [Google Scholar] [CrossRef]
- Daoud, S. Complexity of graphs generated by wheel graph and their asymptotic limits. J. Egypt. Math. Soc. 2017, 25, 424–433. [Google Scholar] [CrossRef]
- Kaliraj, K.; Sivakami, R.; Vernold, V.J. Star edge coloring of corona product of path and wheel graph families. Proyecciones 2018, 37, 593–601. [Google Scholar] [CrossRef]
- Zahid, A.; Saleem, M.; Kashif, A.; Khan, M.; Meraj, M.; Irfan, R. Spanning Simplicial Complex of Wheel Graph Wn. Algebra Colloq. 2019, 26, 309–320. [Google Scholar] [CrossRef]
- Ali, U.; Ahmad, Y.; Sardar, M.S. On 3-total edge product cordial labeling of tadpole, book and flower graphs. Open J. Math. Sci. 2020, 4, 48–55. [Google Scholar] [CrossRef]
- Sathiya, D.; Senthamilselvi, S. On Equitable Edge Coloring of Wheel Graph Families. J. Algebr. Stat. 2022, 13, 1791–1797. [Google Scholar]
- Kaabar, M.K.; Yenoke, K. Radio and Radial Radio Numbers of Certain Sunflower Extended Graphs. Int. J. Math. Math. Sci. 2022, 2022, 9229409. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, H.; Liu, Z.; Mao, Y. Trees with large numbers of subtrees. Int. J. Comput. Math. 2017, 94, 372–385. [Google Scholar] [CrossRef]






| Symbol | Explanation |
| SGF of fan flower containing , | |
| for the case of , we let | |
| the SGF that contain both and path , namely, | |
| . |
| n | m | ||||
|---|---|---|---|---|---|
| 12 | 3 | 808,994,334,366 | 11.90794548 | 112,238,363,816,4 | 12.05014133 |
| 12 | 4 | 998,610,060,032,920 | 14.99939594 | 151,308,674,603,059,0 | 15.17986383 |
| 12 | 5 | 265,280,251,112,307,000 | 17.42370492 | 404,849,273,581,826,000 | 17.60729336 |
| 12 | 6 | 256,550,685,339,735,000,00 | 19.40917318 | 384,650,010,292,476,000,00 | 19.58506575 |
| 12 | 7 | 122,063,734,917,778,000,000,0 | 21.08658665 | 178,548,004,931,270,000,000,0 | 21.251755 |
| 12 | 8 | 344,273,389,923,669,000,000,00 | 22.53690346 | 490,934,797,202,023,000,000,00 | 22.69102382 |
| 12 | 9 | 650,645,762,570,061,000,000,000 | 23.81334461 | 905,809,267,379,347,000,000,000 | 23.95703676 |
| 12 | 10 | 896,628,634,179,120,000,000,000,0 | 24.9526126 | 122,119,065,856,034,000,000,000,00 | 25.08678347 |
| 12 | 11 | 957,232,024,063,896,000,000,000,00 | 25.98101722 | 127,822,905,177,000,000,000,000,000 | 26.10660868 |
| 12 | 12 | 827,993,950,521,421,000,000,000,000 | 26.91802716 | 108,623,009,982,456,000,000,000,000,0 | 27.03592183 |
| 12 | 13 | 600,392,405,365,584,000,000,000,000,0 | 27.77843519 | 775,222,331,646,122,000,000,000,000,0 | 27.88942627 |
| 12 | 14 | 374,744,209,248,582,000,000,000,000,00 | 28.57373493 | 477,004,278,516,100,000,000,000,000,00 | 28.67852227 |
| 12 | 15 | 205,602,572,796,967,000,000,000,000,000 | 29.31302854 | 258,359,754,119,165,000,000,000,000,000,0 | 30.41222486 |
| 12 | 16 | 100,842,557,399,484,000,000,000,000,000,0 | 30.00364385 | 125,251,904,753,382,000,000,000,000,000,0 | 30.09778434 |
| 12 | 17 | 448,296,476,198,180,000,000,000,000,000,0 | 30.65156533 | 550,957,046,116,700,000,000,000,000,000,0 | 30.74111774 |
| 12 | 18 | 182,701,553,239,954,000,000,000,000,000,00 | 31.26174224 | 222,390,527,574,997,000,000,000,000,000,00 | 31.34711629 |
| n | m | ||||
|---|---|---|---|---|---|
| 12 | 3 | 569,170,9 | 6.755,242,688 | 517,527,0 | 6.713933012 |
| 12 | 4 | 980,681,131 | 8.991527819 | 990,109,132 | 8.995683066 |
| 12 | 5 | 168,515,441,557 | 11.2266397 | 181,560,385,458 | 11.2590211 |
| 12 | 6 | 291,422,645,379,48 | 13.4645233 | 327,929,007,285,78 | 13.51577983 |
| 12 | 7 | 506,766,497,010,234,0 | 15.7048079 | 589,052,387,641,233,0 | 15.77015392 |
| 12 | 8 | 884,180,126,963,189,000 | 17.94654075 | 105,597,948,140,887,000,0 | 18.02365548 |
| 12 | 9 | 154,536,766,330,510,000,000 | 20.18903182 | 189,163,078,432,656,000,000 | 20.27683637 |
| 12 | 10 | 270,327,973,135,294,000,000,00 | 22.43189099 | 338,765,521,831,683,000,000,00 | 22.5298992 |
| 12 | 11 | 473,064,933,203,821,000,000,000,0 | 24.67492076 | 606,622,526,889,045,000,000,000,0 | 24.78291853 |
| 12 | 12 | 828,000,782,196,875,000,000,000,000 | 26.91803075 | 108,623,009,982,456,000,000,000,000,0 | 27.03592183 |
| n | m | ||||
|---|---|---|---|---|---|
| 3 | 3 | 102,7 | 3.011570444 | 101,7 | 3.007320953 |
| 4 | 4 | 105,451 | 5.023050703 | 112,636 | 5.051677219 |
| 5 | 5 | 187,184,91 | 7.272270835 | 215,012,25 | 7.332463204 |
| 6 | 6 | 513,612,006,6 | 9.710635168 | 617,934,704,1 | 9.790942587 |
| 7 | 7 | 201,051,445,463,5 | 12.3033072 | 249,018,559,016,5 | 12.39623172 |
| 8 | 8 | 106,896,683,359,669,0 | 15.02896423 | 134,000,723,234,807,0 | 15.12710714 |
| 9 | 9 | 725,328,036,700,938,000 | 17.86053446 | 928,294,891,665,960,000 | 17.96768596 |
| 10 | 10 | 622,370,323,833,015,000,000 | 20.79404888 | 804,6744,796,912,410,000,00 | 20.90562023 |
| 11 | 11 | 654,629,293,559,492,000,000,000 | 23.81599544 | 853,195,489,291,013,000,000,000 | 23.93104855 |
| 12 | 12 | 827,993,950,521,421,000,000,000,000 | 27.03592183 | 108,623,009,982,456,000,000,000,000,0 | 27.03592183 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Jia, Z.; Yang, Y.; Duan, F.; Lv, H.; Zhao, W. Enumerating Subtrees of Flower and Sunflower Networks. Symmetry 2023, 15, 284. https://doi.org/10.3390/sym15020284
Li L, Jia Z, Yang Y, Duan F, Lv H, Zhao W. Enumerating Subtrees of Flower and Sunflower Networks. Symmetry. 2023; 15(2):284. https://doi.org/10.3390/sym15020284
Chicago/Turabian StyleLi, Long, Zongpu Jia, Yu Yang, Fengge Duan, Hailian Lv, and Weiting Zhao. 2023. "Enumerating Subtrees of Flower and Sunflower Networks" Symmetry 15, no. 2: 284. https://doi.org/10.3390/sym15020284
APA StyleLi, L., Jia, Z., Yang, Y., Duan, F., Lv, H., & Zhao, W. (2023). Enumerating Subtrees of Flower and Sunflower Networks. Symmetry, 15(2), 284. https://doi.org/10.3390/sym15020284






