Numerical Solution of Time-Fractional Emden–Fowler-Type Equations Using the Rational Homotopy Perturbation Method

Abstract

The integral-order derivative is not suitable where infinite variances are expected, and the fractional derivative manages to consider effects with more precision; therefore, we considered timefractional Emden–Fowler-type equations and solved them using the rational homotopy perturbation method (RHPM). The RHPM method is based on two power series in rational form. The existence and uniqueness of the equation are proved using the Banach fixed-point theorem. Furthermore, we approximate the term h(z) with a polynomial of a suitable degree and then solve the system using the proposed method and obtain an approximate symmetric solution. Two numerical examples are investigated using this proposed approach. The effectiveness of the proposed approach is checked by representing the graphs of exact and approximate solutions. The table of absolute error is also presented to understand the method′s accuracy.

1. Introduction and Mathematical Preliminaries

Studying singular boundary value problems has received much attention in recent decades. Jonathan Homar Lane [1] proposed the equation in 1870, and Jacob Robert Emden [2] studied it in detail. He introduced a model of the behavior of stellar objects under their gravity. The study of stellar structures [3] involves the design, evolution, life, and death of a star under the laws of physics and chemistry. The star’s core radiates energy, and the star’s gravity compensates for the pressure of the core. Lane–Emden equation [2] is given as

$$\frac{d^{2}z}{d{y}^2}+\frac{2}{y}\frac{dz}{dy}+z^n=0,$$

(1)

where n is the polytropic index. This equation is a dimensionless form of the Poisson equation. Some work based on symmetries and solutions of the Lane–Emden equation can be found in [4]. Furthermore, Muatjetjeja and Khalique [5] found the symmetric solutions of Lane–Emden-type equations.

The Emden–Fowler equation is a generalization of the Lane–Emden equation. Ralph Howard Fowler, a British physicist and astronomer, further explored the Lane–Emden equation ([6,7]) and presented the following equation:

$$\frac{d^{2}z}{d{y}^2}+\frac{b}{y}\frac{dz}{dy}+f\left(y\right)g\left(z\right)=0,b\ge 0,$$

(2)

where $f\left(y\right)$ is a nonlinear function. When $b=2$, $g\left(z\right)=z^n$, and $f\left(y\right)=1$, it leads to the Lane–Emden equation of the standard form. The Emden–Fowler equation has been investigated and studied by many physicists and mathematicians. Some of them solved it for specific polytropic indexes. This equation has many applications in many fields. We can refer to the works of Tajima and Meerson [8] and Ritschell [9] for further details. It is widely used to investigate isothermal gas spheres and thermionic currents [10]. These equations have many applications in radioactive cooling, in the kinetics of combustion, or in the concentration of reactants in a chemical reactor.

Fractional calculus is a powerful tool in applied sciences. Many researchers in fractional control theory, diffusion, and the fractional neutron point model use it. The fractional derivative is global rather than local and is very useful when infinite variances are expected. It manages to consider effects with more precision. This nonlocality is very helpful in understanding physical phenomena that have memory effects. Such systems are difficult to analyze with classical calculus. Fractional differential equations are extensions of ordinary and partial differential equations. These equations have been applied to various mathematical concepts in physics and engineering sciences in recent years. Fractional partial differential equations (FPDEs) are arising as competent tools for challenging modeling phenomena in sciences and engineering. We study fractional equations with the help of fractional calculus [11]. For small deformations in elastic materials, such as in a spring, the mechanical behavior of these nonlinear systems is studied using fractional calculus, which is difficult using classical calculus. We first define fractional integration and derivative as follows:

Definition 1. 

([11]). (Riemann–Liouville fractional derivative) Let ζ be a continuous function; the Riemann–Liouville fractional integral of order μ is given by

$${\mathrm{I}}_{\kappa }^{\mu }\zeta (y,\kappa )=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }\left(\mu \right)}{\int }_0^{\kappa }{(\kappa -w)}^{\mu -1}\zeta (y,w)dw,\hfill & \mu >0,\\ \zeta (y,\kappa ),\hfill & \mu =0\end{array}\right.$$

where Γ represents the Gamma function, $\mu \ge 0$, and $\kappa >0.$

Definition 2. 

([11]). (Caputo fractional derivative) Let ζ be a continuously differentiable function; the Caputo fractional derivative of ζ for $\kappa >0$ and integer l is formulated as

$${\mathrm{D}}_{\kappa }^{\mu }\zeta (y,\kappa )=\left\{\begin{array}{cc}{\mathrm{I}}_{\kappa }^{l-\mu }\frac{{\partial }^l\zeta (y,\kappa )}{\partial {\kappa }^l},\hfill & l-1<\mu <l\hfill \\ \frac{{\partial }^l\zeta (y,\kappa )}{\partial {\kappa }^l},\hfill & \mu =l.\hfill \end{array}\right.$$

In particular, for $0<\mu <1$,

$${\mathrm{D}}_{\kappa }^{\mu }\zeta (y,\kappa )=\frac{1}{\mathsf{\Gamma }(1-\mu )}{\int }_0^{\kappa }{(\kappa -w)}^{-\mu }\frac{\partial }{\partial w}\zeta (y,w)dw.$$

Properties of Caputo derivative

The following properties are satisfied, for $0<\mu \le 1,\rho >-1$:

(1) ${\mathrm{D}}_{\kappa }^{\mu }\beta =0$ for a constant $\beta$;

(2) ${\mathrm{I}}_{\kappa }^{\mu }{\mathrm{D}}_{\kappa }^{\mu }\zeta (y,\kappa )=\zeta (y,\kappa )-\zeta (y,0)$;

(3) ${\mathrm{D}}_{\kappa }^{\mu }{\mathrm{I}}_{\kappa }^{\mu }\zeta (y,\kappa )=\zeta (y,\kappa )$;

(4) ${\mathrm{D}}_{\kappa }^{\mu }{\kappa }^{\rho }=\frac{\mathsf{\Gamma }(1+\rho )}{\mathsf{\Gamma }(1+\rho -\mu )}{\kappa }^{\rho -\mu }$

Over the past few decades, many semi-analytical methods have been used to solve nonlinear differential equations and FPDEs, including Adomian decomposition methods, perturbation methods, Taylor’s series methods, variational iterative methods, etc. We refer to the work of Shah, Chung and chu ([12,13,14,15]) on the multidimensional fractional Navier–Stokes equation using the variational iteration transform method and the fractional analysis of the coupled Burger equation using iterative methods (for more detail, see Lima [16,17], Adomian et al. [18], Horedt [19,20], Shawagfeh [21], Wazwaz [22], Datta [23], and Liao [24]).

The homotopy perturbation method ([25,26]) is based on power series. The rational homotopy perturbation method([27]) is a generalization of the homotopy perturbation method, and we take two power series in the rational form in the rational homotopy perturbation method. The rational homotopy perturbation method takes a nonlinear differential equation and converts it into a series of linear differential equations. This method is very effective, and the major advantage of this method is that it gives accurate results in fewer iterations. For details, we refer readers to ([27,28]).

Definition 3. 

([27]). (Rational Homotopy Perturbation Method)

Consider a nonlinear differential equation as follows:

$$\mathrm{T}\left(z\right)+\mathrm{Y}\left(z\right)-\phi \left(\sigma \right)=0,$$

where$\sigma \in \mathsf{\Theta },$with a boundary condition

$$\mathrm{B}(z,\frac{\partial z}{\partial \lambda }),\sigma \in \mathrm{K},$$

where$\mathrm{T}$is a linear operator,$\mathrm{Y}$is a nonlinear operator,$\phi \left(\sigma \right)$is an analytic function,$\mathrm{K}$denotes the boundary of domain$\mathsf{\Theta }$, $\mathrm{B}$is an operator for the boundary, and$\lambda$is an outward normal from the domain. Formulation of a possible homotopy is

$$\mathrm{H}(\vartheta ,p)=(1-p)(\mathrm{T}\left(\vartheta \right)-\mathrm{T}\left(z_0\right))+p(\mathrm{T}\left(\vartheta \right)+\mathrm{Y}\left(\vartheta \right)-\phi \left(\sigma \right))=0,p\in [0,1],$$

where$z_0$is the initial approximation, and p is the embedding parameter. Clearly,

$$\begin{array}{c}\mathrm{H}(\vartheta ,0)=\mathrm{T}\left(\vartheta \right)-\mathrm{T}\left(z_0\right)=0,\hfill \\ \mathrm{H}(\vartheta ,1)=\mathrm{T}\left(\vartheta \right)+\mathrm{Y}\left(\vartheta \right)-\phi \left(\sigma \right)=0.\hfill \end{array}$$

Now, we consider the solution as a quotient of power series:

$$\vartheta =\frac{p^0{\vartheta }_0+p^1{\vartheta }_1+p^2{\vartheta }_2+\dots }{p^0{\pi }_0+p^1{\pi }_1+p^2{\pi }_2+\dots },$$

where${\vartheta }_i,i=0,1,2,\dots$are unknown functions, and${\pi }_i,i=0,1,2,\dots$are known. When$p\to 1$, we obtain an approximate solution

$$z=\frac{{\vartheta }_0+{\vartheta }_1+{\vartheta }_2+\dots }{{\pi }_0+{\pi }_1+{\pi }_2+\dots }$$

In this paper, we consider the time-fractional Emden–Fowler-type Equation ([29,30]). The equation is taken as

$${}^C{D_{\kappa }}^{\mu }z(y,\kappa )=\frac{{\partial }^2}{\partial y^2}z(y,\kappa )+\frac{v}{y}\frac{\partial z}{\partial y}+r(y,\kappa )h\left(z\right),$$

(3)

with the initial condition $z(y,0)=u\left(y\right)$, where ${}^C{D_{\kappa }}^{\mu }z(y,\kappa )$ is the Caputo derivative, $\kappa$ represents the time variable, $\mu$ is the order of the Caputo derivative, v is a constant, and $h\left(z\right)$ and $r(y,\kappa )$ are nonlinear functions. For a steady-state case, Equation (3) is the Emden–Fowler equation given in Equation (2).

In Section 2 we prove the existence and uniqueness theorem using the Banach fixed-point theorem. Then, in Section 3, we approximate the term $h\left(z\right)$ with a polynomial of a suitable degree and then solve the system using the rational homotopy perturbation method. In Section 4 the condition of convergence is discussed. In Section 5, examples are investigated. The conclusion is presented in Section 6.

2. Existence and Uniqueness

Let us consider the set $z=z(y,\kappa )$ defined in the interval $\overline{\mathsf{\Pi }}\times \left[0,\xi \right]$ to be denoted by $\mathsf{\Phi }$ with a norm

$$\Vert z\Vert =\left\{max\left|z(y,\kappa )\right|,(y,\kappa )\in \overline{\mathsf{\Pi }}\times \left[0,\xi \right]\right\},$$

where $0<\xi <\infty$ is a Banach space. Clearly, the set $\mathsf{\Phi }$ is a Banach space. Let

$$X(z(y,\kappa ),h(z(y,\kappa ),\frac{\partial z(y,\kappa )}{\partial y},\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2})=\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}+\frac{v}{y}\frac{\partial z(y,\kappa )}{\partial y}+r(y,\kappa )h\left(z(y,\kappa )\right).$$

(4)

We can rewrite the above equation as follows:

$$\begin{array}{c}{}^C{D_{\kappa }}^{\mu }z(y,\kappa )=X(z(y,\kappa ),h(z(y,\kappa ),\theta \left(z(y,\kappa )\right),\frac{\partial z(y,\kappa )}{\partial y},\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2})\hfill \\ =\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}+\theta \left(z(y,\kappa )\right)+r(y,\kappa )h\left(z(y,\kappa )\right),\hfill \end{array}$$

(5)

where $\theta \left(z(y,\kappa )\right)=\frac{v}{y}\frac{\partial z(y,\kappa )}{\partial y}.$

Lemma 1. 

For $\mu >0$, the fractional differential equation

$${}^C{D_{\kappa }}^{\mu }z(y,\kappa )=X(z(y,\kappa ),h(z(y,\kappa ),\theta \left(z(y,\kappa )\right),\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}),$$

with condition $z(y,0)=u\left(y\right)$ is equivalent to the integral equation

$$z(y,\kappa )=\frac{1}{\mathsf{\Gamma }\left(\mu \right)}\underset{0}{\overset{\kappa }{\int }}{(\kappa -s)}^{\mu -1}X(z(y,s),h(z(y,s),\theta \left(z(y,s)\right),\frac{{\partial }^{2}z(y,s)}{\partial y^2})ds+u\left(y\right).$$

(6)

This lemma is straightforward.

Lemma 2. 

If $z(y,\kappa )$ and its partial derivatives are continuous on $\overline{\mathsf{\Pi }}\times \left[0,\xi \right]$, then $\frac{\partial z(y,\kappa )}{\partial y}$, $\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}$ are bounded.

This lemma is also straightforward.

We prove existence and uniqueness using the Banach fixed-point theorem ([31]). First of all, we consider the following hypothesis:

• $z(y,\kappa )$ is continuous over $\overline{\mathsf{\Pi }}\times \left[0,\xi \right]$, and the functions $r(y,\kappa )$,$h\left(z\right)$ are continuous with interval $\overline{\mathsf{\Pi }}\times \left[0,\xi \right]$;
• $\theta \left(z\right)$ is differentiable at $y=0$;
• There are non-negative constants $L_1,L_2,L_3$ such that:

  $$\begin{array}{c}\left|\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}-\frac{{\partial }^{2}w(y,\kappa )}{\partial y^2}\right|\le L_1\left|z(y,\kappa )-w(y,\kappa )\right|\hfill \\ \left|\theta \left(z\right(y,\kappa \left)\right)-\theta \left(w\right(y,\kappa \left)\right)\right|\le L_2\left|z(y,\kappa )-w(y,\kappa )\right|\hfill \\ \left|h\left(z\right(y,\kappa \left)\right)-h\left(w\right(y,\kappa \left)\right)\right|\le L_3\left|z(y,\kappa )-w(y,\kappa )\right|\hfill \end{array}$$

  where $z,w$$\in \mathsf{\Phi }(\overline{\mathsf{\Pi }}\times \left[0,\xi \right])$.
• $\underset{(y,\kappa )\in \overline{\mathsf{\Pi }}\times \left[0,\xi \right]}{\overset{max}{︸}}\left|r(y,\kappa )\right|=\gamma$ where $\gamma$ is a non-negative constant.

Using the method mentioned in [32], we will prove the following:

Theorem 1. 

For $\mu >0$, assume that all the hypotheses are satisfied, and let the function X in Equation (6) satisfy the generalized Lipschitz condition

$$\begin{array}{c}\left|X(z(y,\kappa ),\theta \left(z(y,\kappa )\right),h\left(z(y,\kappa )\right),\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2})-X(w(y,\kappa ),\theta \left(z(y,\kappa )\right),h\left(z(y,\kappa )\right),\frac{{\partial }^{2}w(y,\kappa )}{\partial y^2})\right|\hfill \\ \le M\left|z(y,\kappa )-w(y,\kappa )\right|+{L_1}^{\prime }\left|\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}-\frac{{\partial }^{2}w(y,\kappa )}{\partial y^2}\right|\hfill \\ +{L_2}^{\prime }\left|\theta \left(z\right(y,\kappa \left)\right)-\theta \left(w\right(y,\kappa \left)\right)\right|+{L_3}^{\prime }\left|h\left(z\right(y,\kappa \left)\right)-h\left(w\right(y,\kappa \left)\right)\right|,\hfill \end{array}$$

(7)

where ${L_1}^{\prime },{L_2}^{\prime },{L_3}^{\prime },M\ge 0$.and

$$\left|(M+L_1{L_1}^{\prime }+L_2{L_2}^{\prime }+\gamma L_3{L_3}^{\prime })\xi \right|\le \mathsf{\Gamma }(\mu +1),$$

then, Equation (6) has a unique solution.

Proof. 

Consider the integral operator S defined by

$$S\left(z(y,\kappa )\right)=\frac{1}{\mathsf{\Gamma }\left(\mu \right)}\underset{0}{\overset{\kappa }{\int }}{(\kappa -s)}^{\mu -1}X(z(y,s),\theta \left(z(y,\kappa )\right),h\left(z(y,\kappa )\right),\frac{{\partial }^{2}z(y,s)}{\partial y^2})ds+u\left(y\right).$$

Hence, from Lemma 1

$$S\left(z\right(y,\kappa \left)\right)=z(y,\kappa ).$$

Now, we prove this is a contraction.

$$\begin{array}{c}\left|S\left(z\right(y,\kappa \left)\right)-S\left(w\right(y,\kappa \left)\right)\right|=\hfill \\ |\frac{1}{\mathsf{\Gamma }\left(\mu \right)}\underset{0}{\overset{\kappa }{\int }}{(\kappa -s)}^{\mu -1}(X(z(y,s),\theta \left(z(y,s)\right),h\left(z(y,s)\right),\frac{{\partial }^{2}z(y,s)}{\partial y^2})\hfill \\ -X(w(y,s),\theta \left(w(y,s)\right),h\left(z(y,s)\right),\frac{{\partial }^{2}z(y,s)}{\partial y^2})\left)ds\right|\left|S\left(z\right(y,\kappa \left)\right)-S\left(w\right(y,\kappa \left)\right)\right|\hfill \\ \le \frac{1}{\mathsf{\Gamma }\left(\mu \right)}\underset{0}{\overset{\kappa }{\int }}{(\kappa -s)}^{\mu -1}[M\left|z(y,s)-w(y,s)\right|+{L_1}^{\prime }\left|\frac{{\partial }^{2}z(y,s)}{\partial y^2}-\frac{{\partial }^{2}w(y,s)}{\partial y^2}\right|\hfill \\ +{L_2}^{\prime }\left|\theta \left(z\right(y,s\left)\right)-\theta \left(w\right(y,s\left)\right)\right|+\gamma {L_3}^{\prime }\left|h\left(z\right(y,s\left)\right)-h\left(w\right(y,s\left)\right)\right|]ds\hfill \\ \le \frac{(M+L_1{L_1}^{\prime }+L_2{L_2}^{\prime }+\gamma L_3{L_3}^{\prime })}{\mathsf{\Gamma }\left(\mu \right)}∥z-w∥\underset{0}{\overset{\kappa }{\int }}{(\kappa -s)}^{\mu -1}ds\hfill \\ =\frac{(M+L_1{L_1}^{\prime }+L_2{L_2}^{\prime }+\gamma L_3{L_3}^{\prime }){\xi }^{\mu }}{\mathsf{\Gamma }(\mu +1)}∥z-w∥,\hfill \end{array}$$

from our assumption, it is clear that the operator is a contraction. Thus, using the Banach fixed-point theorem, S has a unique fixed point. Hence, the equation has a unique solution. □

3. Method

We approximate $h\left(z\right)$ using a suitable finite-degree polynomial. Let us consider

$$Q\left(z\right)={\alpha }_0+{\alpha }_{1}z+{\alpha }_2{z}^2+{\alpha }_3{z}^3+\dots +{\alpha }_k{z}^k$$

the approximation, where ${\alpha }_i$, $i=0,1,2,3\dots k$ are constants, k is an integer, so the problem becomes as follows:

$${}^C{D_{\kappa }}^{\mu }z(y,\kappa )=\frac{{\partial }^2}{\partial y^2}z(y,\kappa )+\frac{v}{y}\frac{\partial z}{\partial y}+r(y,\kappa )Q\left(z\right),$$

(8)

with initial condition $z(y,0)=u\left(y\right)$,$y\in \overline{\mathsf{\Pi }}$.

Now, we apply the rational homotopy perturbation method [27] in Equation (8). We construct homotopy

$$\begin{array}{c}H(z(y,\kappa ;p),p)=(1-p)\left[{D_{\kappa }}^{\mu }z(y,\kappa ;p)-{D_{\kappa }}^{\mu }{z}_0(y,\kappa ;p)\right]\hfill \\ +p[{D_{\kappa }}^{\mu }z(y,\kappa ;p)-\frac{{\partial }^2}{\partial y^2}z(y,\kappa ;p)-\frac{v}{y}\frac{\partial z(y,\kappa ;p)}{\partial y}-r(y,\kappa )Q\left(z\right)],\hfill \end{array}$$

(9)

where p is the embedding parameter, and $z_0(y,\kappa )$ is the initial approximation.

Consider

$$z(y,\kappa ;p)=\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )},$$

(10)

to be the solution of Equation (9), where $z_j$ are unknown functions, and ${\pi }_n$ are the known analytic functions of independent variables.

Now, putting values of Equation (10) and $Q\left(z\right)$ in Equation (9), we have

$$(1-p)\left[{D_{\kappa }}^{\mu }\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}-{D_{\kappa }}^{\mu }{z}_0(y,\kappa ;p)\right]+p[{D_{\kappa }}^{\mu }\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}-\frac{{\partial }^2}{\partial y^2}\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}$$

$$-\frac{v}{y}\frac{\partial \left[\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}\right]}{\partial y}-r(y,\kappa )({\alpha }_0+{\alpha }_{1}z+{\alpha }_2{z}^2+{\alpha }_3{z}^3+\dots +{\alpha }_k{z}^k)]=0.$$

(11)

After simplifying Equation (11), we obtain

$${D_{\kappa }}^{\mu }\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}={D_{\kappa }}^{\mu }{z}_0(y,\kappa ;p)-p[{D_{\kappa }}^{\mu }{z}_0(y,\kappa ;p)-\frac{{\partial }^2}{\partial y^2}\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}$$

$$-\frac{v}{y}\frac{\partial \left[\frac{{\displaystyle \sum _{j=0}^{\infty }}{p}^j{z}_j(y,\kappa )}{{\displaystyle \sum _{n=0}^{\infty }}{p}^n{\pi }_n(y,\kappa )}\right]}{\partial y}-r(y,\kappa )({\alpha }_0+{\alpha }_{1}z+{\alpha }_2{z}^2+{\alpha }_3{z}^3+\dots +{\alpha }_k{z}^k)],$$

(12)

we compare the coefficients of the powers of p as performed in [33] and [34] for HPM, and we obtain a set of fractional differential equations. After that, we apply the fractional integral operator on those fractional differential equations, and using the properties of fractional operators, we can obtain the values of $z_j$, $j=0,1,2\dots$

In the homotopy perturbation method [33,34,35], the highest power of p determines the order of approximation. In comparison, in the rational homotopy perturbation method, the highest power of p in the numerator and the denominator determines the order of approximation. For example, in our case, the order of approximation is $[j,n]$, as the highest powers of p in the numerator and denominator are j and n, respectively. The solution is provided when the limit of p tends toward 1. That is,

$$z_a=\underset{p\to 1}{lim}z=\frac{z_0+z_1+z_2+\dots }{{\pi }_0+{\pi }_1+{\pi }_2+\dots },$$

(13)

where $z_a$ denotes the approximate solution. The limit in Equation (13) exists if

$$\underset{p\to 1}{lim}\sum _{j=0}^{\infty }{z}_j(y,\kappa )$$

$$\underset{p\to 1}{lim}\sum _{n=0}^{\infty }{\pi }_n(y,\kappa ),$$

exist and

$$\sum _{n=0}^{\infty }{\pi }_n(y,\kappa )\ne 0.$$

4. Convergence of RHPM

Theorem 2. 

(Sufficient condition of convergence) Suppose that W and $W^{\prime }$ are two Banach spaces, and $T:W\to W^{\prime }$ is a contractive nonlinear mapping, that is,

$$\forall z,z^{\prime }\in W;∥T\left(z\right)-T\left(z^{\prime }\right)∥\le \rho ∥z-z^{\prime }∥;0<\rho <1$$

Then, using the Banach fixed-point theorem, T has a unique fixed point a. Assume that the RHPM sequence can be written as

$$Z_m=T\left(Z_{m-1}\right),Z_{m-1}=\sum _{j=0}^{m-1}\frac{z_j}{\eta },m=1,2,3\dots ,$$

where$\eta =\sum _n{\pi }_n$.

$$Z_0=\frac{z_0}{\eta }\in D_b\left(a\right),where,D_b\left(a\right)=\left\{z^{\prime }\in W|∥z^{\prime }-a∥<b\right\},$$

then, under these conditions,

1.

$Z_m\in D_b\left(a\right)$;

2.

$\underset{m\to \infty }{lim}{Z}_m=a$.

Detailed proof of this theorem is found in [27]. □

5. Examples

Example 1. 

Consider the fractional Emden–Fowler equation

$${D_{\kappa }}^{\mu }z(y,\kappa )=\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}+\frac{5}{y}\frac{\partial z(y,\kappa )}{\partial y}-(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2)z(y,\kappa ),$$

(14)

with initial solution $z(y,0)=1$ [30].

Now, we construct the homotopy as

$$\begin{array}{c}(1-p)\left({D_{\kappa }}^{\mu }z(y,\kappa )\right)+\hfill \\ p\left({D_{\kappa }}^{\mu }z(y,\kappa )-\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}-\frac{5}{y}\frac{\partial z(y,\kappa )}{\partial y}+(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2)z(y,\kappa )\right)=0.\hfill \end{array}$$

(15)

After simplification, we can rewrite Equation (15) as follows:

$${D_{\kappa }}^{\mu }z(y,\kappa )-p\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}-p\frac{5}{y}\frac{\partial z(y,\kappa )}{\partial y}+p(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2)z(y,\kappa )=0.$$

(16)

We consider the solution of order $[2,1]$ as

$$z(y,\kappa )=\frac{z_0(y,\kappa )+p{z}_1(y,\kappa )+p^2{z}_2(y,\kappa )}{1+c{y}^2\kappa p},$$

(17)

where c is the adjustment parameter. Using the expansion of ${\left(1+s\right)}^{-1}$, we can rewrite Equation (17) as

$$\left(z_0+p{z}_1+p^2{z}_2\right)\left(1-c{y}^2\kappa p+c^2{y}^4{\kappa }^2{p}^2+\dots \right).$$

Hence,

$$z=z_0+p{z}_1+p^2{z}_2-c{y}^2\kappa p{z}_0-c{y}^2\kappa p^2{z}_1+c^2{y}^4{\kappa }^2{p}^2{z}_0.$$

(18)

After putting the values of Equation (18) in Equation (16), we obtain

$$\begin{array}{c}{D_{\kappa }}^{\mu }{z}_0+p{D_{\kappa }}^{\mu }{z}_1+p^2{D_{\kappa }}^{\mu }{z}_2-pc{y}^2{D_{\kappa }}^{\mu }\left(\kappa z_0\right)\hfill \\ -p^{2}c{y}^2{D_{\kappa }}^{\mu }\left(\kappa z_1\right)+p^2{c}^2{y}^4{D_{\kappa }}^{\mu }\left({\kappa }^2{z}_0\right)-p\frac{{\partial }^2{z}_0}{\partial y^2}-p^2\frac{{\partial }^2{z}_1}{\partial y^2}+p^{2}c\kappa \frac{{\partial }^2{z}_0{y}^2}{\partial y^2}-\hfill \\ \frac{5}{y}\left(p\frac{\partial z_0}{\partial y}+p^2\frac{\partial z_1}{\partial y}-p^{2}c{y}^2\kappa \frac{\partial z_0}{\partial y}-2p^{2}c\kappa z_{0}y\right)+(p{z}_0+p^2{z}_1-p^{2}c{y}^2\kappa z_0)(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2).\hfill \end{array}$$

(19)

After simplifying Equation (19) and comparing the coefficients of the powers of p, we obtain a set of fractional differential equations.

$$p^0:{D_{\kappa }}^{\mu }{z}_0(y,\kappa )=0$$

(20)

$$p^1:{D_{\kappa }}^{\mu }{z}_1(y,\kappa )-c{y}^2{D_{\kappa }}^{\mu }\left(\kappa z_0(y,\kappa )\right)-\frac{{\partial }^2{z}_0(y,\kappa )}{\partial y^2}-\frac{5}{y}\frac{\partial z_0(y,\kappa )}{\partial y}+z_0(y,\kappa )(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2)=0$$

(21)

$$\begin{array}{c}{p}^2:{D_{\kappa }}^{\mu }{z}_2(y,\kappa )-c{y}^2{D_{\kappa }}^{\mu }\left(\kappa z_1(y,\kappa )\right)+c^2{y}^4{D_{\kappa }}^{\mu }\left({\kappa }^2{z}_0(y,\kappa )\right)-\frac{{\partial }^2{z}_1(y,\kappa )}{\partial y^2}+c\kappa \frac{{\partial }^2{y}^2{z}_0(y,\kappa )}{\partial y^2}\hfill \\ -\frac{5}{y}\left(\frac{\partial z_1}{\partial y}-c{y}^2\kappa \frac{\partial z_0}{\partial y}-2yc\kappa z_0\right)+\left(z_1-c{y}^2\kappa z_0\right)(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2).\hfill \end{array}$$

(22)

After applying fractional integration to Equations (14)–(16) and using the initial condition, we obtain the following:

$${I_{\kappa }}^{\mu }{D_{\kappa }}^{\mu }{z}_0(y,\kappa )=0,z_0(y,0)=1$$

(23)

$$\begin{array}{c}{I_{\kappa }}^{\mu }[{D_{\kappa }}^{\mu }{z}_1(y,\kappa )-c{y}^2{D_{\kappa }}^{\mu }\left(\kappa z_0(y,\kappa )\right)-\frac{{\partial }^2{z}_0(y,\kappa )}{\partial y^2}-\frac{5}{y}\frac{\partial z_0(y,\kappa )}{\partial y}+\hfill \\ z_0(y,\kappa )(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2)]=0,z_1(y,0)=0\hfill \end{array}$$

(24)

$$\begin{array}{c}{I_{\kappa }}^{\mu }[{D_{\kappa }}^{\mu }{z}_2(y,\kappa )-c{y}^2{D_{\kappa }}^{\mu }\left(\kappa z_1(y,\kappa )\right)+c^2{y}^4{D_{\kappa }}^{\mu }\left({\kappa }^2{z}_0(y,\kappa )\right)-\hfill \\ \frac{{\partial }^2{z}_1(y,\kappa )}{\partial y^2}+c\kappa \frac{{\partial }^2{y}^2{z}_0(y,\kappa )}{\partial y^2}-\frac{5}{y}\left(\frac{\partial z_1}{\partial y}-c{y}^2\kappa \frac{\partial z_0}{\partial y}-2yc\kappa z_0\right)+\hfill \\ \left(z_1-c{y}^2\kappa z_0\right)(12{\kappa }^2-2\kappa y^2+4{\kappa }^4{y}^2)],z_2(y,0)=0.\hfill \end{array}$$

(25)

For $\mu =1$, the exact solution of Equation (14) is

$$z(y,\kappa )=e^{{\kappa }^2{y}^2}.$$

Thus, after solving Equations (23), (24), and (25) and using the properties of fractional integration and differentiation, we obtain the values of $z_0$, $z_1$, $z_2$ as

$$z_0(y,\kappa )=1$$

(26)

$$z_1(y,\kappa )=c{y}^2\kappa -\frac{24}{\mathsf{\Gamma }(3+\mu )}{\kappa }^{2+\mu }+2y^2\frac{{\kappa }^{1+\mu }}{\mathsf{\Gamma }(2+\mu )}-\frac{96}{\mathsf{\Gamma }(5+\mu )}{y}^2{\kappa }^{4+\mu }$$

(27)

$$\begin{array}{c}{z}_2(y,\kappa )=-c^2{y}^4{\kappa }^2+\frac{12c{\kappa }^{1+\mu }}{\mathsf{\Gamma }(2+\mu )}+\frac{4c{y}^4{\kappa }^{2+\mu }}{\mathsf{\Gamma }(3+\mu )}-\frac{72c{y}^2{\kappa }^{3+\mu }}{\mathsf{\Gamma }(4+\mu )}+\hfill \\ c{y}^2\kappa \left(c{y}^2\kappa +\frac{2y^2{\kappa }^{1+\mu }}{\mathsf{\Gamma }(2+\mu )}-\frac{24{\kappa }^{2+\mu }}{\mathsf{\Gamma }(3+\mu )}-\frac{96y^2{\kappa }^{4+\mu }}{\mathsf{\Gamma }(5+\mu )}\right)\hfill \\ -\frac{480c{y}^4{\kappa }^{5+\mu }}{\mathsf{\Gamma }(6+\mu )}+\frac{24{\kappa }^{1+2\mu }}{\mathsf{\Gamma }(2+2\mu )}+\frac{4y^4{\kappa }^{2+2\mu }\mathsf{\Gamma }(3+\mu )}{\mathsf{\Gamma }(2+\mu )\mathsf{\Gamma }(3+2\mu )}-\hfill \\ \frac{24y^2{\kappa }^{3+2\mu }\mathsf{\Gamma }(4+\mu )}{\mathsf{\Gamma }(2+\mu )\mathsf{\Gamma }(4+2\mu )}-\frac{48y^2{\kappa }^{3+2\mu }\mathsf{\Gamma }(4+\mu )}{\mathsf{\Gamma }(3+\mu )\mathsf{\Gamma }(4+2\mu )}-\frac{864{\kappa }^{4+2\mu }\mathsf{\Gamma }(5+\mu )}{\mathsf{\Gamma }(3+\mu )\mathsf{\Gamma }(5+2\mu )}-\hfill \\ \frac{8y^4{\kappa }^{5+2\mu }\mathsf{\Gamma }(6+\mu )}{\mathsf{\Gamma }(2+\mu )\mathsf{\Gamma }(6+2\mu )}-\frac{192y^4{\kappa }^{5+2\mu }\mathsf{\Gamma }(6+\mu )}{\mathsf{\Gamma }(5+\mu )\mathsf{\Gamma }(6+2\mu )}+\frac{96y^2{\kappa }^{6+2\mu }\mathsf{\Gamma }(7+\mu )}{\mathsf{\Gamma }(3+\mu )\mathsf{\Gamma }(7+2\mu )}+\hfill \\ \frac{1152y^2{\kappa }^{6+2\mu }\mathsf{\Gamma }(7+\mu )}{\mathsf{\Gamma }(5+\mu )\mathsf{\Gamma }(7+2\mu )}+\frac{384y^4{\kappa }^{8+2\mu }\mathsf{\Gamma }(9+\mu )}{\mathsf{\Gamma }(5+\mu )\mathsf{\Gamma }(9+2\mu )}.\hfill \end{array}$$

(28)

For $\mu =1$

$$z_0(y,\kappa )=1$$

$$z_1(y,\kappa )=c{y}^2\kappa +y^2{\kappa }^2-4{\kappa }^3-\frac{4y^2{\kappa }^5}{5}$$

$$z_2(y,\kappa )=6c{\kappa }^2-c^2{y}^4{\kappa }^2+4{\kappa }^3+\frac{2}{3}c{y}^4{\kappa }^3-3c{y}^2{\kappa }^4+\frac{y^4{\kappa }^4}{2}-4y^2{\kappa }^5-24{\kappa }^6$$

$$-\frac{2}{3}c{y}^4{\kappa }^6-\frac{4y^4{\kappa }^7}{5}+\frac{16y^2{\kappa }^8}{5}+\frac{8y^4{\kappa }^{10}}{25}+c{y}^2\kappa \left(c{y}^2\kappa +y^2{\kappa }^2-4{\kappa }^3-\frac{4y^2{\kappa }^5}{5}\right)$$

When $p\to 1$, the solution will be

$$z_a(y,\kappa )=\frac{1}{1+c{y}^2\kappa }[1+c{y}^2\kappa +6c{\kappa }^2+y^2{\kappa }^2-c^2{y}^4{\kappa }^2+\frac{2}{3}c{y}^4{\kappa }^3-3c{y}^2{\kappa }^4+\frac{y^4{\kappa }^4}{2}-\frac{24y^2{\kappa }^5}{5}$$

$$-24{\kappa }^6-\frac{2}{3}c{y}^4{\kappa }^6-\frac{4y^4{\kappa }^7}{5}+\frac{16y^2{\kappa }^8}{5}+\frac{8y^4{\kappa }^{10}}{25}+c{y}^2\kappa \left(c{y}^2\kappa +y^2{\kappa }^2-4{\kappa }^3-\frac{4y^2{\kappa }^5}{5}\right)].$$

(29)

The value of adjustment parameter c is adjusted using the procedure in [33,34,35] using the nonlinear fit command. The value of c is found to be 3.03873 ×${10}^{-6}$.

Example 2. 

Consider the time-fractional Emden–Fowler equation

$${D_{\kappa }}^{\mu }z(y,\kappa )=\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}+\frac{2}{y}\frac{\partial z(y,\kappa )}{\partial y}-(5+4y^2)z(y,\kappa )-(6-5y^2-4y^4),$$

(30)

with initial condition

$$z(y,0)=y^2+e^{y^2}$$

Now, we construct the homotopy as

$$(1-p){D_{\kappa }}^{\mu }z(y,\kappa )+p({D_{\kappa }}^{\mu }z(y,\kappa )-\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}-\frac{2}{y}\frac{\partial z(y,\kappa )}{\partial y}+(5+4y^2)z(y,\kappa )+(6-5y^2-4y^4))=0.$$

(31)

After simplification, we can rewrite the above equation as follows:

$${D_{\kappa }}^{\mu }z(y,\kappa )-p\frac{{\partial }^{2}z(y,\kappa )}{\partial y^2}-p\frac{2}{y}\frac{\partial z(y,\kappa )}{\partial y}+p(5+4y^2)z(y,\kappa )+p(6-5y^2-4y^4))=0.$$

(32)

We consider the solution of order $[2,1]$ as

$$z(y,\kappa )=\frac{z_0(y,\kappa )+p{z}_1(y,\kappa )+p^2{z}_2(y,\kappa )}{1+c{y}^2\kappa p},$$

(33)

where c is the adjustment parameter. Using the expansion of ${\left(1+s\right)}^{-1}$, we can rewrite Equation (33) as

$$\left(z_0+p{z}_1+p^2{z}_2\right)\left(1-c{y}^2\kappa p+c^2{y}^4{\kappa }^2{p}^2+\dots \right).$$

Hence,

$$z=z_0+p{z}_1+p^2{z}_2-c{y}^2\kappa p{z}_0-c{y}^2\kappa p^2{z}_1+c^2{y}^4{\kappa }^2{p}^2{z}_0.$$

(34)

After putting the values of Equation (34) in Equation (32), we obtain

$$\begin{array}{c}{D_{\kappa }}^{\mu }{z}_0+p{D_{\kappa }}^{\mu }{z}_1+p^2{D_{\kappa }}^{\mu }{z}_2-pcy{D_{\kappa }}^{\mu }\left(\kappa z_0\right)-p^{2}cy{D_{\kappa }}^{\mu }\left(\kappa z_1\right)\hfill \\ +p^2{c}^2{y}^2{D_{\kappa }}^{\mu }\left({\kappa }^2{z}_0\right)-p\frac{{\partial }^2{z}_0}{\partial y}-p^2\frac{{\partial }^2{z}_1}{\partial y}+p^{2}c\kappa y\frac{{\partial }^2{z}_0}{\partial y}\hfill \\ +2p^{2}c\kappa \frac{\partial z_0}{\partial y}-\frac{2}{y}\left(p\frac{\partial z_0}{\partial y}+p^2\frac{\partial z_1}{\partial y}-p^{2}cy\kappa \frac{\partial z_0}{\partial y}-p^{2}c\kappa z_0\right)\hfill \\ +(p{z}_0+p^2{z}_1-p^{2}cy\kappa z_0)(5+4y^2)+p(6-5y^2-4y^4)=0.\hfill \end{array}$$

(35)

After simplifying Equation (35) and comparing the coefficients of the powers of p, we obtain a set of fractional differential equations.

$$p^0:{D_{\kappa }}^{\mu }{z}_0(y,\kappa )=0$$

(36)

$$\begin{array}{c}{p}^1:{D_{\kappa }}^{\mu }{z}_1(y,\kappa )-cy{D_{\kappa }}^{\mu }\left(\kappa z_0(y,\kappa )\right)-\frac{{\partial }^2{z}_0(y,\kappa )}{\partial y}\hfill \\ -\frac{2}{y}\frac{\partial z_0(y,\kappa )}{\partial y}+z_0(y,\kappa )(5+4y^2)+(6-5y^2-4y^4)=0\hfill \end{array}$$

(37)

$$\begin{array}{c}{p}^2:{D_{\kappa }}^{\mu }{z}_2(y,\kappa )-cy{D_{\kappa }}^{\mu }\left(\kappa z_1(y,\kappa )\right)+c^2{y}^2{D_{\kappa }}^{\mu }\left({\kappa }^2{z}_0(y,\kappa )\right)-\hfill \\ \frac{{\partial }^2{z}_1(y,\kappa )}{\partial y}+cy\kappa \frac{{\partial }^2{z}_0(y,\kappa )}{\partial y}+2c\kappa \frac{\partial z_0}{\partial y}-\frac{2}{y}\left(\frac{\partial z_1}{\partial y}-cy\kappa \frac{\partial z_0}{\partial y}-c\kappa z_0\right)\hfill \\ +\left(z_1-cy\kappa z_0\right)(5+4y^2)=0.\hfill \end{array}$$

(38)

Applying fractional integration properties and initial conditions, we can write

$${I_{\kappa }}^{\mu }{D_{\kappa }}^{\mu }{z}_0(y,\kappa )=0,z_0(y,0)=y^2+e^{y^2}$$

(39)

$$\begin{array}{c}{I_{\kappa }}^{\mu }[{D_{\kappa }}^{\mu }{z}_1(y,\kappa )-cy{D_{\kappa }}^{\mu }\left(\kappa z_0(y,\kappa )\right)-\frac{{\partial }^2{z}_0(y,\kappa )}{\partial y}-\frac{2}{y}\frac{\partial z_0(y,\kappa )}{\partial y}\hfill \\ +z_0(y,\kappa )(5+4y^2)+(6-5y^2-4y^4)]=0,z_1(y,0)=0\hfill \end{array}$$

(40)

$$\begin{array}{c}{I_{\kappa }}^{\mu }[{D_{\kappa }}^{\mu }{z}_2(y,\kappa )-cy{D_{\kappa }}^{\mu }\left(\kappa z_1(y,\kappa )\right)+c^2{y}^2{D_{\kappa }}^{\mu }\left({\kappa }^2{z}_0(y,\kappa )\right)\hfill \\ -\frac{{\partial }^2{z}_1(y,\kappa )}{\partial y}+cy\kappa \frac{{\partial }^2{z}_0(y,\kappa )}{\partial y}+2c\kappa \frac{\partial z_0}{\partial y}-\frac{2}{y}\left(\frac{\partial z_1}{\partial y}-cy\kappa \frac{\partial z_0}{\partial y}-c\kappa z_0\right)\hfill \\ +\left(z_1-cy\kappa z_0\right)(5+4y^2)]=0,z_2(y,0)=0.\hfill \end{array}$$

(41)

For $\mu =1$, the exact solution of Equation (30) is

$$z(y,\kappa )=e^{\kappa +y^2}+y^2$$

After solving, we obtain the values

$$z_0(y,\kappa )=y^2+e^{y^2}$$

(42)

$$z_1(y,\kappa )=c{\mathrm{e}}^{y^2}\kappa y^2+c\kappa y^4+\frac{{\mathrm{e}}^{y^2}{\kappa }^{\mu }}{\mathsf{\Gamma }(1+\mu )}$$

(43)

$$z_2(y,\kappa )=-c^2{\kappa }^2{y}^4\left({\mathrm{e}}^{y^2}+y^2\right)+c\kappa y^2\left(c{\mathrm{e}}^{y^2}\kappa y^2+c\kappa y^4+\frac{{\mathrm{e}}^{y^2}{\kappa }^{\mu }}{\mathsf{\Gamma }(1+\mu )}\right)+\frac{{\mathrm{e}}^{y^2}{\kappa }^{2\mu }}{\mathsf{\Gamma }(1+2\mu )}$$

(44)

For $\mu =1$ and $c=-0.04725871046550184$, the solution is

$$z(y,\kappa )=\frac{1}{1-0.0472587\kappa y^2}[{\mathrm{e}}^{y^2}+{\mathrm{e}}^{y^2}\kappa +\frac{1}{2}{\mathrm{e}}^{y^2}{\kappa }^2+y^2-0.0472587{\mathrm{e}}^{y^2}\kappa y^2-0.0472587\kappa y^4$$

$$-0.00223339{\kappa }^2{y}^4\left({\mathrm{e}}^{y^2}+y^2\right)-0.0472587\kappa y^2\left({\mathrm{e}}^{y^2}\kappa -0.0472587{\mathrm{e}}^{y^2}\kappa y^2-0.0472587\kappa y^4\right)].$$

(45)

6. Conclusions

We used a rational homotopy perturbation method to solve the time fractional Emden–Fowler equation. This method presented a great potential to solve fractional or partial differential equations. Two numerical examples were investigated using this proposed approach. It is clear from the 2D (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8) and 3D plots (Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14) that this method is approximately accurate. The numerical results obtained in the

Table 1. Comparison of the exact and approximate solution of Example 1 when $\kappa =0.1$ and y varies.

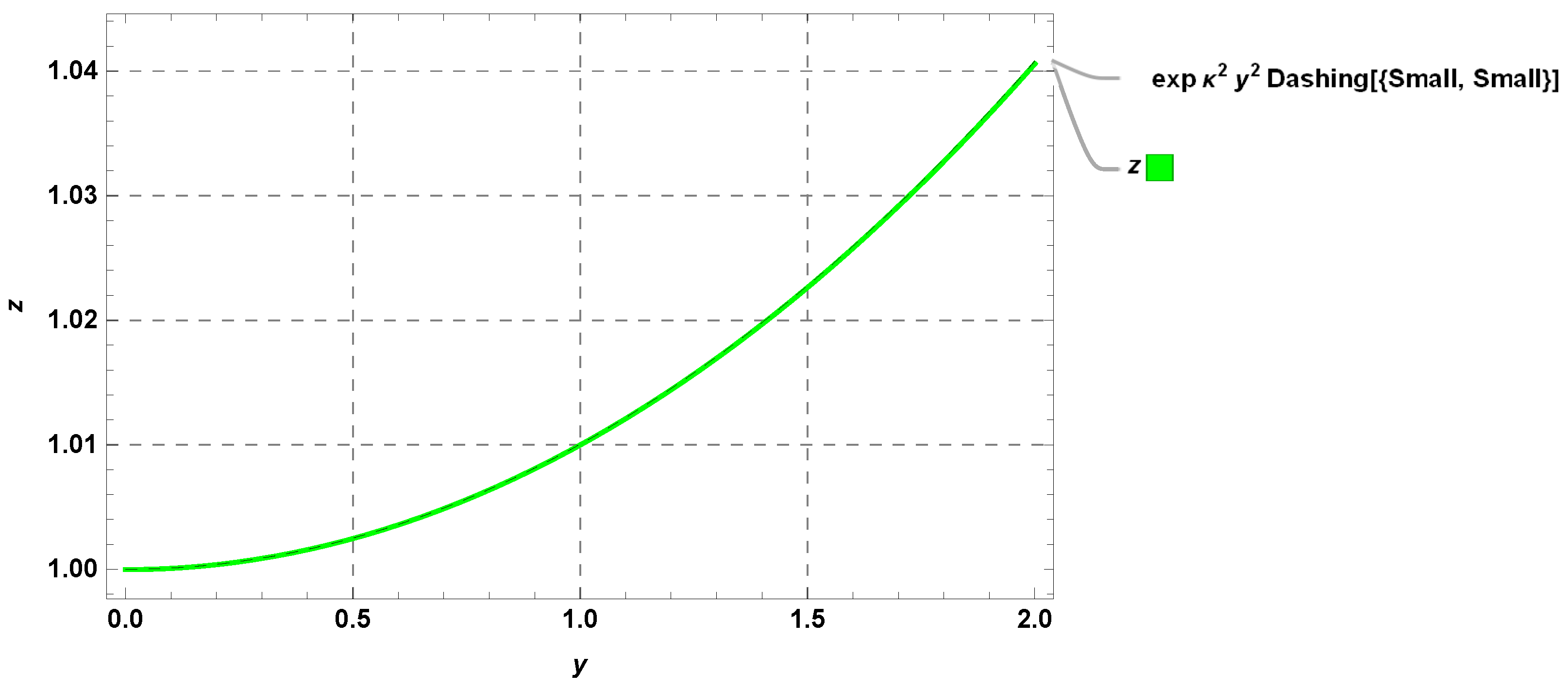
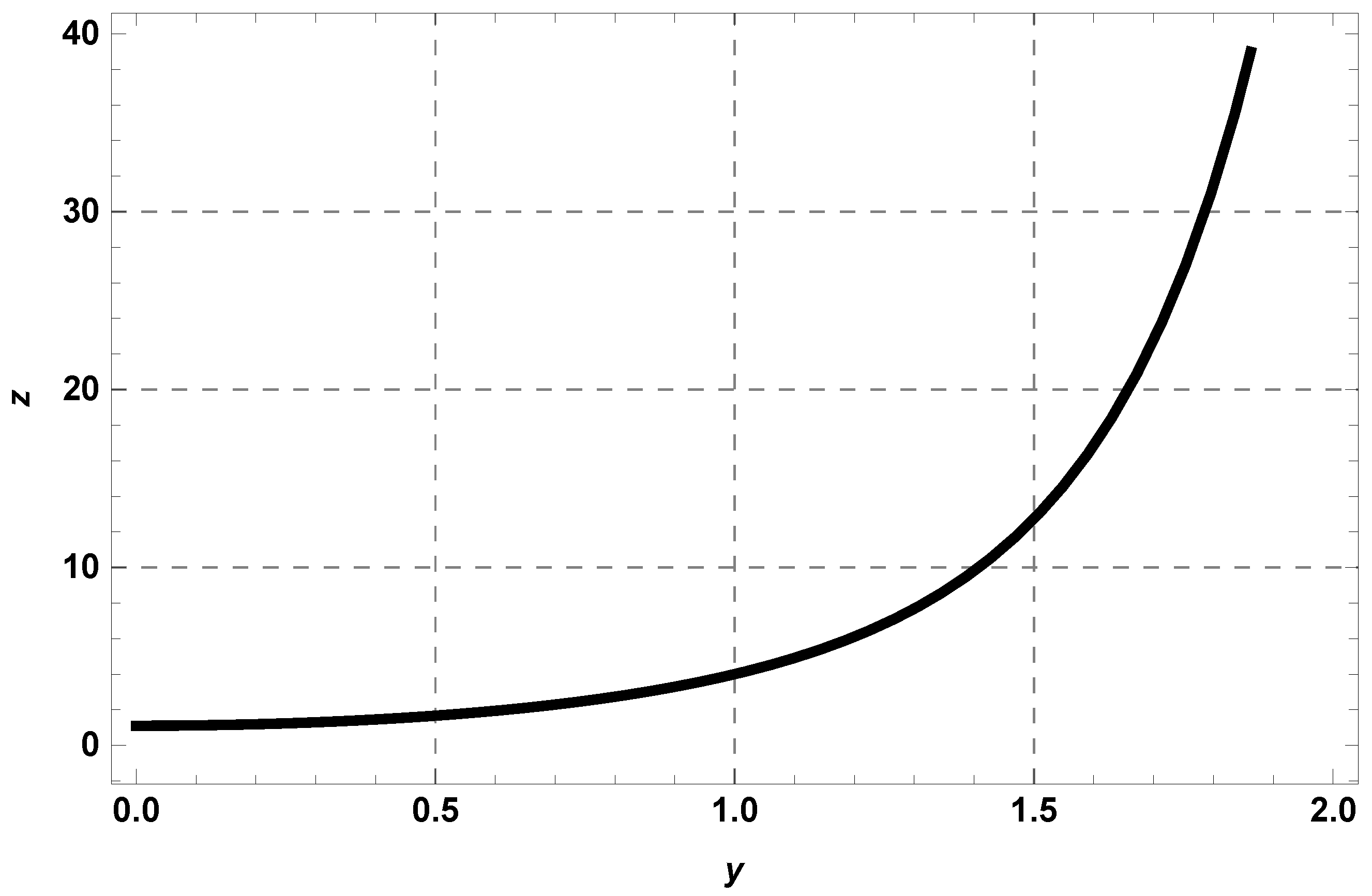
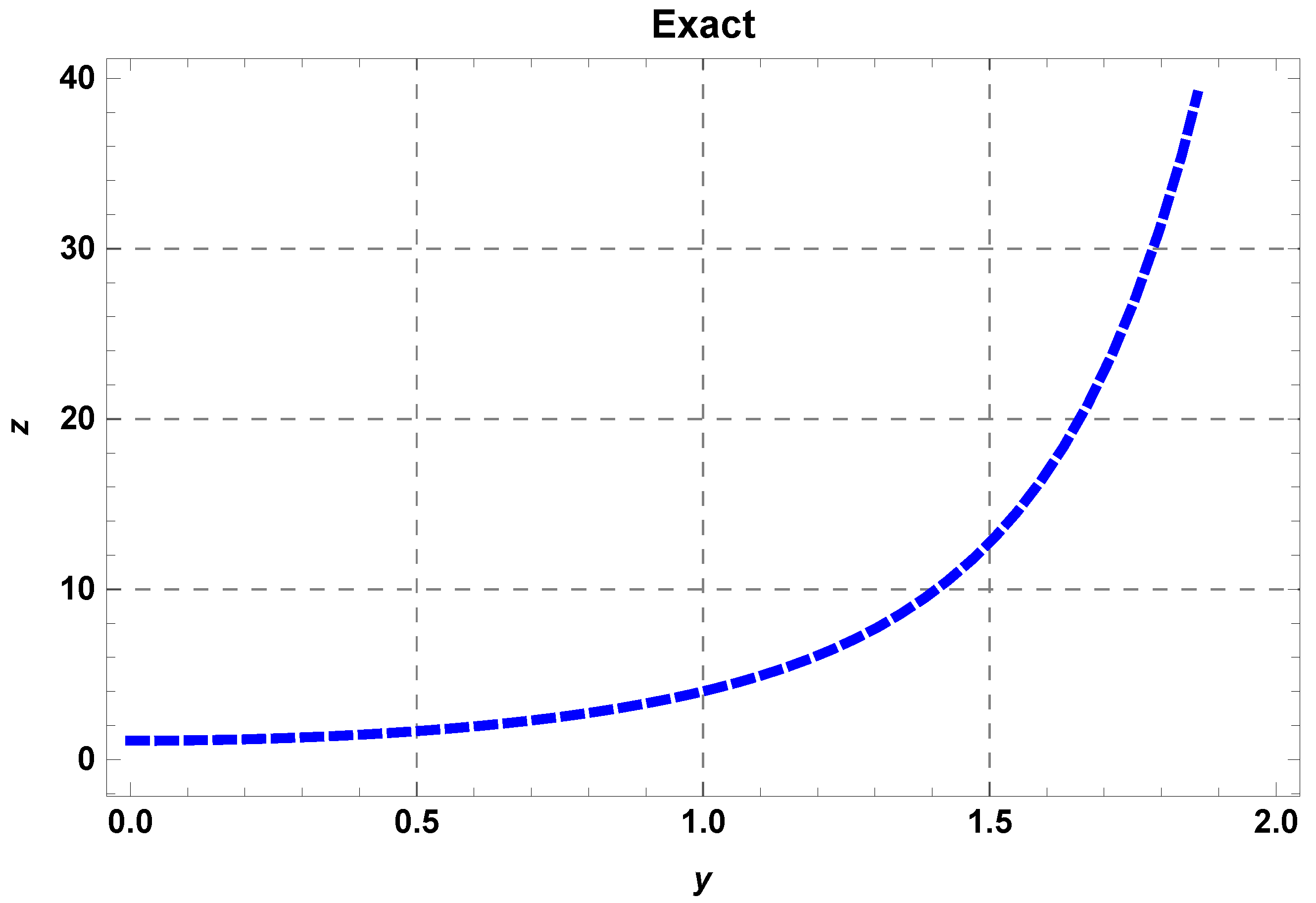
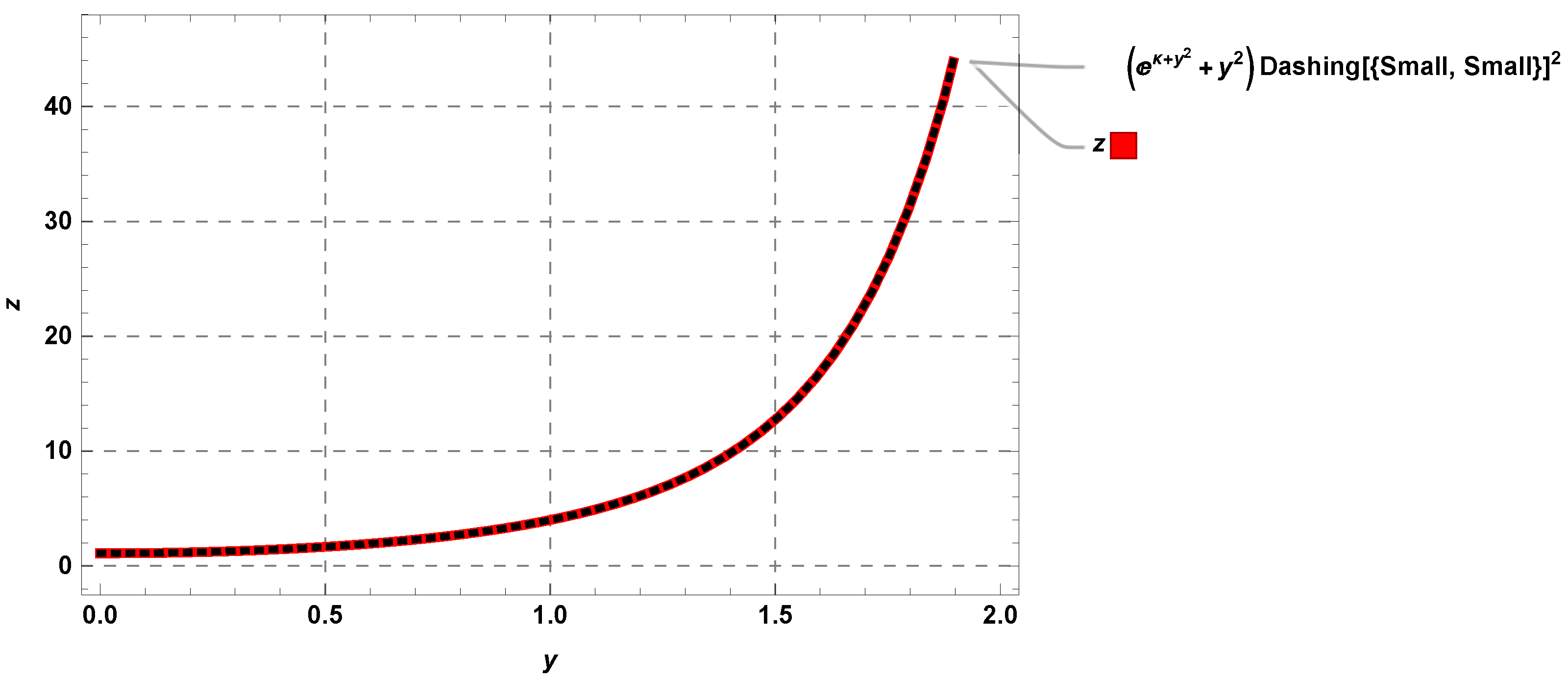
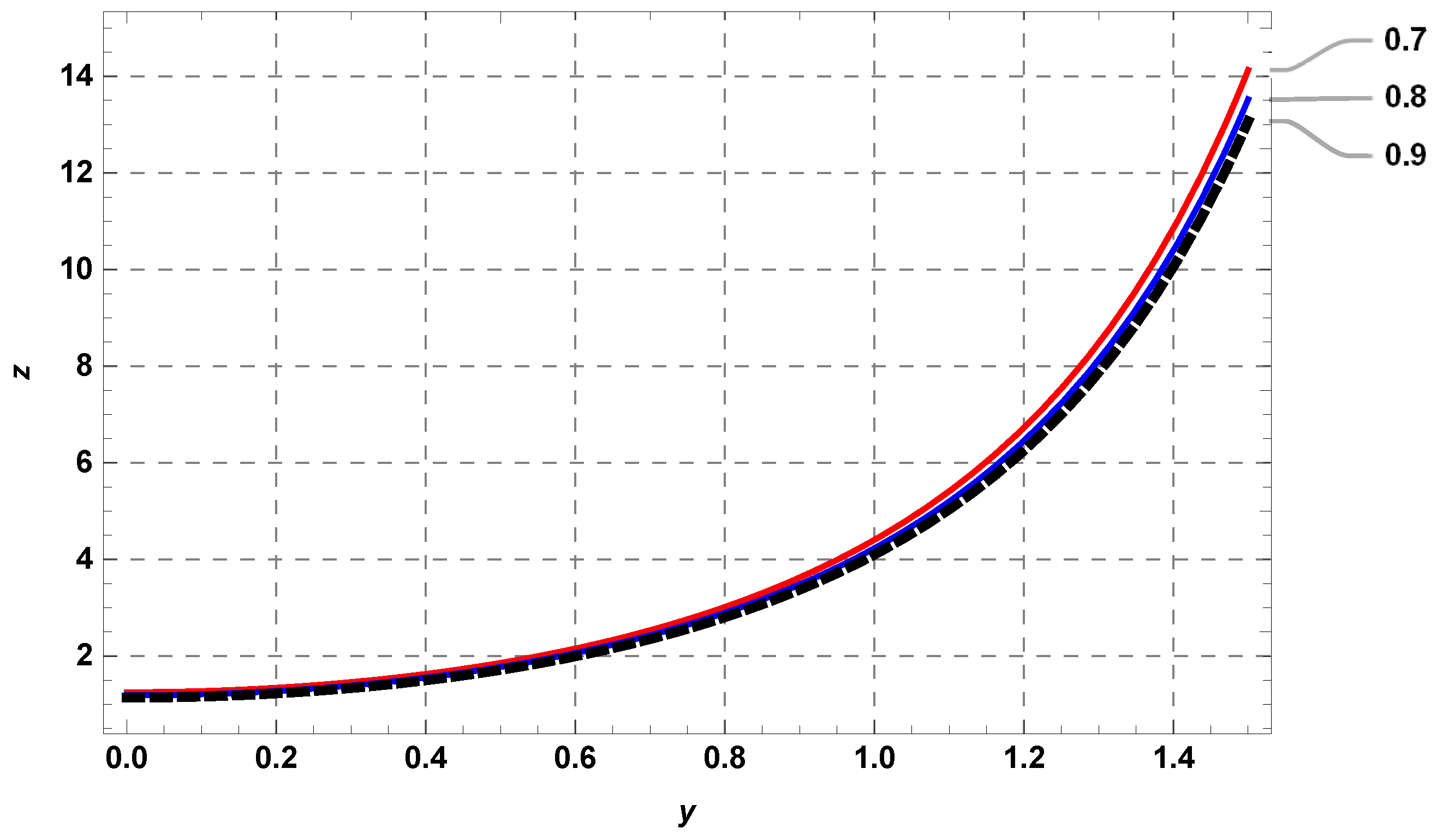
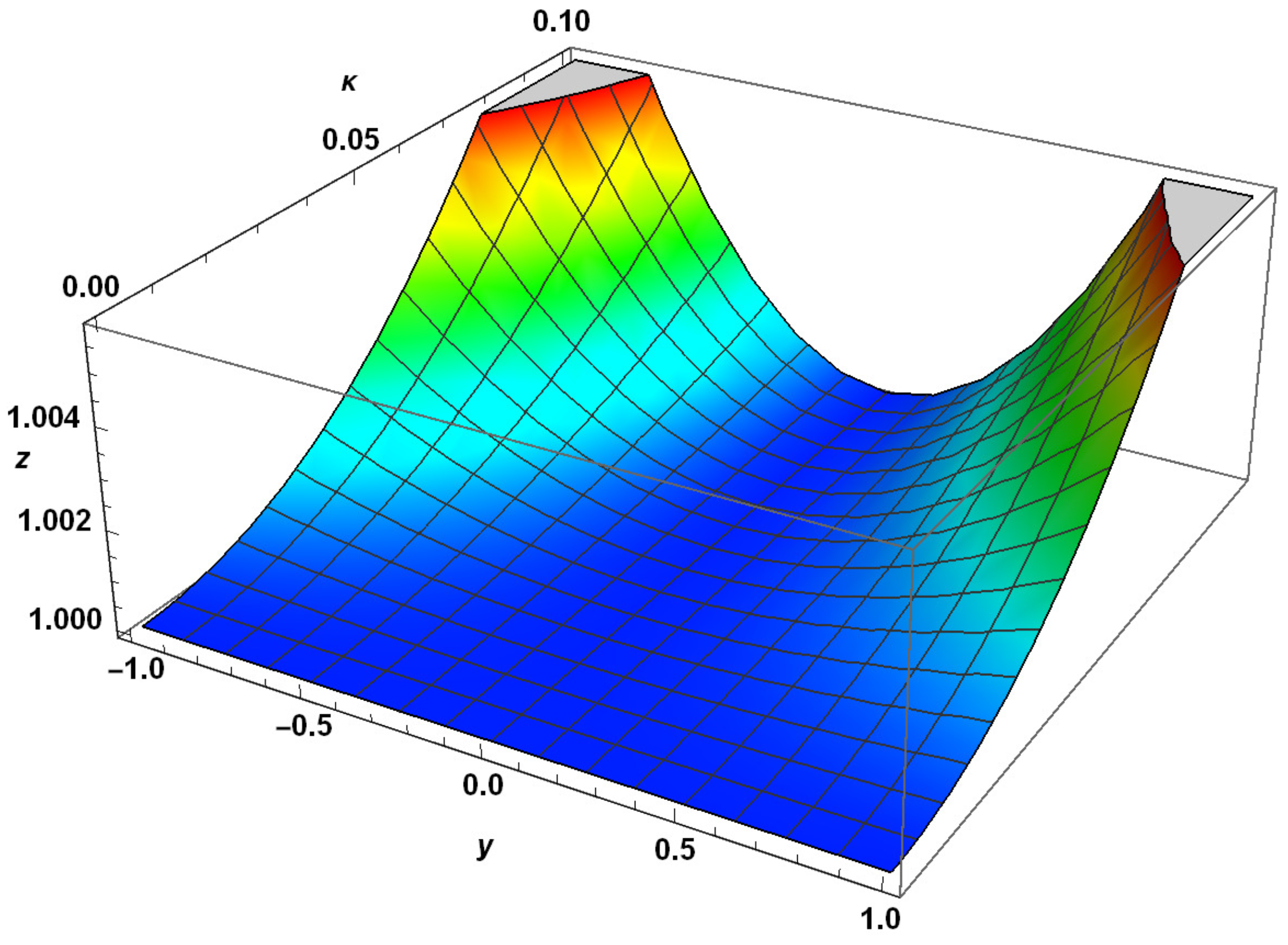
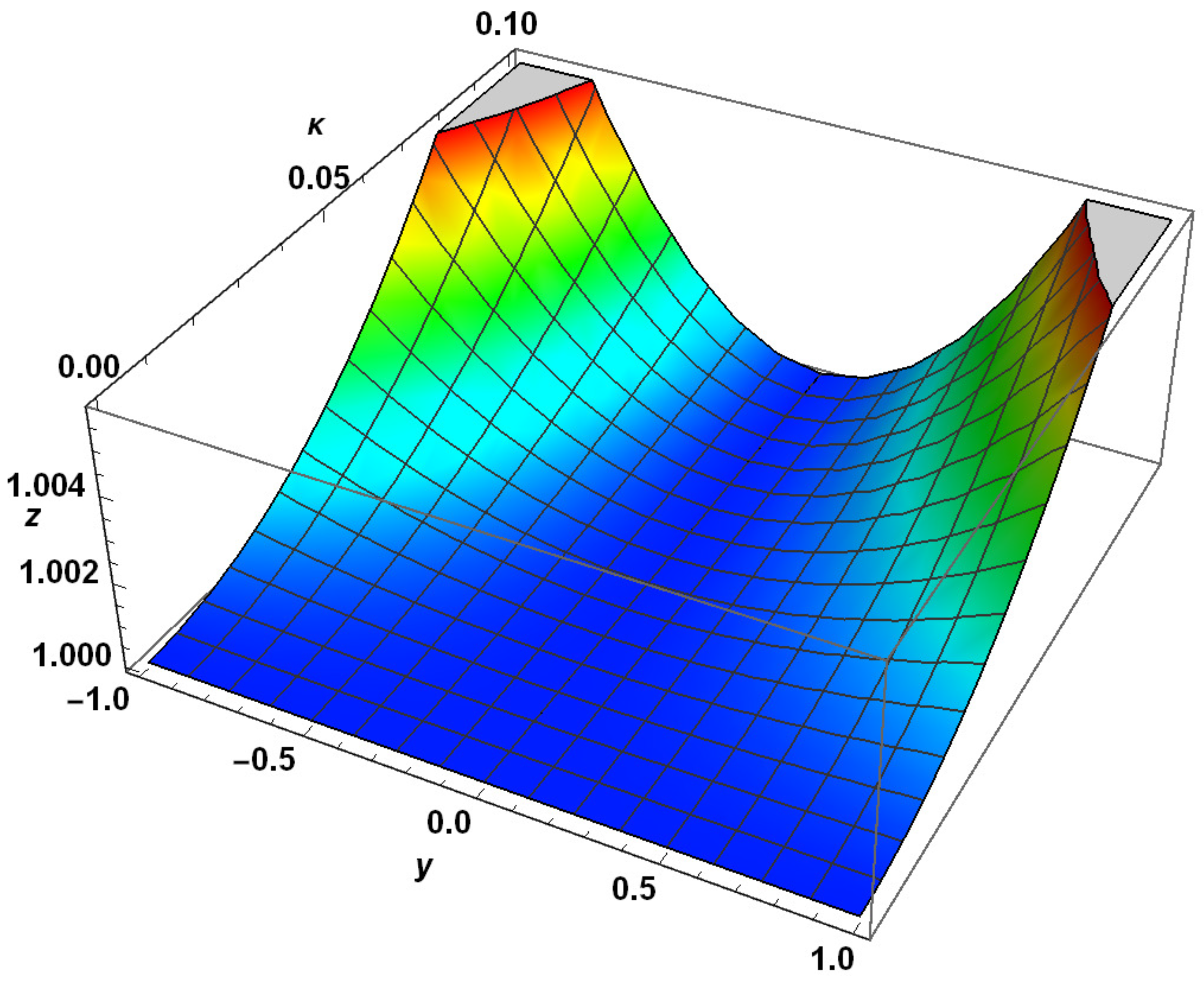
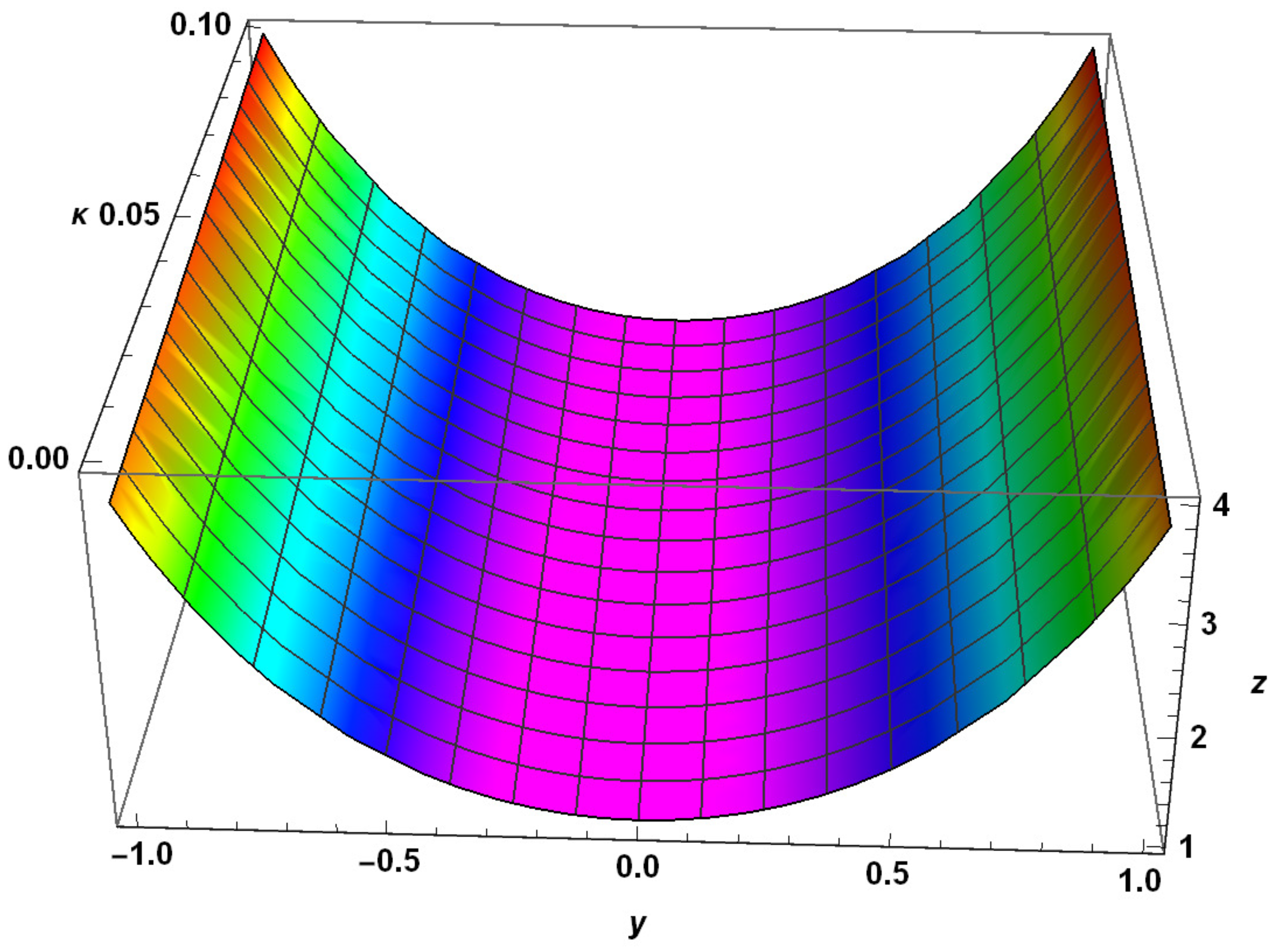
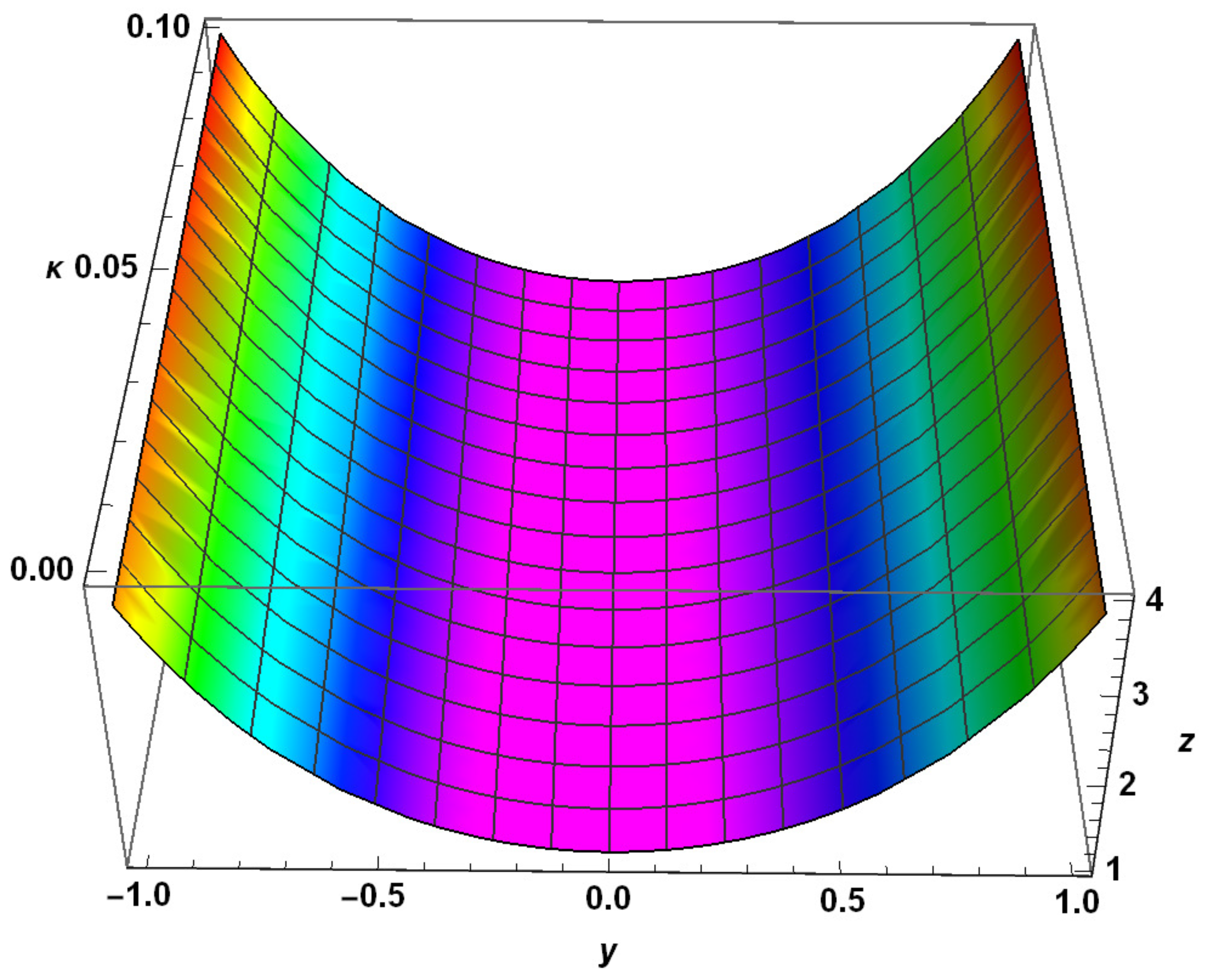
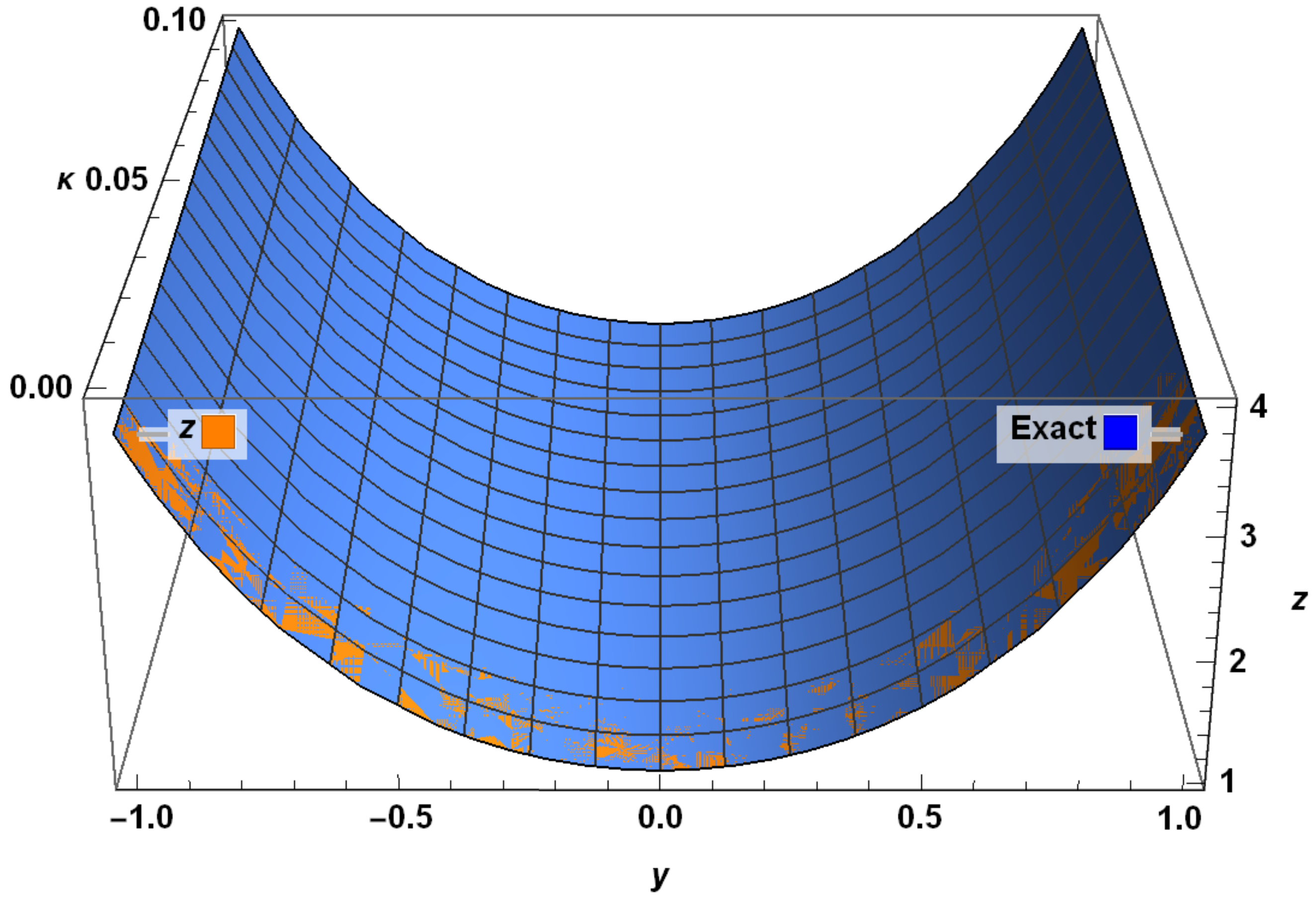
y	Exact Solution	RHPM Solution	Absolute Error	$\mathit{\mu }=0.7$	$\mathit{\mu }=0.8$	$\mathit{\mu }=0.9$
0.1	1.0001	1.00008	0.00092	1.02057	1.00819	1.00249
0.2	1.0004	1.00037	0.00003	1.02134	1.00875	1.0029
0.3	1.0009	1.00087	0.00003	1.02261	1.00969	1.00358
0.4	1.0016	1.00157	0.00003	1.0244	1.011	1.00454
0.5	1.0025	1.00247	0.00003	1.02671	1.01269	1.00578
0.6	1.00361	1.00357	0.00004	1.02953	1.01476	1.00729
0.7	1.00491	1.00486	0.00004	1.03288	1.01722	1.00908
0.8	1.00642	1.00637	0.00005	1.03677	1.02006	1.01115
0.9	1.00813	1.00808	0.00005	1.0412	1.02329	1.0135

and

Table 2. Comparison of the exact and approximate solution of Example 2 when $\kappa =0.1$ and y varies.

y	Exact Solution	RHPM Solution	Absolute Error	$\mathit{\mu }=0.7$	$\mathit{\mu }=0.8$	$\mathit{\mu }=0.9$
0.1	1.1261	1.1262	0.0001	1.27422	1.20967	1.16181
0.2	1.1901	1.1902	0.0001	1.34272	1.27621	1.22689
0.3	1.29906	1.29925	0.00019	1.45952	1.3896	1.33775
0.4	1.45673	1.45693	0.0002	1.62884	1.55384	1.49822
0.5	1.66886	1.66907	0.00021	1.85718	1.77511	1.71425
0.6	1.94384	1.94407	0.00023	2.15409	2.06246	1.99452
0.7	2.29373	2.29399	0.00026	2.53319	2.42883	2.35145
0.8	2.73564	2.73594	0.00030	3.01389	2.89262	2.80271
0.9	3.29398	3.29432	0.00034	3.62384	3.48007	3.37349

also confirm the accuracy of the proposed approach. This method is easy to implement on these types of equations. More research should be carried out to solve other PDEs and nonlinear fractional differential equations using the present approach.