Effects of M-Truncated Derivative and Multiplicative Noise on the Exact Solutions of the Breaking Soliton Equation
Abstract
1. Introduction
2. The SFSBSE’s Wave Equation
Modified F-Expansion Method
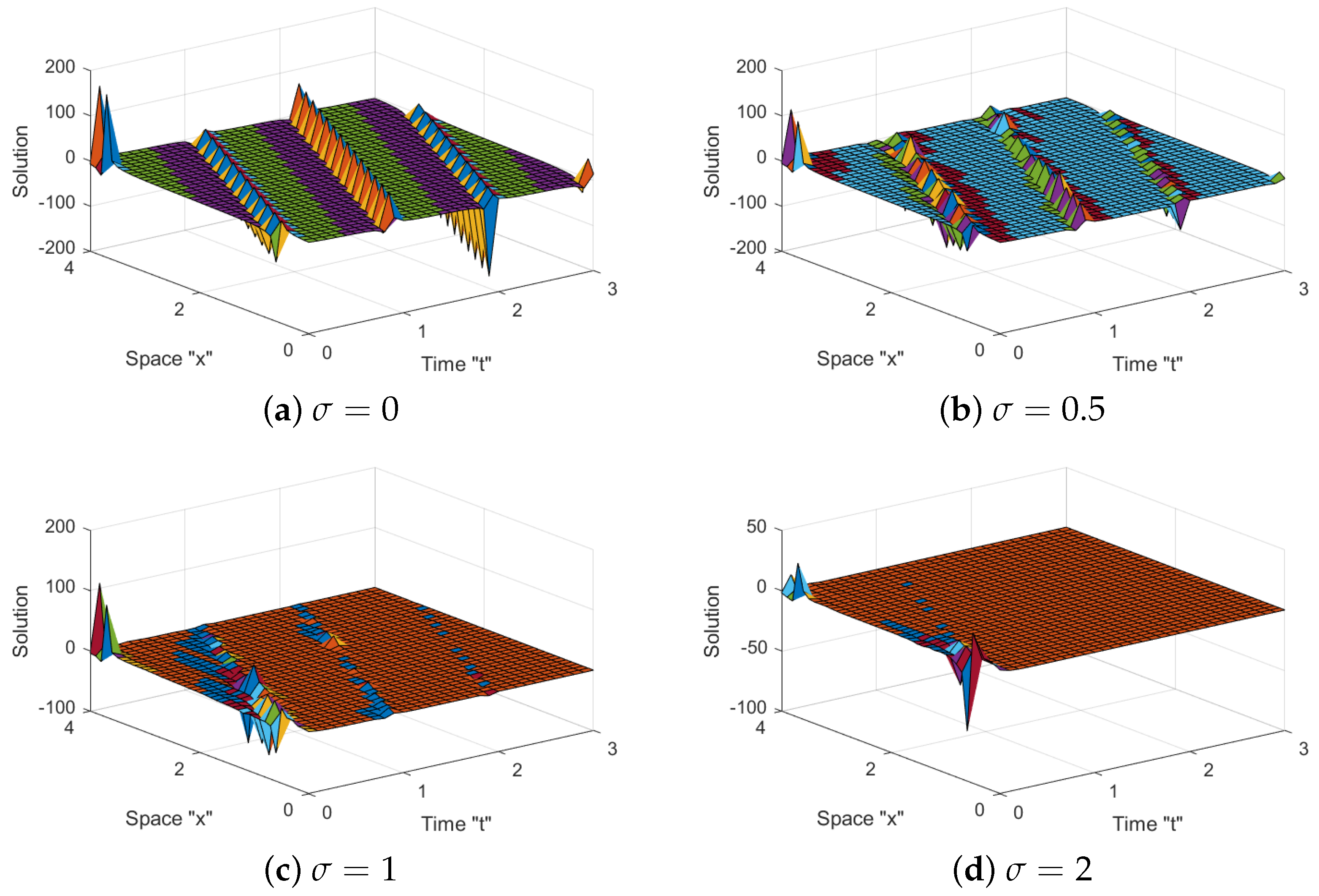
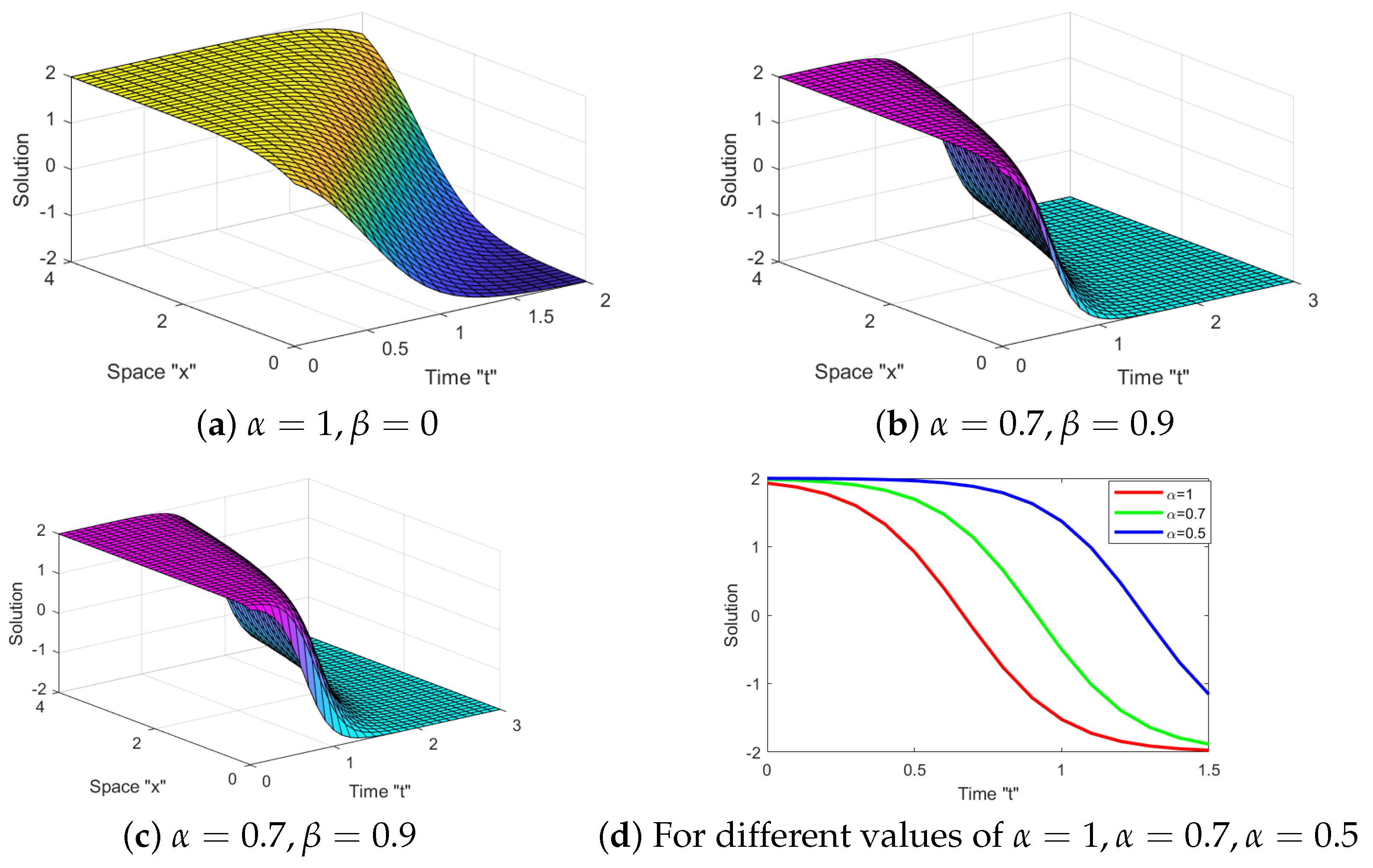
3. The Impact of M-Truncated Derivative and Noise
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Ntegration to Arbitrary Order; Volume 11 of Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M. Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics 2022, 11, 194. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing: Singapore, 2000. [Google Scholar]
- Alshammari, M.; Iqbal, N.; Mohammed, W.W.; Botmart, T. The solution of fractional-order system of KdV equations with exponential-decay kernel. Results Phys. 2022, 38, 105615. [Google Scholar] [CrossRef]
- Riesz, M. L’intégrale de Riemann-Liouville et le problème de Cauchy pour l’équation des ondes. Bulletin de la Société Mathématique de France 1939, 67, 153–170. [Google Scholar] [CrossRef]
- Wang, K.L.; Liu, S.Y. He’s fractional derivative and its application for fractional Fornberg-Whitham equation. Therm. Sci. 2016, 1, 54. [Google Scholar] [CrossRef]
- Miller, S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional differential without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel. Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Sousa, J.V.; de Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The ()-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the ()-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solution of the Kuramoto-Shivashinsky equation on an unbounded domain. Chin. Ann. Math. Ser. B 2018, 39, 145–162. [Google Scholar] [CrossRef]
- Mohammed, W.W. Fast-diffusion limit for reaction–diffusion equations with degenerate multiplicative and additive noise. J. Dyn. Differ. Equ. 2021, 33, 577–592. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-φ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Yan, C. A simple transformation for nonlinear waves. Phys. Lett. A 1996, 224, 77–84. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alshammari, M.; Cesarano, C.; El-Morshedy, M. Brownian Motion Effects on the Stabilization of Stochastic Solutions to Fractional Diffusion Equations with Polynomials. Mathematics 2022, 10, 1458. [Google Scholar] [CrossRef]
- Al-Askar, E.M.; Mohammed, W.W.; Albalahi, A.M.; El-Morshedy, M. The Impact of the Wiener process on the analytical solutions of the stochastic (2+ 1)-dimensional breaking soliton equation by using tanh–coth method. Mathematics 2022, 10, 817. [Google Scholar] [CrossRef]
- Wang, Z.L.; Sun, L.J.; Hua, R.; Zhang, L.H.; Wang, H.F. Lie Symmetry Analysis, Particular Solutions and Conservation Laws of Benjiamin Ono Equation. Symmetry 2022, 14, 9. [Google Scholar] [CrossRef]
- Huo, C.; Li, L. Lie Symmetry Analysis, Particular Solutions and Conservation Laws of a New Extended (3+1)-Dimensional Shallow Water Wave Equation. Symmetry 2022, 14, 1855. [Google Scholar] [CrossRef]
- Kumar, S.; Kour, B.; Yao, S.-W.; Inc, M.; Osman, M.S. Invariance Analysis, Exact Solution and Conservation Laws of (2+1) Dim Fractional Kadomtsev-Petviashvili (KP) System. Symmetry 2021, 13, 477. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equ. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Blömker, D. Fast-diffusion limit for reaction-diffusion equations with multiplicative noise. Stoch. Anal. Appl. 2016, 34, 961–978. [Google Scholar] [CrossRef]
- Imkeller, P.; Monahan, A.H. Conceptual stochastic climate models. Stoch. Dynam. 2002, 2, 311–326. [Google Scholar] [CrossRef]
- Eftekhari, T.; Rashidinia, J. A novel and efficient operational matrix for solving nonlinear stochastic differential equations driven by multi-fractional Gaussian noise. Appl. Math. Comput. 2022, 429, 127218. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M.; El-Morshedy, M. Solitary Wave Solutions for the Stochastic Fractional-Space KdV in the Sense of the M-Truncated Derivative. Mathematics 2022, 10, 4792. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The Analytical Solutions of Stochastic-Fractional Drinfel’d-Sokolov-Wilson Equations via (G’/G)-Expansion Method. Symmetry 2022, 14, 2105. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W. The analytical solutions of the stochastic fractional RKL equation via Jacobi elliptic function method. Adv. Math. Phys. 2022, 2022, 1534067. [Google Scholar] [CrossRef]
- Alshammari, S.; Mohammed, W.W.; Samura, S.K.; Faleh, S. The analytical solutions for the stochastic-fractional Broer–Kaup equations. Math. Probl. Eng. 2022, 2022, 6895875. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. The optical solutions of the stochastic fractional Kundu-Mukherjee-Naskar model by two different methods. Mathematics 2022, 10, 1465. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Integrable (2+1)-dimensional and (3+1)-dimensional breaking soliton equations. Phys. Scr. 2010, 81, 035005. [Google Scholar] [CrossRef]
- Bekir, A. Exact solutions for some (2+1)-dimensional nonlinear evolution equations by using tanh-coth method. World Appl. Sci. J. 2010, 9, 1–6. [Google Scholar]
- Ilhan, O.P.; Manafian, J. Periodic type and periodic cross-kink wave solutions to the (2+1)-dimensional breaking soliton equation arising in fluid dynamics. Mod. Phys. Lett. B 2019, 33, 1950277. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Mohyud-Din, S.T. Assessment of the further improved ()-expansion method and the extended tanh-method in probing exact solutions of nonlinear PDEs. SpringerPlus 2013, 2, 326. [Google Scholar] [CrossRef] [PubMed]
- Darvishi, M.T.; Najafi, M. Some exact solutions of the (2+1)-dimensional breaking soliton equation using the three-wave method. Int. J. Math. Comput. Sci. 2012, 87, 31–34. [Google Scholar]
- Yan-Ze, P. New Exact Solutions for (2+1)-Dimensional Breaking Soliton Equation. Commun. Theor. Phys. 2005, 43, 205–207. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, S. Non-Traveling Wave Solutions for the (2+1)-Dimensional Breaking Soliton System. Appl. Math. 2012, 3, 813–818. [Google Scholar] [CrossRef]
- Zhang, S. New exact non-traveling wave and coefficient function solutions of the (2+1)-dimensional breaking soliton equations. Phys. Lett. A 2007, 368, 470–475. [Google Scholar] [CrossRef]
- Mei, J.Q.; Zhang, H.Q. New types of exact solutions for a breaking soliton equation. Chaos Solitons Fractals 2004, 20, 771–777. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; El-Morshedy, M.; Moumen, A.; Ali, E.E.; Benaissa, M.; Abouelregal, A.E. Effects of M-Truncated Derivative and Multiplicative Noise on the Exact Solutions of the Breaking Soliton Equation. Symmetry 2023, 15, 288. https://doi.org/10.3390/sym15020288
Mohammed WW, El-Morshedy M, Moumen A, Ali EE, Benaissa M, Abouelregal AE. Effects of M-Truncated Derivative and Multiplicative Noise on the Exact Solutions of the Breaking Soliton Equation. Symmetry. 2023; 15(2):288. https://doi.org/10.3390/sym15020288
Chicago/Turabian StyleMohammed, Wael W., M. El-Morshedy, Abdelkader Moumen, Ekram E. Ali, M. Benaissa, and Ahmed E. Abouelregal. 2023. "Effects of M-Truncated Derivative and Multiplicative Noise on the Exact Solutions of the Breaking Soliton Equation" Symmetry 15, no. 2: 288. https://doi.org/10.3390/sym15020288
APA StyleMohammed, W. W., El-Morshedy, M., Moumen, A., Ali, E. E., Benaissa, M., & Abouelregal, A. E. (2023). Effects of M-Truncated Derivative and Multiplicative Noise on the Exact Solutions of the Breaking Soliton Equation. Symmetry, 15(2), 288. https://doi.org/10.3390/sym15020288







