Numerical Solution of Time-Fractional Emden–Fowler-Type Equations Using the Rational Homotopy Perturbation Method
Abstract
1. Introduction and Mathematical Preliminaries
Properties of Caputo derivative
2. Existence and Uniqueness
- is continuous over , and the functions , are continuous with interval ;
- is differentiable at ;
- There are non-negative constants such that:where .
- where is a non-negative constant.
3. Method
4. Convergence of RHPM
- 1.
- ;
- 2.
- .
5. Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lane, J.H. On the theoretical temperature of the Sun under the hypothesis of a gaseous mass maintaining its volume by its internal heat and depending on the laws of gases known to terrestrial experiment. Am. J. Sci. 1870, 50, 57–74. [Google Scholar] [CrossRef]
- Emden, R. Gaskugeln: Anwendungen der Mechanischen Wärmetheorie auf Kosmologische und Meteorologische Probleme; B. G. Teubner: Leipzig, Germany; Berlin, Germany, 1907. [Google Scholar]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; Dover Publications Inc.: New York, NY, USA, 1967. [Google Scholar]
- Kara, A.H.; Mahomed, F.M. A note on the solutions of the Emden-Fowler equation. Int. J. Non-Linear Mech. 1993, 28, 379–384. [Google Scholar] [CrossRef]
- Muatjetjeja, B.; Khalique, C.M. Exact solutions of the generalized Lane–Emden equations of the first and second kind. Pramana 2011, 77, 545–554. [Google Scholar] [CrossRef]
- Fowler, R.H. The form near infinity of real, continuous solutions of a certain differential equation of the second order. Quart. J. Math. 1914, 45, 289–350. [Google Scholar]
- Fowler, R.H. Further studies of Emden’s and similar differential equations. Quart. J. Math. 1931, 2, 259–288. [Google Scholar] [CrossRef]
- Meerson, E.; Megged, E.; Tajima, T. On the quasi-hydrostatic flows of radiatively cooling self-gravitating gas clouds. Astrophys. J. 1996, 457, 321. [Google Scholar] [CrossRef]
- Gnutzmann, S.; Ritschel, U. Analytic solution of Emden-Fowler equation and critical adsorption in spherical geometry. Z. Phys. B Condens. Matter 1995, 96, 391–393. [Google Scholar] [CrossRef]
- Richardson, O.W. The Emission of Electricity from Hot Bodies; Longman, Green and Co.: London, UK, 1921. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Chu, Y.M.; Shah, N.A.; Agarwal, P.; Chung, J.D. Analysis of fractional multi-dimensional Navier–Stokes equation. Adv. Differ. Equ. 2021, 2021, 91. [Google Scholar] [CrossRef]
- Shah, N.A.; Dassios, I.; El-Zahar, E.R.; Chung, J.D. An Efficient Technique of Fractional-Order Physical Models Involving ρ-Laplace Transform. Mathematics 2022, 10, 816. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Chung, J.D. Fractional Analysis of Coupled Burgers Equations within Yang Caputo-Fabrizio Operator. J. Funct. Spaces 2022, 2022, 6231921. [Google Scholar] [CrossRef]
- He, W.; Chen, N.; Dassios, I.; Shah, N.A.; Chung, J.D. Fractional System of Korteweg-De Vries Equations via Elzaki Transform. Mathematics 2021, 9, 673. [Google Scholar] [CrossRef]
- Lima, P.M.; Carpentier, M. Numerical solution of a singular boundary-value problem in non-newtonian fluid mechanics. Appl. Num. Math. 1999, 30, 93–111. [Google Scholar] [CrossRef]
- Lima, P.M. Numerical methods and asymptotic error expansions for the Emden-Fowler equations. J. Comput. Appl. Math. 1996, 70, 245–266. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R.; Shawagfeh, N.T. On the analytic solution of the Lane-Emden equation. Found. Phys. Lett. 1995, 8, 161–181. [Google Scholar] [CrossRef]
- Horedt, G.P. Seven-digit tables of Lane-Emden functions. Astrophys. Space Sci. 1986, 126, 357–408. [Google Scholar] [CrossRef]
- Horedt, G.P. Approximate analytical solutions of the Lane-Emden equation in N-dimensional space. Astron. Astrophys. 1987, 172, 359–367. [Google Scholar]
- Shawagfeh, N.T. Non-perturbative approximate solution for Lane–Emden equation. J. Math. Phys. 1993, 34, 4364–4369. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A new algorithm for solving differential equations of Lane-Emden type. Appl. Math. Comput. 2001, 118, 287–310. [Google Scholar] [CrossRef]
- Datta, B.K. Analytic solution to the Lane-Emden equation. Nuov. Cim. 1996, 111B, 1385–1388. [Google Scholar] [CrossRef]
- Liao, S. A new analytic algorithm of Lane–Emden type equations. Appl. Math. Comput. 2003, 142, 1–16. [Google Scholar] [CrossRef]
- He, J.H. Perturbation Methods: Basic and Beyond; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fract. 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Vazquez-Leal, H. Rational Homotopy Perturbation Method. J. Appl. Math. 2012, 20212, 490342. [Google Scholar] [CrossRef]
- Biazar, J.A.; Asadi, M.; Salehi, F. Rational Homotopy Perturbation Method for solving stiff systems of ordinary differential equations. Appl. Math. Model. 2015, 39, 1291–1299. [Google Scholar] [CrossRef]
- Singh, R.; Singh, S.; Wazwaz, A.M. A modified homotopy perturbation method for singular time-dependent Emden-Fowler equations with boundary conditions. J. Math. Chem. 2016, 54, 918–931. [Google Scholar] [CrossRef]
- Malagi, N.S.; Veeresha, P.; Prasannakumara, B.C.; Prasanna, G.D.; Prakasha, D.G. A new computational technique for the analytic treatment of time-fractional Emden Fowler equations. Math. Comp. Simul. 2021, 190, 362–376. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherlands, 2006; p. 204. [Google Scholar]
- Shokhanda, R.; Goswami, P. Solution of Generalized Fractional Burgers Equation with a Nonlinear Term. Int. J. Appl. Comput. Math. 2022, 8, 235. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Castaneda-Sheissa, R.; Filobello-Nino, U.; Reyes, A.S.; Orea, J.S. High accurate simple approximation of normal distribution-related integrals. Math. Prob. Eng. 2012, 2012, 124029. [Google Scholar] [CrossRef]
- Vazquez-Leal, H.; Filobello-Nino, M. Hpms Inspired Homotopy Contin. Methods. Math. Probl. Eng. 2012, 2012, 309123. [Google Scholar] [CrossRef]
- Filobello-Nino, U.; Vazquez-Leal, H.; Castaneda-Sheissa, R.; Yildirim, A.; Hernandez-Martinez, L.; Pereyra-Diaz, D.; Perez-Sesma, A.; Hoyos-Reyes, C. An approximate solution of blasius equation by using hpm method. Asian J. Math. Stat. 2012, 5, 50–59. [Google Scholar] [CrossRef]



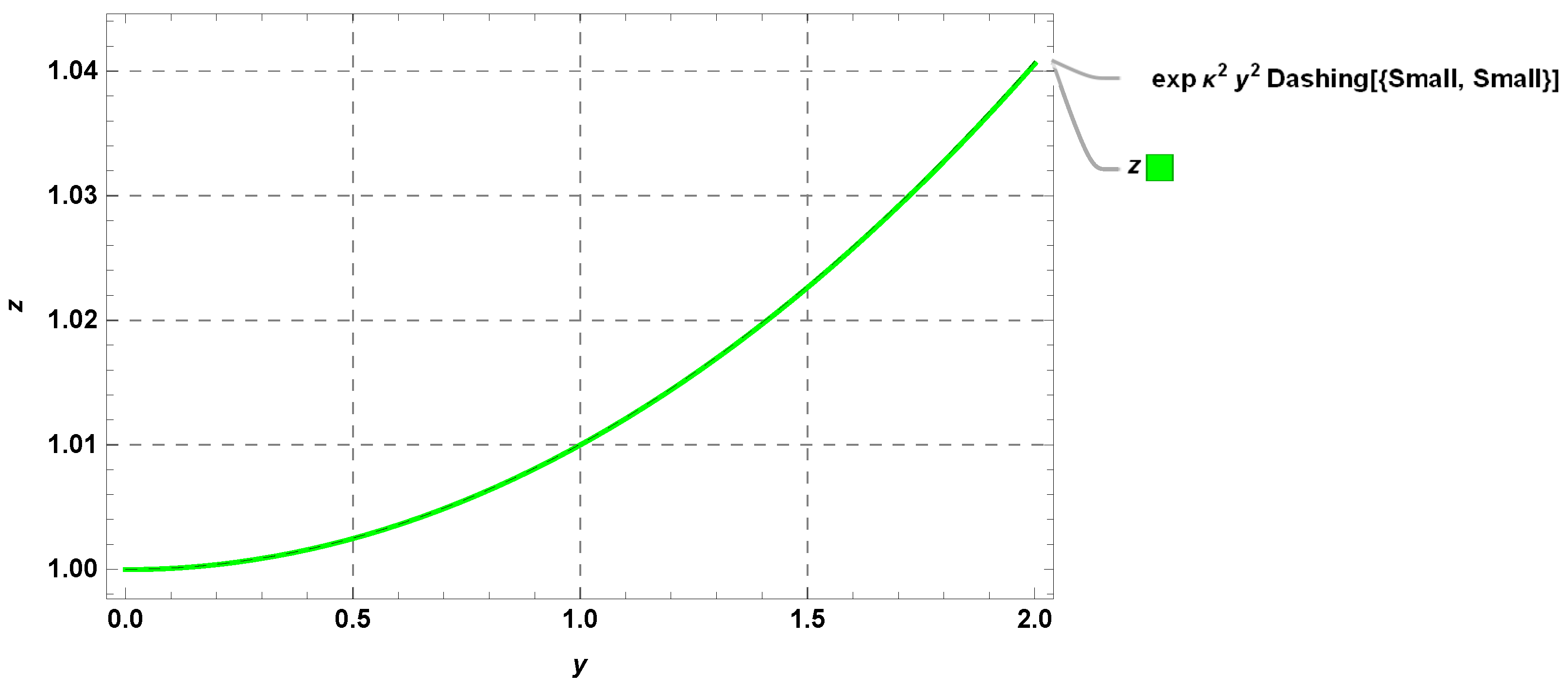
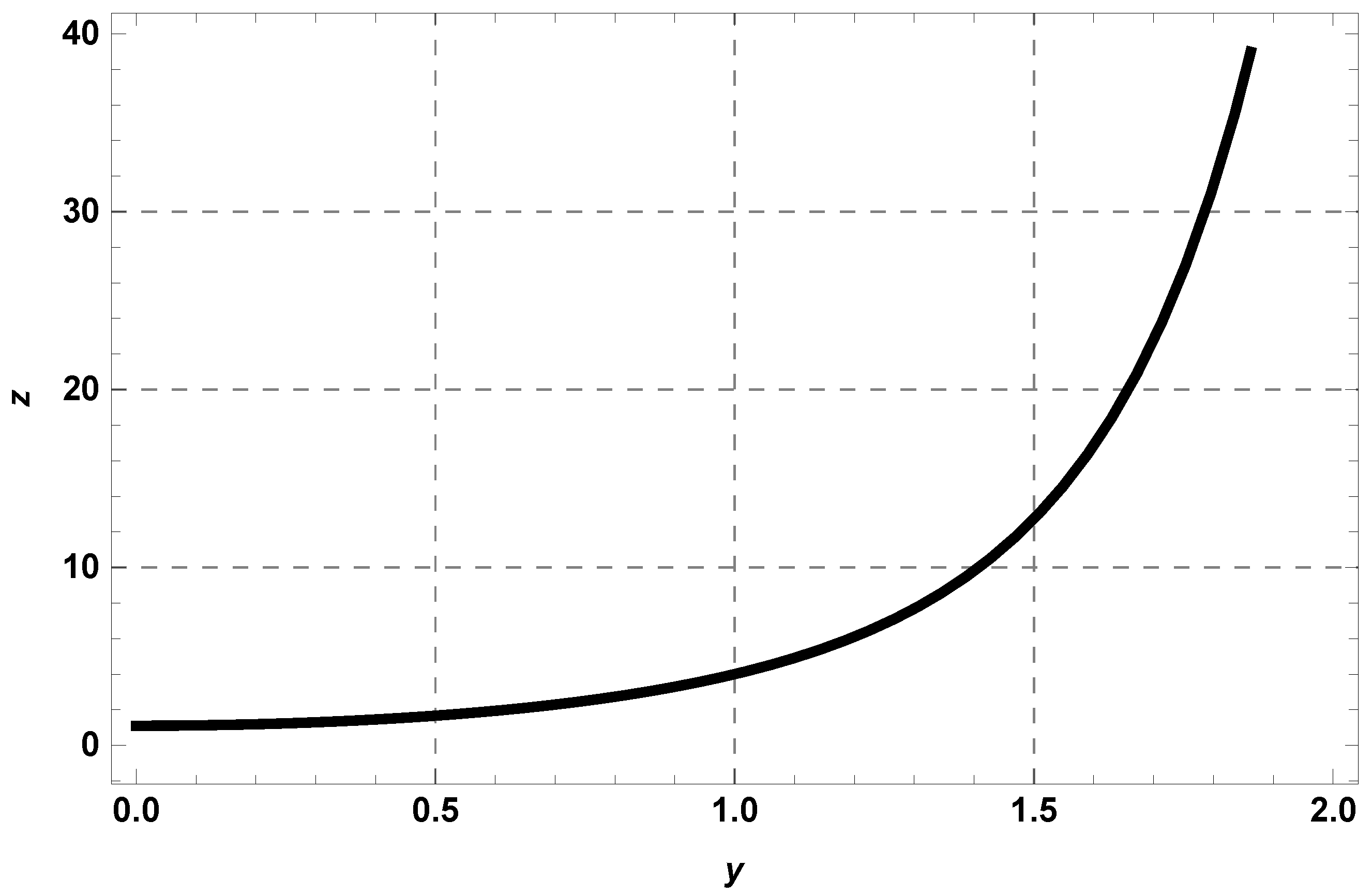
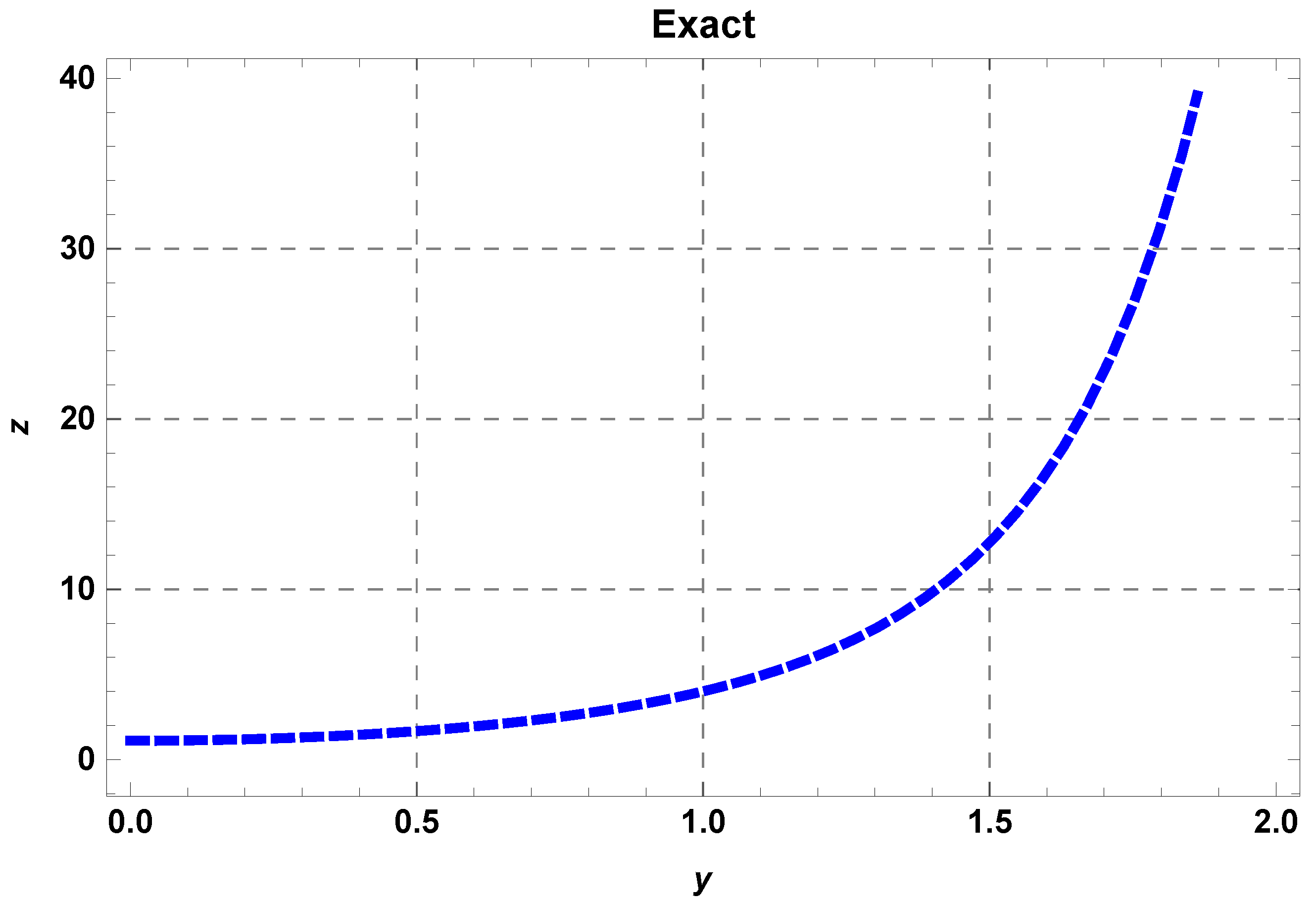
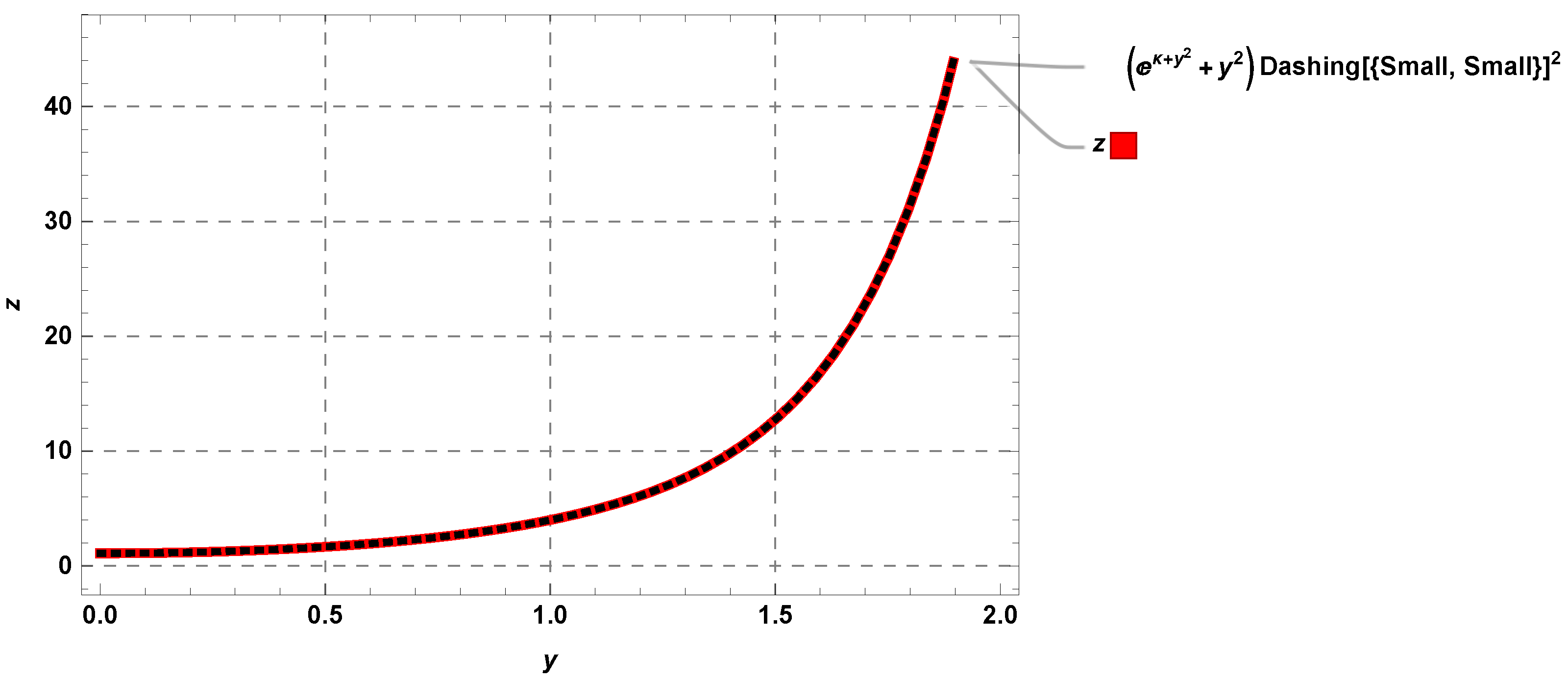
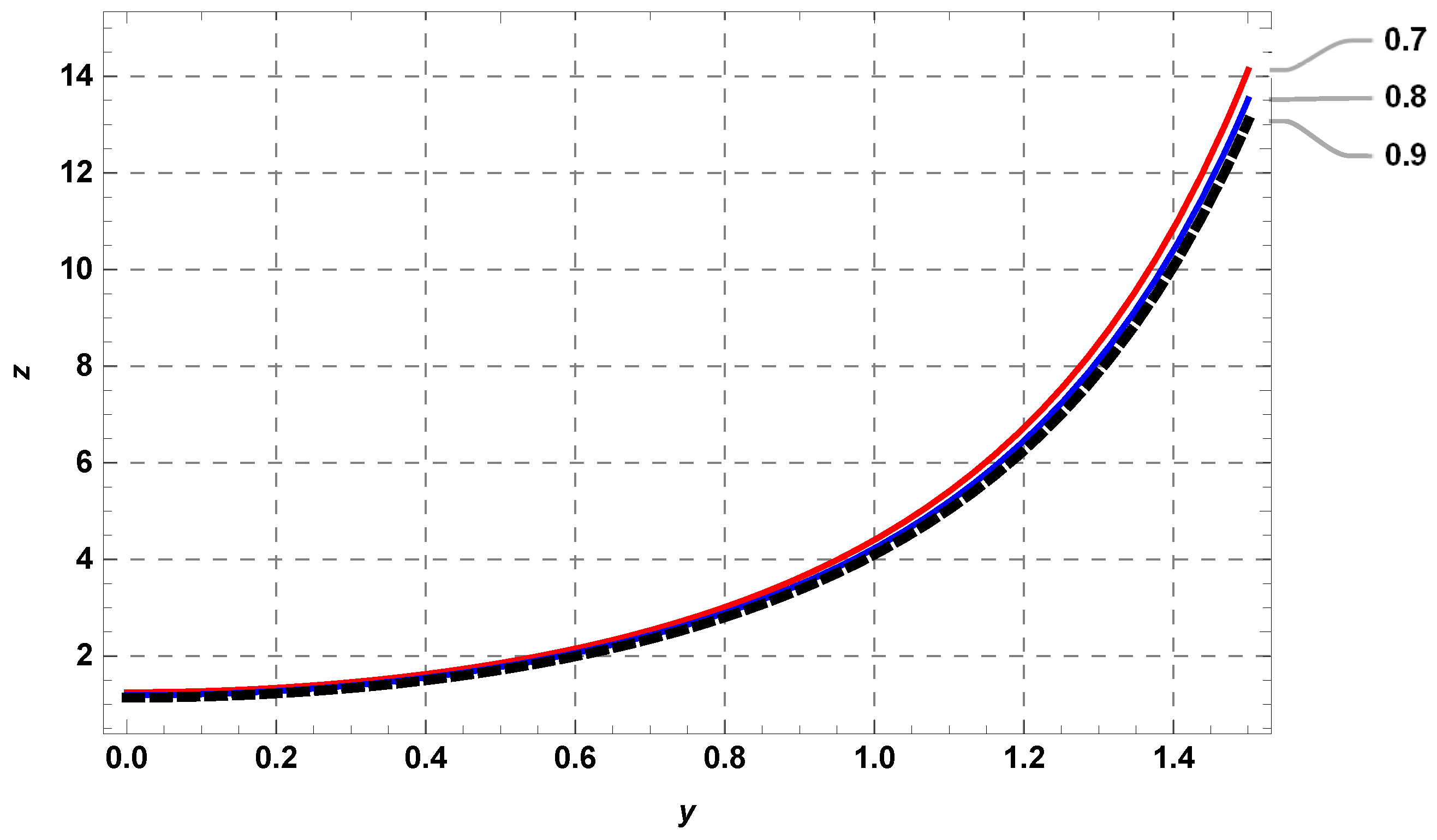
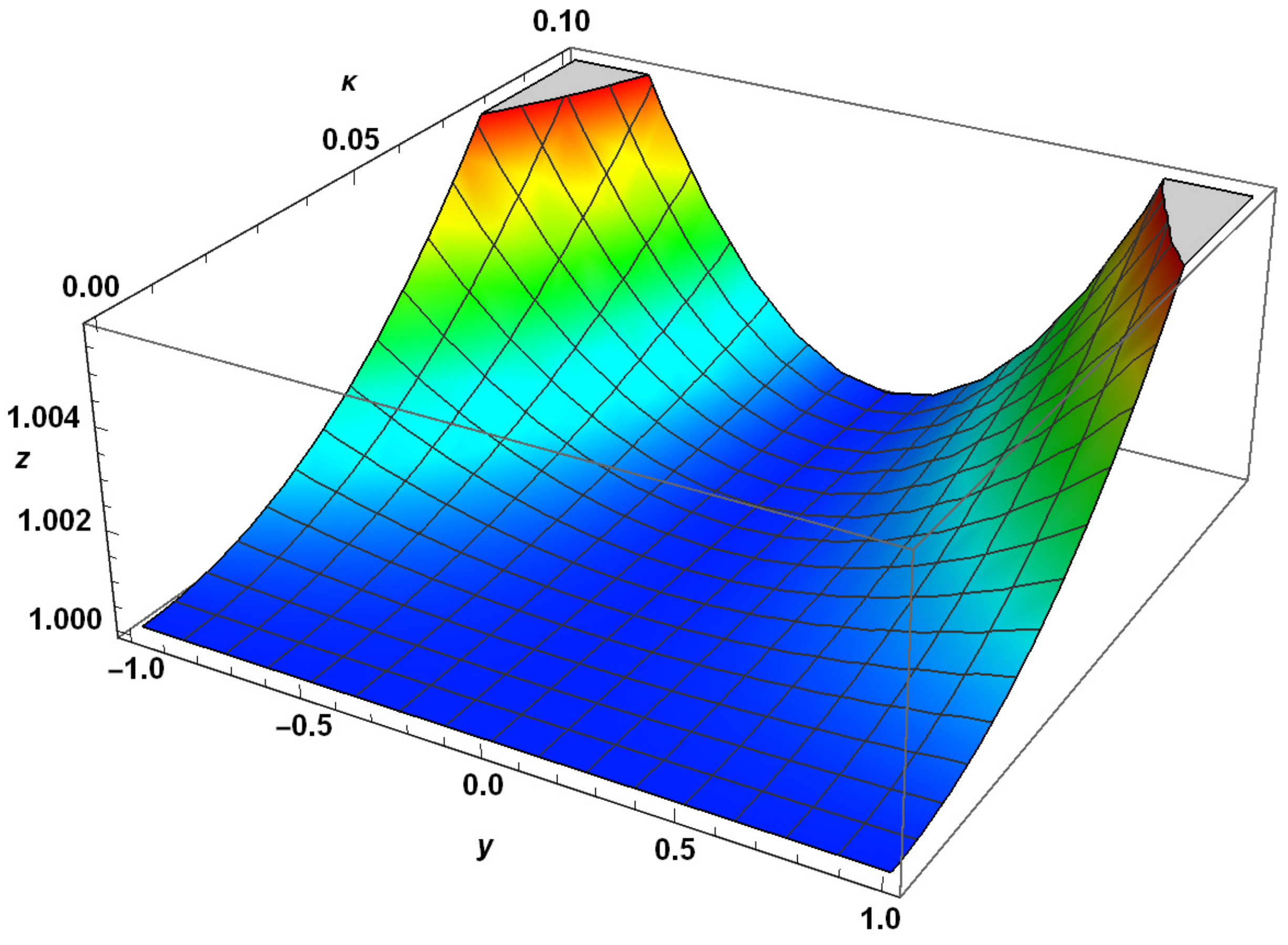
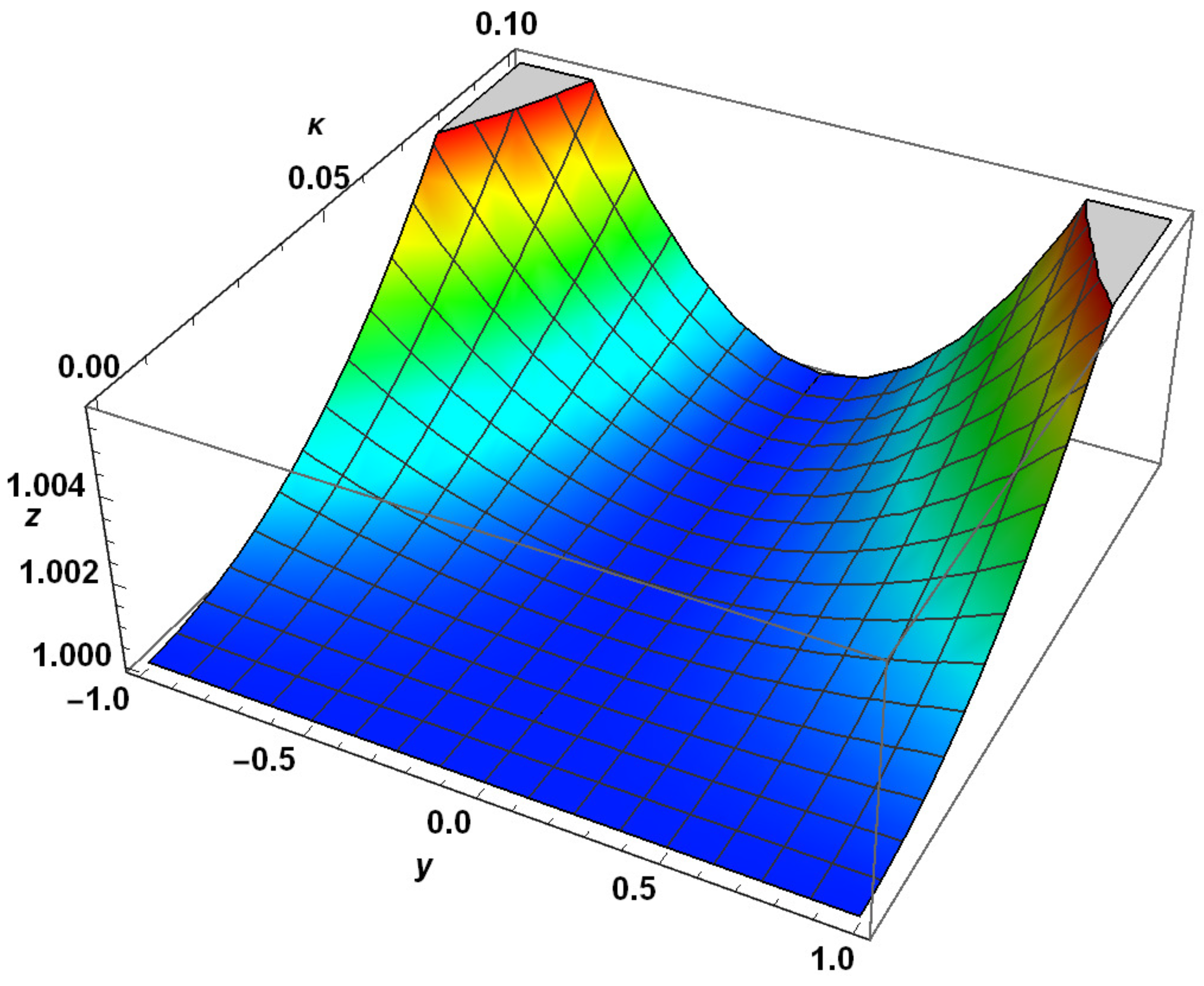

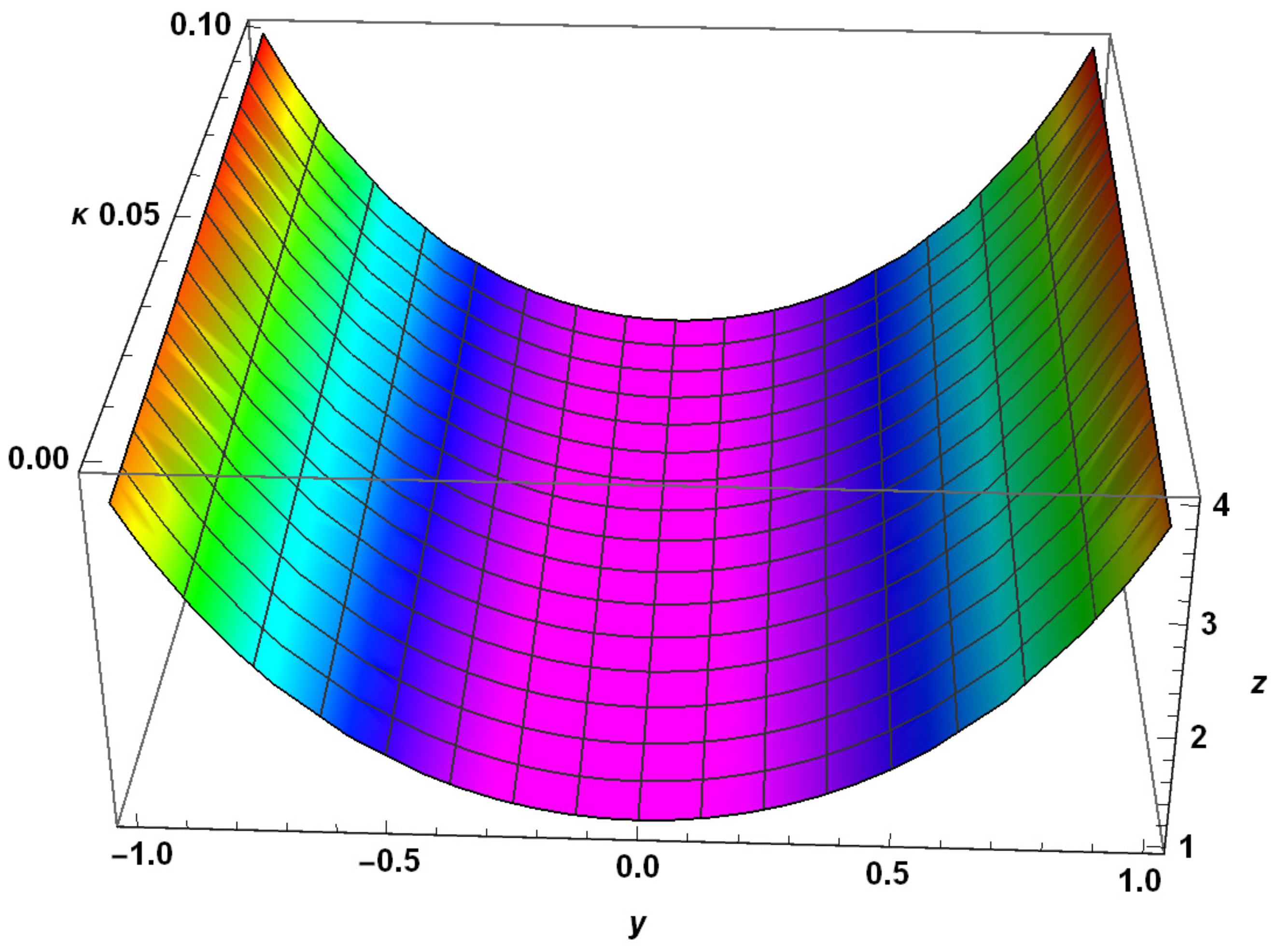
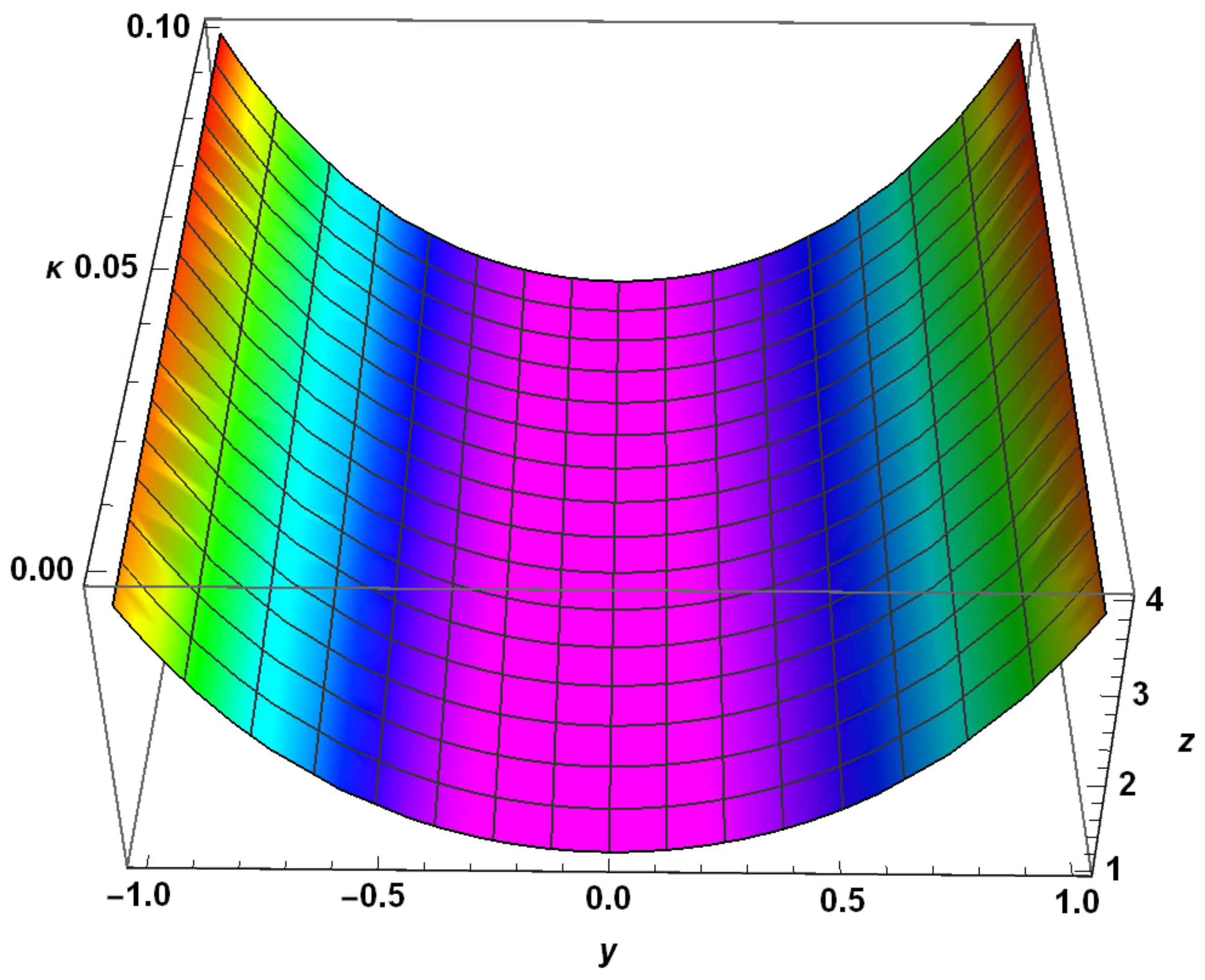
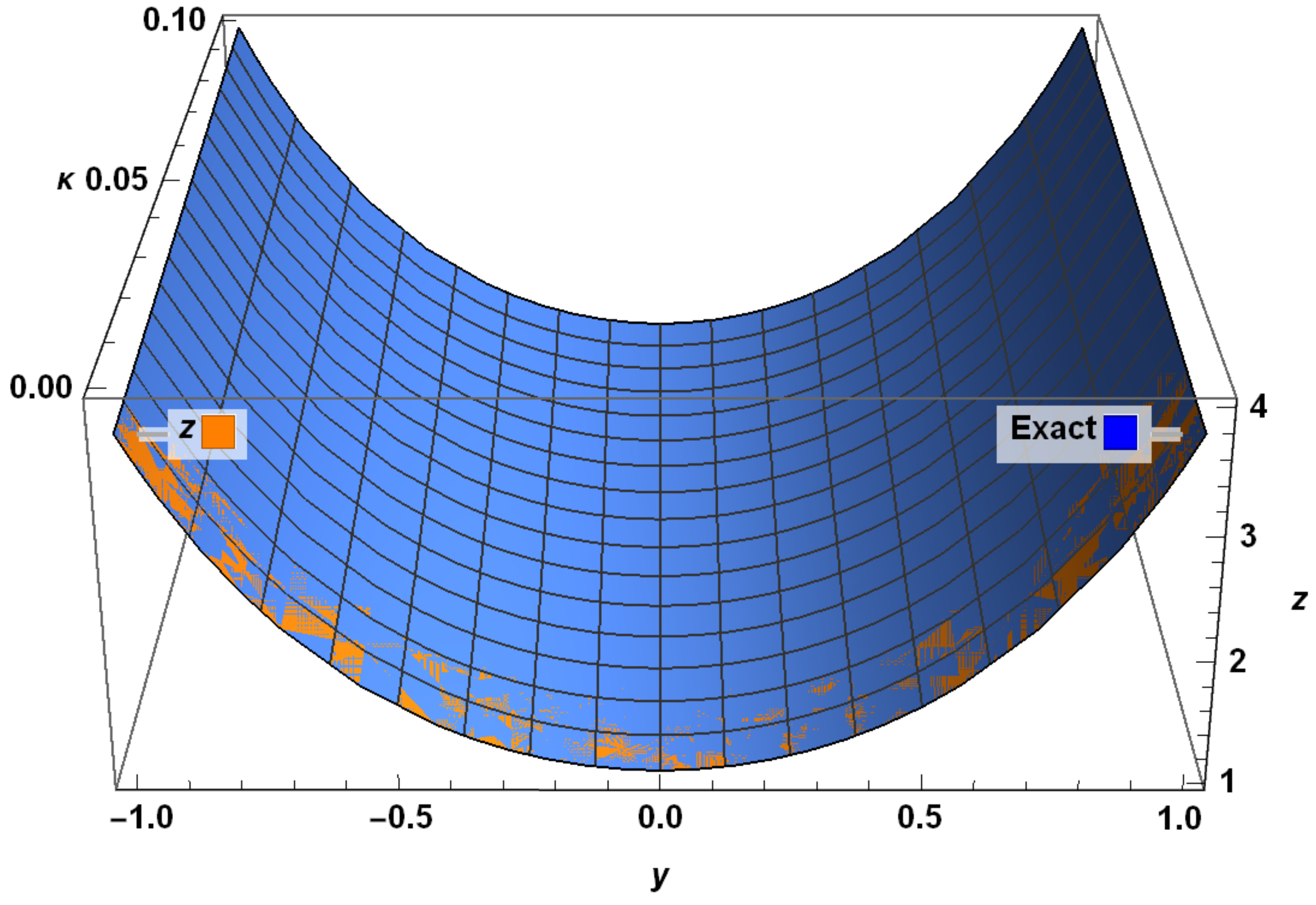
| y | Exact Solution | RHPM Solution | Absolute Error | |||
|---|---|---|---|---|---|---|
| 0.1 | 1.0001 | 1.00008 | 0.00092 | 1.02057 | 1.00819 | 1.00249 |
| 0.2 | 1.0004 | 1.00037 | 0.00003 | 1.02134 | 1.00875 | 1.0029 |
| 0.3 | 1.0009 | 1.00087 | 0.00003 | 1.02261 | 1.00969 | 1.00358 |
| 0.4 | 1.0016 | 1.00157 | 0.00003 | 1.0244 | 1.011 | 1.00454 |
| 0.5 | 1.0025 | 1.00247 | 0.00003 | 1.02671 | 1.01269 | 1.00578 |
| 0.6 | 1.00361 | 1.00357 | 0.00004 | 1.02953 | 1.01476 | 1.00729 |
| 0.7 | 1.00491 | 1.00486 | 0.00004 | 1.03288 | 1.01722 | 1.00908 |
| 0.8 | 1.00642 | 1.00637 | 0.00005 | 1.03677 | 1.02006 | 1.01115 |
| 0.9 | 1.00813 | 1.00808 | 0.00005 | 1.0412 | 1.02329 | 1.0135 |
| y | Exact Solution | RHPM Solution | Absolute Error | |||
|---|---|---|---|---|---|---|
| 0.1 | 1.1261 | 1.1262 | 0.0001 | 1.27422 | 1.20967 | 1.16181 |
| 0.2 | 1.1901 | 1.1902 | 0.0001 | 1.34272 | 1.27621 | 1.22689 |
| 0.3 | 1.29906 | 1.29925 | 0.00019 | 1.45952 | 1.3896 | 1.33775 |
| 0.4 | 1.45673 | 1.45693 | 0.0002 | 1.62884 | 1.55384 | 1.49822 |
| 0.5 | 1.66886 | 1.66907 | 0.00021 | 1.85718 | 1.77511 | 1.71425 |
| 0.6 | 1.94384 | 1.94407 | 0.00023 | 2.15409 | 2.06246 | 1.99452 |
| 0.7 | 2.29373 | 2.29399 | 0.00026 | 2.53319 | 2.42883 | 2.35145 |
| 0.8 | 2.73564 | 2.73594 | 0.00030 | 3.01389 | 2.89262 | 2.80271 |
| 0.9 | 3.29398 | 3.29432 | 0.00034 | 3.62384 | 3.48007 | 3.37349 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalawi, K.S.; Alkahtani, B.S.; Kumar, A.; Goswami, P. Numerical Solution of Time-Fractional Emden–Fowler-Type Equations Using the Rational Homotopy Perturbation Method. Symmetry 2023, 15, 258. https://doi.org/10.3390/sym15020258
Albalawi KS, Alkahtani BS, Kumar A, Goswami P. Numerical Solution of Time-Fractional Emden–Fowler-Type Equations Using the Rational Homotopy Perturbation Method. Symmetry. 2023; 15(2):258. https://doi.org/10.3390/sym15020258
Chicago/Turabian StyleAlbalawi, Kholoud Saad, Badr Saad Alkahtani, Ashish Kumar, and Pranay Goswami. 2023. "Numerical Solution of Time-Fractional Emden–Fowler-Type Equations Using the Rational Homotopy Perturbation Method" Symmetry 15, no. 2: 258. https://doi.org/10.3390/sym15020258
APA StyleAlbalawi, K. S., Alkahtani, B. S., Kumar, A., & Goswami, P. (2023). Numerical Solution of Time-Fractional Emden–Fowler-Type Equations Using the Rational Homotopy Perturbation Method. Symmetry, 15(2), 258. https://doi.org/10.3390/sym15020258






