1. Introduction
Integrals of rational functions can be expressed in terms of elementary functions. Therefore, a natural method of integration consists of using suitable substitutions and integration by parts to reduce our problem to integration of rational functions.
In this paper, we consider irrational integrals containing the quadratic root of a quadratic polynomial, i.e., integrals of the form
where
R is a rational fuction (a quotient of two polynomials) of
x and
y, and
The subject is, in principle, known. A standard method to deal with such integrals consists of using one of the so-called Euler’s substitutions [
1,
2,
3]. However, there are some details which need to be clarified. We will describe in detail a geometric approach to this problem and explain how many Euler substitutions actually exist.
In fact, to the best of our knowledge, all sources and textbooks mention exactly three types of substitutions in this context. It is not clear who was the first to introduce such classification. Leonhard Euler himself used only two of these substitutions (which is sufficient to cover all cases). Three Euler substitutions are usually introduced and discussed in Russian sources; see, e.g., [
4,
5,
6] (Leonhard Euler, although of Swiss origin, lived and worked in Saint Petersburg for many years). Surprisingly enough, the three substitutions appeared in an old textbook, published in 1892 by a Harvard professor, William E. Byerly [
7], without any reference to Euler.
In our paper, we present a clear geometric intepretation of this problem, shortly mentioned in some sources, mainly of Russian origin [
2,
8]. The textbook [
8] is not translated into English. Another book by the same author [
4] does not mention this geometric approach in the section on Euler’s substitutions.
The main novelty of this paper is the introduction of the fourth Euler substitution, which is a natural consequence of the geometric approach discussed in our paper.
2. Three Classical Euler’s Substitutions
The main idea of Euler’s substitutions consists of expressing
as a linear function of
x and a new parameter
t in such a way that the resulting equation is linear with respect to
x. In this paper, we use the most common numbering of these three substitutions, compare [
1,
2,
4,
5,
7]. In some sources, a different order is used; see [
6,
9,
10].
2.1. First Euler Substitution
This substitution can be done only in the case
:
Squaring both sides we get:
Terms quadratic in
x cancel out and the resulting equation is linear in
x. Computing
x, we get a rational dependence on
t:
Then, from (
2) and (
3), we get
2.2. Second Euler Substitution
This substitution can be done only in the case
:
Squaring both sides we get:
The constant
c cancels out and dividing both sides by
x we again derive an equation linear in
x. Hence, similarly as in the previous case,
2.3. Third Euler Substitution
This substitution can be done only in the case
, where
is the discriminant of the quadratic polynomial. Then the polynomial has two distinct real roots
and
, and the third Euler substitution is given by:
Squaring both sides we get:
Computing
x from the resulting equation and then using (
10) and (
2) we obtain
where, of course,
2.4. Original Euler’s Approach
It is interesting that Leonhard Euler himself, in his famous monograph, used only two of these substitutions, see [
11]. He considered two cases:
and
. In the first case (
) he proposed the substitution (
6), while in the second case (
) he proposed the substitution (
3) in a slightly modified form:
Obviously, the case
is not included because then the quadratic polynomial is a square of the linear function in
x and
y is linear is
x as well. Hence, the integrand in (
1) is rational in
x from the very beginning.
3. Geometric Interpretation
It is convenient to square both sides of (
2) resulting in the equation of a quadratic curve
We will denote this curve (a conic section) by , i.e., .
3.1. Elliptic Case:
The canonical form of the quadratic polynomial yields:
We can distinguish three cases, depending on the sign of the discriminant
:
Only in the last case, we get a non-degenerated quadratic curve.
3.2. Parabolic Case:
For (and ) the conic is a parabola with the symmetry axis .
3.3. Hyperbolic Case:
The canonical form of the quadratic polynomial yields:
We can distinguish three cases, depending on the sign of the discriminant
:
Therefore, for we get a non-degenerated quadratic curve.
3.4. Rational Parameterization: Standard Approach
The key idea leading to a rational parameterization consists of fixing an arbitrary point
on the conic
and assigning to any other point
of this conic the line
. Taking as a parameter
t the slope of this line, we obtain a rational parameterization of the conic
[
2,
8]. Thus, we have the system of three equations:
The points
and
belong to the conic
and
t is the slope of the straight line passing through
and
. Subtracting the second equation from the first one we get:
Substituting the last equation into the first one we obtain:
Assuming
, we get
Now, the first and the last equation form a system of two linear equations for two variables
, which can be solved in the standard way. As a result, we obtain:
which means that we expressed
x and
y as rational functions of the parameter
t.
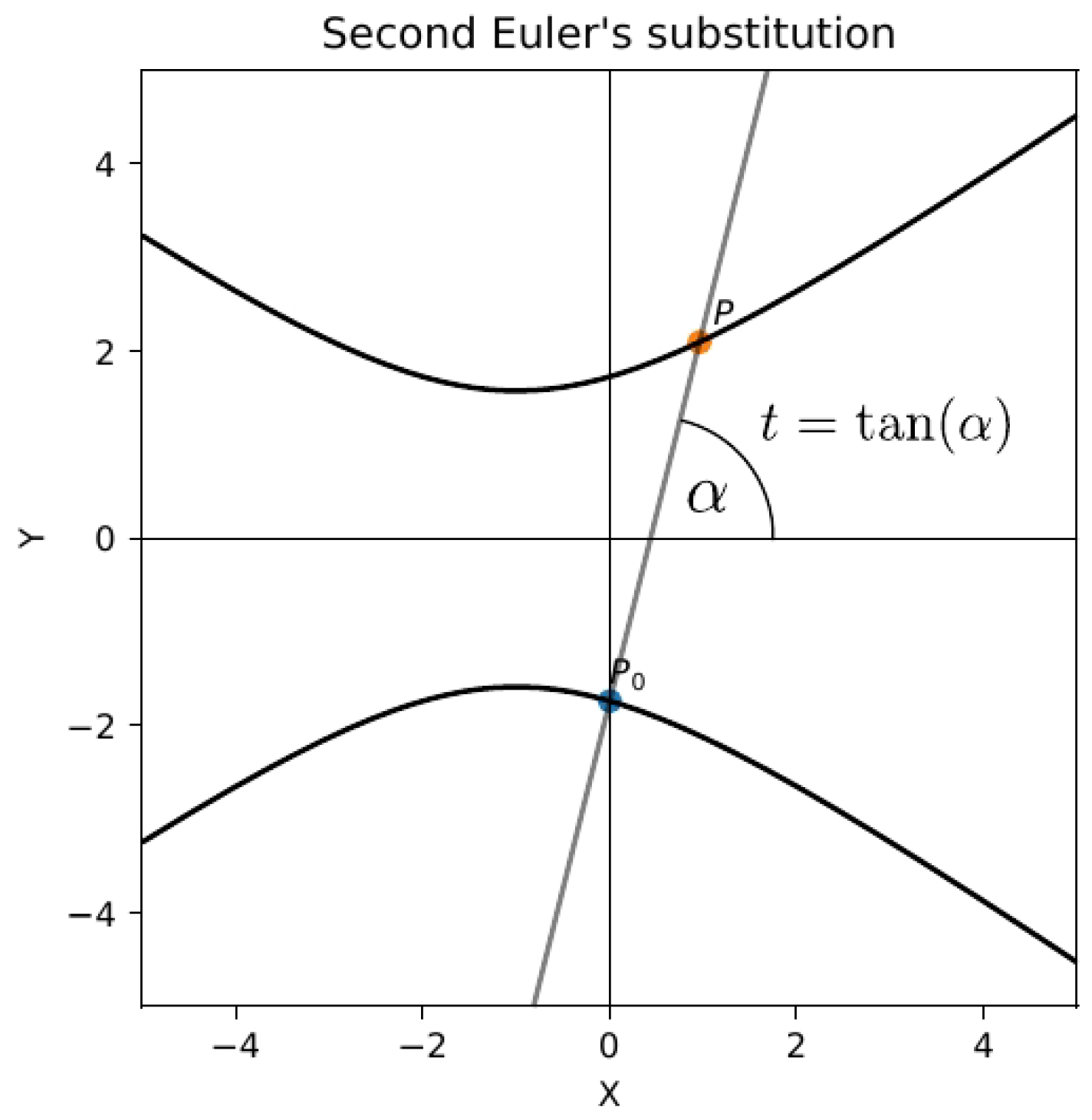
Corollary 1. There are many Euler-like substitutions. Each of them is determined by the choice of , provided that . Then the point is given by:and other points are parameterized by (28). In particular, the second Euler substitution corresponds to
(provided that the graph of the quadric
intersects the axis
y), see
Figure 1 and
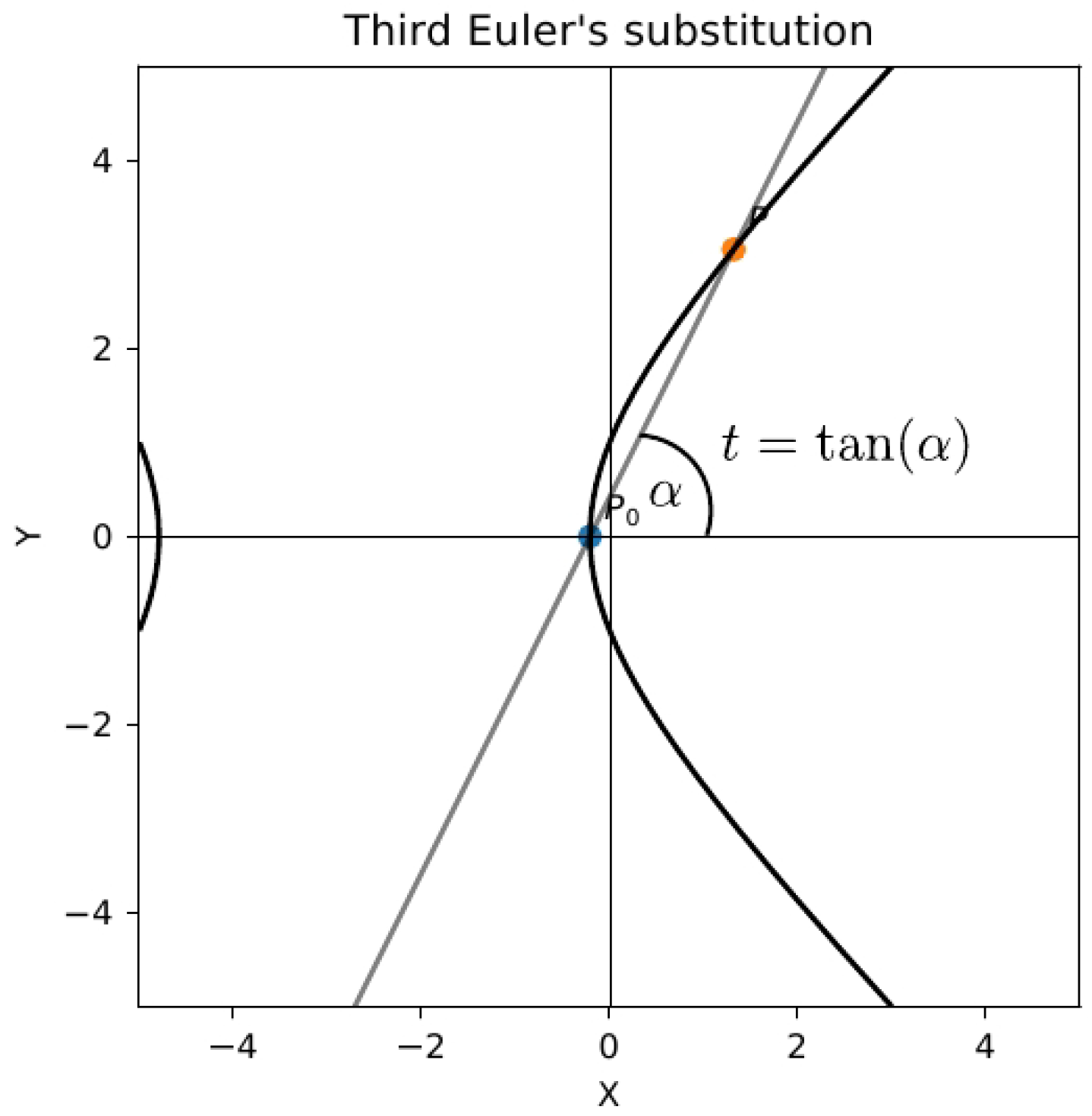
Figure 2. The third Euler substitution corresponds to
being a root of the polynomial
(provided that the graph of
intersects the axis
x), see
Figure 3 and
Figure 4.
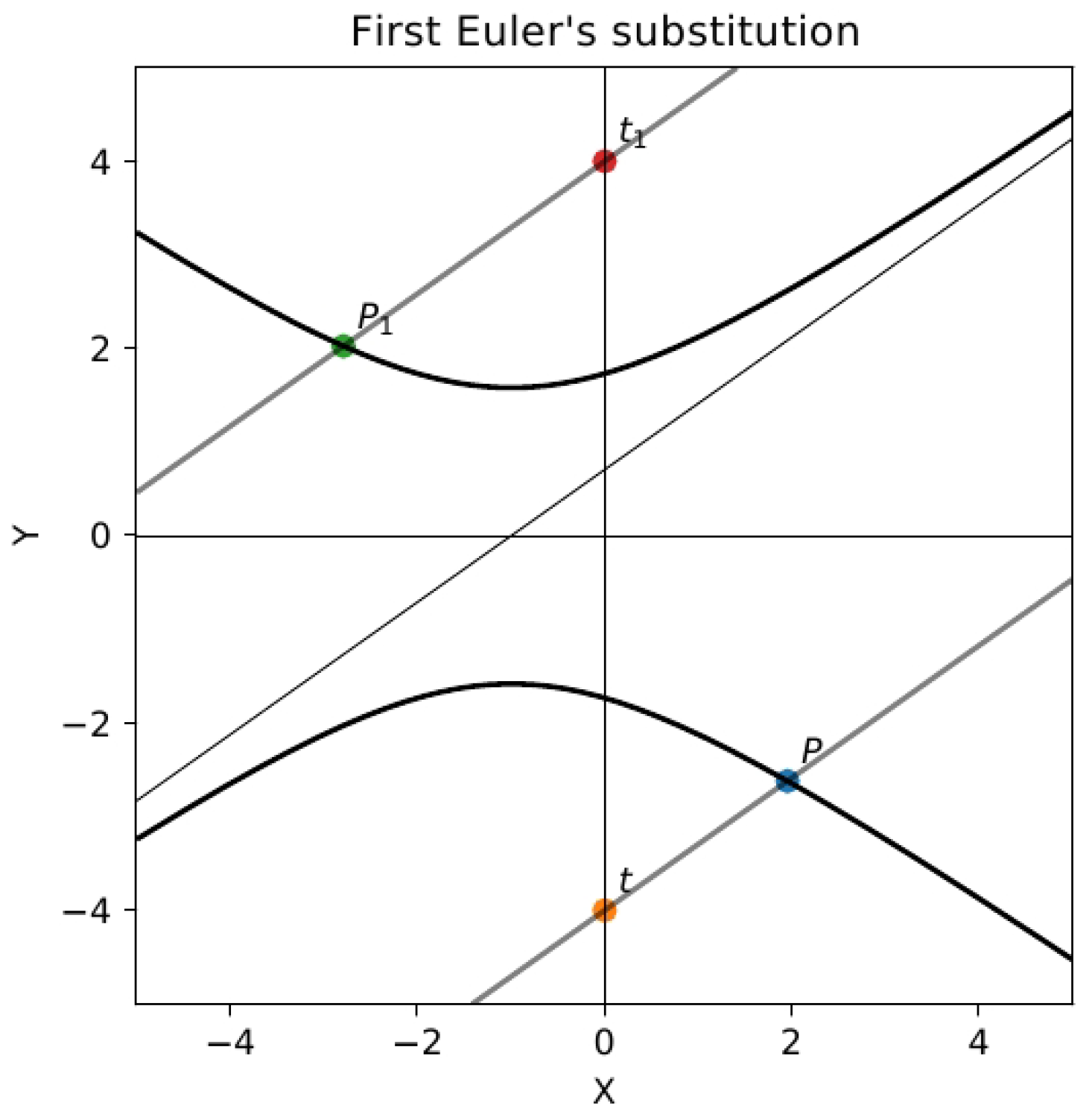
The first Euler substitution apparently does not fit this picture. However, its geometric interpretation is even simpler and more evident. The Formula (
3) describes the family of lines parallel to asymptotes of the corresponding hyperbola, see
Figure 5. We may treat it as a special case of (
28) when the point
lies at a very large number. Note that points
belong to the conic (
15) in the limit for
.
4. New Insights from the Geometric Interpretation
The description given in the previous section is more or less known (see, e.g., [
2,
8]), although we are not aware of any reference containing all these details. We are going to derive from this geometric picture more quite interesting consequences.
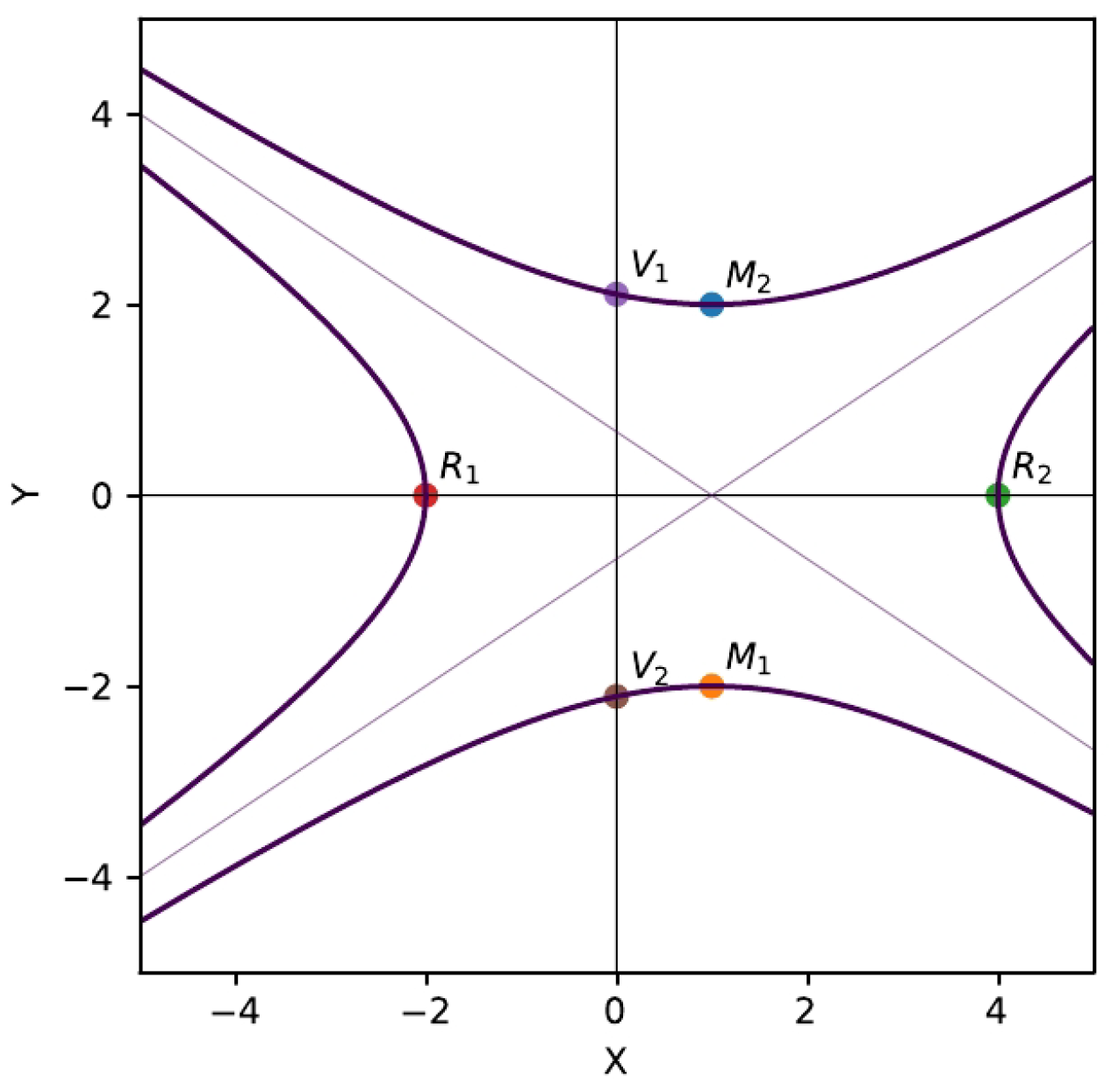
First of all, we identify characteristic points on the graph of a quadratic curve which can be chosen as
in the most natural way: vertices (
,
,
,
) and intersections with coordinate axes (
,
,
,
); see
Figure 6 and
Figure 7.
In particular, in the case of the second Euler substitution,
(see
Figure 1 and
Figure 2) or
, while in the case of the third Euler substitution
(see
Figure 3) or
(see
Figure 4). The first Euler substitution is related to
.
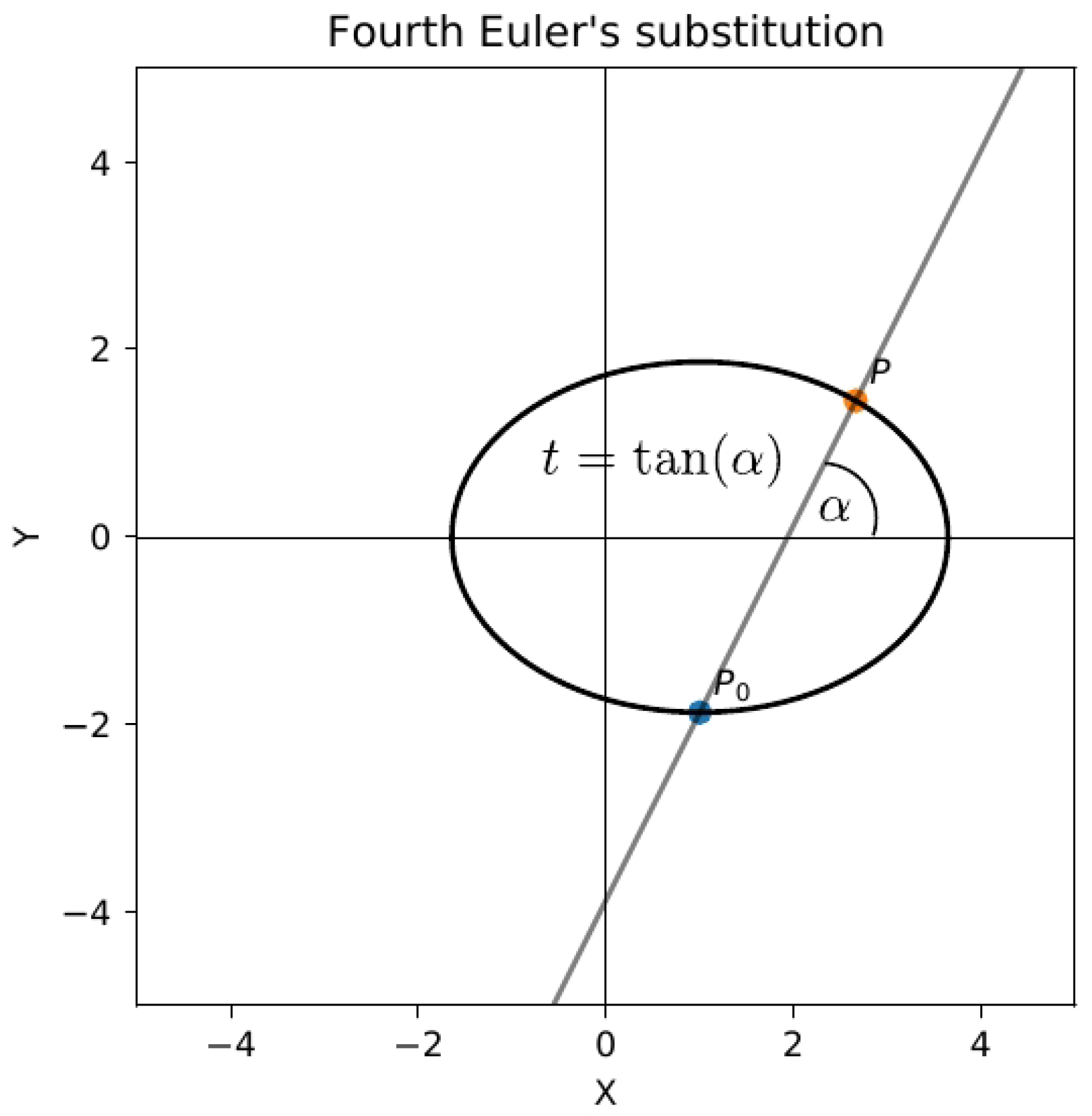
4.1. Fourth Euler’s Substitution
The geometric approach presented above includes all three classical Euler’s substitutions, but it is still missing vertices
and
. Therefore, it is natural to introduce another (fourth) Euler’s substitution, geometrically related to missing vertices:
(see
Figure 8 and
Figure 9) or
.
The algebraic description of the fourth Euler substitution is based on the canonical form of the quadratic polynomial:
where
The fourth Euler substitution is defined by:
Squaring both sides we get:
The constant
q cancels out and dividing both sides by
, we obtain
which is linear in
x. Hence
and using (
32) we get
Thus we have a rational dependence of
x and
y on the parameter
t. Moreover,
and we can easily transform the irrational integral function (
1) into an integral function rational with respect to
t.
4.2. Simplifying Euler’s First Substitution
A geometric approach suggests some modifications or new variants of the existing rational parameterizations. Introducing a new parameter
and substituting it into (
4) and (
5), we obtain the following simplification of the first Euler substitution:
Geometrically, the parameter
t is related to intersections with the
y axis (compare
Figure 5), while the parameter
is related to intersections with the vertical symmetry axis (i.e., the line
). Indeed, the parameter
corresponds to the line passing through the point
and this is one of two asymptotes (that is why
and
for
).
4.3. Euler’s First Substitution as a Limit of the Generic Case
We are going to show that the first Euler substitution can be derived from the generic case (
28) by taking a suitable limit
and
. We consider the pencil of lines
(compare (
24)) but as a parameter we take the ordinate
of the intersection of the line
with the
y-axis (i.e.,
for
). Hence
This change of variable, replacing t with , works for any . Therefore, the second Euler substitution (related to the case ) is excluded.
Substituting (
40) into (
28) we obtain
Assuming
and taking into account
we take the limit
. Hence
and
Comparing (
42) with (
4) and (
5) we easily see that both solutions are identical, provided that we identify
with
t. Note, of course, that the
t parameter given by (
40) is different from the
t parameter used in
Section 2.1.
5. Euler’s Substitutions versus Trigonometric Substitutions
Another popular method for computing irrational integrals (
1) consists of making a suitable trigonometric or hyperbolic substitution. We use the canonical form of the quadratic curve (compare (
30)):
Assuming
(otherwise
y depends linearly on
x) we introduce new variables
as folows:
Then (
43) becomes
because
, etc.
Thus we have three separate cases (in the fourth case –both signs negative– there are no real solutions), where trigonometric or hyperbolic substitutions are well known:
Is it better than Euler’s substitutions? This is a matter of taste. Perhaps it is easier to memorize, however, one has to remember that integrals of trigonometric or hyperbolic functions have to be converted into integrals of rational functions by another substitution:
6. Conclusions
We presented and discussed a geometric approach to Euler substitutions. One consequence of this thorough discussion was the introduction of a fourth Euler substitution, in addition to three traditionally mentioned Euler substitutions. In fact, we can say that more (one parameter family) Euler-like substitutions exist and can be further modified or simplified by suitable linear or fractional linear transformations.
Surprisingly, the subject of constructing rational parametrization of algebraic curves (rationalizing roots) has recently become important in the context of Feynman integrals and computations in high energy particle physics [
12,
13]. Furthermore, Euler’s substitutions were applied for reducing square roots in some mathematical finance calculations [
14]. It would be interesting to appply, in those fields, some geometric ideas presented in this paper.
Author Contributions
Conceptualization, J.L.C.; methodology, J.L.C.; formal analysis, J.L.C. and M.J.; investigation, J.L.C. and M.J.; visualization, M.J.; writing—original draft preparation, J.L.C.; writing—review and editing, J.L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Euler Substitution. Wikipedia. Available online: https://en.wikipedia.org/wiki/Euler_substitution (accessed on 8 August 2023).
- Euler Substitutions. Encyclopedia of Mathematics. Available online: https://encyclopediaofmath.org/wiki/Euler_substitutions (accessed on 18 July 2023).
- Radożycki, T. Solving Problems in Mathematical Analysis; Part I, Section 14.5; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Fikhtengol’ts, G.M. The Fundamentals of Mathematical Analysis; Chapter 10, Section 170; Pergamon Press: Oxford, UK, 1965; Volume 1. [Google Scholar]
- Piskunov, N. Differential and Integral Calculus; Mir Publishers: Moscow, Russia, 1969. [Google Scholar]
- Ryzhik, I.M.; Gradshteyn, I.S. Table of Integrals, Sums, Series, and Products; Gosudarstvennoe Izdatel’stvo Tehniko-Teoretičeskoj Literatury: Moscow, Russia, 1951. (In Russian) [Google Scholar]
- Byerly, W.E. Elements of the Integral Calculus; Ginn and Company: Boston, MA, USA, 1892. [Google Scholar]
- Fikhtengol’ts, G.M. Kurs Differentsial’nogo i Integral’nogo Ischisleniia; Chapter 8, Section 282; Fizmatgiz: Moscow, Russia, 1959; Volume 2. (In Russian) [Google Scholar]
- Lucht, P. The Euler Substitutions. Technical Report. Available online: https://www.researchgate.net/publication/309907150_The_
Eu\protect\discretionary{\char\hyphenchar\font}{}{}ler_Substitutions (accessed on 18 July 2023).
- Boyadzhiev, K.N. Special Techniques for Solving Integrals: Examples and Problems; World Scientific: Singapore, 2021. [Google Scholar]
- Euler, L. Institutiones Calculi Integralis; Part 1, Section 1, Chapter 2; Bruce, I., Translator; Imperial Academy of Sciences: St. Petersburg, Russia, 1768; Volume 1, Available online: http://www.17centurymaths.com/ (accessed on 8 August 2023).
- Besier, M.; van Straten, D.; Weinzierl, S. Rationalizing roots: An algorithmic approach. Commun. Number Theory Phys. 2019, 13, 253–297. [Google Scholar] [CrossRef]
- Besier, M.; Festi, D. Rationalizability of square roots. J. Symb. Comput. 2021, 106, 48–67. [Google Scholar] [CrossRef]
- Trinh, Y.T.; Hanzon, B. Option Pricing and CVA Calculations using the Monte Carlo-Tree (MC-Tree) Method. arXiv 2022, arXiv:2202.00785. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).