Defuzzification of Non-Linear Pentagonal Intuitionistic Fuzzy Numbers and Application in the Minimum Spanning Tree Problem

Abstract

In recent years, with the variety of digital objects around us becoming a source of information, the fields of artificial intelligence (AI) and machine learning (ML) have experienced very rapid development. Processing and converting the information around us into data within the framework of the information processing theory is important, as AI and ML techniques need large amounts of reliable data in the training and validation stages. Even though information naturally contains uncertainty, information must still be modeled and converted into data without neglecting this uncertainty. Mathematical techniques, such as the fuzzy theory and the intuitionistic fuzzy theory, are used for this purpose. In the intuitionistic fuzzy theory, membership and non-membership functions are employed to describe intuitionistic fuzzy sets and intuitionistic fuzzy numbers (IFNs). IFNs are characterized by the mathematical statements of these two functions. A more general and inclusive definition of IFN is always a requirement in AI technologies, as the uncertainty introduced by various information sources needs to be transformed into similar IFNs without neglecting the variety of uncertainty. In this paper, we proposed a general and inclusive mathematical definition for IFN and called this IFN a non-linear pentagonal intuitionistic fuzzy number (NLPIFN), which allows its users to maintain variety in uncertainty. We know that AI technology implementations are performed in computerized environments, so we need to transform the IFN into a crisp number to make such IFNs available in such environments. Techniques used in transformation are called defuzzification methods. In this paper, we proposed a short-cut formula for the defuzzification of a NLPIFN using the intuitionistic fuzzy weighted averaging based on levels (IF-WABL) method. We also implemented our findings in the minimum spanning tree problem by taking weights as NLPIFNs to determine the uncertainty in the process more precisely.

1. Introduction

Today, the fields of artificial intelligence (AI) and machine learning (ML) have shown very rapid development with increasingly diverse data sources. Indeed, various types of digital objects around can serve as sources of information. Processing and converting the information around us into data within the framework of the information processing theory is important, as AI and ML techniques require a large amount of reliable data in the training and validation stages. Although information naturally contains uncertainty, such information needs to be modeled and converted into data without neglecting its inherent uncertainty. For this purpose, mathematical techniques, such as the fuzzy theory and the intuitionistic fuzzy theory, are used. The fuzzy theory, which is actually an extension of the well-known set theory, provides the main foundation for many approaches. Zadeh [1] introduced the fuzzy sets concept as an approach for modeling vagueness and uncertainty. It is possible list lots of different research areas of the theory of fuzzy sets such as applications of medical sciences, business analytics, sociology, psychology, engineering, data sciences, network models, artificial intelligence, machine learning, operations research, optimization, decision support systems.

Atanassov [2] proposed the idea of using intuitionistic fuzzy sets to interpret uncertainty differently from the perspective of the fuzzy sets theory. Atanassov realized this novel concept by merging the membership level and the non-membership level. Generally, fuzzy sets are constructed to assess the membership level of an element in a given set (the non-membership level is directly computed as the complement of membership level), while intuitionistic fuzzy sets present both the membership and the non-membership levels for each element. These two types of sets theoretically are not related to each other; the only restriction is that the sum of these two levels must not be greater than one. The intuitionistic fuzzy theory is frequently applied to optimization problems, especially when dealing with decision-making problems. Xing and Qui [3] examined a matrix game for a situation in which the players of the game approximately know the payoff. The authors used triangular intuitionistic fuzzy numbers to model the uncertainty of the payoff. The authors computed the equilibrium point of the matrix game problem as the solution for a pair of primal-dual single objective intuitionistic fuzzy linear optimization problems. Ghaffar et al. [4] discussed the problem of determining the preference relations between objective functions, which is frequently encountered in fuzzy goal programming problems. The authors used various mathematical forms for intuitionistic fuzzy numbers to define preference relations and analyzed the effects of mathematical forms on the solution set of fuzzy goal programming problems. Büyükselçuk and Sarı [5] investigated a decision-making problem for which the evaluation results of the alternatives according to the criteria were stated to be intuitionistic fuzzy sets. In this study, the authors applied a custom approach to determine which whey protein variety professional athletes should choose as a food supplement. The authors solved the problem using the VIKOR model, in which the evaluation results of the alternatives were circular intuitionistic fuzzy sets. Baklouti [6] evaluated a multi-attribute decision-making problem. For such problems, Baklouti proposed a novel ranking method for IFNs based on the probabilistic dominance relationship between IFNs and fuzzy algebras. Nayagam et al. [7] aimed at ranking IFNs through employing score functions based on membership, non-membership, vagueness, and imprecision functions. The authors obtained a formula for the ranking method of trapezoidal intuitionistic fuzzy numbers. More studies exist in this field. By describing these studies, we sought to emphasize that different scientists use different IFNs according to the structures of their own problems. Moreover, the same type of IFN was commonly used in these studies to model the problem under consideration. However, for some real-life problems, it may not be possible to use only one type of IFN throughout the modeling phase. The need for a general and inclusive mathematical IFN definition for such cases is obvious. Consequently, we proposed the non-linear pentagonal intuitionistic fuzzy number (NLPIFN) definition in this paper.

Intuitionistic fuzzy sets can be evaluated as higher-order fuzzy sets in some cases. Thus, the solution procedure is much more complicated during the application phases of the higher-order fuzzy sets. However, if a better and more elegant result is the goal, then the complexity of computation time, computation volume, or memory space can be neglected. Even though such complexity is acceptable by most of the system designers, a crisp (defuzzified) set or number is still needed for the system to function. Indeed, the current computer systems are created to work with defuzzy information. Thus, a well-defined defuzzification method is a requirement for both fuzzy and intuitionistic fuzzy numbers. For this reason, the IF-WABL method has been deeply discussed in this study. Some mathematical features of the IF-WABL method that offer convenience to users in practical applications have also been presented in this study. A simple formula to calculate the defuzzified value of the newly introduced NLPIFN with IF-WABL was also presented in this study. In the literature, a number of defuzzification methods for fuzzy and intuitionistic fuzzy numbers were proposed and applied in various areas. Nagoorgani and Ponnalagu [8] designed a Simplex-like table to solve the intuitionistic fuzzy linear programming problem. To find better alternative solutions, the authors defuzzified IFNs using an accuracy function which is the average of score function values for membership and non-membership values. The defuzzified value was the weighted average of the components of the IFN in concern. In the defuzzifier stage of the Takagi–Sugeno type intuitionistic fuzzy inference system designed by Hajek and Olej [9], a novel defuzzification method similar to the weighted average was employed. Grzegrorzewski [10] calculated the expected value of the trapezoidal IFN as a defuzzified value. The expected value consisted of two components. The first component was computed as adding half of the difference between the left side membership and non-membership functions to the average of the smallest elements having the largest membership and the smallest non-membership. The second component was computed as adding half of the difference between the right side membership and non-membership functions to the average of the largest elements having the largest membership and the smallest non-membership. Iakovidis and Papageorgiou [11] suggested an intuitionistic fuzzy cognitive map approach enabling an expert’s hesitancy in determining causal relations to be modeled in the medical decision-making area. The authors used the center of gravity defuzzification method to defuzzify the aggregated, linguistically expressed, expert opinions. Akram et al. [12] designed an intuitionistic fuzzy logic control and adapted it to heater fans. In the defuzzifier phase of their controller, the authors employed the Takagi–Sugani type center of area formula. Nayagam and Sivaraman [13] suggested an accuracy function for an interval-valued IFN to calculate the weighted average of the membership degree and the hesitancy degree of the interval-valued IFN. The authors assumed that the weight can be chosen by the user and used to weigh the hesitancy degree. Dongfeng et al. [14] proposed an intuitionistic fuzzy logic reasoning system for threat assessment in air defense systems. All of the input variables of the proposed system were modeled with intuitionistic fuzzy linguistic variables. As a defuzzifier, this system uses the weighted average in which the weights are a combination of values for the membership, non-membership, and hesitancy functions. Yager [15] evaluated various properties and characteristics of intuitionistic fuzzy sets. One of the characteristics was the defuzzification of intuitionistic fuzzy sets that are described in a discreet form. The author proposed two approaches that are similar to weighted averaging. For the first approach, each weight of elements of intuitionistic fuzzy sets was computed by dividing the summation of membership and non-membership values of the element by the total of membership and non-membership values of all elements. For the second approach, each weight of elements of intuitionistic fuzzy sets was computed by dividing the multiplication of the maximum of all memberships and membership values of the element by the total of all multiplications of the maximum of all memberships and membership values of the element. Seikh et al. [16] evaluated a two-person zero-sum matrix game, in which the elements of the payoff matrix are stated as triangular intuitionistic fuzzy numbers. The authors created two intuitionistic fuzzy programming models for each player. Then, to solve these problems, the authors obtained crisp values of the elements of the payoff matrix by defining a defuzzification method that is similar to the weighted average. The authors only used three components of a triangular intuitionistic fuzzy number which these components are used to determine. Hajek and Olej [17] investigated an interval-valued intuitionistic fuzzy inference system that is similar to the Takagi–Sugeno–Kang type system. The authors proposed a defuzzification method to obtain a crisp output from the evaluated system. The authors adopted the center of area method to interval-valued intuitionistic fuzzy outputs. The proposed defuzzification method was similar to the weighted averaging method, in which the weights are computed with respect to the differences between the left sides of the $(\alpha -\beta )$ cuts and the right sides of the $(\alpha -\beta )$ cuts. Giri et al. [18] dealt with a price- and quality-dependent demand multi-item inventory problem in which the price- and quality-dependent demands were intuitionistic fuzzy numbers. The authors stated an intuitionistic fuzzy optimization problem. To solve the problem, the authors obtained the defuzzified values of intuitionistic fuzzy parameters of the model. The authors employed a possibilistic mean method, in which the weight level functions were determined according to the possibility measure of the given IFN. Paramanik et al. [19] investigated the redundancy allocation problem for complex systems in an intuitionistic fuzzy environment. The authors assumed that all the control parameters of the considered system were triangular intuitionistic fuzzy numbers. The authors first computed defuzzified values of the parameters and established an optimization problem using these values. Then, the authors solved the optimization problem with the Genetic Algorithm. The authors utilized Yager’s ranking method to defuzzify all the control parameters. In the employed defuzzification method, there were weights for sides of the membership and non-membership functions and for the membership and non-membership values. Singh et al. [20] dealt with the c-control charts problem with an intuitionistic fuzzy number scenario. With respect to the definition of the intuitionistic fuzzy number given by the authors, there was no hesitancy measure, so they actually employed a fuzzy number. The authors assumed that the limits of the control chart were calculated based on specific$(\alpha -\beta )$ cuts values. On the other hand, intuitionistic fuzzy observations were defuzzified using the method proposed by the authors. The authors obtained defuzzified values using only the membership function and only employed weights to sides of the membership function. Karthick and Uthayakumar [21] evaluated a closed-loop supply chain model with intuitionistic fuzzy parameters. The model was used to investigate the delivery process of an item from a manufacturer to a retailer. In the model, there were various uncertain inventory cost variables that were modeled using intuitionistic triangular fuzzy numbers. The authors first established the model using defuzzified values of these intuitionistic triangular fuzzy numbers and then solved the model by means of theoretical way and using the Genetic Algorithm. The proposed defuzzification method was stated using the distance between the intuitionistic fuzzy number and the origin. If the defuzzification method was applied to an intuitionistic triangular fuzzy number, the result was just the arithmetic mean of the components of the intuitionistic triangular fuzzy number. Maity et al. [22] investigated a green inventory model, in which the demand rate was related to the selling price, stock, and green concern level, and the holding cost was assumed to be a quadratic function of time. To model the demand rate, which possesses uncertainty due to market flexibility, the authors employed a pentagonal intuitionistic fuzzy number. First, the authors stated an intuitionistic fuzzy model, and then, to solve the model, they presented a defuzzification technique and a solution algorithm. The defuzzification technique was an adoption of the centroid method. The authors used the difference between the membership function and non-membership function as the weights of the defuzzification methods. In the aforementioned studies [8,9,10,11,12,13,14,15,16,17,21,22], scientists preferred using weighted-averaging-based defuzzification methods. In actual applications, the authors chose different weights, such as membership values, non-membership values, hesitancy values, accuracy values, the difference between sides of $(\alpha -\beta )$ cuts, and possibility values. All of these methods only use the part of IFN for processing, so the information kept in the shape of the IFN cannot be injected into the defuzzification computations. On the other hand, the IF-WABL method can utilize all information that an IFN contains through its various parameters,$c_L^{\mu },c_R^{\mu },c_L^{\nu },c_R^{\nu }, p\left(\alpha \right),\mathrm{a}\mathrm{n}\mathrm{d} s\left(\beta \right).$ The remaining studies published by the authors of [18,19,20] mentioned this part, in which scientists aimed at using more information kept in the IFN, so they employed various weights to various parts of the IFN. The common disadvantageous part of these methods is that their weights are constant and cannot be adjustable. Thus it is clear that these methods are special cases of the IF-WABL method due to the adjustable manner of the IF-WABL method.

As in the aforementioned studies, there are various precious studies in the literature concerning the implementation of defuzzification methods. However, we have not evaluated one of the important implementation areas of the defuzzification methods which is ordering or ranking. We know that crisp numbers have total ordering; on the other hand, intuitionistic fuzzy numbers have partial ordering. In multi-criteria decision-making problems, ranking or ordering the alternatives has been one of the widely studied topics. Ye [23] investigated intuitionistic trapezoidal fuzzy multi-criteria decision-making problems, in which the preference values of an alternative on the criteria and the weight values of criteria were stated as intuitionistic trapezoidal fuzzy numbers. The author applied Grzegrorzewski’s method to multi-criteria decision-making problems for ranking alternatives in the problem. Yue [24] dealt with interval-valued intuitionistic fuzzy group decision-making problems. The author focused on obtaining the decision makers’ weights in a group decision-making setting. In this setup, the decision information was provided as interval-valued intuitionistic fuzzy numbers. First, the author computed similarity measures between ideal decisions and all individual decisions. Then, the author used these similarity measures to compute the weights of decision makers. To reach the collective decision, all individual decisions, which were stated as interval-valued intuitionistic fuzzy numbers, were aggregated using the weights. To rank all the alternatives, the scores and accuracy degrees of the aggregated overall assessment of each alternative were computed. Wang et al. [25] proposed a novel score function using the prospect value function. This function includes three components: (i) $\alpha$ power of the difference between the average difference of the membership and non-membership values of all interval-valued intuitionistic fuzzy numbers and the difference of the membership and non-membership values of the interval-valued intuitionistic fuzzy number that are being concerned, (ii) $\alpha$ power of the difference between the average total of the membership and non-membership values of all interval-valued intuitionistic fuzzy numbers and, the total of the membership and non-membership values of the interval-valued intuitionistic fuzzy number that are being concerned, (iii) the hesitancy degree. The authors implemented the score function into interval-valued intuitionistic fuzzy multi-criteria decision -making. Wan et al. [26] extended the classic VIKOR method to solve the multi-attribute group decision-making problem with sub-normal triangular IFNs. The authors used weighted possibility means for both membership and non-membership functions as the defuzzifier of the method. The authors employed the defuzzifier and Shannon entropy to compute the attribute weight. Meng et al. [27] proposed two novel approaches to multi-criteria group decision-making under an interval-valued intuitionistic fuzzy environment. These operators were weighted averaging of interval-valued intuitionistic fuzzy numbers. One of these methods was based on arithmetic averaging, which is called the arithmetical interval-valued intuitionistic fuzzy generalized $\lambda$-Shapley Choquet operator, and the other one was based on geometric averaging, which is called the geometric interval-valued intuitionistic fuzzy generalized $\lambda$-Shapley Choquet operator. For these operators, weights were determined by first employing the $\lambda$ fuzzy measure, then Shapley indices, and finally the Choquet integral. These operators were employed to reach the comprehensive interval-valued intuitionistic fuzzy variable of criteria values. Then, using the score and accuracy functions, the authors ranked the alternatives. Wu and Chiclana [28] proposed novel score and accuracy functions for ranking interval-valued intuitionistic fuzzy numbers. The authors used these functions to propose a total order on the set of interval-valued intuitionistic fuzzy numbers and to develop an interval-valued intuitionistic fuzzy multi-attribute decision-making selection process. The expected score function value was the weighted average of the differences between the membership and non-membership value-related $(\alpha -\beta )$ cuts. The expected accuracy function value was the weighted average of the summations of the membership and non-membership value-related $(\alpha -\beta )$ cuts. In both formulas, weights were determined according to a basic unit monotonic function. Qin et al. [29] investigated the Choquet integral for the case that the measure space was an interval intuitionistic fuzzy one. The authors established the interval-valued intuitionistic fuzzy measures system to create the importance measure of attributes. With fuzzy entropy, Shapely values, and the interval-valued intuitionistic fuzzy measure, the authors prepared a theoretical background of calculating the weights of experts to aggregate the decision information of each expert. Finally, the authors employed the score function to rank their alternatives. Li and Wu [30] evaluated the solution method for a multi-criteria group decision environment in which attribute weight information was entirely unknown, and the evaluation information was stated with an interval-valued intuitionistic fuzzy number. The authors proposed a new score function based on the summation of endpoints of $(\alpha -\beta )$ cuts, the difference between the endpoints of the$(\alpha -\beta )$ cuts, and the risk factor determined by a decision-maker. The authors used the score function to compute the crisp values of each attribute and to construct an information entropy function that is used to obtain criterion weight. Xian et al. [31] extended Atanassov’s intuitionistic fuzzy number and Atanassov’s interval-valued intuitionistic fuzzy number concepts to generalized Atanassov’s intuitionistic fuzzy number and generalized interval-valued intuitionistic fuzzy number concepts, respectively. The authors employed these concepts to state an interval-valued intuitionistic fuzzy linguistic variable. The authors used the interval-valued intuitionistic fuzzy linguistic variable concepts to construct the preference degree of each attribute. Then, the authors calculated two interval-valued intuitionistic fuzzy linguistic distance measures of each alternative from the interval-valued intuitionistic fuzzy linguistic positive ideal solution and negative ideal solution. The distance formula was the absolute mean of the differences of membership and non-membership values of the related $(\alpha -\beta )$ cuts. Meng et al. [32] developed a novel approach for group decision-making with interval-valued intuitionistic fuzzy preference relations that can deal with inconsistent and incomplete cases. To check the multiplicative consistency of interval-valued intuitionistic fuzzy preference relations, the authors stated 0–1 mixed programming models. To compute the weights of the decision-makers, the authors proposed a distance measure on interval-valued intuitionistic fuzzy preference relations. The distance is actually the average of absolute differences between two interval-valued intuitionistic fuzzy preference relations that are offered by decision-makers. Kong et al. [33] proposed an alternative way to evaluate the threat assessments of group targets. The authors suggested dealing with this problem using the interval-valued intuitionistic fuzzy multi-attribute group decision-making method. The authors employed the interval-valued intuitionistic fuzzy entropy to calculate attribute weights based on the decision-makers’ decision matrix. The authors used a Shannon entropy-like formula to compute the distance between the judgment value and ideal solutions. Based on this formula, the authors stated a non-linear optimization problem and solved the problem using the improved artificial bee colony algorithm, which was proposed by the authors. Li et al. [34] proposed two operators, namely the intuitionistic fuzzy weighted induced ordered weighted averaging distance operator and the intuitionistic weighted induced ordered weighted averaging weighted average distance operator. Both operators include the ordering phase based on an ordinary intuitionistic fuzzy distance formula. The authors recommended the second operator as a solution to the limitations of the first one. In the intuitionistic fuzzy multi-attribute decision-making model, the authors used the second operator to compute alternative values to rank the alternatives. Hao and Chen [35] investigated ranking problems in multi-attribute decision-making problems with an interval-valued intuitionistic fuzzy environment. The authors proposed two aggregation operators: the interval-valued intuitionistic fuzzy composed ordered weighted arithmetic averaging operator and the interval-valued intuitionistic composed ordered weighted geometric averaging operator. These operators were used to compute the comprehensive attribute values of the alternatives. The authors suggested the maximum and minimum attribute values, similar to the positive and negative ideal solutions. Then, the authors employed the Euclidian distance-like ranking method. Alcantud [36] evaluated multi-attribute group decision-making problems in an intuitionistic fuzzy environment. In that problem’s environment, experts’ ratings were stated as intuitionistic fuzzy variables. The author first aggregated these intuitionistic fuzzy sets through employing a novel intuitionistic fuzzy direct weighted geometric operator, in which pre-determined weights were used to the power of the membership and non-membership values, and these powered results were multiplied. Then, aggregated intuitionistic fuzzy variables were ranked based on the score function, which was the difference between the membership and non-membership functions, and the accuracy function, which was the summation of the membership and non-membership functions. Ding and Wang [37] investigated a TOPSIS-based multi-attribute decision-making problem in which the attribute weights were unknown, and the decision information was in the form of intuitionistic fuzzy numbers. The authors proposed a similarity measure that depends on the minimal absolute differences of the membership and non-membership values. The authors introduced new score and accuracy functions. The score function consists of the summation of the difference between the membership and non-membership values and the weighted difference between the membership and non-membership values, where weights are hesitancy degrees. The accuracy function consists of the summation of the membership and non-membership values and weighted membership and weighted non-membership values, where weights are hesitancy degrees. Based on the proposed score function, the authors proposed a Shannon entropy-like entropy formula to calculate the attribute weights. To rank the alternatives, the authors calculated relative similarity measures between the positive ideal solution and the alternatives and between the negative ideal solution and the alternatives. Faizi et al. [38] evaluated multi-criteria group decision-making problems with an intuitionistic fuzzy environment. The authors modified the COMET method to employ it in an intuitionistic fuzzy environment. The authors computed characteristics objects defined by decision makers and performed pairwise comparisons of the objects by adding decision-makers’ opinions. The authors employed the score function to obtain crisp numbers for the criteria. The authors finally used these crisp numbers in the inference system of COMET. Chen and Tsai [39] proposed an approach to solving multi-attribute decision-making problems by defining a new score function of interval-valued intuitionistic fuzzy values. The score function was based on the average of the square root of membership and non-membership values of interval-valued intuitionistic fuzzy values. The authors ranked alternatives in multi-attribute decision-making problems according to the proposed score function. Wang et al. [40] adopted the intuitionistic fuzzy TOPSIS method for the geo-environmental carrying capacity problem. The authors used geomorphic units as alternatives to be ranked. Using an intuitionistic fuzzy matrix and the positive and negative ideal solutions, the authors computed the weighted distances, of which the formula was very similar to the Hamming distance formula. Finally, using these distances, the authors computed the indicators to rank their alternatives. The authors implemented the approach to the Meishan City, China, data set. Yang et al. [41] investigated the Frank aggregation operators (averaging and geometric) based on the complex intuitionistic fuzzy set theory and proposed a list of averaging operators, such as the complex intuitionistic fuzzy Frank weighted averaging operator, complex intuitionistic fuzzy Frank ordered weighted averaging operator, complex intuitionistic fuzzy Frank hybrid averaging operator, complex intuitionistic fuzzy Frank weighted geometric operator, complex intuitionistic fuzzy Frank ordered weighted geometric operator, and complex intuitionistic fuzzy Frank hybrid geometric operator. The authors embedded these techniques into multi-attribute decision-making problems to measure the performances of the proposed operators. The authors used these operators to aggregate the information in the decision matrix of the multi-attribute decision-making problem. The authors preferred employing the score function to order the alternatives. Jin and Garg [42] proposed a new score function for intuitionistic fuzzy numbers based on a probabilistic perspective. The authors evaluated the value of the score function, like computing the probability of a continuous random variable. An individual’s score was calculated by determining the ratio of the part more minor than the individual to the whole. The authors constructed an entropy index using their proposed score function. The entropy index was used to derive the weights of the criteria in multi-criteria decision-making problems. The authors employed the proposed score function and prospect value function to calculate dominance degrees between alternatives. The authors ranked the alternatives using the dominance degree, negative ideal solution, and positive ideal solution. The score function was similar to computing probability and available for comparison. Huang et al. [43] proposed a new ranking method based on a probabilistic dominance relationship and implemented the ranking method into multi-attribute decision-making problems with an intuitionistic fuzzy environment. In the first step, the authors transformed intuitionistic fuzzy numbers by redefining their membership and non-membership values to mitigate the uncertainty arising from hesitancy. Then, the authors computed the probabilistic dominance degree of an intuitionistic fuzzy number relative to other intuitionistic fuzzy numbers based on the joint probability density function, which concerns the relationship between the membership and non-membership functions. The authors adopted this technique to comparing objects phase of the multi-attribute decision-making problem. Zhengsen et al. [44] implemented the multi-criteria decision problem to the investment decision problem in distributed production. The authors used subjective weights that were expressed as triangular intuitionistic fuzzy numbers. The authors employed the formula to quantify triangular intuitionistic fuzzy numbers. The formula, which is evaluated as a defuzzification, was a weighted averaging of the parameters of triangular intuitionistic fuzzy numbers. The authors used λ to reflect the attitude of decision-makers to the degree of uncertainty. Feng et al. [45] proposed a new perspective to the already used definition of generalized intuitionistic fuzzy soft sets. Based on this novel perspective, some existing concepts and findings about generalized intuitionistic fuzzy soft sets were improved. The authors designed an algorithmic solution approach for multi-attribute decision-making problems by employing generalized intuitionistic fuzzy soft sets and required operators. The authors ordered the alternatives using the proposed expectation score function. The score function was computed as the sum of the constant and the average difference between the membership and non-membership functions. Feng et al. [46] evaluated the problem of ranking intuitionistic fuzzy values and its applications to decision-making problems. The authors first proposed the novel concept of the Minkowski score function. Then, the authors embedded the attitudinal parameter into the first formula to reach a more generalized score function concept. The attitudinal parameter was employed to produce weights for the membership and non-membership functions of the intuitionistic fuzzy value. The Minkowski score function was a parameter-based method that could cover various score functions by adjusting the parameter values. The authors used the Minkowski score function to rank the overall intuitionistic fuzzy preference in the multi-attribute decision-making problem. Agarwal et al. [47] extended the generalized intuitionistic fuzzy soft set by proposing the generalization parameter that was also intuitionistic fuzzy. The authors investigated the novel score and the accuracy functions to compare two intuitionistic fuzzy numbers. Both score and accuracy functions were based on the squared of the membership and non-membership functions. The authors employed these functions to rank alternatives in intuitionistic fuzzy multi-criteria decision-making problems.

In nearly all of the studies mentioned here concerning multi-criteria decision-making problems, the authors only utilized one type of tool to model uncertainty, such as trapezoidal IFN, triangular IFN, intuitionistic fuzzy linguistic variable, and so on. In real-life problems, the weights of attributes and/or the decision-makers’ opinions can be stated through different IFNs. The point is that if we have generally defined and mathematically inclusive IFN, we can use all of the solution methods for multi-criteria decision-making problems. We aimed to fill in the gap with the NLPIFN. Moreover, these studies concerning multi-criteria decision-making problems can be classified according to ranking methods into two classes: (i) weighted averaging-based methods (as published by the authors of [23,26,34,38,42,43,47]) and (ii) distance-based methods (as published by the authors of [24,25,27,28,29,30,31,32,33,35,36,37,39,40,41,45,46,47]). Nearly all of the distance-based methods mentioned here were based on score and/or accuracy functions, of which the main motivation was to measure the similarity between the alternative and ideal solutions. Again, in nearly all of the distance-based methods, interval-valued intuitionistic fuzzy numbers were employed. We assume that interval-valued intuitionistic fuzzy numbers are defined in discrete space. From that point of view, the IF-WABL method is not suitable to process such numbers until a discrete version of IF-WABL is defined, which is highly possible. While we evaluated weighted averaging-based methods, IF-WABL can transform into all of them, providing that the IF-WABL parameters are chosen specially and properly.

As mentioned above, IFNs are employed in many computational areas in various fields, such as artificial intelligence, optimization, decision-making, and operations research. Consequently, the requirements for a general and inclusive mathematical definition of an IFN and a well-defined and easily applicable defuzzification method are obvious. However, converting fuzzy decision-making problems into their equivalent crisp problems using a defuzzifier along with a decision-maker’s opinion is not the only way to solve such problems [48,49,50,51]. Orazbayev et al. [48] developed a method for deriving linguistic models of fuzzyly defined objects and then proposed a heuristic method for solving the multi-criteria optimization problem in a fuzzy environment without employing any defuzzification method. The authors applied the proposed heuristic method to the problem of two-criteria optimization in the delayed petroleum coking process, which is utilized in the production of electrodes and anodes, space technology, electronics, and metallurgy, with fuzzy constraints. In another study, Orazbayev et al. [49] investigated a complex chemical engineering system of an oil refinery under uncertain conditions with respect to various types of information. To handle the aforementioned system as a whole, the authors developed models and then combined these models into a single model. After their modeling efforts, the authors produced a fuzzy optimization problem and then proposed an algorithm that does not include a defuzzification step. To obtain further information concerning the solution of fuzzy decision-making problems without applying a defuzzification method, see topics published by the author of [50].

IFNs have various application areas, making a general and inclusive mathematical definition of IFNs increasingly necessary. As the IFN possesses mathematically superior properties, a general representation can be available for modeling different problems, and it has become possible to use different types of IFNs within the same problem. In this paper, we proposed the non-linear pentagonal intuitionistic fuzzy number (NLPIFN), which has a general and inclusive mathematical definition. We showed that if a user changes the component values of an NLPIFN properly, the user can realize a very large family of IFNs, such as linear pentagonal IFNs, non-linear trapezoidal IFNs, linear trapezoidal IFNs, non-linear triangular IFNs, linear triangular IFNs, and Baloui’s Generalized IFN [52]. For example, if a scientist would like to use a linear pentagonal IFN and non-linear trapezoidal IFN at the same time in their model, they can use the NLPIFN by properly adjusting the component values of the NLPIFN to acquire linear pentagonal IFNs and non-linear trapezoidal IFNs whenever required. In this study, we outlined some definitions and basic arithmetic operations for the newly defined NLPIFN. We also evaluated a flexible, well-defined, and inclusive defuzzification method called IF-WABL [53]. The main idea behind this method was to utilize all relevant information provided by an IFN. The parameters of the IF-WABL method were used to give weights to the ($\alpha -\beta$) cuts of the IFN, the sides of the membership and non-membership functions, and the membership and non-membership functions themselves. As a result of these parameters, every piece of information provided by the IFN is injected into the defuzzification process. The IF-WABL method is also suitable due to the subjectivity of the IF theory. A user who employs the IF-WABL method can determine the parameter values of the method (according to the conditions given in the method’s definition) based on their own desires and/or the nature of the problem being solved. In this study, we presented several mathematical properties of IF-WABL. We also provided a fast and easily applicable formula to compute the defuzzified value of the NLPIFN by employing the IF-WABL method. To show the usage of both the NLPIFN and its IF-WABL formula, we presented an example related to the intuitionistic fuzzy minimum spanning tree problem.

Many research papers have been presented where intuitionistic fuzzy numbers are investigated and implemented in various fields. Still, many more scopes are present to study these topics. In this paper, we aimed to develop an intuitionistic fuzzy number and its application. The possible novelties and contributions of this study can be mentioned as follows:

• The non-linear pentagonal intuitionistic fuzzy number is defined.
• Arithmetic operations of the NLPIFN are formulated using $(\alpha -\beta )$ cuts representation.
• The short-cut formula of the intuitionistic fuzzy weighted averaging based on levels (IF-WABL) value of NLPIFN is derived.
• A solution approach for the intuitionistic fuzzy minimum spanning tree (IF MST) problem based on the IF-WABL value of NLPIFN has been proposed.

In this paper, we have focused on the NLPIFN. We also have presented the arithmetic operations of NLPIFNs using $(\alpha -\beta )$ cuts representation. A modified version of Prim’s algorithm was suggested to solve the (IF MST) problem, of which the edge weights can be any IFNs among the linear pentagonal IFNs, non-linear trapezoidal IFNs, linear trapezoidal IFNs, non-linear triangular IFNs, linear triangular IFNs, and Baloui’s Generalized IFN. Finally, we implemented the solution approach to one numerical illustration.

The structure of the paper is as follows: The second section presents the fundamental preliminary concepts. In the third section, we introduce the NLPIFN and obtain arithmetic operations related to the number using the $(\alpha -\beta )$ cuts approach. Relations between the NLPIFN and IFNs are addressed in this section. A short-cut IF-WABL defuzzification formula is derived in Section 4. The application of NLPIFNs in the IF minimum spanning tree problem is presented in Section 5. Lastly, conclusions are given in Section 6.

2. Preliminaries

This paper sought to model uncertainty by employing different IFNs. Thus, we began with the most fundamental approach to deal with uncertainty problems and provided a definition of fuzzy sets.

Definition 1

([1]). Let X be a space of points (objects), with a generic element of X denoted by x. Thus, X = {x}. A fuzzy set (class) A in X is characterized by a membership (characteristic) function, ${\mu }_A$(x), associated with each point in X a real number in the interval [0, 1] with the value of ${\mu }_A$(x) at x representing the "grade of membership" of x in A. Thus, the nearer the value of ${\mu }_A$(x) is to unity, the higher the grade of membership of x in A.

The previous definition was extended to deal with the different types of uncertainties that are encountered in real-life problems. Thus, a new class of fuzzy sets is created called higher-order fuzzy sets. The type 2 fuzzy set [54] is one element of this new class. With a type 2 fuzzy set, a researcher can employ a fuzzy set to model the membership values of the elements in the relevant fuzzy set. Therefore, based on the novel definition, membership values are also fuzzy sets.

Definition 2

([54]). A Type 2 Fuzzy Set, represented as $\tilde{A}$, is a fuzzy set described by a type 2 membership function, $0\le {\mu }_{\tilde{A}}(x,u)\le 1$, as follows:

$$\tilde{A}=\left\{\left(\left(x,u\right),{\mu }_{\tilde{A}}(x,u)\right)|\forall x\in X, \forall u\in J_X\subseteq [\mathrm{0,1}]\right\}$$

where $x, J_X, and u$ and ${\mu }_{\tilde{A}}(x,u)$ denote the primary variable, the primary membership function in the [0, 1] interval, the secondary variable, and the secondary membership function at $x$ , respectively.

Another member of the higher-order fuzzy set class is IFS. An IFS is characterized by two related functions, namely the membership function, which is the same as the fuzzy set, and the non-membership function. In this paper, we concentrated on IFSs and proposed an alternative mathematical formulation for this member. Thus, we evaluated fundamental definitions related to IFS.

Definition 3

([2]). An IFS A in X is defined as an object in the form of $A=\{〈x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)〉:x\in X\}$ , where the functions ${\mu }_A:X\to \left[\mathrm{0,1}\right]$ and  ${\nu }_A:X\to \left[\mathrm{0,1}\right]$ define the degree of membership and the degree of non-membership of the element $x\in X$, respectively, and for every  $x\in X$ in  $A$, $0\le {\mu }_A\left(x\right)+{\nu }_A\left(x\right)\le 1$ is held.

Definition 4

([2]). For every common fuzzy subset  $A$ on $X$, the intuitionistic fuzzy index of  $x$ in  $A$ is defined as ${\pi }_A\left(x\right)=1-{\mu }_A\left(x\right)-{\nu }_A\left(x\right)$. This phenomenon is also known as the degree of hesitancy or degree of uncertainty of the element $x$ in  $A$. For every $x\in X$,  $0\le {\pi }_A\left(x\right)\le 1$.

Definition 5

([53]). An IFN $\tilde{A}$ is defined as follows:

• An intuitionistic fuzzy subset of the real line.
• Normal, that is, there is some $x_0\in \mathcal{R}$, such that ${\mu }_{\tilde{A}}\left(x_0\right)=1$ and ${\nu }_{\tilde{A}}\left(x_0\right)=0$.
• Convex for the membership function ${\mu }_{A^{*}}\left(x\right)$, that is, ${\mu }_{\tilde{A}}\left({\lambda x}_1+{(1-\lambda )x}_2\right)\ge \mathrm{m}\mathrm{i}\mathrm{n}({\mu }_{\tilde{A}}\left(x_1\right),{\mu }_{\tilde{A}}\left(x_2\right))$ for every $x_1,x_2\in \mathcal{R}$, $\lambda \in \left[\mathrm{0,1}\right]$.
• Concave for the non-membership function ${\nu }_{\tilde{A}}\left(x\right)$, that is, ${\nu }_{\tilde{A}}\left({\lambda x}_1+{(1-\lambda )x}_2\right)\le \mathrm{m}\mathrm{a}\mathrm{x}({\nu }_{\tilde{A}}\left(x_1\right),{\nu }_{\tilde{A}}\left(x_2\right))$ for every $x_1,x_2\in \mathcal{R}$, $\lambda \in \left[\mathrm{0,1}\right]$.

Definition 6

([53]). The support of IFN $\tilde{A}$ on  $\mathcal{R}$ is the crisp set of all $x\in \mathcal{R}$, such that  ${\mu }_{\tilde{A}}\left(x\right)>0$,  ${\nu }_{\tilde{A}}\left(x\right)>0$, and  ${\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\le 1$.

Definition 7.

${\mathcal{F}}_c\left(\mathcal{R}\right)$ will denote the class of (bounded) IFNs which maps ${\mu }_{\tilde{A}}:X\to \left[\mathrm{0,1}\right]$ and  ${\nu }_{\tilde{A}}:X\to \left[\mathrm{0,1}\right]$, such that their $\alpha$ and  $\beta$ cuts are as follows:

• $\alpha ,\beta \in \left[\mathrm{0,1}\right]$ and $\alpha +\beta \le 1$;
• $\widetilde{A_{\alpha }^{\mu }}=\left\{\begin{array}{cc}\left\{x\in R:{\mu }_{\tilde{A}}\left(x\right)\ge \alpha \right\}& if\alpha \in \left(\mathrm{0,1}\right]\\ cl\left\{x\in R:{\mu }_{\tilde{A}}\left(x\right)>0\right\}& if\alpha =0\end{array}\right.;$
• $\widetilde{A_{\alpha }^{\nu }}=\left\{\begin{array}{cc}\left\{x\in R:{\nu }_{\tilde{A}}\left(x\right)\le \beta \right\}& if\beta \in \left(\mathrm{0,1}\right]\\ cl\left\{x\in R:{\nu }_{\tilde{A}}\left(x\right)<1\right\}& if\beta =1\end{array}\right.$.

Definition 8.

A Triangular IFN (TIFN) $\tilde{A}$ is an IFS in $\mathcal{R}$ with the membership function and non-membership function as follows:

$${\mu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{cc}\frac{x-a_1}{a_2-a_1}& a_1\le x\le a_2\\ \frac{a_3-x}{a_3-a_2}& a_2\le x\le a_3\end{array}\right.$$

$$v_{\tilde{A}}\left(x\right)=\left\{\begin{array}{cc}\frac{a_2-x}{a_2-{a_1}^{\prime }}& {a_1}^{\prime }\le x\le a_2\\ \frac{x-a_2}{{a_3}^{\prime }-a_2}& a_2\le x\le {a_3}^{\prime }\end{array}\right.$$

where ${a_1}^{\prime }\le a_1\le a_2\le a_3\le {a_3}^{\prime }$ and the symbolic representation of TIFN is ${\tilde{A}}_{TIFN}=(a_2;a_1,a_3,{a_1}^{\prime },{a_3}^{\prime })$.

Definition 9.

A Trapezoidal IFN (TrIFN) $\tilde{A}$ is an IFS in $\mathcal{R}$ with the membership function and non-membership function as follows:

$${\mu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{cc}\frac{x-a_1}{a_2-a_1}& a_1\le x\le a_2\\ 1& a_2\le x\le a_3\\ \frac{a_4-x}{a_4-a_3}& a_3\le x\le a_4\end{array}\right.$$

$$v_{\tilde{A}}\left(x\right)=\left\{\begin{array}{cc}\frac{a_2-x}{a_2-{a_1}^{\prime }}& {a_1}^{\prime }\le x\le a_2\\ 0& a_2\le x\le a_3\\ \frac{x-a_3}{{a_4}^{\prime }-a_3}& a_3\le x\le {a_4}^{\prime }\end{array}\right.$$

where ${a_1}^{\prime }\le a_1\le a_2\le a_3\le a_4\le {a_4}^{\prime }$. The symbolic representation of TrIFN is ${\tilde{A}}_{TrIFN}=(a_2,a_3; a_1,a_4, {a_1}^{\prime },{a_4}^{\prime })$.

Definition 10

([55]). Let X denote a non-empty set. The Generalized IFS A in X is defined as an object of the form $A=\{〈x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)〉:x\in X\}$, where the functions ${\mu }_A:X\to \left[\mathrm{0,1}\right]$ and  ${\nu }_A:X\to \left[\mathrm{0,1}\right]$ define the degree of membership and the degree of non-membership of A, respectively, $0\le {{\mu }_A\left(x\right)}^{\delta }+{{\nu }_A\left(x\right)}^{\delta }\le 1$ for each $x\in X$, and  $\delta =n$ or  $\frac{1}{n}, n=\mathrm{1,2},\dots ,N$.

3. Representations of the NLPIFN and Its Arithmetic Operations

In this section, we present the membership and non-membership functions of the NLPIFN, its $(\alpha -\beta )$ cuts representation, the arithmetic operations on the NLPIFN using $(\alpha -\beta )$ cuts representation, and the transition between the NLPIFN and other IFNs.

Definition 11.

An NLPIFN $\tilde{A}$ is an IFS in $\mathcal{R}$ with a membership function and non-membership function as follows:

$${\mu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{cc}k{\left(\frac{x-a_1}{a_2-a_1}\right)}^{n_1}& a_1\le x\le a_2\\ k+(1-k){\left(\frac{x-a_2}{a_3-a_2}\right)}^{n_2}& a_2\le x\le a_3\\ \begin{array}{c}k+(1-k){\left(\frac{a_4-x}{a_4-a_3}\right)}^{m_2}\\ k{\left(\frac{a_5-x}{a_5-a_4}\right)}^{m_1}\end{array}& \begin{array}{c}{a}_3\le x\le a_4\\ \begin{array}{c}\\ a_4\le x\le a_5\end{array}\end{array}\end{array}\right.$$

$${\nu }_{\tilde{A}}\left(x\right)=\left\{\begin{array}{cc}{k}^{\prime }+(1-k\prime ){\left(\frac{a_2^{\prime }-x}{a_2^{\prime }-a_1^{\prime }}\right)}^{n_1^{\prime }}& a_1^{\prime }\le x\le a_2^{\prime }\\ k\prime {\left(\frac{a_3-x}{a_3-a_2^{\prime }}\right)}^{n_2^{\prime }}& a_2^{\prime }\le x\le a_3\\ \begin{array}{c}k\prime {\left(\frac{x-a_3}{a_4^{\prime }-a_3}\right)}^{m_2^{\prime }}\\ k^{\prime }+(1-k\prime ){\left(\frac{x-a_4^{\prime }}{a_5^{\prime }-a_4^{\prime }}\right)}^{m_1^{\prime }}\end{array}& \begin{array}{c}{a}_3\le x\le a_4^{\prime }\\ \begin{array}{c}\\ a_4^{\prime }\le x\le a_5^{\prime }\end{array}\end{array}\end{array}\right.$$

where $a_1^{\prime }\le a_1\le a_2^{\prime }\le a_2\le a_3\le a_4\le a_4^{\prime }\le a_5\le a_5^{\prime }$, $n_1>0$,$m_1>0$, $n_2>0$, $m_2>0$,$n_1^{\prime }>0$, $m_1^{\prime }>0$, $n_2^{\prime }>0$, $m_2^{\prime }>0$, $k>0$, $k^{\prime }>0$, $k+k\prime \le 1$, and $k>k\prime$. The symbolic representation of the NLPIFN is $\tilde{A}=(a_3;a_1,a_2,a_4,a_5,{a_1^{\prime },a}_2^{\prime },a_4^{\prime },a_5^{\prime }$). Figure 1 shows the membership and non-membership functions of $\tilde{A}=(a_3=11,a_1=5,a_2=7.5,a_4=12,a_5=16,{a_1^{\prime }=4,a}_2^{\prime }=7,a_4^{\prime }=14,\mathrm{a}\mathrm{n}\mathrm{d} a_5^{\prime }=17)$, $k=0.5, k^{\prime }=0.45,$ $n_1=m_1=0.4,$ and$n_2=m_2=1.3,n_1^{\prime }=m_1^{\prime }=2.1,n_2^{\prime }=m_2^{\prime }=0.7$. In Figure 1, the blue curves represent the graph of membership function of the NLPIFN and the red curves represent the graph of non-membership function of the NLPIFN.

Lemma 1.

If the NLPIFN $\tilde{A}$ is constructed with respect to Definition 11, then $\tilde{A}$ is also an IFN.

Proof of Lemma 1:

It is clear that the condition ${\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\ge 0$ is always satisfied because of the definitions of the membership function and non-membership function. To prove the lemma, we must show that ${\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\le 1$ is valid for all elements of $\tilde{A}$. Based on the definition of the NLPIFN, we know that the membership function increases monotonously with respect to its variable in the intervals $\left[a_1, a_2\right]$ and $\left[a_2, a_3\right]$, and decreases monotonously with respect to its variable in the intervals $\left[a_3, a_4\right]$ and $\left[a_4, a_5\right]$. In addition, the non-membership function increases monotonously with respect to its variable in the intervals $\left[a_3, a_4^{\prime }\right]$ and $\left[a_4^{\prime }, a_5^{\prime }\right]$, and decreases monotonously with respect to its variable in the intervals $\left[a_1^{\prime }, a_2^{\prime }\right]$ and $\left[a_2^{\prime }, a_3\right]$. Thus, if we show that ${\mu }_{\tilde{A}}\left(x\right)+{\nu }_{\tilde{A}}\left(x\right)\le 1$ is valid for just the limit values of the intervals, all of the values in the intervals satisfy the necessary conditions as follows:

• For $a_1^{\prime }$, ${\mu }_{\tilde{A}}\left(a_1^{\prime }\right)=0 \mathrm{a}\mathrm{n}\mathrm{d} {\nu }_{\tilde{A}}\left(a_1^{\prime }\right)=1.0$, so the condition is satisfied.
• For $a_1$, ${\mu }_{\tilde{A}}\left(a_1\right)=0$ and ${\nu }_{\tilde{A}}\left(a_1\right)=k^{\prime }+(1-k\prime ){\left(\frac{a_2^{\prime }-a_1}{a_2^{\prime }-a_1^{\prime }}\right)}^{n_1^{\prime }}$. From Definition 11, we know that $\frac{a_2^{\prime }-a_1}{a_2^{\prime }-a_1^{\prime }}<1.0$. Based on the value of $n_1^{\prime }$, we have two possible limit values for ${\nu }_{\tilde{A}}\left(a_1\right)$: (i) $\underset{n_1^{\prime }\to 0^{+}}{\lim }{\nu }_{\tilde{A}}\left(a_1\right)=1$ and (ii) $\underset{n_1^{\prime }\to \mathrm{\infty }}{\lim }{\nu }_{\tilde{A}}\left(a_1\right)=k^{\prime }$. As a result, the condition is satisfied.
• For $a_2^{\prime }$, ${\mu }_{\tilde{A}}\left(a_2^{\prime }\right)=k{\left(\frac{a_2^{\prime }-a_1}{a_2-a_1}\right)}^{n_1}$ and ${\nu }_{\tilde{A}}\left(a_2^{\prime }\right)=k^{\prime }$. From Definition 11, we know that $\frac{a_2^{\prime }-a_1}{a_2-a_1}<1.0$. Based on the value of $n_1$, we have two possible limit values for ${\mu }_{\tilde{A}}\left(a_2^{\prime }\right)$: (i) $\underset{n_1\to 0^{+}}{\lim }{\mu }_{\tilde{A}}\left(a_2^{\prime }\right)=k$ and (ii) $\underset{n_1\to \mathrm{\infty }}{\lim }{\mu }_{\tilde{A}}\left(a_2^{\prime }\right)=0$. As a result, the condition is satisfied.
• For $a_2$, ${\mu }_{\tilde{A}}\left(a_2\right)=k$ and ${\nu }_{\tilde{A}}\left(a_2\right)=k\prime {\left(\frac{a_3-a_2}{a_3-a_2^{\prime }}\right)}^{n_2^{\prime }}$. From Definition 11, we know that $\frac{a_3-a_2}{a_3-a_2^{\prime }}<1.0$. Based on the value of $n_2^{\prime }$, we have two possible limit values for ${\nu }_{\tilde{A}}\left(a_2\right)$: (i) $\underset{n_2^{\prime }\to 0^{+}}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\nu }_{\tilde{A}}\left(a_2\right)=k\prime$ and (ii) $\underset{n_2^{\prime }\to \mathrm{\infty }}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\nu }_{\tilde{A}}\left(a_2\right)=0$. As a result, the condition is satisfied.
• For $a_3$, ${\mu }_{\tilde{A}}\left(a_3\right)=1.0$ and ${\nu }_{\tilde{A}}\left(a_3\right)=0$, so the condition is satisfied.
• For $a_4$, ${\mu }_{\tilde{A}}\left(a_4\right)=k$ and ${\nu }_{\tilde{A}}\left(a_4\right)=k\prime {\left(\frac{a_4-a_3}{a_4^{\prime }-a_3}\right)}^{m_2^{\prime }}$. From Definition 11, we know that $\frac{a_4-a_3}{a_4^{\prime }-a_3}<1.0$. Based on the value of $m_2^{\prime }$, we have two possible limit values for ${\nu }_{\tilde{A}}\left(a_4\right)$: (i) $\underset{m_2^{\prime }\to 0^{+}}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\nu }_{\tilde{A}}\left(a_4\right)=k\prime$ and (ii) $\underset{m_2^{\prime }\to \mathrm{\infty }}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\nu }_{\tilde{A}}\left(a_4\right)=0$. As a result, the condition is satisfied.
• For $a_4^{\prime }$, ${\mu }_{\tilde{A}}\left(a_4^{\prime }\right)=k{\left(\frac{a_5-a_4^{\prime }}{a_5-a_4}\right)}^{m_1}$ and ${\nu }_{\tilde{A}}\left(a_4^{\prime }\right)=k\prime$. From Definition 11, we know that $\frac{a_5-a_4^{\prime }}{a_5-a_4}<1.0$. Based on the value of $m_1$, we have two possible limit values for ${\mu }_{\tilde{A}}\left(a_4^{\prime }\right)$: (i) $\underset{m_1\to 0^{+}}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\mu }_{\tilde{A}}\left(a_4^{\prime }\right)=k$ and (ii) $\underset{m_1\to \mathrm{\infty }}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\mu }_{\tilde{A}}\left(a_4^{\prime }\right)=0$. As a result, the condition is satisfied.
• For $a_5$, ${\mu }_{\tilde{A}}\left(a_5\right)=0$ and ${\nu }_{\tilde{A}}\left(a_5\right)=k^{\prime }+(1-k\prime ){\left(\frac{x-a_4^{\prime }}{a_5^{\prime }-a_4^{\prime }}\right)}^{m_1^{\prime }}$. From Definition 11, we know that $\frac{x-a_4^{\prime }}{a_5^{\prime }-a_4^{\prime }}<1.0$. Based on the value of $m_1^{\prime }$, we have two possible limit values for ${\nu }_{\tilde{A}}\left(a_5\right)$: (i) $\underset{m_1^{\prime }\to 0^{+}}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\nu }_{\tilde{A}}\left(a_5\right)=1$ and (ii) $\underset{m_1^{\prime }\to \mathrm{\infty }}{\lim }\mathrm{f}\mathrm{o}\mathrm{r} {\nu }_{\tilde{A}}\left(a_5\right)=k^{\prime }$. As a result, the condition is satisfied.
• For $a_5^{\prime }$, ${\mu }_{\tilde{A}}\left(a_5^{\prime }\right)=0 \mathrm{a}\mathrm{n}\mathrm{d} {\nu }_{\tilde{A}}\left(a_5^{\prime }\right)=1.0$, so the condition is satisfied. □

Definition 12.

The $(\alpha -\beta )$ cuts representation of a NLPIFN is written as follows:

$$\begin{gathered} \inf \widetilde{A_{\alpha }^{\mu }}=\left\{\begin{array}{cc}{A}_L^1\left(\alpha \right)=a_1+(a_2-a_1){\left(\frac{\alpha }{k}\right)}^{\frac{1}{n_1}}& \alpha \in (0,k]\\ A_L^2\left(\alpha \right)=a_2+(a_3-a_2){\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{n_2}}& \alpha \in (k,1]\end{array}\right. \\ \sup \widetilde{A_{\alpha }^{\mu }}=\left\{\begin{array}{cc}{A}_R^1\left(\alpha \right)=a_5-(a_5-a_4){\left(\frac{\alpha }{k}\right)}^{\frac{1}{m_1}}& \alpha \in (0,k]\\ A_R^2\left(\alpha \right)=a_4-(a_4-a_3){\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{m_2}}& \alpha \in (k,1]\end{array}\right. \\ \inf \widetilde{A_{\beta }^{\nu }}=\left\{\begin{array}{cc}{A}_L^1\left(\beta \right)=a_3-(a_3-a_2^{\prime }){\left(\frac{\beta }{k\prime }\right)}^{\frac{1}{n_2^{\prime }}}& \beta \in (0,k\prime ]\\ A_L^2\left(\beta \right)=a_2^{\prime }-(a_2^{\prime }-a_1^{\prime }){\left(\frac{\beta -k\prime }{1-k\prime }\right)}^{\frac{1}{n_1^{\prime }}}& \beta \in (k\prime ,1]\end{array}\right. \\ \sup \widetilde{A_{\beta }^{\nu }}=\left\{\begin{array}{cc}{A}_R^1\left(\beta \right)=a_3-(a_3-a_4^{\prime }){\left(\frac{\beta }{k\prime }\right)}^{\frac{1}{m_2^{\prime }}}& \beta \in (0,k\prime ]\\ A_R^2\left(\beta \right)=a_4^{\prime }-(a_4^{\prime }-a_5^{\prime }){\left(\frac{\beta -k\prime }{1-k\prime }\right)}^{\frac{1}{m_1^{\prime }}}& \beta \in (k\prime ,1]\end{array}\right. \end{gathered}$$

After these definitions, we evaluated the arithmetic operations on the NLPIFNs. Letting $\tilde{A}=\left(a_3;a_1,a_2,a_4,a_5,{a_1^{\prime },a}_2^{\prime },a_4^{\prime },a_5^{\prime }\right) \mathrm{a}\mathrm{n}\mathrm{d} \tilde{B}=(b_3;b_1,b_2,b_4,b_5,{b_1^{\prime },b}_2^{\prime },b_4^{\prime },b_5^{\prime })$ represent two NLPIFNs, we assumed that $k$, $k\prime$, $n_1$, $n_2$, $m_1$, $m_2$, $n_1^{\prime }$, $n_2^{\prime }$, $m_1^{\prime }$, and $m_2^{\prime }$ are the same for both NLPIFNs. Employing the $(\alpha -\beta )$ cuts approach, addition and subtraction of the two NLPIFNs proceeded as follows:

$$\tilde{C}=\tilde{A}+\tilde{B}$$

where

$$\begin{gathered} \inf \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}\left(a_1{+b}_1\right)+\left(\right(a_2+b_2)-(a_1+b_1\left)\right){\left(\frac{\alpha }{k}\right)}^{\frac{1}{n_1}}& \alpha \in (0,k]\\ {(a}_2+b_2)+({(a}_3{+b}_3)-(a_2+b_2\left)\right){\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{n_2}}& \alpha \in (k,1]\end{array}\right. \\ \sup \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}(a_5+b_5)-\left(\right(a_5+b_5)-{(a}_4+b_4)){\left(\frac{\alpha }{k}\right)}^{\frac{1}{m_1}}& \alpha \in (0,k]\\ (a_4+b_4)-\left(\right(a_4+b_4)-(a_3+b_3\left)\right){\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{m_2}}& \alpha \in (k,1]\end{array}\right. \\ \inf \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}\left(a_3+b_3\right)-\left({(a}_3{+b}_3\right)-{(a}_2^{\prime }+b_2^{\prime }\left)\right){\left(\frac{\beta }{k\prime }\right)}^{\frac{1}{n_2^{\prime }}}& \beta \in (0,k\prime ]\\ {(a}_2^{\prime }+b_2^{\prime })-({(a}_2^{\prime }+b_2^{\prime })-(a_1^{\prime }+b_1^{\prime }\left)\right){\left(\frac{\beta -k\prime }{1-k\prime }\right)}^{\frac{1}{n_1^{\prime }}}& \beta \in (k\prime ,1]\end{array}\right. \\ \sup \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}{(a}_3+b_3)-((a_3-b_3{)-(a}_4^{\prime }+b_4^{\prime })){\left(\frac{\beta }{k\prime }\right)}^{\frac{1}{m_2^{\prime }}}& \beta \in (0,k\prime ]\\ (a_4^{\prime }+b_4^{\prime })-(\left(a_4^{\prime }+b_4^{\prime }\right)-(a_5^{\prime }+b_5^{\prime }\left)\right){\left(\frac{\beta -k\prime }{1-k\prime }\right)}^{\frac{1}{m_1^{\prime }}}& \beta \in (k\prime ,1]\end{array}\right. \\ \tilde{C}=\tilde{A}-\tilde{B} \end{gathered}$$

where

$$\begin{gathered} \inf \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}\left(a_1{-b}_1\right)+\left(\right(a_2-b_2)-(a_1-b_1\left)\right){\left(\frac{\alpha }{k}\right)}^{\frac{1}{n_1}}& \alpha \in (0,k]\\ {(a}_2-b_2)+(\left(a_3{-b}_3\right)-(a_2-b_2)){\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{n_2}}& \alpha \in (k,1]\end{array}\right. \\ \sup \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}{(a}_5-b_5)-((a_5-b_5)-(a_4-b_4)){\left(\frac{\alpha }{k}\right)}^{\frac{1}{m_1}}& \alpha \in (0,k]\\ (a_4-b_4)-\left(\right(a_4-b_4)-(a_3-b_3\left)\right){\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{m_2}}& \alpha \in (k,1]\end{array}\right. \\ \inf \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}{(a}_3-b_3)-({(a}_3{-b}_3)-{(a}_2^{\prime }-b_2^{\prime })){\left(\frac{\beta }{k\prime }\right)}^{\frac{1}{n_2^{\prime }}}& \beta \in (0,k\prime ]\\ (a_2^{\prime }-b_2^{\prime })-\left(\right(a_2^{\prime }-b_2^{\prime })-{(a}_1^{\prime }-b_1^{\prime })){\left(\frac{\beta -k\prime }{1-k\prime }\right)}^{\frac{1}{n_1^{\prime }}}& \beta \in (k\prime ,1]\end{array}\right. \\ \sup \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}(a_3-b_3)-({{(a}_3-b_3)-(a}_4^{\prime }-b_4^{\prime })){\left(\frac{\beta }{k\prime }\right)}^{\frac{1}{m_2^{\prime }}}& \beta \in (0,k\prime ]\\ (a_4^{\prime }-b_4^{\prime })-(\left(a_4^{\prime }-b_4^{\prime }\right)-(a_5^{\prime }+b_5^{\prime }\left)\right){\left(\frac{\beta -k\prime }{1-k\prime }\right)}^{\frac{1}{m_1^{\prime }}}& \beta \in (k\prime ,1]\end{array}\right. \end{gathered}$$

It became simple to write the membership and non-membership functions of the resulting NLPIFNs with respect to the above $(\alpha -\beta )$ cuts. Multiplication and division of the two NLPIFNs proceeded slightly differently from the addition and subtraction operations. We applied the essentials of interval arithmetic to the $(\alpha -\beta )$ cuts representations to obtain the desired results of the aforementioned operations as follows:

$$\tilde{C}=\tilde{A}\times \tilde{B}$$

where

$$\begin{gathered} \inf \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}min\left\{A_L^1\left(\alpha \right)B_L^1\left(\alpha \right), A_L^1\left(\alpha \right)B_R^1\left(\alpha \right), A_R^1\left(\alpha \right)B_L^1\left(\alpha \right), A_R^1\left(\alpha \right)B_R^1\left(\alpha \right)\right\}& \alpha \in (0,k]\\ min\left\{A_L^2\left(\alpha \right)B_L^2\left(\alpha \right), A_L^2\left(\alpha \right)B_R^2\left(\alpha \right), A_R^2\left(\alpha \right)B_L^2\left(\alpha \right), A_R^2\left(\alpha \right)B_R^2\left(\alpha \right)\right\}& \alpha \in (k,1]\end{array}\right. \\ \sup \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}max\left\{A_L^1\left(\alpha \right)B_L^1\left(\alpha \right), A_L^1\left(\alpha \right)B_R^1\left(\alpha \right), A_R^1\left(\alpha \right)B_L^1\left(\alpha \right), A_R^1\left(\alpha \right)B_R^1\left(\alpha \right)\right\}& \alpha \in (0,k]\\ max\left\{A_L^2\left(\alpha \right)B_L^2\left(\alpha \right), A_L^2\left(\alpha \right)B_R^2\left(\alpha \right), A_R^2\left(\alpha \right)B_L^2\left(\alpha \right), A_R^2\left(\alpha \right)B_R^2\left(\alpha \right)\right\}& \alpha \in (k,1]\end{array}\right. \\ \inf \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}min\left\{A_L^1\left(\beta \right)B_L^1\left(\beta \right), A_L^1\left(\beta \right)B_R^1\left(\beta \right), A_R^1\left(\beta \right)B_L^1\left(\beta \right), A_R^1\left(\beta \right)B_R^1\left(\beta \right)\right\}& \beta \in (0,k\prime ]\\ min\left\{A_L^2\left(\beta \right)B_L^2\left(\beta \right), A_L^2\left(\beta \right)B_R^2\left(\beta \right), A_R^2\left(\beta \right)B_L^2\left(\beta \right), A_R^2\left(\beta \right)B_R^2\left(\beta \right)\right\}& \beta \in (k\prime ,1]\end{array}\right. \\ \sup \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}max\left\{A_L^1\left(\beta \right)B_L^1\left(\beta \right), A_L^1\left(\beta \right)B_R^1\left(\beta \right), A_R^1\left(\beta \right)B_L^1\left(\beta \right), A_R^1\left(\beta \right)B_R^1\left(\beta \right)\right\}& \beta \in (0,k\prime ]\\ max\left\{A_L^2\left(\beta \right)B_L^2\left(\beta \right), A_L^2\left(\beta \right)B_R^2\left(\beta \right), A_R^2\left(\beta \right)B_L^2\left(\beta \right), A_R^2\left(\beta \right)B_R^2\left(\beta \right)\right\}& \beta \in (k\prime ,1]\end{array}\right. \\ \tilde{C}=\tilde{A}/\tilde{B} \end{gathered}$$

where

$$\begin{gathered} \inf \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}min\left\{\frac{A_L^1\left(\alpha \right)}{B_L^1\left(\alpha \right)}, \frac{A_L^1\left(\alpha \right)}{B_R^1\left(\alpha \right)}, \frac{A_R^1\left(\alpha \right)}{B_L^1\left(\alpha \right)}, \frac{A_R^1\left(\alpha \right)}{B_R^1\left(\alpha \right)}\right\}& \alpha \in (0,k]\\ min\left\{\frac{A_L^2\left(\alpha \right)}{B_L^2\left(\alpha \right)}, \frac{A_L^2\left(\alpha \right)}{B_R^2\left(\alpha \right)}, \frac{A_R^2\left(\alpha \right)}{B_L^2\left(\alpha \right)}, \frac{A_R^2\left(\alpha \right)}{B_R^2\left(\alpha \right)}\right\}& \alpha \in (k,1]\end{array}\right. \\ \sup \widetilde{C_{\alpha }^{\mu }}=\left\{\begin{array}{cc}max\left\{\frac{A_L^1\left(\alpha \right)}{B_L^1\left(\alpha \right)}, \frac{A_L^1\left(\alpha \right)}{B_R^1\left(\alpha \right)}, \frac{A_R^1\left(\alpha \right)}{B_L^1\left(\alpha \right)}, \frac{A_R^1\left(\alpha \right)}{B_R^1\left(\alpha \right)}\right\}& \alpha \in (0,k]\\ max\left\{\frac{A_L^2\left(\alpha \right)}{B_L^2\left(\alpha \right)}, \frac{A_L^2\left(\alpha \right)}{B_R^2\left(\alpha \right)}, \frac{A_R^2\left(\alpha \right)}{B_L^2\left(\alpha \right)}, \frac{A_R^2\left(\alpha \right)}{B_R^2\left(\alpha \right)}\right\}& \alpha \in (k,1]\end{array}\right. \\ \inf \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}min\left\{\frac{A_L^1\left(\beta \right)}{B_L^1\left(\beta \right)}, \frac{A_L^1\left(\beta \right)}{B_R^1\left(\beta \right)}, \frac{A_R^1\left(\beta \right)}{B_L^1\left(\beta \right)}, \frac{A_R^1\left(\beta \right)}{B_R^1\left(\beta \right)}\right\}& \beta \in (0,k\prime ]\\ min\left\{\frac{A_L^2\left(\beta \right)}{B_L^2\left(\beta \right)}, \frac{A_L^2\left(\beta \right)}{B_R^2\left(\beta \right)}, \frac{A_R^2\left(\beta \right)}{B_L^2\left(\beta \right)}, \frac{A_R^2\left(\beta \right)}{B_R^2\left(\beta \right)}\right\}& \beta \in (k\prime ,1]\end{array}\right. \\ \sup \widetilde{C_{\beta }^{\nu }}=\left\{\begin{array}{cc}max\left\{\frac{A_L^1\left(\beta \right)}{B_L^1\left(\beta \right)}, \frac{A_L^1\left(\beta \right)}{B_R^1\left(\beta \right)}, \frac{A_R^1\left(\beta \right)}{B_L^1\left(\beta \right)}, \frac{A_R^1\left(\beta \right)}{B_R^1\left(\beta \right)}\right\}& \beta \in (0,k\prime ]\\ max\left\{\frac{A_L^2\left(\beta \right)}{B_L^2\left(\beta \right)}, \frac{A_L^2\left(\beta \right)}{B_R^2\left(\beta \right)}, \frac{A_R^2\left(\beta \right)}{B_L^2\left(\beta \right)}, \frac{A_R^2\left(\beta \right)}{B_R^2\left(\beta \right)}\right\}& \beta \in (k\prime ,1]\end{array}\right. \end{gathered}$$

In this paper, we used the NLPIFN as it covers various forms of IFNs. If we specially determine the components of the NLPIFN, we obtain different IFNs. In

Table 1. Forms of NLPIFNs when selecting different components.

Components of the NLPIFN	Type of IFN
$n_1=n_2=m_1=m_2=n_1^{\prime }=n_2^{\prime }=m_1^{\prime }=m_2^{\prime }=1$	Linear Pentagonal IFN
$k=1$ ,   $k^{\prime }=0$	Non-linear Trapezoidal IFN
$k=1$ ,   $k^{\prime }=0$,   $n_1=m_1=n_1^{\prime }=m_1^{\prime }=1$	Linear Trapezoidal IFN
$k=0$ ,   $k^{\prime }=1$	Non-linear Triangular IFN
$k=0$ ,   $k^{\prime }=1$ ,   $n_2=m_2=n_2^{\prime }=m_2^{\prime }=1$	Linear Triangular IFN
$k=1$ ,   $k^{\prime }=0$,   $n_1=m_1=n_1^{\prime }=m_1^{\prime }=\delta$	Baloui’s Generalized IFN
$k=0$ ,   $k^{\prime }=1$ ,   $n_2=m_2=n_2^{\prime }=m_2^{\prime }=\delta$	Baloui’s Generalized IFN

, we outline the relationships between the NLPIFN and various forms of the IFNs.

Based on Table 1, NLPIFNs may have a variety of application areas and comprise various types of IFNs. Although we defined the corresponding arithmetic operations based on the NLPIFNs, we still require a proper defuzzification approach for the NLPIFNs to employ these numbers in real-life problems.

4. Definition of IF-WABL and Formula for NLPIFNs

The requirement for a flexible, integral, and inclusive defuzzification method for NLPIFNs is obvious. The IF-WABL [53] defuzzification method possesses these properties with the following definition.

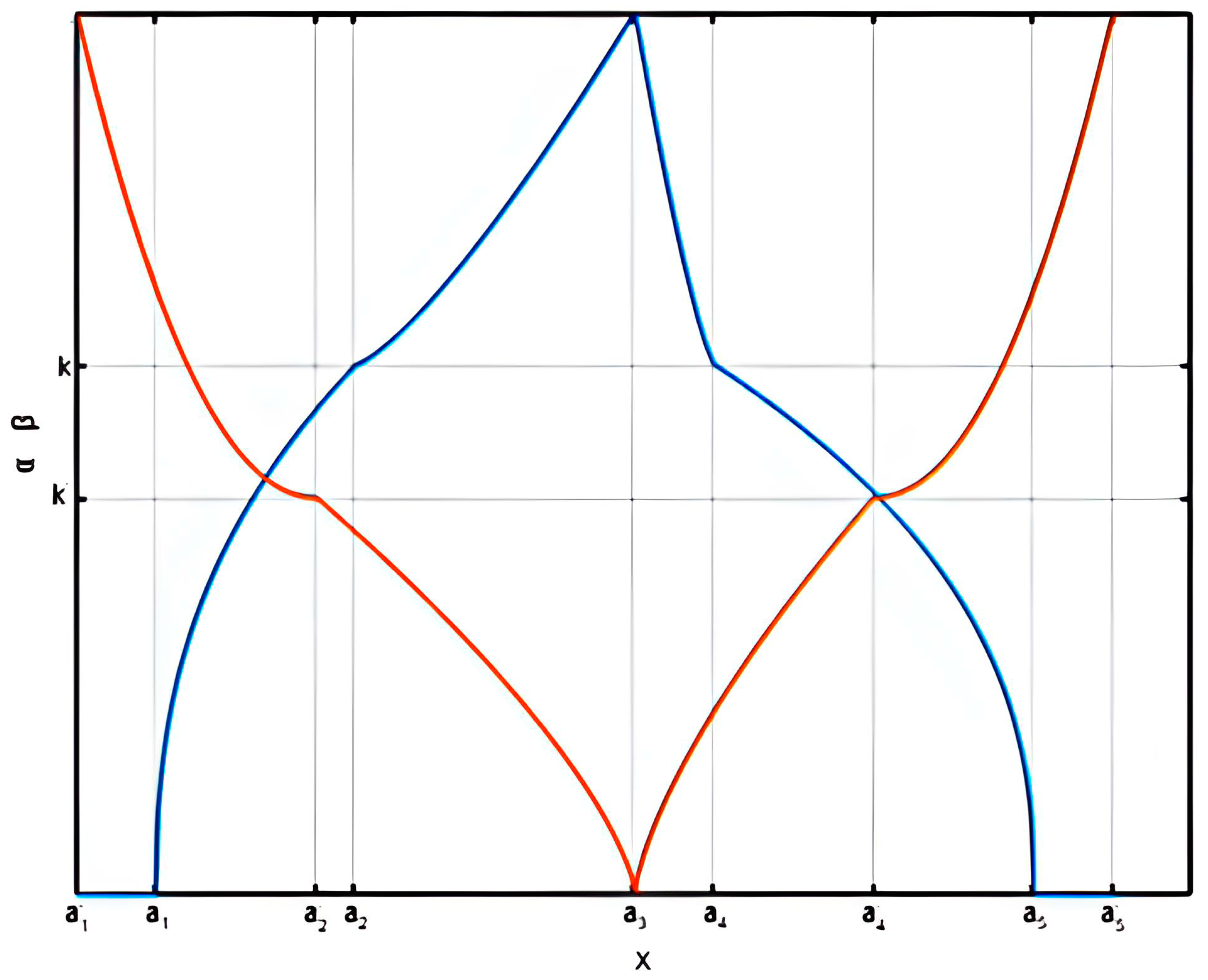
Definition 13.

For an arbitrary IFN  $\tilde{A}$, the IF-WABL defuzzification method can be outlined as follows:

$$IF-WABL\left(\tilde{A}\right)=\theta I\left(\widetilde{A_{\alpha }^{\mu }}\right)+\left(1-\theta \right) I\left(\widetilde{A_{\beta }^{\nu }}\right)$$

where

$$\begin{gathered} I\left(\widetilde{A_{\alpha }^{\mu }}\right)={\int }_0^1\left(c_L^{\mu } inf\widetilde{A_{\alpha }^{\mu }}+c_R^{\mu } sup\widetilde{A_{\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha ; \\ I\left(\widetilde{A_{\beta }^{\nu }}\right)={\int }_0^1\left(c_L^{\nu } inf\widetilde{A_{\beta }^{\nu }}+c_R^{\nu } sup\widetilde{A_{\beta }^{\nu }}\right)s\left(\beta \right)d\beta ; \end{gathered}$$

$\theta \in \left[\mathrm{0,1}\right]$; $c_L^{\mu },c_R^{\mu },c_L^{\nu },c_R^{\nu }\ge 0; c_L^{\mu }+c_R^{\mu }=1; c_L^{\nu }+c_R^{\nu }=1;{\int }_0^{1}p\left(\alpha \right)d\alpha =1; {\int }_0^{1}s\left(\beta \right)d\beta =1.$

Indeed, $I\left(\widetilde{A_{\alpha }^{\mu }}\right)$ and $\mathrm{I}\left(\widetilde{{\mathrm{A}}_{\mathsf{\beta }}^{\mathsf{\nu }}}\right)$ can be understood as special defuzzified values of the membership and non-membership functions of an IFN, respectively. By employing $\theta$, we merged these defuzzified values to obtain a defuzzified value of the IFN. In this way, $\theta$ models the user’s priority related to the membership function over the non-membership function. While $c_L^{\mu }$ and $c_R^{\mu }$ are weights of the left and right sides for the membership function of the IFN, $c_L^{\nu }$ and $c_R^{\nu }$ are weights of the left and right sides for the non-membership function of the IFN, respectively. The user of the IF-WABL method determines the shape of $p\left(\alpha \right)$ to create weights to the $\mathsf{\alpha }$ cuts (membership) of the IFN, and the user of the IF-WABL method designs the function $s\left(\beta \right)$ to assign weights to the $\mathsf{\beta }$ cuts (non-membership) of the IFN. All of these coefficients and functions are called IF-WABL parameters and are determined by the user of the IF-WABL method with respect to the normality and non-negativity conditions of the parameters. The advantages of using the IF-WABL method can be classified into two parts. First, a researcher employing the IF-WABL method can include all of the information contained by the IFN in the relevant process via IF-WABL parameters. IF-WABL parameters generally have two types: weights for sides of the IFN ($c_L^{\mu }, c_R^{\mu }$, $c_L^{\nu }$, and $c_R^{\nu }$) and weight functions for the $(\alpha -\beta )$ cuts of the IFN (p(α) and s(β)). Together, these weights enable the user to employ every piece of information based on the IFN. The other advantage of utilizing IF-WABL is its flexibility property. Due to its flexibility, the IF-WABL defuzzification method can mimic other defuzzification methods by adjusting the values of the IF-WABL parameters. Moreover, a researcher can design their own defuzzification method subject to the normality and non-negativity conditions of the IF-WABL parameters. This application agrees well with the spirit of the IF theory.

Beyond its flexibility and inclusiveness properties, IF-WABL has some mathematical advantages. Based on these properties, some of the arithmetic operations between the IFNs can be easily handled. Before mentioning these characteristics of the IF-WABL method, we offer a definition for the IF extension of a function.

Definition 14.

Let $f(a_1,\dots ,a_n)$ be a function. The IF extension of the function $f$ is  $\Phi :{\mathcal{F}}_c^n\left(\mathcal{R}\right)\to {\mathcal{F}}_c\left(\mathcal{R}\right)$. Moreover, for IFNs $\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)$, $\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)$ is an IF subset and IF extension value of  $f(a_1,\dots ,a_n)$. For this subset, $(\alpha -\beta )$ cuts are as follows:

$$\begin{gathered} {\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)=⌊\mathit{inf}f\left(\widetilde{A_{1,\alpha }^{\mu }},\dots ,\widetilde{A_{n,\alpha }^{\mu }}\right),\mathit{sup}\left(\widetilde{A_{1,\alpha }^{\mu }},\dots ,\widetilde{A_{n,\alpha }^{\mu }}\right)⌋ \\ {\Phi }_{\beta }^{\nu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)=⌊\mathit{inf}f\left(\widetilde{A_{1,\beta }^{\nu }},\dots ,\widetilde{A_{n,\beta }^{\nu }}\right),\mathit{sup}\left(\widetilde{A_{1,\beta }^{\nu }},\dots ,\widetilde{A_{n,\beta }^{\nu }}\right)⌋ \end{gathered}$$

where

$$\begin{gathered} f\left(\widetilde{A_{1,\alpha }^{\mu }},\dots ,\widetilde{A_{n,\alpha }^{\mu }}\right)=\left\{f\left(a_1,\dots ,a_n\right)|a_i\in \widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n\right\}; \\ f\left(\widetilde{A_{1,\beta }^{\nu }},\dots ,\widetilde{A_{n,\beta }^{\nu }}\right)=\left\{f\left(a_1,\dots ,a_n\right)|a_i\in \widetilde{A_{i,\beta }^{\nu }};i=1,\dots ,n\right\}; \\ {\mu }_{\widetilde{A_i}}\left(a_i\right)+{\nu }_{\widetilde{A_i}}\left(a_i\right)\le 1; i=1,\dots ,n. \end{gathered}$$

Lemma 2.

Let the IF extension of the linear function $f(a_1,\dots ,a_n)$ be $\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)$. For  $\forall \alpha ,\beta \in \left[\mathrm{0,1}\right]; \alpha +\beta \le 1$, we write:

$$\begin{gathered} L_{\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)}\left(\alpha \right)=f\left(\overline{inf} \widetilde{A_{1,\alpha }^{\mu }},\dots ,\overline{inf}\widetilde{A_{n,\alpha }^{\mu }}\right) \\ {R}_{\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)}\left(\alpha \right)=f\left(\overline{sup} \widetilde{A_{1,\alpha }^{\mu }},\dots ,\overline{sup}\widetilde{A_{n,\alpha }^{\mu }}\right) \\ {L}_{\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)}\left(\beta \right)=f\left(\overline{inf} \widetilde{A_{1,\beta }^{\nu }},\dots ,\overline{inf}\widetilde{A_{n,\beta }^{\nu }}\right) \\ {R}_{\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)}\left(\beta \right)=f\left(\overline{sup} \widetilde{A_{1,\beta }^{\nu }},\dots ,\overline{sup}\widetilde{A_{n,\beta }^{\nu }}\right) \end{gathered}$$

where

$$\begin{gathered} \overline{inf} \widetilde{A_{i,\alpha }^{\mu }}=\left\{\begin{array}{cc}\mathit{inf}\widetilde{A_{i,\alpha }^{\mu }},& f is non-increasing w.r.t. { a}_i\\ \mathit{sup}\widetilde{A_{i,\alpha }^{\mu }}& else\end{array};\right. \\ \overline{sup} \widetilde{A_{i,\alpha }^{\mu }}=\left\{\begin{array}{cc}\mathit{sup}\widetilde{A_{i,\alpha }^{\mu }},& f is non-decreasing w.r.t. { a}_i\\ \mathit{inf}\widetilde{A_{i,\alpha }^{\mu }}& else\end{array};\right. \\ \overline{inf} \widetilde{A_{i,\beta }^{\nu }}=\left\{\begin{array}{cc}\mathit{inf}\widetilde{A_{i,\beta }^{\nu }},& f is non-decreasing w.r.t. { a}_i\\ \mathit{sup}\widetilde{A_{i,\beta }^{\nu },}& else\end{array};\right. \\ \overline{sup} \widetilde{A_{i,\beta }^{\nu }}=\left\{\begin{array}{cc}\mathit{sup}\widetilde{A_{i,\beta }^{\nu }},& f is non-increasing w.r.t. { a}_i\\ \mathit{inf}\widetilde{A_{i,\beta }^{\nu },}& else\end{array}.\right. \end{gathered}$$

Moreover, let$f$be a monotone and continuous function with respect to each of its components. If$c_L^{\mu }=c_R^{\mu }$and$c_L^{\nu }=c_R^{\nu }$, for$\forall \alpha ,\beta \in \left[\mathrm{0,1}\right]; \alpha +\beta \le 1$, the term is valid as follows:

$$\begin{gathered} {c_L^{\mu }\overline{inf} \widetilde{A_{i,\alpha }^{\mu }}+c_R^{\mu }\overline{sup} \widetilde{A_{i,\alpha }^{\mu }}=c}_L^{\mu }\mathit{inf}\widetilde{A_{i,\alpha }^{\mu }}+c_R^{\mu }\mathit{sup}\widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n \\ {c}_L^{\nu }\overline{inf} \widetilde{A_{i,\beta }^{\nu }}+c_R^{\nu } \overline{sup} \widetilde{A_{i,\beta }^{\nu }}=c_L^{\nu }\mathit{inf}\widetilde{A_{i,\beta }^{\nu }}+c_R^{\nu }\mathit{sup}\widetilde{A_{i,\beta }^{\nu }}; i=1,\dots ,n \end{gathered}$$

Proof of Lemma 2:

In the first part, let $f$ be a monotone non-decreasing function with respect to each of its components. Then, we find the following:

$$\begin{gathered} \overline{inf} \widetilde{A_{i,\alpha }^{\mu }}=\mathit{inf}\widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n \\ \overline{sup} \widetilde{A_{i,\alpha }^{\mu }}=\mathit{sup}\widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n \\ \overline{inf} \widetilde{A_{i,\beta }^{\nu }}=\mathit{inf}\widetilde{A_{i,\beta }^{\nu }}; i=1,\dots ,n \\ \overline{sup} \widetilde{A_{i,\beta }^{\nu }}=\mathit{sup}\widetilde{A_{i,\beta }^{\nu }}; i=1,\dots ,n \end{gathered}$$

Thus, the lemma is valid. In the second case, let $f$ be a monotone decreasing function with respect to each of its components. Then, we can write the following:

$$\begin{gathered} \overline{inf} \widetilde{A_{i,\alpha }^{\mu }}=\sup \widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n \\ \overline{sup} \widetilde{A_{i,\alpha }^{\mu }}=\inf \widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n \\ \overline{inf} \widetilde{A_{i,\beta }^{\nu }}=\sup \widetilde{A_{i,\beta }^{\nu }}; i=1,\dots ,n \\ \overline{sup} \widetilde{A_{i,\beta }^{\nu }}=\inf \widetilde{A_{i,\beta }^{\nu }}; i=1,\dots ,n \end{gathered}$$

We assumed that $c_L^{\mu }=c_R^{\mu }$ and $c_L^{\nu }=c_R^{\nu }$; thus, the lemma is valid. □

Using the lemma, we can write the following theorem.

Theorem 1.

Let$f(a_1,\dots ,a_n)$ be a linear function. For the case $c_L^{\mu }=c_R^{\mu }$, $c_L^{\nu }=c_R^{\nu }$, and IFNs $\widetilde{A_1},\dots ,\widetilde{A_n}$, we state the following:

$$IF-WABL\left(\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)=f\left(IF-WABL\left(\widetilde{A_1}\right),\dots ,IF-WABL\left(\widetilde{A_n}\right)\right)$$

where  $\Phi$ is an IF extension of the function $f$. Moreover, the function $f$ is a monotone non-decreasing function; the above statement is valid when $c_L^{\mu }\ne c_R^{\mu }$ and $c_L^{\nu }\ne c_R^{\nu }$.

Proof of Theorem 1:

Based on the IF-WABL definition, we can write the statement as follows:

$$IF-WABL\left(\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)=\theta I\left({\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)+(1-\theta )I\left({\Phi }_{\beta }^{\nu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)$$

Then, we evaluated the last equality in two pieces:

$$I\left({\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)={\int }_0^1\left(c_L^{\mu }{L}_{\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)}\left(\alpha \right)+c_R^{\mu }{R}_{\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)}\left(\alpha \right)\right)p\left(\alpha \right)d\alpha$$

From Lemma 2, we can write the following:

$$\begin{gathered} I\left({\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ ={\int }_0^1\left(c_L^{\mu }f\right(\overline{inf} \widetilde{A_{1,\alpha }^{\mu }},\dots ,\overline{inf}\widetilde{A_{n,\alpha }^{\mu }}) \\ +c_R^{\mu }f\left(\overline{sup} \widetilde{A_{1,\alpha }^{\mu }},\dots ,\overline{sup}\widetilde{A_{n,\alpha }^{\mu }}\right)\left)p\right(\alpha )d\alpha \end{gathered}$$

where $\overline{inf}\widetilde{A_{i,\alpha }^{\mu }}$ and $\overline{sup}\widetilde{A_{i,\alpha }^{\mu }};i=1,\dots ,n$ are defined as in Lemma 2.

$$\begin{gathered} I\left({\mathsf{\Phi }}_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ ={\int }_0^1{\mathrm{c}}_{\mathrm{L}}^{\mathsf{\mu }}f\left(\overline{inf} \widetilde{A_{1,\alpha }^{\mu }},\dots ,\overline{inf}\widetilde{A_{n,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha \\ +{\int }_0^1{\mathrm{c}}_{\mathrm{R}}^{\mathsf{\mu }}f\left(\overline{sup} \widetilde{A_{1,\alpha }^{\mu }},\dots ,\overline{sup}\widetilde{A_{n,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha \end{gathered}$$

We know that $f$ is a linear function, so we can write the following equality:

$$\begin{gathered} I\left({\mathsf{\Phi }}_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =f\left({\int }_0^1\left({\mathrm{c}}_{\mathrm{L}}^{\mathsf{\mu }}\overline{inf} \widetilde{A_{1,\alpha }^{\mu }}+{\mathrm{c}}_{\mathrm{R}}^{\mathsf{\mu }}\overline{sup} \widetilde{A_{1,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha ,\dots ,{\int }_0^1\left({\mathrm{c}}_{\mathrm{L}}^{\mathsf{\mu }}\overline{inf}\widetilde{A_{n,\alpha }^{\mu }}+{\mathrm{c}}_{\mathrm{R}}^{\mathsf{\mu }}\overline{sup}\widetilde{A_{n,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha \right) \end{gathered}$$

From the definition of IF-WABL, we know that $\theta$ is a positive number. Thus, we can write the following:

$$\begin{gathered} \theta I\left({\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =\theta f\left({\int }_0^1\left(c_L^{\mu }\overline{inf} \widetilde{A_{1,\alpha }^{\mu }}+c_R^{\mu }\overline{sup} \widetilde{A_{1,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha ,\dots ,{\int }_0^1\left(c_L^{\mu }\overline{inf}\widetilde{A_{n,\alpha }^{\mu }}+c_R^{\mu }\overline{sup}\widetilde{A_{n,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha \right) \\ =f\left(\theta {\int }_0^1\left(c_L^{\mu }\overline{inf} \widetilde{A_{1,\alpha }^{\mu }}+c_R^{\mu }\overline{sup} \widetilde{A_{1,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha ,\dots ,\theta {\int }_0^1\left(c_L^{\mu }\overline{inf}\widetilde{A_{n,\alpha }^{\mu }}+c_R^{\mu }\overline{sup}\widetilde{A_{n,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha \right) \end{gathered}$$

Following a similar path, we obtained the statement given below for the second piece:

$$\begin{gathered} (1-\theta )I\left({\Phi }_{\beta }^{\nu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =f\left((1-\theta ){\int }_0^1\left(c_L^{\nu }\overline{inf} \widetilde{A_{1,\beta }^{\nu }}+c_R^{\nu }\overline{sup} \widetilde{A_{1,\beta }^{\nu }}\right)s\left(\beta \right)d\beta ,\dots , \\ (1-\theta ){\int }_0^1\left(c_L^{\nu }\overline{inf}\widetilde{A_{n,\beta }^{\nu }}+c_R^{\mu }\overline{sup}\widetilde{A_{n,\beta }^{\nu }}\right)s\left(\beta \right)d\beta \right) \end{gathered}$$

where $f$ can be a monotone non-decreasing function or not. If $f$ is not a monotone non-decreasing function, then $c_L^{\mu }=c_R^{\mu }$ and $c_L^{\nu }=c_R^{\nu }$ must be satisfied. If $f$ is a monotone non-decreasing function, then $c_L^{\mu }, c_R^{\mu }, c_L^{\nu },$and $c_R^{\nu }$ can be determined arbitrarily. Based on these two alternatives, we can write the following statements:

$$\begin{gathered} \theta I\left({\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =f\left(\theta {\int }_0^1\left(c_L^{\mu }\mathit{inf} \widetilde{A_{1,\alpha }^{\mu }}+c_R^{\mu }\mathit{sup}\widetilde{A_{1,\alpha }^{\mu }} \right)p\left(\alpha \right)d\alpha ,\dots ,\theta {\int }_0^1\left(c_L^{\mu }\mathit{inf}\widetilde{A_{n,\alpha }^{\mu }} \\ +c_R^{\mu }\mathit{sup}\widetilde{A_{n,\alpha }^{\mu }}\right)p\left(\alpha \right)d\alpha \right)=f\left(\theta I\left(\widetilde{A_{1,\alpha }^{\mu }}\right),\dots ,\theta I\left(\widetilde{A_{n,\alpha }^{\mu }}\right)\right) \end{gathered}$$

and

$$\begin{gathered} \left(1-\theta \right)I\left({\Phi }_{\beta }^{\nu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =f\left(\left(1-\theta \right){\int }_0^1\left(c_L^{\nu }\mathit{inf}\widetilde{A_{1,\beta }^{\nu }}+c_R^{\nu }\mathit{sup}\widetilde{A_{1,\beta }^{\nu }} \right)s\left(\beta \right)d\beta ,\dots , \\ \left(1-\theta \right){\int }_0^1\left(c_L^{\nu }\mathit{inf}\widetilde{A_{n,\beta }^{\nu }}+c_R^{\mu }\mathit{sup}\widetilde{A_{n,\beta }^{\nu }}\right)s\left(\beta \right)d\beta \right) \\ =f\left((1-\theta )I\left(\widetilde{A_{1,\beta }^{\nu }}\right),\dots ,(1-\theta )I\left(\widetilde{A_{n,\beta }^{\nu }}\right)\right) \end{gathered}$$

We then merged these two statements knowing that $f$ is a linear function as follows:

$$\begin{gathered} \theta I\left({\Phi }_{\alpha }^{\mu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)+\left(1-\theta \right)I\left({\Phi }_{\beta }^{\nu }\left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =f\left(\theta I\left(\widetilde{A_{1,\alpha }^{\mu }}\right),\dots ,\theta I\left(\widetilde{A_{n,\alpha }^{\mu }}\right)\right)+f\left((1-\theta )I\left(\widetilde{A_{1,\beta }^{\nu }}\right),\dots ,(1-\theta )I\left(\widetilde{A_{n,\beta }^{\nu }}\right)\right) \\ IF-WABL\left(\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right) \\ =f\left(\theta I\left(\widetilde{A_{1,\alpha }^{\mu }}\right)+\left(1-\theta \right)I\left(\widetilde{A_{1,\beta }^{\nu }}\right),\dots ,\theta I\left(\widetilde{A_{n,\alpha }^{\mu }}\right)+(1-\theta )I\left(\widetilde{A_{n,\beta }^{\nu }}\right)\right) \\ IF-WABL\left(\Phi \left(\widetilde{A_1},\dots ,\widetilde{A_n}\right)\right)=f\left(IF-WABL\left(\widetilde{A_1}\right),\dots ,IF-WABL\left(\widetilde{A_n}\right)\right) \end{gathered}$$

 □

As a result of Theorem 1, we can state following relations:

• $\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\mathsf{\gamma }\tilde{A}\right)=\mathsf{\gamma }\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\tilde{A}\right)$, where $\mathsf{\gamma }\ge 0$ and $\mathsf{\gamma }\in \mathrm{R}$.
• $\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\tilde{A}+\tilde{B}\right)=$ $\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\tilde{A}\right)+\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\tilde{B}\right)$.
• If $\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\tilde{A}\right)<\mathrm{I}\mathrm{F}-\mathrm{W}\mathrm{A}\mathrm{B}\mathrm{L}\left(\tilde{B}\right)$, then $\tilde{A}\widetilde{<}\tilde{B}$ for IFNs $\tilde{A}$ and $\tilde{B}$.

These results are very useful for adopting IFNs to real-life problems. Moreover, as noted previously, the IF-WABL method is a flexible approach, as are NLPIFNs. Next, we described the defuzzification short-cut formula for NLPIFNs to merge these two flexible approaches. Based on this short-cut formula, a researcher can easily apply the defuzzification method to their own defuzzification strategy to tackle real-life problems.

Theorem 2.

Let $\tilde{A}=(a_3; a_1,a_2,a_4,a_5, {a_1^{\prime }, a}_2^{\prime },a_4^{\prime },a_5^{\prime }$ be a NLPIFN, with $n_1=m_1$ and  $n_2=m_2$ for the membership function, and  $n_1^{\prime }=m_1^{\prime }$ and $n_2^{\prime }=m_2^{\prime }$ for the non-membership function. The IF-WABL defuzzified value of $\tilde{A}$ is calculated as follows:

$$\begin{array}{cc}\hfill IF-WABL\left(\tilde{A}\right)& =\theta [\left(c_L{a}_2+c_R{a}_4\right)+I_2\left[c_L{(a_3-a}_2)-c_R{(a_4-a}_3)\right]\hfill \\ \hfill & +\left[c_L{(a_2-a}_1)-c_R{(a_5-a}_4)\right](I_1-u)]\hfill \\ \hfill & +(1-\theta )[\left(c_L{a}_2^{\prime }+c_R{a}_4^{\prime }\right)+\left(v-J_1\right)[c_L\left({a_3-a}_2^{\prime }\right)-c_R{(a_4^{\prime }-a}_3\left)\right]\hfill \\ \hfill & -J_2\left[c_L{(a}_2^{\prime }-a_1^{\prime })-c_R(a_5^{\prime }-a_4^{\prime })\right]]\hfill \end{array}$$

where

$$\begin{gathered} {c_L=c}_L^{\mu }=c_L^{\nu }; c_R={c_R^{\mu }=c}_R^{\nu }; u={\int }_0^{k}p\left(\alpha \right)d\alpha ; I_1={\int }_0^k{\left(\frac{\alpha }{k}\right)}^{\frac{1}{n_1}}p\left(\alpha \right)d\alpha ; \\ {I}_2={\int }_k^1{\left(\frac{\alpha -k}{1-k}\right)}^{\frac{1}{n_2}}p\left(\alpha \right)d\alpha ; v={\int }_0^{k^{\prime }}s\left(\beta \right)d\beta ; J_1={\int }_0^{k^{\prime }}{\left(\frac{\beta }{k^{\prime }}\right)}^{\frac{1}{n_2^{\prime }}}s\left(\beta \right)d\beta ; \\ {J}_2={\int }_{k^{\prime }}^1{\left(\frac{\beta -k^{\prime }}{1-k^{\prime }}\right)}^{\frac{1}{n_1^{\prime }}}s(\beta )d\beta . \end{gathered}$$

Proof of Theorem 2:

The $(\alpha -\beta )$ cuts representation of the NLPIFN $\tilde{A}$ given in Definition 12 is written in the IF-WABL formula given in Definition 13. After the application of integral operations, we reached the formula given in Theorem 2. □

The formula outlined in Theorem 2 is a general defuzzification formula that covers all defuzzification formulas for all IFNs given in Table 1. A researcher can easily apply the IF-WABL method after adjusting the parameters of NLPIFN with respect to Table 1 and determining the IF-WABL parameters with respect to the decision-making strategy of the study. Thus, different users can obtain different defuzzified values for the same NLPIFN.

Example 1.

Let $\tilde{A}=(11; 5,7.5,12,16,4,7,14,17)$ be a NLPIFN with $k=0.5$ and $k^{\prime }=0.45$; in addition, $n_1=m_1=0.4$, $n_2=m_2=1.3, n_1^{\prime }=m_1^{\prime }=2.1$, and $n_2^{\prime }=m_2^{\prime }=0.7$. For the same NLPIFN, we can compute various IF-WABL defuzzified values by adjusting the parameters of the IF-WABL method. For the IF-WABL parameter $s\left(\beta \right)=(l+1){\beta }^l$, the chosen values set is $l=0.45, 0.75, 2.0, and 3.7$. For the the IF-WABL parameter $p\left(\alpha \right)=(t+1){\alpha }^t$, the chosen values set is $t=0.3, 0.6, 3.0, and 4.2$. For the IF-WABL parameter $c_L$, the chosen values set is $c_L=0.2, 0.5, 0.6, and 0.9$. For the IF-WABL parameter $\theta$, $\theta =0.35$ is chosen. Employing all of the parameter combinations, we computed various IF-WABL defuzzified values for each given NLPIFN $\tilde{A}$ and present these values in

Table 2. Various defuzzified values for the NLPIFN $\tilde{A}$.

Values of Parameters		${\mathit{c}}_{\mathit{L}}=0.2$ ${\mathit{c}}_{\mathit{R}}=0.8$	${\mathit{c}}_{\mathit{L}}=0.5$ ${\mathit{c}}_{\mathit{R}}=0.6$	${\mathit{c}}_{\mathit{L}}=0.6$ ${\mathit{c}}_{\mathit{R}}=0.4$	${\mathit{c}}_{\mathit{L}}=0.9$ ${\mathit{c}}_{\mathit{R}}=0.1$
$t=0.3$	$l=0.45$	11.19250	9.51232	8.95226	7.27208
	$l=0.75$	11.12610	9.38482	8.80438	7.06306
	$l=2.0$	10.89610	9.04328	8.42566	6.57280
	$l=3.7$	10.71070	8.82510	8.19659	6.31105
$t=0.6$	$l=0.45$	11.12430	9.50938	8.97107	7.35615
	$l=0.75$	11.05800	9.38189	8.82320	7.14714
	$l=2.0$	10.82790	9.04033	8.44447	6.65686
	$l=3.7$	10.64250	8.82218	8.21541	6.39513
$t=3.0$	$l=0.45$	10.92930	9.53205	9.06630	7.66906
	$l=0.75$	10.86290	9.40455	8.91842	7.46004
	$l=2.0$	10.63290	9.06300	8.53969	6.96977
	$l=3.7$	10.44740	8.84484	8.31064	6.70803
$t=4.2$	$l=0.45$	10.90790	9.54557	9.09146	7.72912
	$l=0.75$	10.84160	9.41807	8.94358	7.52011
	$l=2.0$	10.61155	9.07652	8.56485	7.02983
	$l=3.7$	10.42610	8.85836	8.33580	6.76810

.

5. Application of NLPIFNs in the IF Minimum Spanning Tree Problem

In this section, we applied the NLPIFN concept and IF-WABL method to the IF minimum spanning tree problem (MSTP). The MSTP is one of the most fundamental and well-known combinatorial optimization problems in the classical graph theory. The MSTP has many application areas, such as transportation [56], logistics [57], image processing [58], statistical cluster analysis [59], wireless telecommunication networks [60], and distribution systems [61]. In a classical deterministic case, we assumed that the values of all edge weights are crisp numbers. For a deterministic case, the MSTP solution can be derived using the many algorithms in the literature. However, edge weights are not crisp values in some real-world processes. For such cases, various scientists have suggested different approaches. Gao and Lu [62] formulated a fuzzy quadratic MSTP by employing an expected value model, chance-constrained programming, and dependent-chance programming. The authors proposed a genetic algorithm approach to solve this problem. Janiak and Kasperski [63] evaluated a MSTP with fuzzy costs in a given connected graph. The authors used the possibility theory to find the solution to the problem. Nayeem and Pal [64] studied a fuzzy MSTP with constraints. By employing a version of the credibility measure, the authors formulated the problem as dependent-chance and chance-constrained programming problems. Zhou et al. [65] presented a fuzzy MST notion for a fuzzy MSTP based on a credibility measure. The authors evaluated the solutions of the problem for different types of fuzzy numbers. Dey and Pal [66] suggested using a graded mean integration representation of fuzzy numbers to compare and add fuzzy numbers. Using this representation, the authors adopted the famous Prim’s algorithm into a fuzzy MSTP. Broumi et al. [67] investigated an MSTP with trapezoidal fuzzy neutrosophic edge weights. The authors proposed an algorithm using the score function of TrFN. Dey et al. [50] evaluated an MSTP with interval-type 2 fuzzy sets used to represent the arc lengths. The authors introduced a genetic algorithm for finding the solution to the MSTP. In all research [54,62,63,64,65,66,67] mentioned in this part of our study, the authors generally preferred to model the weights of edges in the network using one type of fuzzy number. The authors generally did not include the user’s perspective in the solution process. On the other hand, by utilizing our approach, one can use any of the IFN types, including linear pentagonal IFNs, non-linear trapezoidal IFNs, linear trapezoidal IFNs, non-linear triangular IFNs, linear triangular IFNs, and Baloui’s Generalized IFN. Moreover, by adjusting the IF-WABL parameters according to the user’s perspective on the problem, the user’s subjectivity can be injected into the solution process of the problem.

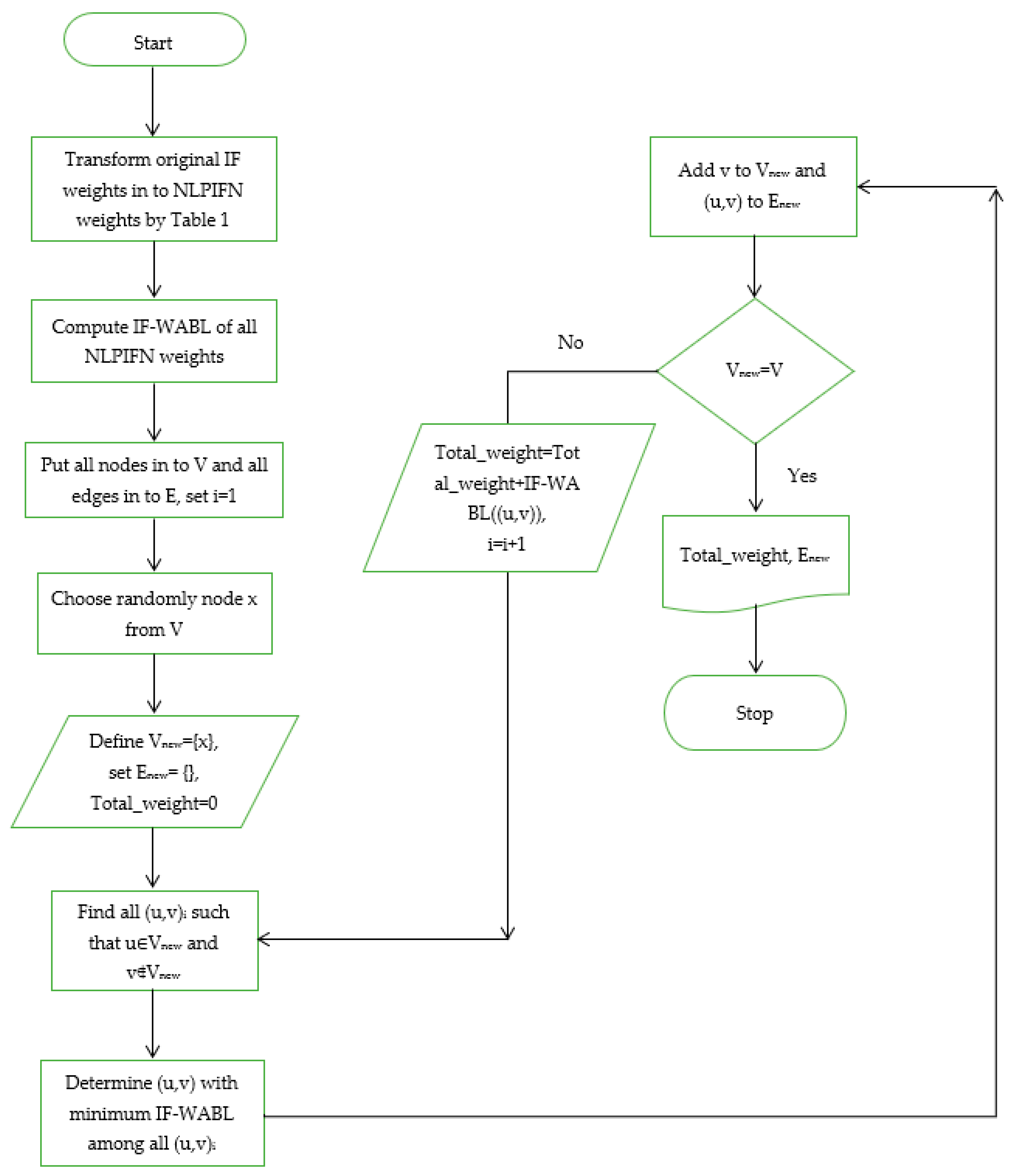
In this study, we proposed a version of Prim’s algorithm to evaluate the IF MSTP. Here, we benefited from the flexibility properties of the NLPIFN and IF-WABL method by redefining Prim’s algorithm for the IF MSTP. In our version, one can use any type of IFN (i.e., Linear Pentagonal, Non-linear Trapezoidal, Linear Trapezoidal, Non-linear Triangular, or Linear Triangular) to state the edge weights of the problem. At the very beginning stage of the problem solution process, we transformed each type of IFN into a NLPIFN by utilizing the component selection alternatives given in Table 1. Next, we employed the IF-WABL defuzzification formula given in Theorem 2 to compute the defuzzified values of the NLPIFN edge weights. In every step of Prim’s algorithm, the arc that has the lowest weight among the remaining arcs must be located. Then, we extended the solution tree to realize a solution to the problem. The re-defined version of Prim’s algorithm for the IF MSTP can be given as follows:

Step 0. Determine the types of IFNs used to define the edge weights and transform all of them into NLPIFNs using Table 1. Compute the IF-WABL defuzzified values of all weights by employing the formula given in Theorem 2. Define V for all nodes and E for all edges.

Step 1. Choose an arbitrary node x from V and define V_new = {x}. Set E_new = $\varnothing$.

Step 2. Find an arc (u, v) with the lowest IF-WABL defuzzified weight, such that u is in V_new and v is not. If there is more than one arc with the same IF-WABL defuzzified weight, arbitrarily pick one of the arcs.

Step 3. Add v to V_new and (u, v) to E_new.

Step 4. If V_new = V, then STOP, keep E^* = E_new, which describes the IFMST, and compute the total IF-WABL defuzzified values of the NLPIFN weights that belong to the chosen arcs to determine the solution for the IF MSTP. Otherwise, go to Step 2.

In Figure 2, we present a flow chart of the re-defined version of Prim’s algorithm. This flowchart, illustrating the proposed approach, was designed to provide a clear overview of the entire process.

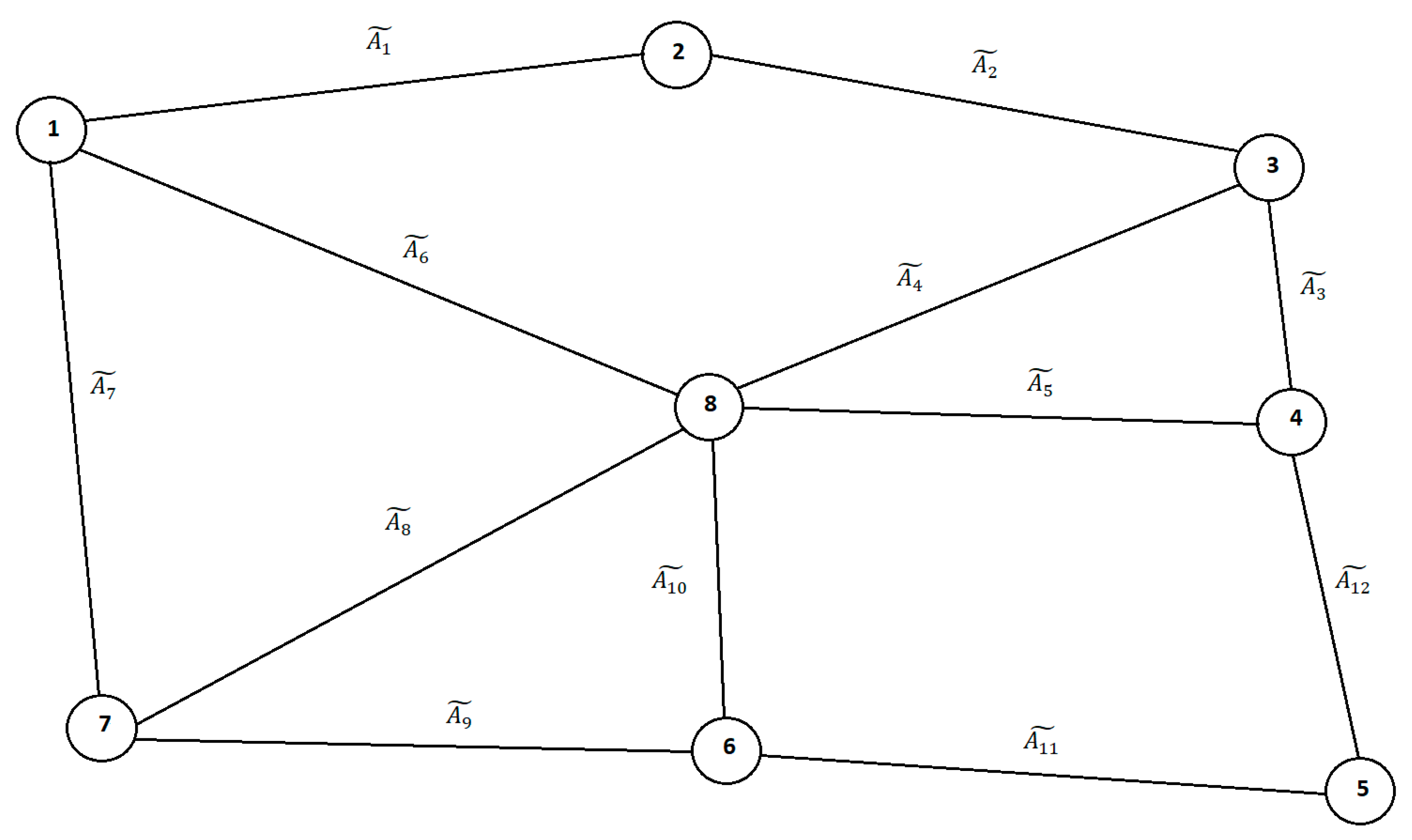
Example 2.

Suppose there are eight oil exploration platforms on the sea. Oil can be extracted from each of these platforms. All the oil obtained must be delivered to land. Laying a pipeline from each platform to the land is a very costly operation; it is a less costly operation to first connect the platforms with pipes and then connect one of the platforms to the land. The most important characteristic when connecting the platforms is the cost. Some platforms cannot be connected to each other due to the lack of suitable physical properties on the seabed. The network given in Figure 3 presents the hypothetical locations of the platforms and possible connections between them. Due to the distance between the platforms, the physical conditions of the seabed, and other natural reasons, the pipe laying costs between the platforms cannot be calculated with certainty. Therefore, these costs expressed in IFNs should be determined by engineers. Without a loss of generality, all of the weights are given as NLPIFNs and their components are given in

Table 3. Weights of the IFMST problem example.

Weight	${\mathit{a}}_1^{\prime }$	${\mathit{a}}_1$	${\mathit{a}}_2^{\prime }$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_4^{\prime }$	${\mathit{a}}_5$	${\mathit{a}}_5^{\prime }$	IF-WABL
$\widetilde{A_1}$	10.6	11.47	11.82	12.12	12.62	12.66	12.85	13.77	13.94	12.761
$\widetilde{A_2}$	2.07	3.07	3.99	4.34	4.44	5.06	5.11	5.96	6.38	4.914
$\widetilde{A_3}$	4.91	5.52	6.10	6.31	6.72	6.89	7.72	8.21	8.52	7.151
$\widetilde{A_4}$	5.38	6.15	6.40	6.79	7.20	7.68	8.24	8.33	8.71	7.568
$\widetilde{A_5}$	6.75	7.30	7.34	7.46	7.88	8.83	9.18	9.82	9.98	8.685
$\widetilde{A_6}$	8.97	9.32	10.13	10.40	10.51	11.17	11.72	11.77	12.70	11.238
$\widetilde{A_7}$	2.93	3.83	3.88	4.36	4.49	4.51	5.27	5.81	6.68	5.081
$\widetilde{A_8}$	10.85	11.74	12.16	12.89	13.22	13.71	14.44	15.27	16.14	14.034
$\widetilde{A_9}$	8.04	8.72	9.61	9.64	10.41	10.52	10.96	11.04	11.47	10.401
$\widetilde{A_{10}}$	5.50	5.80	6.54	6.59	6.88	7.16	7.94	8.39	8.43	7.327
$\widetilde{A_{11}}$	6.10	6.55	7.42	7.77	8.17	8.58	9.29	9.82	10.00	8.616
$\widetilde{A_{12}}$	11.89	12.41	13.27	13.73	14.32	14.79	15.57	15.83	16.04	14.662

. For all NLPIFNs in the example, some values of the components are determined as $k=0.61$ and $k^{\prime }=0.36$; $n_1=m_1=1.4$, $n_2=m_2=0.8, n_1^{\prime }=m_1^{\prime }=2.3$, and $n_2^{\prime }=m_2^{\prime }=0.6$. Here, we sought to obtain the IFMST of the graph by applying the proposed version of Prim’s algorithm. To apply the proposed approach, we must compute the defuzzified values of the given NLPIFN weights presented in Table 3. The IF-WABL parameters for this example were determined as follows:$\theta =0.40; c_L=0.3; c_R=0.7; p\left(\alpha \right)=2.3{\alpha }^{1.3};and s\left(\beta \right)=4.6{\beta }^{3.6}$. The defuzzified values of the NLPIFN weights are computed with respect to the given values of the IF-WABL parameters by utilizing the formula given in Theorem 2.

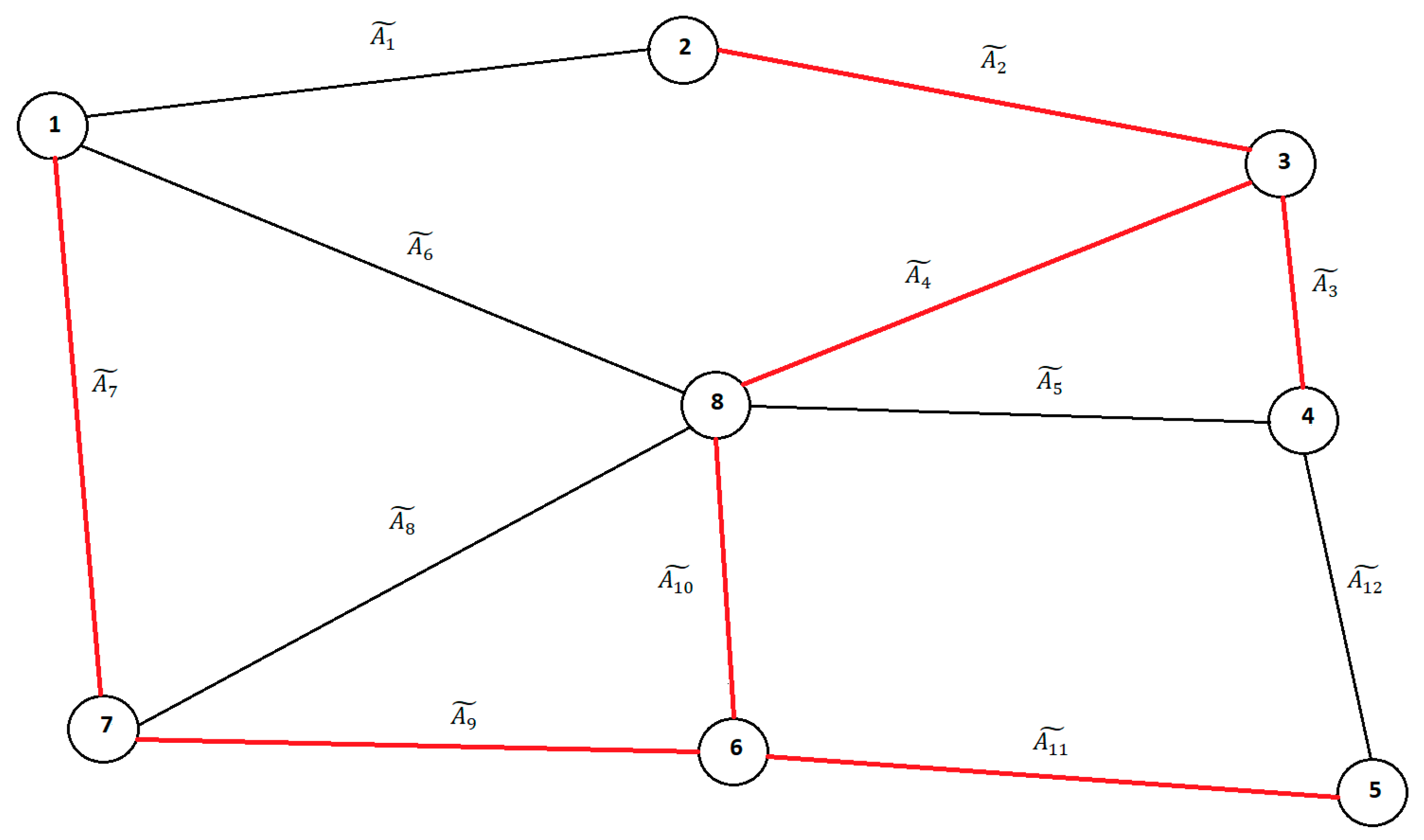
We next used the re-defined version of Prim’s algorithm to solve the given IFMST problem. First, the IF-WABL values of the given NLPIFN weights were calculated. The computed IF-WABL values are presented in Table 3. Node 4 was randomly chosen as the starting point of the algorithm. After Node 4, Nodes 3, 2, 8, 6, 5, 7, and 1 were added to the IFMST. Finally, we reached the solution set of arcs E^* = {(4,3), (3,2), (3,8), (8,6), (6,5), (6,7), and (7,1)} for the problem. A graphical illustration of the final solution is given in Figure 4, where red lines are used to emphasize the chosen arcs. The total edge weight was equal to 51.099.

6. Conclusions

In this paper, we proposed a mathematical definition of a new type of intuitionistic fuzzy number called the non-linear pentagonal intuitionistic fuzzy number (NLPIFN). Moreover, we presented some fundamental characteristics of NLPIFNs that demonstrate $(\alpha -\beta )$ cuts representation and arithmetic operations. We also outlined the relationship between the NLPIFN and other types of IFNs. The results show that the NLPIFN is able to model various types of IFNs, such as linear pentagonal IFNs, non-linear trapezoidal IFNs, linear trapezoidal IFNs, non-linear triangular IFNs, linear triangular IFNs, and Baloui’s Generalized IFN. This property of the NLPIFN allows researchers to create much more flexible models. We also utilized a flexible, strong, and mathematically solid defuzzification method for arbitrary IFNs called IF-WABL [53]. In this study, we also described some mathematical properties of the IF-WABL method and then derived an easy-to-use formula for the IF-WABL method that could be used to defuzzy the NLPIFN. Employing the NLPIFN and IF-WABL together resulted in the following advantages: (i) the NLPIFN was able to transform into various IFNs, enabling researchers to design models that include different types of IFNs together. (ii) Owing to the flexibility of the IF-WABL method, researchers can now create different defuzzification methods that reflect their defuzzification strategies. (iii) Due to the easy-to-use IF-WABL defuzzification formula derived for the NLPIFN, users can easily adopt NLPIFNs and the IF-WABL method into their models. In the final section of the paper, we embedded the NLPIFN definition and IF-WABL method into the solution process of the IF MSTP. For this purpose, we adopted the famous and mathematically sound Prim’s algorithm for the IF edge weight scenario. We also presented a numerical example for the IF MSTP. In the future, we will study the adaptation of the NLPIFN definition and IF-WABL method into multi-attribute decision-making problems. We will adjust the IF-WABL method parameters to reflect the strategic consensus of all decision-makers. Moreover, we will define a discrete version of the IF-WABL to implement the version of the IF-WABL into multi-attribute decision-making problems.