Comparative Analysis of Darcy–Forchheimer Radiative Flow of a Water-Based Al2O3-Ag/TiO2 Hybrid Nanofluid over a Riga Plate with Heat Sink/Source
Abstract
:1. Introduction
- What are the unique rheological characteristics of water-based Ag-AlO and TiO-AlO hybrid nanofluids?
- What is the impact of the Darcy–Forchheimer flow over a Riga plate?
- How do thermal radiation and the non-uniform heat sink/source phenomena impact the heat transfer?
- What is the significance of the slip effect in the velocity profile?
- How is the heat transfer process made by applying the convective heating condition?
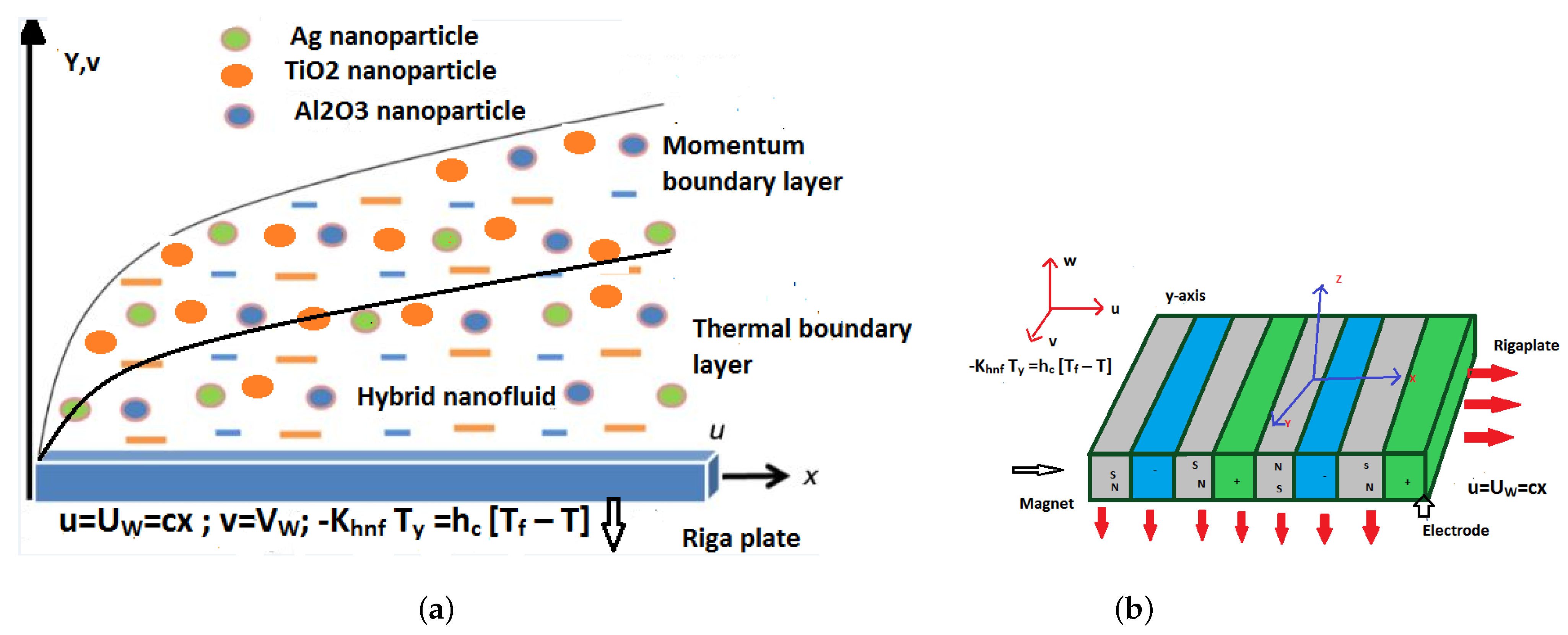
2. Mathematical Formulation
3. Methodology
3.1. Bvp4c Scheme
3.2. ND Solver
4. Results and Discussion
5. Conclusions
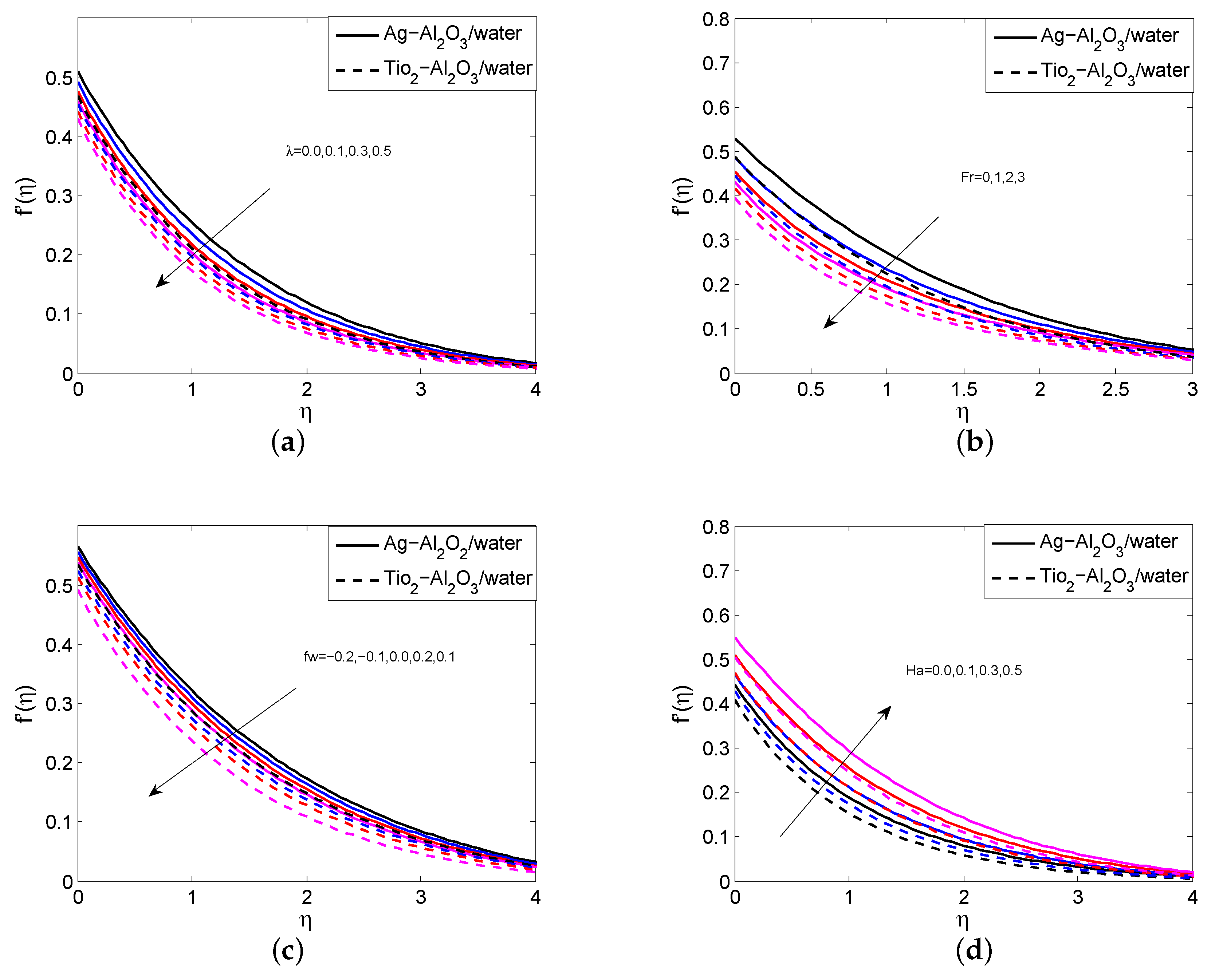
- The fluid velocity downturns when upturning the porosity parameter, Forchheimer number and injection/suction parameter
- The momentum boundary layer thickness is higher in the Ag-AlO hybrid nanofluid than the TiO/AlO hybrid nanofluid.
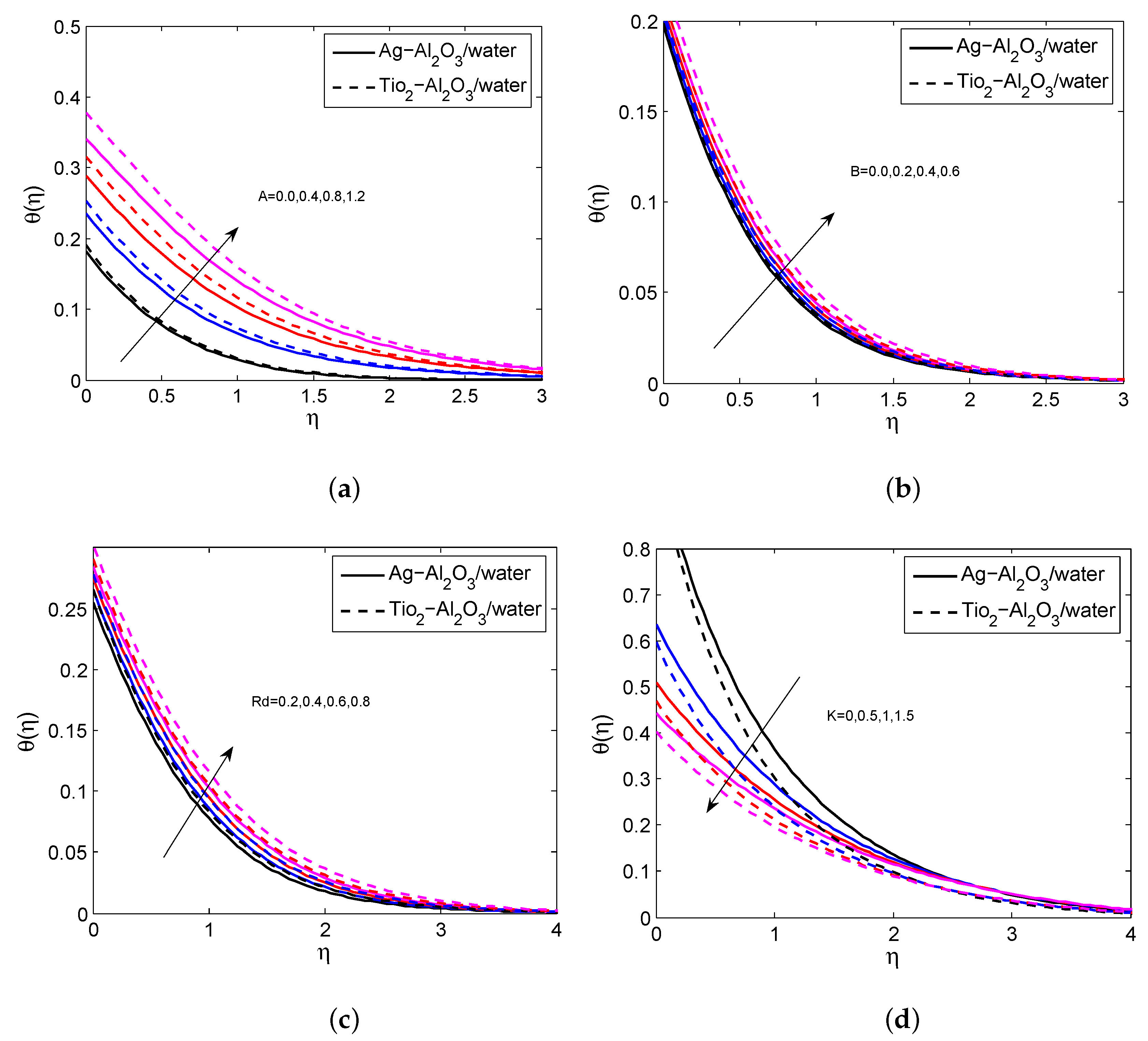
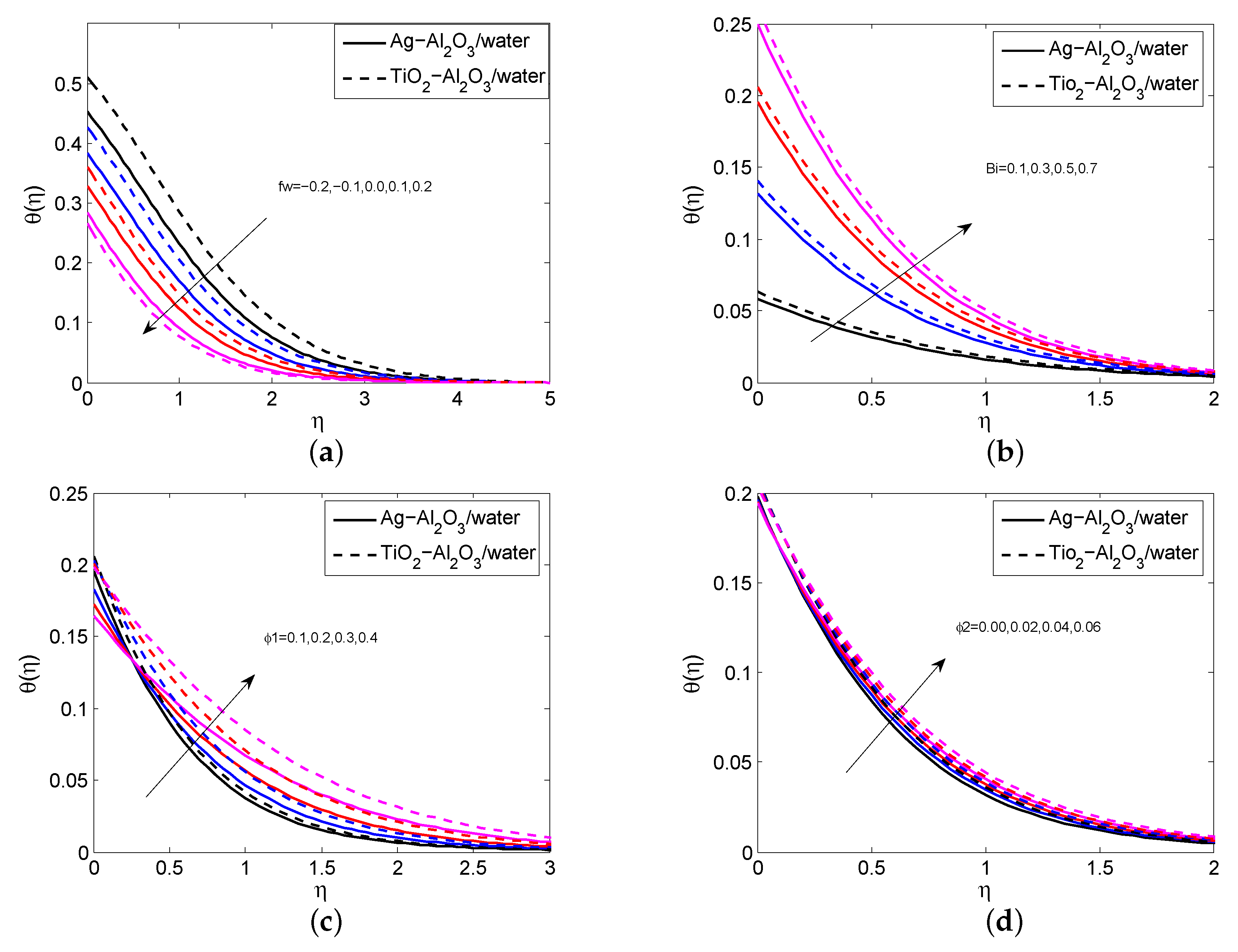
- The radiation, space and temperature-dependent parameters lead to reinforcing the thermal boundary layer.
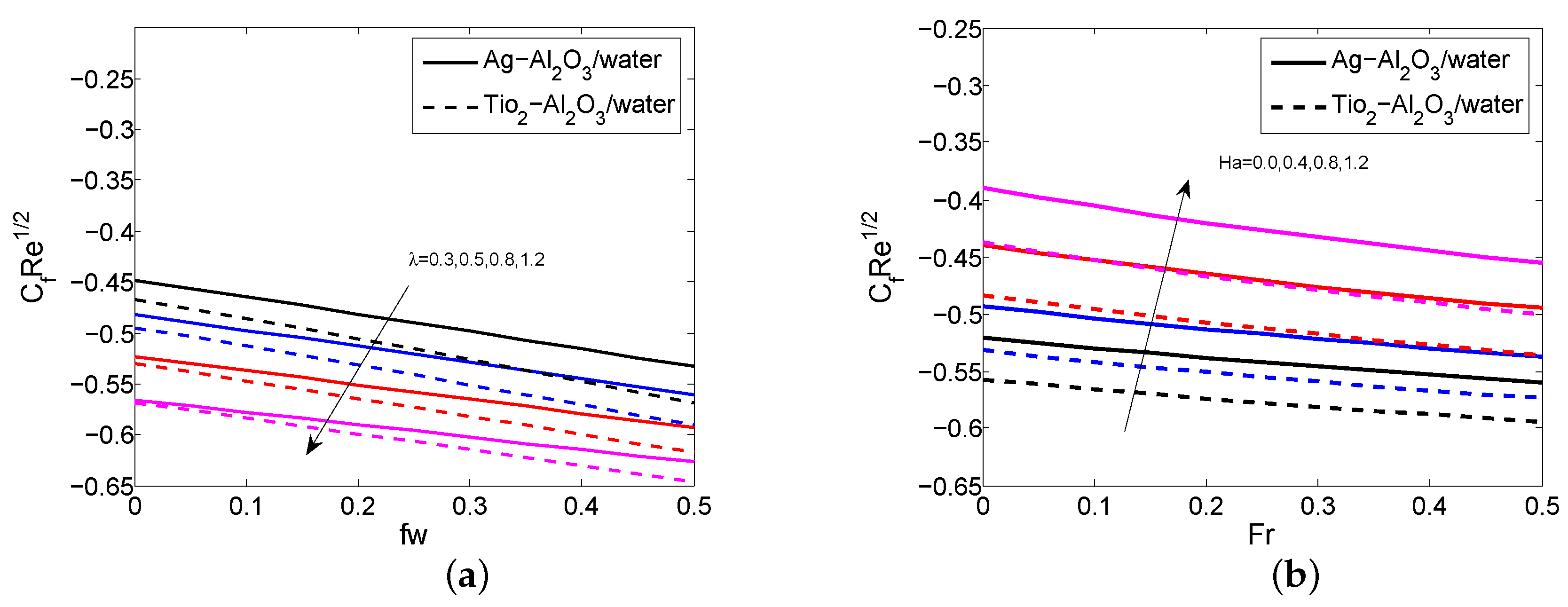
- The skin friction coefficient reduces for a greater quantity of the porosity parameter and Forchheimer number.
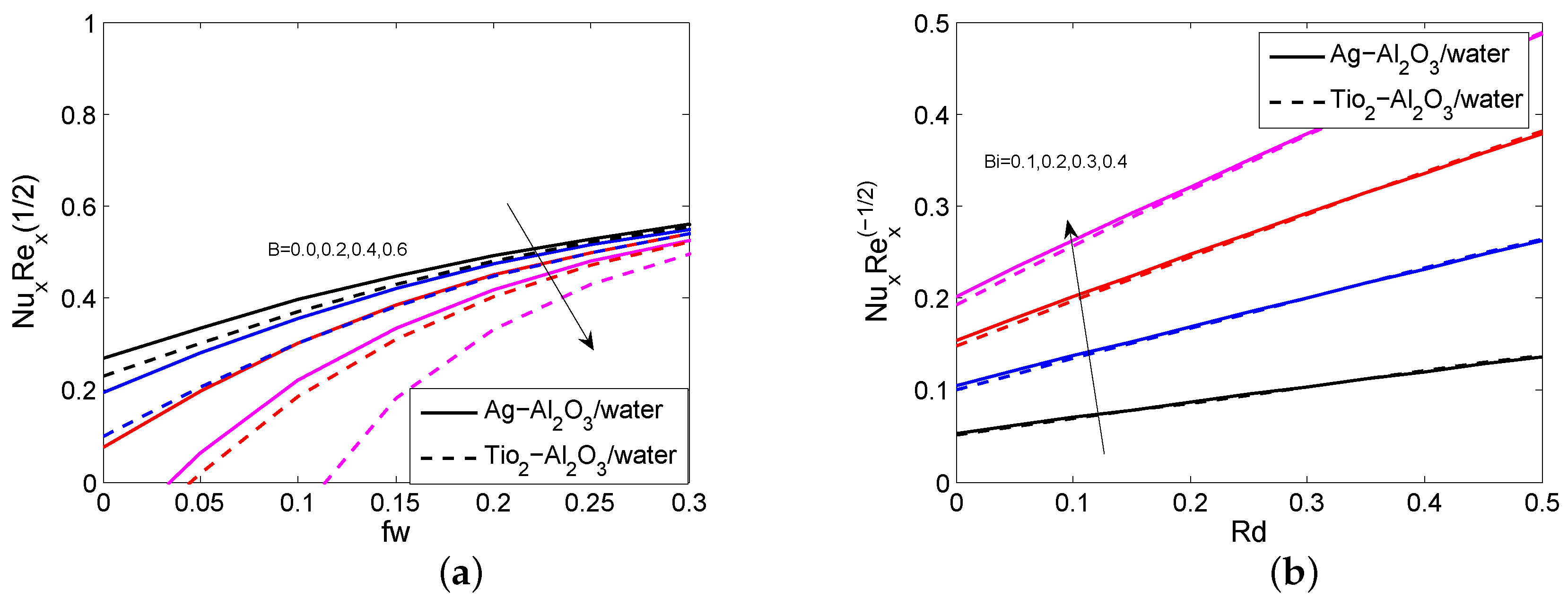
- The Biot number and radiation parameter develop the local Nusselt number.
- The skin friction coefficient and local Nusselt number are higher in the Ag-AlO hybrid nanofluid than the TiO/AlO hybrid nanofluid.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Description |
| applied current density of the electrodes | |
| Cartesian coordinates (m) | |
| dimensionless temperature | |
| drag coefficient | |
| heat transfer coefficient | |
| magnetization of the permanent magnets | |
| magnets positioned in the interval separating the electrodes | |
| Nusselt number | |
| permeability of the porous medium | |
| surface temperature (K) | |
| surface shear stress | |
| surface stretching velocities (m2s−1) | |
| suction/injection parameter | |
| Stefen–Boltzmann coefficient | |
| K | slip parameter |
| specific heat capacity | |
| A | space-dependent coefficient |
| skin friction coefficient | |
| temperature of the hot fluid (K) | |
| T | temperature of the fluid (K) |
| thermal conductivity (K) | |
| temperature away from the sheet (K) | |
| B | temperature-dependent coefficient (K) |
| velocity components | |
| Biot number | |
| dimensionless parameter | |
| Forchheimer number | |
| heating variable | |
| modified Hartmann number | |
| porosity parameter | |
| Prandtl number | |
| radiation parameter | |
| Greek symbols | |
| density | |
| dimensionless variable | |
| density of nanofluid | |
| density of hybrid nanofluid | |
| hybrid nanofluid viscosity | |
| kinematic viscosity | |
| nanofluid viscosity | |
| viscosity | |
| Abbreviation | |
| carbon nanotubes | |
| heat transfer gradient | |
| hybrid nanofluid | |
| heat transfer | |
| heat transfer rate | |
| local Nusselt number | |
| magnetohydrodynamics | |
| momentum boundary layer | |
| nanoparticle volume friction | |
| skin friction coefficient | |
| stretching sheet | |
| thermal boundary layer |
References
- Jamil, F.; Ali, H.M. Applications of hybrid nanofluids in different fields. In Hybrid Nanofluids for Convection Heat Transfer; Academic Press: Cambridge, MA, USA, 2020; pp. 215–254. [Google Scholar]
- Muneeshwaran, M.; Srinivasan, G.; Muthukumar, P.; Wang, C.C. Role of hybrid-nanofluid in heat transfer enhancement-A review. Int. Commun. Heat Mass Transf. 2021, 125, 105341. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag-CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int. J. Heat Fluid Flow 2020, 31, 858–879. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.M.; Bachok, N.; Ali, F.M. Hybrid Nanofluid Flow in a Porous Medium with Second-Order Velocity Slip, Suction and Heat Absorption. Malaysian J. Math. Sci. 2022, 16, 257–272. [Google Scholar] [CrossRef]
- Dadheech, P.K.; Agrawal, P.; Purohit, S.D.; Kumar, D. Study of Flow and Heat Transfer of CuO-Ag/C2H6O2 Hybrid Nanofluid over a Stretching Surface with Porous Media and MHD Effect. Sci. Technol. Asia 2021, 26, 174–181. [Google Scholar]
- Kumar, T.S. Hybrid nanofluid slip flow and heat transfer over a stretching surface. Partial. Differ. Equ. Appl. Math. 2021, 4, 100070. [Google Scholar] [CrossRef]
- Aladdin, N.A.L.; Bachok, N. Boundary layer flow and heat transfer of Al2O3-TiO2/water hybrid nanofluid over a permeable moving plate. Symmetry 2020, 12, 1064. [Google Scholar] [CrossRef]
- Chahregh, H.S.; Dinarvand, S. TiO2-Ag/blood hybrid nanofluid flow through an artery with applications of drug delivery and blood circulation in the respiratory system. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4775–4796. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cul2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Ali, F.; Loganathan, K.; Eswaramoorthi, S.; Prabu, K.; Zaib, A.; Chaudhary, D.K. Heat Transfer Analysis on Carboxymethyl Cellulose Water-Based Cross Hybrid Nanofluid Flow with Entropy Generation. J. Nanomater. 2022, 2022, 5252918. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver. Deutsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Haider, F.; Hayat, T.; Alsaedi, A. Flow of hybrid nanofluid through Darcy-Forchheimer porous space with variable characteristics. Alex. Eng. J. 2021, 60, 3047–3056. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Shah, F.; Kumar, R.N.; Gowda, R.P.; Prasannakumara, B.C.; Chu, Y.M.; Kadry, S. Marangoni convective flow of hybrid nanofluid (MnZnFe2O4-NiZnFe2O4-H2O) with Darcy Forchheimer medium. Ain Shams Eng. J. 2021, 12, 3931–3938. [Google Scholar] [CrossRef]
- Khan, S.A.; Khan, M.I.; Hayat, T.; Alsaedi, A. Darcy-Forchheimer hybrid (MoS2, SiO2) nanofluid flow with entropy generation. Comput. Methods Programs Biomed. 2020, 185, 105152. [Google Scholar] [CrossRef] [PubMed]
- Eswaramoorthi, S.; Loganathan, K.; Reema, J.; Gyeltshen, S. Darcy-Forchheimer 3D Flow of Glycerin-Based Carbon Nanotubes on a Riga Plate with Nonlinear Thermal Radiation and Cattaneo-Christov Heat Flux. J. Nanomater. 2022, 2022, 5286921. [Google Scholar] [CrossRef]
- Tayyab, M.; Siddique, I.; Jarad, F.; Ashraf, M.K.; Ali, B. Numerical solution of 3D rotating nanofluid flow subject to Darcy-Forchheimer law, bio-convection and activation energy. S. Afr. J. Chem. Eng. 2022, 40, 48–56. [Google Scholar] [CrossRef]
- Alzahrani, A.K.; Ullah, M.Z.; Alshomrani, A.S.; Gul, T. Hybrid nanofluid flow in a Darcy-Forchheimer permeable medium over a flat plate due to solar radiation. Case Stud. Therm. Eng. 2021, 26, 100955. [Google Scholar] [CrossRef]
- Prabakaran, R.; Eswaramoorthi, S.; Loganathan, K.; Gyeltshen, S. Thermal Radiation and Viscous Dissipation Impacts of Water and Kerosene-Based Carbon Nanotubes over a Heated Riga Sheet. J. Nanomater. 2022, 2022, 1865763. [Google Scholar] [CrossRef]
- Mumraiz, S.; Ali, A.; Awais, M.; Shutaywi, M.; Shah, Z. Entropy generation in electrical magnetohydrodynamic flow of Al2O3-Cu/H2O hybrid nanofluid with non-uniform heat flux. J. Therm. Anal. Calorim. 2020, 143, 14. [Google Scholar] [CrossRef]
- Thumma, T.; Beg, O.A.; Kadir, A. Numerical study of heat source/sink effects on dissipative magnetic nanofluid flow from a non-linear inclined stretching/shrinking sheet. J. Mol. Liq. 2017, 232, 159–173. [Google Scholar] [CrossRef]
- Mabood, F.; Ibrahim, S.M.; Rashidi, M.M.; Shadloo, M.S.; Lorenzini, G. Non-uniform heat source/sink and Soret effects on MHD non-Darcian convective flow past a stretching sheet in a micropolar fluid with radiation. Int. J. Heat Mass Transf. 2016, 93, 674–682. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Lorenzini, G.; Oudina, F.M.; Animasaun, I.L. Significance of exponential space- and thermal-dependent heat source effects on nanofluid flow due to radially elongated disk with Coriolis and Lorentz forces. J. Therm. Anal. Calorim. 2019, 141, 37–44. [Google Scholar] [CrossRef]
- Ramandevi, B.; Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Combined influence of viscous dissipation and non-uniform heat source/sink on MHD non-Newtonian fluid with Cattaneo–Christov heat flux. Alex. Eng. J. 2018, 57, 1009–1018. [Google Scholar] [CrossRef]
- Gailitis, A.; Lielausis, O. On the possibility to reduce the hydrodynamic drag of a plate in an electrolyte. Appl. Magnetohydrodyn. Rep. Inst. Phys. Riga 1961, 13, 143–146. [Google Scholar]
- Ahmad, A.; Asghar, S.; Afzal, S. Flow of nanofluid past a Riga plate. J. Magn. Magn. Mater. 2016, 402, 44–48. [Google Scholar] [CrossRef]
- Akolade, M.T.; Tijani, Y.O. A comparative study of three dimensional flow of Casson–Williamson nanofluids past a riga plate: Spectral quasi-linearization approach. Partial. Differ. Equ. Appl. Math. 2021, 4, 100108. [Google Scholar] [CrossRef]
- Kumar, R.; Sood, S.; Shehzad, S.A.; Sheikholeslami, M. Radiative heat transfer study for flow of non-Newtonian nanofluid past a Riga plate with variable thickness. J. Mol. Liq. 2017, 248, 143–152. [Google Scholar] [CrossRef]
- Adeosun, A.T.; Gbadeyan, J.A.; Lebelo, R.S. Heat transport of Casson nanofluid flow over a melting Riga plate embedded in a porous medium. Int. J. Eng. Res. Afr. 2021, 55, 15–27. [Google Scholar] [CrossRef]
- Mburu, Z.M.; Mondal, S.; Sibanda, P.; Sharma, R. A numerical study of entropy generation on Oldroyd-B nanofluid flow past a riga plate. J. Therm. Eng. 2021, 7, 845–866. [Google Scholar] [CrossRef]
- Sulochana, C.; Kumar, T.P.; Uma, M.S.; Thulasi, L. MHD Darcy-Forchheimer hybrid nanofluid flow past a nonlinear stretching surface:Numerical study. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1145, 012042. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W.; Abodayeh, K. Computational analysis of MHD nonlinear radiation casson hybrid nanofluid flow at vertical stretching sheet. Symmetry 2022, 14, 1494. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Shafiq, A.; Kumar, M.; Nonlaopon, K. Analysis of heat transfer of mono and hybrid nanofluid flow between two parallel plates in a Darcy porous medium with thermal radiation and heat generation/absorption. Symmetry 2022, 14, 1943. [Google Scholar] [CrossRef]


| Physical Properties | Fluid Phase (HO) | Silver (Ag) | Titanium Dioxide (TiO) | Aluminum Oxide (AlO) |
|---|---|---|---|---|
| (kg/m) | 997.1 | 235 | 4250 | 3970 |
| (J/kg K) | 4179 | 10,500 | 686.2 | 765 |
| k (W/mk) | 0.613 | 429 | 8.9538 | 40 |
| (s/m) | 5.5 × |
| Density | |
| Heat capacity | |
| Viscosity | |
| Thermal conductivity | |
| Electrical conductivity | |
| fw | Present Study | Ref. [33] | |
|---|---|---|---|
| Bvp4c | ND Solver | ||
| 0 | |||
| Ag-AlO/HO | Ag-AlO/HO | TiO-AlO/HO | TiO-AlO/HO | ||
|---|---|---|---|---|---|
| Bvp4c | NDSolver | Bvp4c | NDSolver | ||
| 0 | |||||
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 0 | |||||
| Ag-AlO/HO | Ag-AlO/HO | TiO-AlO/HO | TiO-AlO/HO | ||
|---|---|---|---|---|---|
| Bvp4c | NDSolver | Bvp4c | NDSolver | ||
| 1 | |||||
| A | 0 | ||||
| B | 0 | ||||
| K | 0 | ||||
| 1 | |||||
| 2 | |||||
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sindhu, R.; Alessa, N.; Eswaramoorthi, S.; Loganathan, K. Comparative Analysis of Darcy–Forchheimer Radiative Flow of a Water-Based Al2O3-Ag/TiO2 Hybrid Nanofluid over a Riga Plate with Heat Sink/Source. Symmetry 2023, 15, 199. https://doi.org/10.3390/sym15010199
Sindhu R, Alessa N, Eswaramoorthi S, Loganathan K. Comparative Analysis of Darcy–Forchheimer Radiative Flow of a Water-Based Al2O3-Ag/TiO2 Hybrid Nanofluid over a Riga Plate with Heat Sink/Source. Symmetry. 2023; 15(1):199. https://doi.org/10.3390/sym15010199
Chicago/Turabian StyleSindhu, R., Nazek Alessa, S. Eswaramoorthi, and Karuppusamy Loganathan. 2023. "Comparative Analysis of Darcy–Forchheimer Radiative Flow of a Water-Based Al2O3-Ag/TiO2 Hybrid Nanofluid over a Riga Plate with Heat Sink/Source" Symmetry 15, no. 1: 199. https://doi.org/10.3390/sym15010199
APA StyleSindhu, R., Alessa, N., Eswaramoorthi, S., & Loganathan, K. (2023). Comparative Analysis of Darcy–Forchheimer Radiative Flow of a Water-Based Al2O3-Ag/TiO2 Hybrid Nanofluid over a Riga Plate with Heat Sink/Source. Symmetry, 15(1), 199. https://doi.org/10.3390/sym15010199








