Diffusion Properties of a Brownian Ratchet with Coulomb Friction
Abstract
1. Introduction
2. Langevin Equation with Coulomb Friction and Ratchet Effect
3. Diffusion Properties
4. Constant Force Model
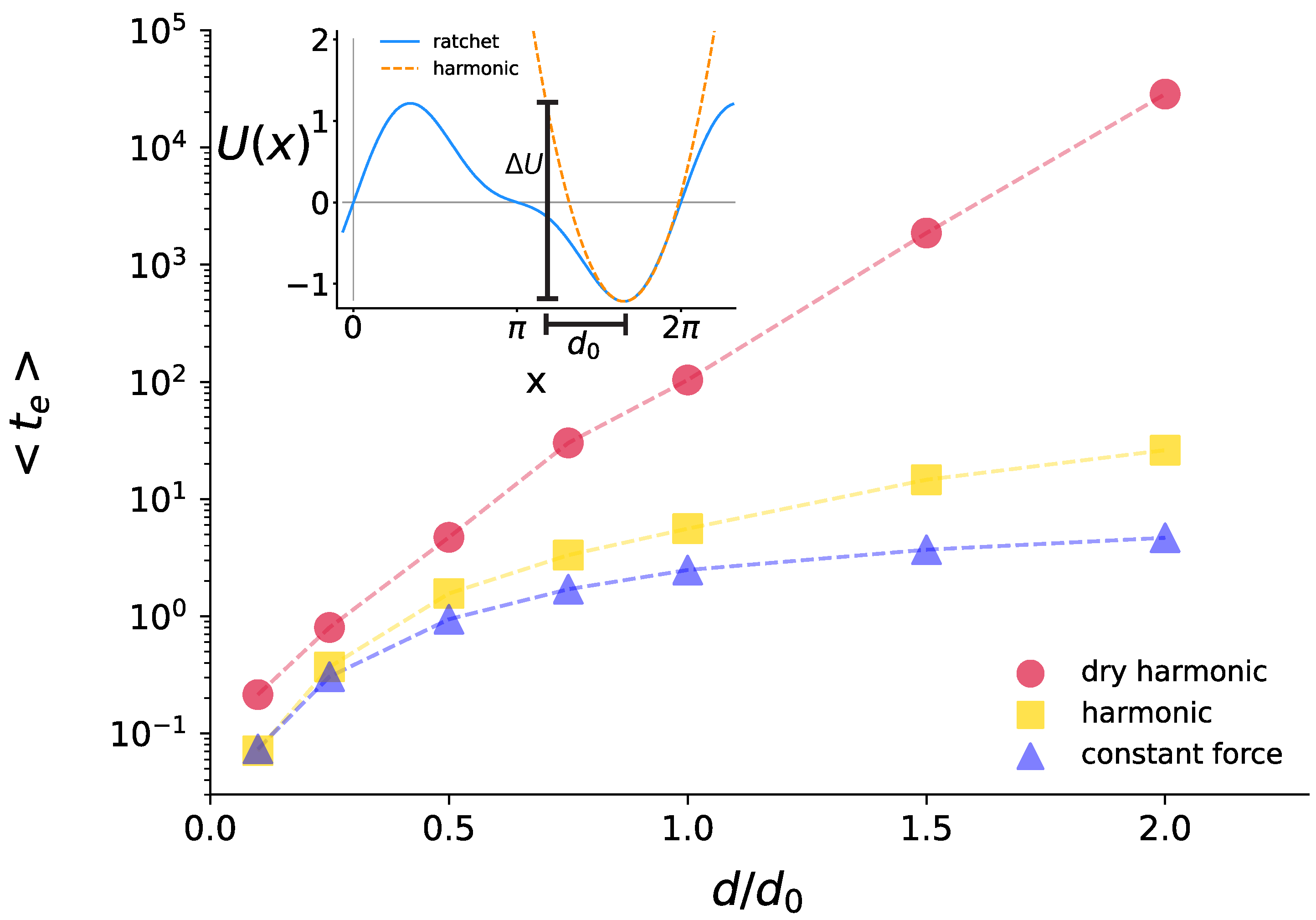
Characteristic Escape Times from a Single Well
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hänggi, P.; Marchesoni, F. Artificial Brownian motors: Controlling transport on the nanoscale. Rev. Mod. Phys. 2009, 81, 387. [Google Scholar] [CrossRef]
- Reimann, P.; Hänggi, P. Introduction to the physics of Brownian motors. Appl. Phys. A 2002, 75, 169–178. [Google Scholar] [CrossRef]
- Dialynas, T.; Lindenberg, K.; Tsironis, G. Ratchet motion induced by deterministic and correlated stochastic forces. Phys. Rev. E 1997, 56, 3976. [Google Scholar] [CrossRef]
- Gradenigo, G.; Sarracino, A.; Villamaina, D.; Grigera, T.S.; Puglisi, A. The ratchet effect in an ageing glass. J. Stat. Mech. Theory Exp. 2010, 2010, L12002. [Google Scholar] [CrossRef]
- Cleuren, B.; Eichhorn, R. Dynamical properties of granular rotors. J. Stat. Mech. Theory Exp. 2008, 2008, P10011. [Google Scholar] [CrossRef]
- Costantini, G.; Marconi, U.M.B.; Puglisi, A. Granular Brownian ratchet model. Phys. Rev. E 2007, 75, 061124. [Google Scholar] [CrossRef]
- Sarracino, A. Time asymmetry of the Kramers equation with nonlinear friction: Fluctuation-dissipation relation and ratchet effect. Phys. Rev. E 2013, 88, 052124. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, R. Current and diffusion of Overdamped Active Brownian Particles in a Ratchet Potential. arXiv 2022, arXiv:2211.04298. [Google Scholar] [CrossRef]
- De Gennes, P.G. Brownian motion with dry friction. J. Stat. Phys. 2005, 119, 953–962. [Google Scholar] [CrossRef]
- Hayakawa, H. Langevin equation with Coulomb friction. Phys. D Nonlinear Phenom. 2005, 205, 48–56. [Google Scholar] [CrossRef]
- Baule, A.; Cohen, E.; Touchette, H. A path integral approach to random motion with nonlinear friction. J. Phys. Math. Theor. 2009, 43, 025003. [Google Scholar] [CrossRef]
- Touchette, H.; Van der Straeten, E.; Just, W. Brownian motion with dry friction: Fokker–Planck approach. J. Phys. Math. Theor. 2010, 43, 445002. [Google Scholar] [CrossRef]
- Baule, A.; Touchette, H.; Cohen, E. Stick–slip motion of solids with dry friction subject to random vibrations and an external field. Nonlinearity 2010, 24, 351. [Google Scholar] [CrossRef]
- Pototsky, A.; Marchesoni, F. Periodically driven Brownian motion with dry friction and ultrarelativistic Langevin equations. Phys. Rev. E 2013, 87, 032132. [Google Scholar] [CrossRef]
- Feghhi, T.; Tichy, W.; Lau, A. Pulling a harmonically bound particle subjected to Coulombic friction: A nonequilibrium analysis. Phys. Rev. E 2022, 106, 024407. [Google Scholar] [CrossRef] [PubMed]
- Cerino, L.; Puglisi, A. Entropy production for velocity-dependent macroscopic forces: The problem of dissipation without fluctuations. EPL (Europhys. Lett.) 2015, 111, 40012. [Google Scholar] [CrossRef]
- Sarracino, A.; Gnoli, A.; Puglisi, A. Ratchet effect driven by Coulomb friction: The asymmetric Rayleigh piston. Phys. Rev. E 2013, 87, 040101. [Google Scholar] [CrossRef] [PubMed]
- Manacorda, A.; Puglisi, A.; Sarracino, A. Coulomb friction driving Brownian motors. Commun. Theor. Phys. 2014, 62, 505. [Google Scholar] [CrossRef]
- Gnoli, A.; Petri, A.; Dalton, F.; Pontuale, G.; Gradenigo, G.; Sarracino, A.; Puglisi, A. Brownian ratchet in a thermal bath driven by coulomb friction. Phys. Rev. Lett. 2013, 110, 120601. [Google Scholar] [CrossRef]
- Gnoli, A.; Puglisi, A.; Touchette, H. Granular Brownian motion with dry friction. EPL (Europhys. Lett.) 2013, 102, 14002. [Google Scholar] [CrossRef]
- Dubkov, A.; Hänggi, P.; Goychuk, I. Non-linear Brownian motion: The problem of obtaining the thermal Langevin equation for a non-Gaussian bath. J. Stat. Mech. Theory Exp. 2009, 2009, P01034. [Google Scholar] [CrossRef]
- Platen, E.; Bruti-Liberati, N. Numerical Solution of Stochastic Differential Equations with Jumps in Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 64. [Google Scholar]
- Lindenberg, K.; Sancho, J.M.; Lacasta, A.; Sokolov, I.M. Dispersionless transport in a washboard potential. Phys. Rev. Lett. 2007, 98, 020602. [Google Scholar] [CrossRef]
- Kaffashnia, A.; Evstigneev, M. Origin of dispersionless transport in spite of thermal noise. Phys. Rev. E 2021, 104, 054113. [Google Scholar] [CrossRef] [PubMed]
- Marchenko, I.; Aksenova, V.Y.; Marchenko, I.; Zhiglo, A. Dispersionless transport in washboard potentials revisited. J. Phys. Math. Theor. 2022, 55, 155005. [Google Scholar] [CrossRef]
- Grebenkov, D.S. First exit times of harmonically trapped particles: A didactic review. J. Phys. A Math. Theor. 2014, 48, 013001. [Google Scholar] [CrossRef]
- Chen, Y.; Just, W. First-passage time of Brownian motion with dry friction. Phys. Rev. E 2014, 89, 022103. [Google Scholar] [CrossRef]
- Vanossi, A.; Manini, N.; Urbakh, M.; Zapperi, S.; Tosatti, E. Colloquium: Modeling friction: From nanoscale to mesoscale. Rev. Mod. Phys. 2013, 85, 529. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semeraro, M.; Gonnella, G.; Lippiello, E.; Sarracino, A. Diffusion Properties of a Brownian Ratchet with Coulomb Friction. Symmetry 2023, 15, 200. https://doi.org/10.3390/sym15010200
Semeraro M, Gonnella G, Lippiello E, Sarracino A. Diffusion Properties of a Brownian Ratchet with Coulomb Friction. Symmetry. 2023; 15(1):200. https://doi.org/10.3390/sym15010200
Chicago/Turabian StyleSemeraro, Massimiliano, Giuseppe Gonnella, Eugenio Lippiello, and Alessandro Sarracino. 2023. "Diffusion Properties of a Brownian Ratchet with Coulomb Friction" Symmetry 15, no. 1: 200. https://doi.org/10.3390/sym15010200
APA StyleSemeraro, M., Gonnella, G., Lippiello, E., & Sarracino, A. (2023). Diffusion Properties of a Brownian Ratchet with Coulomb Friction. Symmetry, 15(1), 200. https://doi.org/10.3390/sym15010200






