Nuclear Structure Investigations of Even–Even Hf Isotopes
Abstract
1. Introduction
2. Physical Quantities and Global Best Fit
2.1. The Intrinsic Quadrupole Moment
2.2. The Electric Quadrupole Moment Q
2.3. The Deformation Parameter
2.4. Global Best Fit
3. Theoretical Models
3.1. Phenomenological Model (PhM)
3.2. Finite-Range Droplet Model (FRDM)
3.3. Hartree–Fock BCS with Skyrme MSk7 Model (HFBCS–MSk7)
3.4. Hartree–Fock–Bogoliubov with Gogny D1S interaction (HFB–Gogny D1S)
- H is the nuclear Hamiltonian of Equation (30).
- is the HFB wavefunction.
- , are the Lagrange parameters fixing the proton and neutron numbers, respectively.
- is the Lagrange parameter to fix the quadrupole moment , defined aswith the operator
3.5. Hatree–Fock–Bogoliubov UNEDF–1 (HFB–UNEDF–1)
3.6. Relativistic Hartree–Bogoliubov Covariant Energy Density Functional NL3* (RHB–NL3*)
| Isotope | Exp. | Global Fit | PhM | FRDM | HFBCS–MSk7 | HFB–Gogny D1S | HFB–UNEDF–1 | RHB–NL3* |
|---|---|---|---|---|---|---|---|---|
| [e b] | ||||||||
| 162Hf | 1.34(10) | 1.6(3) | 1.710 | 2.109 | 2.230 | 2.208 | 2.287 | 2.143 |
| 164Hf | 1.82(17) | 2.1(4) | 2.228 | 2.774 | 3.046 | 3.383 | 2.953 | 2.809 |
| 166Hf | 3.46 | 2.8(5) | 2.866 | 3.452 | 3.407 | 4.766 | 3.744 | 3.692 |
| 168Hf | 4.393(36) | 3.5(6) | 3.585 | 4.240 | 4.815 | 5.925 | 5.118 | 5.283 |
| 170Hf | 5.11(18) | 4.3(8) | 4.339 | 5.148 | 5.719 | 6.514 | 6.138 | 6.132 |
| 172Hf | 5.77(10) | 4.5(8) | 4.546 | 5.172 | 6.257 | 6.935 | 6.511 | 6.421 |
| 174Hf | 5.38(20) | 4.7(8) | 4.711 | 5.592 | 7.086 | 7.002 | 6.480 | 6.132 |
| 176Hf | 5.42(17) | 4.8(8) | 4.814 | 5.138 | 5.364 | 6.620 | 5.967 | 5.695 |
| 178Hf | 4.736(63) | 4.5(8) | 4.526 | 5.103 | 4.633 | 6.087 | 5.145 | 5.375 |
| 180Hf | 4.6470(30) | 4.5(8) | 4.487 | 4.638 | 3.333 | 5.567 | 4.656 | 5.093 |
| 182Hf | — | 4.2(7) | 4.255 | 4.656 | 3.949 | 5.061 | 4.332 | 4.813 |
| 184Hf | — | 3.8(7) | 3.872 | 4.191 | 4.376 | 4.435 | 3.934 | 4.401 |
| [ps] | ||||||||
| 162Hf | 148(11) | 126(22) | 176 | 94 | 89 | 90 | 87 | 93 |
| 164Hf | 435(41) | 376(66) | 467 | 286 | 261 | 235 | 269 | 283 |
| 166Hf | 717(33) | 895(157) | 1010 | 721 | 731 | 522 | 665 | 674 |
| 168Hf | 1239(10) | 1548(271) | 1654 | 1287 | 1134 | 921 | 1067 | 1033 |
| 170Hf | 1740(61) | 2074(363) | 2137 | 1735 | 1562 | 1371 | 1455 | 1457 |
| 172Hf | 1710 | 2199(385) | 2243 | 1924 | 1590 | 1435 | 1528 | 1550 |
| 174Hf | 1986 | 2291(401) | 2317 | 1925 | 1519 | 1537 | 1661 | 1755 |
| 176Hf | 2069 | 2350(411) | 2373 | 2196 | 2103 | 1704 | 1891 | 1981 |
| 178Hf | 2168(29) | 2288(401) | 2304 | 2026 | 2231 | 1698 | 2009 | 1923 |
| 180Hf | 2203.9(14) | 2303(403) | 2322 | 2224 | 3094 | 1853 | 2215 | 2025 |
| 182Hf | — | 2236(392) | 2265 | 2038 | 2403 | 1875 | 2190 | 1971 |
| 184Hf | — | 2063(376) | 2122 | 1893 | 1813 | 1789 | 2017 | 1803 |
| Isotope | “Exp.” | Global Fit | PhM | FRDM | HFBCS–MSk7 | HFB–Gogny D1S | HFB–UNEDF–1 | RHB–NL3* |
|---|---|---|---|---|---|---|---|---|
| 162Hf | 7.13(27) | 7.7(7) | 8.044 | 8.287 | 8.604 | 9.147 | 9.311 | 9.011 |
| 164Hf | 8.2(4) | 8.9(8) | 9.107 | 9.328 | 9.962 | 11.230 | 10.493 | 10.234 |
| 166Hf | 11.27 | 10.1(9) | 10.247 | 10.325 | 10.415 | 13.223 | 11.720 | 11.638 |
| 168Hf | 12.59(5) | 11.3(10) | 11.369 | 11.366 | 12.226 | 14.626 | 13.594 | 13.811 |
| 170Hf | 13.48(24) | 12.4(11) | 12.409 | 12.408 | 13.132 | 15.215 | 14.770 | 14.762 |
| 172Hf | 14.22(14) | 12.6(11) | 12.604 | 12.453 | 13.585 | 15.577 | 15.093 | 14.989 |
| 174Hf | 13.63(27) | 12.7(11) | 12.732 | 13.042 | 14.491 | 15.532 | 14.943 | 14.536 |
| 176Hf | 13.54(23) | 12.8(11) | 12.772 | 12.589 | 12.679 | 14.989 | 14.230 | 13.902 |
| 178Hf | 12.58(8) | 12.3(11) | 12.292 | 12.589 | 11.774 | 14.264 | 13.115 | 13.404 |
| 180Hf | 12.371(4) | 12.1(11) | 12.148 | 12.091 | 9.962 | 13.540 | 12.383 | 12.951 |
| 182Hf | — | 11.7(10) | 11.743 | 12.136 | 10.868 | 12.815 | 11.856 | 12.498 |
| 184Hf | — | 11.1(10) | 11.121 | 11.592 | 11.321 | 11.909 | 11.217 | 11.864 |
| [b] | ||||||||
| 162Hf | 3.67(27) | 4.0(7) | 4.146 | 4.604 | 4.735 | 4.711 | 4.795 | 4.641 |
| 164Hf | 4.28(40) | 4.6(8) | 4.732 | 5.280 | 5.534 | 5.831 | 5.449 | 5.314 |
| 166Hf | 5.90 | 5.3(9) | 5.368 | 5.891 | 5.852 | 6.922 | 6.135 | 6.092 |
| 168Hf | 6.650(54) | 6.0(10) | 6.003 | 6.529 | 6.958 | 7.718 | 7.173 | 7.288 |
| 170Hf | 7.17(25) | 6.6(12) | 6.605 | 7.194 | 7.582 | 8.092 | 7.856 | 7.851 |
| 172Hf | 7.62(13) | 6.7(12) | 6.761 | 7.211 | 7.931 | 8.350 | 8.090 | 8.034 |
| 174Hf | 7.35(27) | 6.9(12) | 6.882 | 7.498 | 8.440 | 8.390 | 8.071 | 7.852 |
| 176Hf | 7.38(23) | 6.9(12) | 6.957 | 7.187 | 7.344 | 8.158 | 7.745 | 7.567 |
| 178Hf | 6.900(92) | 6.7(12) | 6.746 | 7.162 | 6.825 | 7.823 | 7.192 | 7.351 |
| 180Hf | 6.8300(44) | 6.7(12) | 6.716 | 6.828 | 5.788 | 7.481 | 6.842 | 7.155 |
| 182Hf | — | 6.5(11) | 6.541 | 6.841 | 6.300 | 7.133 | 6.599 | 6.956 |
| 184Hf | — | 6.2(11) | 6.239 | 6.491 | 6.633 | 6.677 | 6.289 | 6.652 |
| Q [b] | ||||||||
| 162Hf | −1.05(8) | −1.14(20) | −1.184 | −1.316 | −1.353 | −1.346 | −1.370 | −1.326 |
| 164Hf | −1.22(11) | −1.32(23) | −1.352 | −1.509 | −1.581 | −1.666 | −1.557 | −1.518 |
| 166Hf | −1.69 | −1.51(26) | −1.534 | −1.683 | −1.672 | −1.978 | −1.753 | −1.741 |
| 168Hf | −1.899(16) | −1.7(3) | −1.715 | −1.865 | −1.988 | −2.205 | −2.049 | −2.082 |
| 170Hf | −2.05(7) | −1.9(3) | −1.887 | −2.055 | −2.166 | −2.312 | −2.244 | −2.243 |
| 172Hf | −2.18(4) | −1.9(3) | −1.932 | −2.060 | −2.266 | −2.386 | −2.311 | −2.295 |
| 174Hf | −2.10(8) | −2.0(3) | −1.966 | −2.142 | −2.411 | −-2.397 | −2.306 | −2.243 |
| 176Hf | −2.11(7) | −2.0(3) | −1.988 | −2.053 | −2.098 | −2.331 | −2.213 | −2.162 |
| 178Hf | −1.971(26) | −1.9(3) | −1.927 | −2.046 | −1.950 | −2.235 | −2.055 | −2.100 |
| 180Hf | −1.9528(13) | −1.9(3) | −1.919 | −1.951 | −1.654 | −2.137 | −1.955 | −2.044 |
| 182Hf | — | −1.9(3) | −1.869 | −1.955 | −1.800 | −2.038 | −1.885 | −1.988 |
| 184Hf | — | −1.8(3) | −1.783 | −1.854 | −1.895 | −1.908 | −1.797 | −1.901 |
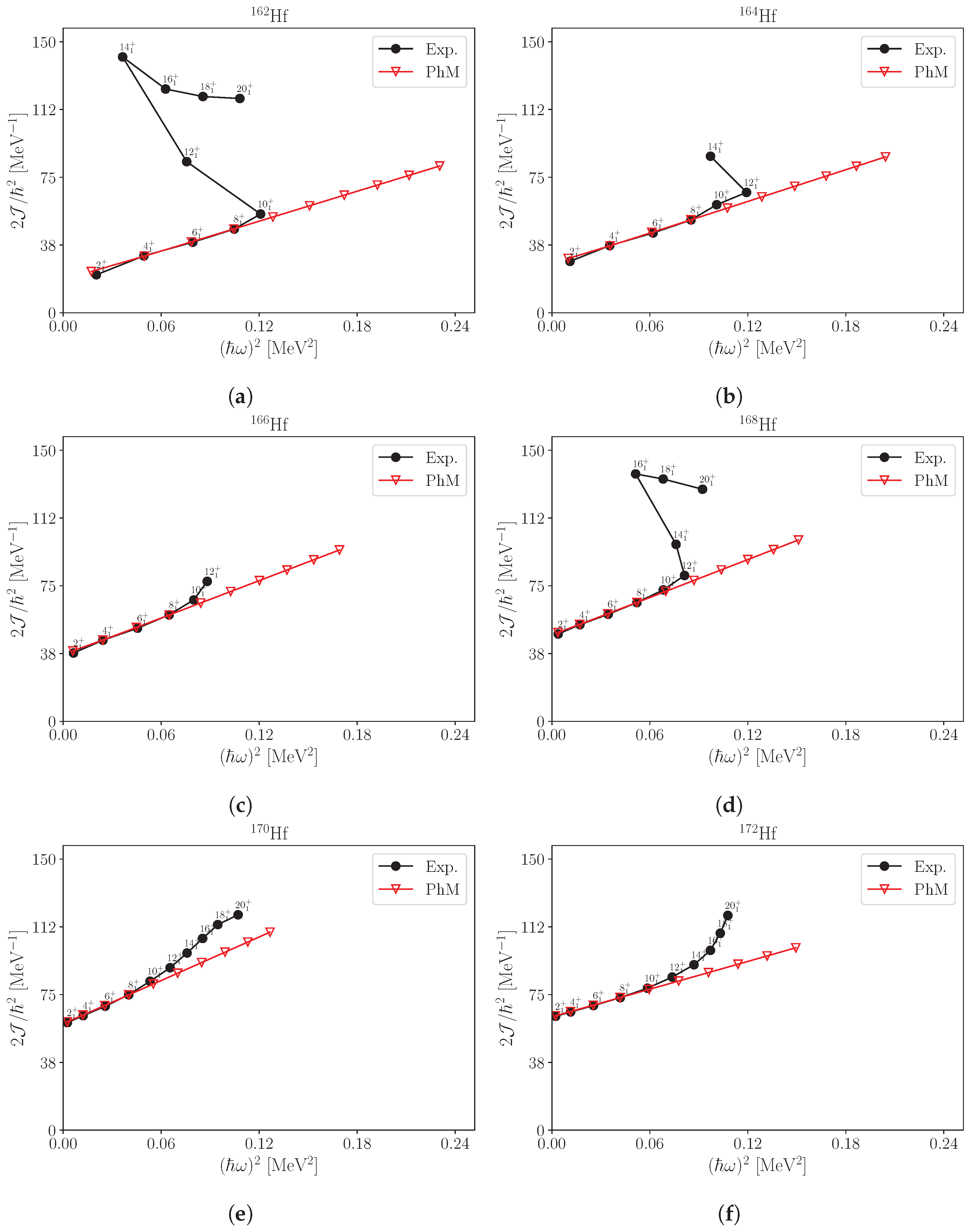
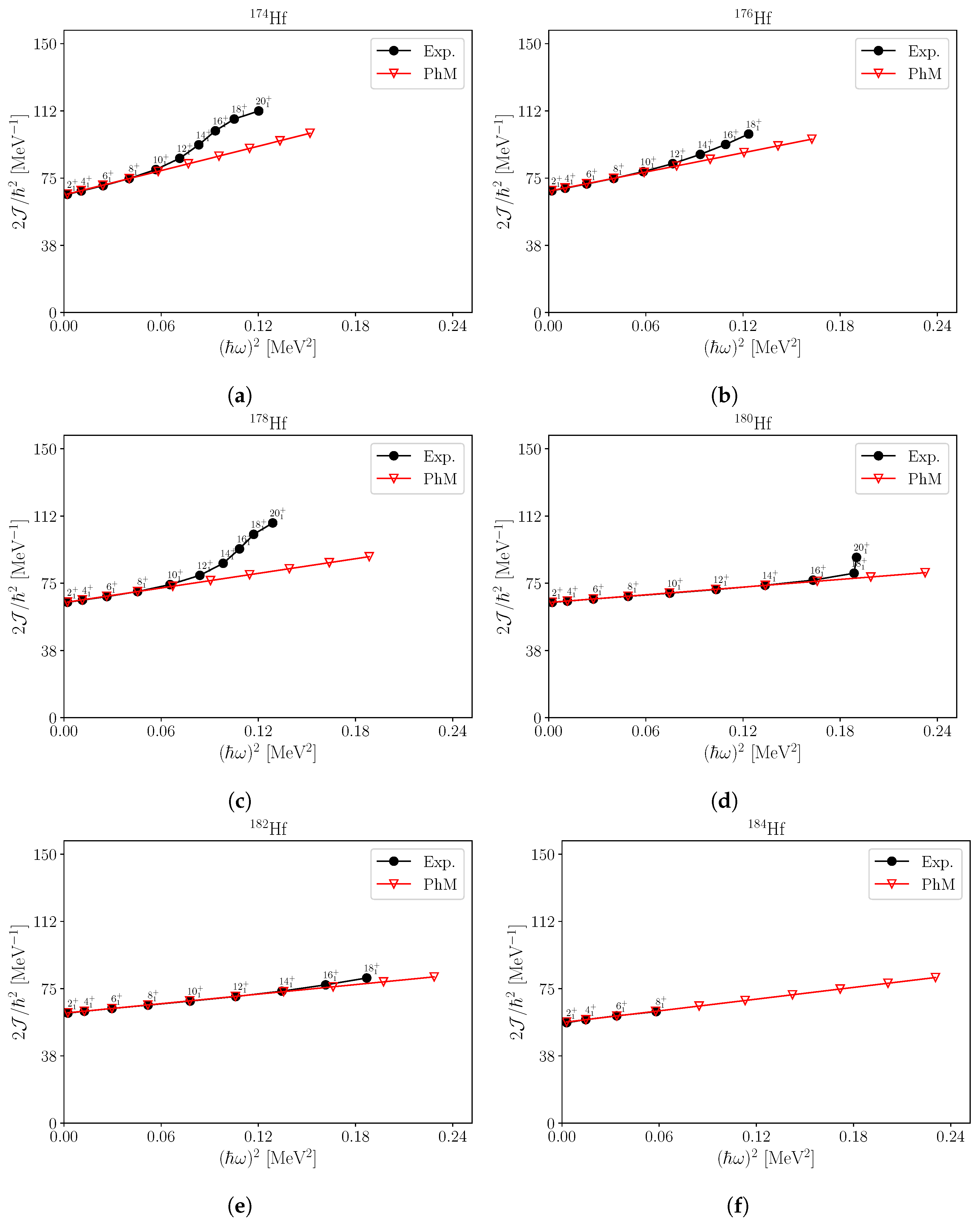
4. Results and Discussion
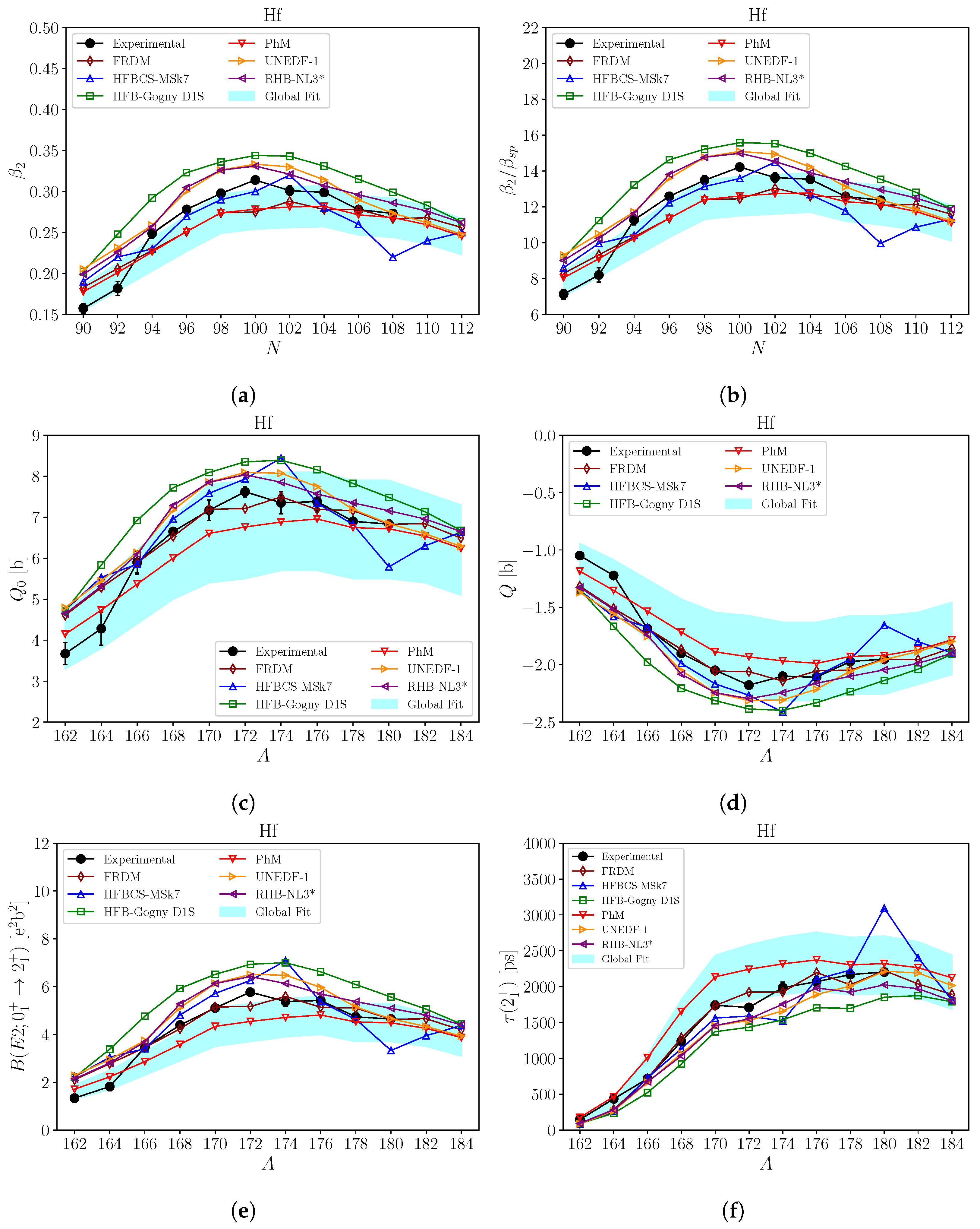
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drout, M.R.; Piro, A.L.; Shappee, B.J.; Kilpatrick, C.D.; Simon, J.D.; Contreras, C.; Coulter, D.A.; Foley, R.J.; Siebert, M.R.; Morrell, N.; et al. Light curves of the neutron star merger GW170817/SSS17a: Implications for r–process nucleosynthesis. Science 2017, 358, 1570. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, O.B.; Ahn, D.S.; Bazin, D.; Fukuda, N.; Gade, A.; Hausmann, M.; Inabe, N.; Ishikawa, S.; Iwasa, N.; Kawata, K.; et al. Discovery of 60Ca and Implications For the Stability of 70Ca. Phys. Rev. Lett. 2018, 121, 022501. [Google Scholar] [CrossRef] [PubMed]
- Walker, P.; Dracoulis, G. Exotic Isomers in Deformed Atomic Nuclei. Hyperfine Interact. 2001, 135, 83–107. [Google Scholar] [CrossRef]
- National Nuclear Data Center. Available online: https://www.nndc.bnl.gov/nudat2 (accessed on 1 December 2022).
- Kota, V. Low lying spectra and electromagnetic transitions for 164Dy, 166Er, and 168Yb nuclei. Phys. Rev. C 1979, 19, 521. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1467–1521. [Google Scholar] [CrossRef]
- Robledo, L.; Rodríguez-Guzmán, R.; Sarriguren, P. Role of triaxiality in the ground–state shape of neutron–rich Yb, Hf, W, Os and Pt isotopes. J. Phys. G Nucl. Part. Phys. 2009, 36, 115104. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.; Sarriguren, P. Collective structural evolution in neutron–rich Yb, Hf, W, Os, and Pt isotopes. Phys. Rev. C 2011, 84, 054316. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.; Minkov, N.; Martinou, A.; Sarantopoulou, S.; Cakirli, R.; Casten, R.; Blaum, K. Analytic predictions for nuclear shapes, prolate dominance, and the prolate-oblate shape transition in the proxy–SU(3) model. Phys. Rev. C 2017, 95, 064326. [Google Scholar] [CrossRef]
- Bonatsos, D. Prolate over oblate dominance in deformed nuclei as a consequence of the SU(3) symmetry and the Pauli principle. Eur. Phys. J. A 2017, 53, 148. [Google Scholar] [CrossRef]
- Bohr, A.N.; Mottelson, B.R. Nuclear Structure; Vol. II: Nuclear Deformations; World Scientific Publishing: Singapore, 1998. [Google Scholar]
- Greiner, W.; Maruhn, J.A. Nuclear Models; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Ogle, W.; Wahlborn, S.; Piepenbring, R.; Fredriksson, S. Single–Particle Levels of Nonspherical Nuclei in the Region 150 < A < 190. Rev. Mod. Phys. 1971, 43, 424–478. [Google Scholar]
- Satula, W.; Wyss, R.; Magierski, P. The Lipkin–Nogami formalism for the cranked mean field. Nucl. Phys. A 1994, 578, 45–61. [Google Scholar] [CrossRef]
- Xu, F.; Satula, W.; Wyss, R. Quadrupole pairing interaction and signature inversion. Nucl. Phys. A 2000, 669, 119–134. [Google Scholar] [CrossRef]
- Zhang, Z.H.; He, X.T.; Zeng, J.Y.; Zhao, E.G.; Zhou, S.G. Systematic investigation of the rotational bands in nuclei with Z ≈ 100 using a particle–number conserving method based on a cranked shell model. Phys. Rev. C 2012, 85, 014324. [Google Scholar] [CrossRef]
- Hara, K.; Sun, Y. Projected shell model and high–spin spectroscopy. Int. J. Mod. Phys. E 1995, 04, 637–785. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, H.; Chen, Q.; Zhang, S.; Meng, J. Shell–model–like approach based on cranking covariant density functional theory: Band crossing and shape evolution in 60Fe. Phys. Rev. C 2018, 97, 034317. [Google Scholar] [CrossRef]
- Stelson, P.; Grodzins, L. Nuclear transition probability, B(E2) for – transitions and deformation parameter, β2. Nucl. Data Sheets Sect. A 1965, 1, 21–102. [Google Scholar] [CrossRef]
- Raman, S.; Malarkey, C.H.; Milner, W.T.; Nestor, C.W., Jr.; Stelson, P.H. Transition probability, B(E2)↑, from the ground to the first–excited 2+ state of even–even nuclides. At. Data Nucl. Data Tables 1987, 36, 1–128. [Google Scholar] [CrossRef]
- Raman, S.; Nestor, C.W., Jr.; Tikkanen, P. Transition Probability from the Ground to the First–Excited 2+ State of Even–Even Nuclides. At. Data Nucl. Data Tables 2001, 78, 1–128. [Google Scholar] [CrossRef]
- Reduced Transition Probabilities or B(E2;0+→2+) Values. Available online: https://www.nndc.bnl.gov/be2 (accessed on 1 December 2022).
- Pritychenko, B.; Birch, M.; Singh, B.; Horoi, M. Tables of E2 transition probabilities from the first 2+ states in even–even nuclei. At. Data Nucl. Data Tables 2016, 107, 1–139. [Google Scholar] [CrossRef]
- Pritychenko, B.; Singh, B.; Verpelli, B. Systematic trends of , , and excited states in even–even nuclei. Nucl. Phys. A 2022, 1027, 122511. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many–Body Problem; Springer: New York, NY, USA, 1980. [Google Scholar]
- Frank, A.; Jolie, J.; van Isacker, P. Symmetries in Atomic Nuclei: From Isospin to Supersymmetry, 2nd ed.; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-21930-7. [Google Scholar]
- Sheith, J.; Ali, R. Symmetry projection in atomic nuclei. Eur. Phys. J. Spec. Top. 2020, 229, 2555–2602. [Google Scholar] [CrossRef]
- Usmanov, P.; Okhunov, A.; Salikhbaev, U.; Vdonin, A. Analysis of Electromagnetic Transitions in Nuclei 176,178Hf. Phys. Part. Nucl. Lett. 2010, 7, 185–191. [Google Scholar] [CrossRef]
- Okhunov, A.; Turaeva, G.; Kassim, H.; Khandaker, M.; Rosli, N.B. Analysis of the energy spectra of ground states of deformed nuclei in the rare–earth region. Chin. Phys. C 2015, 39, 044101. [Google Scholar] [CrossRef]
- Okhunov, A.; Sharrad, F.; Al-Sammarraie, A.A.; Khandaker, M. Correspondence between phenomenological and IBM-1 models of even isotopes of Yb. Chin. Phys. C 2015, 39, 084101. [Google Scholar] [CrossRef]
- Wiederhold, J.; Werner, V.; Kern, R.; Pietralla, N.; Bucurescu, D.; Carroll, R.; Cooper, N.; Daniel, T.; Filipescu, D.; Florea, N.; et al. Evolution of E2 strength in the rare-earth isotopes 174,176,178,180Hf. Phys. Rev. C 2019, 99, 024316. [Google Scholar] [CrossRef]
- Qasim, H.N.; Al-Khudair, F.H. Nuclear shape phase transition in even-even 158–168Hf isotopes. Nucl. Phys. A 2020, 1002, 121962. [Google Scholar] [CrossRef]
- Das, M.; Biswal, N.; Panda, R.; Bhuyan, M. Structural evolution and shape transition in even-even Hf-isotopes within the relativistic mean-field approach. Nucl. Phys. A 2022, 1019, 122380. [Google Scholar] [CrossRef]
- Vasileiou, P.; Mertzimekis, T.; Chalil, A.; Zyriliou, A.; Pelonis, S.; Efstathiou, M.; Lagaki, V.; Siltzovalis, G.; Koseoglou, P.; Bonatsos, D.; et al. Experimental Investigation of the Nuclear Structure in the Neutron–Rich 180Hf. Bulg. J. Phys. 2021, 48, 618–624. [Google Scholar] [CrossRef]
- Mertzimekis, T.; Vasileiou, P.; Zyriliou, A.; Efstathiou, M.; Chalil, A.; Pelonis, S.; Lagaki, V.; Siltzovalis, G.; Koseoglou, P.; Bonatsos, D.; et al. Experimental Investigations of Nuclear Structure around A = 180. Bulg. J. Phys. 2021, 48, 625–633. [Google Scholar] [CrossRef]
- Zyriliou, A.; Mertzimekis, T.; Chalil, A.; Vasileiou, P.; Pelonis, S.; Efstathiou, M.; Mavrommatis, E.; Bonatsos, D.; Martinou, A.; Peroulis, S.; et al. Reviewing Nuclear Structure Properties of Even–Even Yb Isotopes. Bulg. J. Phys. 2021, 48, 608–617. [Google Scholar] [CrossRef]
- Zyriliou, A.; Mertzimekis, T.J.; Chalil, A.; Vasileiou, P.; Mavrommatis, E.; Bonatsos, D.; Martinou, A.; Peroulis, S.; Minkov, N. A study of some aspects of the nuclear structure in the even–even Yb isotopes. Eur. Phys. J. Plus 2022, 137, 352. [Google Scholar] [CrossRef]
- Krane, K.S. Introductory Nuclear Physics; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Sharon, Y.; Benczer-Koller, N.; Kumbartzki, G.; Zamick, L.; Casten, R. Systematics of the ratio of electric quadrupole moments Q() to the square root of the reduced transition probabilities B(E2;→) in even–even nuclei Nucl. Phys. A 2018, 980, 131–142. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B. Collective and Individual–Particle Aspects of Nuclear Structure. Mat. Fys. Medd. Dan. Vid. Selsk. 1953, 27, 1–174. [Google Scholar]
- Rowe, D.J. Nuclear Collective Motion; Metheuen: London, UK, 1970; p. 21. [Google Scholar]
- Grodzins, L. The uniform behaviour of electric quadrupole transition probabilities from first 2+ states in even–even nuclei. Phys. Lett. 1962, 2, 88–91. [Google Scholar] [CrossRef]
- Pritychenko, B.; Birch, M.; Singh, B. Revisiting Grodzins systematics of B(E2) values. Nucl. Phys. A 2017, 962, 73–102. [Google Scholar] [CrossRef]
- Habs, D.; Kester, O.; Ames, F.; Sieber, T.; Bongers, H.; Emhofer, S.; Loewe, M.; Reiter, P.; Lutter, R.; Thirolf, P.; et al. CERN Proposal INTC-P-156. 2002. Available online: https://cds.cern.ch/record/000545918 (accessed on 1 December 2022).
- Usmanov, P.; Mikhailov, I. Non–adiabatic effects of collective motion in even–even deformed nuclei. Phys. Part. Nucl. Lett. 1997, 28, 348. [Google Scholar] [CrossRef]
- Bertulani, C.A. Nuclear Physics in a Nutshell; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Harris, S.M. Higher Order Corrections to the Cranking Model. Phys. Rev. 1965, 138, B509–B513. [Google Scholar] [CrossRef]
- Casten, R.F. Nuclear Structure from a Simple Perspective; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- He, X.T.; Cao, Y.; Gan, X.L. Effects of high-j orbitals, pairing, and deformed neutron shells on upbendings of ground-state bands in the neutron-rich even-even isotopes 170–184Hf. Phys. Rev. C 2020, 102, 014322. [Google Scholar] [CrossRef]
- Möller, P.; Nix, J. Nuclear Masses from a Unified Macroscopic–Microscopic Model. At. Data Nucl. Data Tables 1988, 39, 213–223. [Google Scholar] [CrossRef]
- Möller, P.; Nix, J.; Myers, W.; Swiatecki, W. Nuclear ground–state masses and deformations. At. Data Nucl. Data Tables 1995, 59, 185–381. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.; Ichikawa, T.; Sagawa, H. Nuclear ground–state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109–110, 1–204. [Google Scholar] [CrossRef]
- Myers, W.; Swiatecki, W. Average nuclear properties. Ann. Phys. 1969, 55, 395–505. [Google Scholar] [CrossRef]
- Strutinsky, V. Shell effects in nuclear masses and deformation energies. Nucl. Phys. A 1967, 95, 420–442. [Google Scholar] [CrossRef]
- Lipkin, H. Collective motion in many–particle systems: Part 1. The violation of conservation laws. Ann. Phys. 1960, 9, 272–291. [Google Scholar] [CrossRef]
- Nogami, Y. Improved Superconductivity Approximation for the Pairing Interaction in Nuclei. Phys. Rev. 1964, 134, B313–B321. [Google Scholar] [CrossRef]
- Möller, P.; Nix, J. Calculation of fission barriers with the droplet model and folded Yukawa single–particle potential. Nucl. Phys. A 1974, 229, 269–291. [Google Scholar] [CrossRef]
- Tondeur, F.; Goriely, S.; Pearson, J.; Onsi, M. Towards a Hartree–Fock Mass Formula. Phys. Rev. C 2000, 62, 024308. [Google Scholar] [CrossRef]
- Goriely, S.; Tondeur, F.; Pearson, J. A Hartree–Fock Nuclear Mass Table. At. Data Nucl. Data Tables 2001, 77, 311–381. [Google Scholar] [CrossRef]
- Goriely, S. Capture Gamma-Ray Spectroscopy and Related Topics. In Proceedings of the 10th International Symposium, Santa Fe, NM, USA, 30 August–3 September 1999; Volume 529, pp. 287–294. [Google Scholar]
- Dechargé, J.; Gogny, D. Hartree–Fock–Bogolyubov calculations with the D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568–1593. [Google Scholar] [CrossRef]
- Berger, J.; Girod, M.; Gogny, D. Time–dependent quantum collective dynamics applied to nuclear fission. Comput. Phys. Commun. 1991, 63, 365–374. [Google Scholar] [CrossRef]
- Hilaire, S.; Girod, D. Large-scale mean-field calculations from proton to neutron drip lines using the D1S Gogny force. Eur. Phys. J. A 2007, 33, 237–241. [Google Scholar] [CrossRef]
- Hartree–Fock–Bogoliubov Results Based on the Gogny Force. 2006. Available online: http://www-phynu.cea.fr/science_en_ligne/carte_potentiels_microscopiques/carte_potentiel_nucleaire_eng.htm (accessed on 9 March 2021).
- Delaroche, J.P.; Girod, M.; Libert, J.; Goutte, H.; Hilaire, S.; Péru, S.; Pillet, N.; Bertsch, G. Structure of even-even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction. Phys. Rev. C 2010, 81, 014303. [Google Scholar] [CrossRef]
- Kortelainen, M.; McDonnell, J.; Nazarewicz, W.; Reinhard, P.G.; Sarich, J.; Schunck, N.; Stoitsov, M.; Wild, S. Nuclear energy density optimization: Large deformations. Phys. Rev. C 2012, 85, 024304. [Google Scholar] [CrossRef]
- Mass Explorer UNEDF Project. Available online: http://massexplorer.frib.msu.edu/content/DFTMassTables.html (accessed on 20 February 2021).
- Furnstahl, R. EFT for DFT. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 133–191. [Google Scholar] [CrossRef]
- Agbemava, S.; Afanasjev, A.; Ray, D.; Ring, P. Global performance of covariant energy density functionals: Ground state observables of even–even nuclei and the estimate of theoretical uncertainties. Phys. Rev. C 2014, 89, 054320. [Google Scholar] [CrossRef]
- Agbemava, S.; Afanasjev, A.; Tanina, A. Propagation of statistical uncertainties in covariant density functional theory: Ground state observables and single–particle properties. Phys. Rev. C 2019, 99, 014318. [Google Scholar] [CrossRef]
- Lalazissis, G.; Köning, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Gambhir, X.; Ring, P.; Thimet, A. Relativistic Mean Field Theory for Finite Nuclei. Ann. Phys. 1990, 198, 132–179. [Google Scholar] [CrossRef]
- Walecka, J. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Serot, B.D.; Walecka, J.D. The Relativistic Nuclear Many Body Problem. Adv. Nucl. Phys. 1986, 16, 1–327. [Google Scholar]
- Lalazissis, G.; Karatzikos, S.; Fossion, R.; Arteaga, D.P.; Afanasjev, A.; Ring, P. The effective force NL3 revisited. Phys. Lett. B 2009, 671, 36–41. [Google Scholar] [CrossRef]
- Afanasjev, A.V.; Agbemava, S.E.; Ray, D.; Ring, P. Neutron drip line: Single–particle degrees of freedom and pairing properties as sources of theoretical uncertainties. Phys. Rev. C 2015, 91, 014324. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Stone, N. Table of nuclear electric quadrupole moments. At. Data Nucl. Data Tables 2016, 111–112, 1–28. [Google Scholar] [CrossRef]
- Warda, M.; Staszczak, A.; Próchniak, L. Comparison of Self–Consistent Skyrme and Gogny Calculations for Light Hg Isotopes. Int. J. Mod. Phys. E 2010, 19, 787. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Afanasjev, A.; Bender, M.; Robledo, L.; Shi, Y. Properties of nuclei in the nobelium region studied within the covariant, Skyrme, and Gogny energy density functionals. Nucl. Phys. A 2015, 944, 388–414. [Google Scholar] [CrossRef]
- Vargas, C.E.; Velázquez, V.; Lerma, S. Microscopic study of neutron–rich dysprosium isotopes. Eur. Phys. J. A 2013, 49, 4. [Google Scholar] [CrossRef]
- Rath, A.K.; Stevenson, P.D.; Regan, P.H.; Xu, F.R.; Walker, P.M. Self-consistent description of dysprosium isotopes in the doubly midshell region. Nucl. Phys. Group 2003, 68, 10. [Google Scholar] [CrossRef]
- Patel, Z.; Söderström, P.A.; Podolyák, Z.; Regan, P.H.; Walker, P.M.; Watanabe, H.; Ideguchi, E.; Simpson, G.S.; Liu, H.L.; Nishimura, S.; et al. Isomer Decay Spectroscopy of 164Sm and 166Gd: Midshell Collectivity Around N = 100. Phys. Rev. Lett. 2014, 113, 262502. [Google Scholar] [CrossRef]
- Ideguchi, E.; Simpson, G.S.; Yokoyama, R.; Tanaka, M.; Nishimura, S.; Doornenbal, P.; Lorusso, G.; Söderström, P.A.; Sumikama, T.; Wu, J.; et al. μs isomers of 158,160Nd. Phys. Rev. C 2016, 94, 064322. [Google Scholar] [CrossRef]
| Isotope | ||||
|---|---|---|---|---|
| () | [ keV ] | [ keV ] | [keV] | [keV] |
| 162Hf | 0.880 | 13.804 | 262.249 | 285.000 |
| 164Hf | 1.327 | 14.623 | 199.610 | 210.700 |
| 166Hf | 1.821 | 17.266 | 153.912 | 158.640 |
| 168Hf | 2.373 | 17.522 | 122.068 | 124.100 |
| 170Hf | 2.933 | 20.097 | 100.055 | 100.800 |
| 172Hf | 3.128 | 12.837 | 94.750 | 95.220 |
| 174Hf | 3.276 | 11.366 | 90.728 | 90.985 |
| 176Hf | 3.381 | 8.958 | 88.126 | 88.349 |
| 178Hf | 3.206 | 6.822 | 93.019 | 93.180 |
| 180Hf | 3.211 | 3.584 | 93.137 | 93.324 |
| 182Hf | 3.063 | 4.440 | 97.485 | 97.790 |
| 184Hf | 2.800 | 5.465 | 106.349 | 107.100 |
| Isotope | 162Hf | 164Hf | 166Hf | ||||||
|---|---|---|---|---|---|---|---|---|---|
| I | |||||||||
| 0.285 | 0.262 | 0.183 | 0.211 | 0.200 | 0.148 | 0.158 | 0.154 | 0.119 | |
| 0.730 | 0.709 | 0.253 | 0.587 | 0.577 | 0.220 | 0.470 | 0.465 | 0.185 | |
| 1.293 | 1.269 | 0.302 | 1.085 | 1.072 | 0.270 | 0.897 | 0.889 | 0.234 | |
| 1.940 | 1.915 | 0.341 | 1.669 | 1.655 | 0.310 | 1.406 | 1.398 | 0.273 | |
| 2.635 | 2.632 | 0.374 | 2.304 | 2.311 | 0.344 | 1.972 | 1.978 | 0.306 | |
| 3.185 | 3.409 | 0.402 | 2.995 | 3.028 | 0.372 | 2.566 | 2.619 | 0.334 | |
| 3.567 | 4.239 | 0.427 | 3.618 | 3.799 | 0.398 | — | 3.312 | 0.359 | |
| 4.068 | 5.116 | 0.450 | — | 4.619 | 0.421 | — | 4.053 | 0.381 | |
| 4.653 | 6.036 | 0.470 | — | 5.482 | 0.442 | — | 4.836 | 0.402 | |
| 5.310 | 6.996 | 0.489 | — | 6.386 | 0.461 | — | 5.658 | 0.421 | |
| Isotope | 168Hf | 170Hf | 172Hf | ||||||
| I | |||||||||
| 0.124 | 0.122 | 0.097 | 0.101 | 0.100 | 0.080 | 0.095 | 0.095 | 0.076 | |
| 0.386 | 0.383 | 0.159 | 0.322 | 0.320 | 0.135 | 0.309 | 0.308 | 0.133 | |
| 0.757 | 0.753 | 0.207 | 0.643 | 0.639 | 0.181 | 0.628 | 0.626 | 0.182 | |
| 1.214 | 1.209 | 0.247 | 1.043 | 1.039 | 0.218 | 1.037 | 1.035 | 0.225 | |
| 1.736 | 1.737 | 0.280 | 1.504 | 1.509 | 0.250 | 1.521 | 1.523 | 0.262 | |
| 2.306 | 2.327 | 0.309 | 2.016 | 2.039 | 0.278 | 2.064 | 2.080 | 0.294 | |
| 2.858 | 2.971 | 0.334 | 2.567 | 2.621 | 0.303 | 2.654 | 2.700 | 0.324 | |
| 3.310 | 3.664 | 0.358 | 3.151 | 3.251 | 0.326 | 3.277 | 3.375 | 0.351 | |
| 3.833 | 4.401 | 0.379 | 3.768 | 3.923 | 0.346 | 3.919 | 4.101 | 0.375 | |
| 4.440 | 5.178 | 0.398 | 4.421 | 4.635 | 0.365 | 4.576 | 4.874 | 0.397 | |
| Isotope | 174Hf | 176Hf | 178Hf | ||||||
| I | |||||||||
| 0.091 | 0.091 | 0.073 | 0.088 | 0.088 | 0.071 | 0.093 | 0.093 | 0.075 | |
| 0.297 | 0.296 | 0.129 | 0.290 | 0.289 | 0.127 | 0.307 | 0.306 | 0.134 | |
| 0.608 | 0.606 | 0.178 | 0.597 | 0.595 | 0.177 | 0.632 | 0.631 | 0.188 | |
| 1.010 | 1.008 | 0.221 | 0.998 | 0.996 | 0.222 | 1.059 | 1.057 | 0.237 | |
| 1.486 | 1.490 | 0.260 | 1.481 | 1.482 | 0.262 | 1.570 | 1.575 | 0.280 | |
| 2.021 | 2.044 | 0.294 | 2.035 | 2.044 | 0.299 | 2.150 | 2.177 | 0.320 | |
| 2.598 | 2.663 | 0.324 | 2.647 | 2.676 | 0.332 | 2.778 | 2.854 | 0.356 | |
| 3.209 | 3.340 | 0.352 | 3.308 | 3.370 | 0.362 | 3.435 | 3.600 | 0.389 | |
| 3.857 | 4.070 | 0.378 | 4.011 | 4.123 | 0.390 | 4.119 | 4.409 | 0.420 | |
| 4.551 | 4.850 | 0.401 | — | 4.929 | 0.416 | 4.837 | 5.277 | 0.448 | |
| Isotope | 180Hf | 182Hf | 184Hf | ||||||
| I | |||||||||
| 0.093 | 0.093 | 0.076 | 0.098 | 0.097 | 0.079 | 0.107 | 0.106 | 0.086 | |
| 0.309 | 0.308 | 0.136 | 0.322 | 0.322 | 0.142 | 0.350 | 0.349 | 0.153 | |
| 0.641 | 0.640 | 0.194 | 0.666 | 0.666 | 0.200 | 0.717 | 0.717 | 0.213 | |
| 1.084 | 1.083 | 0.247 | 1.122 | 1.121 | 0.253 | 1.200 | 1.198 | 0.266 | |
| 1.631 | 1.629 | 0.297 | 1.680 | 1.678 | 0.302 | — | 1.780 | 0.314 | |
| 2.274 | 2.271 | 0.344 | 2.332 | 2.329 | 0.347 | — | 2.452 | 0.357 | |
| 3.005 | 3.003 | 0.387 | 3.065 | 3.065 | 0.388 | — | 3.207 | 0.396 | |
| 3.814 | 3.817 | 0.427 | 3.869 | 3.881 | 0.426 | — | 4.036 | 0.432 | |
| 4.682 | 4.709 | 0.464 | 4.734 | 4.769 | 0.461 | — | 4.933 | 0.465 | |
| 5.554 | 5.674 | 0.499 | — | 5.725 | 0.494 | — | 5.893 | 0.495 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasileiou, P.; Mertzimekis, T.J.; Mavrommatis, E.; Zyriliou, A. Nuclear Structure Investigations of Even–Even Hf Isotopes. Symmetry 2023, 15, 196. https://doi.org/10.3390/sym15010196
Vasileiou P, Mertzimekis TJ, Mavrommatis E, Zyriliou A. Nuclear Structure Investigations of Even–Even Hf Isotopes. Symmetry. 2023; 15(1):196. https://doi.org/10.3390/sym15010196
Chicago/Turabian StyleVasileiou, Polytimos, Theo J. Mertzimekis, Eirene Mavrommatis, and Aikaterini Zyriliou. 2023. "Nuclear Structure Investigations of Even–Even Hf Isotopes" Symmetry 15, no. 1: 196. https://doi.org/10.3390/sym15010196
APA StyleVasileiou, P., Mertzimekis, T. J., Mavrommatis, E., & Zyriliou, A. (2023). Nuclear Structure Investigations of Even–Even Hf Isotopes. Symmetry, 15(1), 196. https://doi.org/10.3390/sym15010196








