A Novel Approach for Minimizing Processing Times of Three-Stage Flow Shop Scheduling Problems under Fuzziness
Abstract
1. Introduction
- (1)
- Introducing suitable terminologies and measures that consider the properties of a possible optimal scheduling;
- (2)
- Defining two methods for determining the best schedule, one based on the ordering of pentagonal fuzzy numbers and the other on PFN interval confidence;
- (3)
- Interacting the analyst with the DM to arrive to the optimal sequence.
- (1)
- To minimize the fuzzy professing time of the machines subject to the rental policy;
- (2)
- To study the inclusive study of pentagonal fuzzy numbers in the scheduling problem;
- (3)
- To specific the concept of the optimal scheduling for the scenario;
- (4)
- To validate the proposed study with the support of illustrative example.
2. Preliminaries
- (1)
- is an upper semi—continuous membership function;
- (2)
- is convex fuzzy set, i.e.,for allis normal, i.e.,for which
- (3)
- is the support of, and the closureis compact set.
3. Notations and Assumptions
3.1. Notations
3.2. Assumptions
- i.
- Preemption was prohibited in all jobs. The machine only handled one work at a time.
- ii.
- All jobs were open at the beginning of schedule time. The duration of the production was independent of the schedule.
- iii.
- Each machine’s initial setup time was disregarded. Any machine could be unoccupied.
- iv.
- The deterministic phase was used to process each job. A task must be completed after it had been started.
- v.
- Before the second machine could handle the second work, the first job must have been completed in the first machine.
- vi.
- PFNs were used to represent the due dates.
4. Statement of the Problem
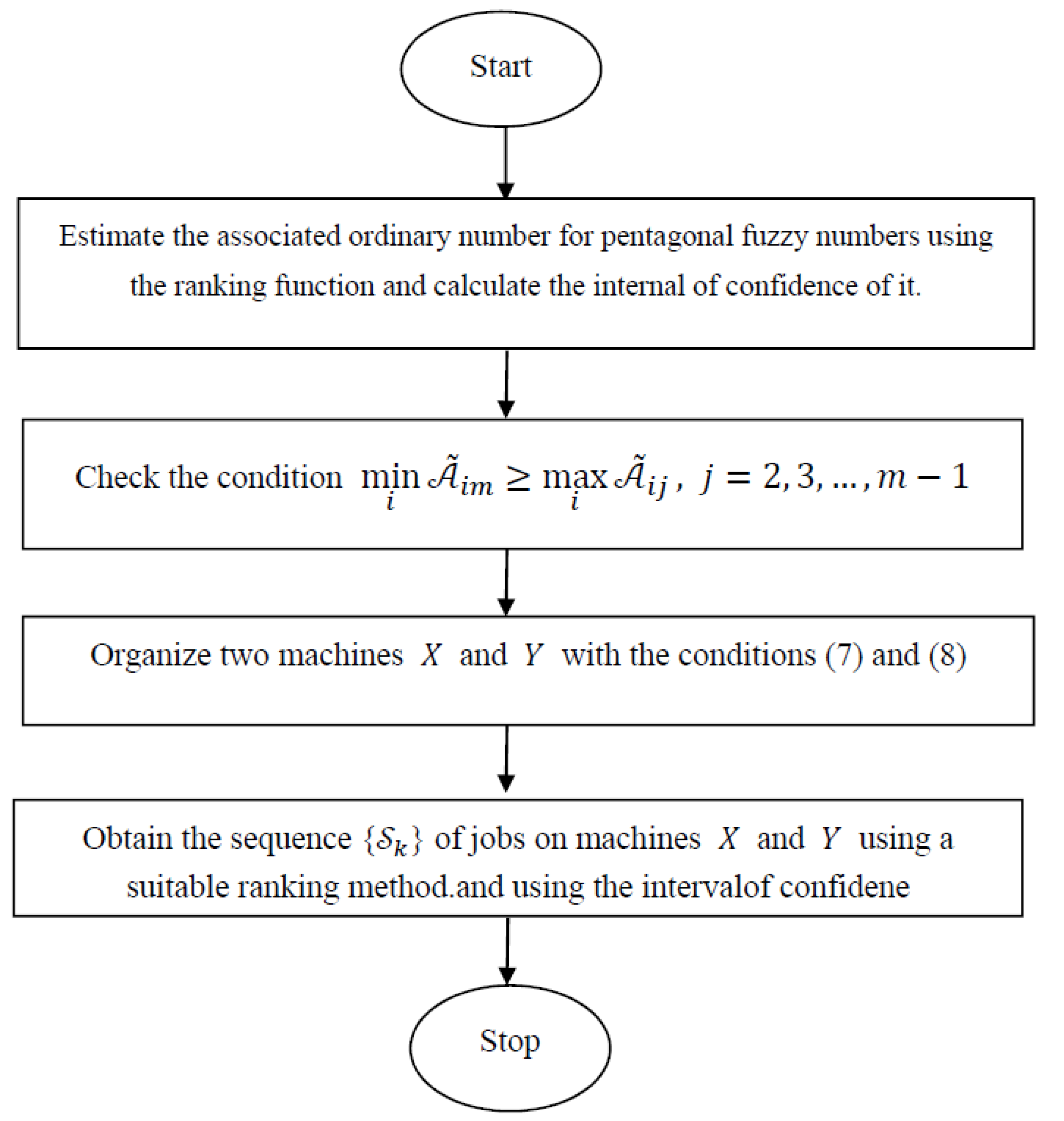
5. Solution Procedure
6. Numerical Example
- Make the optimization with the associated ordinary;
- Compute the true optimum for the intervals of confidence at the level ;
- Compare the results with those obtained using the pentagonal fuzzy numbers. If the divergence is very small within acceptable limits, keep the results obtained by using the PFNs.
7. Comparative Study
- (a)
- The intermediate value of the pentagonal and the triangular fuzzy numbers was equal i.e., when the membership for the total rental cost and for the total processing time;
- (b)
- The left and right fuzziness index values, defined in [24] were smaller than the values we obtained for the idle times of machines, total processing time and the rental cost;
- (c)
Advantages/Limitations of the Proposed Algorithm
- (1)
- The methodology does not involve a unified method because the DM’s vision, kind of fuzzy number, and level set vary from one another, making it impossible to assign a united way for allocating the intriguing scenarios for the DM.
- (2)
- Many factors must be considered such as: (i) the possibility of formulating the problem, (ii) the possibility of formulating the problem and choosing the level set, and (iii) the capability of solving the problem’s selected scenarios and finding their exact optimal scheduling.
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, S.M. Optimal two and three stages production schedule with Set up times included. Nav. Res. Logist. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
- Mir, M.S.S.; Rezaeian, J.; Mohamadian, H. Scheduling parallel machine problem under general effects of deterioration and learning with past-sequence-dependent setup time: Heuristic and meta-heuristic approaches. Soft Comput. 2000, 24, 1335–1355. [Google Scholar]
- Luo, W.; Xu, Y.; Tong, W.; Lin, G. Single-machine scheduling with job-dependent machine deterioration. J. Sched. 2019, 22, 691–707. [Google Scholar] [CrossRef]
- Chen, R.; Yuan, J. Unary NP-hardness of single-machine scheduling to minimize the total tardiness with deadlines. J. Sched. 2019, 22, 595–601. [Google Scholar] [CrossRef]
- Luo, W.; Liu, F. On single-machine scheduling with workload-dependent maintenance duration. Omega 2017, 68, 119–122. [Google Scholar] [CrossRef]
- Atakan, S.; Kerem, B.; Noyan, N. Minimizing value-at-risk in single-machine scheduling. Anal. Oper. Res. 2017, 248, 25–73. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, Q.; Gong, G.; Han, W. A new unrelated parallel machine scheduling problem with tool changes to minimize the total energy consumption. Int. J. Prod. Res. 2019, 58, 6826–6845. [Google Scholar] [CrossRef]
- Ueno, N.; Sotojima, S.; Takeda, J. Multi-Stage Flow-Shop in Steel Works. In Proceedings of the 24th Annual Simulation Symposium, New Orleans, LO, USA, 1 April 1991; Volume 21, pp. 332–337. [Google Scholar]
- Yuan, S.; Li, T.; Wang, B.; Yu, N. Model and algorithm for two-stage flow shop group scheduling problem with special blocking constraint. Control. Decis. 2020, 35, 1773–1779. [Google Scholar]
- Vahedi-Nouri, B.; Fattahi, P.; Tavakkoli-Moghaddam, R.; Ramezanian, R. A algorithm for flow shop scheduling problem with consideration of position-based learning effect and multiple availability constraints. Int. J. Adv. Manuf. Technol. 2014, 73, 601–611. [Google Scholar] [CrossRef]
- Ren, T.; Guo, M.; Lin, L.; Miao, Y. A local search algorithm for the flow-shop scheduling problem with release dates. Discret. Dyn. Nat. Soc. 2015, 2015, 320140. [Google Scholar] [CrossRef]
- Laribi, I.; Yalaoui, F.; Belkaid, F.; Sari, Z. Heuristics for solving flow shop scheduling problem under resources constraints. IFAC-Pap. Online 2016, 49, 1478–1483. [Google Scholar] [CrossRef]
- Yazdani, M.; Naderi, B. Modeling and scheduling no-idle hybrid flow shop problem. J. Optim. Ind. Eng. 2017, 10, 59–66. [Google Scholar]
- Qu, C.; Fu, Y.; Yi, Z.; Tan, J. Solutions to no wait flow-shop scheduling problem using the flower pollination algorithm based on the hormone modulation mechanism. Complexity 2018, 2018, 1973604. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Shymala, A.K.; PAL, M. Triangular fuzzy matrices. Iran. J. Fuzzy Syst. 2007, 4, 75–87. [Google Scholar]
- Shaw, A.K.; Roy, T.K. Generalized trapezoidal fuzzy number with its arithmetic operations and its application in fuzzy system reliability analysis. Int. J. Pure Appl. Sci. Technol. 2011, 5, 60–76. [Google Scholar]
- Panda, A.; Pal, M. A study on pentagonal fuzzy number and its corresponding matrices. Pac. Sci. Rev. B Humanit. Soc. Sci. 2015, 1, 131–139. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mondal, S.P.; Alam, S.; Ahmadian, A.; Senu, N.; De, D.; Salahshour, S. The pentagonal fuzzy number: Its different representations, properties, ranking, defuzzification and application in game problems. Symmetry 2019, 11, 248. [Google Scholar] [CrossRef]
- Pathinathan, T.; Ponnivalavan, K. Pentagonal fuzzy number. Int. J. Comput. Algorithm 2014, 3, 1003–1005. [Google Scholar]
- Kumar, R.; Pathinathan, T. Sieving out the poor using fuzzy decision-making tools. Indian J. Sci. Technol. 2015, 8, 1–7. [Google Scholar] [CrossRef][Green Version]
- Prameela, K.U.; Kumar, P. Execution proportions of multi-server queuing model with pentagonal fuzzy number: DSW algorithm approach. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 1047–1051. [Google Scholar]
- McCahon, C.S.; Lee, E.S. Job sequencing with fuzzy processing times. Comput. Math. Appl. 1990, 19, 31–41. [Google Scholar] [CrossRef]
- Sathish, S.; Ganesan, K. Flow shop scheduling problem to minimize the rental cost under fuzzy environment. J. Nat. Sci. Res. 2012, 2, 62–68. [Google Scholar]
- Khalifa, H.A. On single machine scheduling problem with distinct due dates under fuzzy environment. Int. J. Supply Oper. Manag. 2020, 7, 272–278. [Google Scholar]
- Khalifa, H.A.; Alodhaibi, S.S.; Kumar, P. Solving constrained flow-shop scheduling problem through Multistage Fuzzy Binding Approach with Fuzzy Due Dates. Adv. Fuzzy Syst. 2021, 2021, 6697060. [Google Scholar] [CrossRef]
- Alharbi, M.; Khalifa, H.A. On a flow-shop scheduling problem with fuzzy pentagonal processing time. Hindawi J. Math. 2021, 2021, 6695174. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, Q.; Chica, M. Maintenance costs and makespan minimization for assembly permutation flow shop scheduling by considering preventive and corrective maintenance. J. Manuf. Syst. 2021, 59, 549–564. [Google Scholar] [CrossRef]
- Jabbari, M.; Tavana, M.; Fattahi, P.; Daneshamooz, F. A parameter tuned hybrid algorithm for solving flow shop scheduling problems with parallel assembly stages. Sustain. Oper. Comput. 2022, 3, 22–32. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.; Lu, C.; Wang, A. Learning-based Memetic Algorithm for Energy-Efficient Flexible Job Shop Scheduling with Type-2 Fuzzy Processing Time. IEEE Trans. Evol. Comput. 2022. [Google Scholar] [CrossRef]
- Zhou, T.; Khalifa, H.A.; Najafi, S.E.; Edalatpanah, S.A. Minimizing the machine processing time in a flow shop scheduling problem under piecewise quadratic fuzzy numbers. Discret. Dyn. Nat. Soc. 2022, 2022, 3495228. [Google Scholar] [CrossRef]
- Ren, J.; Ye, C.; Yang, F. Solving flow-shop scheduling problem with a reinforcement-learning algorithm that generalizes the value function with neural network. Alex. Eng. J. 2021, 60, 2787–2800. [Google Scholar] [CrossRef]
- Wang, C.-N.; Hsu, H.-P.; Fu, H.-P.; Phan, N.K.P.; Nguyen, V.T. Scheduling flexible flow shop in labeling companies to minimize the makespan. Comput. Syst. Sci. Eng. 2022, 40, 17–36. [Google Scholar] [CrossRef]
- Wang, C.-N.; Porter, G.A.; Huang, C.C.; Nguyen, V.T.; Husain, S. TFlow-shop scheduling with transportation capacity and time consideration. Comput. Mater. Contin. 2022, 70, 3031–3048. [Google Scholar]
- Jemmali, M.; Hidri, L. Hybrid Flow Shop with Setup Times Scheduling Problem. Comput. Syst. Sci. Eng. 2023, 44, 563–577. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gao, D.; Pedrycz, W. Solving Multi-Objective Fuzzy Job-shop Scheduling Problem by a Hybrid Adaptive Differential Evolution Algorithm. IEEE Trans. Ind. Inform. 2022, 18, 8519–8528. [Google Scholar] [CrossRef]
- Koulamas, C.; Kyparisis, G.J. Flow shop scheduling with two distinct job due dates. Comput. Ind. Eng. 2022, 163, 107835. [Google Scholar] [CrossRef]
- Alajanbi, M.; Malerba, D.; Liu, H. Distributed Reduced Convolution Neural Networks. Mesop. J. Big Data 2021, 2021, 26–29. [Google Scholar] [CrossRef]
- Ali, A.H.; Mohammed, M.A.; Ahmed, M.A. Character Recognition by Implementing FPGA-Based Artificial Neural Network. Mesop. J. Comput. Sci. 2021, 2021, 14–19. [Google Scholar] [CrossRef]

| T | 1 | 2 | … | ||
|---|---|---|---|---|---|
| Machine | … | ||||
| Machine | … | ||||
| Machine | … |
| Job | |||
|---|---|---|---|
| 1 | (7, 7.5, 8, 8.5, 9) | (6, 6.5, 7, 7.5, 8) | (3, 3.5, 4, 4.5, 5) |
| 2 | (12, 12.5,13, 13.5, 14) | (5, 5.5, 6, 6.5, 7) | (4, 4.5, 5, 5.5, 6) |
| 3 | (8, 9, 10, 11, 12) | (4, 4.5, 5, 5.5, 6) | (6, 6.5, 7, 7.5, 8) |
| 4 | (10, 10.5, 11, 11.5, 12) | (5, 5.5, 6, 6.5, 7) | (11, 11.5, 12, 12.5, 13) |
| 5 | (9, 9.5, 10, 10.5, 11) | (5, 5.5, 6, 6.5, 7) | (8, 8.5, 9, 9.5, 10) |
| Job | ||
|---|---|---|
| 1 | (13,14,15,16,17) | (9,10,11,12,13) |
| 2 | (17,18,19,20,21) | (9,10,11,12,13) |
| 3 | (12,13.5, 15,16.5,18) | (10,11,12,13,14) |
| 4 | (15,16,17,18,19) | (16,17,18,19,20) |
| 5 | (14,15,16,17,18) | (13,14,15,16,17) |
| Machine 1 | Machine 2 | Machine 3 | ||||
|---|---|---|---|---|---|---|
| Job | Time in | Time out | Time in | Time out | Time in | Time out |
| 4 | (0, 0, 0, 0, 0) | (10, 10.5, 11, 11.5, 12) | (10, 10.5, 11, 11.5, 12) | (10, 10.5, 11, 11.5, 12) | (15, 16, 17, 18, 19) | (26, 27.5, 29, 30.5, 32) |
| 5 | (10, 10.5, 11, 11.5, 12) | (19, 20, 21, 22, 23) | (19, 20, 21, 22, 23) | (19, 20, 21, 22, 23) | (26, 27.5, 29, 30.5, 32) | (34, 36, 38, 40, 42) |
| 2 | (19, 20, 21, 22, 23) | (31, 32.5, 34, 35.5, 37) | (31, 32.5, 34, 35.5, 37) | (31, 32.5, 34, 35.5, 37) | (36, 38, 40, 42, 44) | (40, 42.5, 45, 47.5, 50) |
| 3 | (31, 32.5, 34, 35.5, 37) | (39, 41.5, 44, 46.5, 49) | (39, 41.5, 44, 46.5, 49) | (39, 41.5, 44, 46.5, 49) | (43, 46, 49, 52, 55) | (49, 52.5, 56, 59.5, 63) |
| 1 | (39, 41.5, 44, 46.5, 49) | (46, 49, 52, 55, 58) | (46, 49, 52, 55, 58) | (46, 49, 52, 55, 58) | (52, 55.5, 59, 62.5, 66) | (55, 59, 63, 67, 71) |
| Jobs | |||
|---|---|---|---|
| 1 | [7, 9] | [6, 8] | [3, 5] |
| 2 | [12, 14] | [5, 7] | [4, 6] |
| 3 | [8, 12] | [4, 6] | [6, 8] |
| 4 | [10, 12] | [5, 7] | [11, 13] |
| 5 | [9, 11] | [5, 7] | [8, 10] |
| Job | ||
|---|---|---|
| 1 | [13, 17] | [9, 13] |
| 2 | [17, 21] | [9, 13] |
| 3 | [12, 18] | [10, 14] |
| 4 | [15, 19] | [16, 20] |
| 5 | [14, 18] | [13, 17] |
| Job | Machine-1 | Machine-2 | Machine-3 | |||
|---|---|---|---|---|---|---|
| Time in | Time out | Time in | Time out | Time in | Time out | |
| 4 | [0, 0] | [10, 12] | [10, 12] | [15, 19] | [15, 19] | (26,32) |
| 5 | [10, 12] | [19, 23] | [19, 23] | [24, 30] | [26, 32] | (34,42) |
| 2 | [19, 23] | [31, 37] | [31, 37] | [36, 44] | [36, 44] | [40, 50] |
| 3 | [31, 37] | [39, 49] | [39, 49] | [43, 55] | [43, 55] | [49, 63] |
| 1 | [39, 49] | [46, 58] | [46, 58] | [52, 66] | [52, 66] | [55, 71] |
| Type of Fuzzy Number | Our Proposed Algorithm | Algorithm by Sathish and Ganesan [24] |
|---|---|---|
| Pentagonal fuzzy number | (55, 59, 63, 67, 71) | (61, 62, 63, 64, 65) |
| Triangular fuzzy number | (59, 63, 67) | (61, 63, 65) |
| Fuzziness index triangular fuzzy number | (63, 4, 4) | (63, 2, 2) |
| Type of Fuzzy Number | Proposed Algorithm | Algorithm by Sathish and Ganesan [24] |
|---|---|---|
| Pentagonal fuzzy number | (229, 340.5, 452, 563.5, 675) | (444, 448, 452, 456, 460) |
| Triangular fuzzy number | (340.5, 452, 563.5) | (444, 452, 460) |
| Fuzziness index triangular fuzzy number | (452, 111.5, 111.5) | (452, 8, 8) |
| Type of Fuzzy Number | Proposed Algorithm | Algorithm by Sathish and Ganesan [24] | |
|---|---|---|---|
| Pentagonal fuzzy number | (9, 10, 11, 12, 13) | ||
| (16, 17, 18, 19, 20) | |||
| (7, 8, 9, 10, 11) | |||
| Triangular fuzzy number | (9, 11, 13) | ||
| (16, 18, 20) | |||
| (7, 9, 11) | |||
| Fuzziness index triangular fuzzy number | (11, 7, 7) | (11, 2, 2) | |
| (18, 15.5, 15.5) | (18, 2, 2) | ||
| (9, 16.5, 16.5) | (9, 2, 2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alburaikan, A.; Garg, H.; Khalifa, H.A.E.-W. A Novel Approach for Minimizing Processing Times of Three-Stage Flow Shop Scheduling Problems under Fuzziness. Symmetry 2023, 15, 130. https://doi.org/10.3390/sym15010130
Alburaikan A, Garg H, Khalifa HAE-W. A Novel Approach for Minimizing Processing Times of Three-Stage Flow Shop Scheduling Problems under Fuzziness. Symmetry. 2023; 15(1):130. https://doi.org/10.3390/sym15010130
Chicago/Turabian StyleAlburaikan, Alhanouf, Harish Garg, and Hamiden Abd El-Wahed Khalifa. 2023. "A Novel Approach for Minimizing Processing Times of Three-Stage Flow Shop Scheduling Problems under Fuzziness" Symmetry 15, no. 1: 130. https://doi.org/10.3390/sym15010130
APA StyleAlburaikan, A., Garg, H., & Khalifa, H. A. E.-W. (2023). A Novel Approach for Minimizing Processing Times of Three-Stage Flow Shop Scheduling Problems under Fuzziness. Symmetry, 15(1), 130. https://doi.org/10.3390/sym15010130







