On the Symmetry Importance in a Relative Entropy Analysis for Some Engineering Problems
Abstract
1. Introduction
2. Historical and Mathematical Background
3. Relative Entropies and Probabilistic Numerical Methods
4. Reliability Structural Analysis and Probabilistic Divergence of the Elastic Pratt Truss Structure
4.1. Numerical Model
- load increment number has been fixed as 5;
- maximum iteration number for a single increment equals 40;
- increment length reduction number was set as 3;
- increment length reduction factor was equal to 0.5;
- the maximum number of line searches equals 0;
- control parameter for the line search method is set as 0.5;
- the maximum number of the BFGS corrections is set as 10;
- relative tolerance for the residual forces and displacements is taken as 0.0001.
4.2. Numerical Results and Discussion
5. Probabilistic Divergence Application to the Homogenization of some Particulate Composite
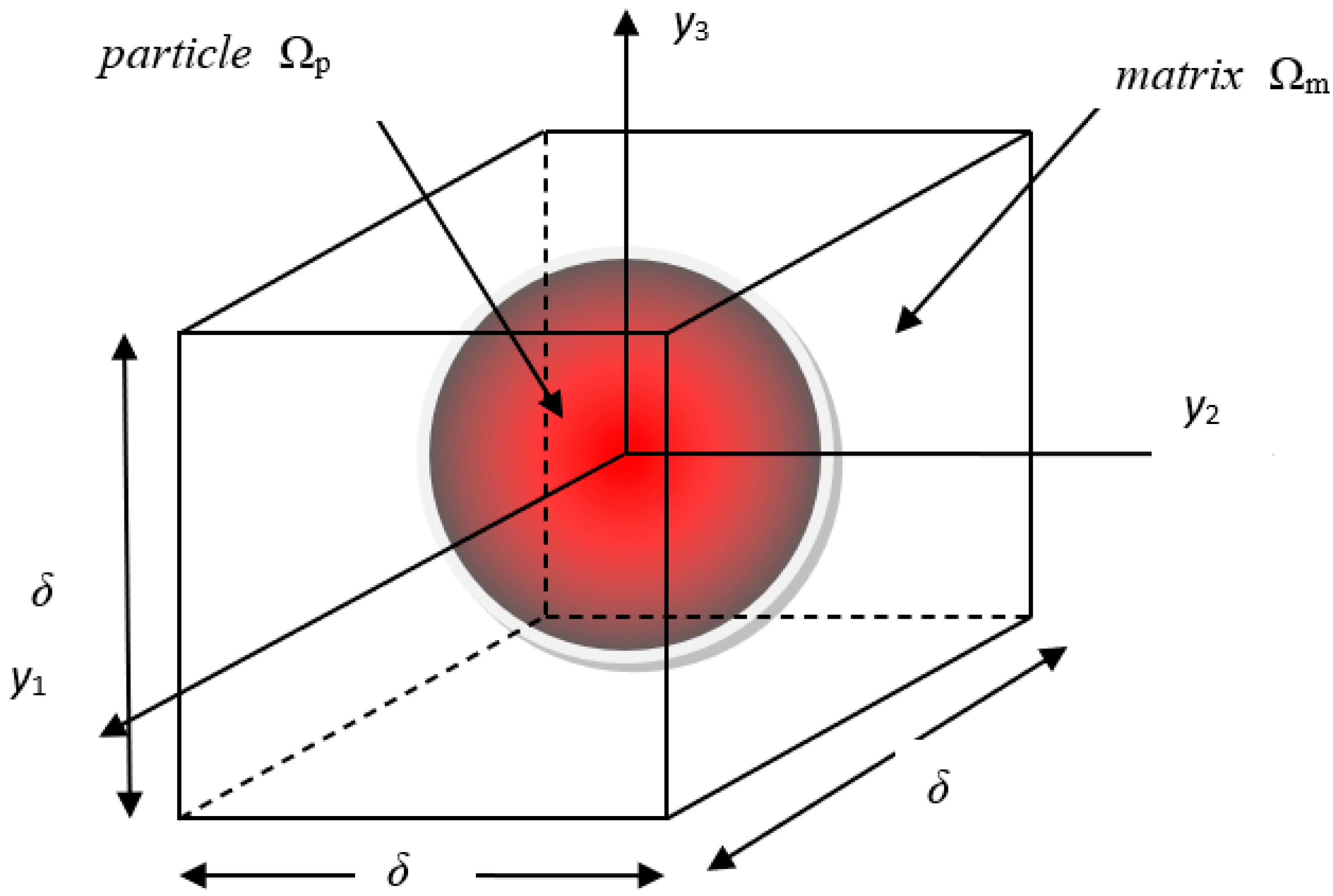
5.1. Composite Material Numerical Model
5.2. Numerical Results and Discussion
6. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haldar, A.; Mahadevan, S. Probability, Reliability and Statistical Methods in Engineering Design; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Hohenbichler, M.; Rackwitz, R. First-order concepts in systems reliability. Struct. Safety 1987, 1, 177–188. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Leinster, T. Entropy and Diversity. The Axiomatic Approach; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis & Fundamentals; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Donald, M.J. On the relative entropy. Comm. Math. Phys. 1986, 105, 13–34. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Part I & II. Bell Sys. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar]
- Hellinger, E. Neue begrűndung der theorie quadratischer formen von unendlichvielen veränderlichen. J. Reine Angew. Math. 1909, 136, 210–271. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. The Annals Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. Roy. Soc. London. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Nielsen, F. On a variational definition for the Jensen-Shannon symmetrization of distances based on the information radius. Entropy 2021, 23, 464. [Google Scholar] [CrossRef]
- Nielsen, F. On the Jensen-Shannon symmetrization of distances relying on abstract means. Entropy 2020, 21, 485. [Google Scholar] [CrossRef]
- Harremoës, P. Interpretation of Rényi entropies and divergences. Phys. A: Stat. Mech. Its Appl. 2006, 365, 57–62. [Google Scholar] [CrossRef]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Mahalanobis, P.C. On the generalized distance in statistics. Proc. Nat. Inst. Sci. India 1936, 2, 49–55. [Google Scholar]
- Kamiński, M. Tsallis entropy in dual homogenization of random composites using the Stochastic Finite Element Method. Int. J. Num. Meth. Engrg. 2018, 113, 834–857. [Google Scholar] [CrossRef]
- Fukui, K.; Sato, K.; Mizusaki, J.; Numao, M. Kullback-Leibler Divergence Based Kernel SOM for Visualization of Damage Process on Fuel Cells. In Proceedings of the 22nd IEEE International Conference on Tools with Artificial Intelligence, Arras, France, 27–29 October 2010; pp. 233–240. [Google Scholar] [CrossRef]
- Bilionis, I.; Koutsourelakis, P.S. Free energy computations by minimization of Kullback–Leibler divergence: An efficient adaptive biasing potential method for sparse representations. J. Comput. Phys. 2012, 231, 3849–3870. [Google Scholar] [CrossRef]
- Jiang, M.; Song, S.; Tang, F.; Li, Y.; Liu, J.; Feng, X. Scan registration for underwater mechanical scanning imaging sonar using symmetrical Kullback–Leibler divergence. J. Electron. Imag. 2019, 28, 013026. [Google Scholar] [CrossRef]
- Wei, S.; Wang, D.; Peng, Z. Principal component analysis based Kullback-Leibler divergence for die cracks detection. In Proceedings of the 2020 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020; pp. 224–228. [Google Scholar] [CrossRef]
- Filippatos, A.; Langkamp, A.; Kostka, P.; Gude, M. A Sequence-Based Damage Identification Method for Composite Rotors by Applying the Kullback–Leibler Divergence, a Two-Sample Kolmogorov–Smirnov Test and a Statistical Hidden Markov Model. Entropy 2019, 21, 690. [Google Scholar] [CrossRef]
- Kumar, P.S.; Kumaraswamidhas, L.A.; Laha, S.K. Bearing degradation assessment and remaining useful life estimation based on Kullback-Leibler divergence and Gaussian processes regression. Measurement 2021, 174, 108948. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Hao, H.; Uy, B.; Xia, Y.; Mirza, O. Dynamic assessment of shear connection conditions in slab-girder bridges by Kullback-Leibler distance. Adv. Struct. Engrg. 2012, 15, 771–780. [Google Scholar] [CrossRef]
- Abbas, A.E.H.; Cadenbach, A.; Salimi, E. A Kullback–Leibler View of Maximum Entropy and Maximum Log-Probability Methods. Entropy 2017, 19, 232. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Asymptotic form of the Kullback–Leibler divergence for multivariate asymmetric heavy-tailed distributions. Phys. A Stat. Mech. Its Appl. 2014, 395, 200–208. [Google Scholar] [CrossRef]
- Garbaczewski, P. Shannon versus Kullback–Leibler entropies in nonequilibrium random motion. Phys. Lett. A 2005, 341, 33–38. [Google Scholar] [CrossRef][Green Version]
- Ferrante, A.; Pavon, M.; Ramponi, F. Hellinger versus Kullback–Leibler multivariable spectrum approximation. IEEE Trans. Autom. Control 2008, 53, 954–967. [Google Scholar] [CrossRef]
- Martín, A.L.; López-Rosa, S.; Angulo, J.; Antolín, J. Jensen–Shannon and Kullback–Leibler divergences as quantifiers of relativistic effects in neutral atoms. Chem. Phys. Letters 2015, 635, 75–79. [Google Scholar] [CrossRef]
- Huang, J.; Yong, W.A.; Hong, L. Generalization of the Kullback–Leibler divergence in the Tsallis statistics. J. Math. Anal. Appl. 2016, 436, 501–512. [Google Scholar] [CrossRef]
- Nielsen, F. Fast approximations of the Jeffreys divergence between univariate Gaussian mixtures via mixture conversions to exponential-polynomial distributions. Entropy 2021, 23, 1417. [Google Scholar] [CrossRef]
- Kamiński, M. The Stochastic Perturbation Method for Computational Mechanics; Wiley: Chichester, UK, 2013. [Google Scholar]
- Kamiński, M. On iterative scheme in determination of the probabilistic moments of the structural response in the Stochastic perturbation-based Finite Element Method. Int. J. Num. Meth. Engrg. 2015, 104, 1038–1060. [Google Scholar] [CrossRef]
- Kamiński, M. Probabilistic entropy in homogenization of the periodic fiber-reinforced composites with random elastic parameters. Int. J. Num. Meth. Engrg. 2012, 90, 939–954. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Giordano, G.; Paternoster, B.; Ventola, A. Perturbative analysis of stochastic Hamiltonian problems under time discretizations. Appl. Math. Letters 2021, 120, 107223. [Google Scholar] [CrossRef]
- Jiang, D.; Zhou, B.; Han, B. Ergodic stationary distribution and extinction of a n-species Gilpin-Ayala competition system with nonlinear random perturbations. Appl. Math. Letters 2021, 120, 107273. [Google Scholar] [CrossRef]
- Eurocode 0, PN-EN-1990-1-1; Structural design basis. European Union: Brussels, Belgium, 2002.
- Kamiński, M.; Błoński, R. Analytical and numerical reliability analysis of certain Pratt steel truss. Appl. Sci. 2022, 12, 2901. [Google Scholar] [CrossRef]
- Oden, J.T. A general theory of finite elements. II. Applications. Int. J. Num. Meth. Engrg. 1969, 1, 247–259. [Google Scholar] [CrossRef]
- Eurocode 3, PN-EN-1993-1-1; Designing of steel structures—general rules. European Union: Brussels, Belgium, 2008.
- Kamiński, M. Design sensitivity analysis for the homogenized elasticity tensor of a polymer filled with rubber particles. Int. J. Sol. Struct. 2014, 51, 612–621. [Google Scholar] [CrossRef]
- Falsone, G.; Laudani, R. A probability transformation method (PTM) for the dynamic stochastic response of structures with non-Gaussian excitations. Engrg. Comput. 2018, 35, 1978–1997. [Google Scholar] [CrossRef]
- Yang, D.Y.; Tian, B.; Qu, Q.X.; Zhang, C.R.; Chen, S.S.; Wei, C.C. Lax pair, conservation law, Darboux transformation and localized waves of a variable-coefficient coupled Hirota system in an inhomogeneous optical fiber. Chaos Solitons Fractals 2021, 150, 110487. [Google Scholar] [CrossRef]
- Shen, Y.; Tian, B. Bilinear auto-Bäcklund transformations and soliton solutions of a (3+1) – dimensional generalized nonlinear evolution equation for the shallow water waves. Appl. Math. Lett. 2021, 122, 107301. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Tian, B.; Chen, Y.Q.; Shen, Y. Painlevé analysis, auto-Bäcklund transformation and analytic solutions of a (2+1) – dimensional generalized Burgers system with the variable coefficients in a fluid. Nonlinear Dynamics 2022, 108, 2417–2428. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Taking into consideration an extended coupled (2+1) – dimensional Burgers system in oceanography, acoustics and hydrodynamics. Chaos Solitons Fractals 2022, 161, 112293. [Google Scholar] [CrossRef]
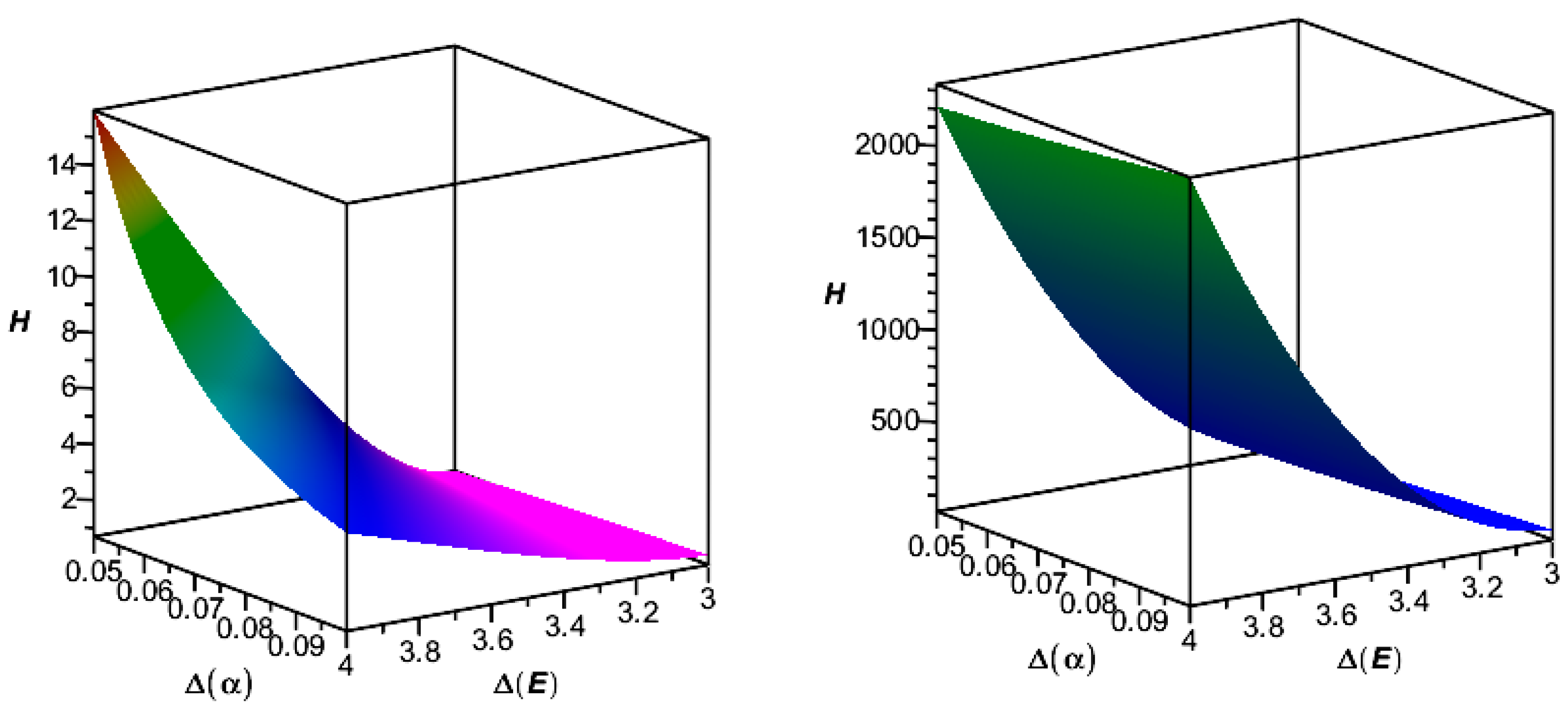
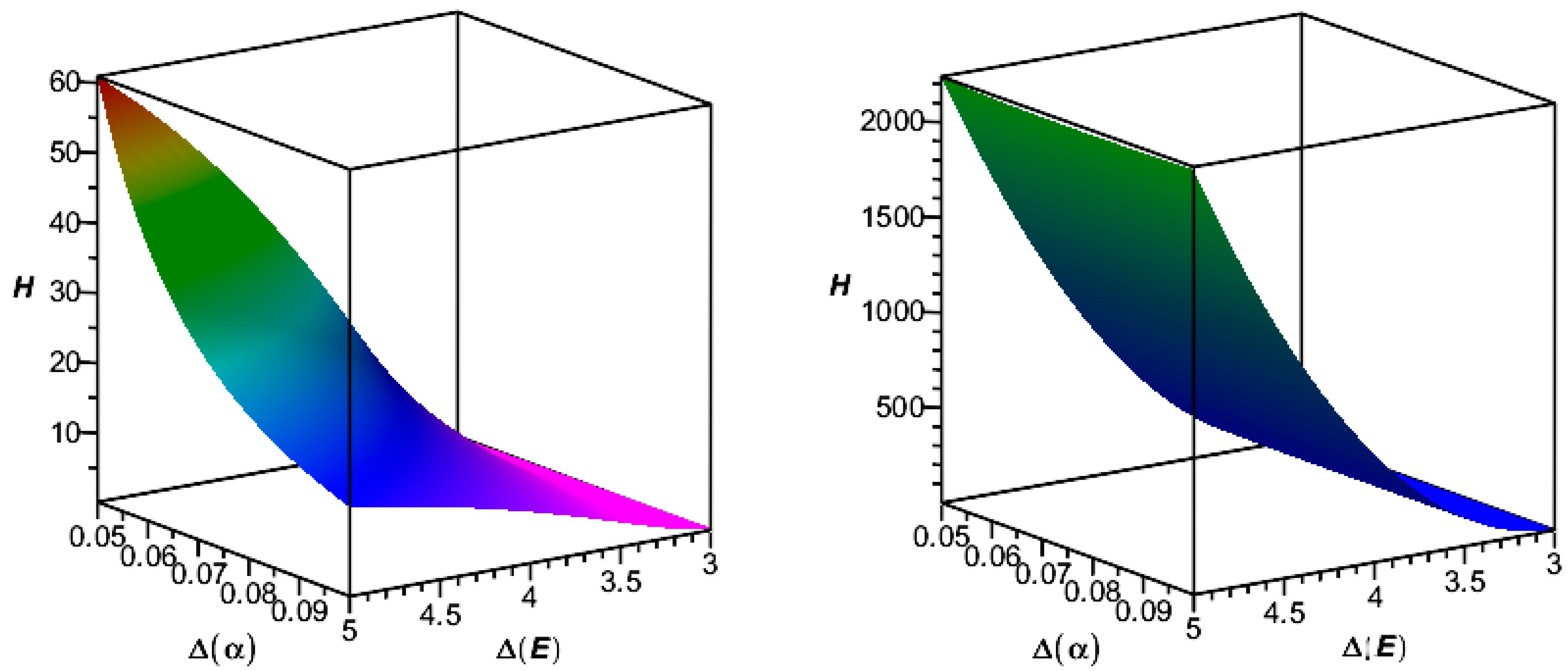





| Numerical Method | Data Type | α = 0.025 | α = 0.050 | α = 0.075 | α = 0.100 | α = 0.125 | α = 0.150 |
|---|---|---|---|---|---|---|---|
| Probabilistic analytical method | α(u) | 0.0914 | 0.1827 | 0.2736 | 0.3639 | 0.4533 | 0.5418 |
| DKL | 6369.278 | 1706.486 | 846.114 | 548.691 | 415.147 | 347.052 | |
| DJ | 6403.883 | 1716.821 | 851.966 | 552.988 | 418.740 | 350.277 | |
| Stochastic perturbation technique | α(u) | 0.0914 | 0.1827 | 0.2736 | 0.3639 | 0.4533 | 0.5417 |
| DKL | 6369.278 | 1706.486 | 846.114 | 548.691 | 415.147 | 347.052 | |
| DJ | 6403.884 | 1716.821 | 851.966 | 552.988 | 418.740 | 350.277 | |
| Monte-Carlo simulation approach | α(u) | 0.0914 | 0.1818 | 0.2722 | 0.3618 | 0.4507 | 0.5385 |
| DKL | 6367.928 | 1702.557 | 842.733 | 545.431 | 411.813 | 343.520 | |
| DJ | 6402.542 | 1712.961 | 848.615 | 549.743 | 415.412 | 346.747 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiński, M. On the Symmetry Importance in a Relative Entropy Analysis for Some Engineering Problems. Symmetry 2022, 14, 1945. https://doi.org/10.3390/sym14091945
Kamiński M. On the Symmetry Importance in a Relative Entropy Analysis for Some Engineering Problems. Symmetry. 2022; 14(9):1945. https://doi.org/10.3390/sym14091945
Chicago/Turabian StyleKamiński, Marcin. 2022. "On the Symmetry Importance in a Relative Entropy Analysis for Some Engineering Problems" Symmetry 14, no. 9: 1945. https://doi.org/10.3390/sym14091945
APA StyleKamiński, M. (2022). On the Symmetry Importance in a Relative Entropy Analysis for Some Engineering Problems. Symmetry, 14(9), 1945. https://doi.org/10.3390/sym14091945






