A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals
Abstract
:1. Introduction
2. Literature Review
2.1. Wavelet Threshold Denoising
2.2. Particle Swarm Optimization Algorithm
2.3. Discussion
3. Background Theory
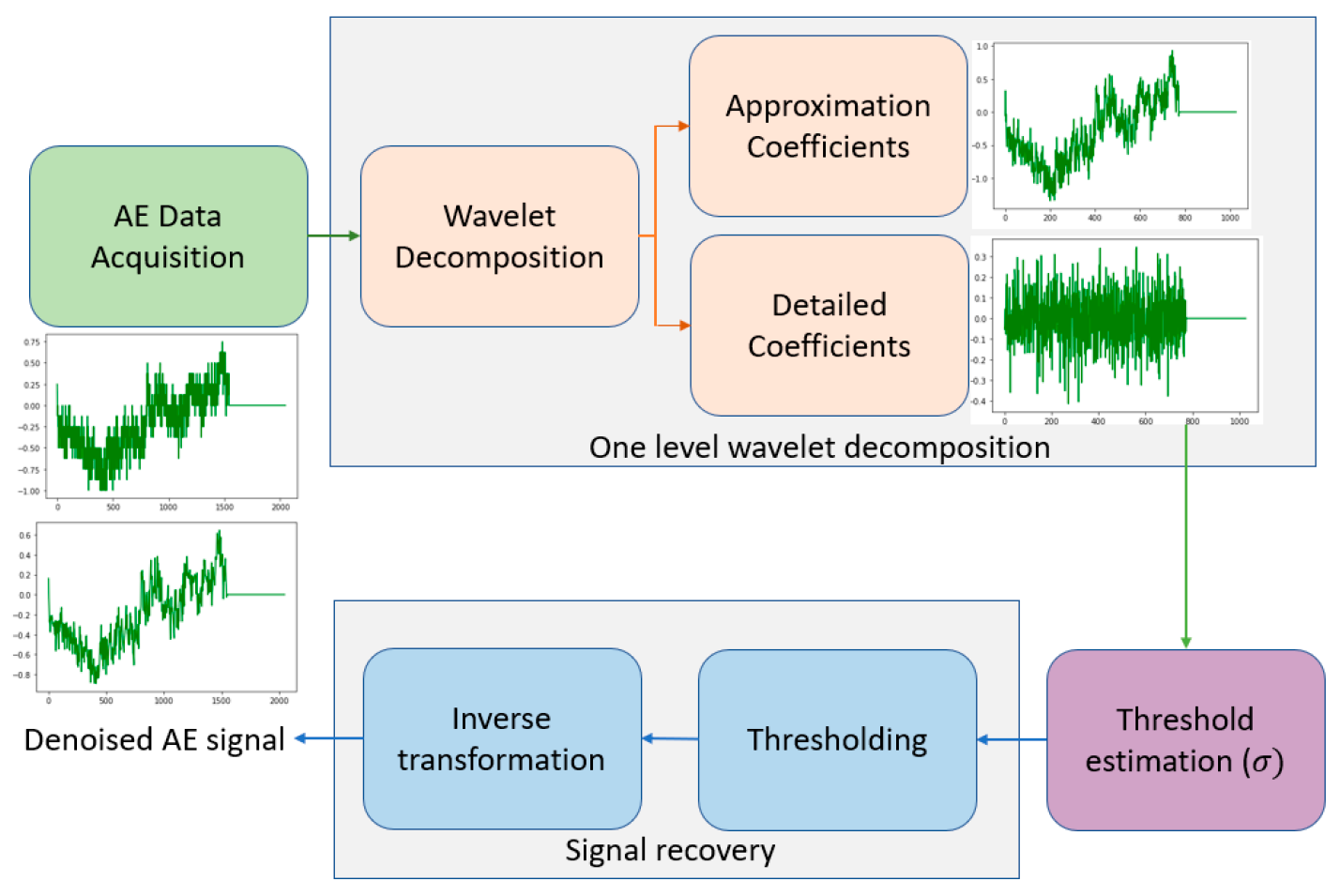
3.1. Wavelet-Based Threshold Denoising
3.2. The Particle Swarm Optimization Algorithm
4. The Proposed Method
Hybrid Particle Swarm Optimization (HPSO)
| Algorithm 1: HPSO. |
|
| Algorithm 2: LAHC. |
|
5. Material and Methods
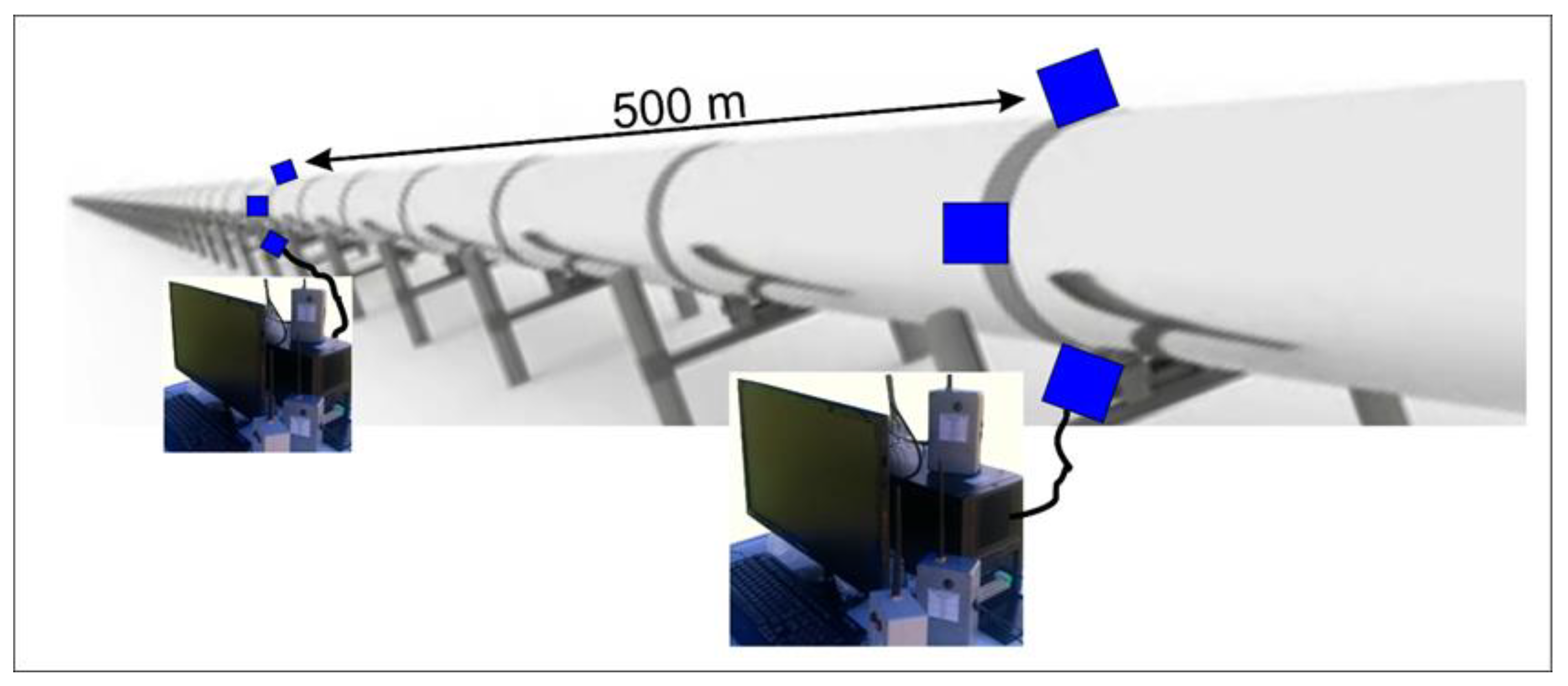
5.1. System Configuration
5.2. Experimental Setup
6. Methodology
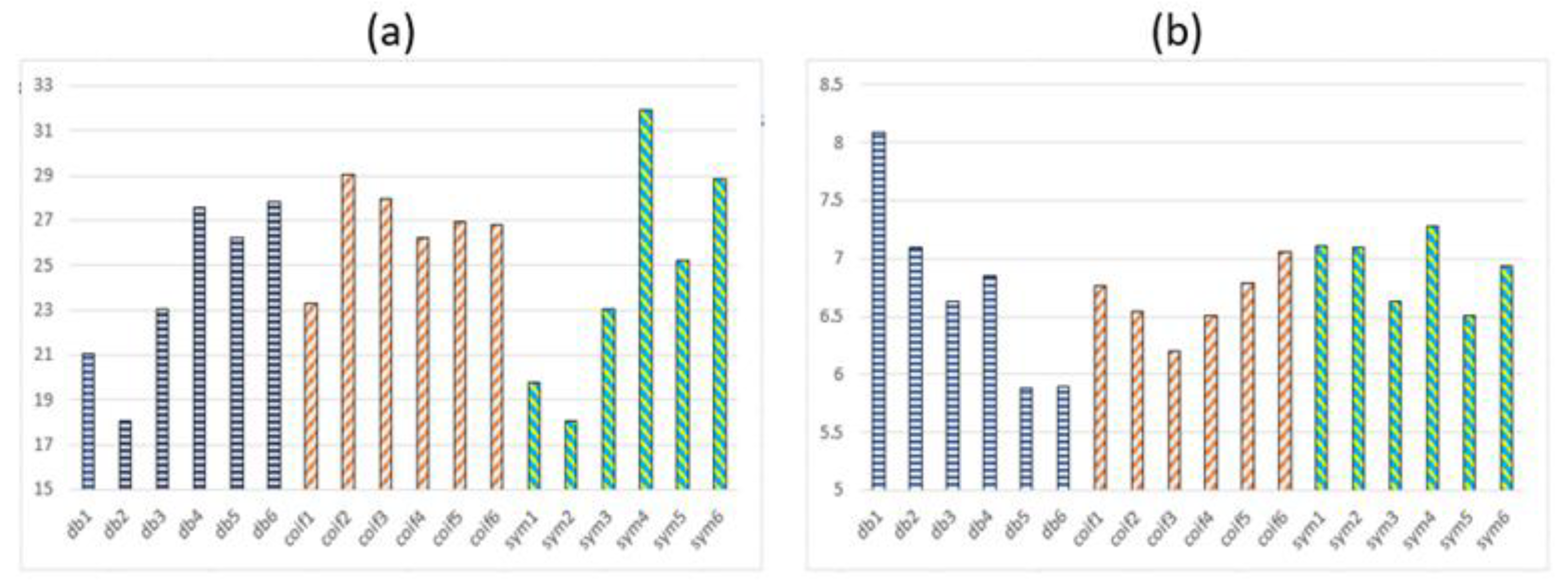
6.1. Wavelet Basis Function
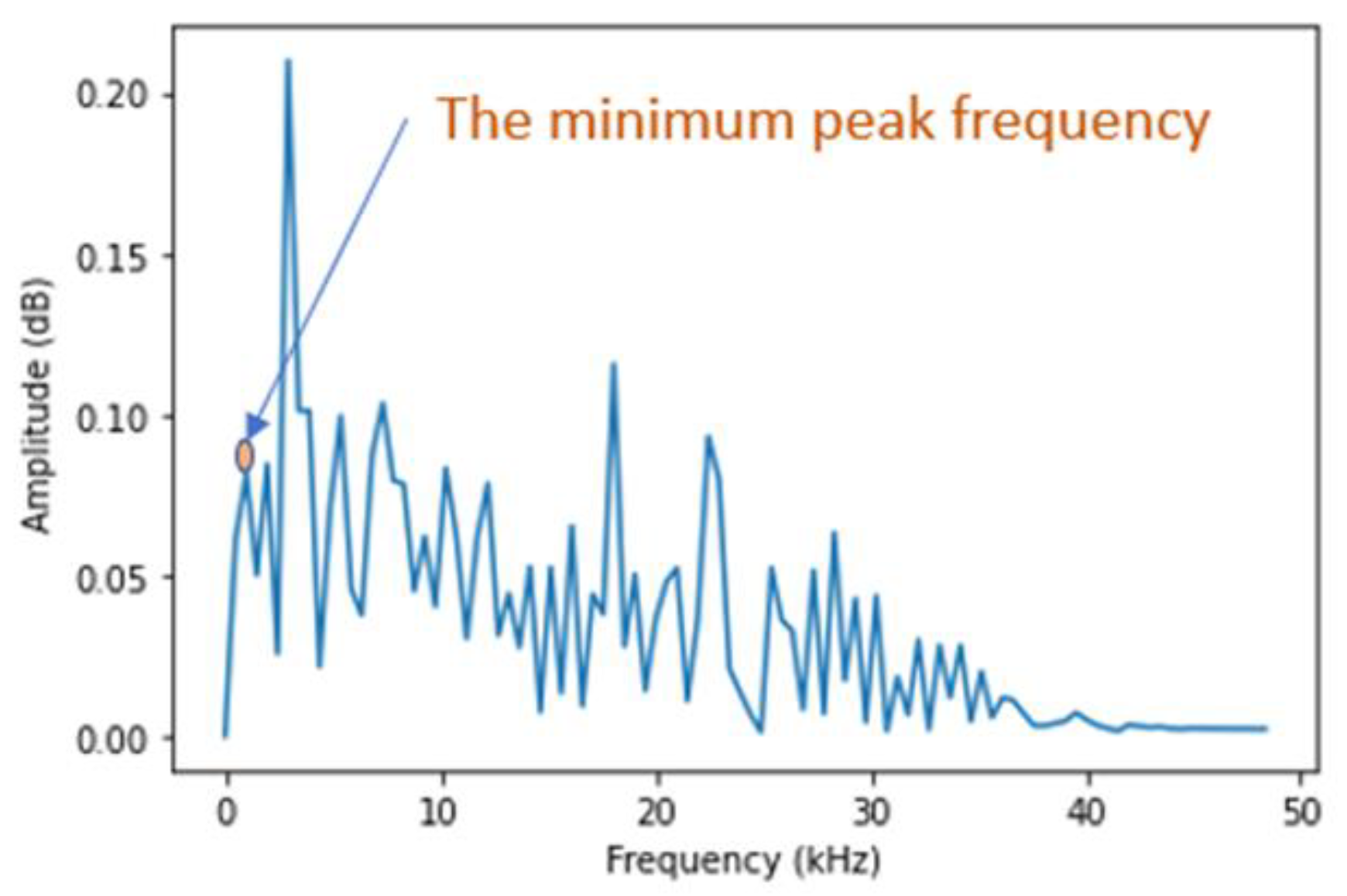
6.2. Decomposition Level
6.3. Signal Denoising
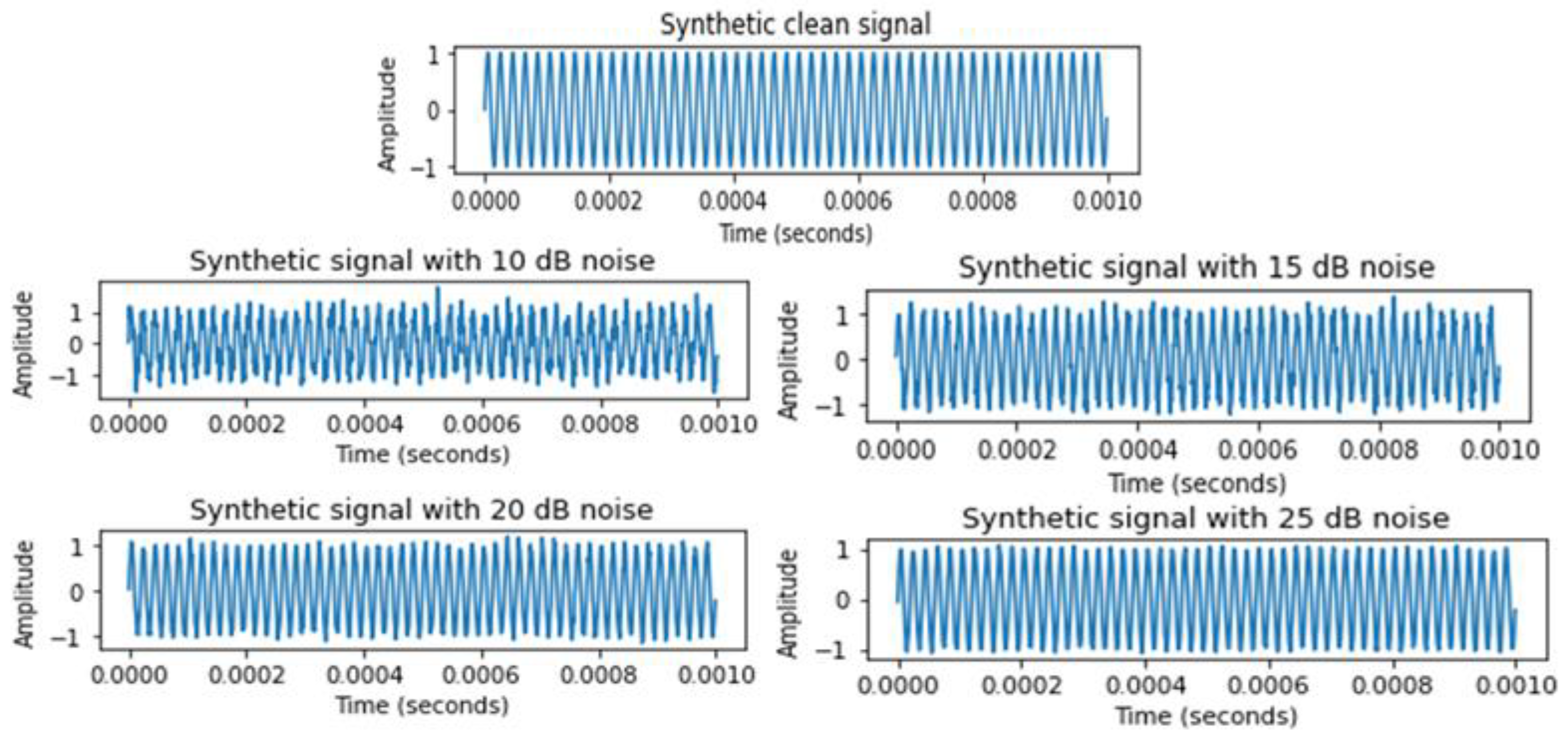
- A 50 KHz sine wave signal was generated, and the original signal was contaminated with various amount of Gaussian white noise. Noisy signal with 10 dB, 15 dB, 20 dB, and 25 dB noise were firstly analysed, and the synthesis was performed in python 3.9 (PyCharm environment). The synthetic signal was then decomposed using ‘db2’ wavelet basis function at level 5.
- Denoising a noisy signal by SSTD requires to first calculate the value range of the wavelet threshold to Equation (3). Donoho recommended to use q = 0.6745 for threshold calculation [21]. Equation (5) is used to shrink the wavelet coefficients at each level. Inverse WT was used to reconstruct the clean signal.
- Denoising a noisy signal by TD-PSO maximum threshold appeared when q = 1 and the minimum threshold was obtained when q = 0.4, so . The population size was set 50, where each the position of each particle was a five-dimensional vector. , , and the maximum iteration were set to 100.
- In case of denoising by TD-GA, maximum threshold appeared when q = 1 and the minimum threshold was obtained when q = 0.4, so . The population size was set 50 where each chromosome was represented by a five-dimensional vector The likelihood of a crossover, as well as the likelihood of a mutation, and maximum iterations were set 0.7, 0.01, and 100, respectively, as recommended by ref. [16]
- Denoising a noisy signal by TD-LAHC maximum threshold appeared when q = 1 and the minimum threshold was obtained when q = 0.4, so . Inverse WT was used to reconstruct the clean signal.
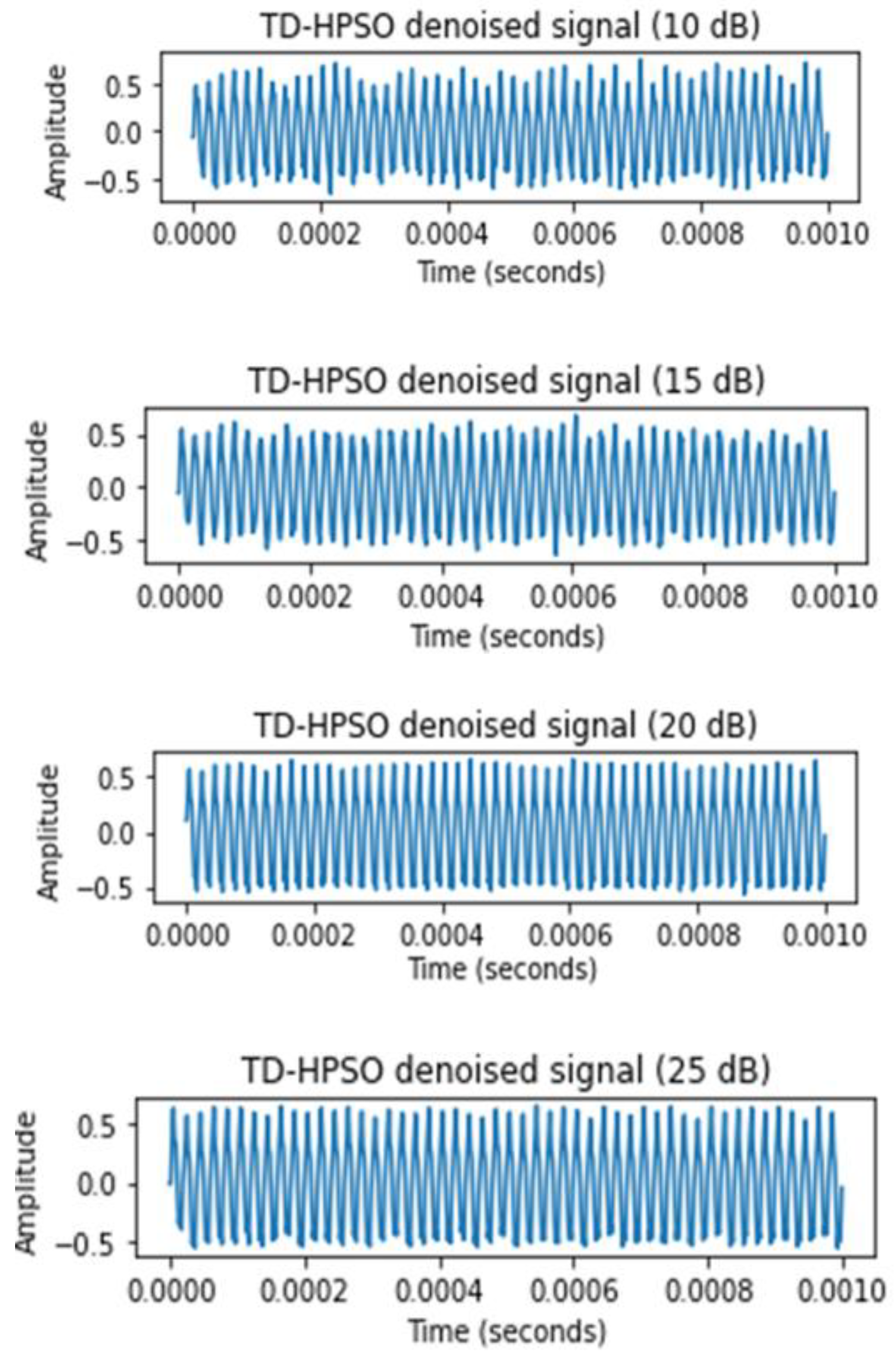
- Denoising a noisy signal by TD-HPSO maximum threshold appeared when q = 1 and the minimum threshold was obtained when q = 0.4, so . The population size was set 50, where the position of each particle was a five-dimensional vector. , , and the maximum number of iterations was set to 100. Inverse WT was used to reconstruct the clean signal.
7. Results and Discussion
7.1. Denoising of Synthetic Datasets Based on HPSO Method
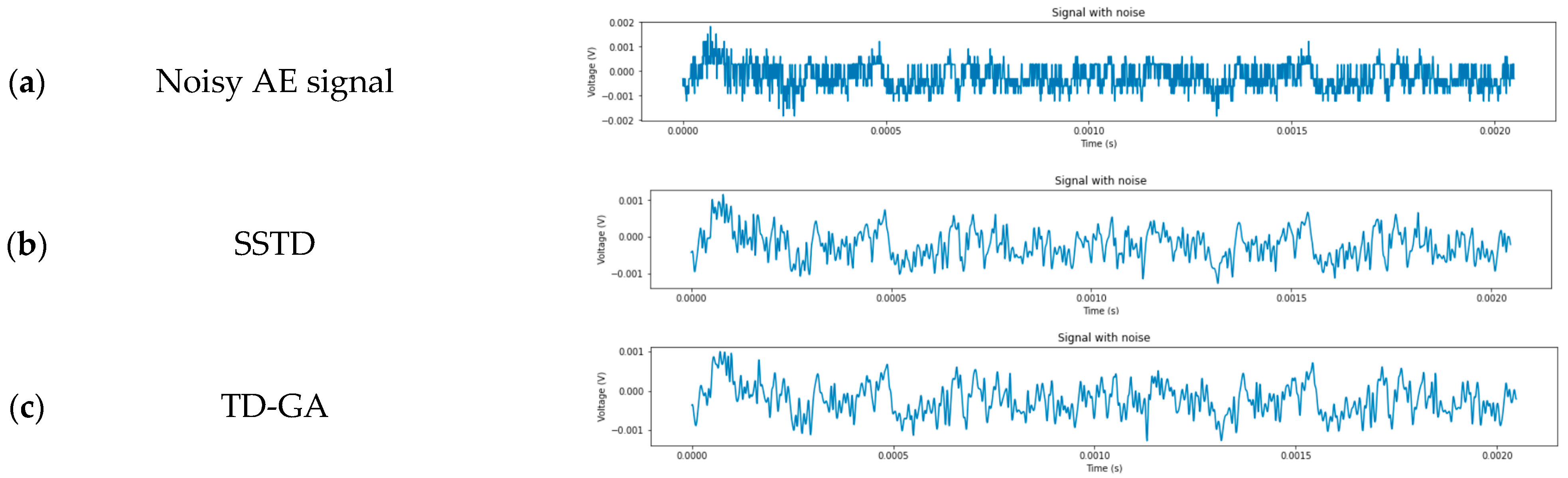
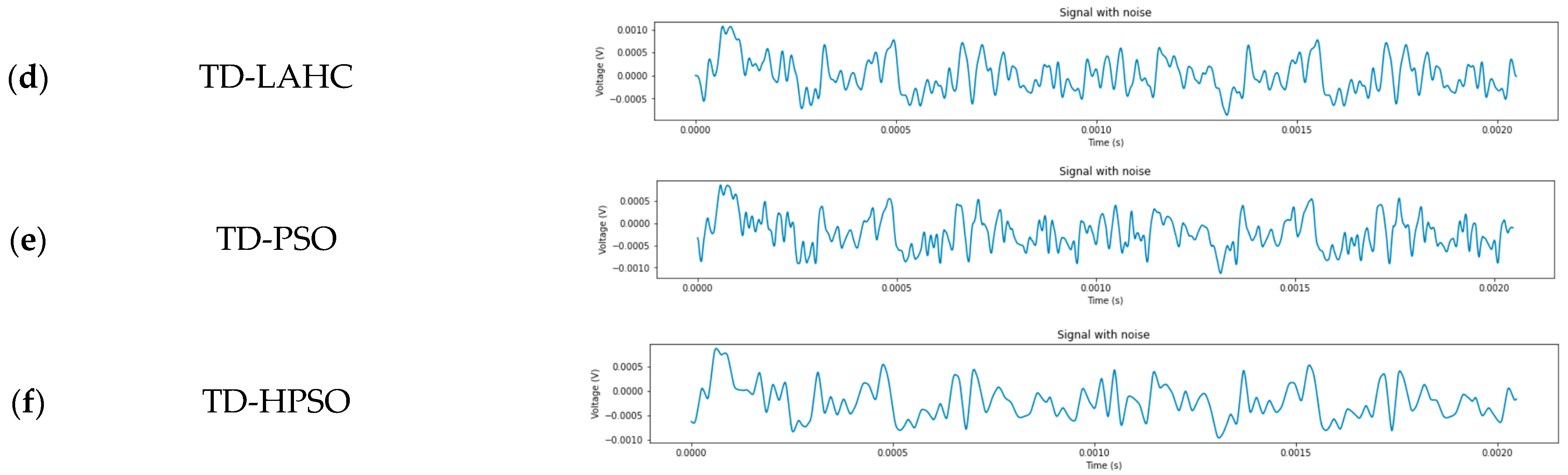
7.2. Denoising of AE Experimental Data Using TD-PSO Method
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A.; Irani, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Dong, L.; Hu, Q.; Tong, X.; Liu, Y. Velocity-Free MS/AE Source Location Method for Three-Dimensional Hole-Containing Structures. Engineering 2020, 6, 827–834. [Google Scholar] [CrossRef]
- Dong, L.; Tong, X.; Ma, J. Quantitative Investigation of Tomographic Effects in Abnormal Regions of Complex Structures. Engineering 2021, 7, 1011–1022. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Yao, X.L.; Liang, P.; Wang, K.X.; Sun, L.; Tian, B.Z.; Liu, X.X.; Wang, S.Y. Fracture evolution and localization effect of damage in rock based on wave velocity imaging technology. J. Cent. South Univ. 2021, 28, 2752–2769. [Google Scholar] [CrossRef]
- Du, Y.; Feng, G.; Kang, H.; Zhang, Y.; Zhang, X. Effects of different pull-out loading rates on mechanical behaviors and acoustic emission responses of fully grouted bolts. J. Cent. South Univ. 2021, 28, 2052–2066. [Google Scholar] [CrossRef]
- Szafran, J.; Juszczyk, K.; Kamiński, M. Experiment-based reliability analysis of structural joints in a steel lattice tower. J. Constr. Steel Res. 2019, 154, 278–292. [Google Scholar] [CrossRef]
- Kamiński, M.; Solecka, M. Optimization of the truss-type structures using the generalized perturbation-based Stochastic Finite Element Method. Finite Elem. Anal. Des. 2013, 63, 69–79. [Google Scholar] [CrossRef]
- Yu, B.; Gabriel, D.; Noble, L.; An, K.-N. Estimate of the optimum cutoff frequency for the Butterworth low-pass digital filter. J. Appl. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
- Sun, H.; He, Z.; Zi, Y.; Yuan, J.; Wang, X.; Chen, J.; He, S. Multiwavelet transform and its applications in mechanical fault diagnosis—A review. Mech. Syst. Signal Process. 2014, 43, 1–24. [Google Scholar] [CrossRef]
- Zhao, M.; Jia, X. A novel strategy for signal denoising using reweighted SVD and its applications to weak fault feature enhancement of rotating machinery. Mech. Syst. Signal Process. 2017, 94, 129–147. [Google Scholar] [CrossRef]
- Mi, X.; Zhao, S. Wind speed prediction based on singular spectrum analysis and neural network structural learning. Energy Convers. Manag. 2020, 216, 112956. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. Fundam. Pap. Wavelet Theory 2009, I, 494–513. [Google Scholar] [CrossRef] [Green Version]
- de Queiroz, R.L.; Rao, K.R. Time-Varying Lapped Transforms and Wavelet Packets. IEEE Trans. Signal Process. 1993, 41, 3293–3305. [Google Scholar] [CrossRef] [Green Version]
- Qiu, X.; Wang, Y.; Xu, J.; Xiao, S.; Li, C. Acoustic emission propagation characteristics and damage source localization of asphalt mixtures. Constr. Build. Mater. 2020, 252, 119086. [Google Scholar] [CrossRef]
- Soni, V.; Bhandari, A.K.; Kumar, A.; Singh, G.K. Improved sub-band adaptive thresholding function for denoising of satellite image based on evolutionary algorithms. IET Signal Process. 2013, 7, 720–730. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Cheng, C.; Jiang, T.; Grzybowski, S. Wavelet de-noising of partial discharge signals based on genetic adaptive threshold estimation. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 543–549. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Tan, C.; Si, L.; Liu, X. A novel denoising method for an acoustic-based system through empirical mode decomposition and an improved fruit fly optimization algorithm. Appl. Sci. 2017, 7, 215. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Part. Swarm Optim. 1995, 4, 1942–1948. [Google Scholar] [CrossRef]
- Banks, A.; Vincent, J.; Anyakoha, C. A review of particle swarm optimization. Part I: Background and development. Nat. Comput. 2007, 6, 467–484. [Google Scholar] [CrossRef]
- Mouna, H.; Azhagan, M.S.M.; Radhika, M.N.; Mekaladevi, V.; Devi, M.N. Velocity Restriction-Based Improvised Particle Swarm Optimization Algorithm. In Progress in Advanced Computing and Intelligent Engineering; Springer: Berlin/Heidelberg, Germany, 2018; pp. 351–360. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Zhao, X.Y. Noise smoothing for structural vibration test signals using an improved wavelet thresholding technique. Sensors 2012, 12, 11205–11220. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.P.; Desai, M.D. Adaptive denoising based on SURE risk. IEEE Signal Process. Lett. 1998, 5, 265–267. [Google Scholar] [CrossRef]
- Meng, B.; Li, Z.; Wang, H.; Li, Q. An improved wavelet adaptive logarithmic threshold denoising method for analysing pressure signals in a transonic compressor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2023–2030. [Google Scholar] [CrossRef]
- Vaiyapuri, T.; Alaskar, H.; Sbai, Z.; Devi, S. GA-based multi-objective optimization technique for medical image denoising in wavelet domain. J. Intell. Fuzzy Syst. 2021, 41, 1575–1588. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, J.; Lu, Z. Structural damage detection using improved particle swarm optimization. Inverse Probl. Sci. Eng. 2017, 5977, 1–19. [Google Scholar] [CrossRef]
- Bhutada, G.G.; Anand, R.S.; Saxena, S.C. PSO-based learning of sub-band adaptive thresholding function for image denoising. Signal Image Video Process. 2012, 6, 1–7. [Google Scholar] [CrossRef]
- Minh, H.; Khatir, S.; Abdel, M.; Cuong-le, T. An Enhancing Particle Swarm Optimization Algorithm ( EHVPSO ) for damage identification in 3D transmission tower. Eng. Struct. 2021, 242, 112412. [Google Scholar] [CrossRef]
- Yang, Q. A new localization method based on improved particle swarm optimization for wireless sensor networks. IET Softw. 2021, 1–8. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; He, G.; Wei, B.; Zhang, Y.; Yu, F.; Wu, H.; Zhan, Z.H. An expanded particle swarm optimization based on multi-exemplar and forgetting ability. Inf. Sci. 2020, 508, 105–120. [Google Scholar] [CrossRef]
- Ji, Y.I.; Liew, A.W. A Novel Improved Particle Swarm Optimization With Long-Short Term Memory Hybrid Model for Stock Indices Forecast. IEEE Access 2021, 9, 23660–23671. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Tan, C.; Si, L.; Zhang, L.; Liu, X. Adaptive wavelet threshold denoising method for machinery sound based on improved fruit fly optimization algorithm. Appl. Sci. 2016, 6, 199. [Google Scholar] [CrossRef] [Green Version]
- van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Lu, H.; Liu, Y.; Cheng, S.; Shi, Y. Adaptive online data-driven closed-loop parameter control strategy for swarm intelligence algorithm. Inf. Sci. 2020, 536, 25–52. [Google Scholar] [CrossRef]
- Qin, Q.; Cheng, S.; Zhang, Q.; Wei, Y.; Shi, Y. Multiple strategies based orthogonal design particle swarm optimizer for numerical optimization. Comput. Oper. Res. 2015, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.J.; Liu, S.J.; Hu, H.X. Best wavelet basis for wavelet transforms in acoustic emission signals of concrete damage process. Russ. J. Nondestruct. Test. 2016, 52, 125–133. [Google Scholar] [CrossRef]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chen, S.J.; Ge, L.; Hu, H.X.; Wang, Y.; Zhou, L. The optimal wavelet threshold de-nosing method for acoustic emission signals during the medium strain rate damage process of concrete. Nondestruct. Test. Eval. 2017, 32, 400–417. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Operating System | Windows 10 (64-bit) |
| Hard disk space | 2 TB (2000 GB) |
| Python version | 3.9 |
| GPU | Alienware NVIDIA GeForce GTX-1070 (8 cores, 2.80 GHz) |
| Parameter | Value |
|---|---|
| Hit definition time (HDT) | 2000 µs |
| Peak definition time (PDT) | 1000 µs |
| Hit lockout time (HLT) | 500 µs |
| Noise threshold | 23 dB |
| Sampling rate | 1 µs per sample |
| Parameter | Value |
|---|---|
| Peak sensitivity, ref (V/(m/s)) | 117 dB |
| Operating frequency range | 40–100 kHz |
| Resonant Frequency, ref (V/(m/s)) | 55 kHz |
| Wavelet Basis | Discrete Transform | Compact Support | Vanishing Moment | Regularity | Symmetry |
|---|---|---|---|---|---|
| Haar (haar) | yes | yes | 1st order | yes | yes |
| Daubecies (db) | yes | Yes | Nth order | yes | Similar |
| Biorthogonal (bior) | yes | Yes | Nth order | ✕ | ✕ |
| Coiflets (coif) | yes | Yes | 2Nth order | yes | Similar |
| Symlets (sym) | yes | Yes | Nth order | yes | Similar |
| Morlet (morlet) | ✕ | ✕ | ✕ | ✕ | yes |
| Meyer (mey) | yes | ✕ | ✕ | yes | yes |
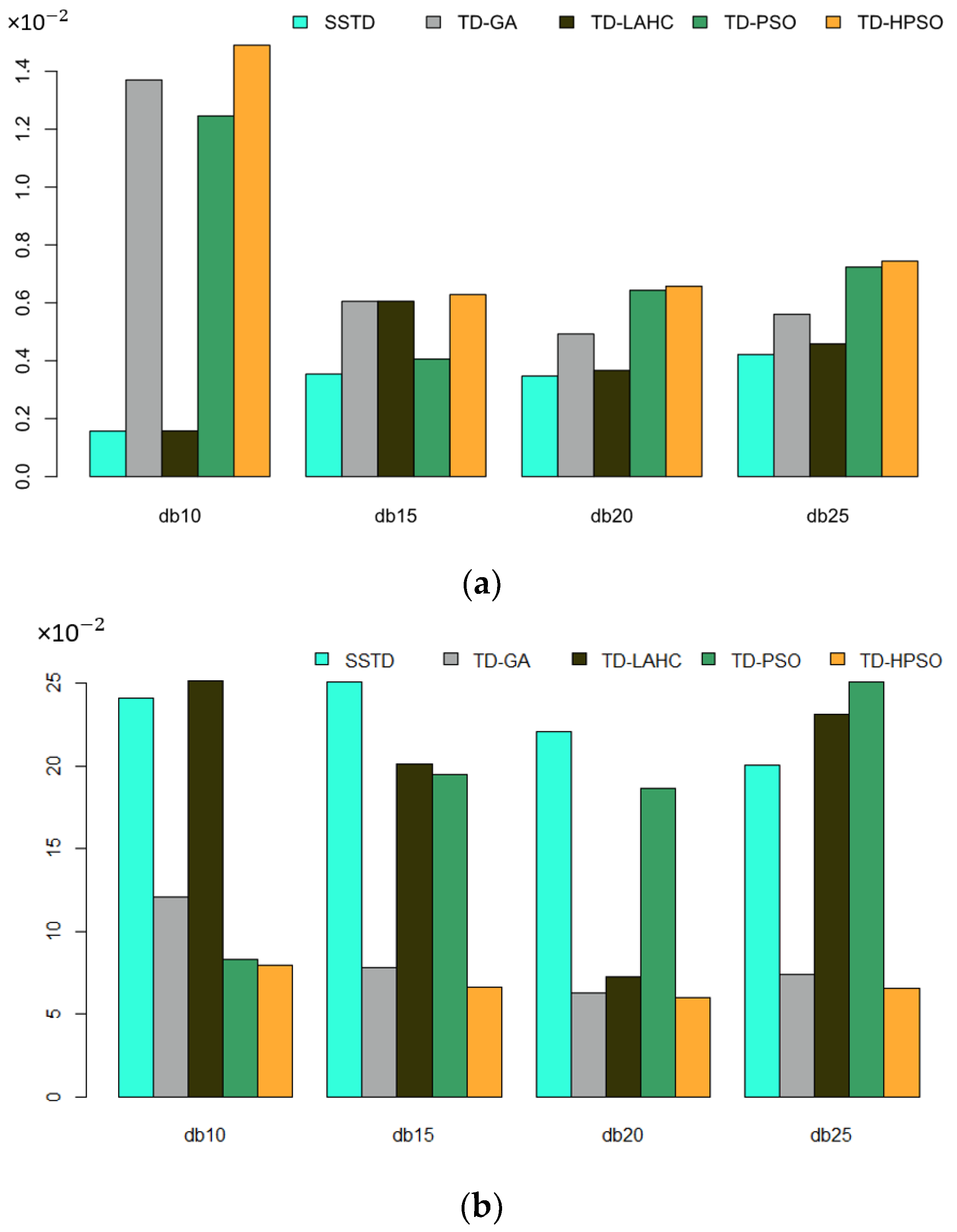
| Index | Added Noise (dB) | SSTD | TD-GA | TD-LAHC | TD-PSO | TD-HPSO |
|---|---|---|---|---|---|---|
| RMSE | 10 | 24.143 | 12.095 | 25.154 | 8.286 | 8.003 |
| 15 | 25.116 | 7.828 | 20.126 | 19.521 | 6.638 | |
| 20 | 22.103 | 6.259 | 7.276 | 18.682 | 6.012 | |
| 25 | 20.095 | 7.376 | 23.135 | 25.098 | 6.543 | |
| SNR | 10 | 0.1569 | 1.3699 | 0.1577 | 1.2458 | 1.4902 |
| 15 | 0.3540 | 0.6053 | 0.6057 | 0.4057 | 0.6285 | |
| 20 | 0.3471 | 0.4924 | 0.3665 | 0.6434 | 0.6572 | |
| 25 | 0.42145 | 0.5605 | 0.4583 | 0.7239 | 0.7441 |
| Index | SSTD | TD-GA | TD-LAHC | TD-PSO | TD-HPSO |
|---|---|---|---|---|---|
| RMSE | 0.16935 | 0.08504 | 0.06221 | 0.11530 | 0.04081 |
| SNR | 2.6071 | 3.1433 | 2.8901 | 3.0799 | 4.2147 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, F.; Rahim, L.A.; Mahmood, A.K.; Abed, S.A. A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals. Symmetry 2022, 14, 1253. https://doi.org/10.3390/sym14061253
Hassan F, Rahim LA, Mahmood AK, Abed SA. A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals. Symmetry. 2022; 14(6):1253. https://doi.org/10.3390/sym14061253
Chicago/Turabian StyleHassan, Farrukh, Lukman Ab. Rahim, Ahmad Kamil Mahmood, and Saad Adnan Abed. 2022. "A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals" Symmetry 14, no. 6: 1253. https://doi.org/10.3390/sym14061253
APA StyleHassan, F., Rahim, L. A., Mahmood, A. K., & Abed, S. A. (2022). A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals. Symmetry, 14(6), 1253. https://doi.org/10.3390/sym14061253






