On an Important Remark Concerning Some MHD Motions of Second-Grade Fluids through Porous Media and Its Applications
Abstract
:1. Introduction
2. Statement of the Problem
3. Applications
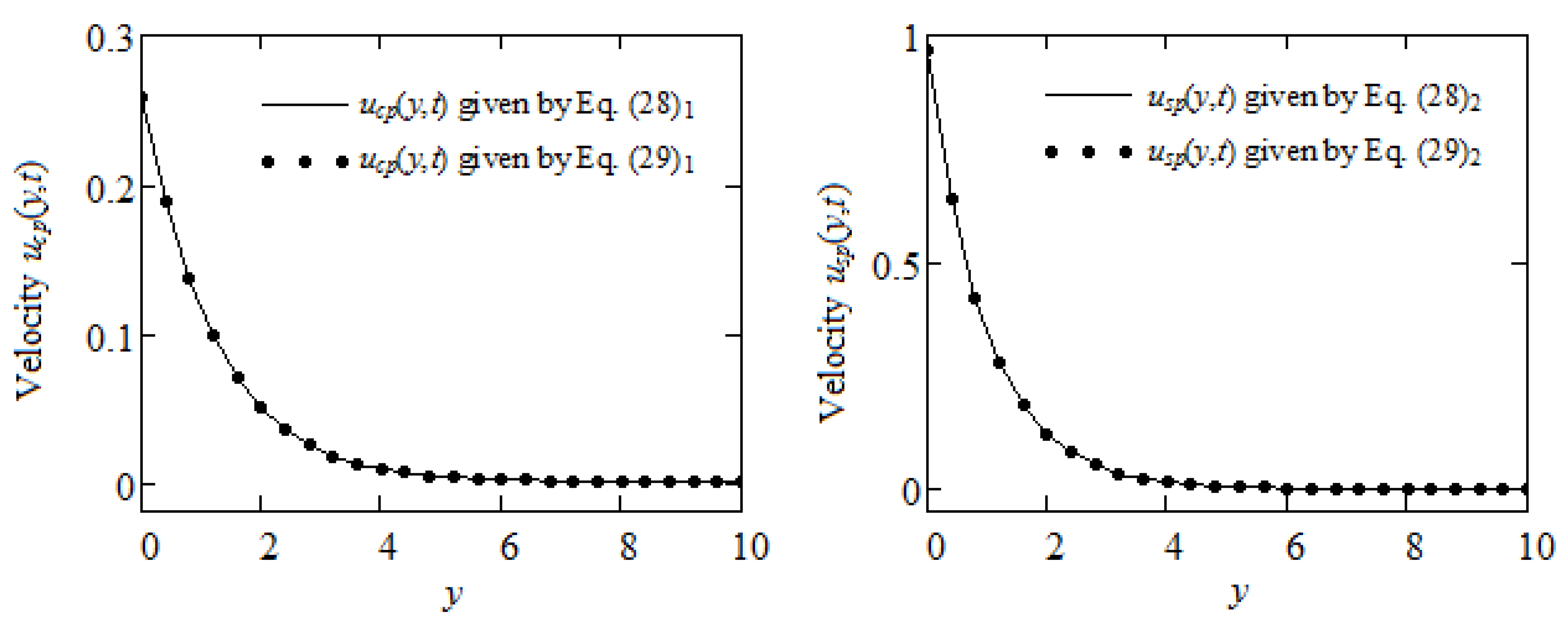
3.1. Motions over an Infinite Flat Plate
3.1.1. Stokes’ Second Problem (Motions with Velocity on the Boundary)
3.1.2. Motions with Shear Stress on the Boundary
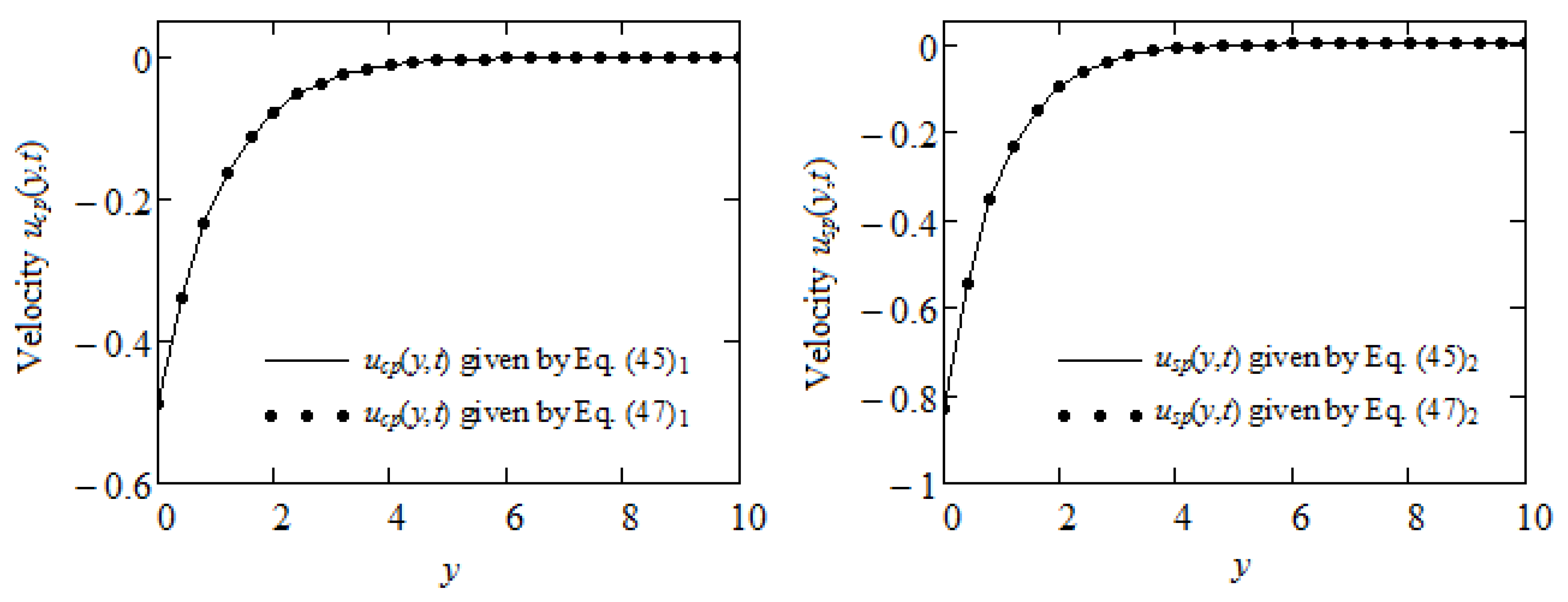
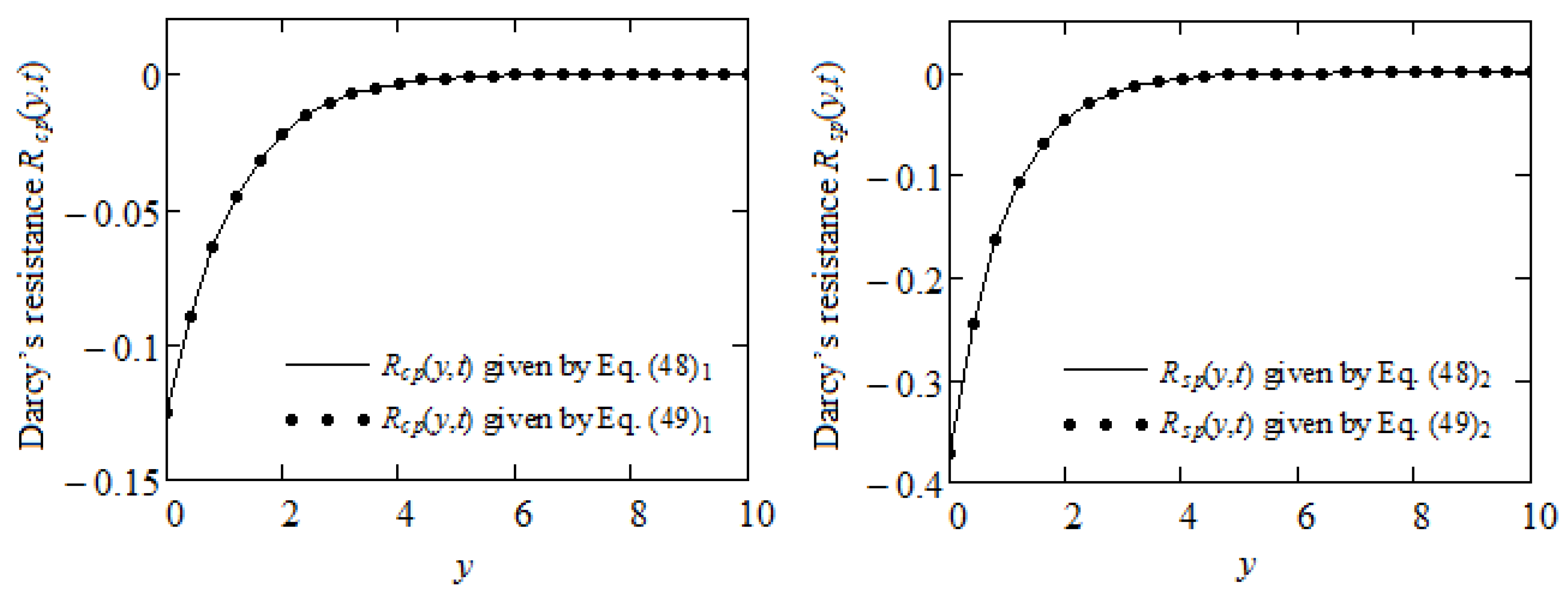
3.2. Motions between Infinite Parallel Plates
3.2.1. Motions with Velocity on the Boundary
3.2.2. Motions Due to Shear Stresses on the Boundary
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | |
| Cauchy stress tensor | |
| First two Rivlin–Ericksen tensors | |
| L | Velocity gradient |
| I | Identity tensor |
| p | Hydrostatic pressure |
| Velocity vector | |
| Darcy’s resistance | |
| Fluid velocity | |
| M | Magnetic parameter |
| K | Porous parameter |
| Permeability of porous medium | |
| B | Magnitude of the applied magnetic field |
| Effective permeability | |
| Greek Symbols | |
| Kinematic viscosity | |
| Dynamic viscosity | |
| Fluid density | |
| Porosity | |
| Electrical conductivity | |
| Frequency of oscillations | |
| Non-trivial shear stress | |
| Material constants | |
References
- Ting, T.W. Certain non-steady flows of second-order fluids. Arch. Rational Mech. Anal. 1963, 14, 1–26. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Hayat, T.; Asghar, S. Periodic flows of a non-Newtonian fluid between parallel plates. Int. J. Non-Linear Mech. 1999, 34, 895–899. [Google Scholar] [CrossRef]
- Hayat, T.; Asghar, S.; Siddiqui, A.M. Some unsteady unidirectional flows of a non-Newtonian fluid. Int. J. Eng. Sci. 2000, 38, 337–346. [Google Scholar] [CrossRef]
- Kiema, D.W.; Manyonge, W.A.; Bitok, J.K.; Adenyah, R.K.; Barasa, J.S. On the steady MHD Couette flow between two infinite parallel plates in a uniform transverse magnetic field. J. Appl. Math. Bioinf. 2015, 5, 87–99. [Google Scholar]
- Onyango, E.R.; Kinyanjui, M.N.; Uppal, S.M. Unsteady hydromagnetic Couette flow with magnetic field lines fixed relative to the moving upper plate. Am. J. Appl. Math. 2015, 3, 206–214. [Google Scholar] [CrossRef]
- Vafai, K. Handbook of Porous Media, 3rd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK; Publisher Boca Raton: Boca Raton, FL, USA, 2015. [Google Scholar]
- Fetecau, C.; Ellahi, R.; Sait, S.M. Mathematical analysis of Maxwell fluid flow through a porous plate channel induced by a constantly accelerating or oscillating wall. Mathematics 2021, 9, 90. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D. Symmetric and non-symmetric flows of Burgers’ fluids through porous media between parallel plates. Symmetry 2021, 13, 1109. [Google Scholar] [CrossRef]
- Dash, G.C.; Ojha, K.L. Viscoelastic hydromagnetic-flow between two porous parallel plates in the presence of a sinusoidal pressure gradient. Alex. Eng. J. 2018, 57, 3463–3471. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, I.; Ellahi, R.; Fetecau, C. Some MHD flows of a second grade fluid through the porous medium. J. Porous Media 2008, 11, 389–400. [Google Scholar] [CrossRef]
- Khan, M.; Malik, R.; Anjum, A. Exact solutions of MHD second Stokes flow of generalized Burgers fluid. Appl. Math. Mech. Engl. Ed. 2015, 36, 211–224. [Google Scholar] [CrossRef]
- Fetecau, C.; Ellahi, R.; Khan, M.; Shah, N.A. Combined porous and magnetic effects on some fundamental motions of Newtonian fluids over an infinite plate. J. Porous Media 2018, 21, 589–605. [Google Scholar] [CrossRef]
- Fetecau, C.; Narahari, M. General solutions for hydromagnetic flow of viscous fluids between horizontal parallel plates through porous medium. J. Eng. Mech. 2020, 146, 04020053. [Google Scholar] [CrossRef]
- Rajagopal, K.R. A note on unsteady unidirectional flows of a non-Newtonian fluid. Int. J. Non-Linear Mech. 1982, 17, 369–373. [Google Scholar] [CrossRef]
- Erdogan, M.E. A note on an unsteady flow of a viscous fluid due to an oscillating plane wall. Int. J. Non-Linear Mech. 2000, 35, 1–6. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Artemov, M.A. Steady flows of second-grade fluids in a channel. Vestn. S.-Peterb. Univ. Prikl. Mat. Inf. Protsessy Upr. 2017, 13, 342–353. (In Russian) [Google Scholar] [CrossRef]
- Erdogan, M.E. On the unsteady unidirectional flows generated by impulsive motion of a boundary or sudden application of a pressure gradient. Int. J. Non-Linear Mech. 2002, 37, 1091–1106. [Google Scholar] [CrossRef]
- Fetecau, C.; Akhter, S.; Corin, F. Note about magnetic and porous effects on the motion of viscous fluids. Bul. Inst. Polit. Iasi 2013, 59, 15–20. [Google Scholar]
- Baranovskii, E.S.; Burmasheva, N.V.; Prosviryakov, E.Y. Exact solutions to the Navier-Stokes equations with couple stresses. Symmetry 2021, 13, 1355. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fetecau, C.; Vieru, D. On an Important Remark Concerning Some MHD Motions of Second-Grade Fluids through Porous Media and Its Applications. Symmetry 2022, 14, 1921. https://doi.org/10.3390/sym14091921
Fetecau C, Vieru D. On an Important Remark Concerning Some MHD Motions of Second-Grade Fluids through Porous Media and Its Applications. Symmetry. 2022; 14(9):1921. https://doi.org/10.3390/sym14091921
Chicago/Turabian StyleFetecau, Constantin, and Dumitru Vieru. 2022. "On an Important Remark Concerning Some MHD Motions of Second-Grade Fluids through Porous Media and Its Applications" Symmetry 14, no. 9: 1921. https://doi.org/10.3390/sym14091921
APA StyleFetecau, C., & Vieru, D. (2022). On an Important Remark Concerning Some MHD Motions of Second-Grade Fluids through Porous Media and Its Applications. Symmetry, 14(9), 1921. https://doi.org/10.3390/sym14091921




