1. Introduction
The compressible multicomponent gas mixture dynamics is of great theoretical and applied interest, and there exist various complicated systems of partial differential equations to describe it under different assumptions; in particular, see [
1,
2,
3,
4,
5,
6]. An important point of both physical and mathematical theories of these equations is the fulfillment of the entropy balance equation with non-negative entropy production, which confirms their physical correctness and makes it possible to prove basic a priori estimates of solutions.
A large amount of numerical methods for solving single-component gas dynamics systems of equations were developed; in particular, see [
7,
8,
9]. Among them, there are various methods based on preliminary regularizations of these equations. These include methods based on the so-called quasi-gasdynamic (QGD) and quasi-hydrodynamic (QHD) regularizations presented in detail in monographs [
10,
11,
12] and many subsequent papers, as well as on other regularizations [
13,
14,
15], etc. The QGD and QHD equations for the general (multi-velocity and multi-temperature) as well as one-velocity and one-temperature gas mixture dynamics were developed, studied and applied, in particular, in [
11,
16,
17,
18,
19,
20,
21,
22], including the validity of the entropy balance equation with non-negative entropy production in [
16,
19,
22].
The construction of entropy correct discretizations of gas dynamics systems of equations is of great interest; in particular, see [
23,
24,
25,
26,
27] and references therein. In [
28], a symmetric three-point version of the 1D QGD-regularized gas dynamics equations for a perfect polytropic single-component gas was constructed, which was conservative in the mass, momentum, and total energy and satisfied the semi-discrete entropy balance equation with a non-negative entropy production. This was achieved, in particular, by introducing non-standard nonlinear averages of the sought functions. In this discretization, the main sought functions (the density, velocity, and specific internal energy of the gas) were defined on a common main mesh, whereas the mass, momentum, and total energy fluxes were defined on another auxiliary mesh. Subsequently, similar discretizations were developed in the case of general equations of state of a gas [
29] as well as the multidimensional case [
30]. Practical testing of these discretizations was accomplished in [
29,
31]. Recall that it is well-known that a regularization is necessary to ensure stability of symmetric spatial discretizations combined with an explicit discretization in time, and the QGD and QHD regularizations applied by us are not trivial and physically motivated [
10,
11,
12].
In this paper, we consider 1D regularized systems of equations for general, multi-velocity and multi-temperature, as well as one-velocity and one-temperature compressible multicomponent gas mixture dynamics of perfect polytropic gases in the absence of chemical reactions. The mixtures are supposed to be homogeneous; i.e., all the components occupy one and the same volume [
2]. In the latter case, where the velocities and temperatures (but not densities) of all components are assumed to be the same, diffusion fluxes between mixture components of type [
1] are taken into account. We develop the mentioned discretization from [
28] further for these systems. The latter system is of primary interest for us in this paper, but first, we need to consider the former system and its discretization as well, in accordance with our aggregation approach. The systems like our main one can be applied to solve numerically gas dynamics problems with contacts between different gases [
19,
20,
21], etc. Vast literature is devoted to problems of such kind, and we refer the reader to the recent paper [
32] for a brief review and a lot of references. Note that the study of the entropy properties of numerical methods for gas mixtures is a complicated matter, and only a few recent papers deal with this subject [
33].
For both the systems, we construct non-standard symmetric three-point spatial discretizations, which are not only conservative in the mass, momentum, and total energy but also satisfy the semi-discrete entropy balance equations with non-negative entropy productions. Importantly, in the one-velocity and one-temperature case, the basic discretization is not constructed directly but rather by aggregation of the discretization in the case of general mixture, and that is a new approach. Additionally, an adequate discretization is accomplished for the terms associated with the diffusion fluxes between the mixture components to guarantee the non-negative entropy production. Notice that both the QGD and QHD regularizations are considered in a unified way (by introducing a parameter into the equations like in [
22]) that essentially shortens the overall study.
The paper is structured as follows. In
Section 2, the 1D regularized system of equations for the dynamics of the general (multi-velocity and multi-temperature) multicomponent gas mixture is presented in the form of mass, momentum, and total energy balance equations for the mixture components. For it, the balance equations for the kinetic and internal energies of the components together with the mixture entropy balance equation with the non-negative entropy production are given. The balance equations for the mass, momentum, and total energy of the mixture are also written. In
Section 3, the 1D regularized system of equations for the dynamics of the one-velocity and one-temperature multicomponent gas mixture is given, additionally taking into account diffusion fluxes between the components. A connection between the solutions to the equations for dynamics of a single-component gas and such a mixture of gases is indicated. For the one-velocity and one-temperature mixture, the corresponding balance equations for the kinetic and internal energies of the mixture as well as the mixture entropy balance equation with a non-negative entropy production are given.
In
Section 4, first, meshes, mesh operators and a set of formulas for the mesh analysis are introduced. Then, a non-standard three-point spatially symmetric discretization of the regularized system of equations for the general multicomponent gas mixture dynamics is performed. Semi-discrete balance equations for the kinetic and internal energies of the components are given. Most importantly, the semi-discrete balance equation for the mixture entropy with a non-negative entropy production is derived in Theorem 1. Semi-discrete balance equations for the momentum and the total energy of the mixture are also presented. In
Section 5, based on the component mass balance equation and the last two mentioned equations, a discretization of the regularized system of equations for the dynamics of the one-velocity mixture of gases is constructed including the diffusion fluxes between the components of the mixture. A connection between the solutions to the semi-discrete equations for dynamics of a single-component gas and the homogeneous mixture of gases is described. Semi-discrete balance equations for the mass, kinetic and internal energies of the mixture are given. The main result (Theorem 2) concerns the derivation of a semi-discrete balance equation for the one-velocity and one-temperature mixture entropy with a non-negative entropy production. Below, we omit words “and one-temperature” for brevity. The final
Section 6 is devoted to numerical experiments in the case of the one-velocity binary mixture, more precisely, the contact between two different gases. Numerical examples concern three cases of subsonic and partially supersonic flows with shock waves, for initial data with pressure jumps up to 2500, well-known in the literature [
34,
35,
36], and both the QGD and QHD regularizations are tested.
Appendix A provides a proof of an important representation for the regularizing terms (together with heat source terms) in the semi-discrete entropy production, ensuring their non-negativity.
2. One-Dimensional (1D) Regularized System of Equations for Dynamics of General Multicomponent Gas Mixtures
A spatially 1D regularized system of equations describes the dynamics of a general multicomponent gas mixture and consists of the following balance equations for the mass, momentum, and total energy of the mixture components
where
(i.e.,
) and
is the amount of mixture components. The main sought functions
,
and
are the density, velocity and absolute temperature of the mixture component
,
, depending on
. Thus, it is assumed that each gas component has its own velocity and temperature. Here
and
are the partial derivatives in
and
; the cases
,
or
are similar. We use the perfect polytropic gas equations of state and the standard expression for the total energy of the components
where
and
are the pressure and specific internal energy of the component
, with the physical constants
,
and
,
. In addition,
, where
is the universal gas constant (the Boltzmann constant) and
is the molecular mass of gas
.
This regularization is the so-called quasi-gasdynamic (QGD) for
or simpler quasi-hydrodynamic (QHD) for
[
16]. Hereafter, by introducing the parameter
ℓ, we can treat both regularizations in a unified manner. The more universal former one is used for flows at any Mach numbers, while the latter is mainly used for subsonic and transonic flows. The regularizing velocities have the form
The viscous stress
and the heat flux
are given by the formulas
where
,
and
are the coefficients of viscosity and heat conductivity (physical or artificial) and the relaxation (regularization) parameter which may depend on the sought functions (here, their specific form is not essential). The terms
and
are of the Navier–Stokes–Fourier type, whereas the terms
and
are relaxation (regularizing) ones. The densities of body forces
and intensities of heat sources
are given functions.
In the case of the binary mixture (
), such equations were considered in [
16] (in the multidimensional version). The above equations for the multicomponent mixture generalize them in a natural way. Note that
The written equations form a set of standard regularized equations for the balance of mass, momentum, and total energy of individual components of the mixture, where
and
are the additional exchange terms. They depend on the sought functions
and satisfy the relations
Hereafter, denotes the summation operation over the index . The second relation is not used in this paper.
In the case of the binary mixtue (
), for any
,
, the exchange terms can be specified, in particular, by means of formulas of the molecular–kinetic type [
16]
where
is the frequency with which molecules of gas
collide (bump into) molecules of gas
,
. Here, it is assumed that the following balance equality holds
where
is the total number of collisions between the molecules of gases 1 and 2, and consequently, relations (
9) are valid; see their derivation in [
16]. Formulas for
and
can be found in [
11,
37] and are not reproduced here.
In the general case
, in particular, the formulas of type [
38] can be used
Here, is the summation operation over the index .
For
,
and
for any
, swapping the indexes
and
, one derives
Consequently, relations (
9) are valid once again provided that
,
and
for any
.
In the absence of the regularization, i.e., for
, the above regularized system of equations is reduced to the 1D compressible Navier–Stokes–Fourier-type system for multicomponent flows for
and
or the Euler-type one for
,
; in particular, see [
6,
38,
39,
40] and references therein.
Now, we present some important balance equations that follow from the basic ones.
Lemma 1. Let be the regularized mass flux of the mixture component α. The following balance equations for the kinetic and internal energies of the mixture components holdfor , where . Proof. To derive these standard type equations, we first multiply the momentum balance equation for the components (2) by
and use the formulas of the same type
Applying the mass balance equation for the components (
1), we obtain Equation (
10).
We subtract it from the balance equation for the total energy of the components (3). By differentiating with respect to
x the products
and
and using the first Formula (
5), we derive the balance equation for the internal energy of the components (11). □
Let us introduce the total density, the specific entropies of the components and the specific total entropy (the mixture entropy)
where
,
and
are constants (reference values of
,
and
). Here,
are the mass concentrations of the mixture components; they will arise below as well.
The entropy balance equation for the general gas mixture has the form
for
. For
, it was derived in [
16] (in the multidimensional case), and the proof was based on a similar equation in the single-component case (
) [
11,
12] (see also [
41]); the derivation in the case
is actually the same.
The sum of all terms on the right-hand side of Equation (
14), except for the divergent first one, is
the entropy production (or the dissipative function). Among these terms, the sum
is the Navier–Stokes–Fourier entropy production, and all its three summands (each in the angular brackets) are non-negative, taking into account the last property (
9).
The remaining terms with the factor
are relaxation ones. The penultimate term on the right in Equation (
14) contains the sum of three quadratic terms with positive coefficients under the sign
, so that term is non-negative. The last term on the right in Equation (
14) is non-negative for
, as well as for
and under the conditions
,
, and then, the total entropy production is also non-negative.
This entropy balance equation and the indicated property of the entropy production non-negativity remain valid for
, where one should switch to another form for the first relaxation term:
Recall that with the help of the specific entropy of the components, the expression for the heat flux (7) can be written in a shortened form
however, this form is not applied below.
Applying the operation
to the balance Equations (
1)–(3) for the mass, momentum, and total energy of the mixture components (i.e., summing them over the index
), we obtain their corollaries which are the balance equations for the mass, momentum and total energy of the mixture
Herein, the aggregated (or total, i.e., for the mixture) pressure, total energy, viscous stress and heat flux are expressed by the formulas
The first of these is Dalton’s law for mixtures. The exchange terms have been cancelled out due to the equalities
and
, see (
9). These equations are used in the next section.
Recall that, for the purposes of discretization, Equations (
1) are often replaced by Equation (
15) and equations for
concentrations
although in this paper, we will not use this approach.
3. One-Dimensional (1D) Regularized System of Equations for the Dynamics of One-Velocity Multicomponent Gas Mixtures in the Presence of Diffusion Fluxes
In this section, we consider the model of the one-velocity mixture, where the velocities and temperatures of all components are assumed to be the same, which drastically reduces the number of sought functions. Let also , . Additionally, diffusion fluxes between the mixture components are introduced.
As in [
19,
22], we write the aggregated regularized system of equations for the one-velocity mixture dynamics (in the diffusion approximation), which is obtained from Equations (
1), (16) and (17) after taking
and
for
, and it consists of the balance equations for the mass of the component and the momentum and total energy of the mixture
with the additional inclusion of the diffusion flux
between the component
and the rest of the components. Now, the main sought functions are the component densities
,
, and their common velocity
u and temperature
. Still,
; also
.
The pressure, specific internal and total energies of the components take a slightly simplified form
and the total density and corresponding quantities appearing in the equations for the one-velocity mixture are as follows
with the coefficients
We emphasize that here,
R and
are
functions rather than constants in contrast to the single-component case (provided that there are different coefficients among
and
). The expression for
p can be rewritten in the standard form
Note that if , then also even for non-coinciding .
In these equations, according to the performed aggregation procedure, we have
where
and
, and the appearance of the additional term
is related to the introduction of diffusion fluxes. We emphasize that a number of new functions (including
and
) here retain their notation from the previous section.
As in [
19,
22], the introduction of total regularizing velocities
makes it possible to simplify the form of the balance equations for the momentum and total energy of the one-velocity mixture (20) and (21):
where
. However, for the purpose of discretization, we prefer to use the original form of these equations below. Recall that
and
are the specific heat capacities at constant volume and pressure and
is the specific enthalpy of the component
. Moreover, in (26), we have
.
In the absence of the regularization, i.e., for
, the presented regularized system of equations for the one-velocity mixture dynamics is reduced to the 1D compressible Navier–Stokes–Fourier-type system for one-velocity and one-temperature multicomponent flows for
and
or the Euler-type one for
,
, in particular, see [
1,
4,
33] and references therein.
In these equations, we define the terms related to the diffusion fluxes between the components by the following formulas
where
and
are the Gibbs potential and specific entropy of the component
(for example, see [
42]).
The quantities
and
are not specified in this paper; they can depend on the sought functions, and it is only assumed that
, whereas
,
and
are constants (reference values of
,
and
). The property
plays an important role and immediately follows from definitions (
32) and the condition
=0.
Note that the formula is valid.
In the case of the binary mixture (
) with
,
, the above equations for the dynamics of the one-velocity mixture were obtained in [
19] (in the multidimensional case). The general multicomponent case (
) with the introduction of
and
has recently been considered in [
22] for
. The above quantities
and
generalize those proposed in [
1] in the case of the binary mixture; this particular case is discussed in more detail in [
22].
Now, we pass to several properties of the above system of equations for the one-velocity gas mixture dynamics.
Proposition 1. Let the functions , u and be a solution to the following regularized system of equations for a single-component gas dynamicsfor , where , and with constant and together withwith , and . Then, for any constant , , such that , the functions , , u and θ are a solution to the regularized system of equations for the one-velocity mixture dynamics (19)–(28) with , , and , , as well as , and with ρ and ε given by formulas (23). Proof. Under the hypotheses of the proposition, Formulas (
22)–(
24) are valid. Moreover, we have
and
in definition (
25), see definition (
38), so Formulas (39) and (40) coincide with the corresponding formulas for the mixture (26)–(28). This means that the momentum and total energy balance equations (36) and (37) coincide with the corresponding equations for the mixture (
30) and (31). Finally, multiplying the mass balance Equation (
35) by
yields the corresponding equation for the mixture components (
19). □
This proposition expresses the natural fact that the formal decomposition of a single-component gas into K components with proportional densities and the same temperatures, velocities and physical constants is a special (trivial) case of the one-velocity mixture. In particular, Proposition 1 is useful for checking various properties of solutions to the equations of the one-velocity mixture dynamics. Of course, its multidimensional version holds as well.
Applying the operation
to the mass balance equation for the mixture components (
19) and using the property
, we obtain the important balance equation for the total mass
where
is the regularized mass flux of the component
; moreover,
according to (
29).
The above balance Equations (
30), (
41) and (31) entail the balance equations for the kinetic and internal energies of the one-velocity mixture [
22]
The specific entropy of the one-velocity mixture is still given by the formula
. The entropy balance equation for the one-velocity mixture has the form [
22]
It is derived from the balance equations for the mass of the components (
19) and the internal energy of the mixture (43).
The sum of all terms on the right-hand side of Equation (
44), except for the divergent first one, is
the entropy production. Among these terms, the sum
is the Navier–Stokes–Fourier entropy production, and all its four terms are non-negative.
The remaining terms with the factor
are relaxation ones, and the three penultimate terms on the right in Equation (
44) contain quadratic terms with positive coefficients under the sign
and therefore are non-negative. The last term on the right in Equation (
44) is again non-negative for
, as well as for
and under the condition
,
, or the more general condition
and then the total entropy production is non-negative as well.
The indicated entropy balance equation and the property of entropy production non-negativity remain valid for
again, where one should pass to a different form for the first relaxation term:
In addition, this property remains valid in the absence of diffusion fluxes (for
): then, in Equation (
44), one should simply omit both terms with
.
4. A Spatial Discretization of the 1D Regularized System of Equations for the Dynamics of General Gas Mixtures
Define the uniform mesh on , with the nodes , , and the step . Let be its internal part. Define also an auxiliary (conjugate) mesh with the nodes , .
Let
be the space of functions defined on a mesh
. For functions
and
, we introduce the averages, shifts of the argument and difference quotients
Here, and . Clearly, : and : .
Below, we need several mesh counterparts of the product rule for differentiation and formulas with averages for
and
[
28]
Hereafter, in order to reduce the amount of parentheses, we write, for example,
(i.e., the multiplication sign · terminates the action of the previous operators on the left). All these formulas are, in fact, simple algebraic identities and can be straightforwardly verified (although some of them are nontrivial). Recall that Formula (47) follows from Formulas (46) and (48):
as well as from the equality
.
Following the single-component case [
28], for the system of equations of the general gas mixture dynamics (
1)–(7) in the absence of body forces (i.e., for
), we construct the following semi-discrete (space-discrete) balance equations for the mass, momentum and total energy of the components
on
, for
. Herein, the pressure, specific internal and total energies of the components have the standard form
The following discretizations are applied for the mass flux and regularizing velocities
along with the viscous stress and heat flux
The main sought functions
,
and
as well as the functions
,
and
are defined in space on the main mesh
, whereas the functions
,
,
,
,
,
,
,
and
are defined on the auxiliary mesh
. In addition, if, for example,
, then one can set
The above semi-discrete equations in the case
represent the set of semi-discrete equations from [
28] that are written for each of the mixture components and contain the additional exchange terms
and
.
Notice that the first Formula (
8) is most often used to discretize
for
[
10,
11,
12], but here, its mesh counterpart does not hold, since
due to Formula (
45), but
.
Along with the standard averages of the functions
and
, this method involves non-standard averages of
,
,
and
of the form [
28]
Here,
is the divided difference for the logarithmic function
The non-standard averages, like the simplest ones, are two-point and symmetric (and therefore, they have the approximation order for twice continuously differentiable functions of the continuous argument). Note that in is an average of the geometric mean type for .
Recall that in order to avoid loss of accuracy at
, instead of Formula (
57) itself, some approximations are used in computations. For this purpose, it is convenient to apply the integral representation of
and the corresponding numerical quadratures, in particular, the trapezoidal rule, the midpoint rule or Simpson’s rule
The first and second of these rules lead to the approximate equalities
and
which we apply in our numerical experiments in
Section 6 below.
Note that using non-standard averages requires some caution. For example, clearly and for any . However, but for .
If one uses only the standard averages, then, in the semi-discrete entropy balance equation, there arise sign-indefinite mesh imbalances in the entropy production [
28].
Let us first derive semi-discrete counterparts of Equations (
10) and (11).
Lemma 2. The semi-discrete balance equations for the kinetic and internal energies of the mixture components holdon , with . Proof. Following [
28], we multiply the semi-discrete momentum balance equation for the mixture components (51) by
and apply Formula (
12). Using the semi-discrete mass balance equation for the components (
50) and Formula (46) twice, we obtain the following equalities
Taking into account also the elementary formulas
we derive the semi-discrete balance equation for the kinetic energy (
58).
We subtract it from the semi-discrete balance equation for the total energy (52). By virtue of Formulas (47) and (46) applied twice, we have, respectively,
Consequently, the semi-discrete balance equation for the internal energy (59) holds as well. □
In this lemma, the choice of averages in and the additional term in the semi-discrete balance equation for the total energy (52) have already played their role, but the specific forms of averages , and have not yet been important and could be arbitrary. They will play their part in the next step of the method analysis.
The following result is a semi-discrete counterpart of the entropy balance equation for the general gas mixture (
14), and it serves as the main one in this section.
Theorem 1. For the semi-discrete method (50)–(56), the entropy balance equation for the mixture holdson (see definitions (13) of the entropies), where The last two terms on the right in Equation (66) compound the entropy production. The first three terms of are non-negative, and the last term is non-negative for , as well as for under the condition , . Moreover, due to the last relation (9). Proof. We use the reasoning from [
28]. According to the formulas
and
, we first have
Due to the semi-discrete mass balance equation for the component (
50) and the expression
see Formula (46), further we obtain
By virtue of the formula
see Formula (46) again, we obtain
By definition (
13) of
, the following equalities hold
The elementary formulas
are also valid. Using the first of them in the first term on the right in Equality (
69), we transform the expression under the sign
:
The latter equality is valid according to the definitions of the averages
and
, and it is this equality that explains their above choice (
55) and (56).
We transform the second term on the right in equality (
69) under the sign
. By virtue of the semi-discrete balance equation for the mixture internal energy (59) and the formulas
see Formula (46), and also by virtue of Formula (48) for the third term on the right in Equation (59), we derive
We apply the operation
to the last equality and use Formula (
72) (as a result, the first term on the right in equality (
69) under the sign
cancels out with
). We also apply the Formulas (
71) and
Then, equality (
69) can be rewritten as the semi-discrete entropy balance equation for the mixture
where
has been introduced above in the statement of the theorem and
The term
can be represented as the sum of three quadratic terms with positive coefficients and a term proportional to
:
according to [
28] (where the case
was considered, while the case
is radically simpler). For the sake of completeness and the reader convenience, the proof is included below in
Appendix A. Therefore, the formula holds
with
introduced above in the statement of the theorem, which completes the proof. □
Remark 1. Theorem 1 can also be derived from the semi-discrete entropy balance equation for the individual mixture componentswith , see [28] in the case . It is proved with the help of transformations quite similar to those performed above, using instead of s. Applying the operation to it, we obtain the semi-discrete entropy balance equation for the mixture (77). Note that the term
in Equation (
66) is a divergent difference imbalance. Of course, the appearance of the first two summands in
is associated with the use of non-standard averages
and
instead of
and
(the second of which, however, also does not coincide with the simplest
). Moreover,
on continuous functions
,
and
having bounded second derivatives
,
and
and for bounded
and
,
.
Similarly to the differential case, the derived semi-discrete entropy balance equation remains valid for
, where one should pass to a different form for the first relaxation term in
:
Applying the operation
to the semi-discrete balance equations for the momentum and total energy of the components (51)–(52), as their corollaries, we obtain the semi-discrete balance equations for the momentum and total energy of the general mixture
on
, compare with the corresponding differential Equations (16) and (17). They involve the total viscous stress, pressure, heat flux and intensity of heat sources
These equations are exploited in the next section.
5. A Spatial Discretization of the 1D Regularized System of Equations for the Dynamics of One-Velocity Gas Mixtures in the Presence of Diffusion Fluxes
In this section, we perform a spatial discretization of the system of equations for the one-velocity mixture dynamics (
19)–(28) and (
32)–(34). It will not be accomplished directly, but rather will be based on the aggregation of the above semi-discrete equations of the general mixture dynamics. Namely this non-standard approach will ultimately ensure the fulfillment of the correct semi-discrete entropy balance equation for the one-velocity mixture.
First, for simplicity, let the body force be absent (i.e.,
). Relying on the semi-discrete balance equations for the mass of the components (
50) and the momentum and total energy of the general mixture (
80)–(81) and setting there
and
for
, we construct the following semi-discrete balance equations for the mass of the components and the momentum and total energy of the one-velocity mixture
on
, where, additionally, there are discrete diffusion fluxes
between the component
and the remaining components of the mixture. The main sought functions
,
,
u and
together with the functions
,
and
are defined in space on the main mesh
. In the equations, the pressure, specific internal and total energies of the components have the familiar form
together with the total density and corresponding quantities for the one-velocity mixture
see also the functions
R and
in (
24).
There arise the following discretizations of the mass flux and regularizing velocities
as well as of the viscous stress and the heat flux
recall that here,
,
and
. Clearly, the following formulas hold
The new term in the heat flux appears due to taking into account the diffusion fluxes between the mixture components.
The functions
,
,
,
,
,
,
,
and
are defined in space on the auxiliary mesh
. Moreover, we have
We emphasize that, at first glance and quite standardly, the direct discretization of the simplified balance equations for the momentum and total energy (
30) and (31) seems to be the most natural. However, it leads to a different method, since even
, and, for such a method, the construction of an entropy balance equation with a non-negative entropy production is problematic.
In addition, we set
where the Gibbs potentials of the components
are given by Formulas (34) and are defined in space on
and still
, whereas the functions
and
are defined in space on
. Moreover, if
, then to preserve the property
on
, one should put, for example,
(but not, say,
) on
.
Now, we present the semi-discrete counterpart of Proposition 1.
Proposition 2. Let the functions , u and be a solution to the following semi-discrete method for the regularized system of equations for a single-component gas dynamics [28]on , where , and with constant and together withwith, for example, , and in space on . Then, for any constant , , such that , the functions , , u and are a solution to the semi-discrete method for the regularized system of equations for the one-velocity mixture dynamics (82)–(90) with , , and , , as well as , and in space on with ρ and ε given by Formulas (86). Proof. Under the hypotheses of the proposition, Formulas (
85) and (
86) are valid. We also have
and
in expressions (88), see definitions (96); furthermore, definitions (97) and (98) coincide with the corresponding formulas for the mixture (
89) and (90). Therefore, the semi-discrete balance equations for the momentum and total energy (93) and (94) coincide with the corresponding balance equations for the mixture (83) and (84). Moreover, the multiplication of the semi-discrete mass balance Equation (
92) by
leads to the corresponding Equation (
82). □
This proposition is useful for checking various properties of solutions to the constructed semi-discrete equations of the one-velocity mixture dynamics and also for testing the codes that implement them.
Let us derive semi-discrete counterparts of Equations (
41)–(43).
Lemma 3. The following semi-discrete balance equations for the total mass and kinetic and internal energies of the one-velocity mixture holdon . Proof. Applying operation
to the semi-discrete mass balance equation for the components (
82) leads to the semi-discrete total mass balance Equation (
99), due to the property
.
Deriving Equations (100) and (101) is similar to the proof of Lemma 2. We multiply the semi-discrete momentum balance Equation (83) by
u, and we use Formulas (
12) and (
60)–(
62), where we omit the index
of
and
, as well as the already derived Equation (
99). As a result, we derive the semi-discrete balance equation for the kinetic energy of the mixture (100).
We subtract it from the semi-discrete balance equation for the total energy (84) and obtain
We apply Formulas (
63) and (65), where we omit the index
of
and
, as well as Formula (64), and prove the semi-discrete balance equation for the internal energy of the mixture (101). □
The next result is a semi-discrete counterpart of the balance equation for the entropy of the one-velocity gas mixture (
44), and it serves as the main one in this section.
Theorem 2. Let . For the semi-discrete method (82)–(91), the balance equation for the entropy of the one-velocity mixture holdon , where The term in Equation (102) is the semi-discrete entropy production. The first three terms of are non-negative, and the last term is non-negative for , as well as for under the condition This condition is certainly true provided that , .
Proof. The derivation of Equation (
102) follows the same plan as in Theorem 1 with an additional transformation of the terms containing
and
.
Due to formulas
and
, we have
By virtue of the semi-discrete mass balance equation for the components (
82) and Formula (
67), we obtain
By virtue of Formulas (
68), where we omit the index
of
, together with
, see (34), we can write
With the help of Formulas (
70) and (
71), where we omit the index
of
, in the first term on the right in equality (
103), the expression under the sign
can be transformed similarly to equalities (
72) as
Let us transform the second term on the right in equality (
103). Due to the semi-discrete balance equation for the internal energy of the mixture (101), as well as Formulas (
73) and (74), where we omit the index
of
and
, together with Formula (48), we obtain
by analogy with equality (
75).
By virtue of Formula (
104), the first term on the right in equality (
103) cancels out the second term on the right in the last formula. Now, due to the definitions of
and
, see expressions (90) and (
89), and using Formulas (
76) and (
71), where we omit the index
of
and
, equality (
103) can be rewritten as the semi-discrete balance equation for the mixture entropy
where
with
Let us transform the terms with
in the balance Equation (
105) with the help of Formula (46):
For the term on the right under the sign of
, with the help of Formula (49), the definition
and the second Formula (
71) with
in the role of
, we have
For the term on the right in (
106) under the sign of
, with the help of formula (
45), the definition of
and formulas (
71) with
in the role of
, as well as the definition of
(see expression (
91)) and the property
, we also obtain
Now, the semi-discrete balance equation for the mixture entropy (
105) takes the form
By virtue of Formula (
79) with
and
for
, the term
can be represented as the following sum
that after applying the operation
allows us to complete the proof. □
As in the differential case, the indicated property of the entropy production non-negativity remains valid for
, where one should pass to a different form for the first relaxation term in
:
In addition, this property is also valid in the absence of diffusion fluxes (for
), when in the balance Equation (
102), one should simply omit all three terms with
, including such terms in
and
.
To complete the section, following [
28], we generalize the constructed semi-discrete method and the obtained results to the case of any
f. Let us generalize the right-hand sides of the semi-discrete momentum and total energy balance Equations (83) and (84):
where the functions
and
f are defined in space on
. We also generalize expression (88) for
as follows
On the right-hand side of the semi-discrete balance equation for the internal energy of the mixture (101), the above expressions with
f generate the following additional term
When deriving the semi-discrete balance equation for the mixture entropy (
102), one should multiply this term by
and apply the formulas
see Formula (48). Further application of Formula (49) makes it possible to cancel out the last term of
, see expression (
109), and the second term on the right in the last formula (this is why the non-standard last term on the right in Equation (
107) was added). This leads to the equalities
with
where two formulas
have additionally been used. As a result, the additional term
appears in
, and the summand
should be added to
. With such
f-dependent extensions (including the generalized Formula (
108) for
), Theorem 2 remains valid.
Notice that
(the same applies to the last term in Equation (
107)) on continuous functions
,
u and
having bounded derivatives
,
and
, and for bounded
and
f.
6. Numerical Experiments
We consider the binary one-velocity mixtures and three test examples well known in the literature, using the following piecewise constant initial data
, with a discontinuity between two gases:
moreover, we have
(although, instead of that, in computations, we set them very small, namely equal
). Their parameters to the left and right of the discontinuity at
and the final time of computations
are given in
Table 1. Note that, in Examples 1–3, the initial pressure drop increases and, respectively, equals
, which amplifies computational complexity. The initial temperature
is calculated according to the above given formulas
, with the simplest choice of
.
We also set in all the examples, and the boundary values of the sought functions at in time are set constant and the same as their values given at .
We define a non-uniform mesh in time
, with the steps
. We take the relaxation parameter and the artificial viscosity and heat conductivity coefficients in the form
standard for the single-component case [
11,
12]. Here,
is a parameter; recall also that
is the step of the spatial mesh,
is the speed of sound in the mixture and, for example,
. In addition,
and
are the inverse Prandtl numbers (which can be considered as adjusting parameters as well); we take them equal 1 except for the last computation.
We apply the discretization in space constructed in the previous
Section 5 combined with the simplest explicit Euler method for the discretization in time. We use the automatic non-uniform mesh in time, with the steps
such that
where
is a parameter (the Courant-type number). Note that if there appear values of
or
less than
at the upper time level, we replace them by
. We adjust the parameters
a and
in each example. Proposition 2 (more precisely, its natural fully discrete counterpart) was used to test the code initially.
Example 1 (moderate two-gas shock-tube problem) from ([
34], Test 5.3), see also ([
35], Test 3.3). The final solution at
has jumps in the values of
,
,
and
but not
p and
u at the contact discontinuity between the two gases, as well as a rarefaction wave in gas 1 to the left and a shock wave (the strong discontinuity, with jumps in the values of
p and
u as well) in gas 2 to the right of the contact discontinuity. The functions
,
and
p are non-increasing, whereas
,
u and
are non-monotone, with the maximal values of
and
u in front of the shock; also,
is piecewise constant. The final maximal Mach number is
, so the flow is subsonic.
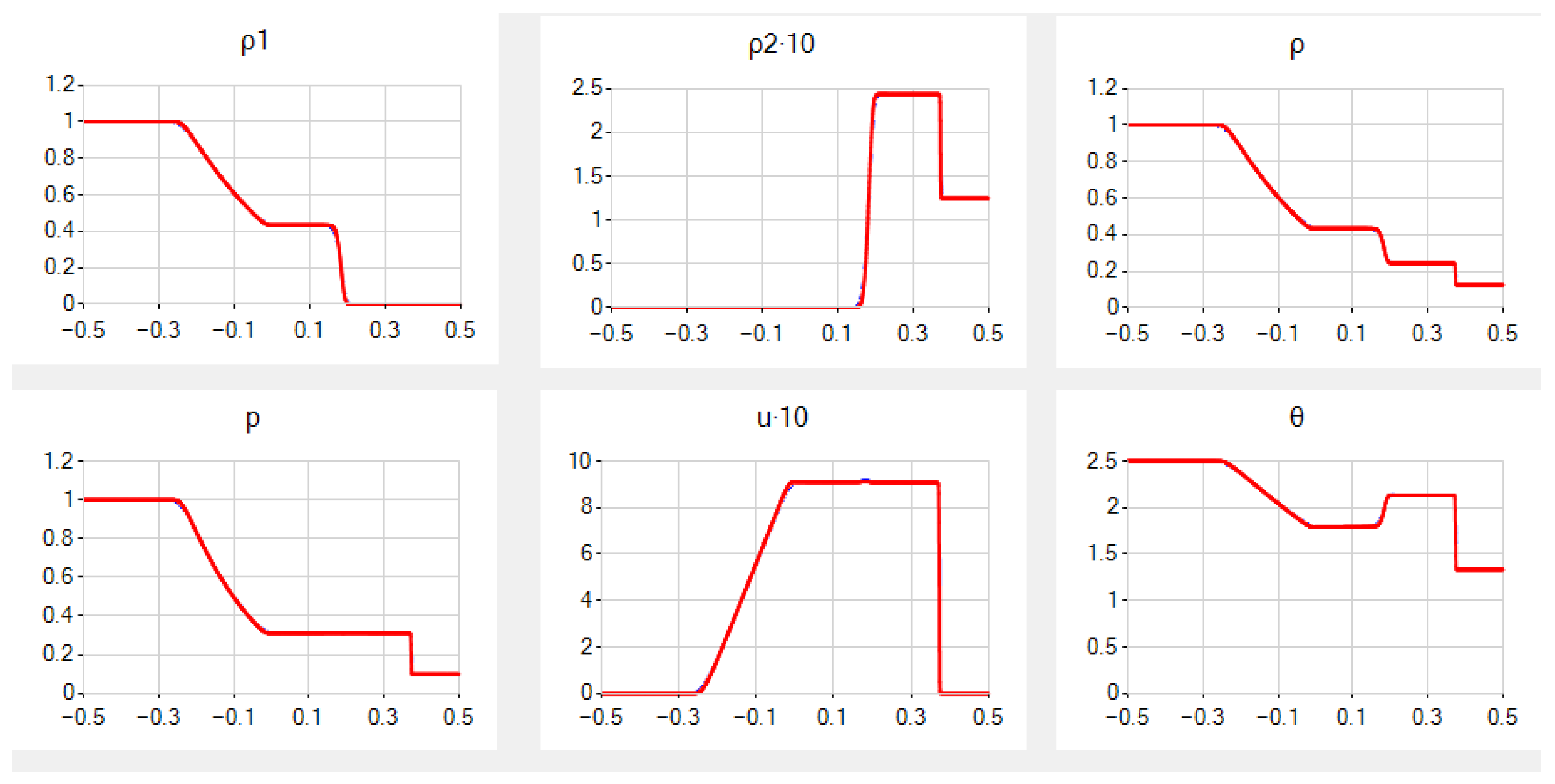
In the QGD case, i.e., for
, the results for
,
and
are shown in
Figure 1 containing the graphs of
,
,
,
p,
u and
. For much smaller
, they are similar; however, as usual, the graph slopes near the points of strong and especially contact discontinuities are smaller, whereas the slopes for
are already much closer to those for
. The results correspond well to those given in [
34,
35].
Moreover, in the simpler QHD case, i.e., for , the results for and the same and N are very close, only with a very small ledge in the graph of u at the contact discontinuity and the graph of just to the right of it, see the same figure. Hereafter, more minor differences become visible after magnifying our figures several times.
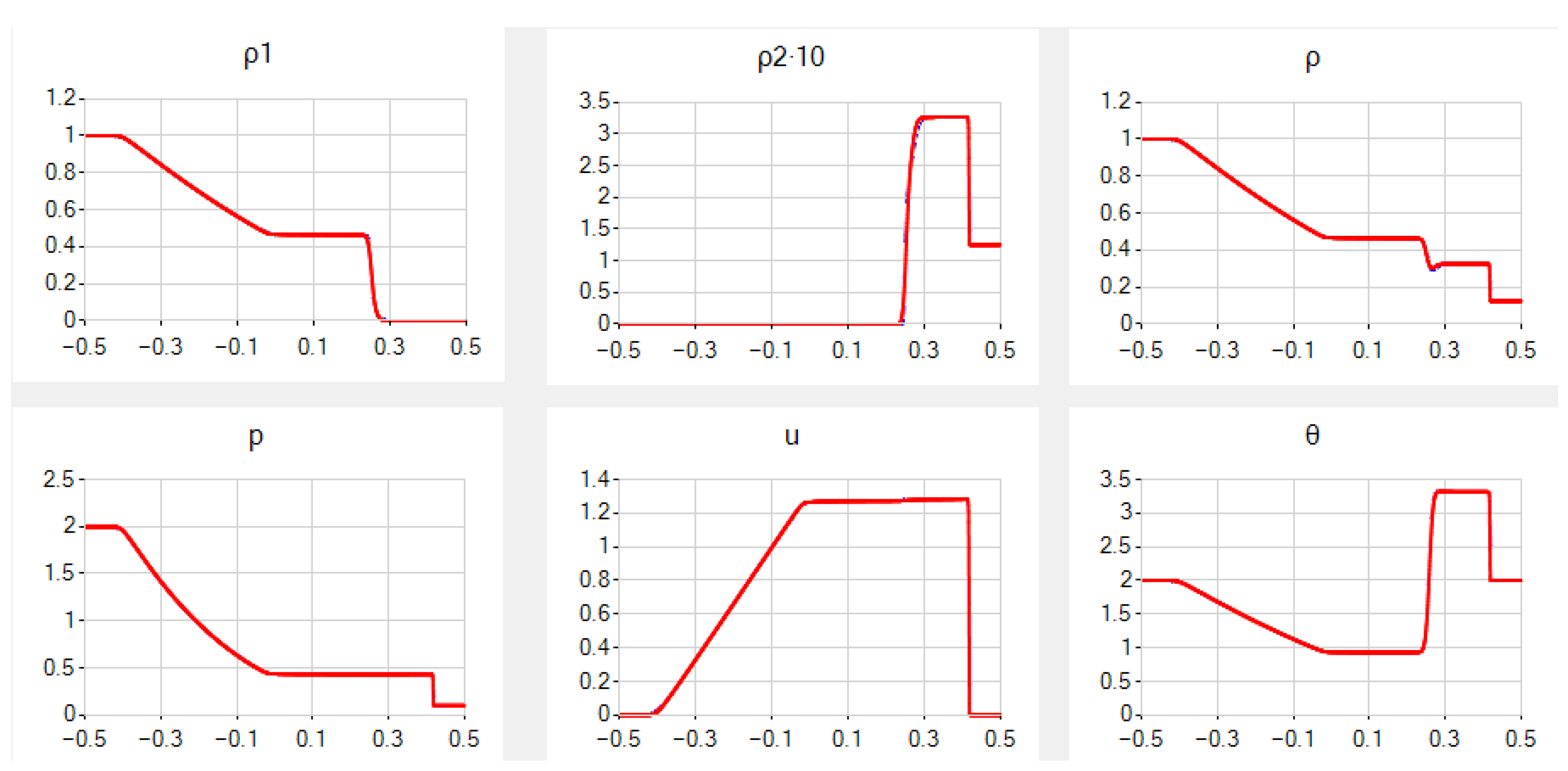
Example 2 (a modified two-gas Sod problem) from ([
36], Test 3.2). In this example,
in contrast to Example 1, and also the difference
is larger. The final solution is in general similar to Example 1, but the maximal value of
is now in front of the shock, not at the left boundary. The final maximal Mach number is
, so the flow is subsonic once again.
In the QGD case, the results for
,
and
are presented in
Figure 2 (for
, they are similar, but the graph slopes near the points of contact and strong discontinuities are smaller once again). They correspond well to those from [
36] except for a very small hollow at the point of contact discontinuity.
In the QHD case, the results for , and are very close once again; a unique visible difference is slightly worse behavior of the graph of just to the right of the contact discontinuity in the same figure.
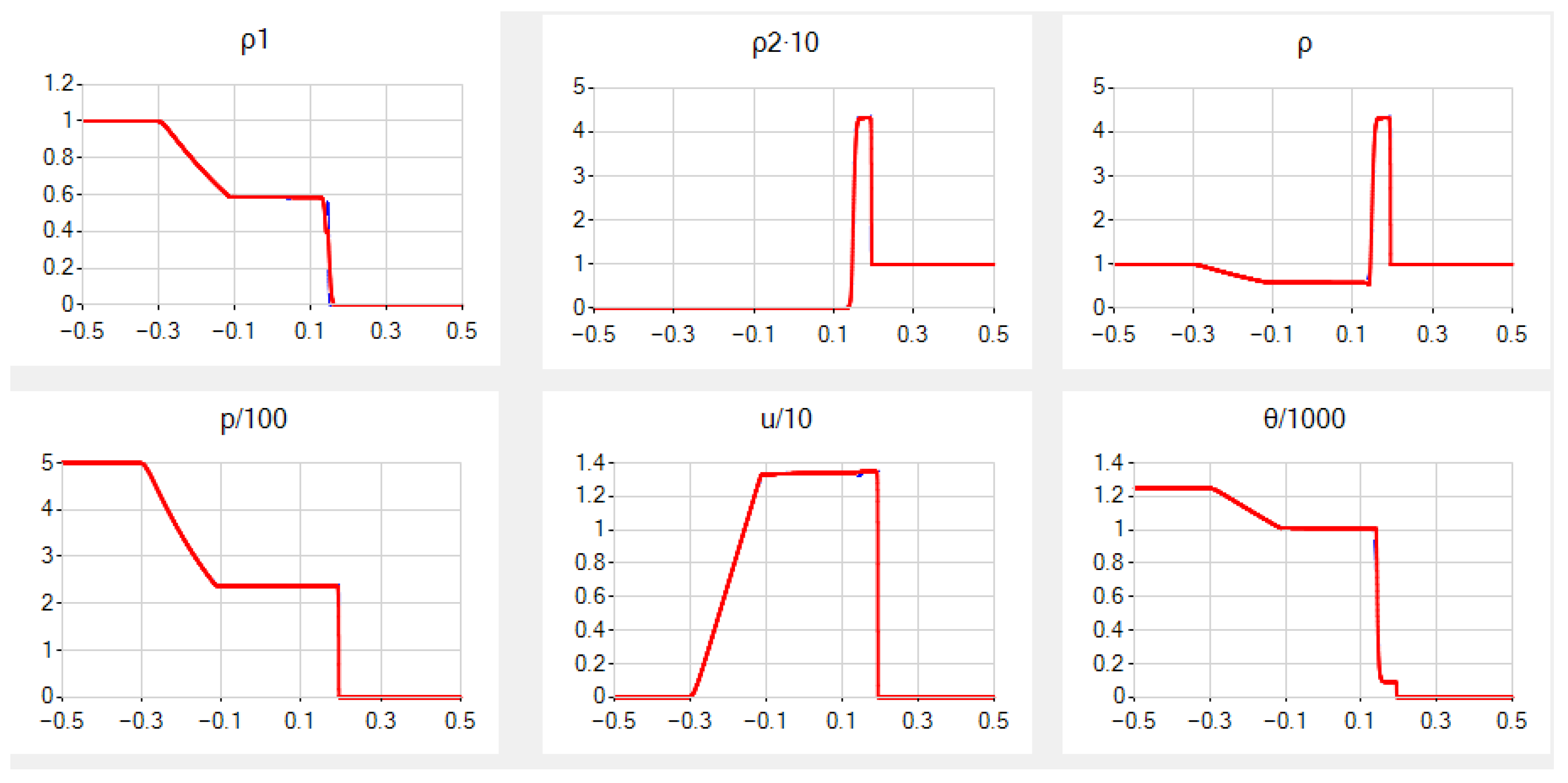
Example 3 (stiff two-gas shock-tube problem) from ([
34], Test 5.4). In the original paper, the initial left and right pressures were confused, and
was not specified, so we adjusted it according to the given graphs; note that it is much less than in the previous examples. Recall that, in this example, the initial pressure drop equals 2500 and is much larger than previously. Concerning the final values, now, the support of the maximal value of
is more narrow, the maximal value of
is in front of the shock and
becomes non-increasing, with large jumps in their values. In addition,
, so the flow is partially supersonic now (recall that
and thus
near the boundaries).
In the QGD case, the results for
,
and
are given in
Figure 3, and they are in accordance with those in [
34]. For smaller
, the quality of graphs of
and
near the contact discontinuity becomes worse.
In contrast, in the QHD case, now, the graphs of
,
u and
p are satisfactory even for
, but the quality of the graphs of
and especially of
and
is much worse near the contact discontinuity (even for larger
), and we omit them. However, the situation can be radically improved by taking larger
and applying another known formula for
:
that is also often used for transonic or supersonic flows. The results become very close and are very slightly worse only for
and
u near the contact discontinuity; see the same figure.