1. Introduction
In a solid the interactions between its constituent atoms or molecules gives rise to elementary excitations from its ground state (GS) when the temperature increases from zero. One has examples of elementary excitations due to atom-atom interactions, known as phonons, or due to spin-spin interactions, known as magnons. Note that magnons are spin waves (SW) when they are quantized. Elementary excitations are defined also for interactions between charge densities in plasma, or for electric dipole-dipole interactions in ferroelectrics, among others. Elementary excitations are thus collective motions which dominate the low-temperature behaviors of solids in general.
For a given system, there are several ways to calculate the energy of elementary excitations from classical treatments to quantum ones. Since those collective motions are waves, their energy depends on the wave vector . The -dependent energy is often called the SW spectrum for spin systems. Note that though the calculation of the SW spectrum is often for periodic crystalline structures, it can also be performed for symmetry-reduced systems such as in thin films or in semi-infinite solids in which the translation symmetry is broken by the presence of a surface.
In this review we focus on the SW excitations in magnetically ordered systems. The history began with ferromagnets and antiferromagnets with collinear spin GSs, parallel or antiparallel configurations in the early 1950s. Most of the works on the SW used either the classical method or the quantum Holstein–Primakoff transformation. The Green’s function (GF) technique has also been introduced in a pioneering paper of Zubarev [
1]. The first application of this method to thin films has been done [
2]. Note that unlike the SW theory, the GF can treat the SW up to higher temperatures. We will come back to this point later.
Let us recall some important breakthroughs in the study of non-collinear spin configurations. The first discovery of the helical spin configuration has been published in 1959 [
3,
4]. Some attempts to treat this non-collinear case have been done in the 1970 and 1980. Let us cite two noticeable works on this subject in Refs. [
5,
6]. In these works, a local system of spin coordinates have been introduced in the way that each spin lies on its quantization axis. One can therefore use the commutation relations between spin deviation operators. These works took into account magnon-magnon interactions by expanding the Hamiltonian up to three-operator terms at temperature
T = 0 [
5] or up to four-operator terms at low
T [
6]. Nevertheless, since these works used the Holstein–Primakoff method, the case of higher
T cannot be dealt with. In Ref. [
7], the GF method has been employed for the first time to calculate the SW spectrum in a frustrated system where the GS spin configuration is non-collinear. Using the SW spectrum, the local order parameters and the specific heat were calculated. Since this work, we have applied the GF method to a variety of systems where the GS is non-collinear. In this review, we will recall results of some of these published works.
Let us comment on the frustration which is the origin of the non-collinear GS. The frustration is caused by either the competing interactions in the system or a geometry frustration as in the triangular lattice with only the antiferromagnetic interaction between the nearest neighbors (NN) (see Ref. [
8]). The frustration causes high GS degeneracy, and for the vector spins (XY and Heisenberg cases) the spin configurations are non-collinear, making the calculation of the SW spectrum harder. A number of examples will be shown in this review paper.
In addition to competing interactions, the Dzyaloshinskii–Moriya (DM) interaction [
9,
10] is also the origin of non-collinear spin configurations in spin systems. While the Heisenberg model between two spins is written as
giving rise to two collinear spins in the GS, the DM interaction is written as
giving rise to two perpendicular spins. The DM model was historically proposed to explain the phenomenon of weak ferromagnetism observed in Mn compounds [
11]. However, the DM interaction is at present known in various materials, in particular at the interface of a multilayer [
12,
13,
14,
15,
16]. Although in this review we do not show the effect of the DM interaction in a magnetic field which gives rise to topological spin swirls known as skyrmions, we should mention a few of the important works given in Refs. [
17,
18,
19,
20,
21]. Skyrmions are among the most studied subjects at the time being due to their potential applications in spin electronics [
22]. We refer the reader to the rich biography given in our recent papers in Refs. [
23,
24].
Since this paper is a review on the method and the results of published works on SW in non-collinear GS spin configurations, it is important to recall the method and show main results of some typical cases. We would like to emphasize that, on the GF technique, to our knowledge there are no authors other than us working with this method. Therefore, the works mentioned in the references of this paper are our works published over the last 25 years. The aim of this review is two-fold. First we show technical details of the GF method by selecting a number of subjects which are of current interest in research: helimagnets, systems including a DM interaction, and surface effects in thin films. Second, we show that these systems possess many striking features due to the frustration.
This paper is organized as follows. In
Section 2, we express the Hamiltonian in a general non-collinear GS and define the local system of spin coordinates. Here, we also present the calculation of the GS and the foundation of the self-consistent GF technique and the calculation of the SW dispersion relation and layer magnetizations at arbitrary temperature (
T). We show in
Section 3 the numerical results obtained from the GF.
Section 4 shows interesting examples using various kinds of interaction including the DM interaction in a variety of systems from two dimensions, to thin films and superlattices.
Section 5 treats a case where the DM interaction competes with the antiferromagnetic interaction in the frustrated antiferromagnetic triangular lattice.
Section 6 presents the surface effect in a thin film where its surface is frustrated. Concluding remarks are given in
Section 7.
2. Hamiltonian of a Chiral Magnet—Local Coordinates
Chiral order in helimagnets has been subject of recent extensive investigations. In Ref. [
25], the surface structure of thin helimagnetic films has been studied. In Ref. [
26] exotic spin configurations in ultrathin helimagnetic holmium films have been investigated. In Refs. [
27,
28] chiral structure and spin reorientations in MnSi thin films have been theoretically studied. In these works, the chiral structures have been considered at
, but not the SW even at
. The main difficulty was due to the non-collinear, non-uniform spin configurations. We have shown that this was possible using the GFs generalized for such spin configurations given in Ref. [
7].
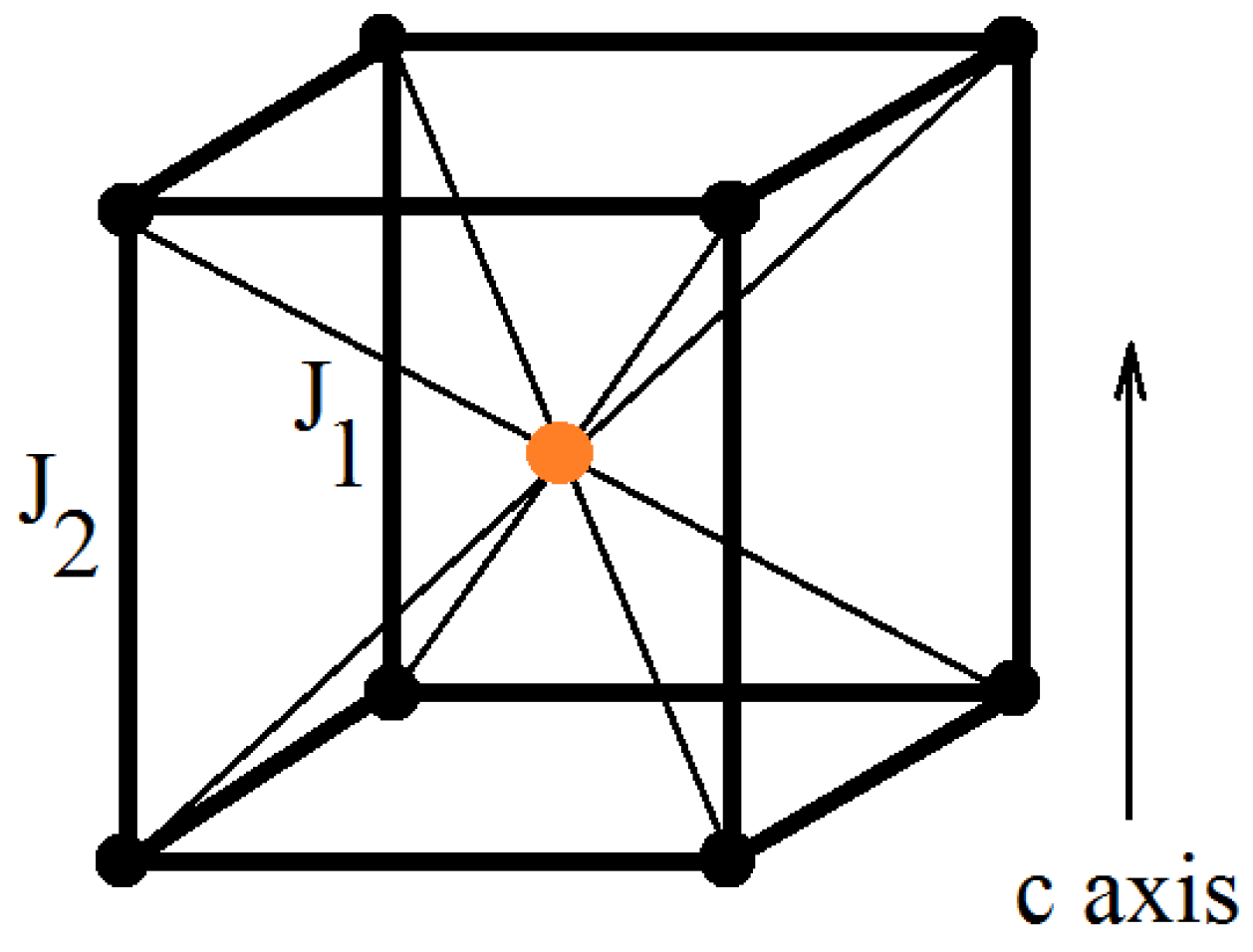
To demonstrate the method, let us follow Ref. [
29]: we consider the body-centered tetragonal (bct) lattice with Heisenberg spins. Each spin interacts with its nearest neighbors (NN) via the exchange constant
and with its next NN (NNN) on the
c-direction via the exchange
(see
Figure 1).
We consider the simplest model of a helimagnet, given by the following Hamiltonian
where
is a quantum spin of magnitude 1/2, the first sum is performed over all NN pairs, and the second sum over pairs on the
c-axis (cf.
Figure 1).
In the case of an infinite crystal, the chiral state occurs when is ferromagnetic and is antiferromagnetic and is larger than a critical value, as will be shown below.
Let us suppose that the energy of a spin
in a chiral configuration when the angle between two NN spin in the neighboring planes is
, one has (omitting the factor
)
The lowest-energy state corresponds to
There are two solutions, and The first solution corresponds to the ferromagnetic state, and the second solution exists if which corresponds to the chiral state.
For a thin helimagnetic film, the angle between spins in adjacent layers varies due to the surface. We can use the method of energy minimization for each layer, then we have a set of coupled equations to solve (see Ref. [
29]).
Figure 2 displays an example of the angle distribution across the film thickness
.
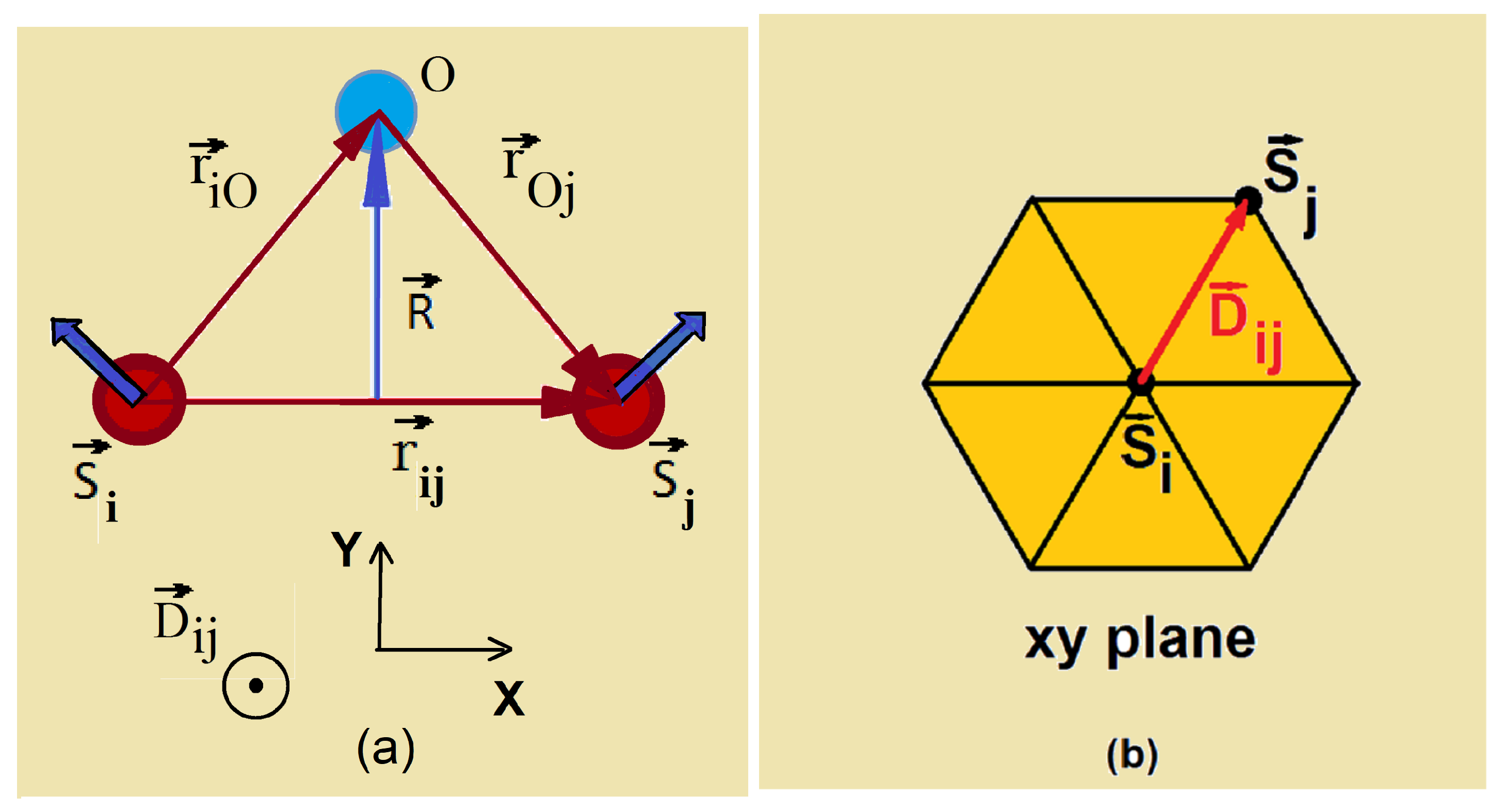
In order to calculate the SW spectrum for systems of non-collinear spin configurations, let us emphasize that the commutation relations between spin operators are established when the spin lies on its quantization
z. In the non-collinear cases, each spin has its own quantization axis. It is therefore important to choose a quantization axis for each spin. We have to use the system of local coordinates defined as follows. In the Hamiltonian, the spins are coupled two by two. Consider a pair
and
. As seen above, in the general case these spins make an angle
determined by the competing interactions in the systems. For quantum spins, in the course of calculation we need to use the commutation relations between the spin operators
. As said above, these commutation relations are derived from the assumption that the spin lies on its quantization axis
z. We show in
Figure 3 the local coordinates assigned to spin
and
. We write
Expressing the axes of
in the frame of
one has
so that
Using Equation (
9) to express
in the
coordinates, we calculate
, we get the following Hamiltonian from (28):
This explicit Hamiltonian in terms of the angle between two NN spins is common for a non-collinear spin configuration due to exchange interactions
. For other types of interactions such as the DM interaction, the explicit Hamiltonian in terms of the angle will be different as shown in
Section 4.
We define the following GFs for the above Hamiltonian:
Writing their equations of motion we have
where
Note that the equation of motion of the G Green’s function generates the F Green’s functions, and vice-versa. Performing the commutators in Equations (
13) and (
14), and using the Tyablikov approximation [
30] for higher-order GFs, for instance
etc., we obtain
Note that the Tyablikov decoupling scheme is equivalent to the so-called “random-phase-approximation” (RPA).
For the sake of clarity, we write separately the NN and NNN sums, we have
For simplicity, we suppose in the following are all equal to for NN interactions and to for NNN interactions. is taken to be for NN pairs. In addition, in the film coordinates defined above, we denote the Cartesian components of the spin position by three indices in three directions x, y and z.
Since there is the translation invariance in the
plane, the in-plane Fourier transforms of the above equations in the
plane are
where
is the SW frequency,
the wave-vector parallel to
planes and
the position of
.
,
and
denote the
z-components of the sites
,
and
. The integral over
is performed in the first Brillouin zone (
) whose surface is
in the
reciprocal plane.
denotes the surface layer,
the second layer etc.
In the 3D case, the Fourier transformation of Equations (
17) and (
18) in the three
directions yields the SW spectrum in the absence of anisotropy:
where
where
is the NN coordination number,
the NNN number on the
c-axis and
where
a is the lattice constant taken the same in three directions. Note that
is zero when
. This is realized at two points as expected in helimagnets:
(
) and
along the helical axis. It is interesting to note that we recover the SW dispersion relation of ferromagnets (antiferromagnets) [
2] with NN interaction only by putting
in the above coefficients.
In the case of a thin film, the in-plane Fourier transformation yields the following matrix equation
where
and
are given by
We take
hereafter. Note that
is a
matrix given by Equation (
24) where
where we recall that
n denotes the layer number, namely
and
. Note that
denotes the angle between a spin in the layer
n and its NN spins in adjacent layers
etc., and
In order to obtain the SW frequency
, we solve the secular equation
for each given (
. Since the linear dimension of the square matrix is 2
, we obtain 2
eigen-values of
, half positive and half negative, corresponding to two opposite spin precessions as in antiferromagnets. These values depend on the input values
(
). Thus, we have to solve the secular equation by iteration until the convergence of input and output values. Note that, even at
,
are not equal to
due to the zero-point spin contraction [
31]. In addition, because of the film surfaces, the spin contractions are not uniform.
The solution for
can be calculated (see Ref. [
29]). The spectral theorem [
1] can be used to obtain, after a somewhat lengthy algebra (see [
29]),:
where
, and
As
depend each other in
, their solutions should be obtained by iteration at a given temperature
T. In the particular case where
one has
Note that the sum is performed over negative since positive yields the zero Bose–Einstein factor at ).
The transition temperature can be calculated self-consistently when all tend to zero.
We show in the following section, the numerical results using the above formulas.
4. Dzyaloshinskii–Moriya Interaction in Thin Films
Let us consider a thin film made of
N square lattices stacked in the
y direction perpendicular to the film surface. The results for this system have been published in Ref. [
38]. Hereafter, we review some of these important results. The Hamiltonian is given by
where
and
are the exchange and DM interactions, respectively, between two quantum Heisenberg spins
and
of magnitude
.
We suppose in this section the in-plane and inter-plane exchange interactions between NN are both ferromagnetic and denoted by
and
, respectively. The DM interaction is defined only between NN in the plane for simplicity. The
J term favors the collinear spin configuration while the DM term favors the perpendicular one. This will lead to a compromise where
makes an angle
with its neighbor
. It is obvious that the quantization axes of
and
are different. Therefore, the transformation using the local coordinates, Equations (
4)–(
9), is necessary. Let us suppose that the vector
is along the
y axis, namely the
axis. We write
where
= +1 (−1) if
(
for NN
j on the
or
axis. One has by definition
.
The easiest way to determine the GS is to minimize the local energy at each spin: taking a spin and calculating the local field acting on it from its neighbors. Then, we align the spin in its local-field direction to minimize its energy. Repeating this procedure for all spins, we say we realize one sweep. We have to make a sufficient number of sweeps to obtain the convergence with a desired precision (see details in Ref. [
39]). This local energy minimization is called “the steepest descent method”. We show in
Figure 8 the configuration obtained for
using
.
We see that each spin has the same angle with its four NN in the plane (angle between NN in adjacent planes is zero). We demonstrate now the dependence of
on
: the energy of the spin
is written as
where
minimizing
with respect to
one obtains
The result is in agreement with that obtained by the steepest descent method. An example has been shown in
Figure 8.
We rewrite the DM term of Equation (30) as
From Equation (
31), we obtain
where we have replaced
by
. Note that
is always positive since for a NN on the positive axis direction,
and
where
is positively defined, while for a NN on the negative axis direction,
and
.
4.1. Formulation of the Green’s Function Technique for the Dzyaloshinskii–Moriya System
Using the transformation into the local coordinates, Equations (
4)–(
9), one has
Note that the quantization axes of the spins are in the
planes as shown in
Figure 3.
We emphasize that, while the sine terms of the DM Hamiltonian, Equation (
35), remain after summing over the NN, the sine terms of
, the 3rd line of Equation (
36), are zero after summing over opposite NN because there is no
term.
It is very important to emphasize again that the commutation relations between spin operators and are valid when the spin lies on its local quantization axis. Therefore, it is necessary ro use the local coordinates for each spin.
In two dimensions (2D) there is no long-range order at non-zero
T for isotropic spin models with short-range interaction [
40]. Thin films have very small thickness, not far from 2D systems. Thus, in order to stabilize the ordering at very low
T, we use a very small anisotropy interaction between between
and
as follows
where
is positive, small compared to
, and limited to NN in the
plane. For simplicity, we suppose
for all such NN pairs. As we will see below, the small value of
does stabilize the SW spectrum when
D becomes large. The Hamiltonian is finally given by
Using the two GF’s in the real space given by Equations (
11) and (12) and using the same method, we study the effect of the DM interaction. For the DM term, the commutation relations
lead to:
which gives rise, using the Tyablikov decoupling, to the following GF’s:
These functions are in fact the G and F functions. There are thus no new GF’s generated by the equations of motion.
As in
Section 2, the Fourier transforms in the
plane
and
of the
G and
F lead to the matrix equation
being given by Equation (
42) below
where
is the SW energy and the matrix elements are given by
where
denotes the layer numbers,
,
,
and
are the wave-vector components in the
planes,
a being the lattice constant. Remarks: (i) if
(surface layer) then there are no
terms in the
, (ii) if
then there are no
terms in
.
For a thin film, the SW frequencies at a given wave vector
are obtained by diagonalizing (
42).
The magnetization of the layer n at finite T is calculated as in the helimagnetic case shown in the previous section. The formula of the zero-point spin contraction is also presented there. The transition temperature can be also calculated by the same method. Let us show in the following the results.
4.2. Results for 2D and 3D Cases
In the 2D case, one has only one layer. The matrix (
42) is
where
is given by (
43) but without
term for the 2D case. Coefficient
is given by (44) and
. The SW frequencies are determined by the following secular equation
Several remarks are in order:
- (i)
when
, the last three terms of
and
are zero: one recovers the ferromagnetic SW dispersion relation
where
is the coordination number of the square lattice (taking
),
- (ii)
when
, one has
,
. One recovers then the antiferromagnetic SW dispersion relation
- (iii)
when there is a DM interaction, one has
(
). If
, the quantity in the square root of Equation (
47) becomes negative at
when
is not zero. The SW spectrum is not stable at
because the energy is not real. The anisotropy
can remove this instability if it is larger than a threshold value
. We solve the equation
to find
. In
Figure 9 we show
versus
. As seen,
increases from zero with increasing
.
As we have anticipated, we need to include an anisotropy in order to allow for SW to be excited even at and for a long-range ordering at non-zero T in 2D as seen below.
We show in
Figure 10 the SW dispersion relation calculated from Equation (
47) for
and 0.6 (radian). As seen, the spectrum is symmetric for positive and negative wave vectors. It is also symmetric for left and right precessions. One observes that for small
, namely small
D,
is proportional to
at low
k (see
Figure 10a). This behavior is that in ferromagnets. For large
, one observes that
becomes linear in
k as seen in
Figure 10b. This behavior is similar to that of antiferromagnets. Note that the change of behavior is progressive with increasing
, we do not observe a sudden transition from
to
k behavior. This behavior is also observed in 3D and in thin films as well.
As said earlier, the inclusion of an anisotropy
d permits a long-range ordering at
in 2D:
Figure 11 displays the magnetization
M (
) calculated by Equation (2) where in each case the limit value
has been used. We note that
M depends strongly on
: at high
T the larger
the stronger
M. However, at
the spin length is smaller for larger
due to the zero-point spin contraction [
31] calculated by Equation (
27). As a consequence there is a cross-over of layer magnetizations at low
T as shown in
Figure 11b. The spin length at
is shown in
Figure 12 for several
.
We now consider the 3D case. The crystal is infinite in three direction. The Fourier transform in the
y direction, namely
and
reduces the matrix (
23) to two coupled equations of
g and
f functions. One has
where
In the ferromagnetic case, , thus . Arranging the Fourier transforms in three directions, one gets the 3D ferromagnetic dispersion relation where and , coordination number of the simple cubic lattice.
As in the 2D case, we find a threshold value
for which is the same for a given
. This is rather obvious because the DM interaction operates in the plane making an angle
between spins in the plane, therefore its effects act on SW in each plane, not in the
y direction perpendicular to the “DM planes”. Using Equation (
53), we calculate the 3D spectrum displayed in
Figure 13 for a small and a large value of
. As in the 2D case, we observe
when
for large
. The main properties of the system are thus governed by the in-plane DM interaction.
Figure 14 displays the magnetization
M versus
T for several values of
. As in the 2D case, when the DM interaction is included, the spins undergo a zero-point contraction which increases with increasing
. The competition between quantum fluctuations at
and thermal effects at high
T gives rise to magnetization cross-over shown in
Figure 14b. The spin length at
vs.
is shown in the inset of
Figure 14b. Comparing these results to those of the 2D case, we see that the spin contraction in 2D is stronger than in 3D. This is physically expected because quantum fluctuations are stronger at lower dimensions.
4.3. The Case of a Thin Film
As in the 2D and 3D cases, in the case of a thin film it is necessary to use a value for
larger or equal to
given in
Figure 9 to stabilize the SW at long wave-length. Note that for thin films with more than one layer, the value of
calculated for the 2D case remains valid.
Figure 15 displays the SW spectrum of a film of eight layers with
for a small and a large
. As in the previous cases,
E is proportional to
k for large
(cf.
Figure 15b) but only for the first mode. The higher modes are proportional to
.
Figure 16 shows the layer magnetizations of the first four layers in a 8-layer film (the other half is symmetric) for two values of
. One observes that the surface magnetization is smaller than the magnetizations of other interior layers. This is due to the lack of neighbors for surface spins [
2].
The spin contraction at
is displayed
Figure 16c.
The effects of the surface exchange and the film thickness have been shown in Ref. [
38].
To close this section, let us mention our work [
41] on the DM interaction in magneto-ferroelectric superlattices where the SW in the magnetic layer have been calculated. We have also studied the stability of skyrmions at finite
T in that work and in Refs. [
42,
43].
6. Other Systems of Non-Collinear Ground-State Spin Configurations: Frustrated Surface in Stacked Triangular Thin Films
In this section, we study by the GF technique the effect of a frustrated surface on the magnetic properties of a film composed triangular layers stacked in the
z direction. Each lattice site is occupied by a quantum Heisenberg spin of magnitude 1/2. Let the in-plane surface interaction be
which can be antiferromagnetic or ferromagnetic. The other interactions in the film are ferromagnetic. We show in the following that the GS spin configuration is non-collinear when
is lower than a critical value
. The film surfaces are then frustrated. In the frustrated case, there are two phase transitions, one corresponds to the disordering of the two surfaces and the other to the disordering of the interior layers. The GF results agree qualitatively with Monte Carlo simulation using the classical spins (see the original paper in Ref. [
39]).
In this section we review some ot the results given in the original paper Ref. [
39], emphasizing the SW calculation and the important results. The Hamiltonian is written as
where the first sum is performed over the NN spin pairs
and
, the second sum over their
z components.
and
are respectively their exchange interaction and their anisotropic one. The latter is small, taken to ensure the ordering at finite
T when the film thickness goes down to a few layers, without this we know that a monolayer with vector spin models does not have a long-range ordering at finite
T [
40].
Let be the exchange between two NN surface spins. We suppose that all other interactions are ferromagnetic and equal to J. We shall use as the unit of energy in the following.
6.1. Ground State
In the case where
is ferromagnetic, the GS of the film is ferromagnetic. When
is antiferromagnetic, the situation becomes complicated. We recall that for a single triangular lattice with antiferromagnetic interaction, the spins are frustrated and arranged in a 120-degree configuration [
8]. This structure is modified when we turn on the ferromagnetic interaction
J with the beneath layer. The competition between the non collinear surface ordering and the ferromagnetic ordering of the bulk leads to an intermediate structure which is determined in the following.
The GS configuration can be determined by using the steepest descent method described below Equation (
31). Let us describe qualitatively the GS configuration: when
is negative and
where
is a critical value, the GS is formed by pulling out the planar
spin structure along the
z axis by an angle
. This is shown in
Figure 23.
Figure 24 shows
and
versus
obtained by the steepest descent method. As seen for
, the angles are zero, namely the GS is ferromagnetic. The critical value
is numerically found between −0.18 and −0.19.
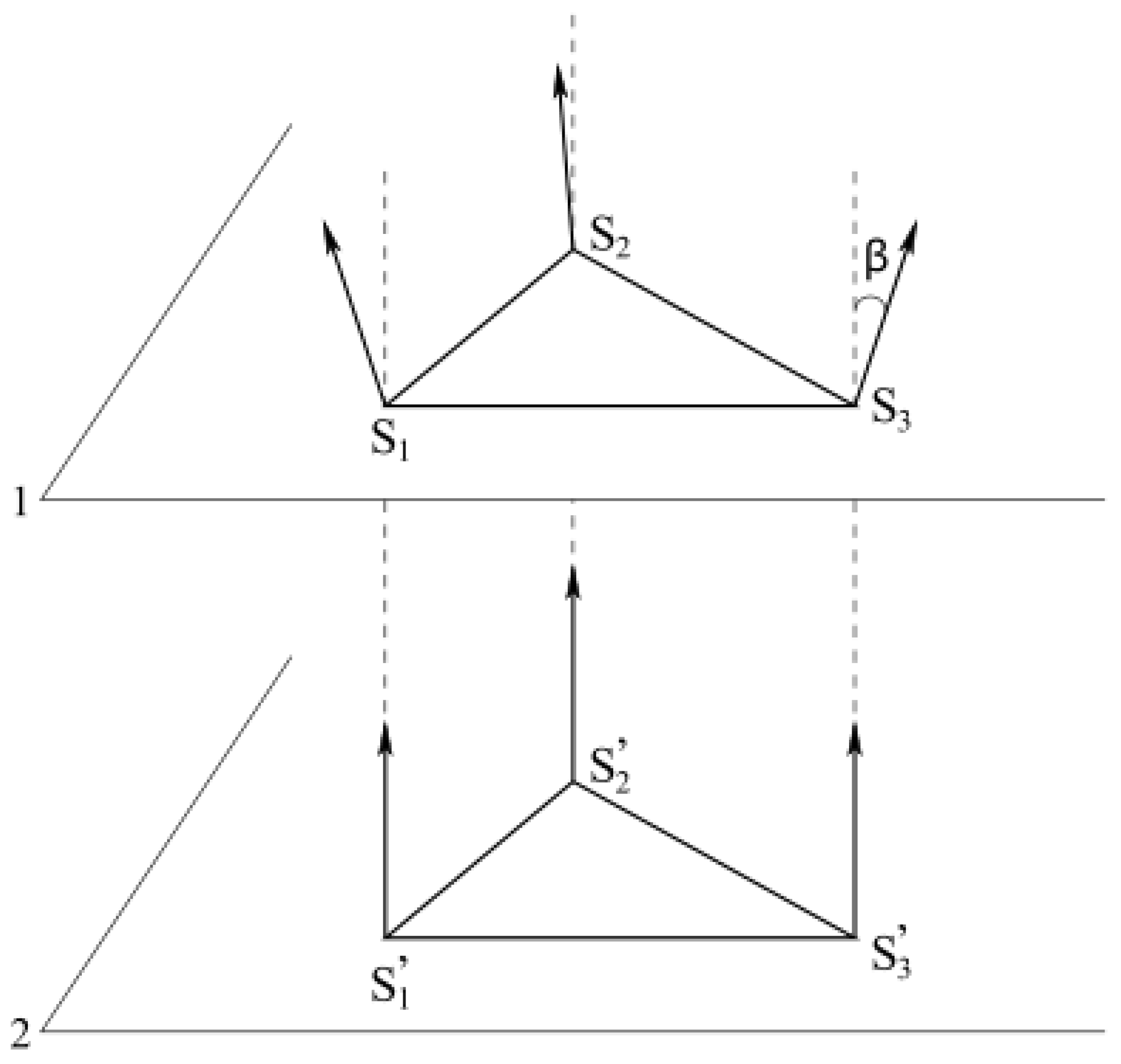
We show in the following that this value can be analytically calculated by assuming the structure shown in
Figure 23). We number the spins as in that figure:
,
and
are the spins in the surface layer,
,
and
are the spins in the second layer. The energy of the cell is
We project the spins on the
plane and on the
z axis. One writes
. One observes that only surface spins have non-zero
vector components. Let the angle between these
components of NN surface spins be
which is in fact the projection of the angle
on the
plane. By symmetry, we have
The angles
and
of
and
formed with the
z axis are by symmetry
The total energy of the cell (
86), with
, is thus
The minimum of the cell energy verifies this condition:
This solution exists under the condition . The critical values are determined from this condition. For , which is in excellent agreement with the results obtained from the steepest descent method.
Now, using the GF method for such a film in the way described in the previous sections, we obtain the full Hamiltonian (
84) in the local framework:
where
is the angle between two NN spins. We define the two coupled GF, and we write their equations of motions in the real space. Taking Tyablikov’s decoupling scheme to reduce higher-order GFs, and then using the Fourier transform in the
plane we arrive at a matrix equation as in the previous section with the matrix
is defined as
where
where
is the in-plane coordination number,
denotes the angle between two NN spins belonging to the adjacent layers
n and
, while
is the angle between two NN spins of the layer
n, and
Note that in the above coefficients, we have used the following notations:
- (i)
and are the in-plane interactions. is equal to for the two surface layers and equal to J for the interior layers. All are taken equal to I.
- (ii)
The interlayer interactions are denoted by and . Note that = 0 if and =0 if .
As described in the previous sections, the SW spectrum is obtained by solving det. Using we calculate the magnetizations layer by layer for typical values of parameters. The results are shown in the following.
6.2. Quantum Surface Phase Transition
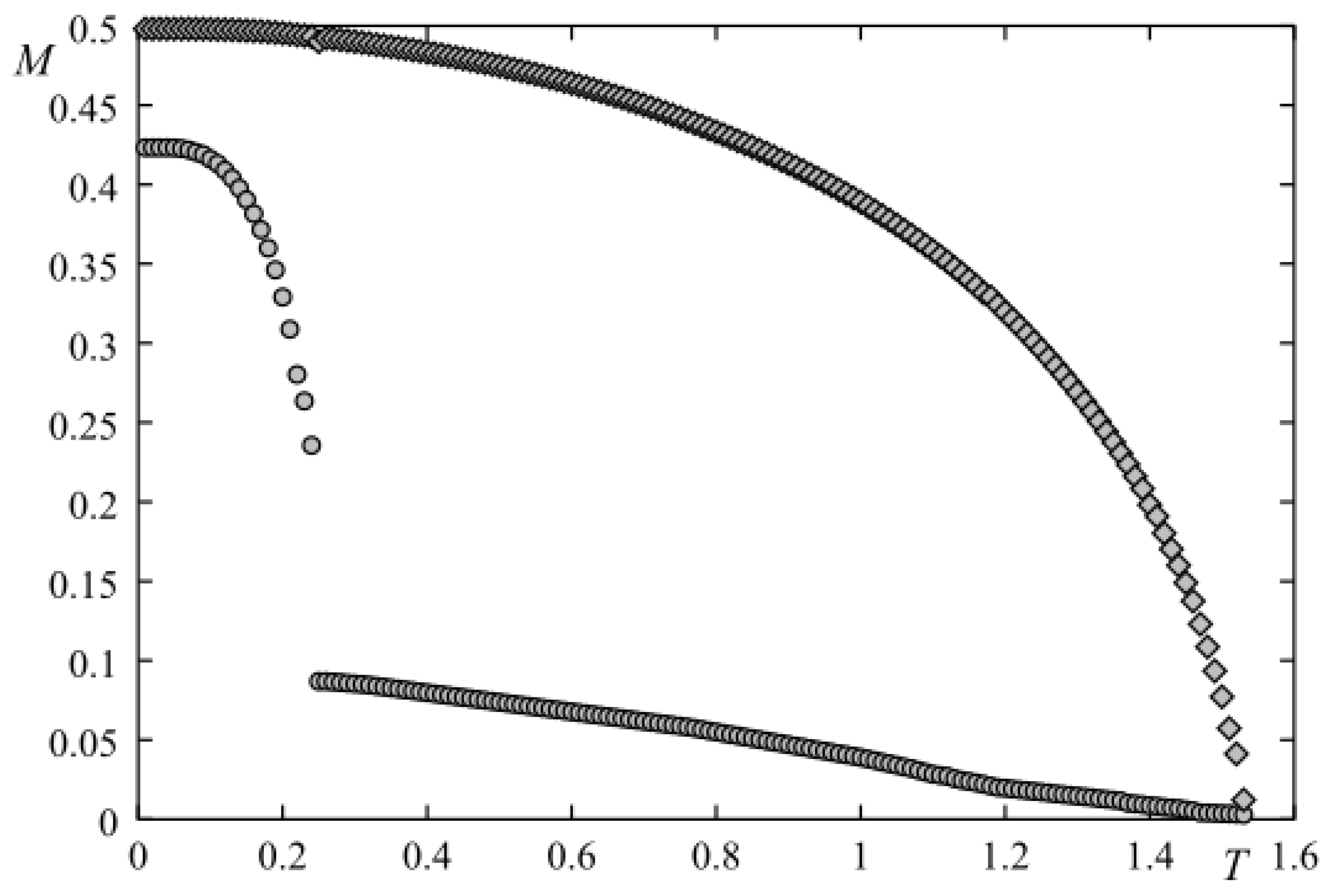
Let us show a typical case in the region of frustrated surface where
in
Figure 25. Several comments are in order:
- (i)
The surface magnetization is very small with respect to the magnetization of the second layer,
- (ii)
At , the length of the surface spin is about 0.425, much shorter than the spin magnitude 1/2. This is due to the antiferromagnetic interaction at the surface which causes a strong spin contraction. For the second layer, the spins are aligned ferromagnetically, their length is fully 0.5,
- (iii)
The surface undergoes a phase transition at while the second layer remains ordered up to . The system is thus disordered at the surface and ordered in the bulk, for temperatures between and . This partial disorder is very interesting. It gives another example of the partial disorder observed earlier in bulk frustrated quantum spin systems.
- (iv)
One observes that between and , the first layer has a small magnetization. This is understood by the fact that the strong magnetization of the second layer acts as an external field on the first layer, inducing therefore a small value of its magnetization.
We plot the phase diagram in the space
in
Figure 26. Phase I denotes the surface canted-spin state, phase IIA denotes the partially ordered phase: the surface is disordered while the bulk is ordered. Phase IIB separated from phase IIA by a vertical line issued from
indicates the ferromagnetic state, and phase III is the paramagnetic phase.
6.3. Classical Phase Transition: Monte Carlo Results
In order to compare with the quantum model shown in the previous subsection, we consider here the classical counterpart model, namely we use the same Hamiltonian (
28) but with the classical Heisenberg spin of magnitude
. The aim is to compare their qualitative features, in particular the question of the partial disordering at finite
T.
We use Monte Carlo simulations for the classical model where the film dimensions are , being the film thickness which is taken to be as in the quantum case shown above. We use here to see the lateral finite-size effect. Periodic boundary conditions are used in the planes. We discard MC steps per spin to equilibrate the system and average physical quantities over the next MC steps per spin.
We show in
Figure 27 the result obtained in the same frustrated case as in the quantum case shown above, namely
. we see that the surface magnetization falls at
while the second-layer magnetization stays ordered up to
. This surface disordering at low
T is similar to the quantum case. Between
and
the system is partially disordered.
Figure 28 shows the phase diagram obtained in the space
. It is interesting to note that the classical phase diagram shown here has the same feature as the quantum phase diagram displayed in
Figure 26. The difference in the values of the transition temperatures is due to the difference of quantum and classical spins.
To close this review, we should mention a few works works where SW in the regime of non-collinear spin configurations have been studied: the frustration effects in antiferromagnetic face-centered cubic Heisenberg films have been studied in Ref. [
49], a frustrated ferrimagnet in Ref. [
50] and a quantum frustrated spin system in Ref. [
51]. These results are not reviewed here to limit the paper’s length. The reader is referred to those works for details.