A Novel Disturbance Rejection Method Based on Robust Sliding Mode Control for the Secure Communication of Chaos-Based System

Abstract

This paper mainly proposes a new disturbance observer (DO) for a secure communication system (SCS) of the chaos-based system (CBS). First, the fractional-order (FO) Chen chaotic system is remodeled by a Takagi–Sugeno (T–S) fuzzy system with the aim of softening in calculation. Second, the robust fixed-time was designed to synchronize two nonidentical chaotic systems. Third, a new disturbance observer was proposed to compensate for the disturbance and uncertainty of the secure communication system. Fourth, the proof of the proposed method based on Lyapunov condition together with simulation are given to illustrate the correctness and effectiveness of the proposed theory. The tested disturbance on the public channel was mostly compensated by the appropriately estimated disturbance value. The states of master and slave systems (MSSs) were closed to each other in fixed-time. These factors are used to confirm that the symmetry of two chaotic systems were obtained by the proposed control methods.

1. Introduction

The disturbance of a control system is well known as the inversed signal from outside of the system. Inside variations of the parameters of the controlled system are uncertain. To handle these inversed signals, the disturbance rejection techniques need to be equipped to the control system. The main problem of the disturbance observer (DO) is the boundary first derivative of the DO. In [1], the nonlinear DO was proposed with the condition of the first derivative disturbance is zero. The applications of the nonlinear DO can be found in [2,3]. To delete the requirement of disturbance conjunction, the improvement of the nonlinear DO can be found in [4,5,6,7]. The DO with the requirement of fixed format can be found in [8]. The DO for secure communication system is a potential area, which can be found in [4,5,6,9]. Other robust control methods for secure communication system (SCS) can be found in [10,11].

In recent years, the secure communication of the chaos-based system (CBS) has been rapidly developed. The request of the 4.0 industrial revolution for secure data has pushed the rate of research regarding SCS growth up. The basic background of the field is the synchronization of two nonidentical chaotic systems and the scheme of encryption and decryption of the date. Therefore, the radar information encryption technique was investigated in [12]. A novel method for the synchronization two chaotic systems can be found in [13]. The finite time synchronization method can be found in [14]. The image encryption technique can be found in [15,16,17,18]. The synchronization of network systems can be found in [19,20,21,22,23]. The synchronization of the chaotic systems in electronic circuits can be found in [24,25,26,27,28]. To simply design the controller and disturbance observer, this paper used the previous model in [9] with the sector nonlinearity method in [29,30] to change the format of a rescaled chaotic system into T–S fuzzy format. The Chen system was proposed in [31], and the fractional-order (FO) Chen system in this paper is reused from previous published paper [9]. To simulate the FO operation, the FOMCON toolbox is used. FOMCON is a toolbox which allows for fractional-order calculus simulation. The guide to using FOMCON can be found in [32]. To synchronize two nonidentical chaotic systems, the fixed-time sliding mode control (SMC) is used to obtain the goal. The basic concept of fixed-time stability (FTS) was proposed in [33]. Taking advantage of the double phase fixed-time SMC in [34], this paper designed the double phases with the fixed-time stability for the synchronization of two nonidentical chaotic systems with the aim of softening the chattering problem. There are several methods to solve the chattering problem, such as adaptive SMC [35,36]. Therefore, the main contributions of this work are as follows: first, the details of the Chen chaotic system were rewritten in the T–S fuzzy format from [9]. The detail of FO Chen chaotic system is represented in this paper. Second, the synchronization of two nonidentical T–S fuzzy chaotic systems obtained a good result with the power of fixed-time SMC. Here, the sliding phase is fixed-time stable is presented with the aim of softening the chattering value. The tracking error will be converged into the zero coordinate in fixed-time. The sliding phase is also in fixed-time. Third, to avoid the perturbations of the SCS, a new DO was proposed. This is a main contribution of this paper. The tested uncertainty in the master system and the disturbance and uncertainty in the slave system are all presented in this paper. All of these values are mostly compensated by the proposed DO. Fourth, to define the power and originality of the proposed theory, the MATLAB simulation was used to verify the provided theories.

The layout of the paper is as follows: first, the introduction is given to illustrate the gap in the research. Next, the preliminary mathematics are presented. In the second section, the analysis of the idea of the proposed DO is illustrated. Third, the proposed control methods are analyzed for the SCS. Fourth, an illustrative example is given to show the effectiveness of the mentioned theories. Finally, the conclusion is given to state that the proposed control method is suitable for the synchronization of two nonidentical chaotic systems.

2. Mathematical Modeling and Preliminary Mathematics

2.1. Mathematical Modeling of MSSs

In this paper, FO T–S fuzzy Chen system in [9] is reused with the mathematical model as below.

$$\{\begin{array}{l}\frac{d^{\alpha }}{d{t}^{\alpha }}{x}_1(t)=-(a+\mathrm{\Delta }a)x_1(t)+(a+\mathrm{\Delta }a)x_2(t)+d_1(t)\\ \frac{d^{\alpha }}{d{t}^{\alpha }}{x}_2(t)=-(\tau +\mathrm{\Delta }\tau )x_1(t)+(c+\mathrm{\Delta }c)x_2(t)-x_1{x}_3+d_2(t)\\ \frac{d^{\alpha }}{d{t}^{\alpha }}{x}_3(t)=x_1(t)x_2(t)-(b+\mathrm{\Delta }b)x_3(t)+d_3(t)\end{array}$$

(1)

where $x_1(t),$ $x_2(t),$ and $x_3(t)$ are states. $\mathrm{\Delta }a,$ $\mathrm{\Delta }b,$ $\mathrm{\Delta }\tau ,$ and $\mathrm{\Delta }c$ are uncertainty parameters of the system. $d_1(\mathit{t}),$ $d_2(\mathit{t}),$ and $d_3(\mathit{t})$ are the disturbance from outside of the system. According to a previous paper [31], the parameters of the system were selected as follows: $a=35,$ $b=3,$ $c=28,$ and $\tau =a-c$.

Assumption 1.

All uncertainties and disturbances must be bounded as follows:$\left|\mathrm{\Delta }a{x}_1(t)\right|\le a_{11},$$\left|\mathrm{\Delta }a{x}_2(t)\right|\le a_{12},$$\left|\mathrm{\Delta }\tau x_1(t)\right|\le {\tau }_{11},$$\left|\mathrm{\Delta }c{x}_2(t)\right|\le {\tau }_{11},$$\left|\mathrm{\Delta }b{x}_3(t)\right|\le b_{11},$$\left|d_1(t)\right|\le d_1,$$\left|d_2(t)\right|\le d_2,$and$\left|d_3(t)\right|\le d_3.$These upper bound values need to be positively defined. In [31], the mathematical formula after rescaling is shown as follows:

$$\left[\begin{array}{c}\frac{d^{\alpha }}{d{t}^{\alpha }}x(t)\\ \frac{d^{\alpha }}{d{t}^{\alpha }}y(t)\\ \frac{d^{\alpha }}{d{t}^{\alpha }}z(t)\end{array}\right]=\left[\begin{array}{ccc}-a& a& 0\\ -\tau & c& -20x(t)\\ 0& 5x(t)& -b\end{array}\right]\left[\begin{array}{c}x(t)\\ y(t)\\ z(t)\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{l}_x(t)\\ l_y(t)\\ l_z(t)\end{array}\right]$$

(2)

where$x_1(t)\to 10x(t),$ $x_2(t)\to 10y(t),$and$x_3(t)\to 20z(t),$and$l_x(t)=-\mathrm{\Delta }ax(t)+\mathrm{\Delta }ay(t)+d_1(t),$ $l_x(t)=-\mathrm{\Delta }\tau x(t)+\mathrm{\Delta }cy(t)+d_2(t),$and$l_x(t)=-\mathrm{\Delta }bz(t)+d_3(t).$These uncertainty values need to be bounded as per Assumption 2 below.

Assumption 2.

All uncertainties must be bounded as follows:$\left|l_x(t)\right|\le L_1,$$\left|ly(t)\right|\le L_2,$and$\left|lz(t)\right|\le L_3,$where$L_1,$$L_2,$$L_3$are positively defined.

This paper used the sector nonlinearity method in [29] to remodel the system (2) into the T–S fuzzy system, then system (2) can be represented as follows:

$$\frac{D^{\alpha }}{dt}X(t)={\displaystyle \sum _{i=1}^2\omega (X_i(t))}{A}_{i}X(t)+B_{i}u(t)+C_{i}l(t)$$

(3)

where$l(t)={\left[\begin{array}{ccc}{l}_x(t)& l_y(t)& l_z(t)\end{array}\right]}^T.$Detail of T-S fuzzy modeling can be found in Appendix A.

Remark 1.

$C_i$and$B_i$should be identity matrices for easy in calculation.

The parameters of (3) are as follows:

$B_i=E_i=I^{3\times 3},$$A_2=\left[\begin{array}{ccc}-35& 35& 0\\ \mathit{-}7& 28& 100\\ 0& \mathit{-}25& \mathit{-}3\end{array}\right],$and$A_1=\left[\begin{array}{ccc}\mathit{-}35& 35& 0\\ \mathit{-}7& 28& \mathit{-}100\\ 0& 25& \mathit{-}3\end{array}\right].$The states and trajectories of the rescaled system are shown in Figure 1 below.

Figure 1. System state, (a) x(t), (b) y(t), and (c) z(t).

The phase portraits are shown in Figure 2 below.

Figure 2. Phase portraits, (a) state on yx-axis, (b) state on zx-axis, (c) state on zy-axis, (d) 3D phase portrait.

To secure the date, the MSS of a SCS, respectively, should selected as follows: the master is

$$\frac{D^{\alpha }}{dt}{X}_m(t)={\displaystyle \sum _{i=1}^2\omega (X_{im}(t))}{A}_i{X}_m(t)+C_i{l}_m(t)$$

(4)

where $l_m(t)$ is perturbation of master system. The slave system is

$$\frac{D^{\alpha }}{d{t}^{\alpha -1}}{X}_s(t)={\displaystyle \sum _{i=1}^2\omega (X_{is}(t))}{A}_i{X}_s(t)+B_i{u}_s(t)+C_i{l}_s(t)$$

(5)

where $l_s(t)$ is perturbation of slave system. System (5) can work if the assumption below is fulfilled.

Remark 2.

The uncertainties of MSSs must be bounded.

Errors of the MSSs are

$$e(t)=X_m(t)-X_s(t)$$

(6)

By taking derivative for Equation (6) corresponding to the degree of$\alpha$leads to

$$\frac{D^{\alpha }}{d{t}^{\alpha -1}}e(t)={\displaystyle \sum _{i=1}^2\omega (X_{im}(t))}{A}_i{X}_m(t)-{\displaystyle \sum _{i=1}^2\omega (X_{is}(t))}{A}_i{X}_s(t)-B_i{u}_s(t)+C_{i}l(t)$$

(7)

where$C_{i}l(t)=C_i[l_m(t)-l_s(t)]$is used to represent the total disturbance and uncertainty on the public channel.

Remark 3.

In this paper,$y_m(t)$and$y_s(t)$were used for encryption and decryption of the data, the structure of secure communication is as follows:

$$\widehat{M}(t)=y_m(t)+M(t)-y_s(t)$$

(8)

where$\widehat{M}(t)$and$M(t)$are the received and sent data.

2.2. Preliminary Mathematics

This section is used to show some preliminary mathematics. First, the fractional-order calculation is rewritten from a previous paper [37]. Second, the fixed-time SMC concept is rewritten from the published paper [37]. Finally, the concept of the proposed DO is presented.

2.2.1. Fractional Calculus

The preliminary mathematics of the fractional-order calculus are as below.

Definition 1.

[37]: The Euler’s Gamma function.

$$\mathrm{\Gamma }(\rho )={\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{\rho -1}{e}^{-t}dt}$$

(9)

where $\rho$ and $t$ are order and time of the operation.

Definition 2.

[37]: Derivation and integration of the fractional calculus.

$$D_t^n=\{\begin{array}{c}\frac{d^n}{d{t}^n},n>0\\ 1, n=0\\ {\displaystyle \underset{a}{\overset{t}{\int }}{(d\tau )}^{-n},n<0}\end{array}$$

(10)

where n is the order of the operation.

Definition 3.

[37]: The Caputo fractional derivative.

$$D_t^{n}h(t)=\frac{1}{\mathrm{\Gamma }(\mathit{l}-n)}{\displaystyle \underset{a}{\overset{t}{\int }}\frac{f^n(\tau )}{{(t-\tau )}^{n-l+1}}}d\tau$$

(11)

with $l-1<n<l.$

Definition 4.

[37]: Stability of the FO system.

Considering FO system as below.

$$D_t^n\xi =h(\xi )$$

(12)

where$\xi ={[{\xi }_1,\dots {\xi }_l]}^T$is state vector. Where 0 < n < 1 is the order of FO calculus. System (12) is stable when the eigenvalues of Jacobian$J=\partial h(\xi )/\partial \xi$are all located in area of

$$\left|arg(eig(J))\right|>n\frac{\pi }{2}$$

(13)

Some properties of FO operation are listed as follows:

Property 1.

Ifn = 0,

$$D_t^{0}h(X)=h(X)$$

(14)

Property 2.

Caputo operation.

$$D_t^{\gamma }(g(X)+h(X))=D_t^{\gamma }g(X)+D_t^{\gamma }h(X)$$

(15)

Property 3.

The product of fractional derivative.

$$D_t^{m+n}h(X)=D_t^m{D}_t^{n}h(X)$$

(16)

2.2.2. Fixed-Time Sliding Mode Control

Herein, the FTS concept in [33,34] are used to design the SMC for the synchronization of two nonidentical chaotic systems. The basic concepts of fixed-time stability are below. The settling-time of the reaching law is as below.

$$\dot{s}=-[K_{s1}{\left|s\right|}^{\frac{a_{11}}{b11}}sign(s)+K_{s2}{\left|s\right|}^{\frac{a12}{b12}}sign(s)]$$

(17)

is calculated as follows:

$$T_{\max }=\frac{b11}{K_{s1}(a11-b11)}+\frac{b12}{K_{s2}(b12-a12)}$$

(18)

where $a11>b11,$ $a12<b12,$ $a11,$ $a12,$ $b11,$ $b12,$ $K_{s1}>0,$ and $K_{s2}>0$. This paper proposed a new structure of DO. Therefore, this section is used to illustrate the idea of the novel DO for such a kind of SCS.

2.2.3. Proposed DO

Based on the mathematical model in Equations (4) and (5), the real disturbance can be approximated by

$${\displaystyle \sum _{i=1}^2\omega (X_{is}(t))}{A}_i{X}_s(t)+B_i{u}_s(t)-{\displaystyle \sum _{i=1}^2\omega (X_{im}(t))}{A}_i{X}_m(t)=\frac{D^{\alpha }}{d{t}^{\alpha -1}}{X}_s(t)-C_i{l}_s(t)-(\frac{D^{\alpha }}{dt}{X}_m(t)-C_i{l}_m(t))$$

(19)

or

$$C_i\mathit{l}(t)={\displaystyle \sum _{i=1}^2\omega (X_{is}(t))}{A}_i{X}_s(t)+B_i{u}_s(t)-{\displaystyle \sum _{i=1}^2\omega (X_{im}(t))}{A}_i{X}_m(t)$$

(20)

if $\frac{D^{\alpha }}{d{t}^{\alpha }}{X}_s(t)\to \frac{D^{\alpha }}{d{t}^{\alpha }}{X}_m(t)$ or $X_s(t)\to X_m(t).$ The proposed DO in this paper is as follows:

$$\widehat{l}(t)=l(t)+{\displaystyle \int K_{l1}{\left|\tilde{l}(t)\right|}^{\frac{a1}{b1}}sign(\tilde{l}(t))+K_{l2}{\left|\tilde{l}(t)\right|}^{\frac{a2}{b2}}sign(\tilde{l}(t))}$$

(21)

or

$$\dot{\tilde{l}}(t)=-[K_{l1}{\left|\tilde{l}(t)\right|}^{\frac{a1}{b1}}sign(\tilde{l}(t))+K_{l2}{\left|\tilde{l}(t)\right|}^{\frac{a2}{b2}}sign(\tilde{l}(t))]$$

(22)

The stability of the proposed DO is fixed-time, with the format of disturbance error similar to the fixed-time SMC in [33].

3. Proposed Approach

Herein, the proposed method for the SCS is presented. The contents of this section are listed as follows: first, the sliding mode control for SCS is analyzed. Second, the DO for estimating perturbations of SCS is illustrated. The calculation is corresponding to the time, therefore writing time (t) is ignored.

3.1. Fixed-Time SMC for SCS

Taking advantage of the double-phase fixed-time SMC [34], the FO fixed-time SMC is designed for the secure communication system with the surface of SMC for each axis designed as below.

$$s_j=\frac{D^{\alpha -1}}{d{t}^{\alpha -1}}{e}_j+\frac{D^{\alpha -2}}{d{t}^{\alpha -2}}[k_{e{1}_j}{\left|e_j\right|}^{\frac{a1e_j}{b1e_j}}sign(e_j)+k_{e{2}_j}{\left|e_j\right|}^{\frac{c1e_j}{d1e_j}}sign(e_j)]$$

(23)

For j goes from 1 to 3. Taking derivative for Equation (23) yields

$${\dot{s}}_j=\frac{D^{\alpha }}{d{t}^{\alpha }}{e}_j+\frac{D^{\alpha -1}}{d{t}^{\alpha -1}}[k_{e{1}_j}{\left|e_j\right|}^{\frac{a1e_j}{b1e_j}}sign(e_j)+k_{e{2}_j}{\left|e_j\right|}^{\frac{c1e_j}{d1e_j}}sign(e_j)]$$

(24)

The equivalent control value of SMC can be calculated by ignoring the disturbance effect. Solving Equation (24) by

$$0=\frac{D^{\alpha }}{d{t}^{\alpha }}{e}_j+\frac{D^{\alpha -1}}{d{t}^{\alpha -1}}[k_{e{1}_j}{\left|e_j\right|}^{\frac{a1e_j}{b1e_j}}sign(e_j)+k_{e{2}_j}{\left|e_j\right|}^{\frac{c1e_j}{d1e_j}}sign(e_j)]$$

(25)

or

$$\begin{array}{l}{\displaystyle \sum _{i=1}^2\omega (X_{im}(t))}{A}_i{X}_m(t)-{\displaystyle \sum _{i=1}^2\omega (X_{is}(t))}{A}_i{X}_s(t)-B_i{u}_s(t)+\\ \frac{D^{\alpha -1}}{d{t}^{\alpha -1}}[k_{e{1}_j}{\left|e_j\right|}^{\frac{a1e_j}{b1e_j}}sign(e_j)+k_{e{2}_j}{\left|e_j\right|}^{\frac{c1e_j}{d1e_j}}sign(e_j)]=0\end{array}$$

(26)

The equivalent control is then calculated

$$\begin{array}{l}{B}_j{u}_{eq{s}_j}={\displaystyle \sum _{i=1}^2\omega ({\mathrm{\Omega }}_{ijm})}{A}_{ij}{X}_{mj}-{\displaystyle \sum _{i=1}^2\omega ({\mathrm{\Omega }}_{ijs})}{A}_{ij}{X}_{sj}+\\ \begin{array}{cccc}& & & \end{array}\frac{D^{\alpha -1}}{d{t}^{\alpha -1}}[k_{e1j}{\left|e_j\right|}^{\frac{a1e_j}{b1ej}}sign(e_j)+k_{e2j}{\left|e\right|}^{\frac{c1ej}{d1ej}}sign(e_j)]\end{array}$$

(27)

In steady-state, the state of the slave system is converged to the state of the master in the fixed-time as below.

$$T_{emax}=\frac{b1ej}{K_{e1j}(a1ej-b1ej)}+\frac{d1ej}{K_{e2j}(d1ej-c1ej)}$$

(28)

The reaching law is designed as follows:

$$B_j{u}_{sw{s}_j}(t)=k_{s{1}_j}{\left|s_j\right|}^{\frac{a1s_j}{b1s_j}}sign(s_j)+k_{s{2}_j}{\left|s_j\right|}^{\frac{c1s_j}{d1s_j}}sign(s_j)$$

(29)

The settling-time of the reaching law is

$$T_{smax}=\frac{b1sj}{K_{s1j}(a1sj-b1sj)}+\frac{d1sj}{K_{s2j}(d1sj-c1sj)}$$

(30)

To soften the effects of the perturbations, a new DO is proposed in the next section.

3.2. Proposed DO for SCS

With the aim of obtaining the reaching law of the DO as Equation (22), the DO is proposed as

$$\begin{array}{l}{\widehat{\mathit{l}}}_j={\displaystyle \sum _{i=1}^2\omega (X_{ijs})}{A}_{ij}{X}_{sj}+B_{ij}{u}_{sj}-{\displaystyle \sum _{i=1}^2\omega (X_{ijm})}{A}_{ij}{X}_{mj}+\\ \begin{array}{cc}& \end{array}{\displaystyle \int }{k}_{\mathit{l}{1}_j}{\left|{\displaystyle \sum _{i=1}^2\omega (X_{ijs})}{A}_{ij}{X}_{sj}+B_{ij}{u}_{sj}-{\displaystyle \sum _{i=1}^2\omega (X_{ijm})}{A}_{ij}{X}_{mj}\right|}^{\frac{a1l_j}{b1{\mathit{l}}_j}}\\ \begin{array}{cc}& \end{array}sign({\displaystyle \sum _{i=1}^2\omega (X_{ijs})}{A}_{ij}{X}_{sj}+B_{ij}{u}_{sj}-{\displaystyle \sum _{i=1}^2\omega (X_{ijm})}{A}_{ij}{X}_{mj})+\\ \begin{array}{cc}& \end{array}{\displaystyle \int }{k}_{\mathit{l}{2}_j}{\left|{\displaystyle \sum _{i=1}^2\omega (X_{ijs})}{A}_{ij}{X}_{sj}+B_{ij}{u}_{sj}-{\displaystyle \sum _{i=1}^2\omega (X_{ijm})}{A}_{ij}{X}_{mj}\right|}^{\frac{c1{\mathit{l}}_j}{d1{\mathit{l}}_j}}\\ \begin{array}{cc}& \end{array}sign({\displaystyle \sum _{i=1}^2\omega (X_{ijs})}{A}_{ij}{X}_{sj}+B_{ij}{u}_{sj}-{\displaystyle \sum _{i=1}^2\omega (X_{ijm})}{A}_{ij}{X}_{mj})\end{array}$$

(31)

or

$${\widehat{\mathit{l}}}_j={\mathit{l}}_j+{\displaystyle \int k_{\mathit{l}{1}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{a1l_j}{b1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)}+{\displaystyle \int k_{\mathit{l}{2}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{c1l_j}{d1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)}$$

(32)

Taking derivative for both sides of Equation (32) we have

$${\dot{\widehat{\mathit{l}}}}_j={\dot{\mathit{l}}}_j+k_{\mathit{l}{1}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{a1{\mathit{l}}_j}{b1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)+k_{\mathit{l}{2}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{c1{\mathit{l}}_j}{d1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)$$

(33)

or

$${\dot{\tilde{\mathit{l}}}}_j=-k_{\mathit{l}{1}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{a1{\mathit{l}}_j}{b1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)-k_{\mathit{l}{2}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{c1{\mathit{l}}_j}{d1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)$$

(34)

This completes the proof of stability of the proposed DO.

3.3. Stability Analysis

The Lyapunov condition is selected as follows:

$$V(t)=\frac{1}{2}{s}^{T}s+\frac{1}{2}{\tilde{l}}^T\tilde{l}$$

(35)

Taking the derivative for Equation (33) leads to

$$\dot{V}(t)=s^T\dot{s}+{\tilde{l}}^T\dot{\tilde{l}}$$

(36)

Equation (34) can be generally rewritten for each element as follows:

$$\begin{array}{l}{\dot{V}}_j=s_j{\dot{s}}_j-{\tilde{\mathit{l}}}_j{\dot{\tilde{\mathit{l}}}}_j\\ \begin{array}{cc}& =-\end{array}{s}_j[k_{s{1}_j}{\left|s_j\right|}^{\frac{a1s_j}{b1s_j}}sign(s_j)+k_{s{2}_j}{\left|s_j\right|}^{\frac{c1s_j}{d1s_j}}sign(s_j)]-\\ \begin{array}{cc}& \end{array}{\tilde{\mathit{l}}}_j(k_{\mathit{l}{1}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{a1{\mathit{l}}_j}{b1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j)+k_{\mathit{l}{2}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{c1{\mathit{l}}_j}{d1{\mathit{l}}_j}}sign({\tilde{\mathit{l}}}_j))\\ \begin{array}{cc}& =-\end{array}[k_{s{1}_j}{\left|s_j\right|}^{\frac{a1s_j}{b1s_j}+1}+k_{s{2}_j}{\left|s_j\right|}^{\frac{c1s_j}{d1s_j}+1}]-{\tilde{\mathit{l}}}_j(k_{\mathit{l}{1}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{a1{\mathit{l}}_j}{b1{\mathit{l}}_j}+1}+k_{\mathit{l}{2}_j}{\left|{\tilde{\mathit{l}}}_j\right|}^{\frac{c1{\mathit{l}}_j}{d1{\mathit{l}}_j}+1})\\ \begin{array}{cc}& \le 0\end{array}\end{array}$$

(37)

This completes the proof.

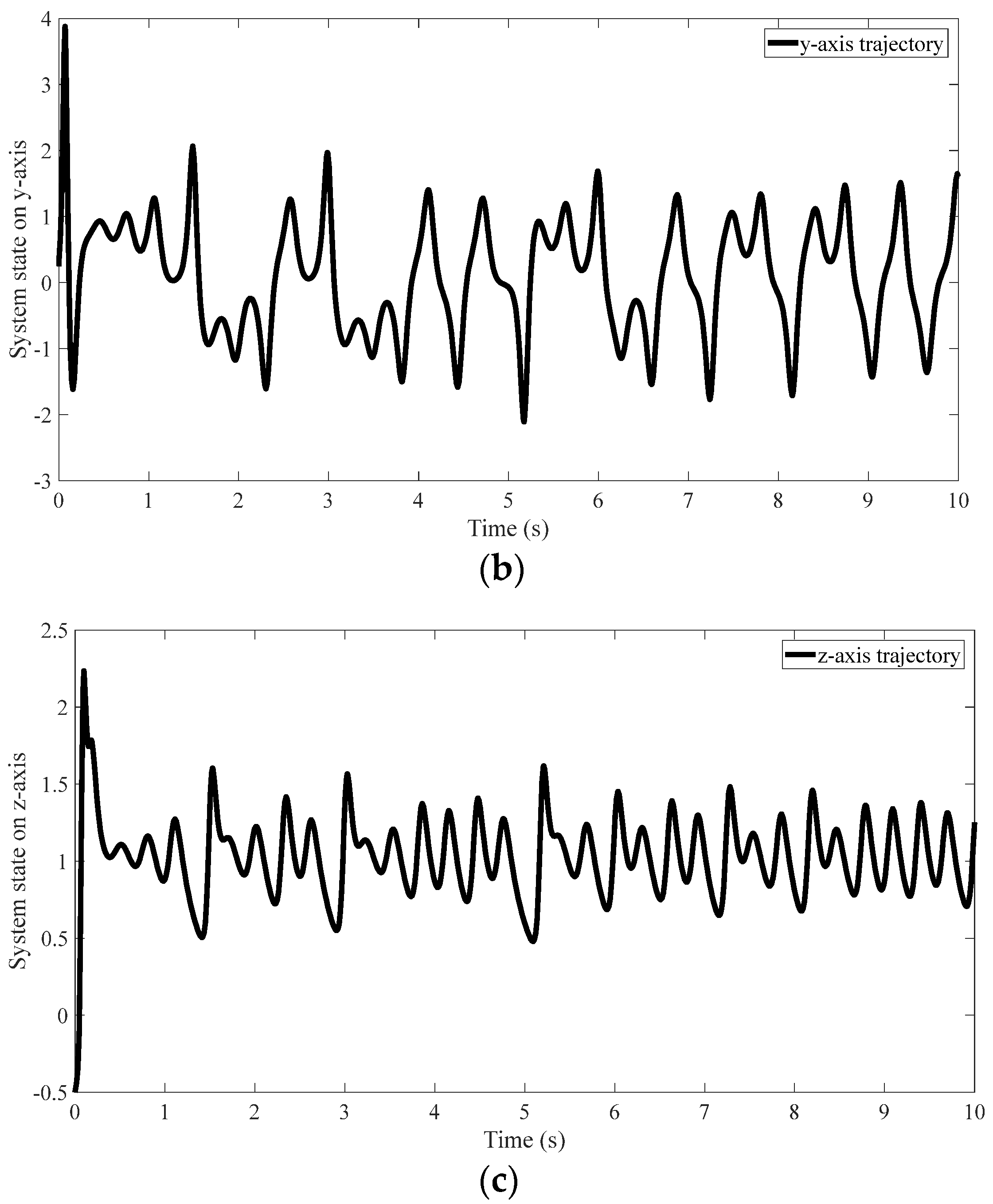
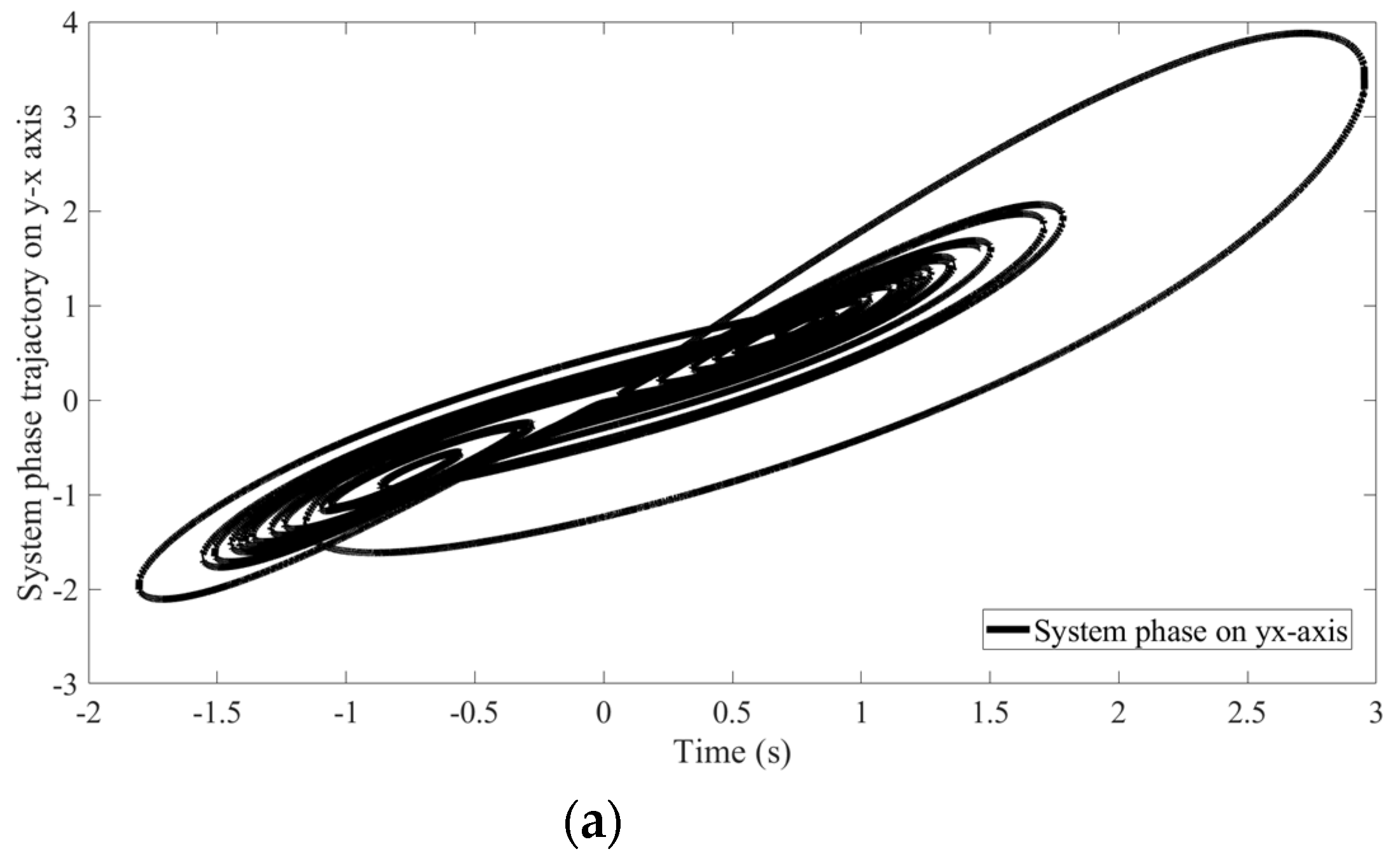
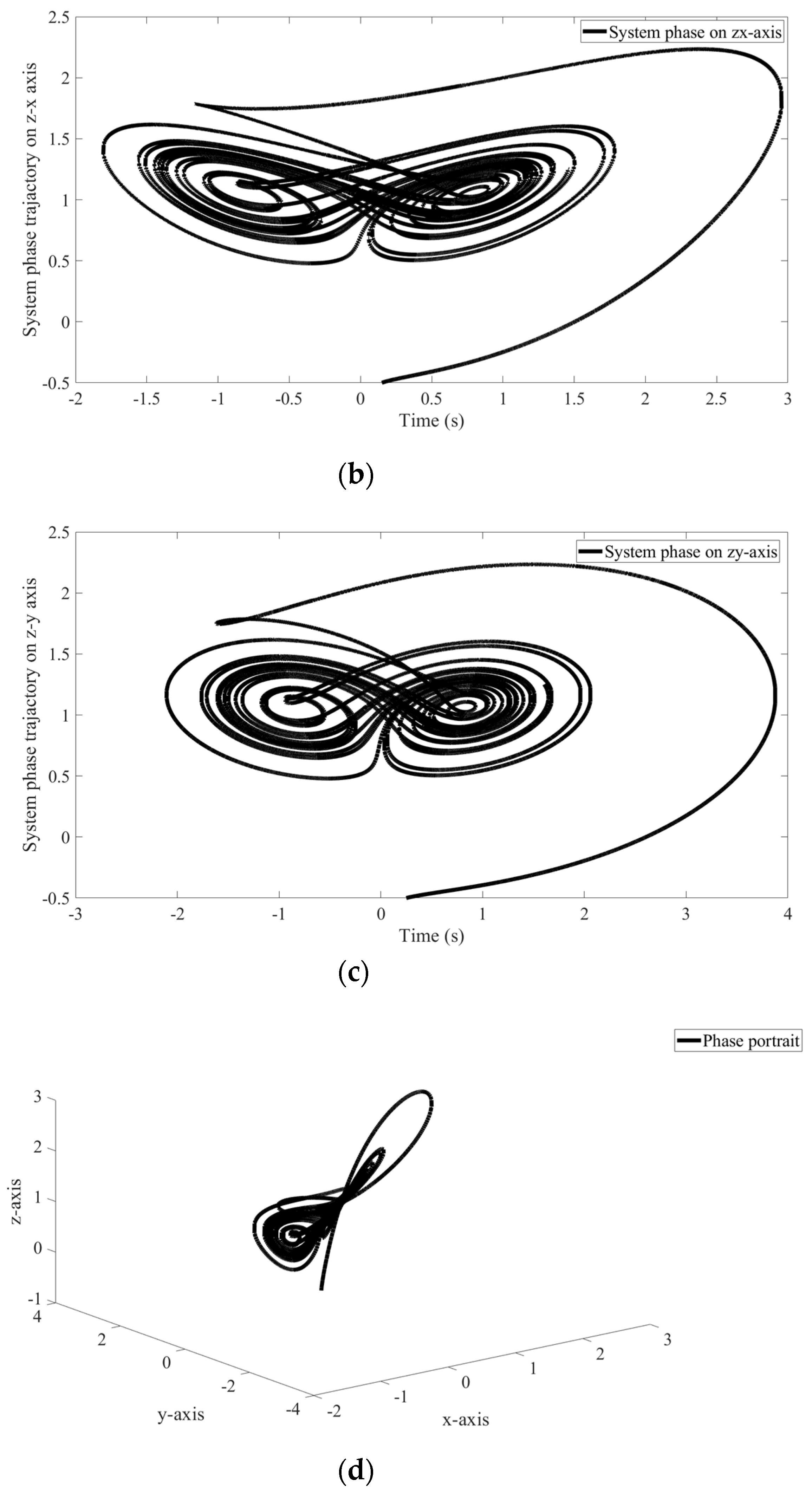
4. An Illustrative Example

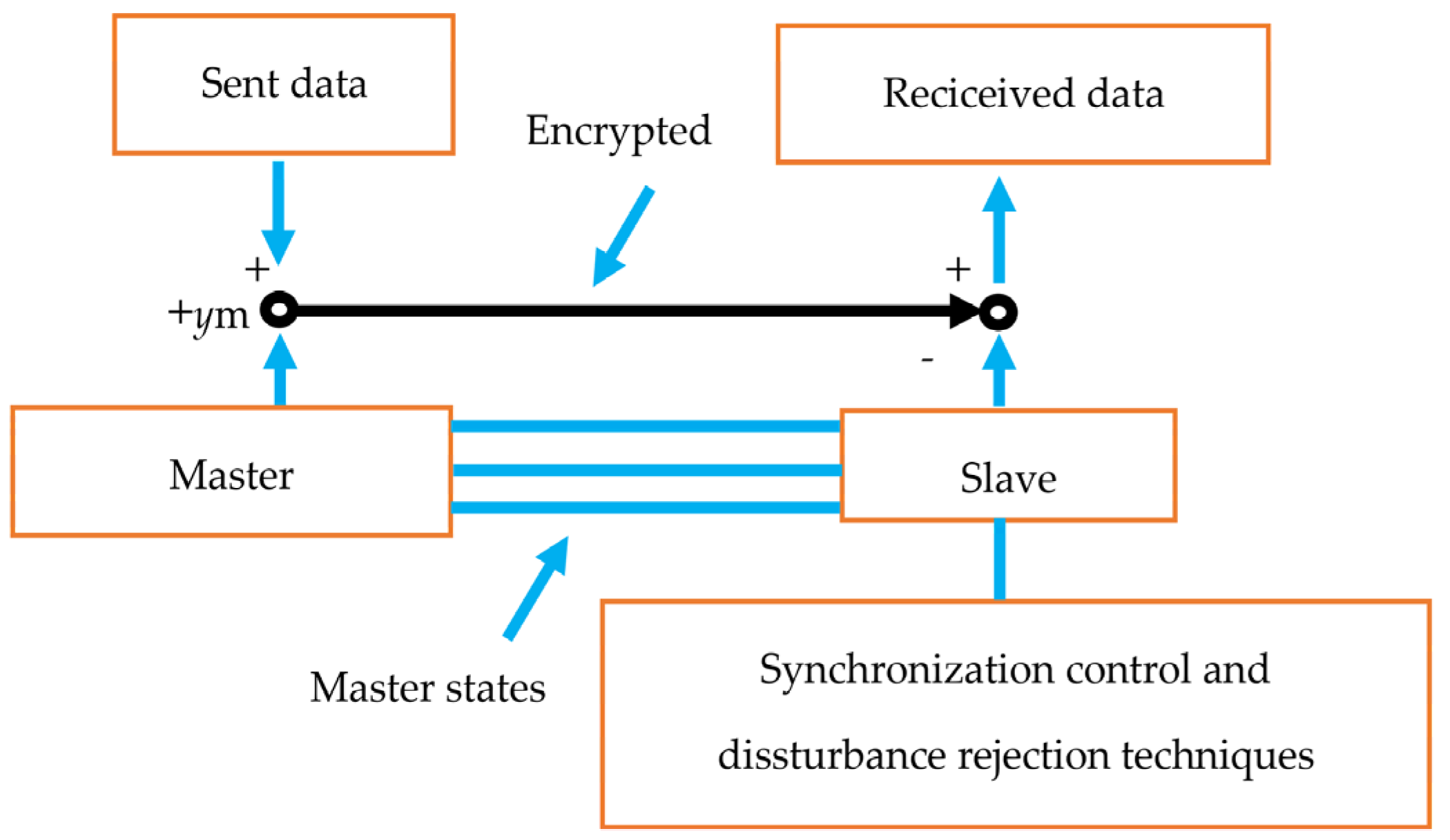
4.1. Scheme of SCS of the CBS and Parameters of Proposed Method

In this section, the performances of the proposed methods are given. First, the tracking of states of MSSs are shown. Second, the phases of MSSs are shown together in one figure for each axis. Third, the tracking errors are shown together with the analysis data. Fourth, the disturbance observer effectiveness is shown. Fifth, the secure data and encrypted date are shown. The secure communication scheme is shown in Figure 3.

Figure 3. Scheme of SCS of the CBS.

The secure date from the master area need to be mixed with the state of the master system and the mixed signal is provided onto the public channel, the received signal can be obtained with the decryption technique, which used the state of the slave system to archive the goal. As shown in Figure 3 above, to obtain the goal of transmission, the synchronization control and disturbance rejection are required. The control gains are as follows: first, the sliding phase gains of Equation (23) are $a1e1/b1e1=1.75,$ $a2e1/b2e1=0.85,$ $K_{e11}=2,$ $K_{e21}=2,$ $a1e2/b1e2=1.75,$ $a2e2/b2e2=0.85,$ $K_{e12}=2,$ $K_{e22}=2,$ $a1e3/b1e3=1.75,$ $a2e3/b2e3=0.85,$ $K_{e13}=2,$ $K_{e23}=2$. Second, the reaching phase gains of Equation (29) are $a1s1/b1s1=1.25,$ $a2s1/b2s1=0.75,$ $K_{s11}=50,$ $K_{s21}=50,$ $a1s2/b1s2=1.25,$ $a2s2/b2s2=0.75,$ $K_{s12}=50,$ $K_{s22}=50,$ $a1s3/b1s3=1.25,$ $a2s3/b2s3=0.75,$ $K_{s13}=50,$ $K_{s23}=50$. The gains of the DO in Equation (31) are $a1l1/b1l1=1.25,$ $a2l1/b2l1=0.95,$ $K_{l11}=100,$ $K_{l21}=100,$ $a1l2/b1l2=1.25,$ $a2l2/b2l2=0.95,$ $K_{l12}=100,$ $K_{l22}=100,$ $a1l3/b1l3=1.25,$ $a2l3/b2l3=0.95,$ $K_{l13}=100,$ and $K_{l23}=100$. The fractional order in Equation (1) is 0.99.

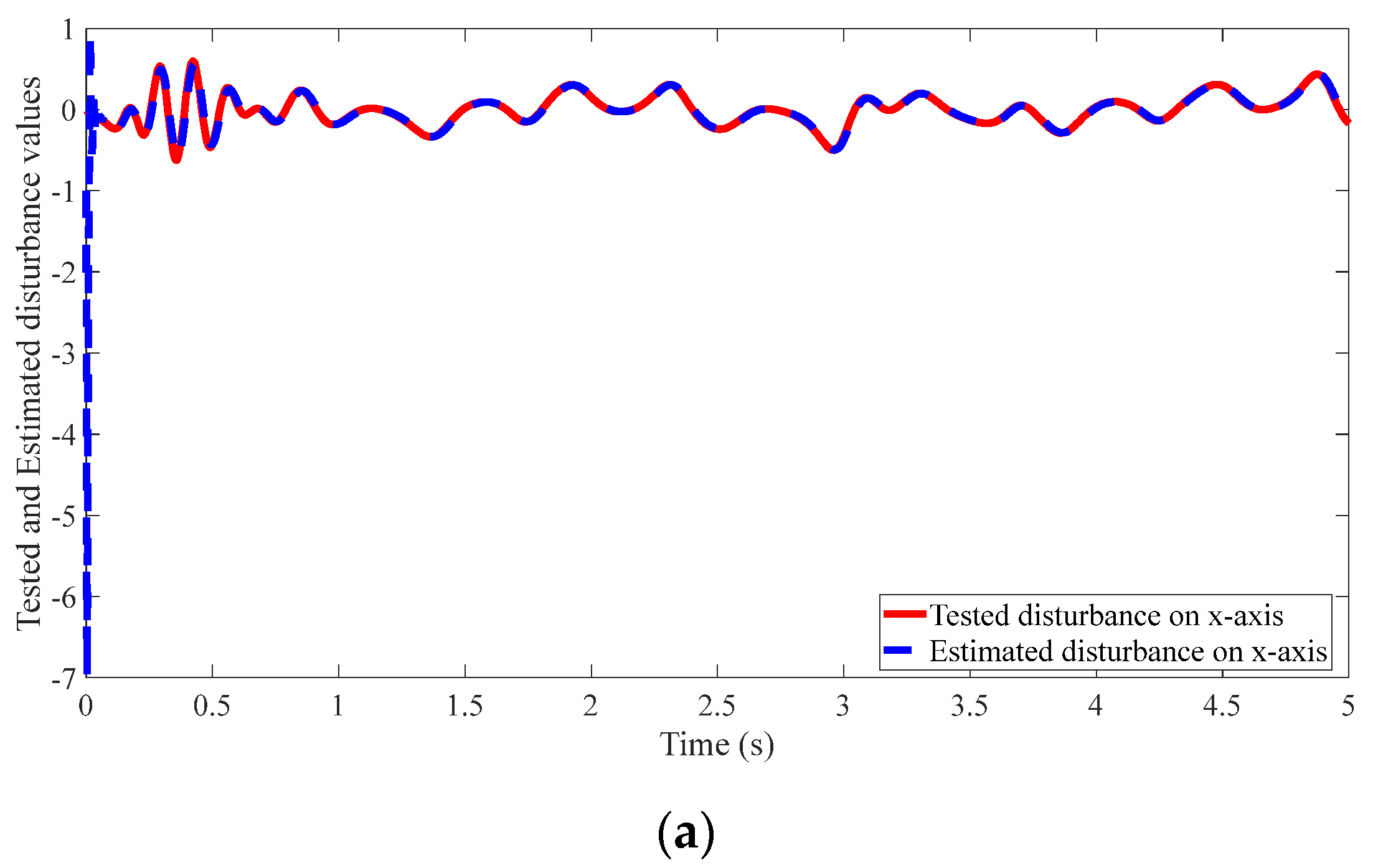
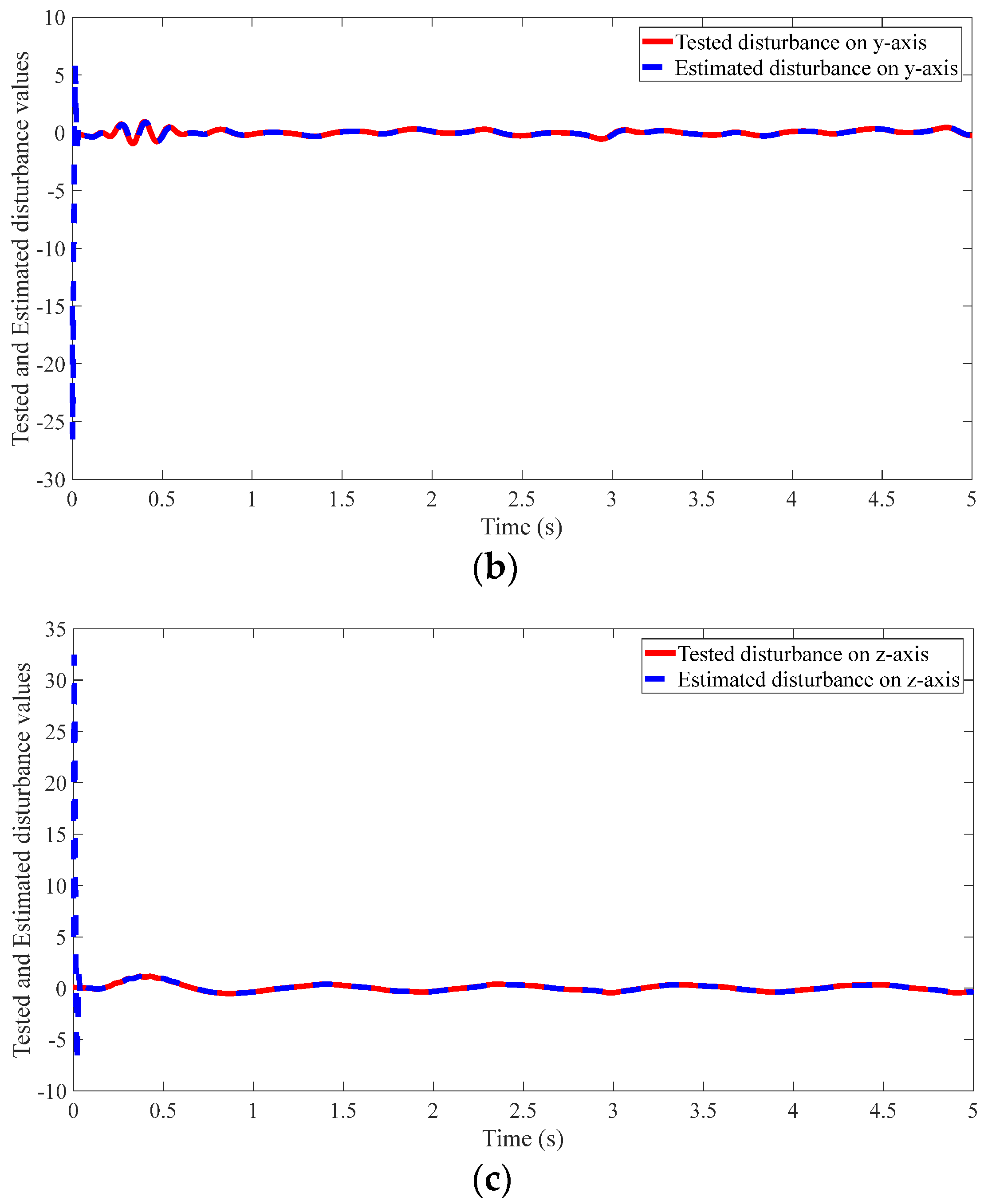
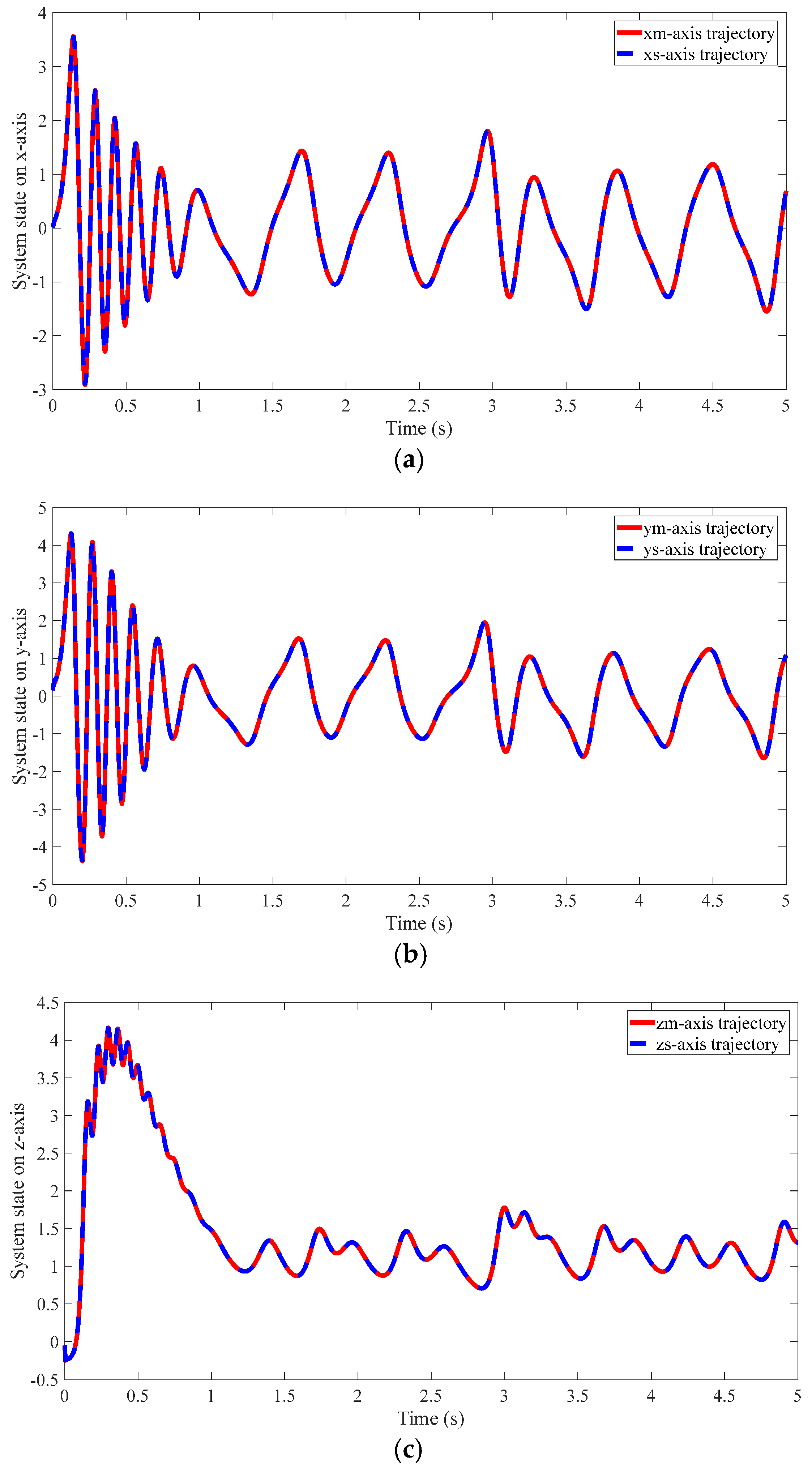
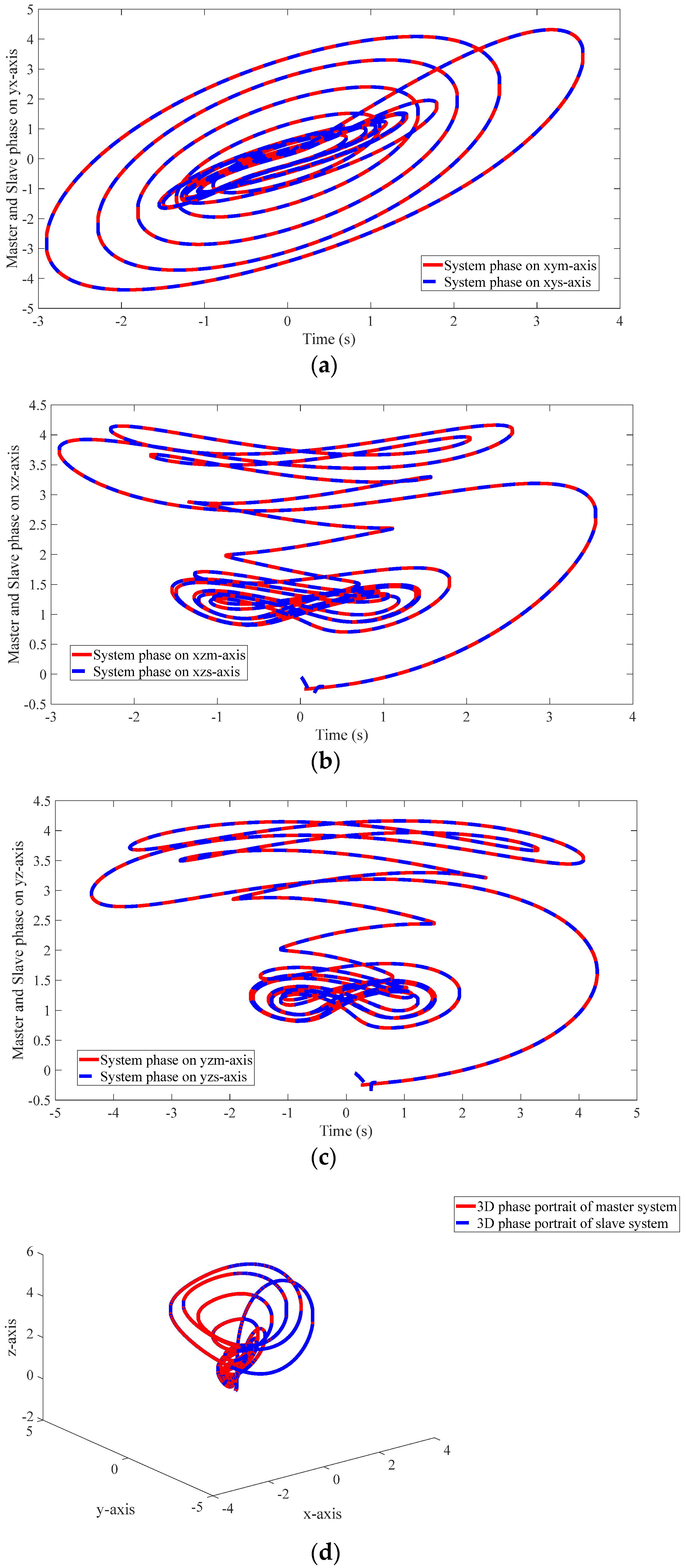
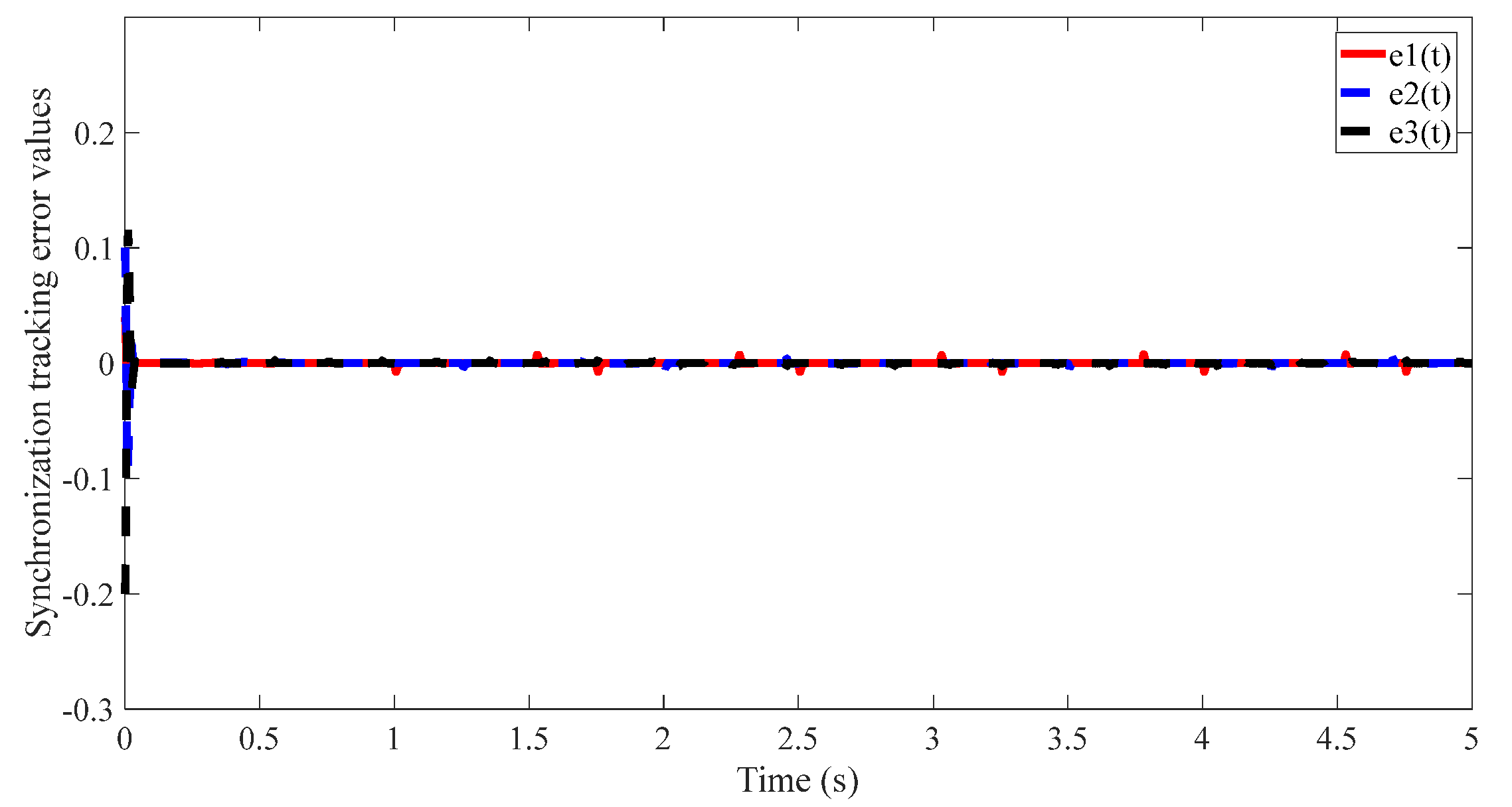
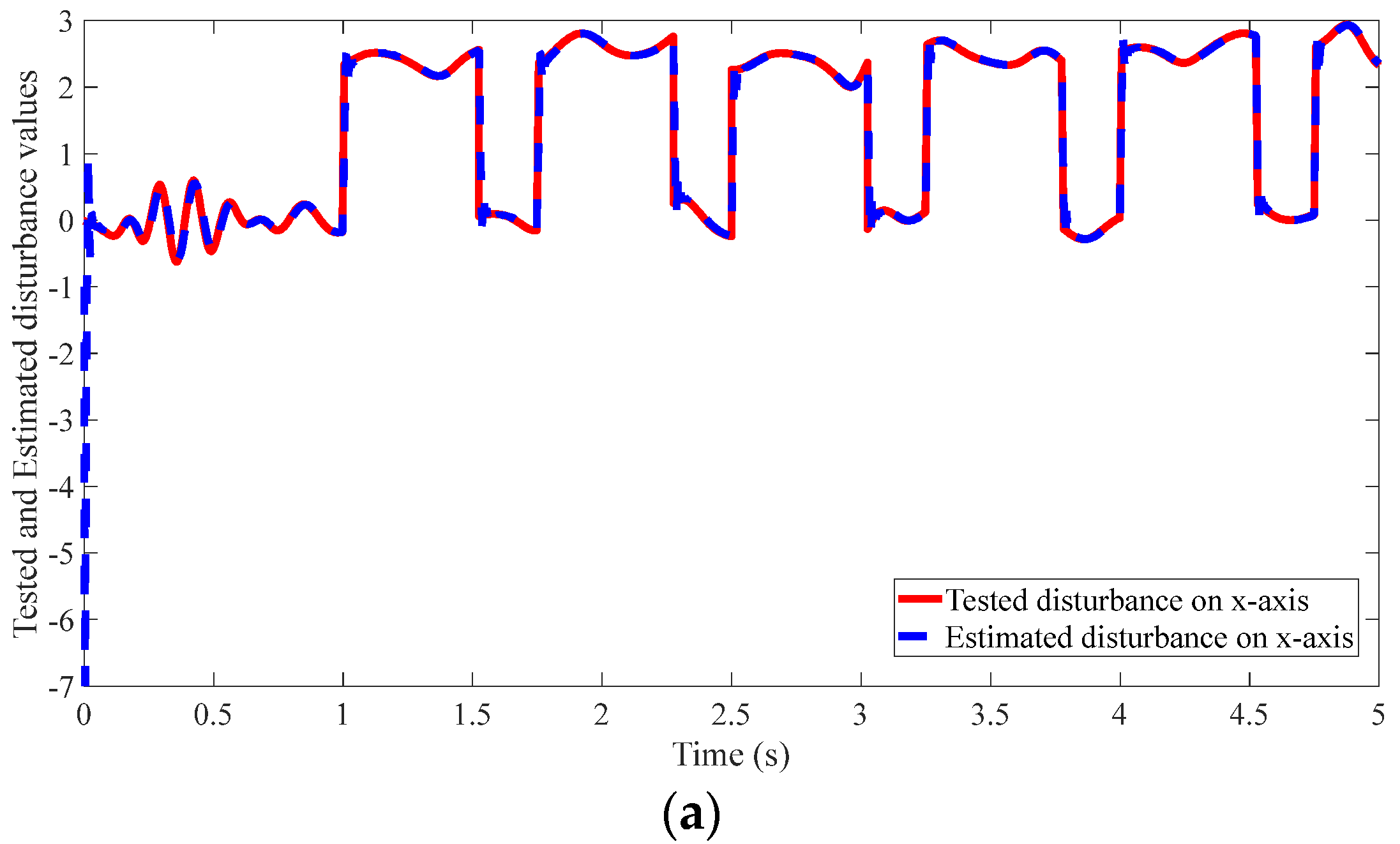
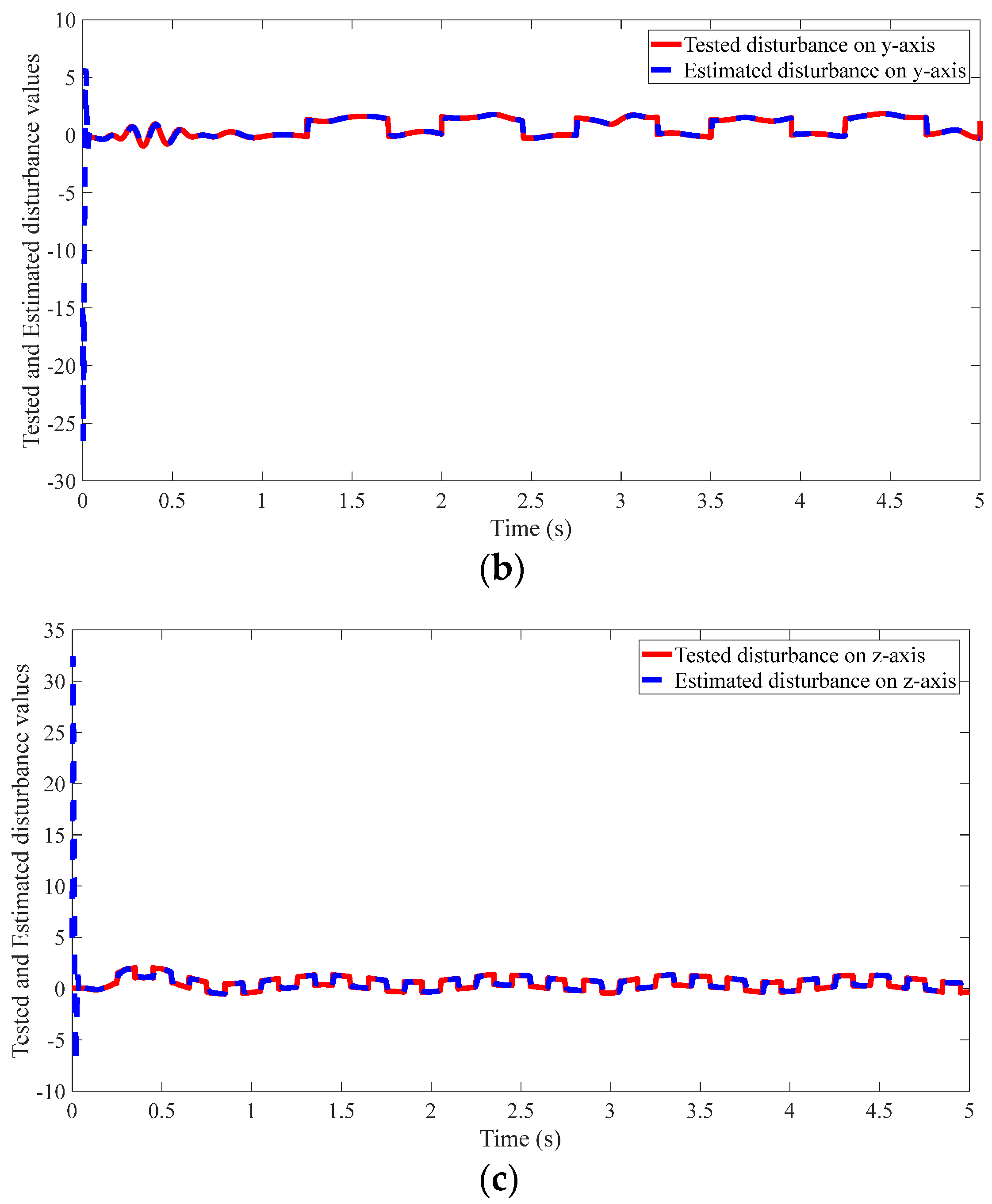
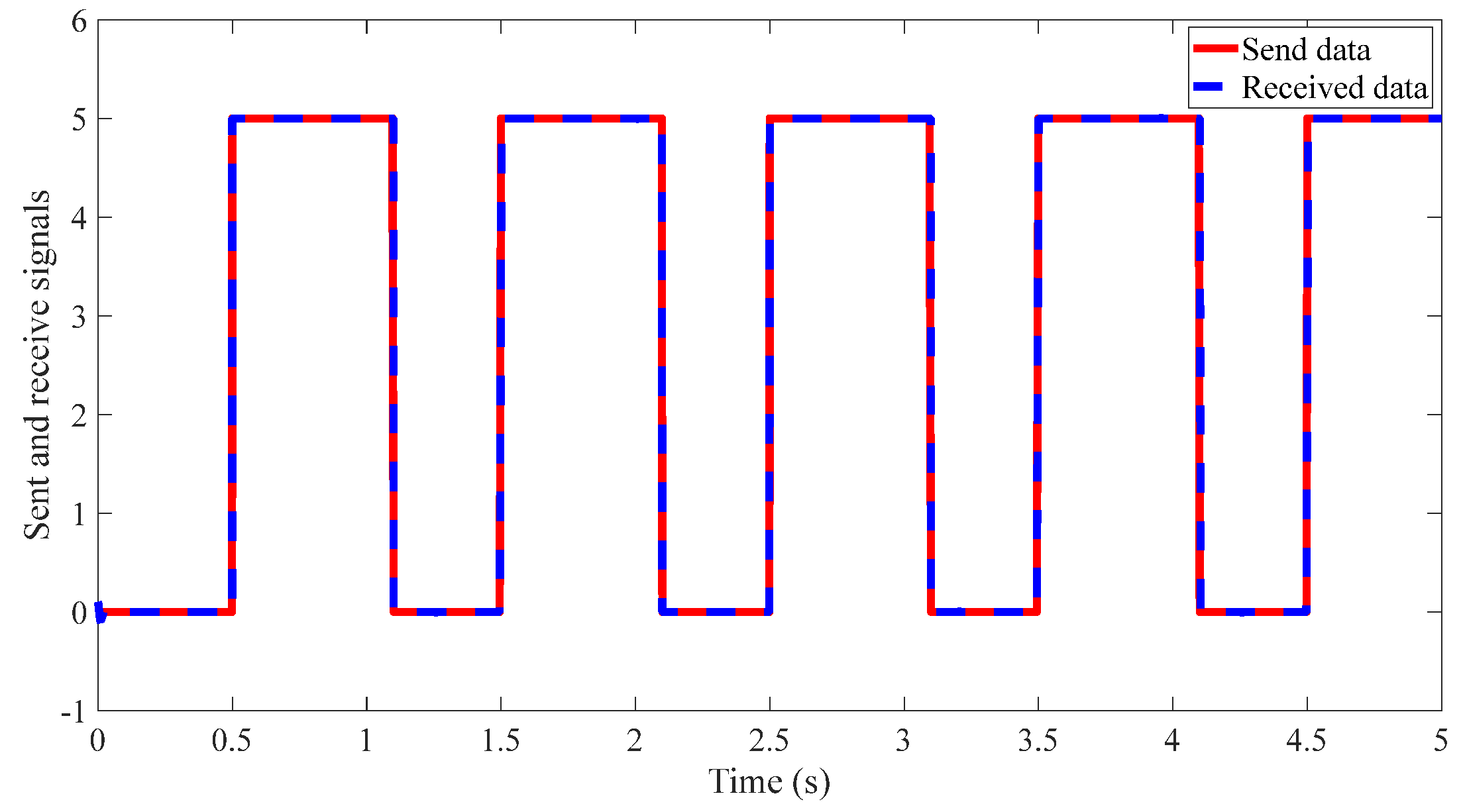
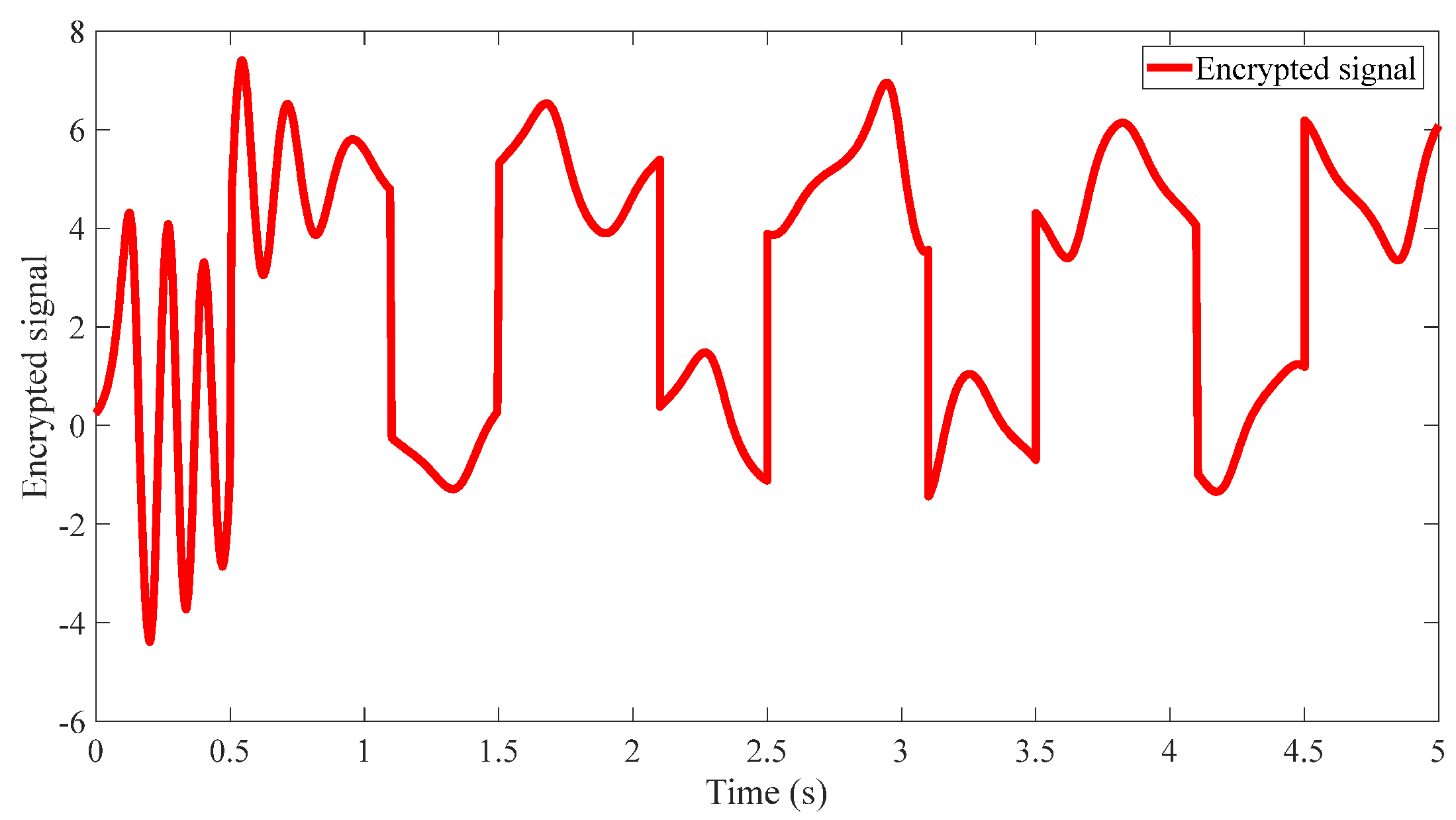
4.2. Results of the Proposed Method

The sine and cosine, and complicated disturbance and uncertainty were tested on the SCS of chaos-based system. However, the hash condition is mainly analyzed in this paper. Otherwise, the simple disturbance conditions were just used to analyze the effectiveness of the proposed DO.

Case 1.

Perturbations are periodic signals.

The uncertainties of master system are $l_{xm}(t)=-\mathrm{\Delta }a{x}_m(t)+\mathrm{\Delta }a{y}_m(t)=0.25cos(2\pi t)x_m(t),$ $l_{ym}(t)=-\mathrm{\Delta }\tau x_m(t)+\mathrm{\Delta }c{y}_m(t)=0.25cos(2\pi t)y_m(t),$ and $l_{zm}(t)=-\mathrm{\Delta }b{z}_m(t)=0.25cos(2\pi t)z_m(t)$ on xm-, ym-, and zm-axes, respectively. The uncertainties of slave system are $l_{xs}(t)=-\mathrm{\Delta }a{x}_s(t)+\mathrm{\Delta }a{y}_s(t)=0.15sin(2\pi t)x_s(t),$ $l_{ym}(t)=-\mathrm{\Delta }\tau x_s(t)+\mathrm{\Delta }c{y}_s(t)=0.15sin(2\pi t)y_s(t),$ and $l_{zm}(t)=-\mathrm{\Delta }b{z}_s(t)=0.25cos(2\pi t)z_s(t)$ on xs-, ys-, and zs-axes, respectively. The performance of the proposed DO is shown as in Figure 4 below.

Figure 4. Tested and estimated disturbances on three axes, (a) $l_x$ and ${\widehat{l}}_x,$ (b) $l_y$ and ${\widehat{l}}_y,$ and (c) $l_z$ and ${\widehat{l}}_z.$ .

The tested uncertainties on three channels of MSSs were compensated by the estimated disturbance values. To show the effectiveness of the proposed control method with both disturbance and uncertainty rejection ability, the disturbance and uncertainty were tested in case 2 as below.

Case 2.

Perturbations are periodic signals together with square disturbances.

The uncertainties of the master system are $l_{xm}(t)=-\mathrm{\Delta }a{x}_m(t)+\mathrm{\Delta }a{y}_m(t)=0.25cos(2\pi t)x_m(t),$ $l_{ym}(t)=-\mathrm{\Delta }\tau x_m(t)+\mathrm{\Delta }c{y}_m(t)=0.25cos(2\pi t)y_m(t),$ and $l_{zm}(t)=-\mathrm{\Delta }b{z}_m(t)=0.25cos(2\pi t)z_m(t)$ on xm-, ym-, and zm-axes, respectively. The uncertainties of the slave system are $l_{xs}(t)=-\mathrm{\Delta }a{x}_s(t)+\mathrm{\Delta }a{y}_s(t)=0.15sin(2\pi t)x_s(t),$ $l_{ym}(t)=-\mathrm{\Delta }\tau x_s(t)+\mathrm{\Delta }c{y}_s(t)=0.15sin(2\pi t)y_s(t),$ and $l_{zm}(t)=-\mathrm{\Delta }b{z}_s(t)=0.25cos(2\pi t)z_s(t)$ on xs-, ys-, and zs-axes, respectively. The tested disturbance are as follows: $d_1(t)$ with 2.5 amplitude, 0.75 period, 70% pulse width, and delay time is 1 s, $d_2(t)$ with 1.5 amplitude, 0.75 period, 60% pulse width, and delay time is 1.25 s, and $d_3(t)$ with 1 amplitude, 0.2 period, 50% pulse width, and delay time is 0.25 s for x-, y-, and z-axes, respectively. The performance of the proposed DO is shown as in Figure 5 below.

Figure 5. States of MSSs, (a) $x_m$ and $x_s,$ (b) $y_m$ and $y_s,$ and (c) $z_m$ and $z_s.$

The states of MSSs are mostly identical with very fast convergent speeds. The red color state is used for the master and blue color state for the slave systems. The states of the MSSs are unpredicted signals, which correspond with the original state of chaotic system. To show the effectiveness of proposed method for synchronizing two different chaotic systems, the phase trajectories of MSSs are displayed in Figure 6 below.

Figure 6. Phase portraits of MSSs, (a) state on yx-axis, (b) state on zx-axis, (c) state on zy-axis, (d) 3D phase portrait.

In Figure 6, the phase of the states of both the master and slave systems are mostly converged to each other. These phases are the most similar to the original phases. The phase portraits of the MSSs were mostly identical and correspond to the original one. The simulations performed demonstrated that the synchronization control method is satisfied for the secure communication of chaos-based system. To show the effectiveness of the proposed method, the synchronization errors are shown in Figure 7 below.

Figure 7. Tracking errors on three axes.

The tracking errors of these axes are converged to zero in the settling-times $T_{e1}<0.07$ (s), $T_{e1}<0.07$ (s), and $T_{e1}<0.07.$ The maximum errors are $Ma{x}_{e1}<0.022,$ $Ma{x}_{e2}<0.095,$ and $Ma{x}_{e3}<0.116.$ In steady-states, the errors are located in the areas of $e_1\in (-7.3;7.3)\times {10}^{-3},$ $e_2\in (-4.5;4.5)\times {10}^{-3},$ and $e_1\in (-2.65;2.65)\times {10}^{-3}.$ The effectiveness of the proposed DO for estimating both disturbance and uncertainty are shown in Figure 8 below.

Figure 8. Tested and estimated disturbances and uncertainty on three axes, (a) $l_x$ and ${\widehat{l}}_x,$ (b) $l_y$ and ${\widehat{l}}_y,$ and (c) $l_z$ and ${\widehat{l}}_z.$

As shown in Figure 8 above, the tested disturbances with system parameter variations were all tested on the SCS. The expectation of disturbance rejection is met. The tested disturbance and uncertainty in both master and slave systems were mostly rejected by the proposed DO. There are simple and complicated disturbances which were mostly rejected by the proposed DO. In Figure 8, the disturbances and uncertainties were nonidentical, the disturbances were square waves and uncertainties were periodic signals. These signals were mixed together and challenged the performances of the proposed DO. Therefore, Figure 8 was used to validate the correctness and effectiveness of the proposed DO. The sent and received data are shown in Figure 9 below.

Figure 9. Sent and received data.

In this work, the square wave signal was used to test the performance of the SCS. The received and sent date are mostly identical. From this, we can state that the proposed control method is good for the synchronization and robustness with regards to disturbance and uncertainty. If a hacker wanted to extract the data on the public channel, they would have been able to see the signal such as that in Figure 10 below.

Figure 10. Encrypted data.

The signal as in Figure 10 has no meaning. This is the expectation of the work in secure communication. The obtained results are good enough for such complicated disturbance values. To show the effectiveness of the proposed method, the comparison of this paper and a previous paper is shown in Table 1 below.

Table 1. Comparison of this paper and a previous paper [11].

Paper	Maximum Settling-Time	Maximum Error	Disturbance Rejection
This paper	0.07 s	$Ma{x}_{e3}<0.116.$	Yes
Previous paper [11]	$>$1 s	$>$5	Was not mentioned

Therefore, the proposed method in this paper is good for synchronizing two nonidentical chaotic systems and rejecting the perturbations from inside and outside of the SCS.

5. Conclusions

A new DO for SCS of the CBS was successfully proposed. The conditions of boundary disturbance value and the frequency of disturbance were deleted. A new DO only needs the states of MSSs to be closed to each other. The estimated and tested disturbances are closed to each other in a predefined time. This is also a new concept of the DO for SCS of CBS. In this paper, the chattering of conventional SMC was deleted by the fixed-time SMC with double reaching and sliding phases. The correction of the proposed methods was proved by using Lyapunov condition. The effectiveness of the proposed methods was verified by MATLAB simulation. The achievement of disturbance rejection was used to show the novelty and originality of proposed DO. This has huge implications for our next research in SCS of CBS. In our next study, the proposed concept of the DO will be improved and verified by experiments for the secure communication of the chaos-based system.