Abstract
The thermodynamics and phase transitions of magnetic Anti-de Sitter black holes were studied. We considered extended-phase-space thermodynamics, with the cosmological constant being a thermodynamic pressure and the black hole mass being treated as a chemical enthalpy. The extended-phase-space thermodynamics of black holes mimic the behavior of a Van der Waals liquid. Quantities conjugated to the coupling of nonlinear electrodynamics (NED) and a magnetic charge are obtained. Thermodynamic critical points of phase transitions are investigated. It was demonstrated that the first law of black hole thermodynamics and the generalized Smarr relation hold. The Joule–Thomson adiabatic expansion of NED-AdS black holes is studied. The dependence of inversion temperature on pressure and the minimum of the inversion temperature are found.
1. Introduction
Black hole thermodynamics are important for the understanding and development of quantum gravity. The matter is that the microscopic structure of a black hole is unknown. Now, there is evidence that black holes behave as thermodynamic systems [1,2,3]. The area of a black hole is considered as the entropy, and the surface gravity is connected with the temperature [4,5]. The interest in AdS space-time is increased because of a holographic picture where black holes are systems that are dual to conformal field theories [6,7,8]. In addition, space-time with a negative cosmological constant allows phase transitions in black holes [9]. Holography helps solve some problems in quantum chromodynamics [10] and condensed matter physics [11,12]. The cosmological constant in gravity theory is understood as a vacuum expectation value of fields; therefore, it may vary. Hence, the cosmological constant should be included in black hole thermodynamics. In extended-phase-space thermodynamics of black holes, the cosmological constant is treated as a thermodynamic pressure, which is a conjugate to a volume, and the phase transitions mimic Van der Waals liquid–gas behavior [13,14].
In this paper, we study nonlinear electrodynamics (NED)—proposed in [15,16,17]—coupled with AdS gravity in extended-phase-space thermodynamics. In some NED [18,19,20,21] (and others), singularities in the centers of point-like electric charges are absent. In addition, quantum corrections are taken into account in the Euler–Heisenberg NED [22]. Born–Infeld AdS gravity was studied in [23,24,25,26,27,28,29,30,31,32], where an analogy with Van der Waals fluids was shown. criticality and extended-phase thermodynamics were studied in [14,23,33,34,35,36,37,38,39,40].
Here, the Joule–Thomson adiabatic thermal expansion of NED–AdS black holes with heating and cooling regimes is studied. The black hole’s mass is considered as the enthalpy, which is constant during the Joule–Thomson expansion.
The structure of the paper is as follows. We obtain the NED–AdS metric function of magnetic black holes and corrections to the Reissner–Nordström solution in Section 2. In Section 3, the first law of black hole thermodynamics in the extended phase space with a negative cosmological constant, which is a pressure, is studied. We define the thermodynamic magnetic potential and the thermodynamic conjugate to the NED coupling. It is shown that the generalized Smarr relation holds. The critical specific volume, critical temperature, and critical pressure are found in Section 4. In Section 4.1, the Gibbs free energy is analyzed to show the critical behavior. The Joule–Thomson adiabatic NED–AdS black hole expansion is studied in Section 5. The inversion temperature and pressure are obtained, and their dependence on the model parameters is investigated. Section 6 is a summary.
We use units with , , and .
2. NED–AdS Black Hole Solution
The action of NED coupled with Einstein–AdS gravity is given by
where is Newton’s constant, is the negative cosmological constant, and l is the AdS radius. Here, the NED Lagrangian proposed in [15] (see also [16,17]) is
where is the field strength invariant, B and E are the magnetic and electric fields, respectively, and . At , Equation (2) is converted into Maxwell’s electrodynamic Lagrangian. The reason for choosing the theory with the NED Lagrangian (2) is its simplicity. The metric and other functions are simple elementary functions. The gravitation and electromagnetic field equations are obtained through the variation of action (1) with respect to the metric and potential :
with . Making use of Equation (2), we obtain the energy–momentum tensor of the NED:
Equations (3)–(5) hold for a general function . Here, we consider space-time with spherical symmetry:
The metric function is given by [41]
with the mass function
M is the ADM black hole’s mass and is the energy density. We study magnetic black holes because models with electrically charged black holes and with the Maxwell weak-field limit have singularities [41]. Then, , and the Lorentz invariant is , where q is the magnetic charge. Therefore, we consider black holes as magnetic monopoles. By virtue of Equation (5), the energy density with the cosmological constant term is given by
This and the following equations are obtained for the NED Lagrangian (2). The mass function follows from Equations (8) and (9):
It is worth mentioning that, in our NED model (2), the total magnetic mass is infinite. From Equations (7) and (10), one finds the metric function
With the help of Equation (11), ignoring the cosmological constant (), we obtain the metric function when r approaches infinity:
Making use of Equation (12), at , one finds the metric function of the Reissner–Nordström space-time. From Equation (12), one can obtain corrections to the Reissner–Nordström black holes in the order of . In Figure 1, the plots of the metric function (11) are depicted at and for different parameters.
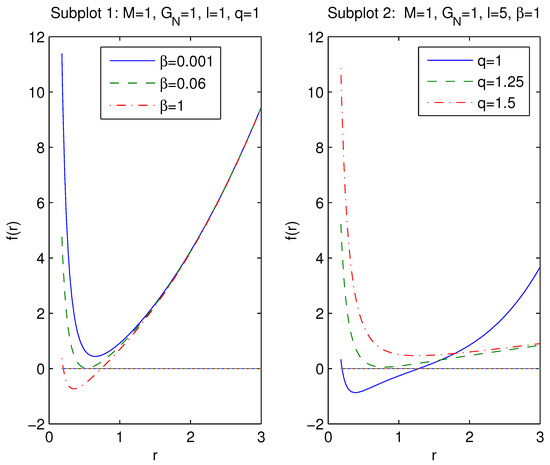
Figure 1.
The plots of the function at and .
According to Figure 1 black holes could have two event horizon radii or one extreme event horizon radius for various parameters. It should be noted that, when there is no horizon, it is not a black hole, and there is a naked singularity. In Figure 1, subplot 1 shows that, when the coupling increases—with a fixed magnetic charge q and the AdS radius l—the event horizon radius (the largest root of the equation ) increases. However, if the magnetic charge increases, at a fixed NED parameter and with the cosmological constant, the event horizon radius decreases.
3. The First Law of Black Hole Thermodynamics and the Smarr Relation
By introducing the pressure that is connected with a negative cosmological constant [42,43,44], we can formulate the generalized first law of black hole thermodynamics: . Here, M is treated as a chemical enthalpy [42] so that , where U is the internal energy. Making use of the Euler scaling argument [42,45], we can find the generalized Smarr relation from the first law of BH thermodynamics. The dimensional analysis, with , gives , , , , , and . Here, is considered as a thermodynamic variable. By using the Euler theorem, one obtains the mass
where is the thermodynamic conjugate to the NED coupling . The black hole’s entropy S, volume V, and pressure P are given by [46,47]
With the aid of Equation (11) and the equation for the event horizon radius , we obtain the black hole’s mass:
Making the limit in Equation (15), one finds the mass function of Maxwell–AdS black holes:
By virtue of Equation (15), for a non-rotating black hole, where and , we obtain
The Hawking temperature is given by
with . From Equations (11) and (18) and with at , one finds
Making use of Equations (14), (17), and (19), we obtain the first law of black hole thermodynamics:
From Equations (17) and (20), one finds the magnetic potential and vacuum polarization :
It should be noted that , and the potential at corresponds to the potential of a point-like magnetic monopole . Thus, the coupling smoothes the singularity at . Plots of the potential and versus are depicted in Figure 2.
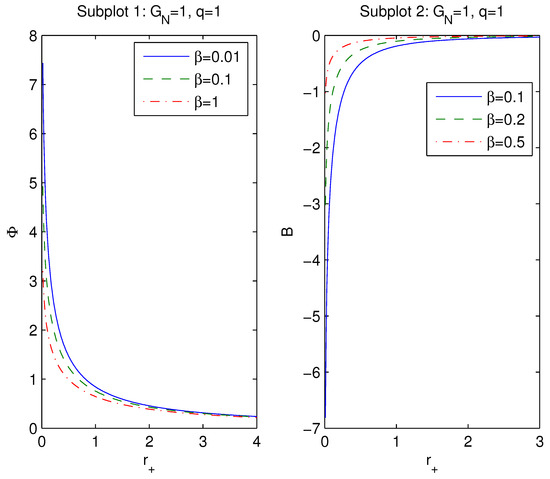
Figure 2.
Plots of the functions and vs. at .
In Figure 2, subplot 1 shows that, when the coupling increases, the magnetic potential decreases, and at , it vanishes (). In accordance with subplot 2 of Figure 2, when the parameter increases, the vacuum polarization decreases, and as , we have . Making use of Equations (14), (15), (19), and (21), one can verify that the generalized Smarr relation holds:
4. Black Hole Thermodynamics
Making use of Equation (19), we obtain the black hole’s equation of state (EoS):
At , Equation (23) becomes the EoS for a charged Maxwell–AdS black hole [40]. The EoS of the charged AdS black hole is similar to the EoS of a Van der Waals fluid when the specific volume [40] with . Then, Equation (23) is rewritten as
Critical points that correspond to inflection points in the diagram can be found by solving the following equations:
Making use of Equation (25), one finds the equation for the critical points:
Solutions (which are approximate) to Equation (26), as well as the critical temperatures and pressures, are presented in Table 1.

Table 1.
Critical values of the specific volume and temperature at .
The plots of diagrams for various parameters are depicted in Figure 3.

Figure 3.
Plots of the function P vs. v at , . The critical isotherm corresponds to .
The approximate solution to Equation (26) at , is , and the critical temperature and pressure are and , respectively. The critical isotherm corresponds to , but the non-critical behavior of the diagrams is for , , and . The two upper curves in Figure 3 show the one-phase state for and correspond to an “ideal gas". The lower solid line shows a two-phase behavior for . From Equations (27) and (28), we obtain the critical ratio:
By virtue of Equation (29), at (), one finds the ratio , which corresponds to a Van der Waals fluid.
4.1. The Gibbs Free Energy
The Gibbs free energy is given by
where the black hole’s mass M is treated as a chemical enthalpy. From Equations (20) and (30), one finds . Therefore, G is stationary at fixed (). With the help of Equations (15), (19), and (30), we obtain ():
We will study the dependence of the Gibbs free energy G on the temperature T for different fixed () values. The plots of G versus T, where we took into account that is a function of P and T (see Equation (23)), are depicted in Figure 4.
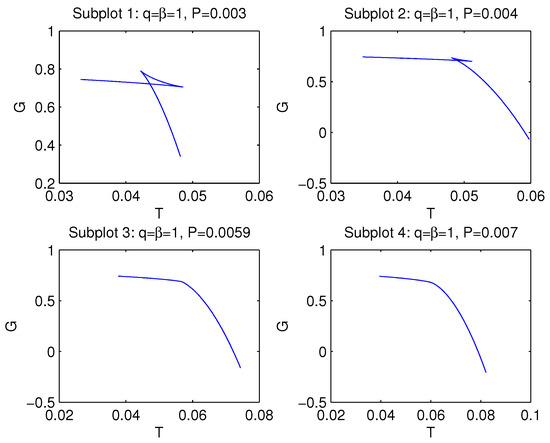
Figure 4.
Plots of the Gibbs free energy G vs. T with , .
Subplots 1 and 2 in Figure 4 show first-order phase transitions between small and large black holes. The Gibbs free energy at has a “swallowtail” behavior. The points on the curves correspond to different event horizon radii of black holes. At the critical point— (), , and at in subplot 3—a second-order phase transition takes place. Subplot 3 shows that there is a cusp at the critical point. Hence, the second derivative of the Gibbs free energy G with respect to temperature T is discontinuous at that point. We check this analytically in Appendix A. The behavior is similar to that of the Reissner–Nordström–AdS black hole. In subplot 4, for , only a single phase exists, and we have a smooth single-valued curve. Plots of entropy S versus temperature T at are depicted in Figure 5. According to subplots 1 and 2 of Figure 5, the entropy is an ambiguous function of the temperature for some regions. This confirms that, for such a region, first-order phase transitions occur. Subplot 3 of Figure 5 shows the second-order phase transition, where the tangent of the slope at the critical point at , , and is infinite. The critical point separates a low-entropy state and a high-entropy state. In accordance with subplot 4 of Figure 5, there is not a critical behavior of a black hole.
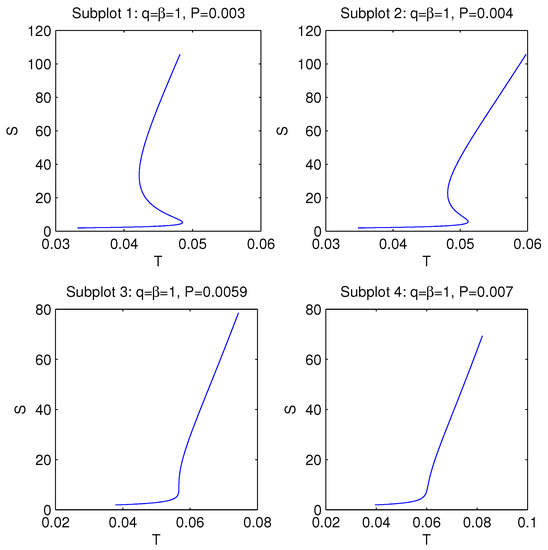
Figure 5.
Plots of the entropy S vs. temperature T at , .
5. Joule–Thomson Expansion of Black Holes
In Joule–Thomson adiabatic expansion (isenthalpic), the black hole’s mass M, which is the enthalpy, is constant. The Joule–Thomson thermodynamic coefficient, which characterizes cooling–heating phases, is given by
The Joule–Thomson coefficient , according to Equation (32), is the slope of the tangent in diagrams. At the inversion temperature , when , the sign of is changed. When the initial temperature during the isenthalpic expansion is higher than the inversion temperature , the temperature decreases, which is a cooling phase (); however, if the initial temperature is lower than , the final temperature increases for this heating phase. Making use of Equation (32) and , one obtains the inversion temperature:
In fact, the inversion temperature is a border between cooling and heating processes. The inversion temperature goes through the maxima of diagrams, the slopes of the diagrams are changed, and the cooling and heating phases of black holes are separated [48,49]. The black hole EoS (23) can be represented as
At , Equation (34) is converted into the Maxwell–AdS black hole EoS. From Equation (15) and , we obtain
Equations (34) and (35) represent the diagrams in parametric form, and they are depicted in Figure 6.
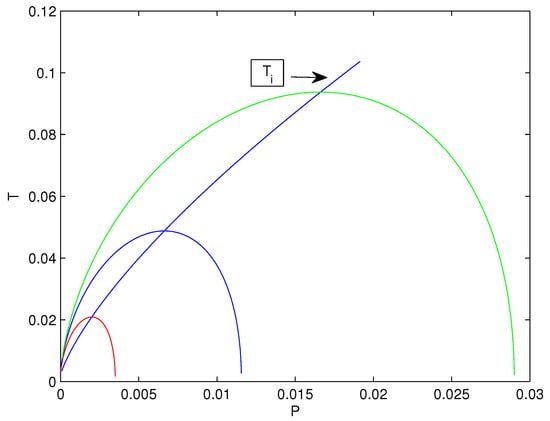
Figure 6.
Plots of the temperature T vs. pressure P and the inversion temperature with , . The diagrams correspond to the masses , 14, and 16, from bottom to top.
In accordance with Figure 6, when the black hole’s mass increases, the inversion point increases. Making use of Equations (33) and (34), one finds the equation for the inversion pressure :
By using Equations (34) and (36), we obtain the inversion temperature:
Equations (36) and (37) are equations for the inversion temperature versus in the parametric form. The plots of versus are depicted in Figure 7. According to subplot 1 of Figure 7, the inversion temperature increases with q. Subplot 2 of Figure 7 shows that the inversion temperature decreases when the coupling increases.
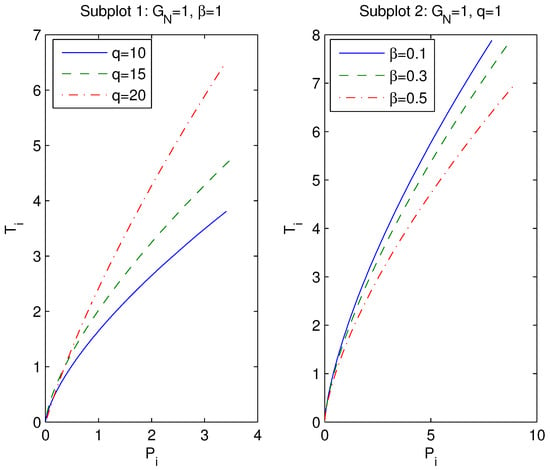
Figure 7.
Plots of the inversion temperature vs. pressure .
If , we have a cooling process, while when , a heating process occurs. In Figure 6, the area with belongs to the left side of the inversion temperature border line; however, corresponds to the right site of the border line . Putting into Equation (36), we obtain the equation for the minimum of the event horizon radius :
where . The discriminant of cubic Equation (38) is negative; therefore, Equation (38) possesses three real solutions—one is a positive physical solution and two are negative non-physical solutions: . The positive physical solution to Equation (38) is given by
Making use of Equations (37) and (39), the plot of the minimum inversion temperature versus the coupling is depicted in Figure 8.
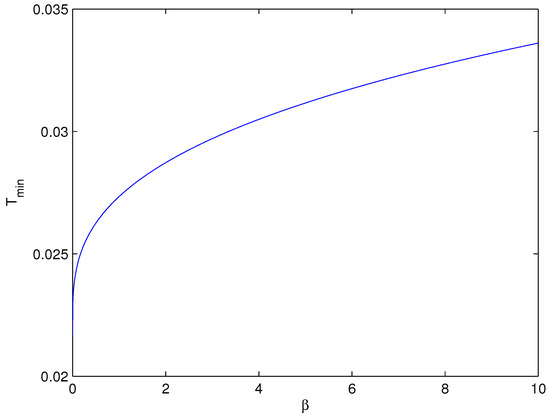
Figure 8.
Plots of the minimum inversion temperature vs. for .
By virtue of Equations (38) and (39), at , we obtain the minimum of the inversion temperature for Maxwell–AdS magnetic black holes:
From Equations (26) and (27), at (), and from Equation (40), one finds the relation , which is valid for electrically charged AdS black holes [50].
6. Summary
We studied NED coupled with Einstein–AdS black holes and obtained their metric and mass functions. Black holes can have one or two horizons depending on the magnetic charge q, coupling , and AdS radius l. At and , the corrections to the Reissner–Nordström solution are in the order of . We formulated NED–AdS black hole thermodynamics in an extended thermodynamic phase space where the cosmological constant was considered as a thermodynamic pressure and the mass of the black hole was treated as the chemical enthalpy. The vacuum polarization conjugated to the NED parameter and the thermodynamic potential conjugated to the magnetic charge q were obtained. It was demonstrated that the first law of black hole thermodynamics and the generalized Smarr relation hold. NED–AdS black hole thermodynamics mimic the Van der Walls liquid–gas behavior. The critical temperature, pressure, and Gibbs free energy were calculated, and we showed that first- and second-order phase transitions occur at some parameter settings. We obtained the critical ratio of to show corrections to the Van der Waals critical ratio of . A similar behavior took place in another model of an NED–AdS black hole [51].
The Joule–Thomson adiabatic isenthalpic expansion of NED–AdS black holes was studied. Cooling- and heating-phase transitions occur depending on the model’s parameters. We obtained the inversion temperature and pressure as functions of the magnetic charge and NED coupling of black holes; they define the border between cooling and heating phases. The radii corresponding to the minima of the inversion temperature and pressure were found. As a particular case, we obtained the relation at to connect the critical temperature with the minimum inversion temperature. Previously, this formula was obtained for Einstein–AdS black holes [50].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
One can calculate the second derivative of the Gibbs free energy G with respect to temperature T with the relation
It follows from Equation (A1) that the second derivative of G with respect to T is discontinuous when . Making use of Equation (34), we obtain the second derivative of the temperature at a constant pressure:
From Equation (A2), we obtain the equation corresponding to , giving the second derivative of G with respect to T being infinite:
The approximate real and positive solution to Equation (A3) at is the critical event horizon radius corresponding to the second-order phase transition presented in Figure 4, subplot 3. One can verify that the approximate real and positive solutions to Equation (A3) for various are in accordance with Table 1. This confirms that the second-order phase transition takes place when the second derivative of G with respect to T is discontinuous.
References
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The Four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of space-time: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Padmanabhan, T. Thermodynamical Aspects of Gravity: New insights. Rept. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W.; Page, D.N. Thermodynamics of Black Holes in anti-De Sitter Space. Commun. Math. Phys. 1983, 87, 577–588. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef] [Green Version]
- Hartnoll, S.A.; Kovtun, P.K.; Muller, M.; Sachdev, S. Theory of the Nernst effect near quantum phase transitions in condensed matter, and in dyonic black holes. Phys. Rev. B 2007, 76, 144502. [Google Scholar] [CrossRef] [Green Version]
- Hartnoll, S.A.; Herzog, C.P.; Horowitz, G.T. Building a Holographic Superconductor. Phys. Rev. Lett. 2008, 101, 031601. [Google Scholar] [CrossRef] [Green Version]
- Dolan, B.P. Black holes and Boyle’s law? The thermodynamics of the cosmological constant. Mod. Phys. Lett. A 2015, 30, 1540002. [Google Scholar] [CrossRef] [Green Version]
- Kubiznak, D.; Mann, R.B.; Teo, M. Black hole chemistry: Thermodynamics with Lambda. Class. Quant. Grav. 2017, 34, 063001. [Google Scholar] [CrossRef] [Green Version]
- Kruglov, S.I. Nonlinear Electrodynamics and Magnetic Black Holes. Ann. Phys. 2017, 529, 1700073. [Google Scholar] [CrossRef] [Green Version]
- Kruglov, S.I. 4D Einstein–Gauss–Bonnet Gravity Coupled with Nonlinear Electrodynamics. Symmetry 2021, 13, 204. [Google Scholar] [CrossRef]
- Kruglov, S.I. Einstein–Gauss–Bonnet Gravity with Nonlinear Electrodynamics: Entropy, Energy Emission, Quasinormal Modes and Deflection Angle. Symmetry 2021, 13, 944. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. Roy. Soc. Lond. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Kruglov, S.I. A model of nonlinear electrodynamics. Ann. Phys. 2014, 353, 299–306. [Google Scholar] [CrossRef] [Green Version]
- Kruglov, S.I. Modified nonlinear model of arcsin-electrodynamics. Commun. Theor. Phys. 2016, 66, 59–65. [Google Scholar] [CrossRef]
- Kruglov, S.I. Notes on Born–Infeld-type electrodynamics. Mod. Phys. Lett. A 2017, 32, 1750201. [Google Scholar] [CrossRef] [Green Version]
- Heisenberg, W.; Euler, H. Consequences of the Dirac Theory of Positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Mann, R.B.; Kubiznak, D. Extended phase space thermodynamics for charged and rotating black holes and Born—Infeld vacuum polarization. J. High Energy Phys. 2012, 1211, 110. [Google Scholar] [CrossRef] [Green Version]
- Hendi, S.H.; Panahiyan, S.; Panah, B.E. P-V criticality and geometrical thermodynamics of black holes with Born-Infeld type nonlinear electrodynamics. Int. J. Mod. Phys. D 2015, 25, 1650010. [Google Scholar] [CrossRef] [Green Version]
- Zou, D.-C.; Zhang, S.-J.; Wang, B. Critical behavior of Born-Infeld AdS black holes in the extended phase space thermodynamics. Phys. Rev. D 2014, 89, 044002. [Google Scholar] [CrossRef] [Green Version]
- Fernando, S.; Krug, D. Charged black hole solutions in Einstein–Born–Infeld gravity with a cosmological constant. Gen. Rel. Grav. 2003, 35, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Dey, T.K. Born–Infeld black holes in the presence of a cosmological constant. Phys. Lett. B 2004, 595, 484–490. [Google Scholar]
- Cai, R.-G.; Pang, D.-W.; Wang, A. Born–Infeld black holes in (A)dS spaces. Phys. Rev. D 2004, 70, 124034. [Google Scholar] [CrossRef] [Green Version]
- Fernando, S. Thermodynamics of Born–Infeld-anti-de Sitter black holes in the grand canonical ensemble. Phys. Rev. D 2006, 74, 104032. [Google Scholar] [CrossRef] [Green Version]
- Myung, Y.S.; Kim, Y.-W.; Park, Y.-J. Thermodynamics and phase transitions in the Born–Infeld-anti-de Sitter black holes. Phys. Rev. D 2008, 78, 084002. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, R.; Roychowdhury, D. Critical phenomena in Born-Infeld AdS black holes. Phys. Rev. D 2012, 85, 044040. [Google Scholar] [CrossRef] [Green Version]
- Miskovic, O.; Olea, R. Thermodynamics of Einstein–Born–Infeld black holes with negative cosmological constant. Phys. Rev. D 2008, 77, 124048. [Google Scholar] [CrossRef] [Green Version]
- Majhi, B.R.; Samanta, S. P-V criticality of AdS black holes in a general framework. Phys. Lett. B 2017, 773, 203–207. [Google Scholar] [CrossRef]
- Jafarzade, K.; Sadeghi, J.; Panah, B.E.; Hendi, S.H. Geometrical thermodynamics and P-V criticality of charged accelerating AdS black holes. Ann. Phys. 2021, 432, 168577. [Google Scholar] [CrossRef]
- Pradhan, P. P–V criticality of conformal gravity holography in four dimensions. Mod. Phys. Lett. A 2018, 33, 1850030. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, P. Thermodynamic Products in Extended Phase Space. Int. J. Mod. Phys. D 2017, 26, 1750010. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, K. Extended phase space thermodynamics of black holes: A study in Einstein’s gravity and beyond. arXiv 2021, arXiv:2112.00938. [Google Scholar]
- Cong, W.; Kubiznak, D.; Mann, R.B. Thermodynamics of AdS Black Holes: Critical Behavior of the Central Charge. Phys. Rev. Lett. 2021, 127, 091301. [Google Scholar] [CrossRef]
- Hansen, D.; Kubiznak, D.; Mann, R.B. Universality of P-V Criticality in Horizon Thermodynamics. J. High Energy Phys. 2017, 1, 47. [Google Scholar] [CrossRef] [Green Version]
- Kubiznak, D.; Mann, R.B. P-V criticality of charged AdS black holes. J. High Energy Phys. 2012, 1207, 33. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef] [Green Version]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the Mechanics of AdS Black Holes. Class. Quant. Grav. 2009, 26, 195011. [Google Scholar] [CrossRef] [Green Version]
- Dolan, B.P. The cosmological constant and the black hole equation of state. Class. Quant. Grav. 2011, 28, 125020. [Google Scholar] [CrossRef] [Green Version]
- Cvetic, M.; Gibbons, G.W.; Kubiznak, D.; Pope, C.N. Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef] [Green Version]
- Smarr, L. Mass formula for Kerr black holes. Phys. Rev. Lett. 1973, 30, 71–73. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef] [Green Version]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Holography, thermodynamics and uctuations of charged AdS black holes. Phys. Rev. D 1999, 60, 104026. [Google Scholar] [CrossRef] [Green Version]
- Ghaffarnejad, H.; Yaraie, E.; Farsam, M. Quintessence Reissner–Nordstrom anti de Sitter black holes and Joule Thomson effect. Int. J. Theor. Phys. 2018, 57, 1671–1682. [Google Scholar] [CrossRef] [Green Version]
- Rizwan, C.L.A.; Kumara, A.N.; Vaid, D.; Ajith, K.M. Joule–Thomson expansion in AdS black hole with a global monopole. Int. J. Mod. Phys. A 2018, 33, 1850210. [Google Scholar] [CrossRef] [Green Version]
- Okcu, O.; Aydiner, E. Joule—Thomson expansion of the charged AdS black holes. Eur. Phys. J. C 2017, 77, 24. [Google Scholar] [CrossRef] [Green Version]
- Kruglov, S.I. Rational nonlinear electrodynamics of AdS black holes and extended phase space thermodynamics. Eur. Phys. J. C 2022, 82, 292. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).