Mathematical Assessment of Convection and Diffusion Analysis for A Non-Circular Duct Flow with Viscous Dissipation: Application of Physiology

Abstract

The present analysis has interesting applications in physiology, industry, engineering and medicine. Peristaltic pumps acquire an elliptical cross-section during motion. Peristaltic pumps, roller pumps and finger pumps also have highly useful applications. Transportation through these pumps provides an effective fluid movement and the substance remains separate from the duct walls. Convection and diffusion analyses were executed with accentuated viscous dissipation for the non-Newtonian flow that occurs inside a duct. The viscous effects are reviewed with an integrated convection and diffusion analysis that elucidates in-depth heat flux. Viscous dissipation appears to be the primary cause of increased heat generation. The Cartesian coordinate system is availed to develop this problem under consideration. A dimensionless set of coupled partial differential equations is attained by utilizing the relevant transformations that eventually simplify this complex problem. These coupled equations are solved step by step with a consideration of a polynomial solution method for coupled equations. The unfolded graphical outcomes of velocity, temperature and concentration reveal an axial symmetric flow. A higher rate of convection is observed due to viscous effects. Both the velocity and temperature profiles have an increasing function of $Q$.

1. Introduction

The pumping of viscid fluid through various ducts against an opposite pressure gradient and through a series of moving constrictive rings on a wall is known as peristalsis. It has an extensive variety of applications within the nuclear industry, the medical sciences and as a natural mechanism for pumping material through the human physiological system [1]. The fluids contained in the ducts of a living organism are called bio-fluids. The majority of bio-fluids are non-Newtonian in nature. The extensive details of non-Newtonian fluid are referenced in [2,3]. The steady flow of Couette fluid under non-linear slip conditions was interpreted through the Chebyshev spectral technique. Furthermore, the steady and incompressible flow over a wedge, while considering a second grade fluid, was numerically investigated. The movement of non-Newtonian Jeffrey fluid inside a non-circular duct with MHD effects was given in [4]. An unsteady flow of electrically conducting fluid inside a rectangular duct possessing sinusoidal moving walls was studied and exact solutions were computed. The flow analysis inside a duct that has a sinusoidal traveling pattern on its wall was discussed by Bohme et al. [5]. They had taken a very low Reynolds value with ignorable inertial forces for this creeping flow problem. The research on Casson fluid transportation inside a sinusoidal channel was discussed by Akbar [6]. They computed exact solutions for Casson flow under MHD effects for an asymmetric domain. Rashid et al. [7] explored the impacts of a magnetic field on the peristaltic flow of an incompressible, non-Newtonian Williamson fluid within a curved tube. The physical consequences of peristaltic flow and heat transfer through a curved channel having a ciliated wall were discussed by Saleem et al. [8]. An analysis is highlighted in their work wherein a comparison is made between the phase flow, which has one type of nanoparticle model, and the hybrid flow, which has two kinds of nanoparticles in the base fluid. Many researchers have shown an interest in elliptical channel flow problems. The non-Newtonian fluid flow in ducts has been examined extensively [9]. For an elliptic cross-section, the fluid flow through a non-circular channel was examined in [10]. Numerical solutions were computed, and cooling effects were highlighted in their study. They also highlighted the iso-thermal surrounding effects on this elliptic flow domain. Sharma and Shaw [11] numerically elucidated the non-Newtonian flow with viscous effects. Heat and mass flux consequences are highlighted for Williamson and Casson models with radiation impacts. Shaw et al. [12] also discussed the three-dimensional geometric flow of nanofluid with viscous effects. They utilized the local linearization technique to solve this nanofluid flow problem by considering distinct geometrical models. Some recent research in convection and diffusion analysis are referred to in [13,14]. Some recent and important research on circular ducts are also referenced in [15,16,17]. In addition to this, a number of recent works discuss the topic of heat transfer across elliptical channels [18,19]. In the literature, the researchers discussed various configurations such as rectangular, cylindrical and asymmetrical channels. However, the analysis of peristalsis in elliptic channels with convection and diffusion effects remains somewhat unexamined. Some relevant and recent articles that discuss non-circular duct flow problems with heat and mass transfer are given [20,21,22,23,24,25,26,27,28,29,30,31].

The research highlighted above clearly shows that the convection and diffusion interpretation with viscous dissipation has not been considered by anyone for an elliptic domain. Furthermore, the solution to such a complex problem involves some coupled partial differential equations that are not easy to solve. We have disclosed the exact solution to this complex mathematical problem. There are exact velocity, concentration and temperature solutions provided in Section 3. Moreover, no one has considered such convection and diffusion analysis in addition to viscous dissipation for a Jeffrey fluid inside an elliptic domain with sinusoidal walls. Thus, the elucidation of peristalsis flow with convection, diffusion and viscous dissipation effects inside an elliptical duct is handled mathematically. The current analysis is taken into account by considering non-Newtonian Jeffrey fluid. A polynomial solution method is utilized to solve the final coupled equations in dimensionless form. The viscous effects are highlighted in detail for current convection and diffusion analysis. The graphical assessment verifies the result validation.

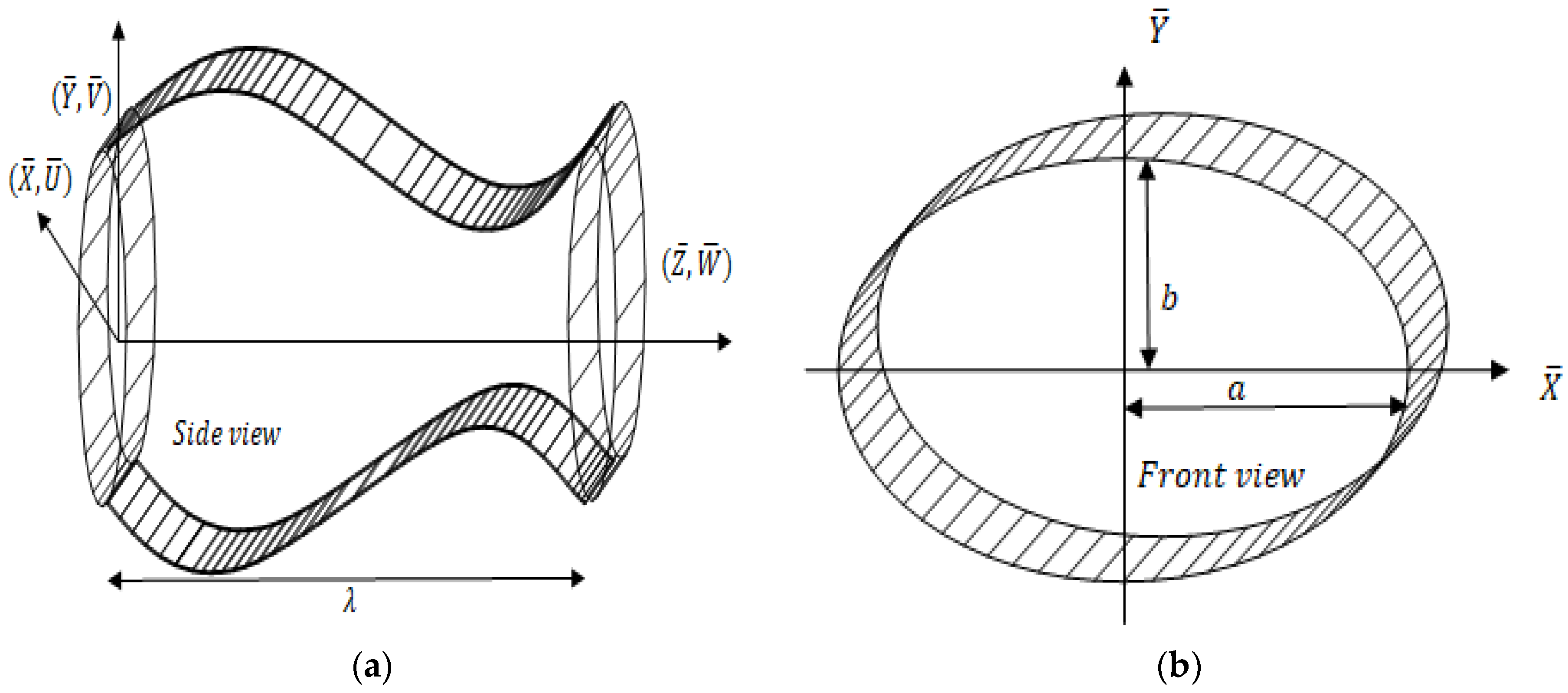
2. Mathematical Modeling

A Cartesian ($\overline{X}$,$\overline{Y},\overline{Z})$ coordinate system is considered for this problem and the non-circular shape of the duct is achieved by taking the equation of an ellipse in boundary conditions. The geometry is referred to in [32] and shown in Figure 1.

The sinusoidal behavior of a traveling wall is considered by the equations given below:

$$\overline{a}\left(\overline{Z},\overline{t}\right)=\pm a_o\pm dsin\left[\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right], \overline{b}\left(\overline{Z},\overline{t}\right)=\pm b_o\pm dsin\left[\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right]$$

(1)

Consider the dimensional form of the following equations.

Continuity equation:

$$\frac{\partial \overline{U}}{\partial \overline{X}}+\frac{\partial \overline{V}}{\partial \overline{Y}}+\frac{\partial \overline{W}}{\partial \overline{Z}}=0,$$

(2)

X-direction momentum equation:

$$\rho (\frac{\partial \overline{U}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{U}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{U}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{U}}{\partial \overline{Z}})=-\frac{\partial \overline{P}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{XX}}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{YX}}}{\partial \overline{Y}}+\frac{\partial {\overline{S}}_{\overline{ZX}}}{\partial \overline{Z}},$$

(3)

Y-direction momentum equation:

$$\rho (\frac{\partial \overline{V}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{V}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{V}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{V}}{\partial \overline{Z}})=-\frac{\partial \overline{P}}{\partial \overline{Y}}+\frac{\partial {\overline{S}}_{\overline{XY}}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{YY}}}{\partial \overline{Y}}+\frac{\partial {\overline{S}}_{\overline{YZ}}}{\partial \overline{Z}},$$

(4)

Z-direction momentum equation:

$$\rho (\frac{\partial \overline{W}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{W}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{W}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{W}}{\partial \overline{Z}})=-\frac{\partial \overline{P}}{\partial \overline{Z}}+\frac{\partial {\overline{S}}_{\overline{XZ}}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{YZ}}}{\partial \overline{Y}}+\frac{\partial {\overline{S}}_{\overline{ZZ}}}{\partial \overline{Z}},$$

(5)

Energy equation:

$$\begin{array}{c}\rho C_P\left(\frac{\partial \overline{T}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{T}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{T}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{T}}{\partial \overline{Z}}\right)=k\left(\frac{{\partial }^2\overline{T}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Z}}^2}\right)+\\ {\overline{S}}_{\overline{XX}}\frac{\partial \overline{U}}{\partial \overline{X}} +{\overline{S}}_{\overline{YX}}\frac{\partial \overline{U}}{\partial \overline{Y}} +{\overline{S}}_{\overline{ZX}}\frac{\partial \overline{U}}{\partial \overline{Z}} +{\overline{S}}_{\overline{XY}}\frac{\partial \overline{V}}{\partial \overline{X}} +{\overline{S}}_{\overline{YY}}\frac{\partial \overline{V}}{\partial \overline{Y}}+{\overline{S}}_{\overline{YZ}}\frac{\partial \overline{V}}{\partial \overline{Z}}+{\overline{S}}_{\overline{XZ}}\frac{\partial \overline{W}}{\partial \overline{X}}+{\overline{S}}_{\overline{YZ}}\frac{\partial \overline{W}}{\partial \overline{Y}}+{\overline{S}}_{\overline{ZZ}}\frac{\partial \overline{W}}{\partial \overline{Z}},\end{array}$$

(6)

Concentration equation:

$$\frac{\partial \overline{C}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{C}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{C}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{C}}{\partial \overline{Z}}=D\left(\frac{{\partial }^2\overline{C}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{C}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{C}}{\partial {\overline{Z}}^2}\right)+\frac{D{K}_T}{T_b}\left(\frac{{\partial }^2\overline{T}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Z}}^2}\right)$$

(7)

The dimensional form of boundary conditions that give the shape of an ellipse to this non-circular duct is given as

$$\overline{W}=0, \overline{T}={\overline{T}}_W, \overline{C}={\overline{C}}_w \mathrm{for} \frac{{\overline{x}}^2}{{\overline{a}}^2}+\frac{{\overline{y}}^2}{{\overline{b}}^2}=1.$$

(8)

For the considered non-Newtonian fluid, the extra stress tensor is provided as [33]:

$$\overline{S}=\frac{\mu }{1+{\lambda }_1}(\dot{\gamma }+{\lambda }_2\ddot{\gamma } )$$

(9)

where $\ddot{\gamma }$ is the time derivative of shear rate.

The transformations between two frames are:

$$\overline{x}=\overline{ X}, \overline{y}=\overline{ Y}, \overline{z}=\overline{Z}-c\overline{ t}, \overline{u}=\overline{U}, \overline{v}=\overline{V}, \overline{w}=\overline{W}-c, \overline{p}=\overline{P},\overline{ T}=T, \overline{C}=C,$$

(10)

The dimensionless parameters are [34]:

$$\begin{array}{c}x\frac{\overline{x}}{D_h} , y\frac{\overline{y}}{D_h}, z=\frac{\overline{z}}{\lambda }, u=\frac{\overline{u}\lambda }{D_{h}c}, v=\frac{\overline{v}\lambda }{D_{h}c}, w=\frac{\overline{w}}{c}, t=\frac{c\overline{t}}{\lambda }, p=\frac{\overline{p}{D}_h{}^2}{c\mu \lambda }, a=\frac{\overline{a}}{D_h}, b=\frac{\overline{b}}{D_h}, \sigma =\frac{\overline{C}-{\overline{C}}_w}{{\overline{C}}_b-{\overline{C}}_w},\\ S_r=\frac{\rho D{k}_T\left({\overline{T}}_b-{\overline{T}}_w\right)}{\mu T_b\left({\overline{C}}_b-{\overline{C}}_w\right)}, S_c=\frac{\mu }{D\rho },\\ \theta =\frac{\overline{T}-{\overline{T}}_w}{{\overline{T}}_b-{\overline{T}}_w}, B_r=\frac{c^2{\mu }_f}{k_f ({\overline{T}}_b-{\overline{T}}_w)}, \delta =\frac{b_o}{a_o}, \varphi =\frac{d}{b_o}, S\frac{D_h\overline{S}}{c\mu }.\end{array}$$

(11)

$D_h \mathrm{is} \mathrm{hydrolic} \mathrm{diameter}$ for ellipse and is given as $D_h$=$\frac{b_o\pi }{E\left(e\right)}$;

where E(e) = ${{\displaystyle \int }}_0^{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{1-e^{2}si{n}^2\alpha d\alpha }$, and e = $\sqrt{1-{\mathsf{\delta }}^2}$.

The dimensionless set of governing equations is attained by using Equations (10) and (11) with approximation, $\lambda \to \infty$.

$$\frac{\partial p}{\partial x}=0,$$

(12)

$$\frac{\partial p}{\partial y}=0,$$

(13)

$$\frac{\partial p}{\partial z}=\frac{1}{1+{\lambda }_1}\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}\right),$$

(14)

$$\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2}+B_r\frac{1}{1+{\lambda }_1}\left[{\left(\frac{\partial w}{\partial x}\right)}^2+{\left(\frac{\partial w}{\partial y}\right)}^2\right]=0,$$

(15)

$$\frac{{\partial }^2\sigma }{\partial x^2}+\frac{{\partial }^2\sigma }{\partial y^2}+S_r{S}_c\mathit{(}\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2} )=0,$$

(16)

The corresponding dimensionless boundary conditions are

$$\mathit{w}=\mathit{1} \mathit{for} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

(17)

$$Ɵ=\mathit{0} \mathit{for} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

(18)

$$\sigma =\mathit{0} \mathit{for} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

(19)

where a = $\frac{E\left(e\right)}{\pi }\left(\frac{1}{\delta }+\varphi \sin \left(2\pi z\right)\right) , b=\frac{E\left(e\right)}{\pi }\left(1+\varphi \sin \left(2\pi z\right)\right)$.

3. Exact Solution

A polynomial of order 4 is considered in its present form since such a polynomial gives a total of six equations to solve with six constants and the system was exactly evaluated using Mathematica.

$$\mathit{w}\mathit{(}\mathit{x}\mathit{,}\mathit{y}\mathit{)}=m_1{x}^4+m_2{y}^4+m_3{x}^2{y}^2+m_4{x}^2+m_5{y}^2+m_6,$$

(20)

Insert Equation (20) in (14) and compare the coefficients of $x^2,y^2,x^0{y}^0$; thus, we obtain

$$12m_1+2m_3=0,$$

(21)

$$12m_2+2m_3=0,$$

(22)

$$2m_4+2m_5=\left(1+{\lambda }_1\right)\frac{dp}{dz},$$

(23)

Furthermore, by putting Equation (20) in Equation (17) and comparing the coefficients of $x^4,x^2,x^0$

$$a^4{m}_1+b^4{m}_2-a^2{b}^2{m}_3=0,$$

(24)

$$a^2{b}^2{m}_3-2b^4{m}_2+a^2{m}_4-b^2{m}_5=0,$$

(25)

$$b^4{m}_2+b^2{m}_5+m_6=-1,$$

(26)

Solving Equations (21)–(26) we obtain values of constants, which are:

$m_1=0, m_2=0, m_3=0, m_4=-\frac{-b^2\frac{dp}{dz}\left(1+{\lambda }_1\right)}{2\left(a^2+b^2\right)},m_5=\frac{a^2\frac{dp}{dz}\left(1+{\lambda }_1\right)}{2\left(a^2+b^2\right)}, m_6=\frac{-2a^2+2b^2+a^2{b}^2\frac{dp}{dz}\left(1+{\lambda }_1\right)}{2\left(a^2+b^2\right)},$

Putting the above constant values in Equation (20), we obtain

$$w\left(x,y\right)=-1+\frac{1}{2}\frac{dp}{dz}\frac{a^2{b}^2}{\left(a^2+b^2\right)}\left(1+{\lambda }_1\right)\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right),$$

(27)

Taking the integral of Equation (27) over the cross-sectional area of this elliptic duct provides the non-dimensional flow rate given as

$$qz=-\pi ab-\frac{\pi }{4}\frac{dp}{dz}\frac{a^3{b}^3}{\left(a^2+b^2\right)}\left(1+{\lambda }_1\right),$$

(28)

where q(z) = Q − ${{\displaystyle \int }}_0^{1}abdz$. From Equation (28), the pressure gradient solution is calculated as follows

$$\frac{dp}{dz}=-\frac{4\left(a^2+b^2\right)}{\pi a^3{b}^3\left(1+{\lambda }_1\right)}(ab\pi +Q-{{\displaystyle \int }}_0^{1}abdz),$$

(29)

For a single wavelength the pressure rise is:

$$∆P={{\displaystyle \int }}_0^1\frac{\partial p}{\partial z}dz,$$

(30)

By following a similar procedure for the temperature solution, we have

$$\begin{array}{c}\theta \left(x,y\right)\hfill \\ =\frac{-B_r{\left(\frac{\mathit{dp}}{\mathit{dz}}\right)}^2{a}^2{b}^2\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)\left(b^6{x}^2+a^2{b}^4\left(b^2+6x^2-y^2\right)+a^6\left(b^2+y^2\right)+a^4{b}^2\left(4b^2-x^2+6y^2\right)\right)\left(1+{\lambda }_1\right)}{12{\left(a^2+b^2\right)}^2\left(a^4+6a^2{b}^2+b^4\right)},\hfill \end{array}$$

(31)

Substituting the above temperature solution in the concentration equation, the final concentration solution is given as

$$\begin{array}{c}\sigma \left(x,y\right)\hfill \\ =\frac{B_r{\left(\frac{\mathit{dp}}{\mathit{dz}}\right)}^2{S}_c{S}_r{a}^2{b}^2\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)\left(b^6{x}^2+a^2{b}^4\left(b^2+6x^2-y^2\right)+a^6\left(b^2+y^2\right)+a^4{b}^2\left(4b^2-x^2+6y^2\right)\right)\left(1+{\lambda }_1\right)}{12{\left(a^2+b^2\right)}^2\left(a^4+6a^2{b}^2+b^4\right)}\hfill \end{array}$$

(32)

4. Validation

The obtained exact solutions satisfy the considered boundary conditions, if we set $\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}\right)=1$ in Equations (20), (24) and (25) then we obtain w = −1, θ = 0 and σ = 0, which shows that the boundary conditions are fully satisfied. Furthermore, these solutions fully satisfy the governing equations. Thus, the obtained solutions are exact solutions. The graphical results also validate the mathematical computations.

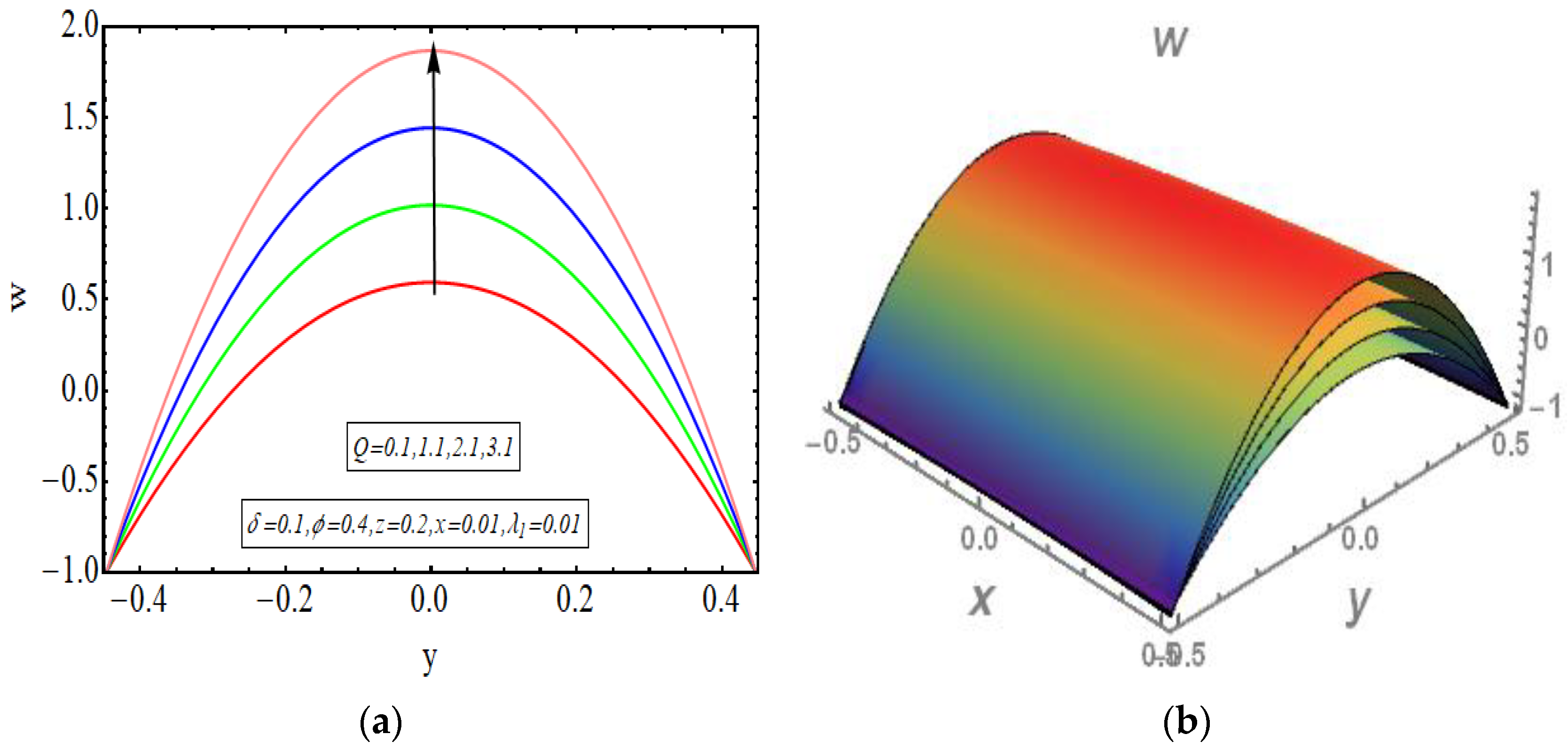
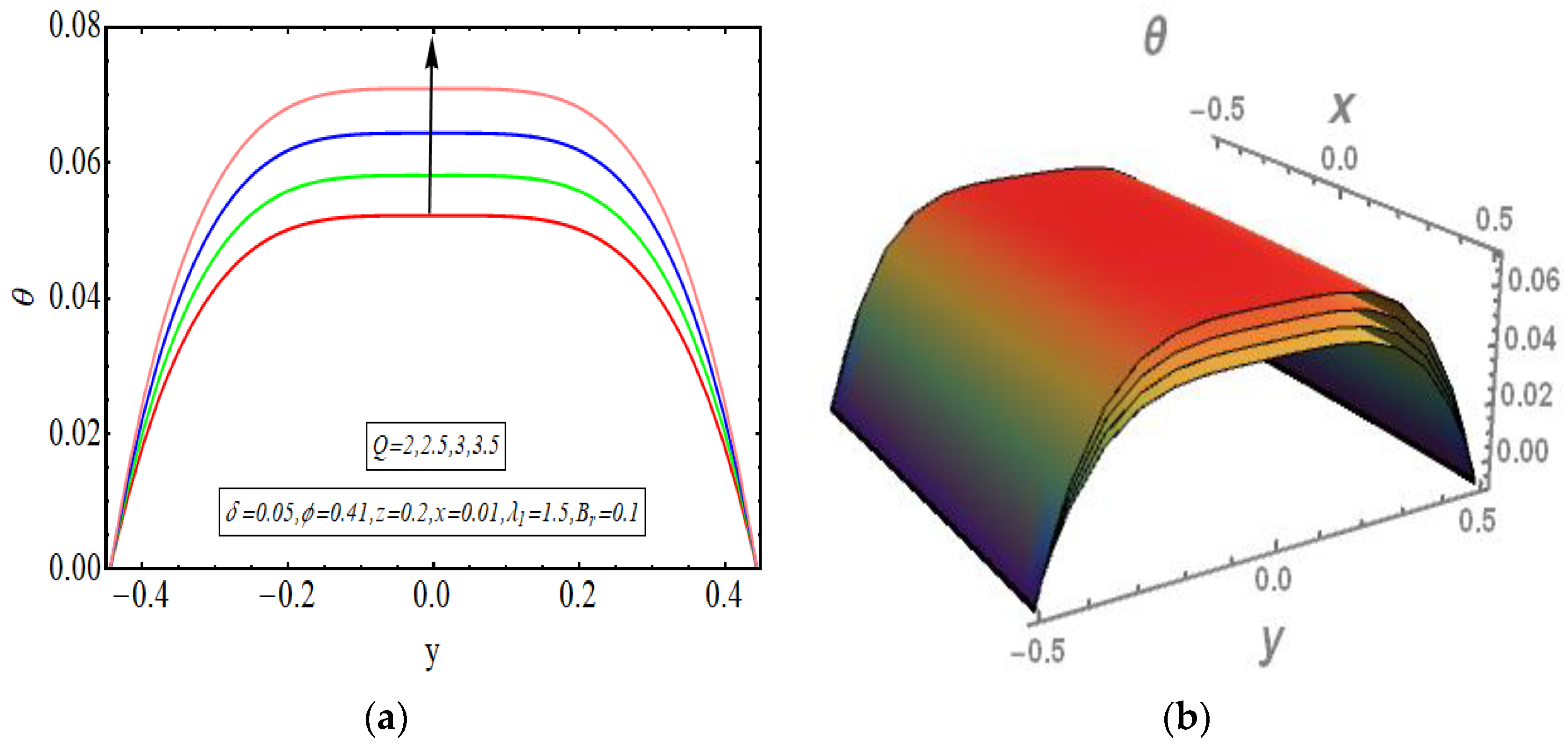
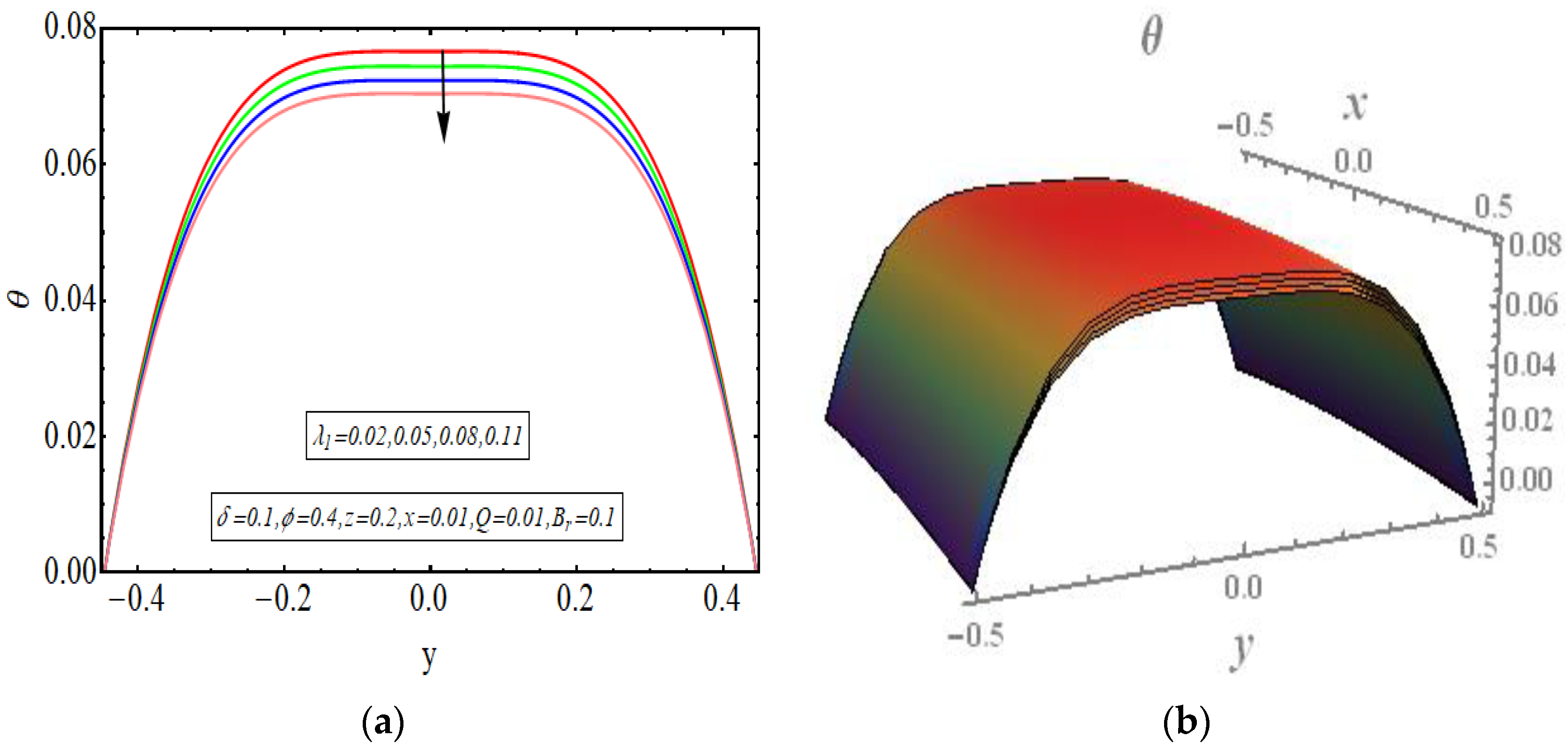
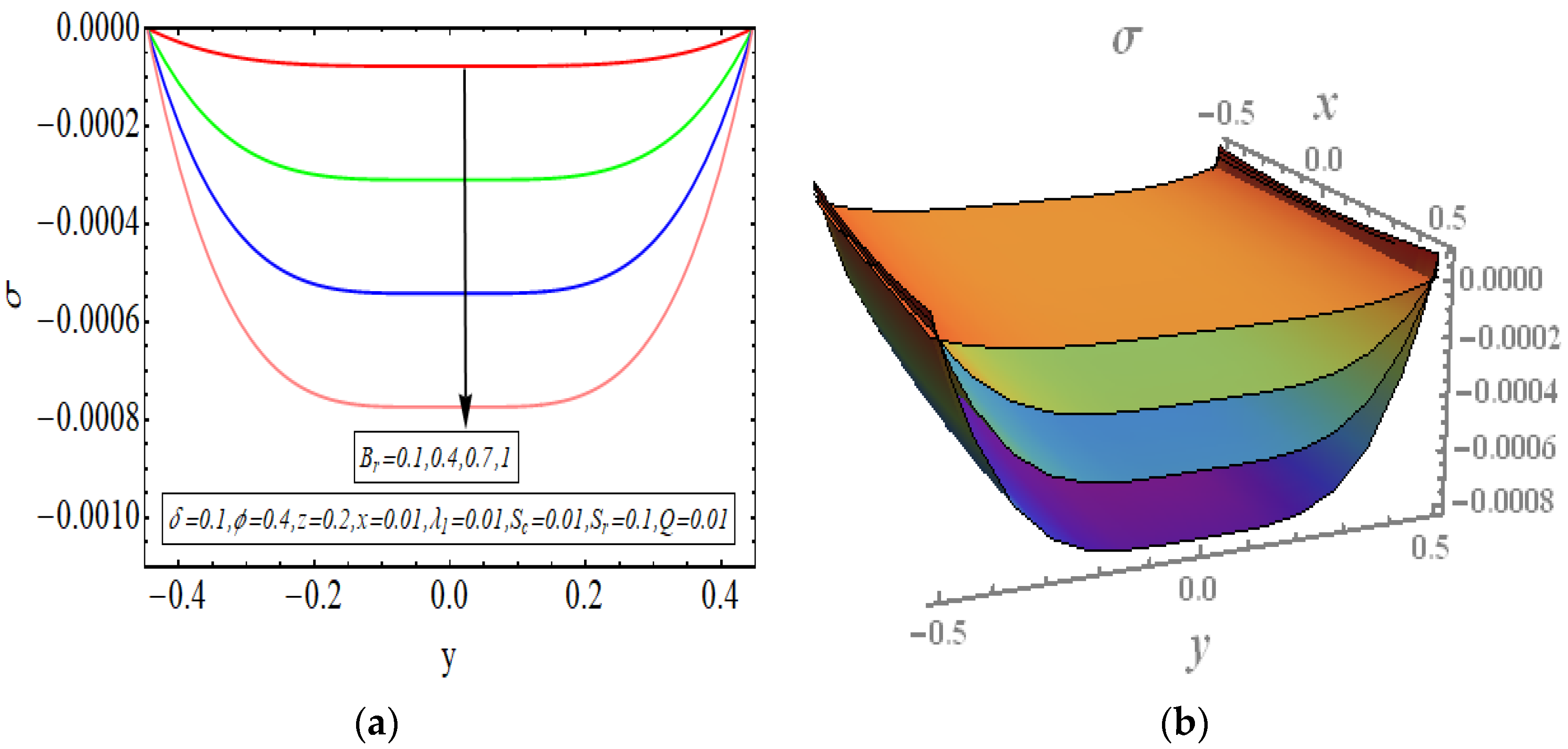
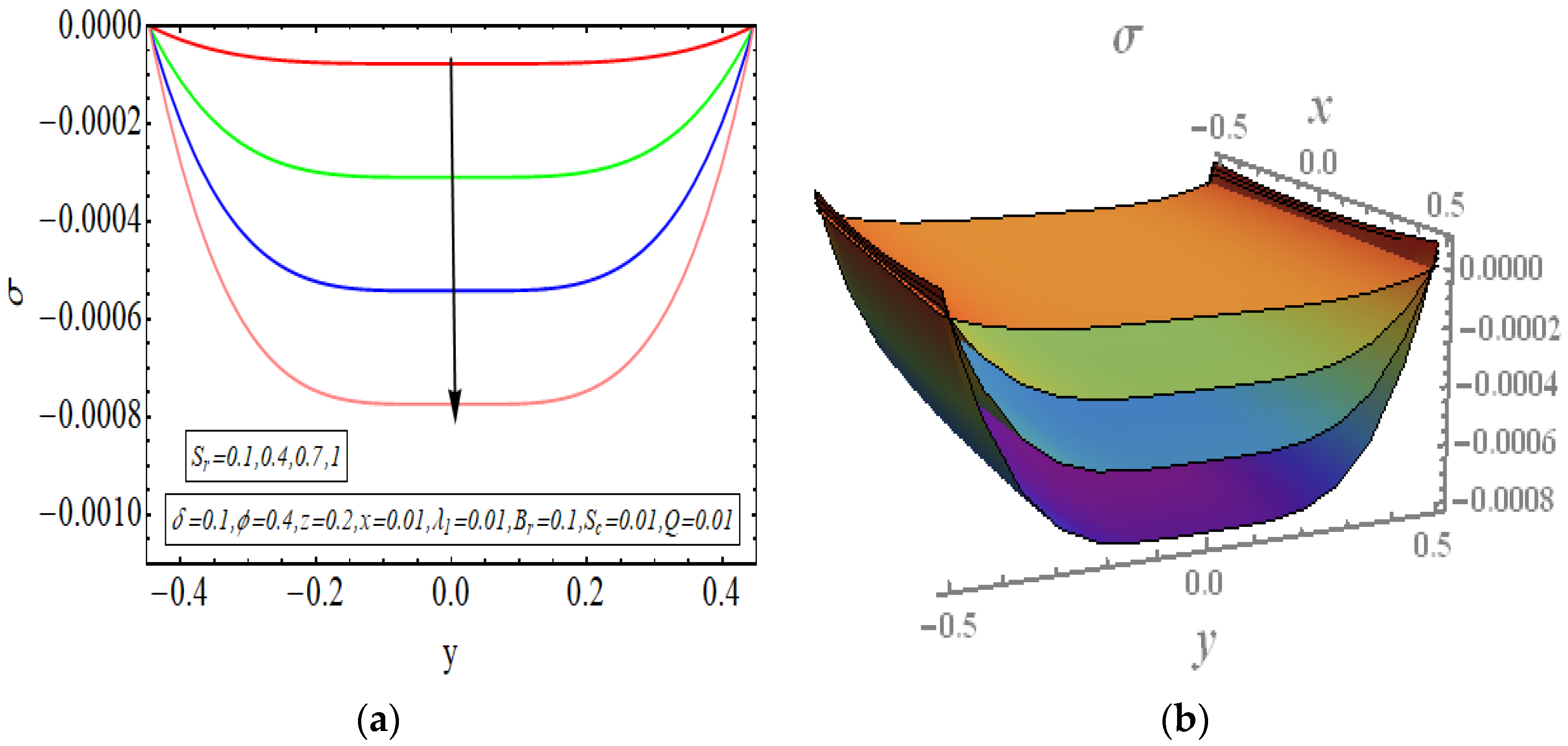
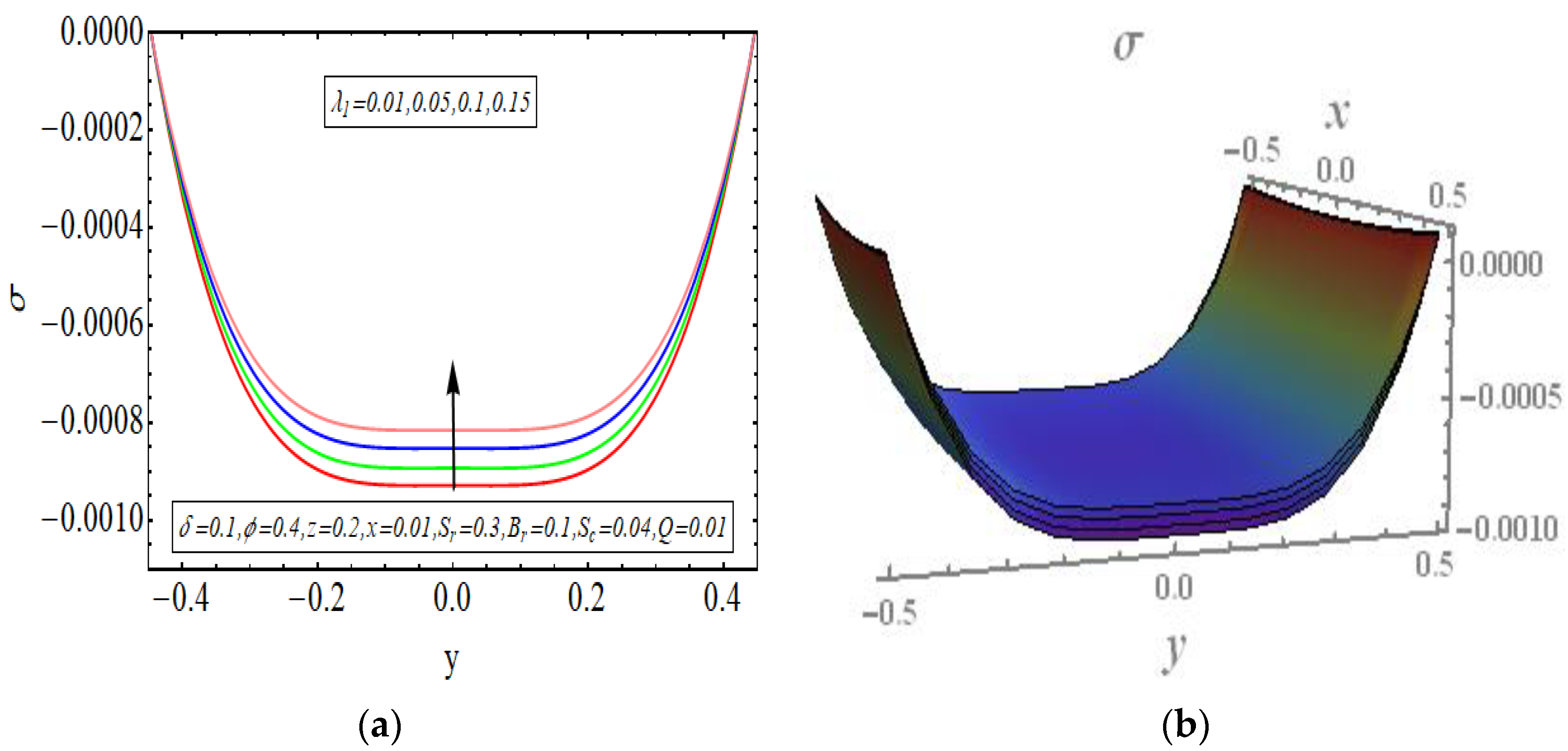
5. Results and Discussion

This section explains the behavior of graphs with respect to different parameters. Figure 2a shows the increment in a two-dimensional velocity profile for flow rate Q, while Figure 2b explains the three-dimensional graphical outcome of the velocity profile which rises for flow rate Q. Figure 3 illustrates the graphical description which is for a two-dimensional temperature profile in the case of flow rate Q. As a result, it shows an increment in the value for both two-dimensional and three-dimensional graphs disclosed in Figure 3a,b, respectively. The increasing flow rate results in an enhanced flow and convection profile. Figure 4 represents the graphical description for a two-dimensional temperature profile in the case of ${\lambda }_1$. As a result, it shows a reduction in temperature for both two-dimensional and three-dimensional graphical outcomes revealed in Figure 4a,b, respectively. As the nature of fluid tends to be non-Newtonian, the convection declines.

Figure 5 represents the graphical description which is for a two-dimensional temperature profile in the case of $B_r$. As a result, it shows an increment for both two-dimensional and three-dimensional outcomes shown in Figure 5a,b, respectively. Figure 5a,b show that the temperature is an increasing function of $B_r$ and a slight enhance in $B_r$ results in a higher increase in temperature. Thus, viscous dissipation has a clear and prime impact on heat transfer as compared to conduction only. Figure 6 illustrates the graphical description for dp/dz. Figure 6a shows that the pressure gradient decreases in case of increase in the flow rate Q. Figure 6b shows the increment in the pressure gradient with an enhancing value of dimensionless parameter $\lambda { }_1$. The graph in Figure 6c shows an uprise in the value of $\delta$ and, finally, Figure 6d illustrates that the value is increasing at the left side of graph while declining at the right side for the increase in value of ϕ. In Figure 6a–c, the points $z=0.25, z=0.75$ are points of inflection. In Figure 6d, the points $z=0.25, 0.5, 0.75$ are inflection points as well. Figure 7 shows the graphical plotting of pressure rise against flow rate $Q$. There are three graphical areas that are portrayed. In (i) $∆P>0$ is referred to as peristaltic pumping, in (ii) $∆P=0$ is referred to as free pumping and in (iii) $∆P<0$ is referred to as an augmented pumping region. Figure 7a shows the result with an increased value of ${\lambda }_1$. Figure 7b shows the increment in the pressure rise for the peristaltic pumping region but a reduction in the augmented pumping area with an uprising value of ϕ. Figure 7c shows the result for $\delta$. It goes higher in the peristaltic pumping region but goes down in the augmented pumping area. Figure 8 reveals the 2D and 3D concentration graphs for $Q$. Figure 8a reveals the reduction by incrementing the value of $Q$. The graphs in Figure 9 depict the 2D and 3D results of the concentration profile. Figure 9a illustrates the lower graph value with higher B_r value in the two-dimensional graph and Figure 9b shows three-dimensional graphs for B_r. Figure 10 shows the graphs of concentration for S_c in 2D and 3D. Figure 10a shows that the concentration is reducing while S_c is increasing and same can be seen in Figure 10b. Figure 11 discloses the graphs of concentration for S_r in 2D and 3D. Figure 11a shows that the concentration is reducing while S_r is increasing and the same is observed in Figure 11b. Figure 12 shows the graphs of concentration for ${\lambda }_1$ in 2D and 3D. Figure 12a shows that the concentration is increasing with the increasing value of ${\lambda }_1$ and same is noted in Figure 12b. As the fluid tends to be non-Newtonian, the concentration profile gains magnitude. Figure 13 illustrates the streamlines that are drawn for this elliptical duct. The trapping of streamlines increases as the value of $Q$increases. In Figure 13a–d, streamlines are plotted to visualize the flow pattern for increasing dimensionless flow rate $Q$. It is evident from these graphical plots that the closed contours are enhancing in size for incrementing $Q$ but the number of closed contour lines are surprisingly the same in all Figure 13a–d. Moreover, these results depict an axially symmetric flow behavior in this sinusoidal elliptic duct.

In comparison to the already existing literature [32,33,34] on peristaltic flow problems, the results presented here show the same parabolic profile for flow domain and a maximum and fully developed profile is observed in the center. In our case, temperature follows a similar behavior as in most peristaltic flow domain cases, i.e., a maximum and steady convection was noted in the center that reduces towards the walls of the duct. Pressure gradient graphs have a sinusoidal wall fluctuation profile that is seen in the majority of peristaltic flow literature reviews. As presented in the majority of the literature, the pressure rise has three evident peristaltic pumping zones ($∆P<0, ∆P=0, ∆P>0$) and streamlines are perfectly in accordance with the already existing literature reviews that have a sinusoidal propelling wave profile at the walls of this duct.

6. Conclusions

In an elliptical cross-sectional duct, the peristaltic flow with integrate convection and diffusion effects was inspected. A non-Newtonian Jeffrey fluid model was considered and viscous effects were also highlighted in this study. Major outcomes are given as follows:

• In an elliptic duct, the velocity profile graph shows that the nature of flow is axially symmetric.
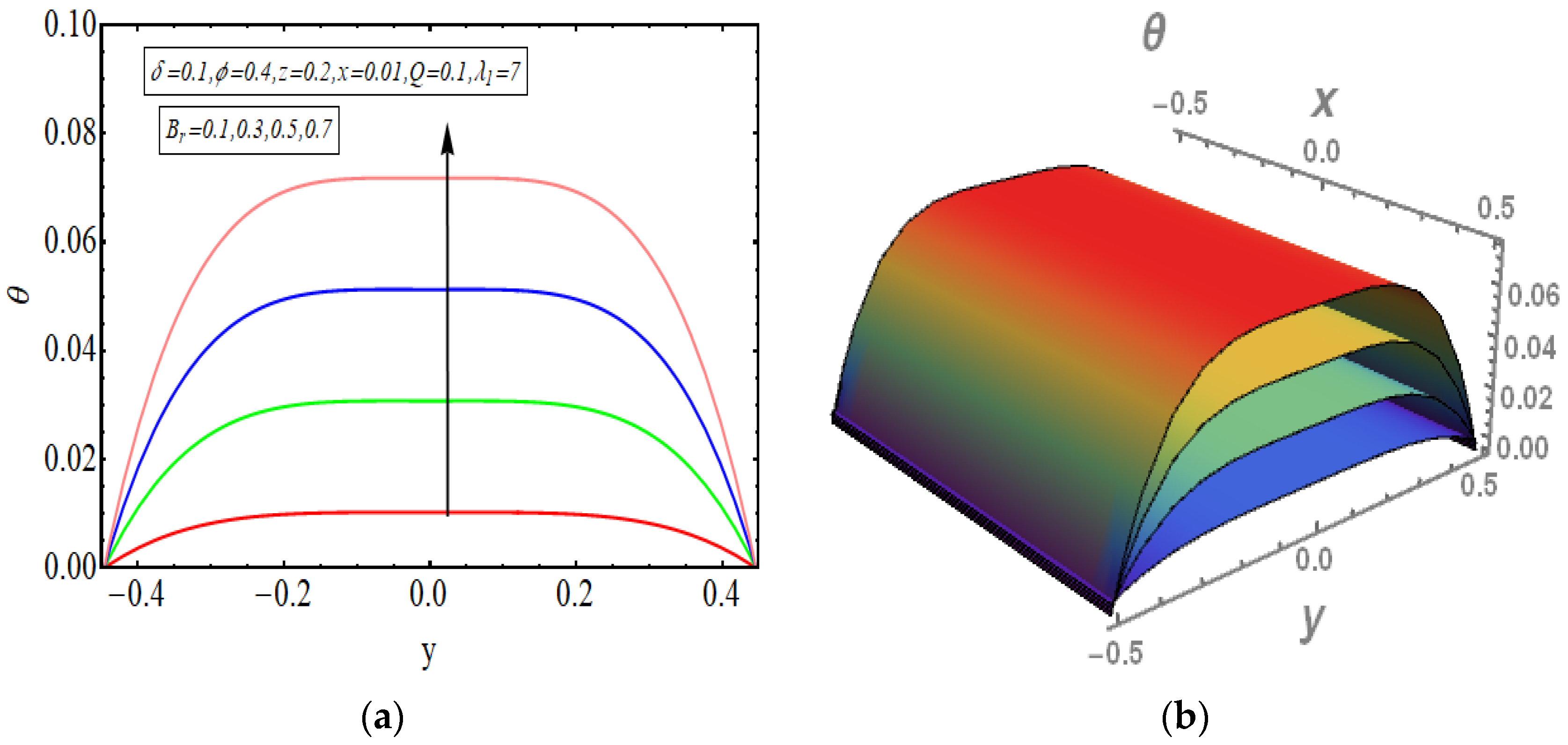
• As the value of flow rate Q increases, the behavior of velocity and temperature graphs also goes higher.
• Several interesting research problems can be considered for future work by applying complex non-Newtonian models to the present problem.
• Viscous effects are the core reason behind high convection rates. The rise in temperature is primarily happening due to viscous dissipation.
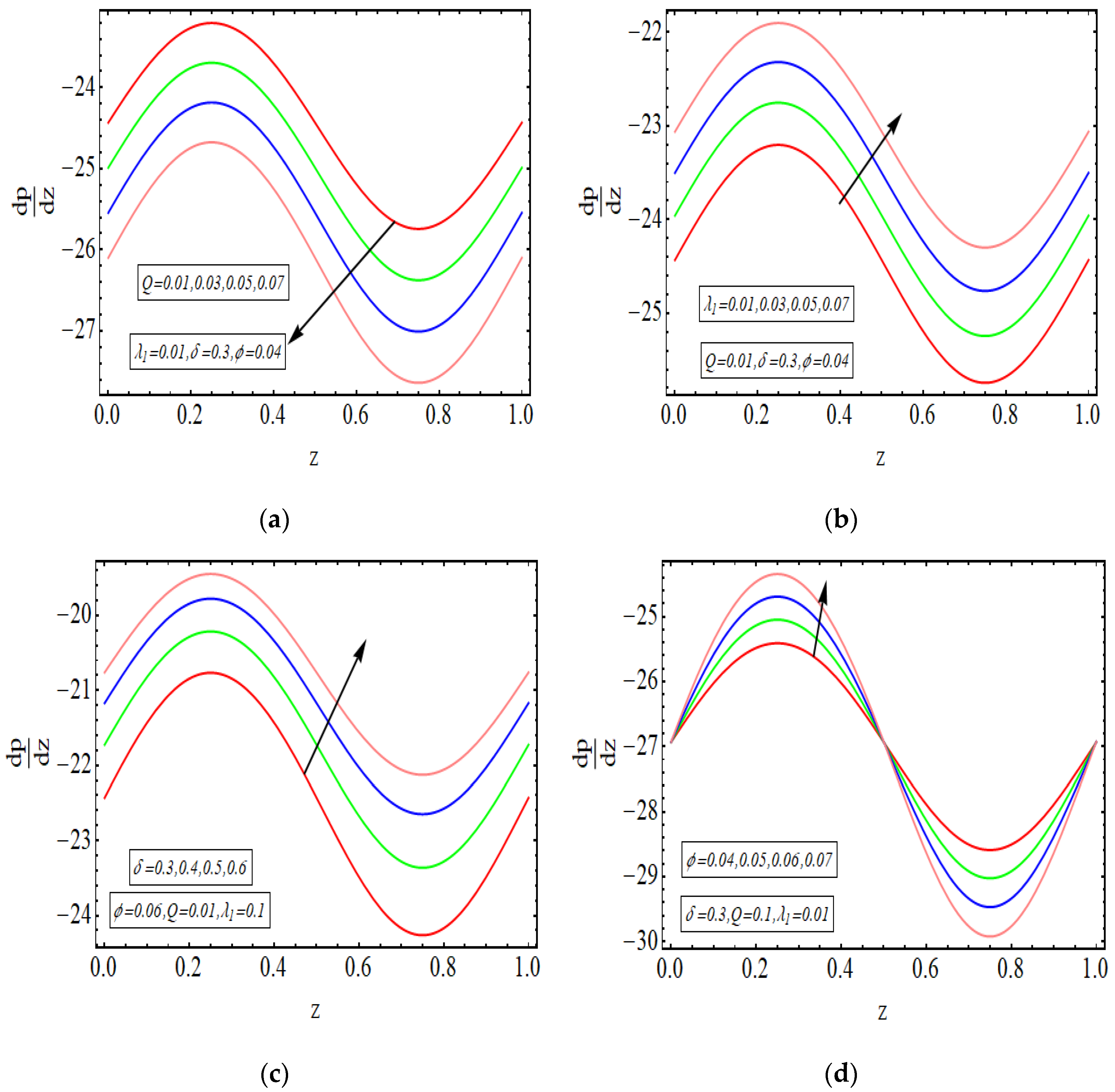
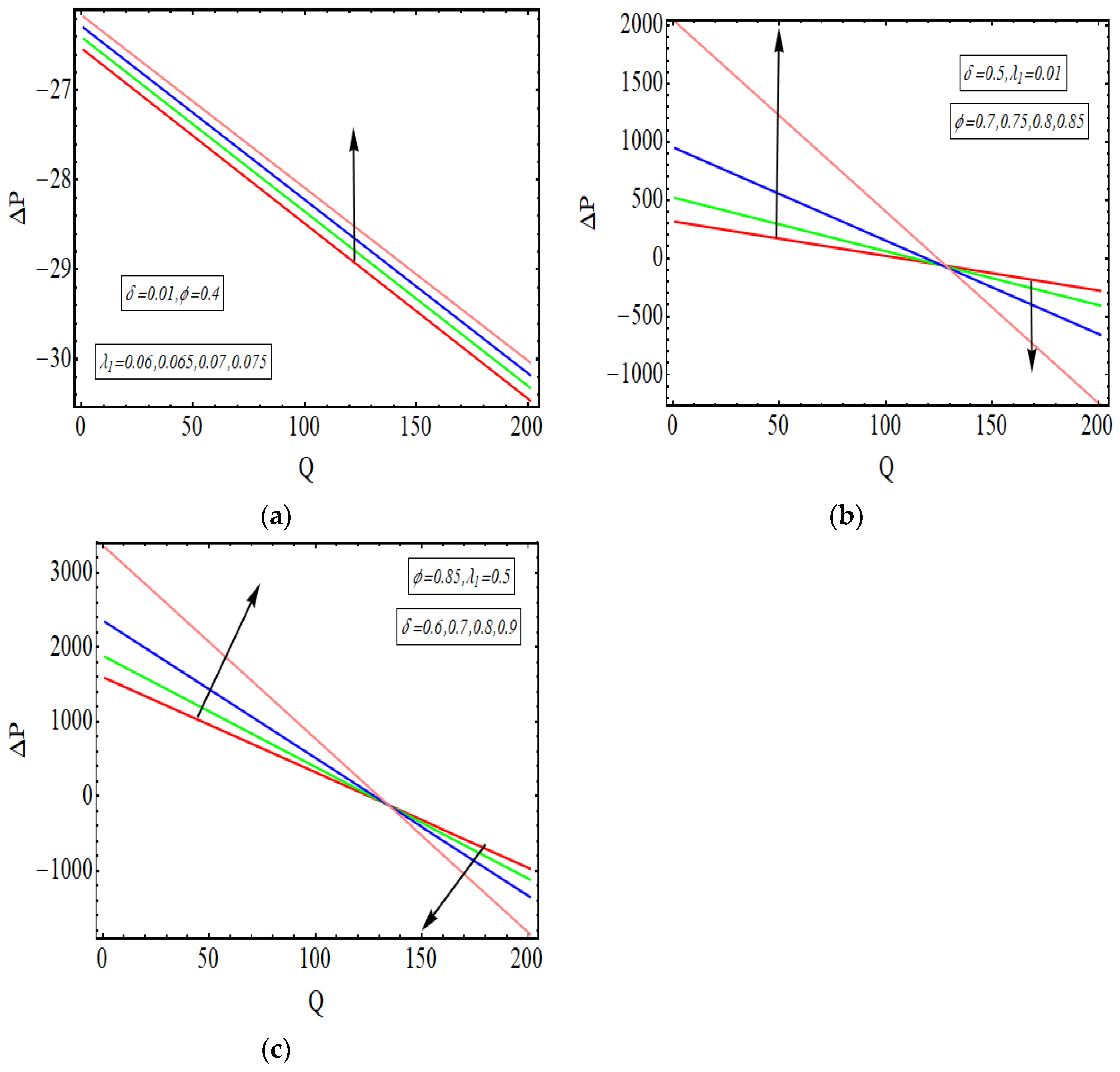
• The pressure rise graphs disclose the three core sections of multiple pumping regions: free pumping, augmented pumping and co-pumping. There are increasing values in co-pumping but declining values in the augmented pumping section.
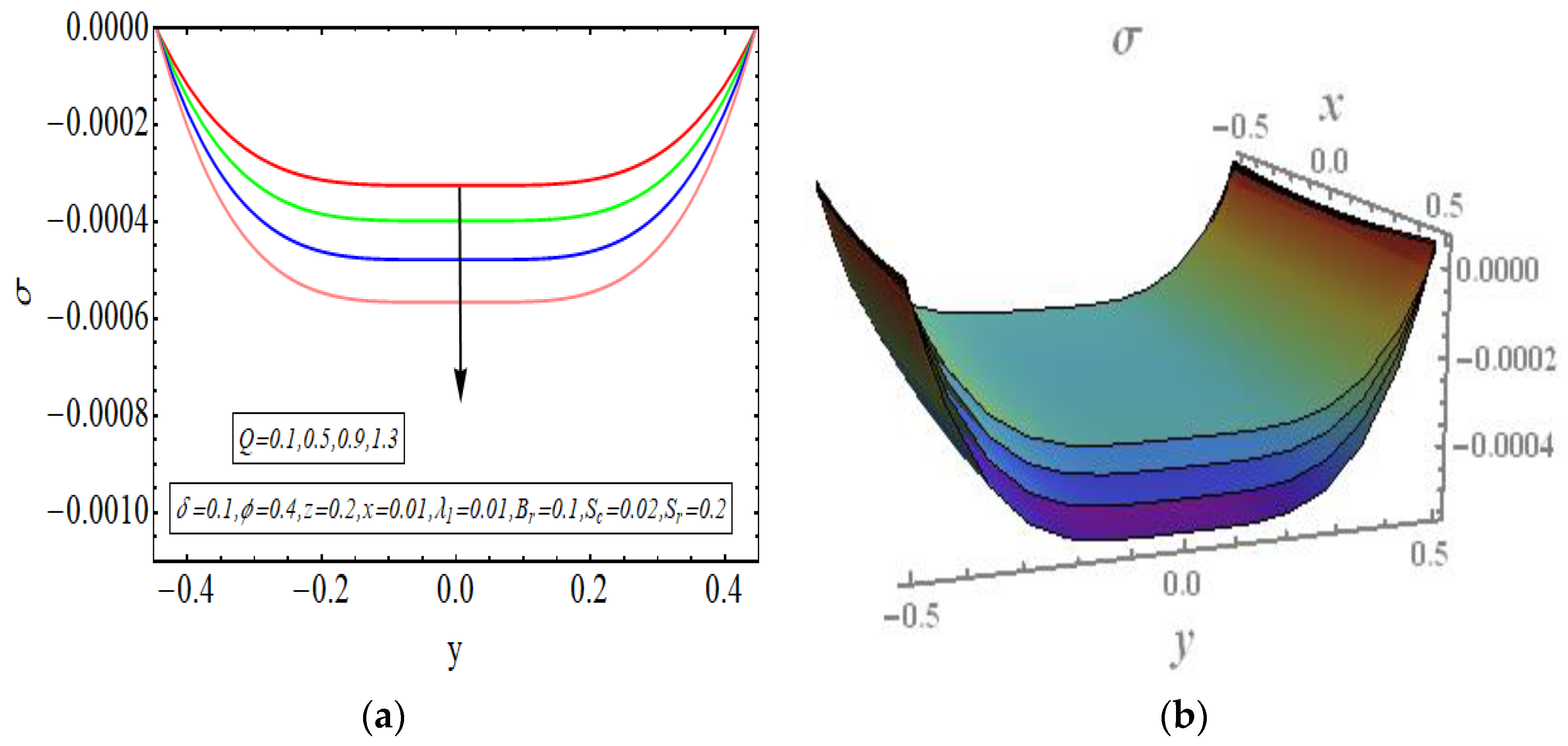
• Positive velocity and temperature profiles are observed but a negative concentration profile has also been observed.
• The value of Q is directly proportional to the trapping of streamlines e.g., the size of the trapping of streamlines increases as the value of flow rate increases.