The Stability of a Hydrodynamic Bravais Lattice
Abstract
1. Introduction
2. Normal Mode Analysis
2.1. Review of Theoretical Model
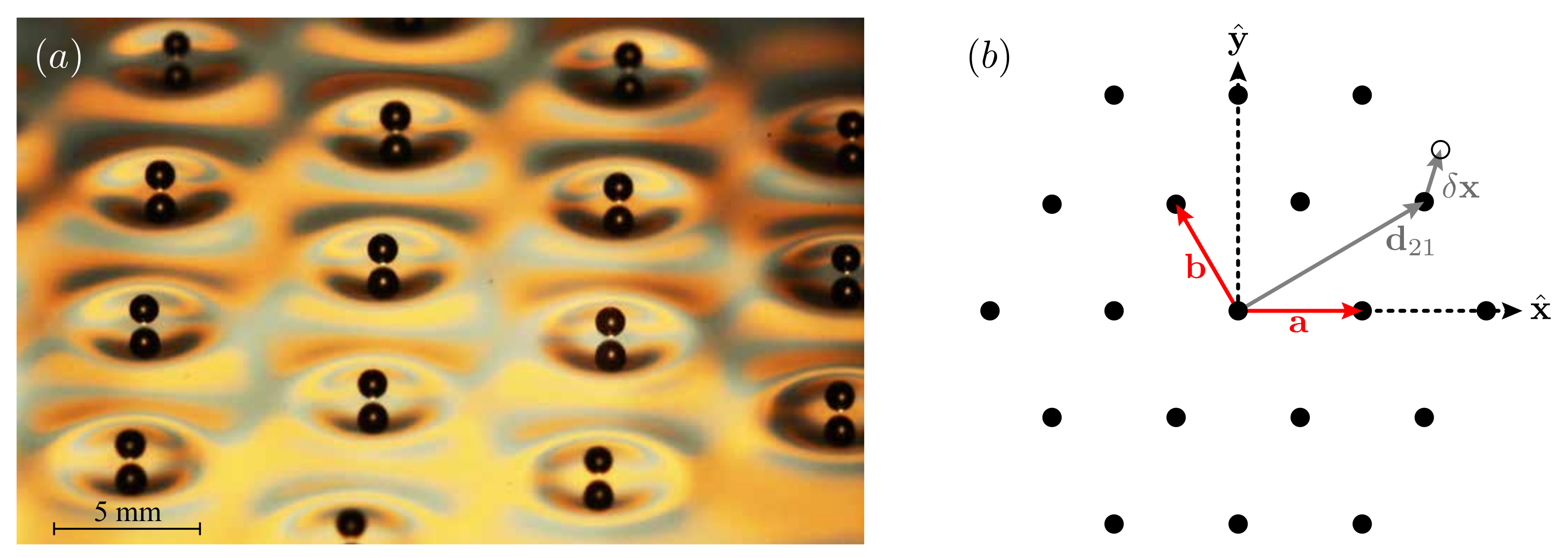
2.2. Base State of the Bravais Lattice
2.3. Dispersion Relation of the Perturbed Lattice
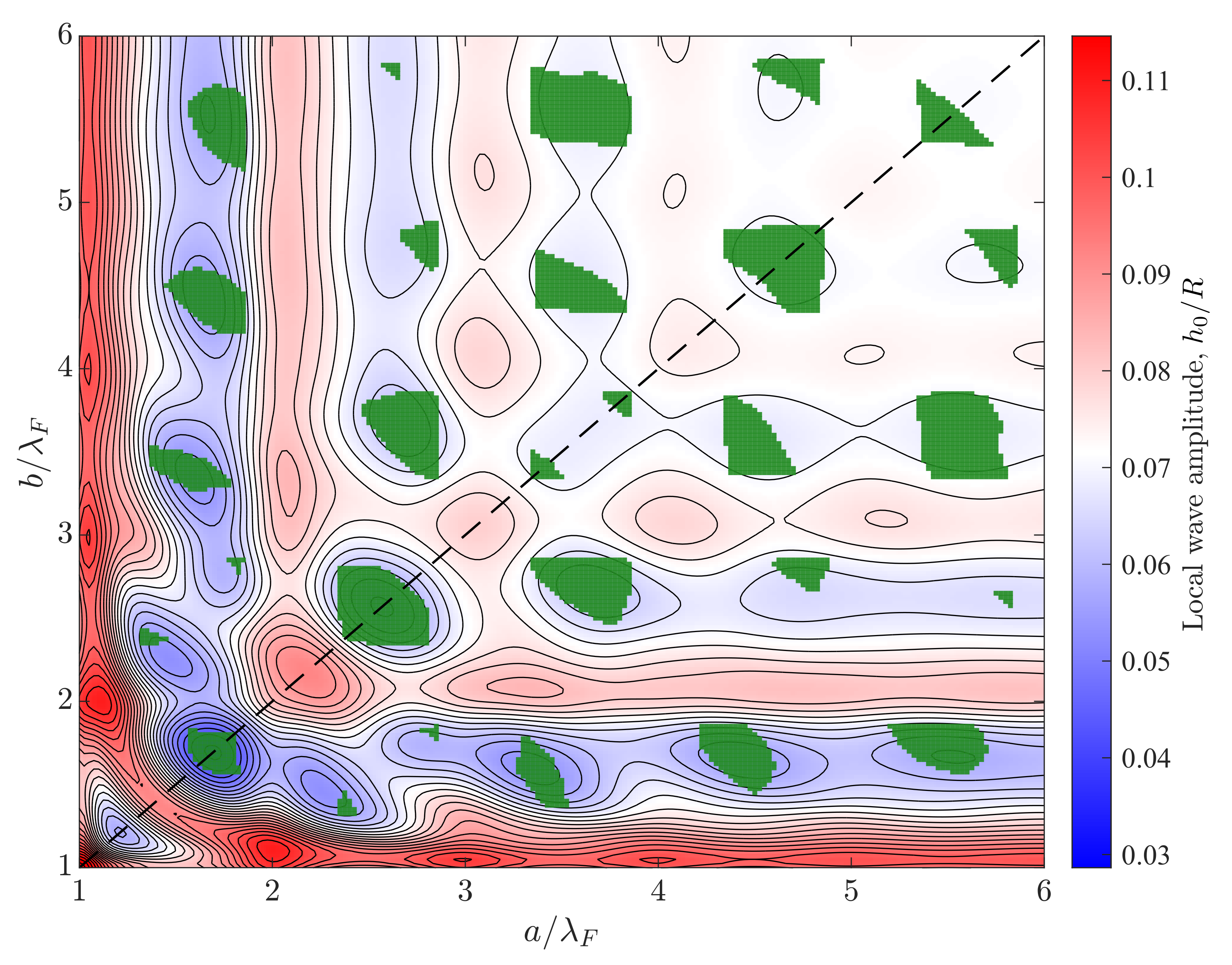
3. Results
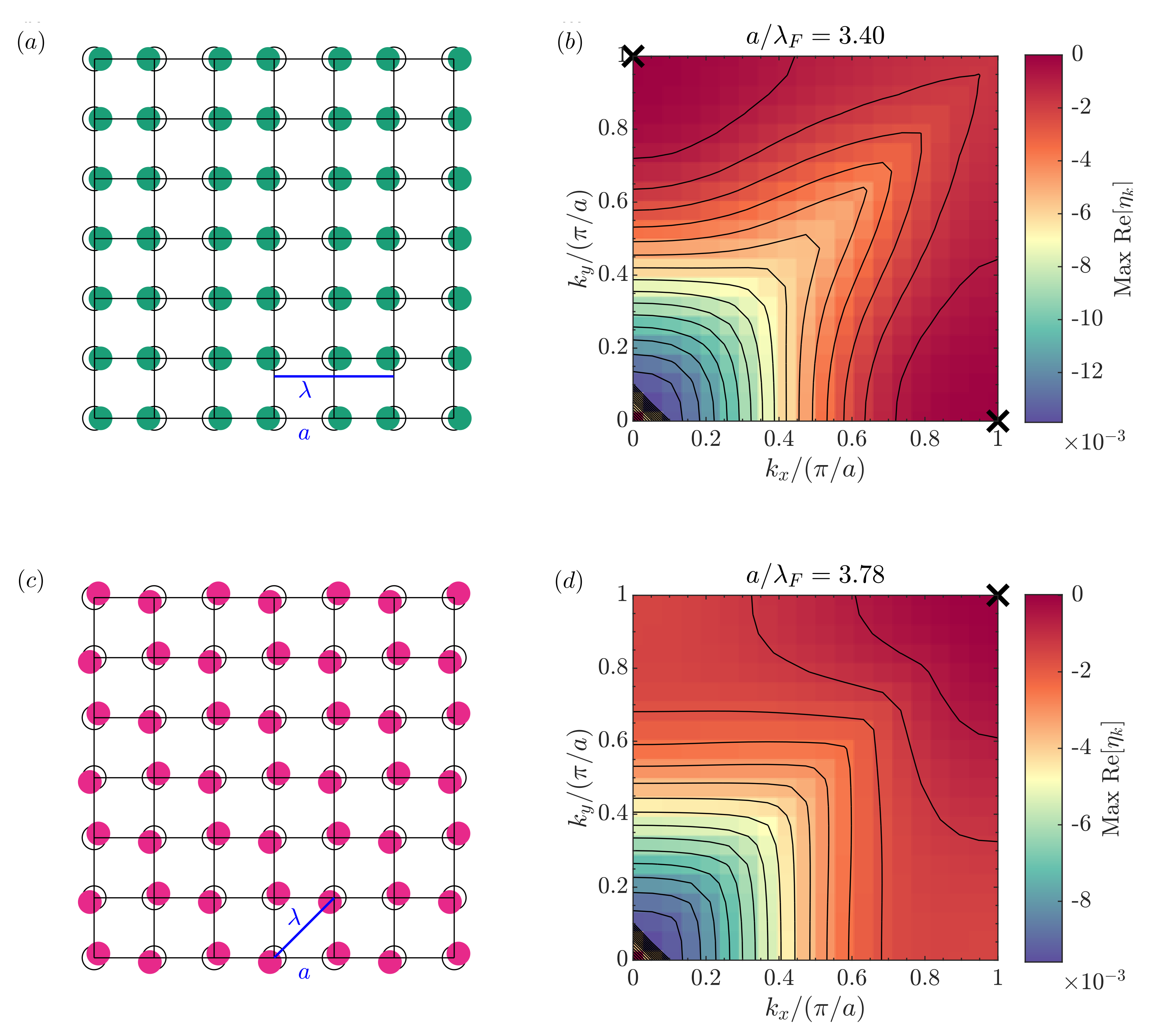
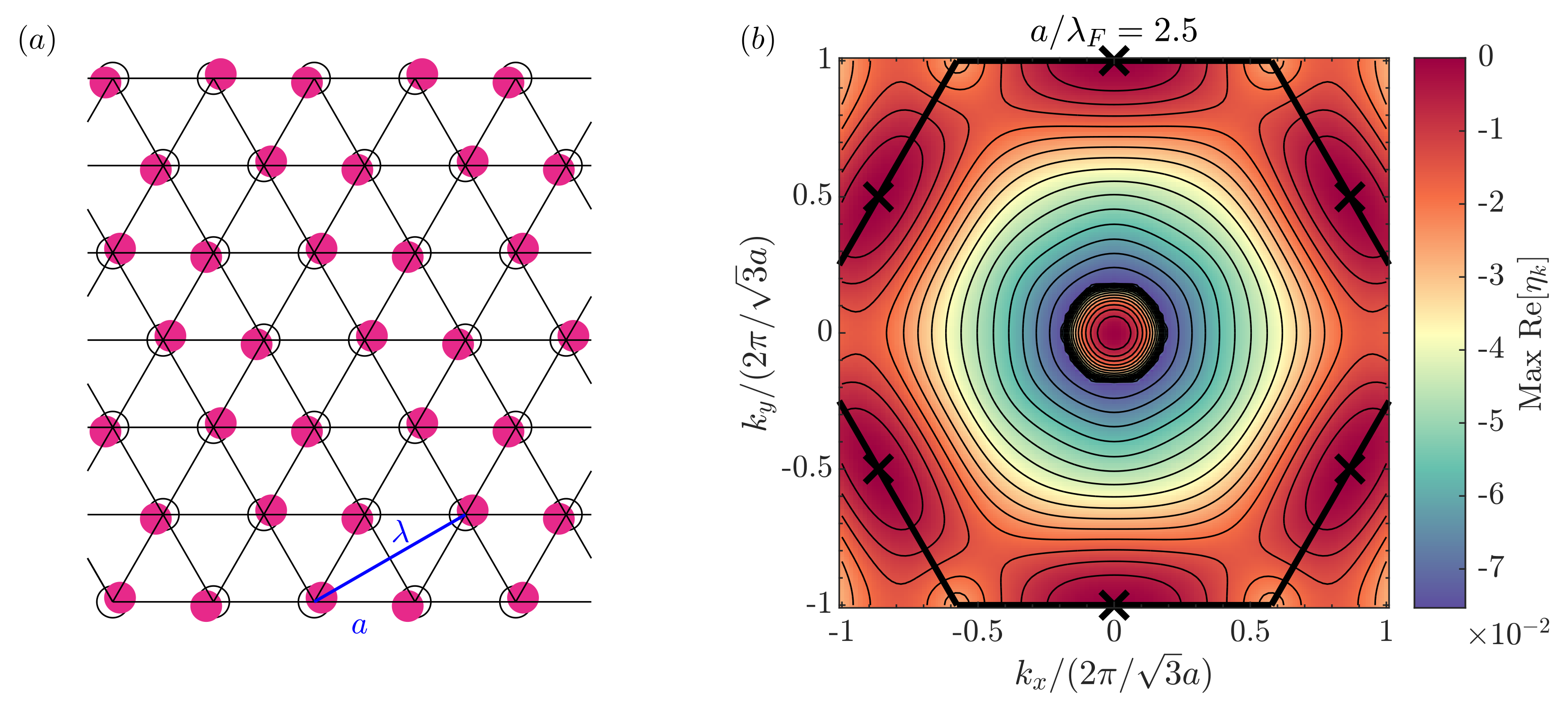
3.1. Square and Triangular Lattices
3.2. Geometric Instabilities in the Low-Memory Limit
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Impact-Phase Parameters
Appendix B. Rotational Symmetries of the Square and Triangular Lattices
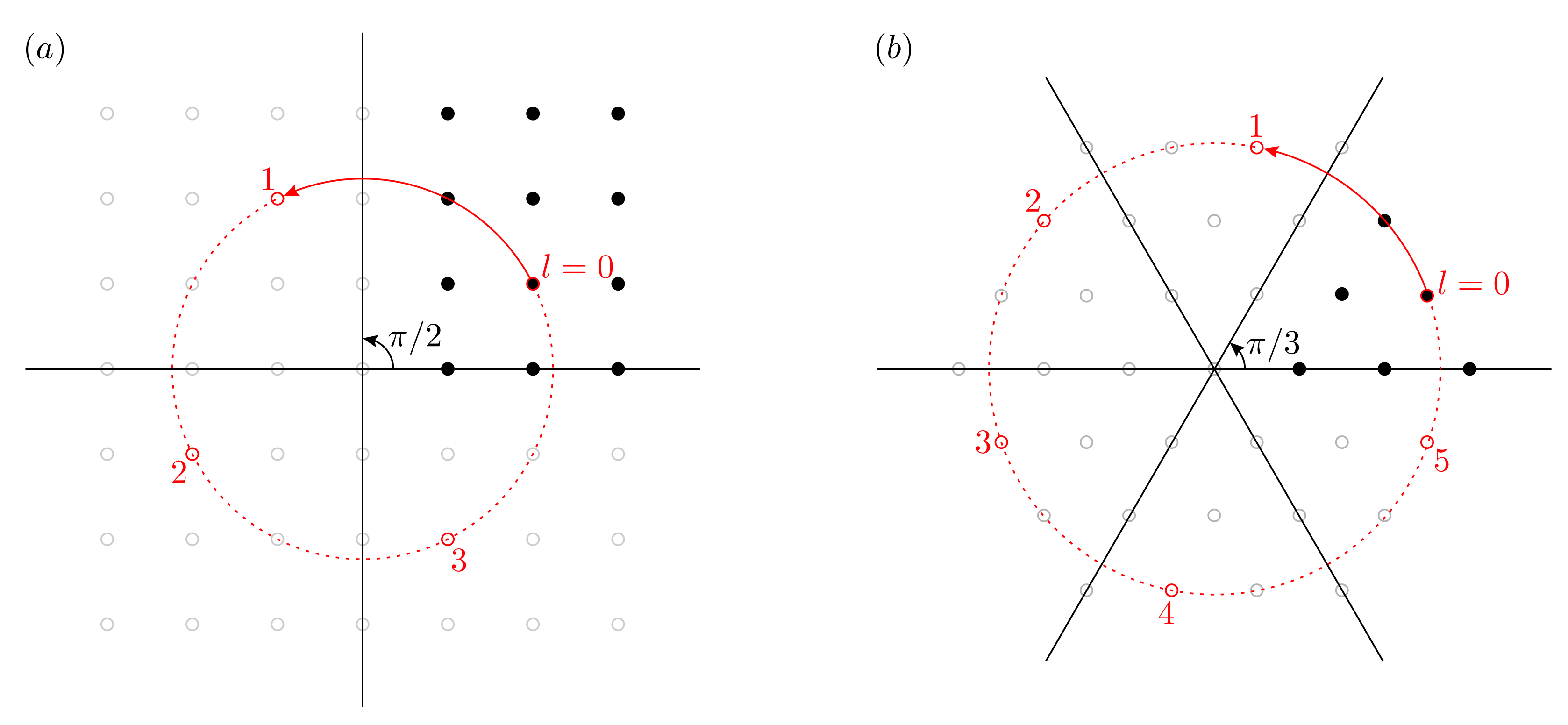
Appendix B.1. Square Lattice
Appendix B.2. Triangular Lattice
References
- Krumhansl, J. Lattice vibrations in solids. J. Appl. Phys. 1962, 33, 307–319. [Google Scholar] [CrossRef]
- Cochran, W. Lattice vibrations. Rep. Prog. Phys. 1963, 26, 1. [Google Scholar] [CrossRef]
- Dean, P. Atomic vibrations in solids. IMA J. Appl. Math. 1967, 3, 98–165. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Kane, C.; Lubensky, T. Topological boundary modes in isostatic lattices. Nat. Phys. 2014, 10, 39–45. [Google Scholar] [CrossRef]
- Lubensky, T.; Kane, C.; Mao, X.; Souslov, A.; Sun, K. Phonons and elasticity in critically coordinated lattices. Rep. Prog. Phys. 2015, 78, 073901. [Google Scholar] [CrossRef]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495–14500. [Google Scholar] [CrossRef]
- Süsstrunk, R.; Huber, S.D. Classification of topological phonons in linear mechanical metamaterials. Proc. Natl. Acad. Sci. USA 2016, 113, E4767–E4775. [Google Scholar] [CrossRef]
- Bragg, W.L.; Nye, J.F. A dynamical model of a crystal structure. Proc. R. Soc. A 1947, 190, 474–481. [Google Scholar]
- Penciu, R.; Kriegs, H.; Petekidis, G.; Fytas, G.; Economou, E. Phonons in colloidal systems. J. Chem. Phys. 2003, 118, 5224–5240. [Google Scholar] [CrossRef]
- Keim, P.; Maret, G.; Herz, U.; von Grünberg, H.H. Harmonic lattice behavior of two-dimensional colloidal crystals. Phys. Rev. Lett. 2004, 92, 215504. [Google Scholar] [CrossRef]
- Kaya, D.; Green, N.; Maloney, C.; Islam, M. Normal modes and density of states of disordered colloidal solids. Science 2010, 329, 656–658. [Google Scholar] [CrossRef][Green Version]
- Chen, K.; Still, T.; Schoenholz, S.; Aptowicz, K.B.; Schindler, M.; Maggs, A.; Liu, A.J.; Yodh, A. Phonons in two-dimensional soft colloidal crystals. Phys. Rev. E 2013, 88, 022315. [Google Scholar] [CrossRef]
- Ghosh, A.; Mari, R.; Chikkadi, V.; Schall, P.; Maggs, A.; Bonn, D. Low-energy modes and Debye behavior in a colloidal crystal. Phys. A Stat. Mech. Its Appl. 2011, 390, 3061–3068. [Google Scholar] [CrossRef]
- Beatus, T.; Tlusty, T.; Bar-Ziv, R. Phonons in a one-dimensional microfluidic crystal. Nat. Phys. 2006, 2, 743–748. [Google Scholar] [CrossRef]
- Schiller, U.D.; Fleury, J.B.; Seemann, R.; Gompper, G. Collective waves in dense and confined microfluidic droplet arrays. Soft Matter 2015, 11, 5850–5861. [Google Scholar] [CrossRef]
- Tsang, A.C.H.; Shelley, M.J.; Kanso, E. Activity-induced instability of phonons in 1D microfluidic crystals. Soft Matter 2018, 14, 945–950. [Google Scholar] [CrossRef]
- Ono-dit-Biot, J.C.; Soulard, P.; Barkley, S.; Weeks, E.R.; Salez, T.; Raphaël, E.; Dalnoki-Veress, K. Mechanical properties of 2D aggregates of oil droplets as model mono-crystals. Soft Matter 2021, 17, 1194–1201. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Ursell, F. The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. A 1954, 225, 505–515. [Google Scholar]
- Miles, J.; Henderson, D. Parametrically forced surface waves. Annu. Rev. Fluid Mech. 1990, 22, 143–165. [Google Scholar] [CrossRef]
- Walker, J. The amateur scientist. Drops of liquid can be made to float on liquid. What enables them to do so? Sci. Am. 1978, 238, 151. [Google Scholar] [CrossRef]
- Couder, Y.; Fort, E.; Gautier, C.H.; Boudaoud, A. From bouncing to floating: Noncoalescence of drops on a fluid bath. Phys. Rev. Lett. 2005, 94, 177801. [Google Scholar] [CrossRef] [PubMed]
- Moláček, J.; Bush, J.W.M. Drops bouncing on a vibrating bath. J. Fluid Mech. 2013, 727, 582–611. [Google Scholar] [CrossRef]
- Couder, Y.; Protiere, S.; Fort, E.; Boudaoud, A. Dynamical phenomena: Walking and orbiting droplets. Nature 2005, 437, 208. [Google Scholar] [CrossRef] [PubMed]
- Protière, S.; Boudaoud, A.; Couder, Y. Particle–wave association on a fluid interface. J. Fluid Mech. 2006, 554, 85–108. [Google Scholar] [CrossRef]
- Eddi, A.; Sultan, E.; Moukhtar, J.; Fort, E.; Rossi, M.; Couder, Y. Information stored in Faraday waves: The origin of a path memory. J. Fluid Mech. 2011, 674, 433–463. [Google Scholar] [CrossRef]
- Fort, E.; Eddi, A.; Boudaoud, A.; Moukhtar, J.; Couder, Y. Path-memory induced quantization of classical orbits. Proc. Natl. Acad. Sci. USA 2010, 107, 17515–17520. [Google Scholar] [CrossRef]
- Bush, J.W.M. Pilot-wave hydrodynamics. Annu. Rev. Fluid Mech. 2015, 47, 269–292. [Google Scholar] [CrossRef]
- Bush, J.W.M.; Couder, Y.; Gilet, T.; Milewski, P.A.; Nachbin, A. Introduction to focus issue on hydrodynamic quantum analogs. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 096001. [Google Scholar] [CrossRef]
- Bush, J.W.M.; Oza, A.U. Hydrodynamic quantum analogs. Rep. Prog. Phys. 2020, 84, 017001. [Google Scholar] [CrossRef]
- Rahman, A.; Blackmore, D. Walking droplets through the lens of dynamical systems. Mod. Phys. Lett. B 2020, 34, 2030009. [Google Scholar] [CrossRef]
- Couchman, M.M.P.; Turton, S.E.; Bush, J.W.M. Bouncing phase variations in pilot-wave hydrodynamics and the stability of droplet pairs. J. Fluid Mech. 2019, 871, 212–243. [Google Scholar] [CrossRef]
- Couchman, M.M.P.; Bush, J.W.M. Free rings of bouncing droplets: Stability and dynamics. J. Fluid Mech. 2020, 903. [Google Scholar] [CrossRef]
- Thomson, S.J.; Couchman, M.M.P.; Bush, J.W.M. Collective vibrations of confined levitating droplets. Phys. Rev. Fluids 2020, 5, 083601. [Google Scholar] [CrossRef]
- Barnes, L.; Pucci, G.; Oza, A.U. Resonant interactions in bouncing droplet chains. C. R. Mécanique 2020, 348, 573–589. [Google Scholar] [CrossRef]
- Protière, S.; Bohn, S.; Couder, Y. Exotic orbits of two interacting wave sources. Phys. Rev. E 2008, 78, 036204. [Google Scholar] [CrossRef]
- Oza, A.U.; Siéfert, E.; Harris, D.M.; Moláček, J.; Bush, J.W.M. Orbiting pairs of walking droplets: Dynamics and stability. Phys. Rev. Fluids 2017, 2, 053601. [Google Scholar] [CrossRef]
- Borghesi, C.; Moukhtar, J.; Labousse, M.; Eddi, A.; Fort, E.; Couder, Y. Interaction of two walkers: Wave-mediated energy and force. Phys. Rev. E 2014, 90, 063017. [Google Scholar] [CrossRef]
- Arbelaiz, J.; Oza, A.U.; Bush, J.W.M. Promenading pairs of walking droplets: Dynamics and stability. Phys. Rev. Fluids 2018, 3, 013604. [Google Scholar] [CrossRef]
- Lieber, S.I.; Hendershott, M.C.; Pattanaporkratana, A.; Maclennan, J.E. Self-organization of bouncing oil drops: Two-dimensional lattices and spinning clusters. Phys. Rev. E 2007, 75, 056308. [Google Scholar] [CrossRef]
- Eddi, A.; Terwagne, D.; Fort, E.; Couder, Y. Wave propelled ratchets and drifting rafts. Europhys. Lett. 2008, 82, 44001. [Google Scholar] [CrossRef]
- Eddi, A.; Decelle, A.; Fort, E.; Couder, Y. Archimedean lattices in the bound states of wave interacting particles. Europhys. Lett. 2009, 87, 56002. [Google Scholar] [CrossRef][Green Version]
- Eddi, A.; Boudaoud, A.; Couder, Y. Oscillating instability in bouncing droplet crystals. Europhys. Lett. 2011, 94, 20004. [Google Scholar] [CrossRef]
- Thomson, S.J.; Durey, M.; Rosales, R.R. Collective vibrations of a hydrodynamic active lattice. Proc. R. Soc. A 2020, 476, 20200155. [Google Scholar] [CrossRef]
- Oza, A.U.; Rosales, R.R.; Bush, J.W.M. A trajectory equation for walking droplets: Hydrodynamic pilot-wave theory. J. Fluid Mech. 2013, 737, 552–570. [Google Scholar] [CrossRef]
- Thomson, S.J.; Durey, M.; Rosales, R.R. Discrete and periodic complex Ginzburg-Landau equation for a hydrodynamic active lattice. Phys. Rev. E 2021, 103, 062215. [Google Scholar] [CrossRef]
- Moláček, J.; Bush, J.W.M. Drops walking on a vibrating bath: Towards a hydrodynamic pilot-wave theory. J. Fluid Mech. 2013, 727, 612–647. [Google Scholar] [CrossRef]
- Turton, S.E.; Couchman, M.M.P.; Bush, J.W.M. A review of the theoretical modeling of walking droplets: Towards a generalized pilot-wave framework. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 096111. [Google Scholar] [CrossRef]
- Harris, D.M.; Quintela, J.; Prost, V.; Brun, P.T.; Bush, J.W.M. Visualization of hydrodynamic pilot-wave phenomena. J. Vis. 2017, 20, 13–15. [Google Scholar] [CrossRef]
- Damiano, A.P.; Brun, P.T.; Harris, D.M.; Galeano-Rios, C.A.; Bush, J.W.M. Surface topography measurements of the bouncing droplet experiment. Exp. Fluids 2016, 57, 163. [Google Scholar] [CrossRef]
- Tadrist, L.; Shim, J.B.; Gilet, T.; Schlagheck, P. Faraday instability and subthreshold Faraday waves: Surface waves emitted by walkers. J. Fluid Mech. 2018, 848, 906–945. [Google Scholar] [CrossRef]
- Wind-Willassen, Ø.; Moláček, J.; Harris, D.M.; Bush, J.W.M. Exotic states of bouncing and walking droplets. Phys. Fluids 2013, 25, 082002. [Google Scholar] [CrossRef]
- Blackman, M. Contributions to the theory of the specific heat of crystals II—On the vibrational spectrum of cubical lattices and its application to the specific heat of crystals. Proc. R. Soc. A 1935, 148, 384–406. [Google Scholar]
- Montroll, E.W. Dynamics of a square lattice I. Frequency spectrum. J. Chem. Phys. 1947, 15, 575–591. [Google Scholar] [CrossRef]
- Bell, R. The dynamics of disordered lattices. Rep. Prog. Phys. 1972, 35, 1315–1409. [Google Scholar] [CrossRef]
- Kosevich, A.M. The Crystal Lattice: Phonons, Solitons, Dislocations, Superlattices; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]



| Symbol | Definition |
|---|---|
| Fluid | |
| Density, surface tension, effective kinematic viscosity [47] | |
| Bath driving frequency, Faraday period, wavelength, wavenumber | |
| Peak driving acceleration of bath, walking threshold of single drop, lattice instability threshold, Faraday threshold | |
| Trajectory equation | |
| , t, g | Horizontal position, time, gravitational acceleration |
| R, | Droplet radius, mass |
| Wave amplitude strobed at bouncing period | |
| Wave kernel | |
| Wave decay timescale [47] | |
| Memory parameter | |
| Wave-amplitude coefficient | |
| , | Spatio-temporal damping coefficient, viscosity induced wavenumber correction [48] |
| Non-dimensional spatial-damping coefficient | |
| , | Horizontal drag coefficient [47], air viscosity |
| Non-dimensional droplet mass | |
| Non-dimensional wave-force coefficient | |
| , | Impact phase parameters (see Appendix A) [32] |
| Lattice | |
| Basis vectors defining geometry of Bravais lattice | |
| Horizontal position of droplets in base lattice, | |
| Wave vector, polarization vector, complex-valued frequency of vibrational mode |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Couchman, M.M.P.; Evans, D.J.; Bush, J.W.M. The Stability of a Hydrodynamic Bravais Lattice. Symmetry 2022, 14, 1524. https://doi.org/10.3390/sym14081524
Couchman MMP, Evans DJ, Bush JWM. The Stability of a Hydrodynamic Bravais Lattice. Symmetry. 2022; 14(8):1524. https://doi.org/10.3390/sym14081524
Chicago/Turabian StyleCouchman, Miles M. P., Davis J. Evans, and John W. M. Bush. 2022. "The Stability of a Hydrodynamic Bravais Lattice" Symmetry 14, no. 8: 1524. https://doi.org/10.3390/sym14081524
APA StyleCouchman, M. M. P., Evans, D. J., & Bush, J. W. M. (2022). The Stability of a Hydrodynamic Bravais Lattice. Symmetry, 14(8), 1524. https://doi.org/10.3390/sym14081524






