Analytical Results for Classical Axially Symmetric States of Relativistic Hydrogenic Ions in Collinear Electric and Magnetic Fields of Arbitrary Strengths
Abstract
1. Introduction
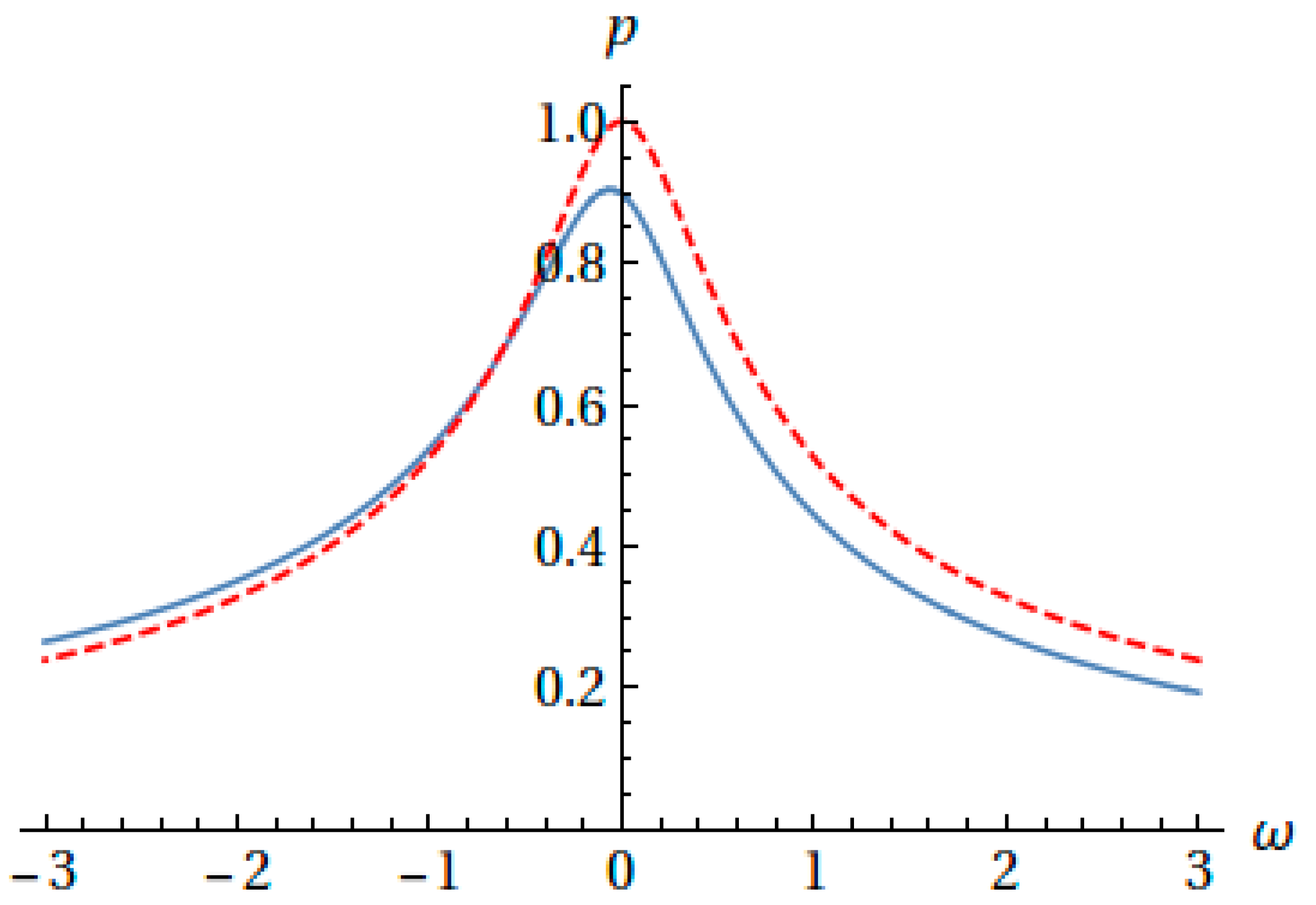
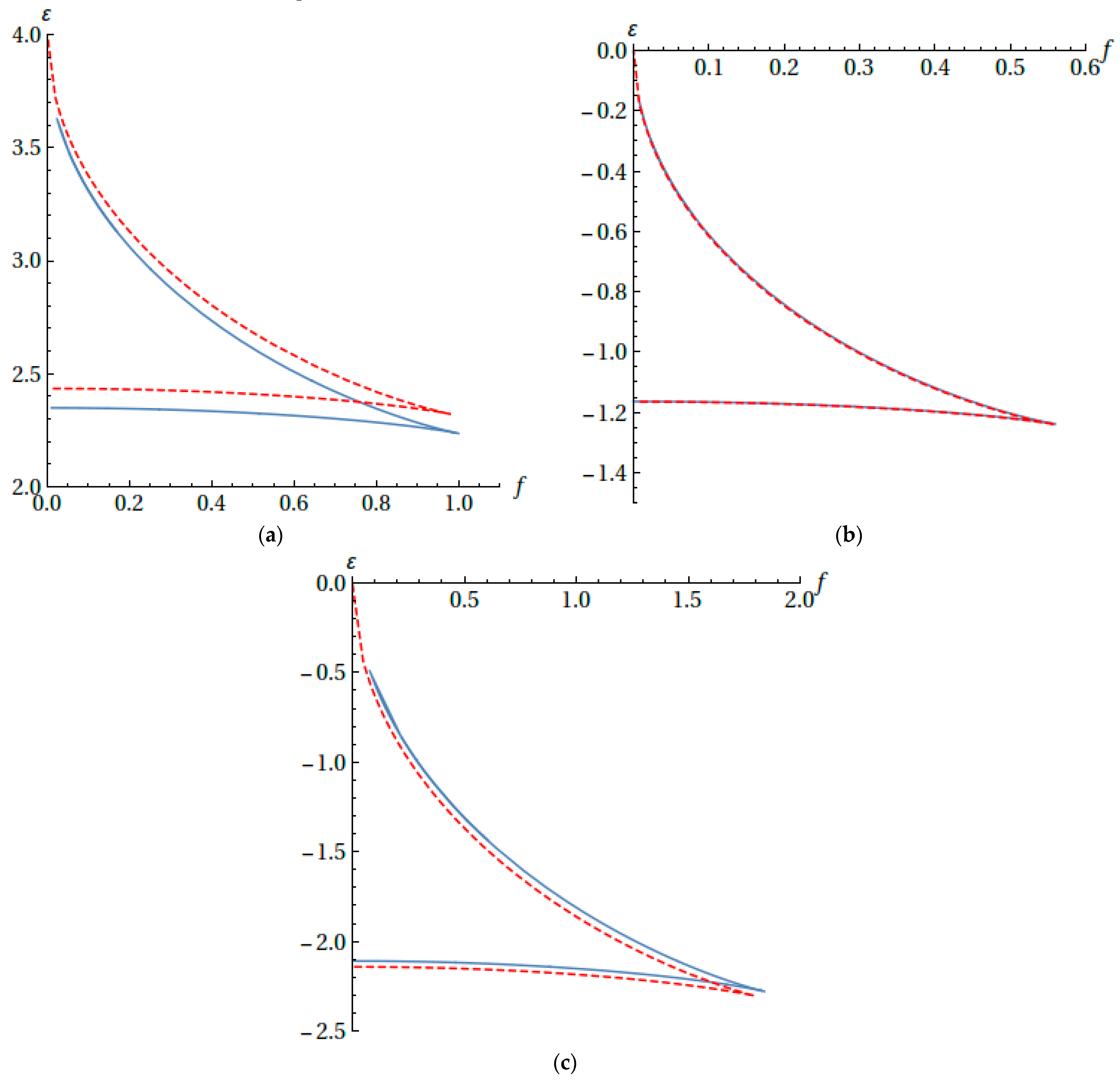
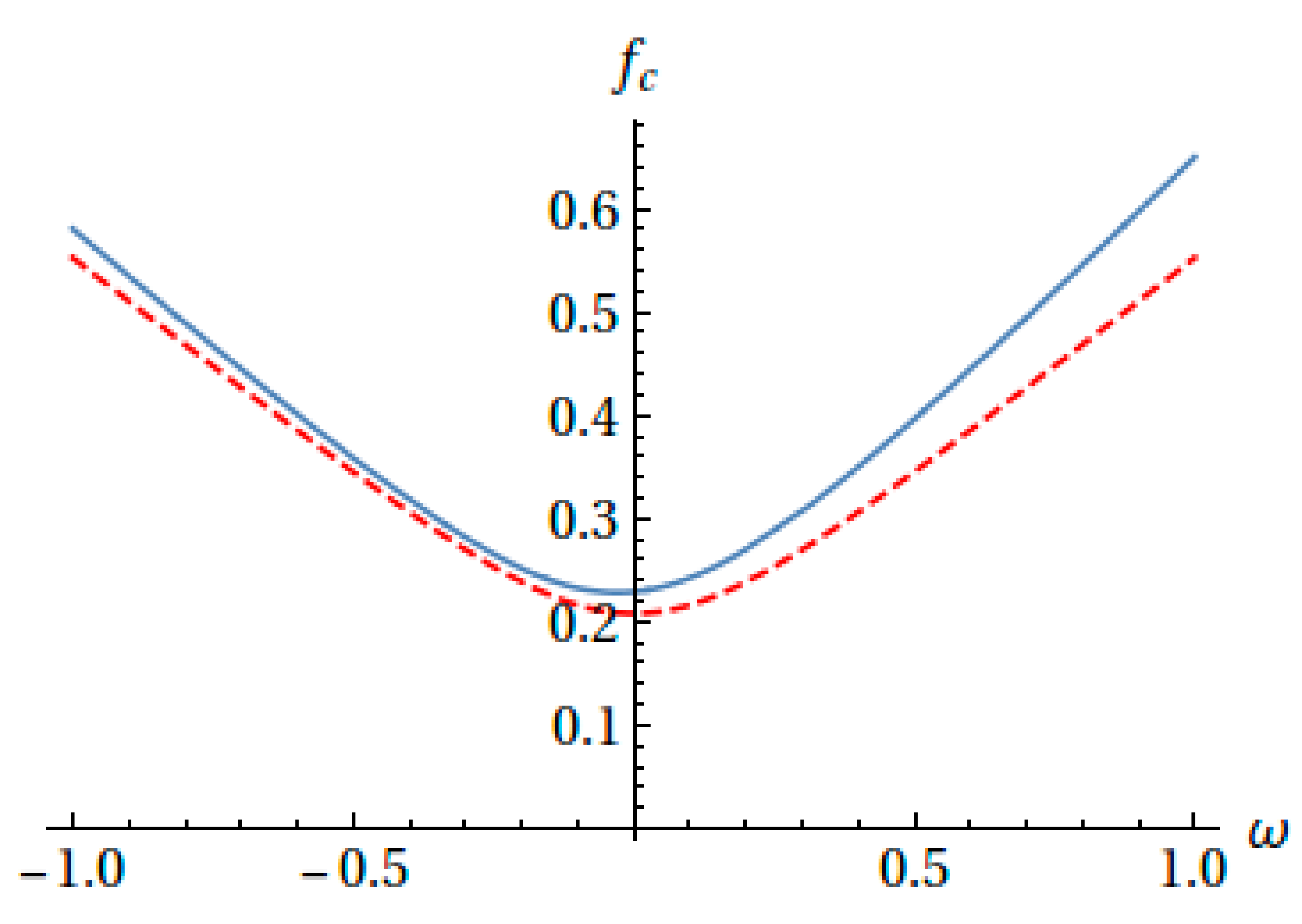
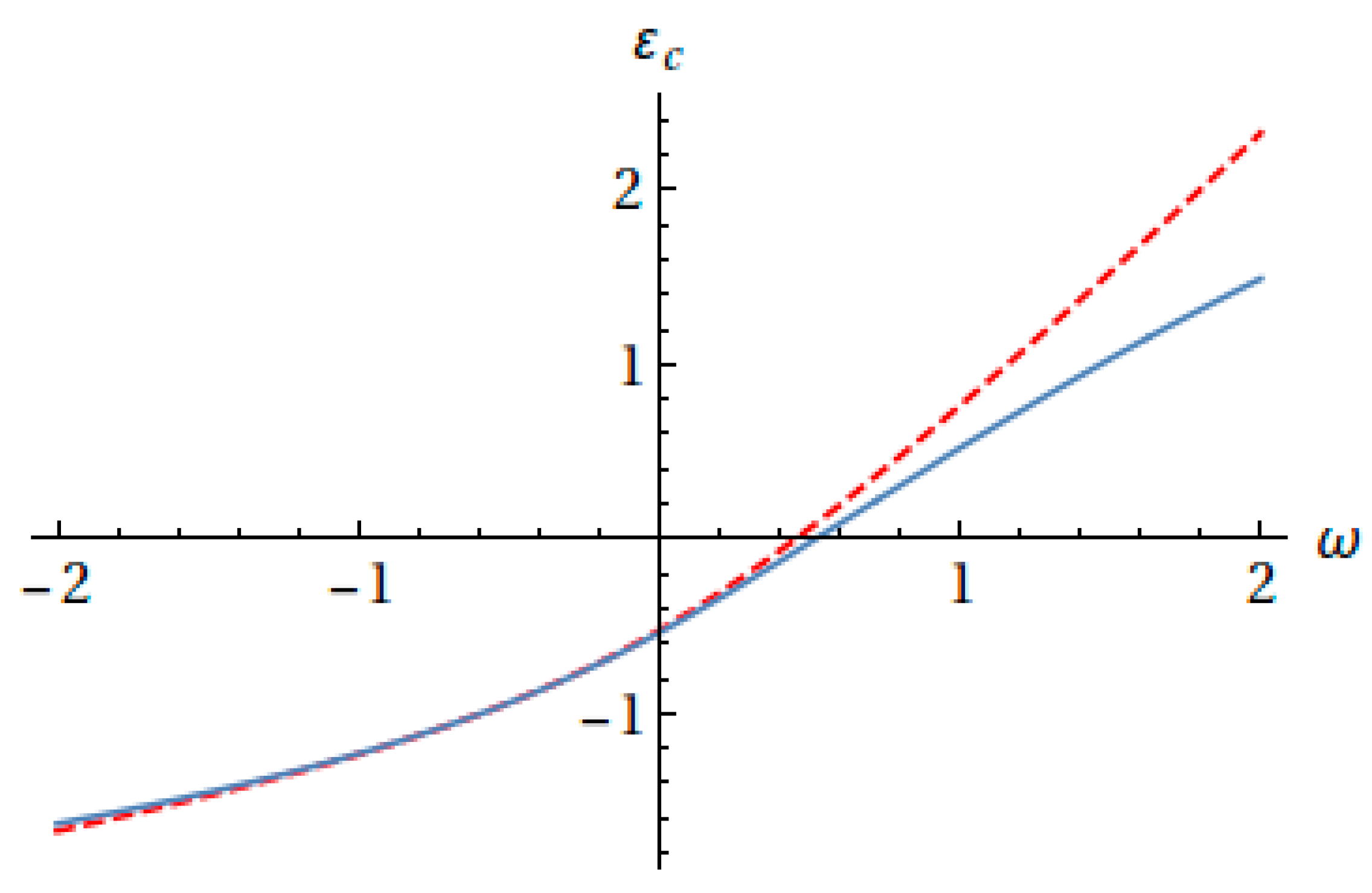
2. Results
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, E.; Farrelly, D.; Uzer, T. A Saturnian atom. Opt. Express 1997, 1, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Germann, T.C.; Herschbach, D.R.; Dunn, M.; Watson, D.K. Circular Rydberg states of the hydrogen atom in a magnetic field. Phys. Rev. Lett. 1995, 74, 658. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.H.; Lee, C.Y.; Gallagher, T.F. Production of circular Rydberg states with circularly polarized microwave fields. Phys. Rev. Lett. 1994, 73, 3078. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Cheret, M.; Roussel, F.; Spiess, G. New scheme for producing circular orbital states in combined RF and static fields. J. Phys. B At. Mol. Opt. Phys. 1993, 26, L437. [Google Scholar] [CrossRef]
- Dutta, S.K.; Feldbaum, D.; Walz-Flannigan, A.; Guest, J.R.; Raithel, G. High-angular-momentum states in cold Rydberg gases. Phys. Rev. Lett. 2001, 86, 3993. [Google Scholar] [CrossRef] [PubMed]
- Hulet, R.G.; Hilfer, E.S.; Kleppner, D. Inhibited spontaneous emission by a Rydberg atom. Phys. Rev. Lett. 1985, 55, 2137. [Google Scholar] [CrossRef] [PubMed]
- MacAdam, K.B.; Horsdal-Pedersen, E. Charge transfer from coherent elliptic states. J. Phys. B At. Mol. Opt. Phys. 2003, 36, R167. [Google Scholar] [CrossRef][Green Version]
- Vainberg, V.M.; Popov, V.S.; Sergeev, A.V. The 1/n expansion for a hydrogen atom in an external field. Sov. Phys. JETP 1990, 71, 470–477. [Google Scholar]
- Oks, E. Circular Rydberg states of hydrogenlike systems in collinear electric and magnetic fields of arbitrary strengths: An exact analytical classical solution. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2004, 28, 171–179. [Google Scholar] [CrossRef]
- Haba, Y.; Nagaoka, K.; Tsumori, K.; Kisaki, M.; Takahashi, K.; Nakano, H.; Ikeda, K.; Yoshimura, S.; Osakabe, M. Response of beam focusing to plasma fluctuation in a filament-arc-type negative ion source. Jpn. J. Appl. Phys. 2020, 59, SHHA01. [Google Scholar] [CrossRef]
- Zhu, C.; Gao, Z.F.; Li, X.D.; Wang, N.; Yuan, J.P.; Peng, Q.H. Modified Fermi energy of electrons in a superhigh magnetic field. Mod. Phys. Lett. A 2016, 31, 1650070. [Google Scholar] [CrossRef]
- Wang, H.; Gao, Z.F.; Jia, H.Y.; Wang, N.; Li, X.D. Estimation of electrical conductivity and magnetization parameter of neutron star crusts and applied to the high-braking-index pulsar PSR J1640-4631. Universe 2020, 6, 63. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kryukov, N.; Oks, E. Analytical Results for Classical Axially Symmetric States of Relativistic Hydrogenic Ions in Collinear Electric and Magnetic Fields of Arbitrary Strengths. Symmetry 2022, 14, 1515. https://doi.org/10.3390/sym14081515
Kryukov N, Oks E. Analytical Results for Classical Axially Symmetric States of Relativistic Hydrogenic Ions in Collinear Electric and Magnetic Fields of Arbitrary Strengths. Symmetry. 2022; 14(8):1515. https://doi.org/10.3390/sym14081515
Chicago/Turabian StyleKryukov, N., and E. Oks. 2022. "Analytical Results for Classical Axially Symmetric States of Relativistic Hydrogenic Ions in Collinear Electric and Magnetic Fields of Arbitrary Strengths" Symmetry 14, no. 8: 1515. https://doi.org/10.3390/sym14081515
APA StyleKryukov, N., & Oks, E. (2022). Analytical Results for Classical Axially Symmetric States of Relativistic Hydrogenic Ions in Collinear Electric and Magnetic Fields of Arbitrary Strengths. Symmetry, 14(8), 1515. https://doi.org/10.3390/sym14081515






