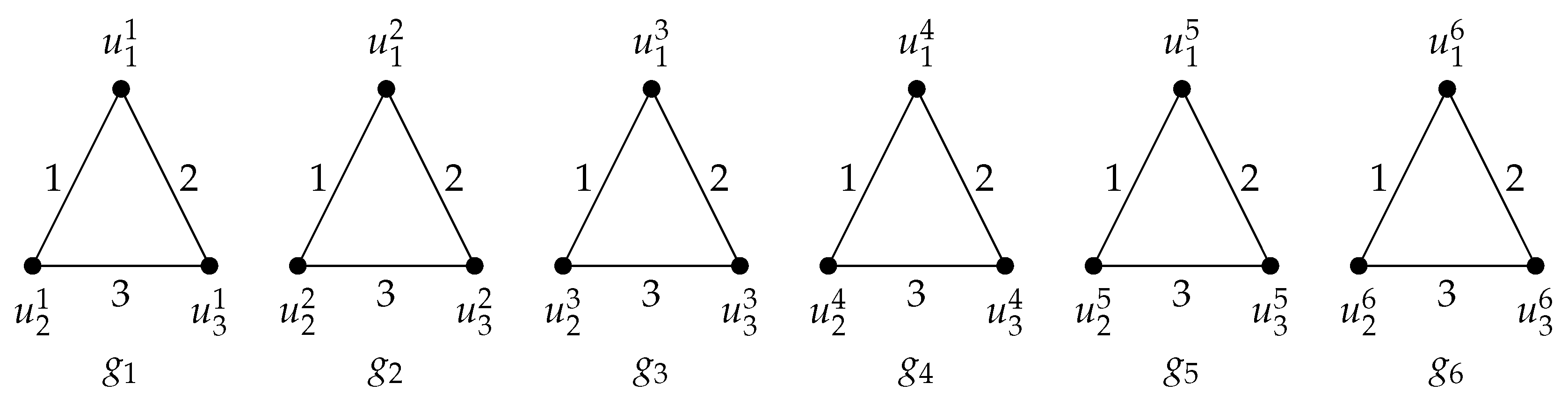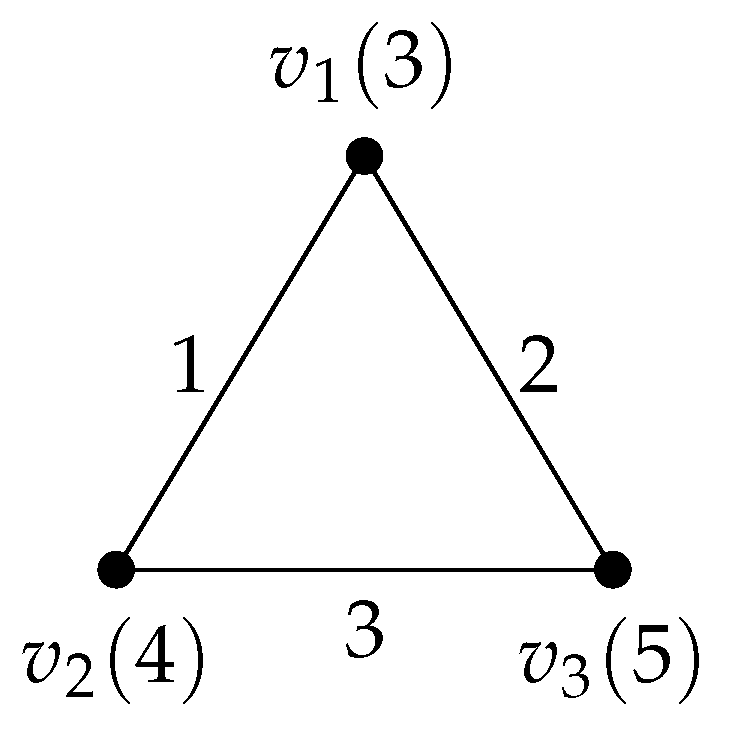1. Introduction
Graphs that are considered in this paper are finite, undirected, connected, and simple. The concept of antimagic labeling of a graph was introduced by Hartsfield and Ringel [
1].
An antimagic labeling of a graph G with m edges and n vertices is a one-to-one correspondence f between the edge set of G to the label set such that , for any two distinct vertices of in , where is defined as the sum of the labels of the edges that are incident to a vertex v in G. A graph that has at least one antimagic labeling is called an antimagic graph.
It is clear that
does not have any antimagic labeling. Except for
, it is believed that all other connected graphs admit at least some antimagic labeling. This is proposed as a conjecture by Hartsfield and Ringel [
1] which states that “Every connected graph other than
are antimagic”. Hartsfield and Ringel [
1] proved that stars, paths, cycles, wheels, complete graphs and complete bipartite graphs,
admit antimagic labeling.
In cryptography, Data Encryption Standard (DES) is a block cipher in which the data is encrypted in blocks. Compared to DES, the Advanced Encryption Standard (AES is a symmetric block cipher cryptographic algorithm used for carrying out the encryption) has more security. Antimagic labeling of a network (graph) is used in AES to perform the encryption of data in blocks of a size of 128 bits each. Likewise, antimagic labeling is used in many fields of engineering. By also using an antimagic labeling of a graph
G, we can give a proper colouring to the graph
G. For the study on antimagic labeling and its connection with the vertex colouring, refer to [
2,
3,
4].
Alon et al. [
5] confirmed that the conjecture stands true for some classes of graphs. That is, if
G is a graph with
n vertices and there exist a absolute constant
c such that either
or
, then the graph
G admits an antimagic labeling. Later, Yilma [
6] proved that a graph with maximum degree greater than or equal to
is antimagic.
Researchers have adopted various new techniques to prove some interesting classes of graphs that have an antimagic labeling. For detailed survey, one can refer to [
7,
8,
9,
10,
11,
12,
13,
14,
15]. Although researchers studied the antimagicness of several classes of graph, the conjecture of Hartsfield and Ringel still remains open, even for trees.
Regular graphs are well-studied networks in computer science and most of them are symmetric nature. So, studying the antimagicness of regular graphs is more attractive. Initially, the antimagicness of regular graphs were extensively studied by many researchers and finally, in 2016, it was shown that all regular graphs are antimagic. Cranston et al. [
16] proved that all odd regular graphs are antimagic, while the antimagicness of the even regular graphs were verified by Chang et al. [
17] in 2016. In 2015, Bèrczi et al. [
18] gave proof of the antimagicness of even regular graphs but they realized that the proof of the main theorem of the step uses an invalid assumption. Hence, 4 years later in 2019, they rectified the error and proved that all regular graphs admit antimagic labeling.
Theorem 1 (See [
17]).
For every k-regular graph is antimagic. Once regular graphs were proven to be antimagic, researchers focused on proving the antimagicness of graph products using the base as a regular graphs. Liang and Zhu [
19] proved that if
G is a
k-regular graph and
H is any arbitrary graph with
, then the Cartesian product of graph
G and
H admits an antimagic labeling. Cheng [
20] considers a regular graph
and
that has the degree bounded with some inequality, and in this case the Cartesian product of
and
again admits antimagic labeling. In addition, they investigated whether two or more regular graphs with positive degree (mandatorily not connected) admit an antimagic labeling. Wang and Hsiao [
21] explored new classes of sparse antimagic graphs through Cartesian products. Additionally, Wang and Hsiao [
21] considers
G as an arbitrary graph and
H as a
—regular graph with
, and then they proved that the lexicographic product of graph
G and
H admits an antimagic labeling. Oudone Phanalasy et al. [
22] proved that certain families of Cartesian products of regular graphs are antimagic. Daykin et al. [
23] constructed two families of graphs known to be antimagic, namely sequential generalized corona graph and generalized snowflake graph. Wenhui et al. [
24] investigated antimagicness for lexicographic product
and
where
. Yingyu et al. [
25] assumed
G as a complete bipartite graph
and
H as a path graph
, and then they proved that the lexicographic product of graph
G and
H admits an antimagic labeling. Recently, Yingyu et al. [
26] constructed oriented Eulerian circuit and used Siamese method to achieve an antimagic labeling for the composition of graph
G and
. The antimagicness of joined graphs is considered by Wang et al. [
27]. If
G is a graph with minimum degree of at least
r and
H is a graph with maximum degree of at most
then the join of
G and
H admits an antimagic labeling for
. Bača et al. [
28] used the antimagic labeling of join graphs to prove the antimagicness of complete multi-partite graphs.
Inspired by the results on the antimagicness of product graphs, in this paper we discuss the antimagicness for rooted and corona products of regular graphs. More particularly, we proved that if we let G be a connected t-regular graph and H be a connected k-regular graph, then the rooted product of G and H admits antimagic labeling when . We also proved that if we let G be a connected t-regular graph and H be a connected k-regular graph, then the corona product of G and H admits antimagic labeling for all .
A rooted graph H is a graph that has one vertex, named a root vertex, as its fixed vertex. Let G be a n vertex graph and be a sequence of n rooted graphs such that and v is the root vertex of H. The rooted product of the graphs G and H obtained from G such that by identifying the root vertex of to the ith vertex of G. The rooted product of graph G and H is denoted by . The corona product of the graph G and H is the graph obtained by taking one copy of G and n copies of H, and joining the ith vertex of G to each vertex from the copy of H and it is denoted by .
2. Main Results
In this section, we prove our main results. Before proving the main result we prove some basic lemmas and observations which will be used in the main results.
Lemma 1. If G is a k-regular graph with m edges, then for any vertex u in , , where f is an antimagic labeling of G.
Proof. Let G be a k-regular graph with m edges. By Theorem 1 it admits an antimagic labeling. Let f be an antimagic labeling of G, then for any vertex u in , takes minimum when their incident edges obtain labels from the set and take the maximum value when their incident edges obtain labels from the set .
Hence, . □
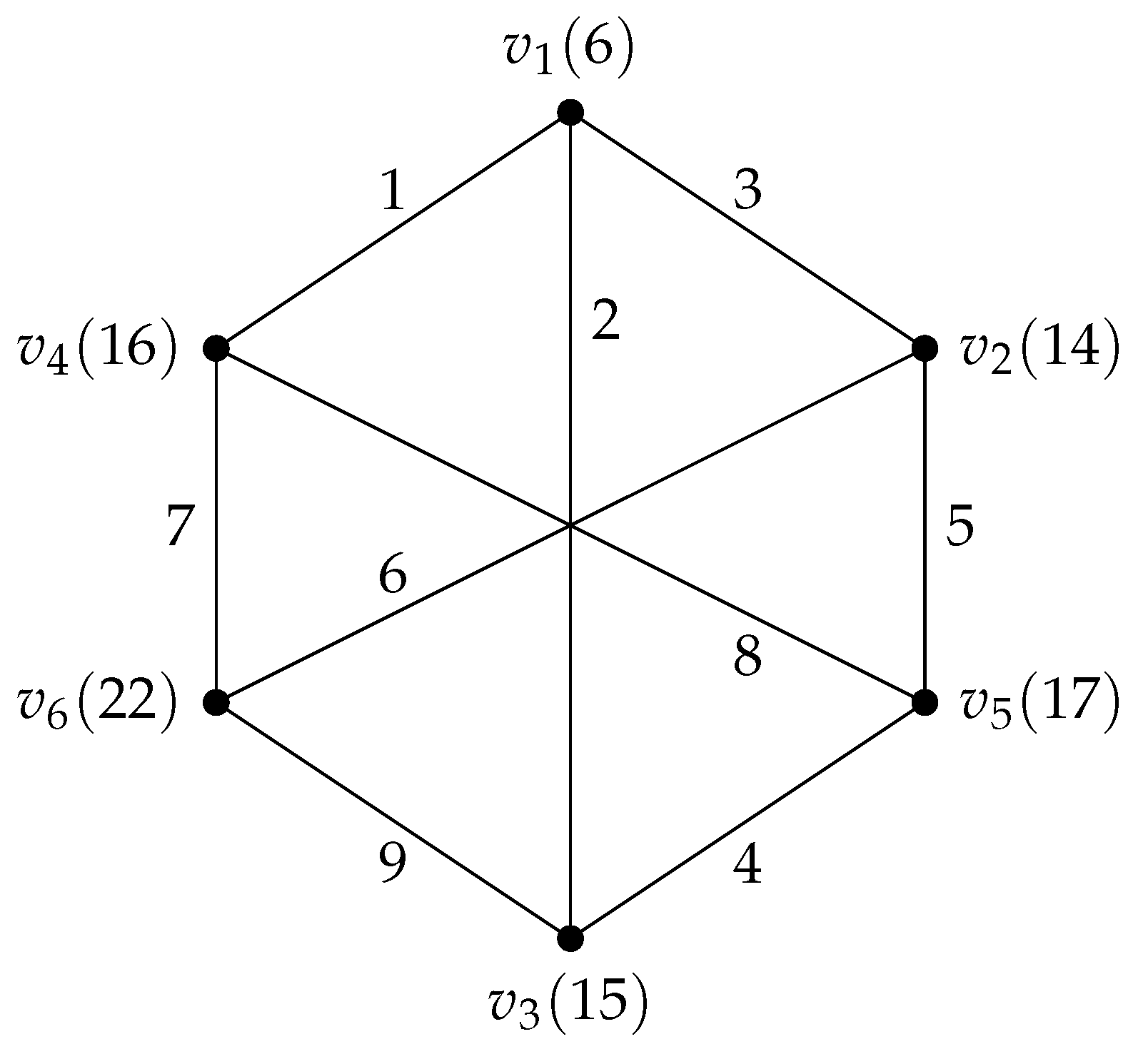
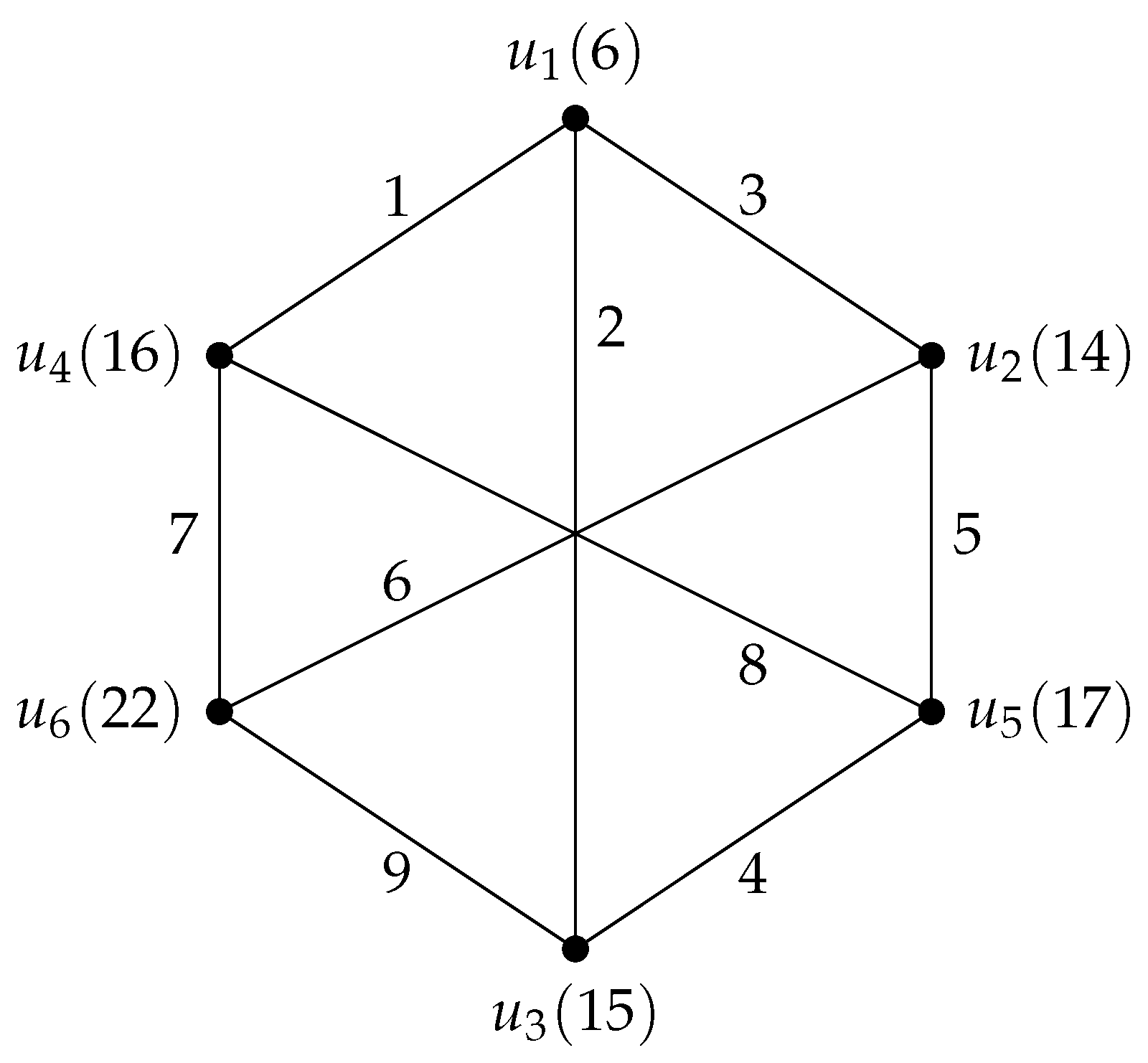
Figure 1 shows the antimagic labeling of a 3-regular graph
G with 9 edges. From
Figure 1, we also observe that the range of the vertex sum of the vertices of
G are from 6 to 22.
From Lemma 1, we have the following observation.
Observation 1. If G be a k-regular graph with f as its antimagic labeling. Letbe any two vertices of G such that ifthen.
An antimagic labeling of a 2-regular graph
H with 3 edges is given in
Figure 2. From
Figure 2 we also observe that the range in the difference of the vertex sum of any two vertices of
H are from 0 to 2.
Theorem 2. Let G be a connected t-regular graph and let H be a connected k-regular graph, then the rooted product of G and H admits antimagic labeling.
Proof. Let G be a t-regular graph with n vertices and m edges and let H be a k-regular graph with p vertices and q edges. By Theorem 1, the graphs G and H admit antimagic labeling. Let f and g be the antimagic labeling of G and H respectively. By definition of f, such that for any two distinct vertices u and v in G. By definition of g, such that for any two distinct vertices x and y in H.
Let us name the vertices of
G as
such that,
and also name the vertices of
H as
such that,
Construct the rooted product of
G and
H,
by fixing the root vertex of
H as
. Note that the number of edges in
is
. Let us name the vertices of
as follows. The vertices of
G are named as the same as the earlier, that is
and then name the vertices of
, for
(
isomorphic copy of H) as
. That is the vertex
in
H is now has the name
in
for
. Note that
. That is, the set of vertices
induces the graph
G. Before defining the antimagic labeling of
, we label the edges of
by using the edge labeling
g of
H as follows:
for an edge
in
,
where
as an edge
in
H. Then by definition of
g and (
2) for each
.
where
are the vertices of
in
.
Now we define
by,
From the above labeling
h, we observe that, for all
and
In order to prove that h is an antimagic labeling of , we need to prove that for any two distinct vertices x and y in such that We consider the following possible cases on the vertices of x and the vertices of y in .
- (i)
x in and y in for and & .
- (ii)
x in G and y in when ,
- (iii)
x and y are the vertices of G.
Case 1. For any two distinct vertices x and y in , where x is in and y in , for and .
Case 1.1. When
, then both the vertex
x and
y are from
. By definition on the naming of the vertices of
,
and
for some
Then by definition of
h and by (
7) we have,
Without loss of generality, we assume that
. By (
4), we have
, therefore
. Hence
Case 1.2. When , then the vertex x in and the vertex y in .
By definition on the naming of vertices of and , and for some .
Without loss of generality we assume
. Then by definition of
h and by (
7) we have,
Case 1.2.1. If
. Then by (
2),
Case 1.2.2. If
. Then by (
2),
Consider,
Since
and
are antimagic labeling of
and
respectively, by Observation 1, we have,
Case 2. For any two distinct vertices x and y in such that x in G and y in for such that .
By definition on naming the vertices of
G,
and by definition on the naming of the vertices of
,
for some
r,
. Then by definition of
h and by (
6) and (
7). We have
Case 2.1. When
for
. Consider
Since, , , . Hence, .
Case 2.2. When
for
. Consider
By definition of
f,
.
Since
&
Case 3. Both the vertices are from
G. By definition on the naming of the vertices of
G,
and
for some
&
. By (
6),
Without loss of generality, we consider
, therefore by (
1) and
and by (
4),
. Consider,
Since, . Hence, . □
Figure 1,
Figure 2,
Figure 3 and
Figure 4 illustrate the proof Theorem 2. An antimagic labeling of a 3-regular graph
G and the antimagic labeling of a 2-regular graph
H are given in
Figure 1 and
Figure 2, respectively. In
Figure 3, the six copies of the graph
H are considered with their labeling function
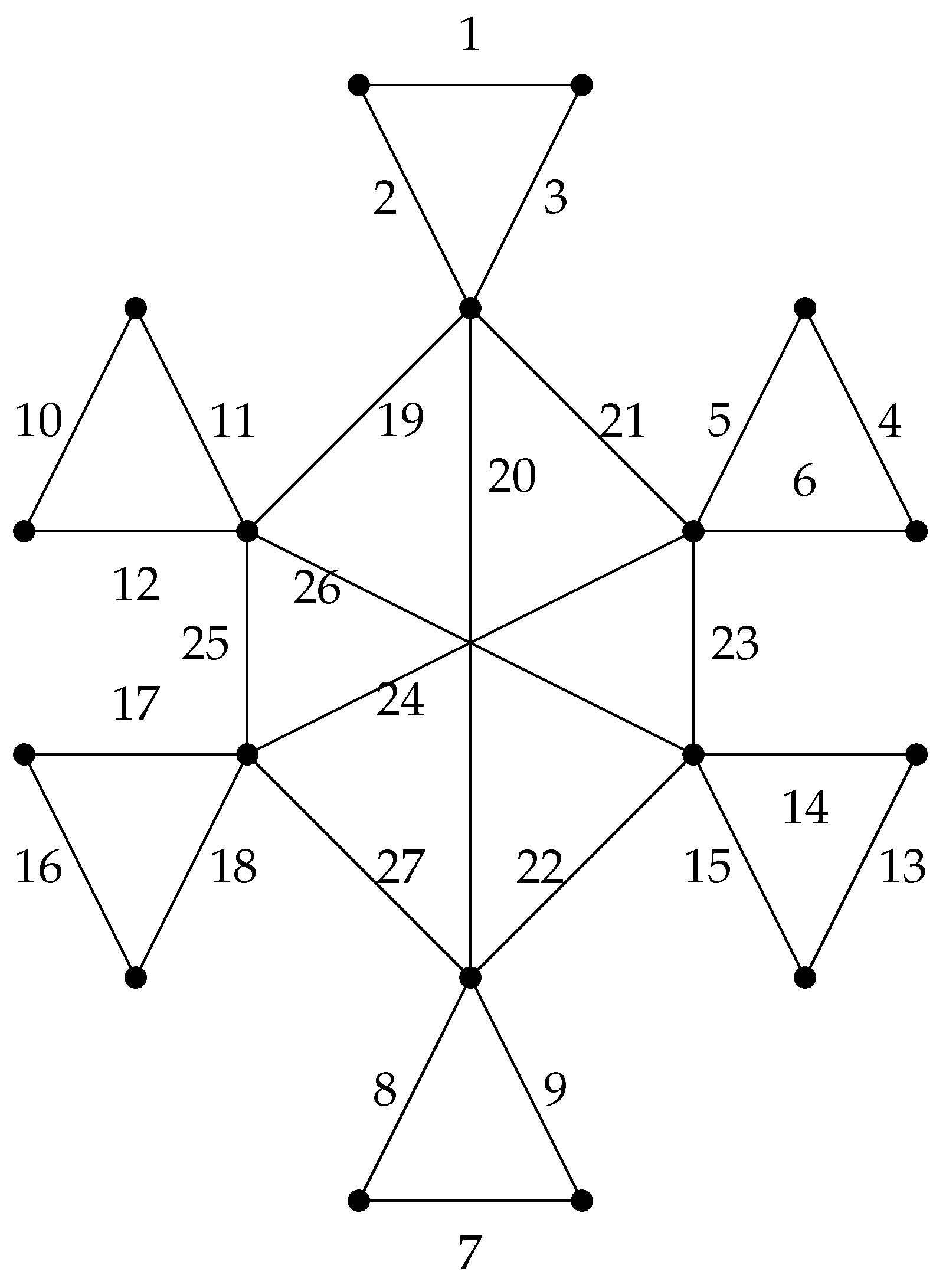
. The rooted product of the graph
G and
H with their antimagic labeling is given in
Figure 4. Here, the root vertex of the graph
H is chosen as
.
Theorem 3. Let G be a connected t-regular graph and H be a connected k-regular graph then the corona product of G and H admits antimagic labeling, .
Proof. Let G be a t-regular graph with n vertices and m edges and let H be a k-regular graph with p vertices and q edges. As G and H are regular graphs, by Theorem 1, they admits an antimagic labeling. Let f and g be antimagic labeling of G and H respectively. By definition of f, such that for any two distinct vertices u and v in G. By definition of g, such that for any two distinct vertices x and y in H.
Let us name the vertices of
G as
such that,
and also name the vertices of
H as
such that,
Construct the corona product of
G and
H,
by joining the edge with
vertex of G with each vertex from
copy of
H. Note that the number of edges in
is
. Let us name the vertices of
as follows. The vertices of
G are named as the same as the earlier, that is
and then name the vertices of
, for
(
isomorphic copy of
H) as
. That is the vertex
in
H is now has the name
in
for
. Before defining the antimagic labeling of
, we label the edges of
by using the edge labeling
g of
H as follows:
for an edge
in
,
where
as an edge
in
H that corresponding to the edge
e in
. Then by definition of
and (
11) for each
.
where
are the vertices of
in
.
Now we define
by,
From the above labeling
h, we observe that, for all
and
In order to prove that h is an antimagic labeling of , we need to prove that for any two distinct vertices x and y in such that We consider the following possible cases on the vertices of x and the vertices of y in .
- (i)
x in and y in for .
- (ii)
x in G and y in for .
- (iii)
x and y are the vertices of G.
Case 1. For any two distinct vertices x and y in , where x is in and y in , for each .
Case 1.1. When
, then both the vertex
x and
y are from
. By definition on the naming of the vertices of
,
and
for some
. Then, by definition of
h and by (
16), we have
Without loss of generality, we assume that
. By (
13), we have
, therefore
. Hence
Case 1.2. When , then the vertex x in and the vertex y in . By definition on the naming of vertices of and , let and for some .
Without loss of generality we assume
. Then by definition of
h and by (
16) we have
Case 1.2.1. If
. Then by (
13) we have,
. Consider
Since
Case 1.2.2. If
. Then by (
13) we have,
Consider
Since
and
are the antimagic labelings of
and
, respectively, and by Observation 1,
and also
.
Case 2. For any two distinct vertices x and y in such that x in G and y in for .
By definition on naming the vertices of
G,
and by definition on the naming of the vertices of
, let
for some
s,
. Then, by definition of
h and by (
15) and (
16), we have
We apply maximum value for the negative terms of above equations i.e.,
and by Lemma 1,
Since, .
Case 3.
x and
y are the vertices of
G. By definition on the naming of the vertices of
G,
and
for some
&
. By (
15),
Without loss of generality, we consider
, therefore by (
10),
Consider
□
Figure 5,
Figure 6 and
Figure 7 illustrate the proof Theorem 3. An antimagic labeling of a 2-regular graph
G and the antimagic labeling of a 3-regular graph
H are given in
Figure 5 and
Figure 6 respectively. The corona product of the graph
G and
H with their antimagic labeling is given in
Figure 7.