Open Support of Hypergraphs under Addition

Abstract

For a vertex v in a graph G, the open support of v under addition is the sum of degrees of all its neighbors. The open support of G under addition is the sum of open supports of all its vertices. The results for open support of graphs are deeply dependent on the structure property of the graph considered, such as its symmetry. In this paper, we generalize the concept of open support to hypergraphs. We give some examples and prove a general formula for open support of hypergraphs by using the adjacency and incidence matrices method.

1. Introduction

A hypergraph, H, is an ordered pair $\left(V\right(H),E(H\left)\right)$, where $V\left(H\right)$ is the vertex set of H and $E\left(H\right)$ is the edge set of H. Each edge in $E\left(H\right)$ is a subset of $V\left(H\right)$. A hypergraph is said to be k-uniform (also called a k-graph for short) if each edge contains exactly k vertices of H. Two vertices, $v_i$, $v_j$, are called adjacent if there exists some edge $e\in E$, such that $v_i\in e$ and $v_j\in e$. We say $v_i$ is a neighbor of $v_j$ if $v_i$ and $v_j$ are adjacent. The neighborhood of $v_i$, denoted by $N_H\left(v_i\right)$, consists of all neighbors of $v_i$. A vertex, v, is said to be incident with an edge e if $v\in e$. The degree of a vertex $v_i$, denoted by $d\left(v_i\right)$, is the number of edges that are incident with v. In this paper, we consider k-uniform, finite, simple hypergraphs.

The study of open support of graphs has important applications in many fields, such as chemical structure, urban planning, computer science, etc. The concept of open support of a graph under addition was introduced by Balamurugan et al. [1], where they showed the open support of paths, cycles, and some other graphs. Results for the open support of graphs are deeply dependent on the structure property of the graph to be considered, such as its symmetry. In [2], the authors obtained a general formula for the open support of a graph. In addition, Balamurugan et al. [3,4] also defined the closed support of graphs under addition. For more information concerning the open support of graphs under addition, see [5,6,7].

The open support of a graph is closed related to the Graph Labeling Problems, which usually focus on some particular types of graphs (like a wheel graph, middle graph, and so on) and try to find some useful indices of them [8,9,10,11,12]. In addition, the concept of open support can be extended to fuzzy/interval-valued fuzzy graphs too [13,14]. Note that a graph may look at a k-uniform hypergraph with $k=2$, but the open support’s result can be applied to more areas if similar conclusions in general hypergraphs are studied. In this paper, we give the open support of some hypergraphs and show a general formula for it. In Section 2, we give some definitions and notations. Section 3 provides the open support of some special hypergraphs. In Section 4, we give a definition of open support of an edge and show a formula for the open support of hypergraphs by using the graph matrix method.

2. Definitions

In this section, we introduce the definition of an open support of a hypergraph. In graphs such as a lily graph, twig graph, etc., open support is defined in [15,16,17,18,19,20]. Here, we give the concept of these graphs in the hypergraph. Furthermore, by studying the open support of these special graph classes, we can draw generalized results about hypergraphs.

Definition 1.

The open support of a vertex, v, under addition is defined by ${\sum }_{u\in N_H\left(v\right)}d\left(u\right)$ and it is denoted by supp$\left(v\right)$.

Definition 2.

The open support of a hypergraph, H, under addition is defined by ${\sum }_{v\in V\left(H\right)}supp\left(v\right)$ and it is denoted by $supp\left(H\right)$.

Definition 3.

For two edges, $e_i$, $e_j$$\in E$, the set $T:e_i\bigcap e_j$ is called the joint of $e_i$ and $e_j$. We say $e_i$, $e_j$ is disjoint if its joint is empty.

Definition 4.

A path is a hypergraph $P_m=e_1{T}_1{e}_2{T}_2\dots e_{m-1}{T}_{m-1}{e}_m$, where $E=(e_1, e_2, \dots , e_m)$ is the edge set of $P_m$ and for $i\in \{1, 2, \dots , m-1\}$, $T_i=e_i\bigcap e_{i+1}$ are the joints of $P_m$.

In order to find new hypergraphs, we define an adding edge operation, adding an edge at some joint T means adding a vertex set disjoint with V, which, together with T, forms a new edge. Now we can define some hypergraphs that are obtained by adding an edge at some joint of a path.

Definition 5.

The twig graph is obtained from a path $P_m$ by adding two edges to the i-th joint for each $1\le i\le m-1$. It is denoted by $T{W}_m$.

Definition 6.

The lily graph is obtained from a path $P_{2m}$ by adding two $K_{1,m}$$(m\ge 2)$ to the m-th joint. It is denoted by $L_m$.

Definition 7.

The hypergraph $P_{m-1}$$(1, 2, \dots , m)$ is obtained from a path $P_{m-1}$, where l vertices are fixed as joints on the starting and ending edges of the path, respectively, and an i edge is added to the i-th for each $1\le i\le m$ joint.

Let C be a k-uniform hypergraph, where C is a cycle of order n if there exists a cyclic ordering $(v_1, v_2, \dots , v_n)$ of the vertex set such that each continuous pair $v_i{v}_{i+1}$ is located in some edge of C. It is denoted by $C_n$. Each edge of C is composed of k consecutive vertices. The following definition is obtained by adding edges on a cycle.

Definition 8.

The jellyfish graph is obtained from a 4-cycle, where in the 4-cycle, there are two pairs of nonadjacent joints and we add an edge between the fist pair of joints, and then add m and n edges on another pair of nonadjacent joints, respectively. It is denoted by $J_{m,n}$.

All hypergraphs considered in this paper are those with joints of size one.

3. Examples

In this section, we show open support results of hypergraphs, including paths, twig graphs, jellyfish graphs, lily graphs, and $p_{m-1}(1, 2, \dots , m)$. We give an example behind each conclusion to make it easier to understand.

Theorem 1.

Let $H=P_m$ be a path. Then, $supp\left(H\right)=(k-1)\left[m\right(k+2)-2]$.

Proof. 

Let the vertex set of H be $V\left(H\right)=\{t_i;1\le i\le m-1\}\bigcup \{v_i^j;i=1\mathrm{or}i=m,1\le j\le k-1\}\bigcup \{v_i^j;2\le i\le m-1,1\le j\le k-2\}$, the edge set of H be $E\left(H\right)=\{e_i;1\le i\le m\}$, in which $e_i$ means the i-th edge in the path; $t_i$ means the i-th joint in the path; and $v_i^j$ means the j-th vertex (except the joint vertices) in the i-th edge. See Figure 1 for the case $m=5$, $k=3$.

Figure 1. The 3-graph $P_5$.

Obviously, for $1\le i\le m-1$, $d\left(t_i\right)=2$, for $i=1,m$, $1\le j\le k-1$, $d\left(v_i^j\right)=1$, and for $2\le i\le m-1,1\le j\le k-2$, $d\left(v_i^j\right)=1$.

First, the open supports for the vertices in the joint are calculated. It is easy to see, $supp\left(t_1\right)=$${\sum }_{u\in N\left(t_1\right)}d\left(u\right)=2k-1$, in the same way, we have $supp\left(t_{m-1}\right)={\sum }_{u\in N\left(t_{m-1}\right)}d\left(u\right)=2k-1$, and for $2\le i\le m-2$,

$$supp\left(t_i\right)=\sum _{u\in N\left(t_i\right)}d\left(u\right)=2k.$$

Second, by classifying the remaining vertices in the path, we can get the following results.

• For $i=1,m$, $1\le j\le k-1$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k$.
• For $2\le i\le m-1,1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+1$.

To sum it up, we conclude that

$$\begin{array}{cc}\hfill supp\left(H\right)=& supp\left(t_1\right)+\sum _{i=2}^{m-2}supp\left(t_i\right)+supp\left(t_{m-1}\right)+\sum _{j=1}^{k-1}supp\left(v_1^j\right)\hfill \\ \hfill +& \sum _{j=1}^{k-1}supp\left(v_m^j\right)+\sum _{i=2}^{m-1}\sum _{j=1}^{k-2}supp\left(v_i^j\right)\hfill \\ \hfill =& (k-1)\left[m\right(k+2)-2].\hfill \end{array}$$

□

Example 1.

By Theorem 1, we have $supp\left(P_5\right)=(3-1)[5(3+2)-2]=46$.

Now we are ready to calculate the open support of a twig graph, and the twig graph is obtained by adding edges on to the path.

Theorem 2.

Let $H=T{W}_m$ be a twig graph. Then, $supp\left(H\right)=(k-1)\left[3m\right(k+4)-2(k+6\left)\right]$.

Proof. 

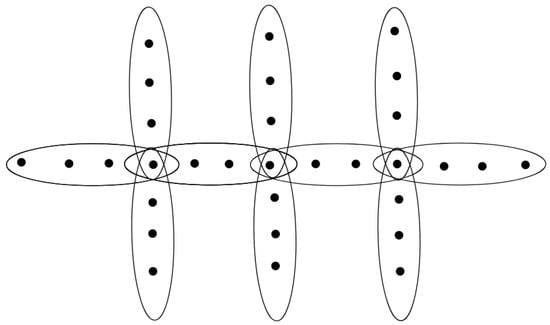
Let the vertex set of H be $V\left(H\right)=\{t_i;1\le i\le m-1\}\bigcup \{v_1^j;1\le j\le k-1\}\bigcup \{v_i^j;2\le i\le m-1,1\le j\le k-2\}\bigcup \{v_i^j;m\le i\le 3m-2,1\le j\le k-1\}$, and edge set of H be $E\left(H\right)=\{e_i;1\le i\le 3m-2\}$, when we are regarding $T{W}_m$ as a path adding $2(m-1)$ edges, $e_i(1\le i\le m)$ represents the i-th edge in the path; $e_i(m+1\le i\le 3m-2)$ is the edge adding to the path; $t_i(1\le i\le m-1)$ means the i-th joint in the path; and $v_i^j$ means the j-th vertex (except the joint vertices) in the i-th edge. See Figure 2 for the case $m=4$, $k=4$.

Figure 2. The 4-graph $T{W}_4$.

Clearly, for $1\le i\le m-1$, $d\left(t_i\right)=4$, for $1\le j\le k-1$, $d\left(v_1^j\right)=1$, for $2\le i\le m-1,1\le j\le k-2$, $d\left(v_i^j\right)=1$, and for $m\le i\le 3m-2,1\le j\le k-1$, $d\left(v_i^j\right)=1$.

First of all, the open support of vertices in the joint is calculated, it follows that, $supp\left(t_1\right)={\sum }_{u\in N\left(t_1\right)}d\left(u\right)=4k-1$, and for $2\le i\le m-2$,

$$supp\left(t_i\right)=\sum _{u\in N\left(t_i\right)}d\left(u\right)=4k+2,$$

and $supp\left(t_{m-1}\right)={\sum }_{u\in N\left(t_{m-1}\right)}d\left(u\right)=4k-1$.

Then, we discuss the open support of the remaining vertices in the graph.

• For $1\le j\le k-1$, $supp\left(v_1^j\right)={\sum }_{u\in N\left(v_1^j\right)}d\left(u\right)=k+2$;
• For $2\le i\le m-1,1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+5$;
• For $1\le j\le k-1$, $supp\left(v_m^j\right)={\sum }_{u\in N\left(v_m^j\right)}d\left(u\right)=k+2$;
• For $m+1\le i\le 3m-2$, $1\le j\le k-1$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+2$.

Therefore, we conclude that

$$\begin{array}{cc}\hfill supp\left(H\right)=& supp\left(t_1\right)+\sum _{i=2}^{m-2}supp\left(t_i\right)+supp\left(t_{m-1}\right)+\sum _{j=1}^{k-1}supp\left(v_1^j\right)\hfill \\ \hfill +& \sum _{i=2}^{m-1}\sum _{j=1}^{k-2}supp\left(v_i^j\right)+\sum _{j=1}^{k-1}supp\left(v_m^j\right)+\sum _{i=m+1}^{3m-2}\sum _{j=1}^{k-1}supp\left(v_i^j\right)\hfill \\ \hfill =& (k-1)\left[3m\right(k+4)-2(k+6\left)\right].\hfill \end{array}$$

□

Example 2.

By Theorem (2), we have $supp\left(T{W}_4\right)=(4-1)[3\times 4(4+4)-2(4+6)]=228.$

Next, we continue to prove the next theorem, and the jellyfish graph in the next theorem can be regarded as adding some edges to the 4-cycle.

Theorem 3.

Let $H=J(m,n)$ be a jellyfish graph. Then, $supp\left(H\right)=(k-1)[m^2+n^2+(m+n)(k+3)+5k+16]$.

Proof. 

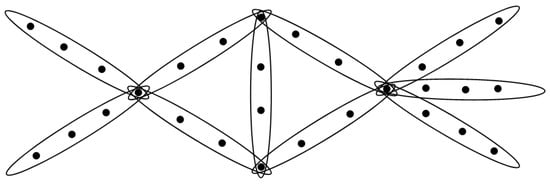
Let the vertex set of H be $V\left(H\right)=\{t_i;1\le i\le 4\}\bigcup \{v_i^j;1\le i\le m+n,1\le j\le k-1\}\bigcup \{v_i^j;m+n+1\le i\le m+n+5,1\le j\le k-2\}$, and the edge set of H be $E\left(H\right)=\{e_i;1\le i\le m+n+5\}$, when we are regarding $J(m,n)$ as a 4-cycle adding $m+n+1$ edges, $e_i(m+n+1\le i\le m+n+4)$ means the $(i-m-n)$-th edge in 4-cycle; $t_i(1\le i\le 4)$ represents the i-th joint in the cycle; $e_i(1\le i\le m)$ is the edge adding to the cycle associate with the 4-th joint; $e_i(m+1\le i\le m+n)$ is the edge adding to the cycle associate with the 2-th joint; $e_{m+n+5}$ means associate with the 1-th joint and 3-th joint; and $v_i^j$ means the j-th vertex (except the joint vertices) in the i-th edge. See Figure 3 for the case $m=2$, $n=3$, $k=4$.

Figure 3. The 4-graph $J(2,3)$.

Clearly, $d\left(t_1\right)=d\left(t_3\right)=3$, $d\left(t_2\right)=n+2$, $d\left(t_4\right)=m+2$, for $1\le i\le m+n,1\le j\le k-1$, $d\left(v_i^j\right)=1$, and for $m+n+1\le i\le m+n+5,1\le j\le k-2$, $d\left(v_i^j\right)=1$.

We start with the open supports for the vertices in the joint, where $supp\left(t_1\right)={\sum }_{u\in N\left(t_1\right)}d\left(u\right)=3k+n+m+1$, $supp\left(t_2\right)={\sum }_{u\in N\left(t_2\right)}d\left(u\right)=(n+2)(k-1)+4$, $supp\left(t_3\right)={\sum }_{u\in N\left(t_3\right)}d\left(u\right)=3k+n+m+1$, and $supp\left(t_4\right)={\sum }_{u\in N\left(t_4\right)}d\left(u\right)=(m+2)(k-1)+4$.

Next, we discuss the remaining vertices in the graph and classify them according to their neighbors.

• For $1\le i\le m,1\le j\le k-1$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+m$;
• For $m+1\le i\le m+n,1\le j\le k-1$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+n$;
• For $m+n+1\le i\le m+n+2$, $1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+n+2$;
• For $m+n+3\le i\le m+n+4$, $1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+m+2$;
• For $1\le j\le k-2$, $supp\left(v_{m+n+5}^j\right)={\sum }_{u\in N\left(v_{m+n+5}^j\right)}d\left(u\right)=k+3$.

Therefore, we conclude that

$$\begin{array}{cc}\hfill supp\left(H\right)=& \sum _{i=1}^{4}supp\left(t_i\right)+\sum _{i=1}^m\sum _{j=1}^{k-1}supp\left(v_i^j\right)\hfill \\ \hfill +& \sum _{i=m+1}^{m+n}\sum _{j=1}^{k-1}supp\left(v_i^j\right)+\sum _{i=m+n+1}^{m+n+5}\sum _{j=1}^{k-2}supp\left(v_i^j\right)\hfill \\ \hfill =& (k-1)[m^2+n^2+(m+n)(k+3)+5k+16].\hfill \end{array}$$

□

Example 3.

By Theorem 3, we have $supp\left(J(2,3)\right)=(4-1)[2^2+3^2+(2+3)(4+3)+5\times 4+16]=252.$

Recall that the lily graph is obtained by adding $2m$ edges to the $P_{2m}$.

Theorem 4.

Let $H=L_m(m\ge 2)$ be a lily graph. Then, $supp\left(H\right)=2(k-1)\left[2m\right(k+2)+(m+1\left)\right(2m-1\left)\right]$.

Proof. 

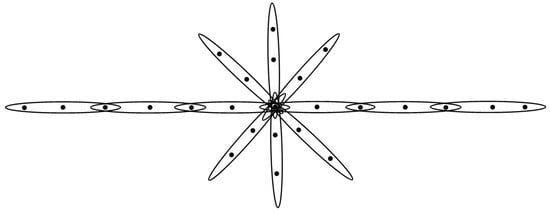
Let the vertex set of H be $V\left(H\right)=\{t_i;1\le i\le 2m-1\}\bigcup \{v_1^j;1\le j\le k-1\}\bigcup \{v_i^j;2\le i\le 2m-1,1\le j\le k-2\}\bigcup \{v_{2m}^j;1\le j\le k-1\}\bigcup \{v_i^j;2m+1\le i\le 4m,1\le j\le k-1\}$, and the edge set of H be $E\left(H\right)=\{e_i;1\le i\le 4m\}$, when we are regarding $l_m$ as a $P_{2m}$ adding $2m$ edges, $e_i(1\le i\le 2m)$ represents the i-th edge in the path; $e_i(2m+1\le i\le 4m)$ is the edge adding to the path; $t_i(1\le i\le 2m-1)$ means the i-th joint in the path; and $v_i^j$ means the j-th vertex (except the joint vertices) in the i-th edge. See Figure 4 for the case $m=3$, $k=3$.

Figure 4. The 3-graph $L_3$.

Clearly, the degree of each vertex in the graph is for $1\le i\le m-1$, $d\left(t_i\right)=2$, and $d\left(t_m\right)=2m+2$, and for $m+1\le i\le 2m-1$, $d\left(t_i\right)=2$, and for $1\le j\le k-1$, $d\left(v_1^j\right)=1$, for $2\le i\le m-1,1\le j\le k-2$, $d\left(v_i^j\right)=1$, for $2\le i\le 2m-1,1\le j\le k-2$, $d\left(v_i^j\right)=1$, for $1\le j\le k-1$, $d\left(v_{2m}^j\right)=1$, and for $2m+1\le i\le 4m,1\le j\le k-1$, $d\left(v_i^j\right)=1$.

First, we calculate the open support of the joint vertices: $supp\left(t_1\right)={\sum }_{u\in N\left(t_1\right)}d\left(u\right)=2k-1$, $supp\left(t_{m-1}\right)={\sum }_{u\in N\left(t_{m-1}\right)}d\left(u\right)=2k+2m$, $supp\left(t_m\right)={\sum }_{u\in N\left(t_m\right)}d\left(u\right)=2m(k-1)+2k$, $supp\left(t_{m+1}\right)={\sum }_{u\in N\left(t_{m+1}\right)}d\left(u\right)=2k+2m$, $supp\left(t_{2m-1}\right)={\sum }_{u\in N\left(t_{2m-1}\right)}d\left(u\right)=2k-1$, and for $2\le i\le m-2$,

$$supp\left(t_i\right)=\sum _{u\in N\left(t_i\right)}d\left(u\right)=2k,$$

for $m+2\le i\le 2m-2$,

$$supp\left(t_i\right)=\sum _{u\in N\left(t_i\right)}d\left(u\right)=2k.$$

Now we consider the remaining vertices:

• For $1\le j\le k-1$, $supp\left(v_1^j\right)={\sum }_{u\in N\left(v_1^j\right)}d\left(u\right)=k;$
• For $2\le i\le m-1,1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+1;$
• For $m\le i\le m+1$, $1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+2m+1;$
• For $m+2\le i\le 2m-1,1\le j\le k-2$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+1;$
• For $1\le j\le k-1$, $supp\left(v_{2m}^j\right)={\sum }_{u\in N\left(v_{2m}^j\right)}d\left(u\right)=k;$
• For $2m+1\le i\le 4m,1\le j\le k-1$, $supp\left(v_i^j\right)={\sum }_{u\in N\left(v_i^j\right)}d\left(u\right)=k+2m.$

Therefore, we conclude that

$$\begin{array}{cc}\hfill supp\left(H\right)=& \sum _{i=1}^{2m-1}supp\left(t_i\right)+\sum _{j=1}^{k-1}supp\left(v_1^j\right)+\sum _{i=2}^{2m-1}\sum _{j=1}^{k-2}supp\left(v_i^j\right)\hfill \\ \hfill +& \sum _{j=1}^{k-1}supp\left(v_{2m}^j\right)+\sum _{i=2m+1}^{4m}\sum _{j=1}^{k-1}supp\left(v_i^j\right)\hfill \\ \hfill =& 2(k-1)\left[2m\right(k+2)+(m+1\left)\right(2m-1\left)\right].\hfill \end{array}$$

□

Example 4.

By Theorem 4, we have $supp\left(L_3\right)=2(3-1)[2\times 3(3+2)+(3+1)(2\times 3-1)]=200.$

The $P_{m-1}(1, 2, \dots , m)$ in the next theorem can be regarded as a graph generated by adding $\frac{m(m+1)}{2}$ edges to the $P_{m-1}$.

Theorem 5.

Let $H=P_{m-1}(1, 2, \dots , m)$. Then, $supp\left(H\right)=\frac{m^3}{3}(k-1)+\frac{m^2}{2}(k^2+k+2)+\frac{m}{6}(9k^2+19k-64)-(k-1)(k+6)$.

Proof. 

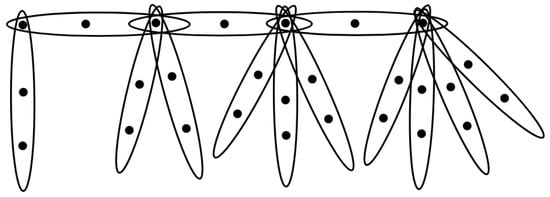
Let the vertex set of H be $V\left(H\right)=\{t_i;1\le i\le m\}\bigcup \{v_i^q;1\le i\le m-1,1\le q\le k-2\}\bigcup \{v_{i,j}^q;1\le i\le m,1\le j\le i,1\le q\le k-1\}$, and the edge set of H be $E\left(H\right)=\{e_i;1\le i\le m-1\}\bigcup \{e_{i,j};1\le i\le m,1\le j\le i\}$, where we are regarding $P_{m-1}(1, 2, \dots , m)$ as a path adding $\frac{m(m+1)}{2}$ edges, $e_i(1\le i\le m-1)$ represents the i-th edge in the path; $e_{i,j}(1\le i\le m,1\le j\le i)$ is the edge adding to the path; $t_i(1\le i\le m)$ means the i-th joint; $v_i^q(1\le i\le m-1)$ means the q-th vertex in the $e_i$; and $v_{i,j}^q(1\le i\le m,1\le j\le i)$ means the q-th vertex (except the joint vertices) in the $e_{i,j}$. See Figure 5 for the case $m=4$, $k=3$.

Figure 5. The 3-graph $P_3(1,2,3,4)$.

The degree of vertices in the graph is obviously, for $1\le i\le m-1$, $d\left(t_i\right)=i+2$, and $d\left(t_m\right)=m+1$, for $1\le i\le m-1,1\le q\le k-2$, $d\left(v_i^q\right)=1$, for $1\le i\le m-1,1\le j\le i,1\le q\le k-1$, $d\left(v_{i,j}^q\right)=1$, and for $1\le j\le m,1\le q\le k-1$, $d\left(v_{m,j}^q\right)=1$.

The open support of the vertices in the joint is as follows: $supp\left(t_1\right)={\sum }_{u\in N\left(t_1\right)}d\left(u\right)=2k+1$, $supp\left(t_2\right)={\sum }_{u\in N\left(t_2\right)}d\left(u\right)=4k+1$, and for $3\le i\le m-2$,

$$supp\left(t_i\right)=\sum _{u\in N\left(t_i\right)}d\left(u\right)=ik+2k+6,$$

and $supp\left(t_{m-1}\right)={\sum }_{u\in N\left(t_{m-1}\right)}d\left(u\right)=mk+m+k-2$, $supp\left(t_m\right)={\sum }_{u\in N\left(t_m\right)}d\left(u\right)=mk+k-1$.

Next, we consider the open support of the remaining vertices in $p_{m-1}(1, 2, \dots , m)$:

• For $1\le q\le k-2$, $supp\left(v_1^q\right)={\sum }_{u\in N\left(v_1^q\right)}d\left(u\right)=k+3$;
• For $2\le i\le m-2,1\le q\le k-2$, $supp\left(v_i^q\right)={\sum }_{u\in N\left(v_i^q\right)}d\left(u\right)=2i+k+2$;
• For $1\le t\le k-2$, $supp\left(v_{m-1}^q\right)={\sum }_{u\in N\left(v_{m-1}^q\right)}d\left(u\right)=2m+k-1$;
• For $1\le q\le k-1$, $supp\left(v_{1,1}^q\right)={\sum }_{u\in N\left(v_{1,1}^q\right)}d\left(u\right)=k$;
• For $2\le i\le m-1,1\le j\le i,1\le t\le k-1$, $supp\left(v_{i,j}^q\right)={\sum }_{u\in N\left(v_{i,j}^q\right)}d\left(u\right)=k+i$;
• For $1\le j\le m,1\le q\le k-1$, $supp\left(v_{m,j}^q\right)={\sum }_{u\in N\left(v_{m,j}^q\right)}d\left(u\right)=k+m+1$.

Therefore, we conclude that

$$\begin{array}{cc}\hfill supp\left(H\right)=& supp\left(t_1\right)+supp\left(v_2\right)+\sum _{i=3}^{m-2}supp\left(t_i\right)+supp\left(t_{m-1}\right)+supp\left(t_m\right)\hfill \\ \hfill +& \sum _{q=1}^{k-2}supp\left(v_1^q\right)+\sum _{i=2}^{m-2}\sum _{q=1}^{k-2}supp\left(v_i^q\right)+\sum _{t=1}^{k-2}supp\left(v_{m-1}^q\right)+\sum _{q=1}^{k-1}supp\left(v_{1,1}^q\right)\hfill \\ \hfill +& \sum _{i=2}^{m-1}\sum _{j=1}^i\sum _{q=1}^{k-1}supp\left(v_{i,j}^q\right)+\sum _{j=1}^m\sum _{q=1}^{k-1}supp\left(v_{m,j}^q\right)\hfill \\ \hfill =& \frac{m^3}{3}(k-1)+\frac{m^2}{2}(k^2+k+2)+\frac{m}{6}(9k^2+19k-64)-(k-1)(k+6).\hfill \end{array}$$

□

Example 5.

By Theorem 5, we have $supp\left(P_3(1,2,3,4)\right)=\frac{4^3}{3}(3-1)+\frac{4^2}{2}(3^2+3+2)+\frac{4}{6}(9\times 3^2+19\times 3-64)-(3-1)(3+6)=186.$

4. Concluding Remarks

In this paper, we generalized the concept of open support of graphs to hypergraphs. We obtained the open support of some special types of hypergraphs. The method used in this paper can be extended to study the open support of other hypergraphs.

The skeleton support of an edge e under addition is defined by ${\sum }_{v\in e}d\left(v\right)$ and it is denoted by $ske\left(e\right)$. The skeleton support of a hypergraph H under addition is defined by ${\sum }_{e\in E\left(H\right)}ske\left(e\right)$ and it is denoted by $ske\left(H\right)$.

Theorem 6.

For any hypergraph H, $ske\left(H\right)={\sum }_{v\in V\left(H\right)}{\left(d\left(v\right)\right)}^2$.

Proof. 

Let $V\left(H\right)=\{v_1, v_2, \dots , v_n\}$ and $E\left(H\right)=\{e_1, e_2, \dots , e_m\}$ be the vertex set and edge set of H, respectively. Considering Table 1, the degree-incidence matrix with entry $a_{i,j}$, where for $i\in \{1, 2, \dots , n\}$ and $j\in \{1, 2, \dots , m\}$,

$$a_{i,j}=\left\{\begin{array}{cc}d\left(v_i\right)\hfill & v_i\in e_j,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Table 1. Degree-incidence matrix.

	${\mathit{e}}_1$	${\mathit{e}}_2$	…	${\mathit{e}}_{\mathit{m}}$
$v_1$	$a_{1,1}$	$a_{1,2}$	…	$a_{1,m}$
$v_2$	$a_{2,1}$	$a_{2,2}$	…	$a_{2,m}$
…	…	…	…	…
$v_n$	$a_{n,1}$	$a_{n,2}$	…	$a_{n,m}$

On one hand, summing up entries in the i-th row, corresponding to vertex $v_i$, we get ${\sum }_{j=1}^n{a}_{i,j}={\left(d\left(v_i\right)\right)}^2$; next, summing up over all vertices, we get

$$\sum _{i=1}^n\sum _{j=1}^n{a}_{i,j}=\sum _{i=1}^n{\left(d\left(v_i\right)\right)}^2.$$

(1)

On the other hand, summing up entries in the j-th column, corresponding to edge $e_j$, we get ${\sum }_{i=1}^n{a}_{i,j}=ske\left(e_j\right)$, and summing up over all edges, we obtain

$$\sum _{j=1}^n\sum _{i=1}^n{a}_{i,j}=ske\left(H\right).$$

(2)

It follows from (1) and (2) that

$$\begin{array}{c}\hfill ske\left(H\right)=\sum _{v\in V\left(H\right)}{\left(d\left(v\right)\right)}^2.\end{array}$$

□

Theorem 7.

For any hypergraph H, $supp\left(H\right)={\sum }_{v\in V\left(H\right)}\left|N_H\left(v\right)\right|d\left(v\right)$.

Proof. 

Let $V\left(H\right)=\{v_1, v_2, \dots , v_n\}$ be the vertex set of H. Considering Table 2, the degree-adjacency matrix with entry $a_{i,j}$, where for $i,j\in \{1, 2, \dots , n\}$,

$$a_{i,j}=\left\{\begin{array}{cc}d\left(v_i\right)\hfill & v_j\in N_H\left(v_i\right),\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Table 2. Degree-adjacency matrix.

	${\mathit{v}}_1$	${\mathit{v}}_2$	…	${\mathit{v}}_{\mathit{n}}$
$v_1$	$a_{1,1}$	$a_{1,2}$	…	$a_{1,n}$
$v_2$	$a_{2,1}$	$a_{2,2}$	…	$a_{2,n}$
…	…	…	…	…
$v_n$	$a_{n,1}$	$a_{n,2}$	…	$a_{n,n}$

Since there are $|N_H\left(v_i\right)|$ vertices adjacent to $v_i$, summing the elements of the i-th row of the degree-adjacency matrix, we get ${\sum }_{j=1}^n{a}_{i,j}=\left|N_H\left(v_i\right)\right|d\left(v_i\right)$, then the summation results of all rows are summed

$$\sum _{i=1}^n\sum _{j=1}^n{a}_{i,j}=\sum _{i=1}^n|N_H\left(v_i\right)|d\left(v_i\right)=\sum _{v\in V\left(H\right)}|N_H\left(v\right)|d\left(v\right).$$

(3)

Next, we sum the elements of the j-th column of the degree-adjacency matrix, and the result is the sum of the degrees of all neighbors of the vertex $v_j$; we get ${\sum }_{i=1}^n{a}_{i,j}=supp\left(v_j\right)$, then sum over all columns

$$\sum _{j=1}^n\sum _{i=1}^n{a}_{i,j}=\sum _{j=1}^{n}supp\left(v_j\right)=supp\left(H\right).$$

(4)

From (3) and (4), we can see that

$$supp\left(H\right)=\sum _{v\in V\left(H\right)}|N_H\left(v\right)|d\left(v\right).$$

(5)

□

In the following corollary, we show the connection of $supp\left(H\right)$ and $ske\left(H\right)$.

Corollary 1.

For any k-graph with $k=2$, we have $supp\left(H\right)=ske\left(H\right)$.