Monitoring the Ratio of Two Normal Variables Based on Triple Exponentially Weighted Moving Average Control Charts with Fixed and Variable Sampling Intervals
Abstract
:1. Introduction
2. A Brief Review of the Distribution of the Ratio Z
3. Construction of the TEWMA-RZ Control Charts
3.1. A Brief Review of the VSI-EWMA-RZ Control Chart
3.2. A Brief Review of the VSI-DEWMA-RZ Chart
3.3. The Proposed TEWMA-RZ Charts
3.3.1. The FSI-TEWMA-RZ Chart
3.3.2. The VSI-TEWMA-RZ Chart
4. Design of the Proposed TEWMA-RZ Charts
4.1. Design of the Proposed FSI-TEWMA-RZ Chart
4.2. Design of the Proposed VSI-TEWMA Charts
5. Numerical Results and Analysis
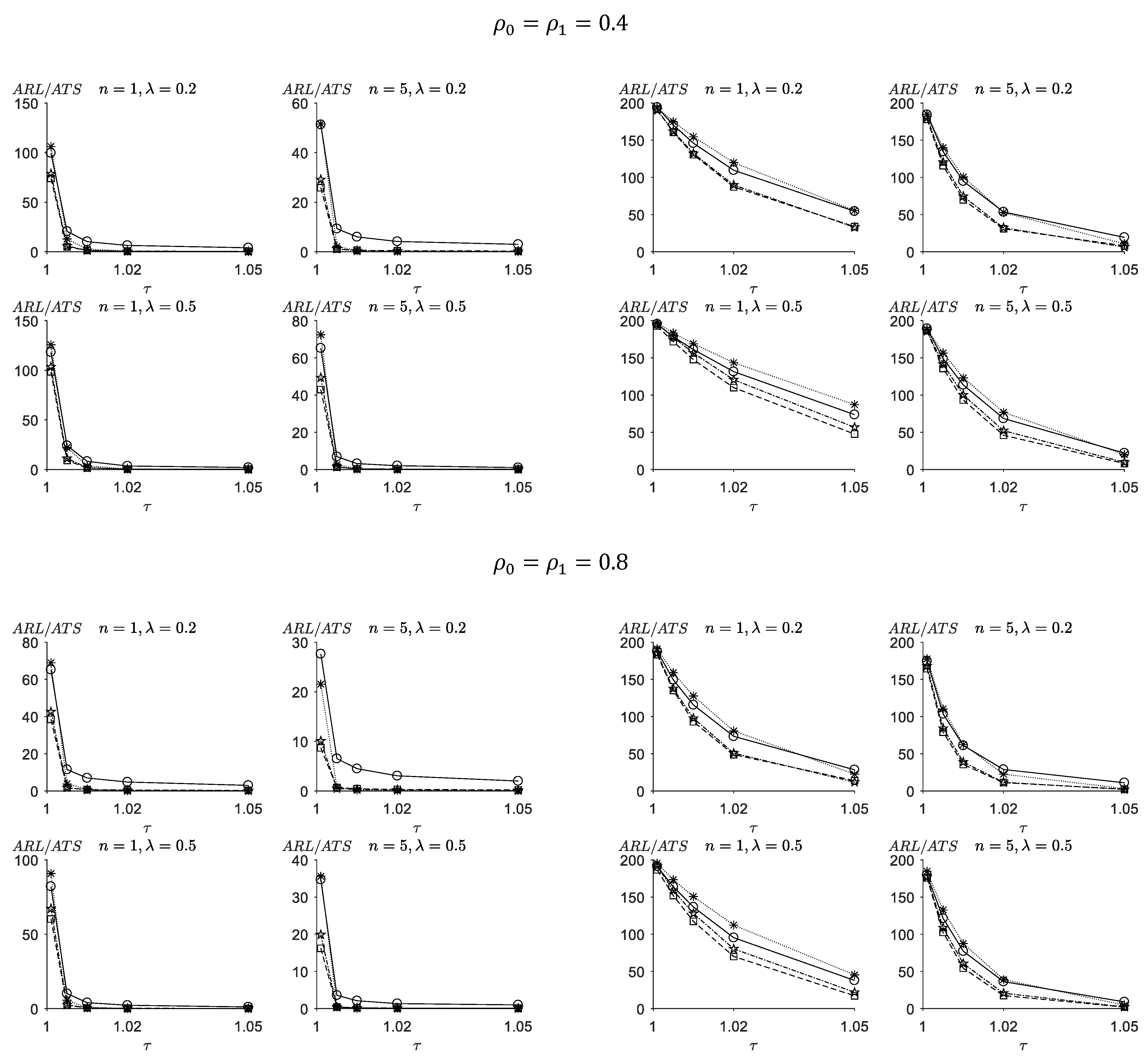
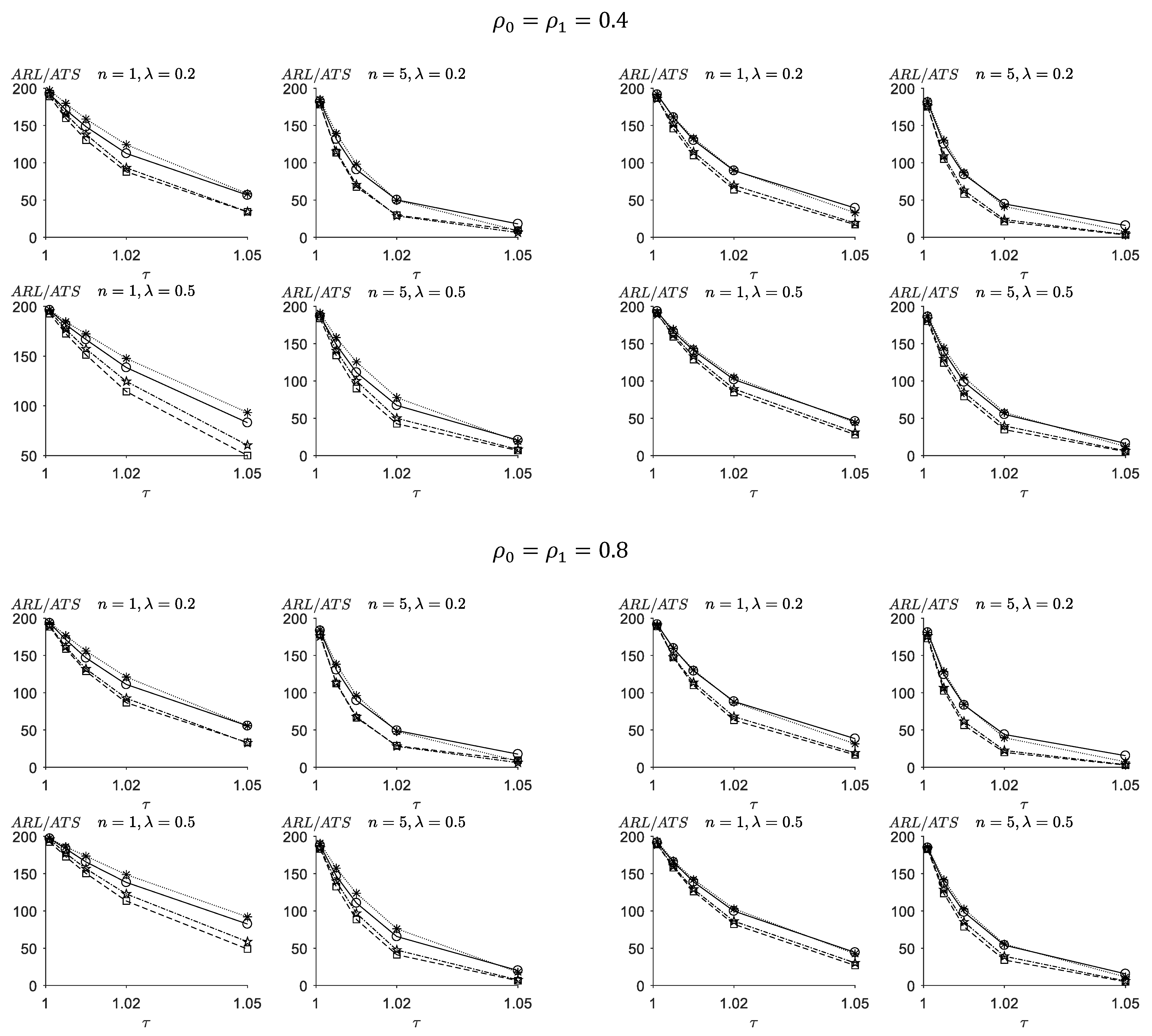
5.1. Comparisons between the VSI-TEWMA-RZ and the FSI-TEWMA-RZ Charts
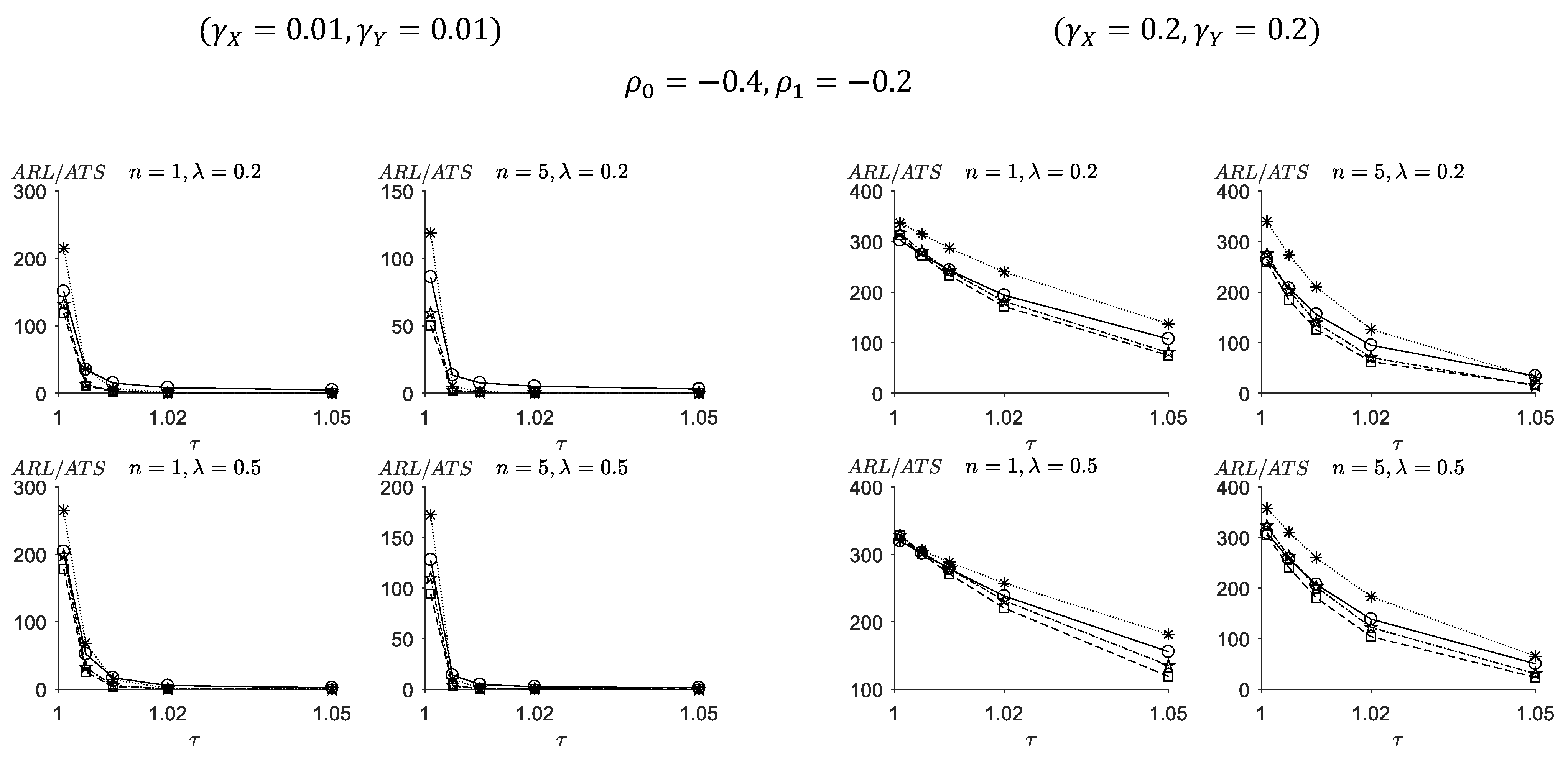
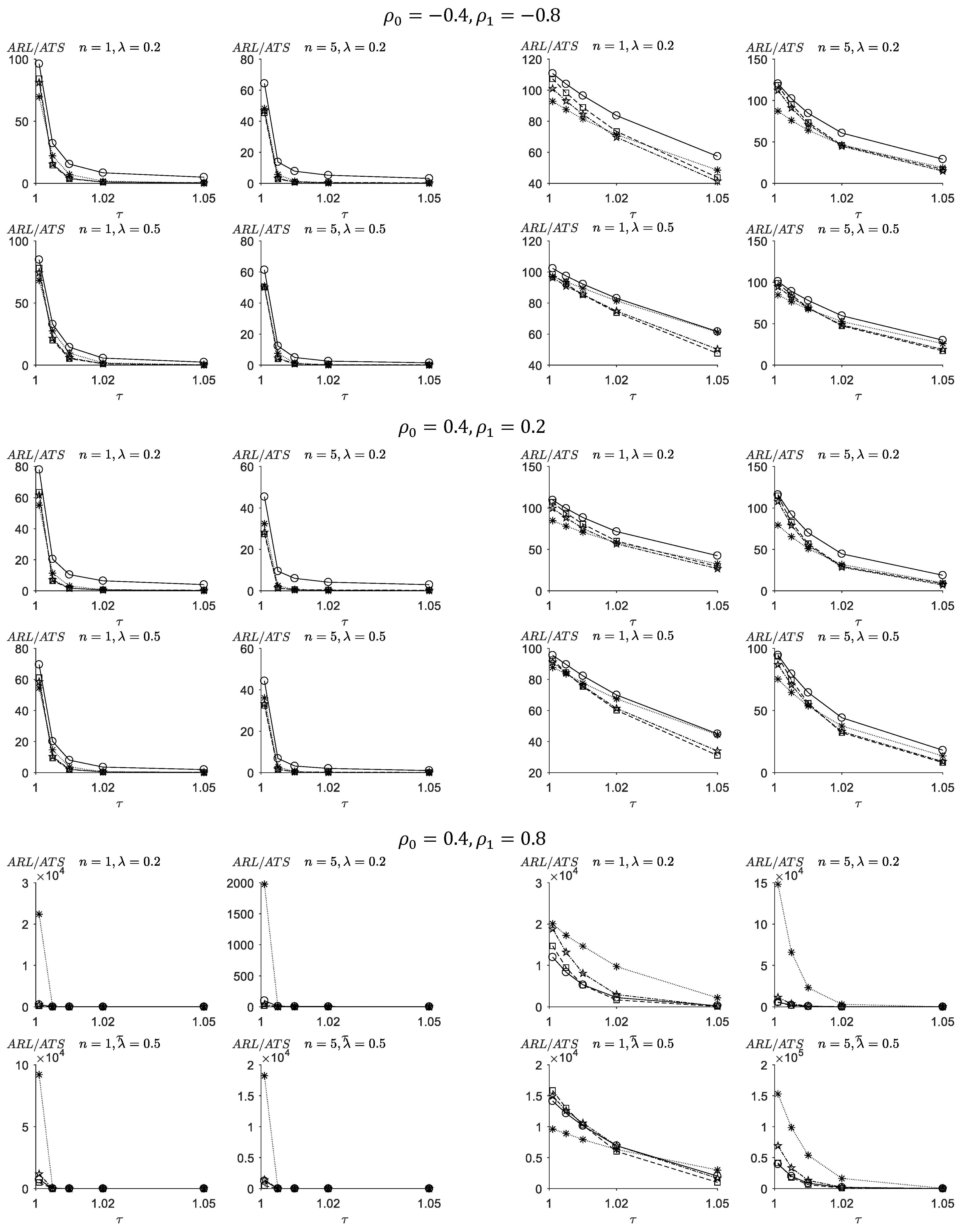
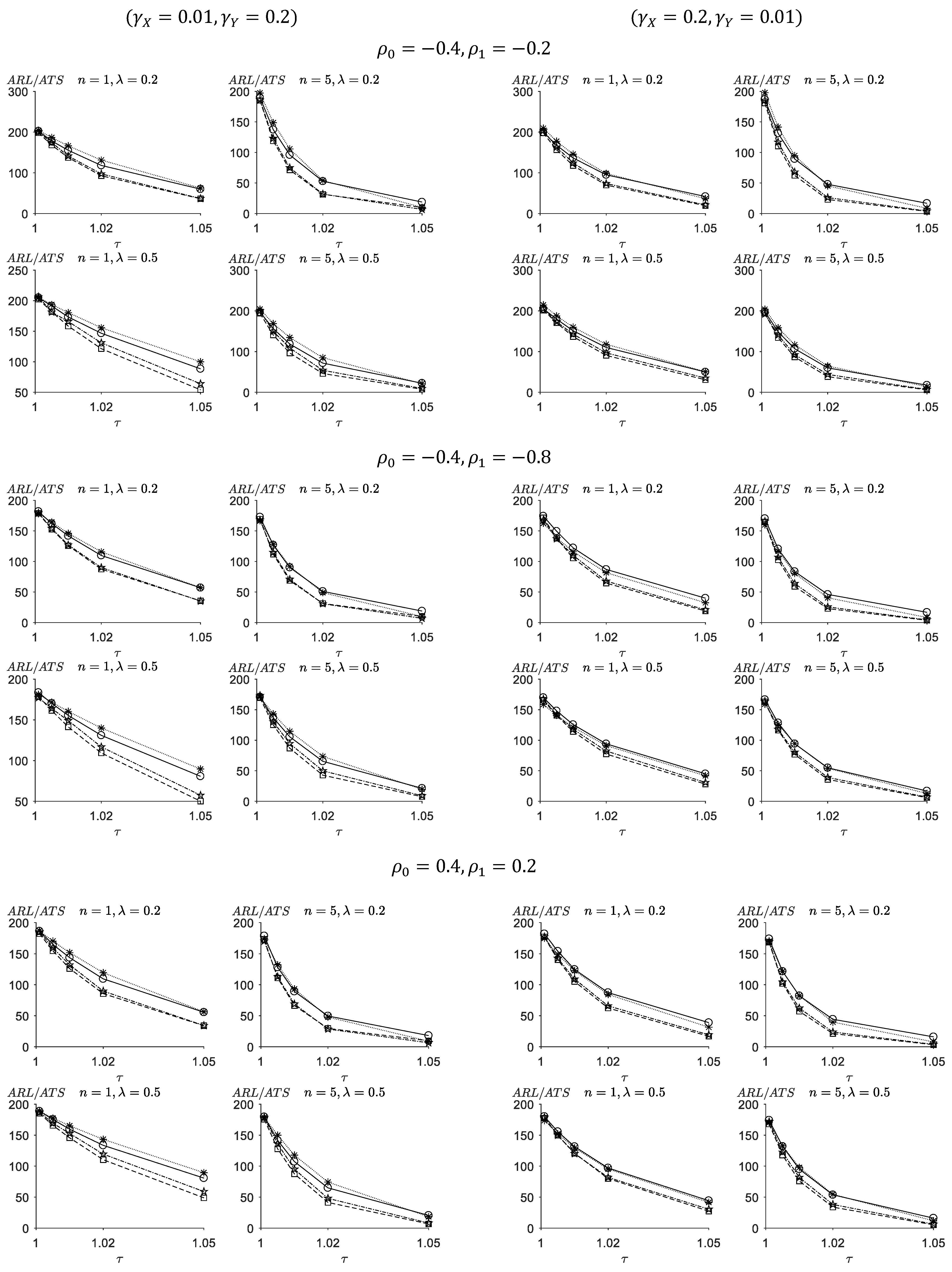
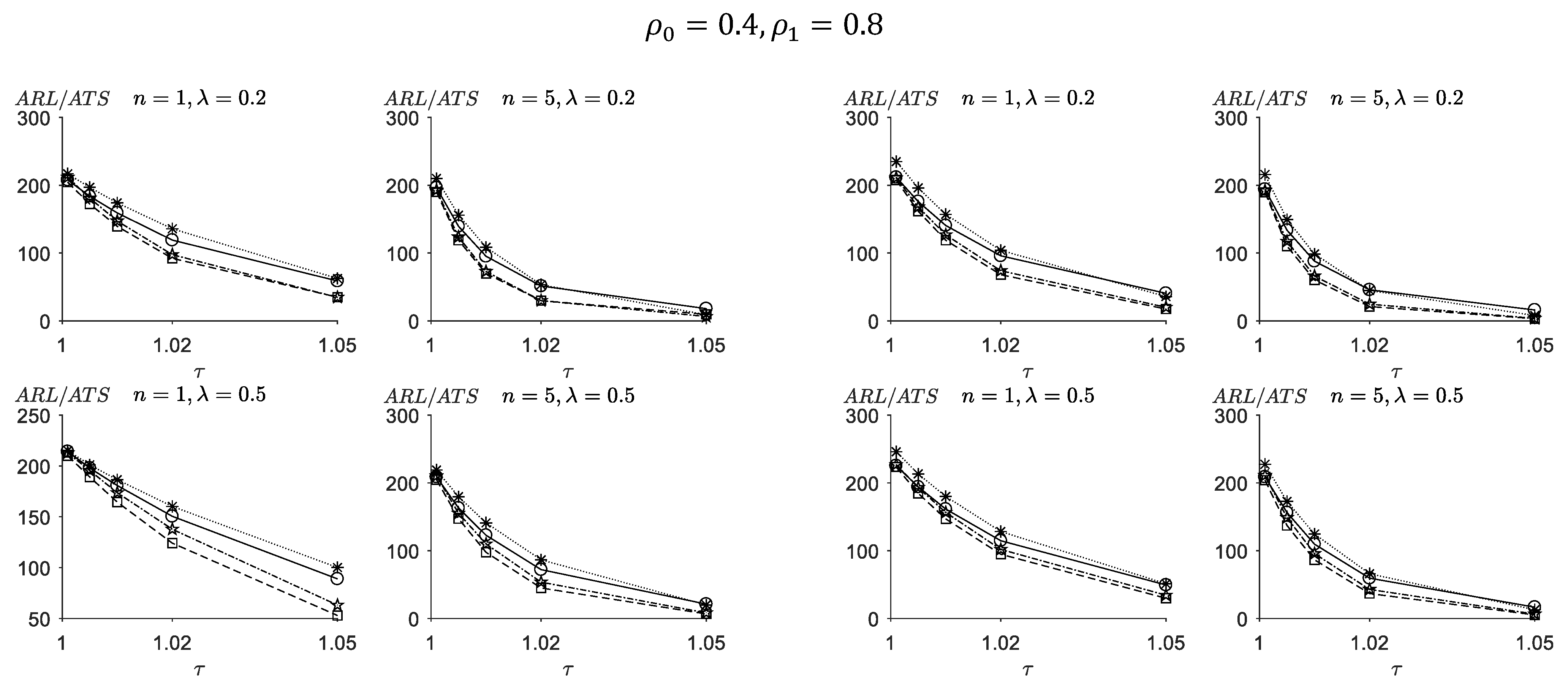
5.2. Comparisons between the VSI-TEWMA-RZ Chart and the VSI-EWMA-RZ Chart
5.3. Comparisons between the VSI-TEWMA-RZ Chart and the VSI-DEWMA-RZ Chart
6. An Illustrative Example
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Celano, G.; Castagliola, P.; Faraz, A.; Fichera, S. Statistical performance of a control chart for individual observations monitoring the ratio of two normal variables. Qual. Reliab. Eng. Int. 2014, 30, 1361–1377. [Google Scholar] [CrossRef]
- Spisak, A.W. A Control Chart for Ratios. J. Qual. Technol. 1990, 22, 34–37. [Google Scholar] [CrossRef]
- Davis, R.B.; Woodall, W.H. Evaluation of control charts for ratios. In Proceedings of the 22nd Annual Pittsburgh Conference on Modeling and Simulation, Pittsburgh, PA, USA, 24–25 April 1975. [Google Scholar]
- Öksoy, D.; Boulos, E.; Pye, L.D. Statistical process control by the quotient of two correlated normal variables. Qual. Eng. 1993, 6, 179–194. [Google Scholar] [CrossRef]
- Celano, G.; Castagliola, P. Design of a phase II control chart for monitoring the ratio of two normal variables. Qual. Reliab. Eng. Int. 2016, 32, 291–308. [Google Scholar] [CrossRef]
- Celano, G.; Castagliola, P. A synthetic control chart for monitoring the ratio of two normal variables. Qual. Reliab. Eng. Int. 2016, 32, 681–696. [Google Scholar] [CrossRef]
- Antzoulakos, D.; Rakitzis, A. Runs rules schemes for monitoring process variability. J. Appl. Stat. 2010, 37, 1231–1247. [Google Scholar] [CrossRef]
- Rakitzis, A.C. On the performance of modified runs rules charts with estimated parameters. Commun. Stat. Simul. Comput. 2017, 46, 1360–1380. [Google Scholar] [CrossRef]
- Oh, J.; Wei, C.H. On the individuals chart with supplementary runs rules under serial dependence. Methodol. Comput. Appl. Probab. 2020, 22, 1257–1273. [Google Scholar] [CrossRef]
- Tran, K.P. The efficiency of the 4-out-of-5 runs rules scheme for monitoring the ratio of population means of a bivariate normal distribution. Int. J. Reliab. Qual. Saf. Eng. 2016, 23, 1650020. [Google Scholar] [CrossRef]
- Tran, K.P.; Castagliola, P.; Celano, G. Monitoring the ratio of two normal variables using Run Rules type control charts. Int. J. Prod. Res. 2015, 54, 1670–1688. [Google Scholar] [CrossRef]
- Tran, K.P.; Castagliola, P.; Celano, G. Monitoring the ratio of two normal variables using EWMA type control charts. Qual. Reliab. Eng. Int. 2016, 32, 1853–1869. [Google Scholar] [CrossRef]
- Tran, K.P.; Knoth, S. Steady-State ARL analysis of ARL-unbiased EWMA-RZ control chart monitoring the ratio of two normal variables. Qual. Reliab. Eng. Int. 2018, 34, 377–390. [Google Scholar] [CrossRef]
- Tran, K.P.; Castagliola, P.; Celano, G. Monitoring the ratio of population means of a bivariate normal distribution using CUSUM type control charts. Stat. Pap. 2016, 59, 387–413. [Google Scholar] [CrossRef]
- Shamma, S.E.; Amin, R.W.; Shamma, A.K. A double exponentially weigiited moving average control procedure with variable sampling intervals. Commun. Stat.-Simul. Comput. 1991, 20, 511–528. [Google Scholar] [CrossRef]
- Shamma, S.E.; Shamma, A.K. Development and evaluation of control charts using double exponentially weighted moving averages. Int. J. Qual. Reliab. Manag. 1992, 9, 6. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, G. An extended EWMA mean chart. Qual. Technol. Quant. Manag. 2005, 2, 39–52. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Woodall, W.H. An evaluation of the double exponentially weighted moving average control chart. Commun. Stat. -Simul. Comput. 2010, 39, 933–949. [Google Scholar] [CrossRef]
- Alevizakos, V.; Koukouvinos, C. A double exponentially weighted moving average chart for time between events. Commun. Stat. -Simul. Comput. 2020, 49, 2765–2784. [Google Scholar] [CrossRef]
- Adeoti, O.A.; Malela-Majika, J.-C. Double exponentially weighted moving average control chart with supplementary runs-rules. Qual. Technol. Quant. Manag. 2020, 17, 149–172. [Google Scholar] [CrossRef]
- Malela-Majika, J.-C. New distribution-free memory-type control charts based on the Wilcoxon rank-sum statistic. Qual. Technol. Quant. Manag. 2021, 18, 135–155. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. The triple exponentially weighted moving average control chart. Qual. Technol. Quant. Manag. 2021, 18, 326–354. [Google Scholar] [CrossRef]
- Alevizakos, V.; Chatterjee, K.; Koukouvinos, C. A triple exponentially weighted moving average control chart for monitoring time between events. Qual. Reliab. Eng. Int. 2021, 37, 1059–1079. [Google Scholar] [CrossRef]
- Chatterjee, K.; Koukouvinos, C.; Lappa, A. A new S2-TEWMA control chart for monitoring process dispersion. Qual. Reliab. Eng. Int. 2021, 37, 1334–1354. [Google Scholar] [CrossRef]
- Letshedi, T.I.; Malela-Majika, J.-C.; Castagliola, P.; Shongwe, S.C. Distribution-free triple EWMA control chart for monitoring the process location using the Wilcoxon rank-sum statistic with fast initial response feature. Qual. Reliab. Eng. Int. 2021, 37, 1996–2013. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Tran, K.P.; Heuchenne, C. Monitoring the ratio of two normal variables using variable sampling interval exponentially weighted moving average control charts. Qual. Reliab. Eng. Int. 2019, 35, 439–460. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Tran, K.P.; Heuchenne, H.L. CUSUM control charts with variable sampling interval for monitoring the ratio of two normal variables. Qual. Reliab. Eng. Int. 2019, 36, 474–497. [Google Scholar] [CrossRef]
- Cedilnik, A.; Košmelj, K.; Blejec, A. The distribution of the ratio of jointly normal variables. Metodoloski Zv. 2004, 1, 99–108. [Google Scholar] [CrossRef]
- Pham-Gia, T.; Turkkan, N.; Marchand, E. Density of the ratio of two normal random variables and applications. Commun. Stat. Theory Methods 2006, 35, 1569–1591. [Google Scholar] [CrossRef]
- Oliveira, A.; Oliveira, T.; Macías, S.; Antonio. Distribution function for the ratio of two normal random variables. AIP Conf. Proc. 2015, 1648, 840005. [Google Scholar] [CrossRef]
- Geary, R.C. The Frequency Distribution of the quotient of two normal variates. J. R. Stat. Soc. 1930, 93, 442–446. [Google Scholar] [CrossRef]
- Sun, G.; Hu, X.; Xie, F.; Zhou, X.; Jiang, C. One-Sided double exponentially weighted moving average control charts for monitoring the ratio of two normal variables. Sci. Iran. 2022. under review. [Google Scholar]
- Reynolds, M.R.; Amin, R.W.; Arnold, J.C. CUSUM Charts with variable sampling intervals. Technometrics 1990, 32, 371–384. [Google Scholar] [CrossRef]
- Haq, A.; Akhtar, S. Auxiliary information based maximum EWMA and DEWMA charts with variable sampling intervals for process mean and variance. Commun. Stat. -Theory Methods 2020, 51, 3985–4005. [Google Scholar] [CrossRef]
- Malela-Majika, J.-C.; Rapoo, E. Distribution-free cumulative sum and exponentially weighted moving average control charts based on the Wilcoxon rank-sum statistic using ranked set sampling for monitoring mean shifts. J. Stat. Comput. Simul. 2016, 86, 3715–3734. [Google Scholar] [CrossRef]




| 0.2 | 1.0067 | 0.9998 | 1.0030 | 0.9999 | 1.2480 | 1.0601 | 1.0762 | 1.0083 |
| 0.5 | 1.0161 | 1.0000 | 1.0071 | 0.9999 | 1.5315 | 1.0581 | 1.1699 | 1.0106 |
| 0.2 | 1.0059 | 0.9998 | 1.0026 | 0.9999 | 1.2061 | 1.0467 | 1.0653 | 1.0061 |
| 0.5 | 1.0141 | 0.9999 | 1.0063 | 1.0000 | 1.4454 | 1.0452 | 1.1466 | 1.0069 |
| 0.2 | 1.0050 | 0.9998 | 1.0022 | 0.9999 | 1.1618 | 1.0316 | 1.0534 | 1.0042 |
| 0.5 | 1.0119 | 0.9999 | 1.0053 | 1.0000 | 1.3544 | 1.0305 | 1.1210 | 1.0047 |
| 0.2 | 1.0038 | 0.9998 | 1.0017 | 0.9999 | 1.1146 | 1.0179 | 1.0397 | 1.0019 |
| 0.5 | 1.0092 | 0.9999 | 1.0041 | 1.0000 | 1.2543 | 1.0179 | 1.0912 | 1.0028 |
| 0.2 | 1.0022 | 0.9999 | 1.0010 | 1.0000 | 1.0574 | 1.0045 | 1.0216 | 1.0002 |
| 0.5 | 1.0053 | 1.0000 | 1.0024 | 1.0000 | 1.1316 | 1.0051 | 1.0504 | 1.0008 |
| Sample Number | Box Size | VSI-EWMA | VSI-DEWMA | VSI-TEWMA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 250 gr | 25.479 | 25.355 | 24.027 | 25.792 | 24.960 | 25.122 | 1.003 | 1.00150 | 0.1 | 1.00075 | 0.1 | 1.00038 | 0.1 |
| 25.218 | 25.171 | 24.684 | 25.052 | 25.107 | 25.046 | |||||||||
| 2 | 250 gr | 25.359 | 25.172 | 24.508 | 25.292 | 24.449 | 24.956 | 1.000 | 1.00075 | 0.2 | 1.00075 | 0.2 | 1.00056 | 0.2 |
| 25.211 | 25.115 | 24.679 | 24.933 | 24.831 | 24.954 | |||||||||
| 3 | 250 gr | 24.574 | 24.864 | 25.865 | 25.107 | 24.811 | 25.044 | 1.005 | 1.00288 | 2.1 | 1.00181 | 0.3 | 1.00119 | 0.3 |
| 24.784 | 24.868 | 25.377 | 24.879 | 24.734 | 24.929 | |||||||||
| 4 | 250 gr | 25.313 | 24.483 | 24.088 | 25.184 | 25.681 | 24.950 | 0.999 | 1.00094 | 2.2 | 1.00138 | 0.4 | 1.00128 | 0.4 |
| 25.338 | 24.859 | 24.305 | 25.115 | 25.251 | 24.974 | |||||||||
| 5 | 250 gr | 25.557 | 24.959 | 25.023 | 24.482 | 25.531 | 25.111 | 0.998 | 1.00000 | 2.3 | 1.00042 | 0.5 | 1.00085 | 0.5 |
| 25.277 | 25.402 | 25.012 | 24.937 | 25.148 | 25.163 | |||||||||
| 6 | 250 gr | 24.882 | 24.473 | 24.814 | 25.418 | 24.732 | 24.864 | 0.997 | 1.00000 | 4.2 | 0.99933 | 0.6 | 1.00009 | 0.6 |
| 24.962 | 24.644 | 24.817 | 25.419 | 24.818 | 24.932 | |||||||||
| 7 | 500 gr | 49.848 | 48.685 | 49.994 | 49.910 | 49.374 | 49.562 | 0.999 | 1.00000 | 6.1 | 0.99897 | 2.5 | 0.99953 | 0.7 |
| 49.993 | 49.128 | 49.830 | 49.566 | 49.422 | 49.588 | |||||||||
| 8 | 500 gr | 49.668 | 50.338 | 49.149 | 47.807 | 49.064 | 49.205 | 0.990 | 1.00000 | 8 | 0.99664 | 4.4 | 0.99809 | 2.6 |
| 49.695 | 50.681 | 49.640 | 48.969 | 49.612 | 49.720 | |||||||||
| 9 | 500 gr | 51.273 | 48.303 | 48.510 | 50.594 | 48.591 | 49.454 | 0.993 | 1.00000 | 9.9 | 0.99515 | 6.3 | 0.99662 | 4.5 |
| 50.366 | 49.210 | 49.844 | 49.890 | 49.595 | 49.781 | |||||||||
| 10 | 500 gr | 48.720 | 51.566 | 49.677 | 50.651 | 50.344 | 50.192 | 1.002 | 1.00100 | 11.8 | 0.99649 | 8.2 | 0.99655 | 6.4 |
| 49.721 | 50.215 | 50.178 | 50.324 | 50.071 | 50.102 | |||||||||
| 11 | 500 gr | 53.173 | 51.079 | 51.636 | 49.187 | 49.779 | 50.971 | 1.015 | 1.00800 | 11.9 | 1.00145 | 10.1 | 0.99900 | 8.3 |
| 51.081 | 50.660 | 50.468 | 49.787 | 49.197 | 50.239 | |||||||||
| 12 | 500 gr | 51.255 | 48.578 | 49.657 | 49.971 | 50.675 | 50.027 | 1.004 | 1.00600 | 12 | 1.00333 | 10.2 | 1.00116 | 10.2 |
| 49.899 | 49.476 | 49.400 | 49.909 | 50.365 | 49.810 | |||||||||
| 13 | 500 gr | 48.760 | 50.206 | 51.216 | 51.997 | 49.818 | 50.399 | 1.010 | 1.00800 | 12.1 | 1.00547 | 10.3 | 1.00332 | 10.3 |
| 48.919 | 50.032 | 50.497 | 50.627 | 49.483 | 49.912 | |||||||||
| 14 | 500 gr | 51.599 | 49.257 | 52.077 | 49.874 | 48.791 | 50.319 | 1.004 | 1.00600 | 12.2 | 1.00563 | 10.4 | 1.00447 | 10.4 |
| 50.351 | 49.885 | 51.044 | 49.898 | 49.506 | 50.137 | |||||||||
| 15 | 500gr | 49.178 | 51.188 | 50.602 | 50.221 | 50.433 | 50.325 | 1.006 | 1.00600 | 12.3 | 1.00577 | 10.5 | 1.00512 | 10.5 |
| 49.104 | 50.348 | 50.621 | 50.018 | 50.085 | 50.035 | |||||||||
| 16 | 500gr | 50.667 | 50.600 | 50.601 | 49.517 | 50.578 | 50.393 | 1.010 | 1.00800 | 12.4 | 1.00686 | 10.6 | 1.00599 | 10.6 |
| 50.011 | 49.870 | 49.779 | 50.020 | 49.877 | 49.911 | |||||||||
| 17 | 500gr | 50.925 | 49.036 | 50.971 | 51.888 | 50.741 | 50.712 | 1.009 | 1.00850 | 12.5 | 1.00767 | 10.7 | 1.00683 | 10.7 |
| 50.579 | 49.735 | 50.196 | 50.740 | 49.959 | 50.242 | |||||||||
| 18 | 500gr | 50.673 | 50.653 | 50.346 | 50.749 | 51.338 | 50.752 | 1.010 | 1.00925 | 12.6 | 1.00845 | 10.8 | 1.00764 | 10.8 |
| 50.459 | 49.990 | 50.281 | 50.251 | 50.281 | 50.252 | |||||||||
| 19 | 250gr | 25.390 | 25.554 | 25.799 | 23.869 | 25.041 | 25.131 | 1.006 | 1.00763 | 12.7 | 1.00804 | 10.9 | 1.00784 | 10.9 |
| 25.158 | 25.278 | 25.073 | 24.349 | 25.085 | 24.989 | |||||||||
| 20 | 250gr | 24.343 | 26.087 | 25.431 | 24.799 | 26.440 | 25.420 | 1.002 | 1.00481 | 12.8 | 1.00642 | 11.0 | 1.00713 | 11.0 |
| 24.771 | 25.427 | 25.005 | 24.711 | 25.258 | 25.035 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Sun, G.; Xie, F.; Tang, A. Monitoring the Ratio of Two Normal Variables Based on Triple Exponentially Weighted Moving Average Control Charts with Fixed and Variable Sampling Intervals. Symmetry 2022, 14, 1236. https://doi.org/10.3390/sym14061236
Hu X, Sun G, Xie F, Tang A. Monitoring the Ratio of Two Normal Variables Based on Triple Exponentially Weighted Moving Average Control Charts with Fixed and Variable Sampling Intervals. Symmetry. 2022; 14(6):1236. https://doi.org/10.3390/sym14061236
Chicago/Turabian StyleHu, Xuelong, Guan Sun, Fupeng Xie, and Anan Tang. 2022. "Monitoring the Ratio of Two Normal Variables Based on Triple Exponentially Weighted Moving Average Control Charts with Fixed and Variable Sampling Intervals" Symmetry 14, no. 6: 1236. https://doi.org/10.3390/sym14061236
APA StyleHu, X., Sun, G., Xie, F., & Tang, A. (2022). Monitoring the Ratio of Two Normal Variables Based on Triple Exponentially Weighted Moving Average Control Charts with Fixed and Variable Sampling Intervals. Symmetry, 14(6), 1236. https://doi.org/10.3390/sym14061236






