Forbidden Pairs of Disconnected Graphs for Traceability of Block-Chains

Abstract

Each traceable graph must be a block-chain; however, a block-chain is not necessarily traceable in general. Whether a given graph is a block-chain or not can be easily verified by a polynomial algorithm. It occurs to us that forbidden subgraph conditions for a block-chain are traceable. In this article, we characterize all pairs of disconnected forbidden subgraphs for the traceability of block-chains, so as to completely solve pairs of forbidden subgraphs for the traceability of block-chains (including disconnected and connected).

1. Introduction

The Hamiltonicity of graphs is a very important and far-reaching research topic in structural graph theory. The origin and development of this problem is closely related to the famous Four-Color Conjecture. Therefore, it has attracted the attention of many experts and scholars at home and abroad. The traceability of graphs is also closely related to the research of Hamiltonicity in structural graph theory. In terms of algorithmic complexity, it is NP-complete to determine whether a graph is traceable.

In the paper, we only discuss the finite simple graphs. The undefined terminology and notations can be found in Bondy and Murty [1].

Let $G=\left(V\right(G),E(G\left)\right)$ be a connected graph. We denote the size, order, connectivity, independence number, and component number of G by $e\left(G\right),n\left(G\right),\kappa \left(G\right),\alpha \left(G\right)$, and $\omega \left(G\right)$, respectively. Let u be a vertex of G. The set of vertices that are the neighbors of u in the graph G can be denoted by $N_G\left(u\right)$. Let S be a subset of $V\left(G\right)$(or $E\left(G\right)$). We denote the induced subgraph of G by $G\left[S\right]$. Moreover, we use $G-S$ to denote the subgraph $G\left[V\right(G)\backslash S]$, respectively. For a positive integer l, we define $V_l\left(G\right)=\{v\in V\left(G\right)|d_G\left(v\right)=l\}$.

If a graph includes a Hamilton cycle, then it is said to be to be Hamiltonian, and if it includes a Hamilton path, then it is said to be traceable. Sufficient conditions for the traceability of graphs mainly include the following two categories: one is described from the perspective of parameters, among which the independence number, degree sum, minimum degree, and neighborhood union are commonly used; the other is forbidden certain subgraphs from the perspective of structural graph theory.

Let H be a given graph. If G does not include induced copies of H, then a graph of G is called H-free, and H is said to be a forbidden subgraph of G. For a class of graphs $\mathcal{H}$, if G is H-free for each $H\in \mathcal{H}$, then the graph G is $\mathcal{H}$-free. It should be mentioned that each $H_1$-free graph is also $H_2$-free if $H_1$ is an induced subgraph of $H_2$.

As always, $K_n$ is used to denote the complete graph of order n, and $K_{m,n}$ is used to denote the complete bipartite graph such that partition sets are of size m and n. As a result, a vertex is denoted by $K_1$, a triangle is denoted by $K_3$, and a star is denoted by $K_{1,r}$ (moreover, the $K_{1,3}$ is said to be a claw). Let $K_{2,t}(u,u^{\prime })$ be a $K_{2,t}$ satisfying $u,u^{\prime }$, being the nonadjacent vertices of degree t. Let $K_{2,t}^{\prime }(u,u^{\prime },u^{″})$ be the graph acquired from a $K_{2,t}(u,u^{\prime })$ by adding a new vertex $u^{″}$ that is adjacent to $u^{\prime }$ only. Let $S(m,l)$ be the graph acquired from a $K_{2,m}(u,u^{\prime })$ and a $K_{2,l}^{\prime }(w,w^{\prime },w^{″})$ by identifying u with w and $w^{″}$ with $u^{\prime }$ (see Figure 1).

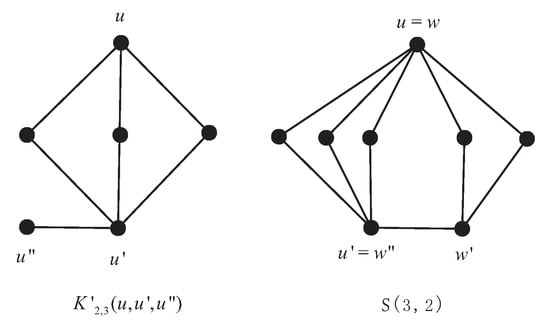
Figure 1. Some graphs with small parameters.

Here are some graphs that will be used later (see Figure 2):

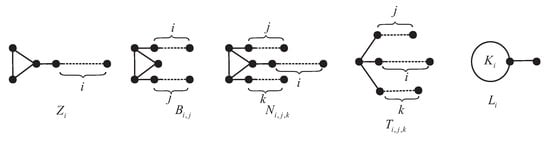
Figure 2. Some classes of graphs.

• $P_i$, the path having i vertices (it should be noted that $P_1=K_1$ and $P_2=K_2$);
• $Z_i$, a graph acquired by identifying an end-vertex of a $P_{i+1}$ with a vertex of a $K_3$;
• $B_{i,j}$, a graph acquired by identifying an end-vertex of a $P_{i+1}$ and $P_{j+1}$ with the two vertices of a $K_3$, respectively;
• $N_{i,j,k}$, a graph acquired by identifying an end-vertex of a $P_{i+1},P_{j+1}$, and $P_{k+1}$ with the three vertices of a $K_3$, respectively;
• $T_{i,j,k}\left(v\right)$, a graph acquired by identifying an end-vertex of three paths $P_{i+1},P_{j+1}$, and $P_{k+1}$ with one vertex v, respectively; moreover, when there is no scope for confusion, we use the notation $T_{i,j,k}$ to denote $T_{i,j,k}\left(v\right)$;
• $L_i$, a graph acquired by identifying an end-vertex of a $P_2$ with a vertex of a $K_i$.

A graph is an empty graph (no edge in the graph), if it is $P_2$-free. A graph is a clique if it is $2K_1$-free. It is not too difficult to check that the graph is traceable. For fear of this trivial case, we just consider that our forbidden subgraphs have at least three vertices throughout the whole article.

Bedrossian [2] characterized all pairs $\{R,S\}$ of connected forbidden subgraphs for Hamiltonicity. Chen et al. [3] considered pairs of forbidden subgraphs that force Hamiltonicity in a graph of high connectivity. Xiong et al. [4] considered pairs of forbidden subgraphs for the edge-connectivity of a connected graph. The most representative result of a traceable graph obtained by adding the forbidden subgraph condition is the conclusion about pairs of forbidden subgraphs [5].

Faudree and Gould [5] extended Bedrossian’s result and characterized all the pairs $\{R,S\}$ of connected subgraphs for traceability.

Theorem 1

([5]). Let R and S be connected graphs such that $R,S\ne P_3$, and let G be a connected graph. Then, G with $\{R,S\}$-free indicates G is traceable if and only if (up to symmetry) $R=K_{1,3}$ and S is an induced subgraph of $N_{1,1,1}$.

With more and more in-depth research on forbidden subgraphs, most studies focus on connected forbidden subgraphs, while the research on disconnected forbidden subgraphs is very few and just started. The first people who studied disconnected forbidden subgraphs were Li and Vrána [6]. They come up with the disconnected forbidden subgraphs and characterized all pairs of disconnected forbidden subgraphs for Hamiltonicity.

Theorem 2

([6]). Let S be a graph with $\left|V\right(S\left)\right|\ge 3$. Then, every two-connected S-free graph is Hamiltonian if and only if S is $P_3$ or $3K_1$.

Theorem 3

([6]). Let R and S be graphs of order at least three other than $P_3$ and $3K_1$. Then, there exists an integer $n_0$ satisfying every two-connected $\{R,S\}$-free graph of order at least $n_0$ that is Hamiltonian, if and only if one of the following is true (up to symmetry):

• $R=K_{1,3}$ and S is an induced subgraph of $P_6,Z_3,N_{0,1,2},N_{1,1,1},K_1\bigcup Z_2,K_2\cup Z_1$, or $K_3\cup P_4$;
• $R=K_{1,k}$ with $k\ge 4$ and S is an induced subgraph of $2K_1\cup K_2$;
• $R=k{K}_1$ with $k\ge 4$ and S is an induced subgraph of $L_l$ with $l\ge 3$, or $2K_1\cup K_{l^{\prime }}$ with $l^{\prime }\ge 2$.

So far, more and more scholars have begun to study pairs of disconnected forbidden subgraphs and many results have been obtained. Xiong et al. [7] considered the pairs of disconnected forbidden subgraphs for a two-factor connected graph. In [8], Du, Li and Xiong extended the result made by Faudree and Gould [5] and characterized all pairs of disconnected forbidden subgraphs for traceability.

Theorem 4

([8]). Let S be a graph with $\left|V\right(S\left)\right|\ge 3$. Then, every connected S-free graph is traceable if and only if S is $P_3$ or $3K_1$.

Theorem 5

([8]). Let R and S be graphs of order at least three other than $P_3$ and $3K_1$. Then, there exists an integer $n_0$ satisfying every connected $\{R,S\}$-free graph of order at least $n_0$ where is traceable, if and only if one of the following is true (up to symmetry):

• $R=K_{1,3}$ and S is an induced subgraph of $N_{1,1,1},K_1\cup Z_1$, or $2K_1\cup K_3$;
• $R=K_{1,k}$ with $k\ge 4$ and S is an induced subgraph of $2K_1\cup K_2$;
• $R=k{K}_1$ with $k\ge 4$ and S is an induced subgraph of $L_l$ with $l\ge 3$, or $2K_1\cup K_{l^{\prime }}$ with $l^{\prime }\ge 2$.

Let G be a graph. If it does not have separating vertices and is connected, then G is called nonseparable. We define a maximal nonseparable subgraph ($P_1$, or $P_2$, or two-connected) of G as a block of G. We use end-block to denote the block that includes exactly one cut vertex of G. If a graph has connectivity 1 and has exactly two end-blocks or is nonseparable, then it is called a block-chain. We should pay attention that each traceable graph must be a block-chain; however, a block-chain is not necessarily traceable in general. Whether a given graph is a block-chain or not can be easily verified by a polynomial algorithm. Many graphs employed in the “only if” part of the proof of Theorem 1 are not block-chains (and are therefore trivially non-traceable). It occurs to us that forbidden subgraph conditions for a block-chain are traceable. In [9], Li, Broersma, and Zhang characterized all pairs of connected graphs R and S other than $P_3$, ensuring that every $\{R,S\}$-free block-chain is traceable.

Theorem 6

([9]). The only connected graph S satisfying a block-chain with S-free indicates it is traceable $P_3$.

Theorem 7

([9]). Let R and S be connected graphs such that R, $S\ne P_3$. Then, a block-chain with $\{R,S\}$-free indicates it is traceable if and only if (up to symmetry) $R=K_{1,3}$ and S is an induced subgraph of $N_{1,1,3}$, or $R=K_{1,4}$ and $S=P_4$.

It is natural that we consider pairs of disconnected forbidden subgraphs for the traceability of block-chains.

We define the Ramsey number $r(k,l)$ as the smallest integer satisfying that each graph of order $r(k,l)$ includes either a clique of k vertices or an independent set of l vertices [10].

In [11], Lei et al. characterized all pairs of disconnected forbidden subgraphs excepting a claw for the traceability of block-chains.

Theorem 8

([11]). Let S be a graph with $\left|V\right(S\left)\right|\ge 3$. Then, every S-free block-chain of order at least $r(10,4)$ is traceable if and only if S is $P_3$ or $4K_1$.

Theorem 9

([11]). Let R and S be graphs of order at least three other than $P_3$, $4K_1$, and $K_{1,3}$. Then, there exists an integer $n_0=max\{r(10,4),r(3k+5,k+2),r(2l-3,k)+k-2,r(2k+l^{\prime }-2,k)\}$ satisfying every $\{R,S\}$-free block-chain of order at least $n_0$ being traceable, if and only if one of the following is true (up to symmetry):

• $R=K_{1,4}$ and S is an induced subgraph of $P_4,P_3\cup K_1$, or $3K_1\cup K_2$;
• $R=K_{1,k}$ with $k\ge 5$ and S is an induced subgraph of $3K_1\cup K_2$;
• $R=k{K}_1$ with $k\ge 5$ and S is an induced subgraph of $L_l$ with $l\ge 3$, or $3K_1\cup K_{l^{\prime }}$ with $l^{\prime }\ge 2$.

Clearly, Lei et al. [11] did not characterize all pairs of disconnected forbidden subgraphs for the traceability of block-chains. The authors did not consider the case where one of the forbidden subgraphs in pairs of forbidden subgraphs is a claw. Li et al. [9] characterized all pairs of connected forbidden subgraphs for the traceability of block-chains. They did not consider disconnected forbidden subgraphs for the traceability of block-chains. In this paper, we will characterize all pairs of disconnected forbidden subgraphs for the traceability of block-chains, so as to completely solve pairs of forbidden subgraphs for the traceability of block-chains (including disconnected and connected).

In the following sections, Section 1 is devoted to the main results and discussions in this paper, Section 2 is devoted to the conclusions, and gives possible avenues for future work, Appendix A.1 is devoted to the preliminaries for the proof of Theorems 10–12, Appendix A.2 is devoted to the proofs of Theorem 10, and Appendix A.3 is devoted to the proofs of Theorem 11.

2. Results and Discussions

In this paper, we will characterize all pairs of disconnected forbidden subgraphs for the traceability of block-chains.

We construct families of block-chains ${\mathcal{G}}_0$ that are not traceable. ${\mathcal{G}}_0$ is a family of graphs H obtained from six complete graphs $B_i$ for $i\in \{1,\dots ,6\}$ with $V\left(B_1\right)\cap V\left(B_2\right)=\left\{v_1\right\}$, $V\left(B_2\right)\cap V\left(B_3\right)=\left\{v_2\right\}$, $V\left(B_2\right)\cap V\left(B_4\right)=\left\{v_3\right\}$, $V\left(B_3\right)\cap V\left(B_5\right)=\left\{v_4\right\}$, $V\left(B_4\right)\cap V\left(B_5\right)=\left\{v_5\right\}$, $V\left(B_5\right)\cap V\left(B_6\right)=\left\{v_6\right\}$, and $\left|V\right(B_j\left)\right|\ge 2$ for $j\in \{1,6\}$, $\left|V\right(B_k\left)\right|\ge 3$ for $k\in \{2,3,4\}$, $\left|V\right(B_5\left)\right|=3$. We also construct families of graph ${\mathcal{F}}_0$ such that $L\left({\mathcal{F}}_0\right)={\mathcal{G}}_0$; see Figure 3 (where the edge that is possibly zero is shown as a dotted line).

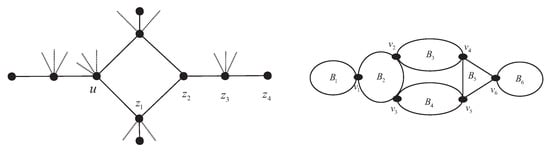
Figure 3. (Left) ${\mathcal{F}}_0$; (right) ${\mathcal{G}}_0$.

We will characterize all pairs of disconnected $\{R,S\}$ of graphs such that there is an integer $n_0$ satisfying every disconnected $\{R,S\}$-free block-chain of order at least $n_0$ being traceable by the following theorems.

Theorem 10.

Let G be a $K_{1,3}$-free block-chain. Then:

(1) 

If G is also $P_6\cup K_1$-free, then G is traceable;

(2) 

If G is also $Z_2\cup 2K_1$-free and $n\left(G\right)\ge 183$, then G is traceable;

(3) 

If G is also $Z_3\cup K_1$-free and $n\left(G\right)\ge 32$, then G is traceable;

(4) 

If G is also $K_3\cup P_4\cup K_1$-free and $n\left(G\right)\ge 3482$, then G is traceable;

(5) 

If G is also $N_{1,1,1}\cup K_2$-free, then G is traceable;

(6) 

If G is also $N_{1,1,2}\cup K_1$-free, then either G is traceable or G is isomorphic to a member of ${\mathcal{G}}_0$.

See Appendix A.2 for the proof of Theorem 10.

Corollary 1.

If G is a $\{K_{1,3},B_{1,2}\cup K_1\}$-free block-chain, then G is traceable.

Proof of Corollary 1.

By contradiction, suppose that G is a $\{K_{1,3},B_{1,2}\cup K_1\}$-free non-traceable block-chain. Note that G is $B_{1,2}\cup K_1$-free, then G must be $N_{1,1,2}\cup K_1$-free. By Theorem 10 (6), the closure $cl\left(G\right)$ of G is isomorphic to a member of ${\mathcal{G}}_0$. Note that $B_i$ is a clique in $cl\left(G\right)$; possibly, $G\left[V\left(B_i\right)\right]$ is not a clique. However, $G\left[V\left(B_i\right)\right]$ must be connected. Moreover, if $\left|V\right(B_i\left)\right|\ge 3$, then $G\left[V\left(B_i\right)\right]$ must be two-connected.

Then, for $\{v_2,v_4\}\in V\left(B_3\right)$ (see Figure 3), there exists a shortest path joining $v_2$ and $v_4$ in $G\left[V\left(B_3\right)\right]$. The length of a shortest such path is called the distance of $G\left[V\left(B_3\right)\right]$ between $v_2$ and $v_4$ and denoted $d_{G\left[V\left(B_3\right)\right]}(v_2,v_4)$. We shall distinguish the following cases to prove Corollary 1.

Case 1$d_{G\left[V\left(B_3\right)\right]}(v_2,v_4)=1$.

Note that $\left|V\right(B_3\left)\right|\ge 3$. Then, there is at least one vertex $x_1\in V\left(B_3\right)$ with $N_{G\left[V\left(B_3\right)\right]}\left(x_1\right)\cap \{v_2,v_4\}\ne \varnothing$. Since G is $K_{1,3}$-free, $G\left[\{v_2,v_4,x_1\}\right]$ is a clique. By the definition of ${\mathcal{F}}_0$, there exist two vertices $\{x_2,x_3\}\subseteq V(B_1\cup B_2)$ such that $v_2{x}_2{x}_3$ is a path of G. Then, $G\left[\{x_1,v_2,v_4,v_6,x_2,x_3\}\right]\cong B_{1,2}$. There exists a vertex $x_4\in V\left(B_4\right)$ with $N_G\left(x_4\right)\cap V\left(G\left[\{x_1,v_2,v_4,v_6,x_2,x_3\}\right]\right)=\varnothing$. Then, $G\left[\{x_1,v_2,v_4,v_6,x_2,x_3,x_4\}\right]\cong B_{1,2}\cup K_1$, a contradiction.

Case 2$d_{G\left[V\left(B_3\right)\right]}(v_2,v_4)>1$.

There exists at least two vertices $\{y_1,y_2\}\subseteq V\left(B_3\right)$ such that $v_4{y}_1{y}_2$ is a path of $G\left[V\left(B_3\right)\right]$.There exists a vertex $y_3\in V\left(B_6\right)$ with $v_6{y}_3\in E\left(G\right)$. Then, $G\left[\{v_4,v_5,v_6,y_1,y_2,y_3\}\right]\cong B_{1,2}$. There exists a vertex $y_4\in V\left(B_1\right)$ with $N_G\left(y_4\right)\cap V\left(G\left[\{v_4,v_5,v_6,y_1,y_2,y_3\}\right]\right)=\varnothing$. Then, $G\left[\{v_4,v_5,v_6,y_1,y_2,y_3,y_4\}\right]\cong B_{1,2}\cup K_1$, a contradiction.

These contradictions show that Corollary 1 holds. □

Theorem 11.

Let G be a $K_{1,3}$-free block-chain. Then, if G is also $S\cup P_4$-free for $S\in \{Z_1,P_4\}$ and $n\left(G\right)\ge 212$, then G is traceable.

See Appendix A.3 for the proof of Theorem 11.

Ultimately, we may propose our main result as below.

Theorem 12.

Let R and S be graphs of order at least three other than $P_3$ and $4K_1$. Then, there is an integer $n_0$ such that every $\{R,S\}$-free block-chain of order at least $n_0$ is traceable, if and only if one of the following is true (up to symmetry):

• $R=K_{1,3}$ and S is an induced subgraph of $N_{1,1,3},P_6\cup K_1,Z_2\cup 2K_1,$$Z_3\cup K_1,K_3\cup P_4\cup K_1,Z_1\cup P_4,P_4\cup P_4,N_{1,1,1}\cup K_2$, or $B_{1,2}\cup K_1$;
• $R=K_{1,4}$ and S is an induced subgraph of $P_4,P_3\cup K_1$ or $3K_1\cup K_2$;
• $R=K_{1,k}$ with $k\ge 5$ and S is an induced subgraph of $3K_1\cup K_2$;
• $R=k{K}_1$ with $k\ge 5$ and S is an induced subgraph of $L_l$ with $l\ge 3$, or $3K_1\cup K_{l^{\prime }}$ with $l^{\prime }\ge 2$.

Proof of Theorem 12.

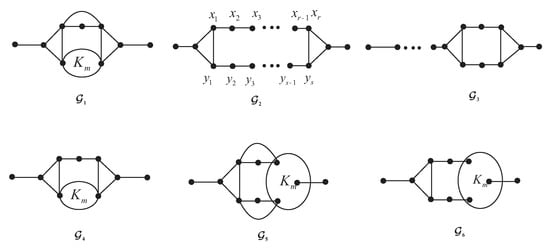
By Theorem 1 and Theorems 9–11, the sufficiency is proven. Then, we only need to prove the necessity.

Firstly, some families of block-chains ${\mathcal{G}}_i,i=1,\dots ,6$, which are not traceable (see Figure 4), are constructed.

Figure 4. Some classes of graphs that are connected and non-traceable.

Let R and S be graphs of order at least three other than $P_3$ and $4K_1$, such that there exists an integer $n_0$ such that every connected $\{R,S\}$-free block-chain of order at least $n_0$ is traceable. Then, all graphs in ${\mathcal{G}}_i,i=1,\dots ,6$, of order large enough, contain either R or S as an induced subgraph. By Theorem 9, it suffices to consider that either R or S is $K_{1,3}$. We can assume without loss of generality that $R=K_{1,3}$. Note that all graphs in ${\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4,{\mathcal{G}}_5,{\mathcal{G}}_6$ are $K_{1,3}$-free. Thus, each of them contains S being an induced subgraph. Since all graphs in ${\mathcal{G}}_1$ are $5K_1$-free, S is also $5K_1$-free, i.e., $\alpha \left(S\right)\le 4$. This indicates that $\omega \left(S\right)\le 4$. If $\omega \left(S\right)=1$, i.e., S is connected, then, by Theorem 7, S is an induced subgraph of $N_{1,1,3}$. Therefore, we assume that $\omega \left(S\right)>1$, i.e., S is disconnected. Note that S is an induced subgraph of all graphs in ${\mathcal{G}}_2$, and S is also an induced subgraph of all graphs in ${\mathcal{G}}_3$. Then, if there exists one component of S such that it contains a cycle, then the cycle is triangle. If every component of S does not contain a triangle, then S is a forest. Since G is $K_{1,3}$-free, every component of S is a path. Note that all graphs in ${\mathcal{G}}_4$ are $K_3\cup K_3$-free. Therefore, if there exists one component of S such that it contains a triangle, say $H_i$ for $1\le i\le 4$, then every component of $S-H_i$ is a path. Suppose that $\omega \left(S\right)=2$, say, $H_1,H_2$ are the two components of S. Suppose first that $H_1$ and $H_2$ are paths of G. Observe that all graphs in ${\mathcal{G}}_5$ are $P_7$-free. Then, $H_1$ is an induced subgraph of $P_6$. If $H_1=K_1$, then noting that all graphs in ${\mathcal{G}}_5$ are $K_1\cup P_7$-free, we have that $H_2$ is an induced subgraph of $P_6$; if $H_1=K_2$, then observing that all graphs in ${\mathcal{G}}_5$ are $K_2\cup P_5$-free, we have that $H_2$ is an induced subgraph of $P_4$; if $H_1=P_3$, then observing that all graphs in ${\mathcal{G}}_5$ are $P_3\cup P_5$-free, we have that $H_2$ is an induced subgraph of $P_4$; if $H_1=P_4$; then observing that all graphs in ${\mathcal{G}}_5$ are $P_4\cup P_5$-free, we have that $H_2$ is an induced subgraph of $P_4$; if $H_1=P_5$; then observing that all graphs in ${\mathcal{G}}_5$ are $P_5\cup K_2$-free, we have that $H_2$ is an induced subgraph of $K_1$; if $H_1=P_6$, then observing that all graphs in ${\mathcal{G}}_5$ are $P_6\cup K_2$-free, we have that $H_2$ is an induced subgraph of $K_1$. Furthermore, note that $P_5\cup K_1$ is an induced subgraph of $P_6\cup K_1$ and $P_4\cup P_3$ is an induced subgraph of $P_4\cup P_4$. Thus, S is an induced subgraph of $P_6\cup K_1$ or $P_4\cup P_4$. Suppose now that $H_1$ contains a triangle and $H_2$ is a path of G. Then, $H_1$ is an induced subgraph of $K_3,Z_i,B_{i,j},N_{i,j,k}$. If $H_1$ is an induced subgraph of $N_{i,j,k}$, then, by $\alpha \left(S\right)\le 4$, $H_2$ is $K_1$ or $K_2$. Note that all graphs in ${\mathcal{G}}_1$ are $\{N_{1,1,2}\cup K_1,N_{1,1,1}\cup P_3\}$-free. Thus, S is an induced subgraph of $N_{1,1,1}\cup K_2$. If $H_1$ is an induced subgraph of $B_{i,j}$, then, by $\alpha \left(S\right)\le 4$, $H_2$ is $K_1$ or $K_2$. All graphs in ${\mathcal{G}}_5$ are $\{B_{1,2}\cup K_2\}$-free, and all graphs in ${\mathcal{G}}_6$ are $\{B_{2,2}\cup K_1\}$-free. Thus, S is an induced subgraph of $B_{1,2}\cup K_1$. If $H_1$ is an induced subgraph of $Z_i$, then noting that all graphs in ${\mathcal{G}}_5$ are $\{Z_3\cup K_2,Z_2\cup K_2,Z_1\cup P_5\}$-free, also note that $Z_2\cup K_1$ is an induced subgraph of $Z_3\cup K_1$. Thus, S is an induced subgraph of $Z_3\cup K_1$ or $Z_1\cup P_4$. If $H_1$ is $K_3$, then note that all graphs in ${\mathcal{G}}_5$ are $K_3\cup P_5$-free. Thus, $H_2$ is an induced subgraph of $K_3\cup P_4$. Suppose that $\omega \left(S\right)=3$, say $H_1,H_2$, and $H_3$ are three components of S. By $\omega \left(S\right)\le 4$, up to symmetry, $H_1$ and $H_2$ are complete and $\omega \left(S\right)\le 2$. This implies that $H_3$ is either an induced subgraph of $Z_2$ or an induced subgraph of $P_6$. Note that all graphs in ${\mathcal{G}}_5$ are $\{Z_2\cup K_1\cup K_2,Z_1\cup K_2\cup K_2,K_3\cup P_5\cup K_1\}$-free, and also observe that $K_3\cup P_4$ is an induced subgraph of $K_3\cup P_4\cup K_1$. Thus, S is an induced subgraph of $Z_2\cup 2K_1$ or $K_3\cup P_4\cup K_1$. Suppose that $\omega \left(S\right)=4$. Then, every component of S is complete and of order at most three. Note that all graphs in ${\mathcal{G}}_5$ are $K_3\cup 2K_2\cup K_1$-free; also note that $K_3\cup K_2\cup 2K_1$ is an induced subgraph of $K_3\cup P_4\cup K_1$. We conclude that S is an induced subgraph of $K_3\cup P_4\cup K_1$. This completes the proof of the necessity. □

Concluding remark: In this paper, we characterized all pairs $\{R,S\}$ of graphs (not necessary connected) such that there exists an integer $n_0$ such that every connected $\{R,S\}$-free graph of order at least $n_0$ is traceable.

3. Conclusions

In 2013, Li, Broersma, and Zhang [9] characterized all the pairs of connected forbidden subgraphs for the traceability of block-chains. We characterized all pairs of disconnected forbidden subgraphs for the traceability of block-chains, so as to completely solve pairs of forbidden subgraphs for the traceability of block-chains (including disconnected and connected). This further reveals the profound connotation of graph traceability and the Hamiltonicity property.

In the future, we can consider the triples’ disconnected forbidden subgraphs for traceability and Hamiltonicity. Forbidden subgraphs are closely related to many path and cycle properties of graphs, which have attracted the attention of many graph theory experts. Many meaningful research results have been obtained, and many problems worth further study have been left. The study of disconnected forbidden subgraphs is just beginning, and the properties of many graphs are related to disconnected forbidden subgraphs. In terms of disconnected forbidden subgraphs and pancyclicity, the disconnected forbidden subgraphs and Hamiltonian-connected onescan be further studied. With the application of disconnected forbidden subgraphs, people can also study the color, matching, factor, and other problems of the graph. The research prospect of disconnected forbidden subgraphs is very broad, and there are still many problems to break through.

Appendix A.1. Preliminaries

Some preliminary notations and theorems preparing for the proofs of Theorems 12 will be introduced in this section.

Let G be a given graph. To reduce the repetition rate, the definition of the line graph of G (denoted by $L\left(G\right)$), the closure of a claw-free graph G (denoted by cl$\left(G\right)$) and closed claw-free graph G can refer to [12]. The following theorem is significant when we deal with the traceability of claw-free graphs.

Theorem A1

(Ryjáček [12]). Let G be a claw-free graph. Then

• cl$\left(G\right)$ is uniquely determined;
• cl$\left(G\right)$ is claw-free;
• cl$\left(G\right)$ is the line graph of a triangle-free graph.

Theorem A2

(Brandt, Favaron and Ryjáček [13]). G is traceable if and only if cl$\left(G\right)$ is traceable.

Following [14], if for each graph in a class $\mathcal{H}$, its closure is also in $\mathcal{H}$, then the class $\mathcal{H}$ of graphs is called stable.

Theorem A3.

(Brousek, Ryjáček and Favaron [14]) Let S be a connected claw-free closed graph of order at least 3. If $S\in \left\{K_3\right\}\cup \{Z_i:i>0\}\cup \{N_{i,j,k}:i,j,k>0\}$, then the class of $\{K_{1,3},S\}$-free graphs is stable.

Theorem A4

([6]). Let S be a disconnected claw-free closed graph. Then the class of $\{K_{1,3},S\}$-free graphs is stable, if and only if for every component C of S, the class of $\{K_{1,3},C\}$-free graphs is stable.

By Theorems A3 and A4, the class of $\{K_{1,3},P_6\cup K_1\}$, $\{K_{1,3},Z_2\cup 2K_1\},$$\{K_{1,3},Z_3\cup K_1\}$, $\{K_{1,3},K_3\cup P_4\cup K_1\}$ and $\{K_{1,3},N_{1,1,1}\cup K_2\}$-free graphs are stable.

For a closed claw-free graph G, let $L^{-1}\left(G\right)$ be a $K_3$-free graph satisfying G is its line graph. Clearly G is S-free if and only if $L^{-1}\left(G\right)$ contains no (not necessary induced) copies of $L^{-1}\left(S\right)$.

Theorem A5

([15]). Every $K_3$-free graph of order n has at most $n^2/4$ edges.

Theorem A6

(Wang and Xiong [16]). Every 2-connected $\{K_{1,3},N_{1,1,5}\}$-free graph is traceable.

Theorem A7

(Wang and Xiong [17]). Let G be a 2-connected graph with circumference $c\left(G\right)$. Then if $c\left(G\right)\le 5$, then G has a spanning trail that starts from any given vertex.

In 1972, Chvátal and Erdos [18] also gave the condition for Hamiltonicity and traceability by $\alpha \left(G\right)$ and $\kappa \left(G\right)$.

Theorem A8

([18]). Let G be a graph on at least three vertices with stability number $\alpha \left(G\right)$ and connectivity $\kappa \left(G\right)$.

• If $\alpha \left(G\right)\le \kappa \left(G\right)-1$, then G is Hamilton-connected;
• If $\alpha \left(G\right)\le \kappa \left(G\right)$, then G is Hamiltonian;
• If $\alpha \left(G\right)\le \kappa \left(G\right)+1$, then G is traceable.

Lemma A1.

Let G be a block-chain. Each block of G has at most two cut vertex of G.

Proof. 

Suppose, otherwise, that there exists a block $B_0$ of G such that it has at least three cut vertex of G. Let $B\left(G\right)$ be the block tree of G. Then the maximum degree of $B\left(G\right)$ at least 3. Note that every tree with maximum degree k has at least k leaves. Then $B\left(G\right)$ has at least 3 leaves. Therefore, G has at least three end-blocks, a contradiction. □

Lemma A2.

Let H be a graph. Then, if $L\left(H\right)$ is a block-chain, then the number of cut edges in H that is not pendent is at most two.

Proof. 

By contradiction, suppose that the number of cut edges in H that is not pendent is at least three. Let $H^{\prime }$ be the maximal 2-edge-connected subgraph of H with $\left|V\right(H^{\prime }\left)\right|$ is as large as possible. Then the number of cut edges of H that is not pendent incident with $V\left(H^{\prime }\right)$ is at least three. Then there exists at least one block of $L\left(H\right)$ has at least three cut vertex of $L\left(H\right)$, contradicting Lemma A1. □

Appendix A.2. Proofs of Theorem 10

Proof of Theorem 10.

We assume that G is a $K_{1,3}$-free block-chain with non-traceable. By Theorems A1 and A2, we only need to consider the case that G is closed. By Theorem 7, G contains an induced copy of $N_{1,1,3}$. Let H be a $K_3$-free graph with $H=L^{-1}\left(G\right)$. By Theorem 7, H contains a (not necessary induced) copy of $T^{\prime }=T_{2,2,4}\left(u\right)=L^{-1}\left(N_{1,1,3}\right)$, that is a graph consisting of three paths $Q_1=u{x}_1{x}_2$, $Q_2=u{y}_1{y}_2$, $Q_3=u{z}_1\dots z_4$. Let F be a subgraph of H and $\mathcal{D}(F,H)$ be the set of all components of $H-F$ and ${\mathcal{D}}_F(v,H)=\{D:D\in \mathcal{D}(F,H),N_G\left(v\right)\cap V\left(D\right)\ne \varnothing \}$ for $v\in V\left(F\right)$. Let Q be a subgraph of F and ${\mathcal{D}}_F(Q,H)=\{D:D\in \mathcal{D}(F,H),N\left(V\left(Q\right)\right)\cap V\left(D\right)\ne \varnothing \}$, respectively. In the absence of confusion of definitions, we use $\mathcal{D}\left(F\right)$, ${\mathcal{D}}_F\left(v\right)$ and ${\mathcal{D}}_F\left(Q\right)$ to denote the $\mathcal{D}(F,H)$, ${\mathcal{D}}_F(v,H)$ and ${\mathcal{D}}_F(Q,H)$.

Proof of (1):

Let G be $\{K_{1,3},P_6\cup K_1\}$-free block-chain. By Theorem 7, the subgraph $H\left[\{y_2{y}_1,y_{1}u,u{z}_1,z_1{z}_2,z_2{z}_3,z_3{z}_4\}\right]\cup H\left\{x_1{x}_2\right\}]$ is a $L^{-1}\left(P_6\right)\cup L^{-1}\left(K_1\right)$, a contradiction. This implies that the statement (1) holds. □

Proof of (2):

Let G be $\{K_{1,3},2K_1\cup Z_2\}$-free block-chain.

Claim 1.$\mid {\mathcal{D}}_{T^{\prime }}\left(x\right)\mid \le 1$ for any $x\in V\left(T^{\prime }\right)$.

Proof. 

By contradiction, suppose that there is one vertex, say $x_0\in V\left(T^{\prime }\right)$, with $|{\mathcal{D}}_{T^{\prime }}\left(x_0\right)|>1$. Then there exist at least two vertices $\{x_0^{\prime },x_0^{″}\}\subseteq N\left(x_0\right)\cap (V\left(H\right)\setminus V\left(T^{\prime }\right)$. If $x_0=u$, then the subgraph $H\left[\{u{u}^{\prime },u{u}^{″},u{z}_1,z_1{z}_2,z_2{z}_3\}\right]\cup H\left[\left\{x_1{x}_2\right\}\right]\cup H\left[\left\{y_1{y}_2\right\}\right]$ is a $L^{-1}\left(Z_2\right)\cup L^{-1}\left(K_1\right)\cup L^{-1}\left(K_1\right)$, a contradiction. If $x_0=z_2$, then the subgraph $H\left[\{z_2{z}_2^{\prime },z_2{z}_2^{″},z_2{z}_1,z_{1}u,u{x}_1\}\right]\cup H\left[\left\{y_1{y}_1\right\}\right]\cup H\left[\left\{z_3{z}_4\right\}\right]$ is a $L^{-1}\left(Z_2\right)\cup L^{-1}\left(K_1\right)\cup L^{-1}\left(K_1\right)$, a contradiction. If $x_0\in \{x_1,x_2,y_1,y_2\}$, then $H[V(Q_1\cup Q_2)\cup \{x_0^{\prime },x_0^{″}\}]$ contains a subgraph $F_1\cong L^{-1}\left(Z_2\right)$. Then $H\left[\{E\left(F_1\right),z_1{z}_2,z_3{z}_4\}\right]$ is a $L^{-1}(2K_1\cup Z_2)$, a contradiction. If $x_0\in \{z_1,z_3,z_4\}$, then $H\left[V(Q_3\cup \{x_0^{\prime },x_0^{″}\})\right]$ contains a subgraph $F_2\cong L^{-1}\left(Z_2\right)$. Then $H\left[\{E\left(F_1\right),x_1{x}_2,y_1{y}_2\}\right]$ is a $L^{-1}(2K_1\cup Z_2)$, a contradiction. □

Moreover, ${\mathcal{D}}_{T^{\prime }}\left(x\right)$ contain at most one element of $\{P_1,P_2\}$, otherwise a $L^{-1}(2K_1\cup Z_2)$ could be found. It implies that $n\left(H\right)\le 27$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 182$ and $n\left(G\right)\le 182$. This deduces that every connected $\{K_{1,3},2K_1\cup Z_2\}$-free graph of order at least 183 is traceable. □

Proof of (3):

Let G be $\{K_{1,3},K_1\cup Z_3\}$-free block-chain.

Claim 2. Each element of ${\mathcal{D}}_{T^{\prime }}\left(z_1\right)$ is isomorphic to $K_1$.

Proof. 

Suppose, by contradiction, that there exists a component $D_0$ (say) in ${\mathcal{D}}_{T^{\prime }}\left(z_1\right)$ such that it is not isomorphic to a connected subgraph of $K_1$. Then $D_0$ contains a subgraph F that it is isomorphic to $P_2$. Then the subgraph $H\left[\{u{x}_1,u{y}_1,u{z}_1,z_1{z}_2,z_2{z}_3,z_3{z}_4\}\right]\cup H\left[E\left(P_2\right)\right]$ is a $L^{-1}\left(Z_3\right)\cup L^{-1}\left(K_1\right)$, a contradiction. □

Claim 3.${\mathcal{D}}_{T^{\prime }}\left(v\right)=\varnothing$ for any $v\in V\left(T^{\prime }\right)\setminus \{z_1,z_4\}$.

Proof. 

By contradiction, suppose that there exists one vertex $v_0\in V\left(T^{\prime }\right)\setminus \{z_1,z_4\}$ such that ${\mathcal{D}}_{T^{\prime }}\left(v_0\right)\ne \varnothing$. Let $v_0^{\prime }\in N\left(v_0\right)\cap (V\left(H\right)\setminus V\left(T^{\prime }\right))$. If $v_0=u$, then $H\left[\{u{u}^{\prime },u{x}_1,u{z}_1,z_1{z}_2,z_2{z}_3,z_3{z}_4,y_1{y}_2\}\right]$ is a $L^{-1}(Z_3\cup K_1)$, a contradiction. If $v_0\in \{x_1,y_1\}$, then, by symmetry, we only consider the case that $v_0=x_1$. Then $H\left[\{x_1{x}_1^{\prime },x_1{x}_2,x_{1}u,u{z}_1,z_1{z}_2,z_2{z}_3,y_1{y}_2\}\right]$ is a $L^{-1}(Z_3\cup K_1)$, If $v_0\in \{x_2,y_2\}$, then, by symmetry, we only consider the case that $v_0=x_2$. Then the subgraph $H\left[\{u{x}_1,u{y}_1,u{z}_1,z_1{z}_2,z_2{z}_3,z_3{z}_4,x_2^{\prime }{x}_2\}\right]$ is a $L^{-1}(Z_3\cup K_1)$, a contradiction. If $v_0\in \{z_2,z_3\}$, then $H[V(Q_1\cup Q_3)\cup \left\{x^{\prime }\right\}$ contains a subgraph $F\cong L^{-1}\left(Z_3\right)$. Then $H\left[\{E\left(F\right),y_1{y}_2\}\right]$ is a $L^{-1}(Z_3\cup K_1)$, a contradiction. □

$\mid {\mathcal{D}}_{T^{\prime }}\left(z_4\right)\mid \le 1$ and ${\mathcal{D}}_{T^{\prime }}\left(z_4\right)$ contain at most one element of $\left\{K_1\right\}$, otherwise we also can find a $L^{-1}(K_1\cup Z_3)$. And $\mid {\mathcal{D}}_{T^{\prime }}\left(z_1\right)\mid >1$. Otherwise, by Claims A.2, 3, $n\left(H\right)\le 11$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 31$ and $n\left(G\right)\le 31$. This deduces that every $\{K_{1,3},K_1\cup Z_3\}$-free block-chain of order at least 32 is traceable, a contradiction. Therefore, there exist at least two vertices $z_1^{\prime }$ and $z_1^{″}$ such that $\{z_1^{\prime },z_1^{″}\}\subseteq N\left(z_1\right)\cap (V\left(H\right)\setminus V\left(T^{\prime }\right))$.

Claim 4.$u{x}_1$ and $u{y}_1$ are cut edges of H.

Proof. 

By symmetry, we just need to prove that $u{x}_1$ is a cut edge of H. By contradiction, suppose that $u{x}_1$ is not a cut edge of H. Note that H is $K_3$-free. Then, by Claims A.2 and A.2, there exists at least one vertex $x_{i_0}$ (say) such that $N\left(x_{i_0}\right)\cap V(T^{\prime }\setminus Q_1)\ne \varnothing$ for $i_0\in \{1,2\}$. Let $x_{i_0}^{\prime }\in N\left(x_{i_0}\right)\cap V(T^{\prime }\setminus Q_1)$ for $i_0\in \{1,2\}$. If $x_{i_0}^{\prime }\in \{y_1,y_2,z_1,z_2\}$, then $H[V(Q_1\cup Q_2)\cup \{z_1,z_1^{\prime },z_1^{″}\}]$ contains a subgraph $F_1\cong L^{-1}\left(Z_3\right)$. Then $H\left[\{E\left(F_1\right),z_3{z}_4\}\right]$ is a $L^{-1}(K_1\cup Z_3)$, a contradiction. If $x_{i_0}^{\prime }\in \{z_3,z_4\}$, then $H[V(Q_1\cup Q_3)\cup \{z_1^{\prime },z_1^{″}\}]$ contains a subgraph $F_2\cong L^{-1}\left(Z_3\right)$. Then $H\left[\{E\left(F_2\right),y_1{y}_2\}\right]$ is a $L^{-1}(K_1\cup Z_3)$, a contradiction. These contradictions show that $u{x}_1$ is a cut edge of H. □

By Claim 4, $u{x}_1$ and $u{y}_1$ are cut edges of H. Then, by Lemma A2, the edge $u{z}_1$ is not cut edge of H. By Claims 3,4, u has a neighbor in $V\left(Q_3\right)\setminus \{u,z_1\}$. Let $u^{\prime }\in N_H\left(u\right)$. Then $u^{\prime }\in \{z_2,z_3,z_4\}$. Since H is $K_3$-free, $u^{\prime }\ne z_2$. This implies that $u^{\prime }\in \{z_3,z_4\}$. Then $H[V(Q_2\cup Q_3)\cup \{z_1^{\prime },z_1^{″}\}]$ contains a subgraph $F\cong L^{-1}\left(Z_3\right)$. Then $H\left[\{E\left(F\right),x_1{x}_2\}\right]$ is a $L^{-1}(K_1\cup Z_3)$, a contradiction. This contradiction implies that every connected $\{K_{1,3},Z_3\cup K_1\}$-free graph of order at least 32 is traceable. □

In order to prove the statements (4), (5) and (6), we choose a maximal $T_{k_1,k_2,k_3}\left(u\right)$ in H consisting of three paths $Q_1=u{x}_1\dots x_{k_1}$, $Q_2=u{y}_1\dots y_{k_2}$, $Q_3=u{z}_1\dots z_{k_3}$ and it satisfies

(I) $k_3\ge k_2\ge k_1\ge 2$;

(II) $k_3$ is maximized;

(III) $k_2$ is maximized subject to $\left(I\right)$;

(IV) $k_1$ is maximized subject to $\left(I\right)$, $\left(II\right)$ and $\left(III\right)$.

By Theorem 7, $T_{k_1,k_2,k_3}\left(u\right)$ contains a (not necessary induced) copy of $T_{2,2,4}\left(u\right)=L^{-1}\left(N_{1,1,3}\right)$. Then $k_3\ge 4$. Let $T=T_{k_1,k_2,k_3}\left(u\right)$. Then $T^{\prime }\subseteq T$. Let $Q_i^{\prime }=H[(V\left(Q_i\right)\setminus \left\{u\right\})\cup V\left({\mathcal{D}}_T(Q_i\setminus \left\{u\right\})\right)]$ for $i\in \{1,2,3\}$.

Proof of (4):

Let G be $\{K_{1,3},K_3\cup P_4\cup K_1\}$-free block-chain.

Claim 5. Each element of $\mathcal{D}\left(T\right)$ is isomorphic to a connected subgraph of $C_4$, i.e., $\{K_1,K_2,P_3,P_4,C_4\}$.

Proof. 

Suppose, by contradiction, that there exists a component $D_0$ (say) in $\mathcal{D}\left(T\right)$ such that it is not isomorphic to a connected subgraph of $C_4$. Then $D_0$ contains a subgraph F that it is isomorphic to $P_5$ or $K_{1,3}$. If $F\cong P_5$, then the subgraph $H\left[\{u{x}_1,u{y}_1,u{z}_1\}\right]\cup H\left[E\left(P_5\right)\right]\cup H\left[\left\{z_3{z}_4\right\}\right]$ is a $L^{-1}\left(K_3\right)\cup L^{-1}\left(P_4\right)\cup L^{-1}\left(K_1\right)$, a contradiction. If $F\cong K_{1,3}$, then $H\left[E\left(F\right)\right]\cup H\left[\{u{z}_1,z_1{z}_2,z_2{z}_3,z_3{z}_4\}\right]\cup H\left[\left\{y_1{y}_2\right\}\right]$ is a $L^{-1}\left(K_3\right)\cup L^{-1}\left(P_4\right)\cup L^{-1}\left(K_1\right)$, a contradiction. □

Claim 6. For $i\in \{1,2\}$, $H[V(Q_i\cup \mathcal{D}\left(T\right))\setminus \left\{u\right\}]$ does not contain subgraph which is isomorphic to $K_{1,3}$.

Proof. 

Suppose, by contradiction, that there exists a integer $i_0\in \{1,2\}$ such that $H[V(Q_{i_0}\cup \mathcal{D}\left(T\right))\setminus \left\{u\right\}]$ contains subgraph which is isomorphic to $K_{1,3}$. Then $H[V(Q_1\cup Q_2\cup \mathcal{D}\left(T\right))\setminus \left\{u\right\}]$ contains a subgraph $F\cong K_{1,3}\cup K_2$. Then $H\left[\{E\left(F\right),u{z}_1,z_1{z}_2,z_2{z}_3,z_3{z}_4\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. □

Claim 7.$|{\mathcal{D}}_T\left(v\right)|\le 1$ for every $v\in V\left(T\right)\setminus \left\{u\right\}$.

Proof. 

Suppose, by contradiction, that there exists a vertex $v_0\in V\left(T\right)\setminus \left\{u\right\}$ with $|{\mathcal{D}}_T\left(v_0\right)|\ge 2$. Then we assume that $D,D^{\prime }\subseteq {\mathcal{D}}_T\left(v_0\right)$. By Claim 6, $v_0\notin V(Q_1\cup Q_2)\setminus \left\{u\right\}$. This implies that $v_0\in V\left(Q_3\right)\setminus \left\{u\right\}$. Then $H[V(Q_3\cup D\cup D^{\prime })\setminus \left\{u\right\}]$ contains a subgraph $F\cong K_{1,3}\cup K_2$. However, $H\left[\{E\left(F\right),x_1{x}_2,x_{2}u,u{y}_2,y_2{y}_1\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. □

Claim 8.$|{\mathcal{D}}_T\left(u\right)|\ge 3$.

Proof. 

Suppose, by contradiction, that $|{\mathcal{D}}_T\left(u\right)|\le 2$. Then $k_3\le 7$. Otherwise, then the subgraph $H\left[\{u{x}_1,u{y}_1,u{z}_1,z_4{z}_5,z_5{z}_6,z_6{z}_7,z_7{z}_8,z_2{z}_3\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction.

Note that $k_1\le k_2\le k_3\le 7$. Then, by Claims 5-7, $n\left(H\right)\le 118$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 3481$ and $n\left(G\right)\le 3481$. This implies that every $\{K_{1,3},K_3\cup P_4\cup K_1\}$-free block-chain of order at least 3482 is traceable, a contradiction. □

Then $k_3=4$. Otherwise, $k_3>4$. By Claim 8, $H\left[V\right(\mathcal{D}\left(T\right))\cup \{u\left\}\right]$ contains a subgraph $F\cong K_{1,3}$. Then the subgraph $H\left[\{E\left(F\right),z_1{z}_2,z_2{z}_3,z_3{z}_4,z_4{z}_5,x_1{x}_2\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. Therefore, $2\le k_1\le k_2\le k_3\le 4$. Let $u^1,u^2,u^3$ be the vertex u’s neighbor in different element in $\mathcal{D}\left(T\right)$, respectively. □

Claim 9. For any $i\in \{1,2,3\}$, $H[V(Q_i\cup \mathcal{D}\left(T\right))\setminus \left\{u\right\}]$ does not contain subgraph which is isomorphic to $P_5$.

Proof. 

Suppose, by contradiction, that there exists a integer $i_0\in \{1,2,3\}$ with $H[V(Q_{i_0}\cup \mathcal{D}\left(T\right))\setminus \left\{u\right\}]$ contains subgraph $F_1$ (say) which is isomorphic to $P_5$. Let $Q_{i_0}=u{v}_1\dots v_{k_{i_0}}$. Then $k_{i_0}\in \{2,3,4\}$. By Claim 5, $V\left(F_1\right)\cap (V\left(Q_{i_0}\right)\setminus \left\{u\right\})\ne \varnothing$. If $|V\left(F_1\right)\cap \{u^1,u^2,u^3\}|\le 1$, then there exist at least two vertices $u_1$, $u_2\in \{u^1,u^2,u^3\}$ such that $\{u_1,u_2\}\cap V\left(F_1\right)=\varnothing$. Note that $H[V(T\setminus Q_{i_0})\cup \{u,u_1,u_2\}]$ contains a subgraph $F_2\cong K_{1,3}\cup K_2$. Then $H\left[\{E\left(F_1\right),E\left(F_2\right)\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. This implies that $|V\left(F_1\right)\cap \{u^1,u^2,u^3\}|\ge 2$. Suppose that $\{u^1,u^2,u^3\}\subseteq V\left(F_1\right)$. Note that $u^1,u^2,u^3$ belong to different components of $\mathcal{D}\left(T\right)$, and so are not connected by a path in $\mathcal{D}\left(T\right)$. Then $F_1$ is a path whose vertices are alternately in $V\left(Q_{i_0}\right)\setminus \left\{u\right\}$ and $\{u^1,u^2,u^3\}$. By Claim 7, $|V\left(F_1\right)\cap (V\left(Q_{i_0}\right)\setminus \left\{u\right\})|\ge 3$. Then $\left|V\right(F_1\left)\right|\ge 6$, contradicting $\left|V\right(F_1\left)\right|=5$. This implies that $|V\left(F_1\right)\cap \{u^1,u^2,u^3\}|=2$. Without loss of generality, suppose that $\{u^1,u^2\}\subseteq V\left(F_1\right)$. By Claim 7, $|V\left(F_1\right)\cap (V\left(Q_{i_0}\right)\setminus \left\{u\right\})|\ge 2$. Since H is $K_3$-free, $N\left(v_1\right)\cap \{u^1,u^2\}=\varnothing$. By choice of T, $N\left(v_{k_{i_0}}\right)\cap \{u^1,u^2\}=\varnothing$. Therefore, $k_{i_0}=4$ and $\{u^1,u^2,v_2,v_3\}\subseteq V\left(F_1\right)$. Note that $u^1,u^2,u^3$ belong to the different component of $\mathcal{D}\left(T\right)$ and H is $K_3$-free. Then, $v_1\notin V\left(F_1\right)$. Therefore, $H[V(T\setminus Q_{i_0})\cup \{u,u^3,v_1\}]$ contains a subgraph $F_2^{\prime }\cong K_{1,3}\cup K_2$. Then $H\left[\{E\left(F_1\right),E\left(F_2^{\prime }\right)\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. □

Claim 10. For any component $D\in \mathcal{D}\left(T\right)$, $N_H\left(V\left(D\right)\right)\cap V\left(T\right)\subseteq \{x_1,y_1,z_2,z_3,u\}$. Moreover, if $N_H\left(V\left(D\right)\right)\cap V\left(T\right)\ne \left\{u\right\}$, then $D\cong K_1$.

Proof. 

By Claim 6, $N_H\left(V\left(D\right)\right)\cap (V(Q_1\cup Q_2)\setminus \{u,x_1,x_{k_1},y_1,y_{k_2}\})=\varnothing$. By Claim 9, $N_H\left(V\left(D\right)\right)\cap (V\left(Q_3\right)\setminus \{u,z_2,z_3\})=\varnothing$. By the choice of T, $N_H\left(V\left(D\right)\right)\cap \{x_{k_1},y_{k_2},z_{k_3}\}=\varnothing$. Therefore, $N_H\left(V\left(D\right)\right)\cap V\left(T\right)\subseteq \{x_1,y_1,z_2,z_3,u\}$.

Moreover, suppose, by contradiction, that there exists an element $D_0\in \mathcal{D}\left(T\right)$ such that $N_H\left(V\left(D_0\right)\right)\cap V\left(T\right)\ne \left\{u\right\}$ and $D_0\ncong K_1$. Note that $N_H\left(V\left(D_0\right)\right)\cap V\left(T\right)\ne \varnothing$ and $N_H\left(V\left(D_0\right)\right)\cap V\left(T\right)\subseteq \{x_1,y_1,z_2,z_3,u\}$. Then there exist a vertex $v_0\in \{x_1,y_1,z_2,z_3\}$ such that $v_0\in N_H\left(V\left(D_0\right)\right)\cap V\left(T\right)$. Then, by Claim 5, $H[V\left(D_0\right)\cup \left\{v_0\right\}]$ contains a path $P_{v_0}=v_0{v}_1{v}_2$ starting from $v_0$ such that $\{v_1,v_2\}\subseteq V\left(D_0\right)$. By Claim 9, $v_0\notin \{z_2,z_3\}$. Then we only consider the case that $v_0\in \{x_1,y_1\}$. By Claim A.2 again, $k_1<3$ or $k_2<3$, contradicting the choice of $T_{k_1,k_2,k_3}\left(u\right)$. □

Claim 11.$d_{H-\left\{u\right\}}\left(v\right)=1$ for every vertex $v\in N_{\mathcal{D}\left(T\right)}(V\left(Q_i\right)\setminus \left\{u\right\})$ for $i\in \{1,2,3\}$.

Proof. 

Suppose, by contradiction, that there exists a vertex $v_0\in N_{\mathcal{D}\left(T\right)}(V\left(Q_i\right)\setminus \left\{u\right\})$ for $i\in \{1,2,3\}$ with $d_{H-\left\{u\right\}}\left(v_0\right)>1$. By Claim10, $v_0$ has no neighbor outside $V\left(T\right)$ and $N_{H-\left\{u\right\}}\left(v_0\right)\subseteq \{x_1,y_1,z_2,z_3\}$. Since H is $K_3$-free, $|N_{H-\left\{u\right\}}\left(v_0\right)\cap \{z_2,z_3\}|\le 1$. It means that $|N_{H-\left\{u\right\}}\left(v_0\right)\cap \{x_1,y_1\}|\ge 1$. Since H is $K_3$-free, $v_0\notin \{u^1,u^2,u^3\}$.

Suppose first that $|N_{H-\left\{u\right\}}\left(v_0\right)\cap \{z_2,z_3\}|=0$. Then $N_{H-\left\{u\right\}}\left(v_0\right)\subseteq \{x_1,y_1\}$. Then $H\left[\{u{u}^1,u{u}^2,u{u}^3,x_2{x}_1,x_1{v}_0,v_0{y}_1,y_1{y}_2,z_1{z}_2\}\right]$ is an $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction.

Suppose now that $|N_{H-\left\{u\right\}}\left(v_0\right)\cap \{z_2,z_3\}|=1$. Then $N_{H-\left\{u\right\}}\left(v_0\right)\cap \{x_1,y_1\}\ne \varnothing$. Without loss of generality, we assume that $v_0{x}_1\in E\left(H\right)$. Then $H[V(Q_1\cup Q_3\cup Q_2)\setminus \left\{u\right\})]$ contains a subgraph $F\cong P_5\cup K_2$. Then $H\left[\{u{u}^1,u{u}^2,u{u}^3,E\left(F\right)\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. □

Claim 12. each element of $\{Q_1^{\prime },Q_2^{\prime },Q_3^{\prime }\}$ is the component of $H-\left\{u\right\}$.

Proof. 

By contradiction, suppose that there exists a pair of vertices $x_0\in V\left(Q_i^{\prime }\right)$ for $i\in \{1,2,3\}$, $y_0\in V\left(Q_j^{\prime }\right)$ for $j\in \{1,2,3\}\setminus \left\{i\right\}$ such that $x_0{y}_0\in E\left(H\right)$. Then, by Claim11, $x_0\in V\left(Q_i\right)\setminus \left\{u\right\}$ for $i\in \{1,2,3\}$ and $y_0\in V\left(Q_j\right)\setminus \left\{u\right\}$ for $j\in \{1,2,3\}\setminus \left\{i\right\}$.

Suppose, first, that $i,j\in \{1,2\}$. Without loss of generality, we assume that $i=1$ and $j=2$. First, we assume that $x_0\in \{x_{k_1},x_{k_1-1}\}$ and $y_0\in \{y_{k_2},y_{k_2-1}\}$. If each component of ${\mathcal{D}}_T\left(u\right)$ is trivial component, then, by Claim 10, a cycle C can be found in $H[V(Q_1\cup Q_2)\cup \left\{u\right\}]$ passing through u that dominates $E\left(H[V(Q_1^{\prime }\cup Q_2^{\prime })\cup \left\{u\right\}]\right)$. By Claim 10 again, $H\left[E(C\cup Q_3)\right]$ is a dominating trail of H, a contradiction. This indicates that there exists at least one component D (say) in $\mathcal{D}\left(u\right)$ with it is non-trivial component, then $H\left[V\right(D)\cup \{u\left\}\right]$ contains a path P of length at least two with starting from u. Note that $x_0{y}_0\in E\left(H\right)$. Then $H\left[V(Q_1\cup Q_2)\right]$ contains a path ${\widehat{Q}}_2$ starting from u that it longer than $Q_2$. We can construct a new $T_{k_1,k_2,k_3}^{\prime }\left(u\right)=\{P,{\widehat{Q}}_2,Q_3\}$ larger than T, which is opposite to the choice to T. Now, we assume that $x_0\notin \{x_{k_1},x_{k_1-1}\}$ or $y_0\notin \{y_{k_2},y_{k_2-1}\}$. Then $H[V(Q_1\cup Q_2)\setminus \left\{u\right\}]$ contains a path $P_5$. Then $H\left[\{u{u}^1,u{u}^2,u{u}^3,E\left(P_5\right),z_1{z}_2\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction.

Suppose, now, that $i\in \{1,2\}$ and $j=3$. Then $H[V(Q_1\cup Q_2\cup Q_3)\setminus \left\{u\right\}]$ contains a subgraph $F\cong P_5\cup K_2$. Then $H\left[\{u{u}^1,u{u}^2,u{u}^3,E\left(F\right)\}\right]$ is a $L^{-1}(K_3\cup P_4\cup K_1)$, a contradiction. □

Let $D_1,\dots ,D_t$ be all the non-trivial components of $H-\left\{u\right\}$. By Claim 12, $\{Q_1^{\prime },Q_2^{\prime },Q_3^{\prime }\}\subseteq \{D_1,\dots ,D_t\}$ and $t\ge 3$. Let $D_1=Q_3^{\prime }$, $D_2=Q_2^{\prime }$ and $D_3=Q_1^{\prime }$. By Claims 6,9, $D_i$ is isomorphic to a connected subgraph of $C_4$ for $i\in \{2,3\}$. Note that $D_4,\dots ,D_t$ also are components of $H-T$. Then, by Claim 5, each element of $\{D_4,\dots ,D_t\}$ is isomorphic to a connected subgraph of $C_4$. Therefore, $D_i$ is isomorphic to a connected subgraph of $C_4$ for $i\in \{2,\dots ,t\}$. Let $D_i^{\prime }=H[V\left(D_i\right)\cup \left\{u\right\}]$ for $i\in \{1,\dots ,t\}$ and $\mathcal{D}=\{D_1^{\prime },\dots ,D_t^{\prime }\}$.

Claim 13. For $i\in \{1,\dots ,t\}$, either $D_i^{\prime }$ contains a cut edge of H that is not pendent or there exists a cycle $C_i$ in $D_i^{\prime }$ passing through u that dominates $E\left(D_i^{\prime }\right)$.

Proof. 

We assume on the contrary that $D_i^{\prime }$ does not contain a cut edge of H that is not pendent. We will show that there exists a cycle $C_i$ in $D_i^{\prime }$ passing through u that dominates $E\left(D_i^{\prime }\right)$. Note that $D_i$ is a non-trivial components of $H-\left\{u\right\}$. Then

$$N_H\left(V\left(D_i\right)\right)\cap V(H\setminus D_i)=\left\{u\right\}fori\in \{1,\dots ,t\}$$

(A1)

Suppose first that $i=1$. Since H is $K_3$-free, $u{z}_2\notin E\left(H\right)$. Note that the edge $z_2{z}_3$ is not a cut edge of H. Then, by (A1), $N_H\left(u\right)\cap (V\left({\mathcal{D}}_T\left(z_3\right)\right)\cup \{z_3,z_4\})\ne \varnothing$. Then, by Claim 11, a cycle $C_1$ can be found in $D_1^{\prime }$ passing through u that dominates $E\left(D_1^{\prime }\right)$.

Suppose now that $i\in \{2,\dots ,t\}$. Note that H is $K_3$-free and $D_i^{\prime }$ does not contain a cut edge of H that is not pendent. Then, by (A1), $D_i\ncong K_2$. Since $D_i$ is isomorphic to a connected subgraph of $C_4$ for $i\in \{2,\dots ,t\}$, $D_i\in \{P_3,P_4,C_4\}$. Note that H is $K_3$-free and $D_i^{\prime }$ does not contain a cut edge of H that is not pendent. Then, by (A1), a cycle $C_i$ can be found in $D_i^{\prime }$ passing through u that dominates $E\left(D_i^{\prime }\right)$. □

Claim 14. For $i\in \{1,\dots ,t\}$, if $D_i^{\prime }$ contains a cut edge of H that is not pendent, then $D_i^{\prime }$ has a dominating path $P^i$ with one end is u that dominates $E\left(D_i^{\prime }\right)$.

Proof. 

Suppose first that $i=1$. Then, by Claim 11, $D_1^{\prime }$ has a dominating path $P^1=z_4{z}_3{z}_2{z}_{1}u$ terminating at u that dominates $E\left(D_1^{\prime }\right)$.

Suppose now that $i\in \{2,\dots ,t\}$. Note $D_i$ is isomorphic to a connected subgraph of $C_4$ for $i\in \{2,\dots ,t\}$. Then $D_i\cup \left\{u\right\}$ has a dominating path $P^i$ of $D_i^{\prime }$ which terminates at u for $i\in \{2,\dots ,t\}$. □

By Lemma A2, there exists at most two element of $\mathcal{D}$ which contains cut edges in H that is not pendent. Firstly, we assume that no element of $\mathcal{D}$ contains cut edges in H that is not pendent. It means that all cut edges in H are pendent. Then, by Claim 13, we can find a dominating trail $T_1=H\left[{\bigcup }_{i=1}^{t}E\left(C_i\right)\right]$ that dominates every edge in H, a contradiction.

Secondly, suppose that there exists exactly one element of $\mathcal{D}$ which contains cut edges in H that is not pendent, say $D_k^{\prime }$ for $k\in \{1,\dots ,t\}$. Then, by Claim 13, $H\setminus D_k$ contains a closed trail $T_2=H[{\bigcup }_{i=1}^{t}E\left(C_i\right)\setminus E\left(C_k\right)]$ starting at u and terminating at u that dominates $E(H\setminus D_k)$. By Claim 14, we can find a dominating trail $T=H\left[E(T_2\cup P^k)\right]$ that dominates every edge in H, a contradiction.

Finally, suppose that there are exactly exactly two elements of $\mathcal{D}$ which contains cut edges in H that is not pendent, say $D_{k_1}^{\prime }$ and $D_{k_2}^{\prime }$ for $\{k_1,k_2\}\subseteq \{1,2,\dots ,t\}$. Then, by Claim 13, $H\setminus (D_{k_1}\cup D_{k_2})$ contains a closed trail $T_3=H[{\bigcup }_{i=1}^{t}E\left(C_i\right)\setminus E(C_{k_1}\cup C_{k_2})]$ starting at u and terminating at u that dominates $E(H\setminus (D_{k_1}\cup D_{k_2}))$. By Claim 14, we can find a dominating trail $T=H\left[E(P^{k_1}\cup P^{k_2}\cup T_3)\right]$ that dominates every edge in H, a contradiction.

These contradictions imply that every connected $\{K_{1,3},K_3\cup P_4\cup K_1\}$-free block-chain of order at least 3482 is traceable. □

Proof of (5):

Let G be $\{K_{1,3},N_{1,1,1}\cup K_2\}$-free block-chain.

Note that $k_3\ge 4$. Then $k_3=4$. Otherwise, the subgraph $H\left[\{u{x}_1,x_1{x}_2,u{y}_1,y_1{y}_2,u{z}_1,z_1{z}_2\}\right]\cup H\left[\{z_3{z}_4,z_4{z}_5\}\right]$ is a $L^{-1}\left(N_{1,1,1}\right)\cup L^{-1}\left(K_2\right)$, a contradiction. This implies that $2\le k_1\le k_2\le k_3=4$

Claim 15. For any component $D\in \mathcal{D}\left(T\right)$, if $N_H\left(V\left(D\right)\right)\cap V(Q_1\cup Q_2)\ne \varnothing$, then $D\cong K_1$.

Proof. 

Suppose, by contradiction, that there exists an element $D_0\in \mathcal{D}\left(T\right)$ with $D_0\ncong K_1$. Then there exist a vertex $v_0\in V(Q_1\cup Q_2)$ such that $v_0\in N_H\left(V\left(D_0\right)\right)\cap V(Q_1\cup Q_2)$. Then, $H[V\left(D_0\right)\cup \left\{v_0\right\}]$ contains a path $P_{v_0}=v_0{v}_1{v}_2$ starting from $v_0$ such that $\{v_1,v_2\}\subseteq V\left(D_0\right)$. By the choice of $T_{k_1,k_2,k_3}\left(u\right)$, $v_0\notin \{x_{k_1},x_{k_1-1},y_{k_2},y_{k_2-1}\}$. Then $H[V(Q_1\cup Q_2)\cup \{v_1,v_2\}]$ contains a subgraph $F\cong T_{2,2,2}$. Then $H\left[\{E\left(F\right)\cup \{z_1{z}_2,z_2{z}_3\}\}\right]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. □

Claim 16. For any component $D\in \mathcal{D}\left(T\right)$, if $N_H\left(V\left(D\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})\ne \varnothing$, then $N_H\left(V\left(D\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})=\left\{z_2\right\}$. Moreover, D is isomorphic to $K_1$.

Proof. 

Suppose, by contradiction, that there exists a vertex $v_0\ne z_2$ with $v_0\in N_H\left(V\left(D\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})$. Note that $k_3=4$. Then $v_0\ne z_4$. Hence, $v_0\in \{z_1,z_3\}$. If $v_0=z_1$, then $H[V(Q_1\cup Q_2\cup D)\cup \left\{z_1\right\}]$ contains a subgraph $F_1\cong T_{2,2,2}$. Then $H\left[\{E\left(F_1\right)\cup \{z_2{z}_3,z_3{z}_4\}\}\right]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. This implies that $v_0=z_3$. Then $H[V\left(D\right)\cup \{z_3,z_4\}]$ contains a subgraph $F_2\cong P_3$. Then $H[\{u{x}_1,x_1{x}_2,u{y}_1,y_1{y}_2,u{z}_1,z_1{z}_2\}\cup E\left(F_2\right)]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction.

Moreover, suppose, by contradiction, that there exists a component $D_0\in \mathcal{D}\left(T\right)$ with $N_H\left(V\left(D_0\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})\ne \varnothing$ and $D_0$ is not isomorphic to $K_1$. Then there exist a vertex $v_0\in V\left(Q_3\right)\setminus \left\{u\right\}$ with $v_0\in N_H\left(V\left(D_0\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})$. Then, $H[V\left(D_0\right)\cup \left\{v_0\right\}]$ contains a path $P_{v_0}=v_0{v}_1{v}_2$ starting from $v_0$ with $\{v_1,v_2\}\subseteq V\left(D_0\right)$. By Claim 16, $v_0=z_2$. Then $H\left[V(D_0\cup Q_3)\right]$ contains a subgraph $F_3\cong T_{2,2,2}$. It is now easily seen that

$$H\left[V(H\setminus (D_0\cup Q_3))\right]doesnotcontainasubgraph{P}_3.$$

(A2)

By (A2), $k_1=k_2=2$ and ${\mathcal{D}}_T\left(v\right)=\varnothing$ for $v\in V(Q_1\cup Q_2)\setminus \left\{u\right\}$. Next, we will show that

$$eachelementof\{Q_1^{\prime },Q_2^{\prime },Q_3^{\prime }\}isthecomponentofH-\left\{u\right\}.$$

(A3)

Proof of (A3):

By contradiction, suppose that there exists a pair of vertices $x_0\in V\left(Q_i^{\prime }\right)$ for $i\in \{1,2,3\}$, $y_0\in V\left(Q_j^{\prime }\right)$ for $j\in \{1,2,3\}\setminus \left\{i\right\}$ such that $x_0{y}_0\in E\left(H\right)$. Note that ${\mathcal{D}}_T\left(v\right)=\varnothing$ for $v\in V(Q_1\cup Q_2)\setminus \left\{u\right\}$. Then, $x_0\in V\left(Q_i\right)\setminus \left\{u\right\}$ for $i\in \{1,2,3\}$ and $y_0\in V\left(Q_j\right)\setminus \left\{u\right\}$ for $j\in \{1,2,3\}\setminus \left\{i\right\}$. By (A2), we just need to consider the case $x_0\in V(Q_1\cup Q_2)\setminus \left\{u\right\}$ and $y_0\in V\left(Q_3\right)\setminus \left\{u\right\}$. Without loss of generality, we assume that $x_0\in V\left(Q_1\right)\setminus \left\{u\right\}$ and $y_0\in V\left(Q_3\right)\setminus \left\{u\right\}$. If $y_0\in \{z_1,z_2\}$, then, $H[V(D_0\cup Q_1\cup Q_3)\setminus \left\{u\right\}]$ contains a subgraph $F_4\cong T_{2,2,2}$. Then $H[\{u{y}_1,y_1{y}_2\}\cup E\left(F_4\right)]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. This implies that $y_0\in \{z_3,z_4\}$. Note that $k_1=k_2=2$. Then, by Claims 15,16 we can find a dominating trail T that dominates every edge in H, a contradiction. This implies that (A3) holds. □

Note that $k_1=k_2=2$. Then, by (A3), the edges $\left\{u{x}_1\right\}$ and $\left\{u{y}_1\right\}$ are the cut edges of H. Note that $H[V\left(D_0\right)\cup \left\{z_2\right\}]$ contains a path $P_{z_2}=z_2{v}_1{v}_2$ starting from $z_2$ such that $\{v_1,v_2\}\subseteq V\left(D_0\right)$. By Lemma A2, the edges $\left\{z_2{v}_1\right\}$ and $\left\{z_2{z}_3\right\}$ are not the cut edges of H. Then $N\left(u\right)\cap \{v_1,v_2\}\ne \varnothing$ and $N\left(u\right)\cap \{z_3,z_4\}\ne \varnothing$. We assume that $u^{\prime }\in N\left(u\right)\cap \{v_1,v_2\}$ and $u^{″}\in N\left(u\right)\cap \{z_3,z_4\}$.

$$ForanycomponentD\in \mathcal{D}\left(T\right)\setminus \left\{D_0\right\},D\cong K_1.$$

(A4)

Proof of (A4):

Otherwise, there exist a component $D_1\in \mathcal{D}\left(T\right)\setminus \left\{D_0\right\}$ such that $D_1$ is not isomorphic to $K_1$. By Claim 15, $N_H\left(V\left(D_1\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})\ne \varnothing$. By Claim 16, $N_H\left(V\left(D_1\right)\right)\cap (V\left(Q_3\right)\setminus \left\{u\right\})=\left\{z_2\right\}$. Then, $H[V(D_0\cup D_1\cup Q_3)\setminus \left\{u\right\}]$ contains a subgraph $F_5\cong T_{2,2,2}$. Then $H[\{u{y}_1,y_1{y}_2\}\cup E\left(F_5\right)]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. This implies that (A4) holds. □

Then, by (A4) and Claim 16, we can find a cycle $C=u{u}^{″}{Q}_3{z}_2{P}_{v_0}{u}^{\prime }u$ in $Q_3^{\prime }$ passing through u that dominates $E\left(Q_3^{\prime }\right)$. By Claim 15, we can find a dominating trail $T^{\prime }=H\left[E(Q_1\cup Q_2\cup C)\right]$ that dominates every edge in H, a contradiction. This contradiction shows that Claim 16 holds. □

Let $X=\{x_{k_1},x_{k_1-1}\}\cup V\left({\mathcal{D}}_T\left(x_{k_1-1}\right)\right)$, $Y=\{y_{k_2},y_{k_2-1}\}\cup V\left({\mathcal{D}}_T\left(y_{k_2-1}\right)\right)$ and $Z=\{z_3,z_4\}$.

Claim 17.$N_H\left(u\right)\cap (X\cup Y\cup Z)=\varnothing$.

Proof. 

By contradiction, suppose that $N_H\left(u\right)\cap (X\cup Y\cup Z)\ne \varnothing$. If $N_H\left(u\right)\cap X\ne \varnothing$, then, by Claim 15, a cycle $C_1$ can be found in $Q_1^{\prime }$ passing through u that dominates $E\left(D_1^{\prime }\right)$. By Claims 15,16, we can find a dominating trail $H\left[E(C_1\cup Q_3\cup Q_2)\right]$ that dominates every edge in H, a contradiction. If $N_H\left(u\right)\cap Z\ne \varnothing$, then, by Claim 16, a cycle $C_2$ can be found in $Q_3^{\prime }$ passing through u that dominates $E\left(D_3^{\prime }\right)$. By Claims 15,16, we can find a dominating trail $H\left[E(C_3\cup Q_1\cup Q_2)\right]$ that dominates every edge in H, a contradiction. If $N_H\left(u\right)\cap Y\ne \varnothing$, then, by Claims 15,16, we can find a dominating trail that dominates every edge in H, a contradiction. □

Claim 18. Each element of $\{Q_1^{\prime },Q_2^{\prime },Q_3^{\prime }\}$ is the component of $H-\left\{u\right\}$.

Proof. 

By contradiction, suppose that there exists a pair of vertices $x_0\in V\left(Q_i^{\prime }\right)$ for $i\in \{1,2,3\}$, $y_0\in V\left(Q_j^{\prime }\right)$ for $j\in \{1,2,3\}\setminus \left\{i\right\}$ such that $x_0{y}_0\in E\left(H\right)$. First, we will show that

$$noedgehasoneendinV\left(Q_1^{\prime }\right)andoneendinV\left(Q_2^{\prime }\right).$$

(A5)

Proof of (A5):

Suppose, by contradiction, that $x_0\in V\left(Q_1^{\prime }\right)$ and $y_0\in V\left(Q_2^{\prime }\right)$. If $x_0\in X$ and $y_0\in Y$, then, by Claim 15, we can find a cycle $C_1$ in $H[V(Q_1^{\prime }\cup Q_2^{\prime })\cup \left\{u\right\}]$ passing through u that dominates $E\left(H[V(Q_1^{\prime }\cup Q_2^{\prime })\cup \left\{u\right\}]\right)$. By Claims 15,16, we can find a dominating trail $H\left[E(C_1\cup Q_3)\right]$ that dominates every edge in H, a contradiction. This implies that $x_0\notin X$ or $y_0\notin Y$. Without loss of generality, we assume that $x_0\notin X$. Then $k_1\in \{3,4\}$. Since H is $K_3$-free, $H[V(Q_1^{\prime }\cup Q_2^{\prime })\cup \{u,z_1\}]$ contains a subgraph $F_1\cong T_{2,2,2}$. Then $H[E\left(F_1\right)\cup \{z_2{z}_3,z_3{z}_4\}]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. This implies that (A5) holds. □

Next, we will prove that

$$noedgehasoneendinX\cup YandoneendinV\left(Q_3^{\prime }\right).$$

(A6)

Proof of (A6):

Suppose, by contradiction, that $x_0\in X\cup Y$ and $y_0\in V\left(Q_3^{\prime }\right)$. Without loss of generality, we assume that $x_0\in X$. If $y_0\in Z$, then, by Claims 15,16, we can find a cycle $C_2$ in $H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]$ passing through u that dominates $E\left(H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]\right)$. By Claims 15,16, we can find a dominating trail $H\left[E(C_2\cup Q_2)\right]$ that dominates every edge in H, a contradiction. This implies that $y_0\notin Z$. By Claim 16, $z_1$ has no neighbor outside $T_{k_1,k_2,k_3}\left(u\right)$. We can find a path P in $H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]$ starting with u that dominates $E\left(H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]\right)$. By Claim 15, we can find a dominating trail $H\left[E(P\cup Q_2)\right]$ that dominates every edge in H, a contradiction. This implies that (A6) holds. □

Then we will prove that

$$noedgehasoneendinV(Q_1^{\prime }\cup Q_2^{\prime })andoneendinZ.$$

(A7)

Proof of (A7):

Suppose, by contradiction, that $x_0\in V(Q_1^{\prime }\cup Q_2^{\prime })$ and $y_0\in Z$. Without loss of generality, suppose that $x_0\in V\left(Q_1^{\prime }\right)$. By (A6), $x_0\notin X$. Then $k_1\in \{3,4\}$. If $x_0\in \left\{x_1\right\}\cup V\left({\mathcal{D}}_T\left(x_1\right)\right)$, then, by Claims 15,16, we can find a path $P^{\prime }$ in $H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]$ from u to $x_{k_1}$ that dominates $E\left(H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]\right)$. By Claim 15, we can find a dominating trail $H\left[E(P^{\prime }\cup Q_2)\right]$ that dominates every edge in H, a contradiction. This implies that $k_1=4$ and $x_0\in \left\{x_2\right\}\cup V\left({\mathcal{D}}_T\left(x_2\right)\right)$. Then the vertex $x_1$ has no neighbor outside T. Otherwise, we can find a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. Combining this with Claims 15,16, we can find a path $P^{″}$ in $H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]$ from u to $x_{k_1}$ that dominates $E\left(H[V(Q_1^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\}]\right)$. By Claim 15, we can find a dominating trail $H\left[E(P^{″}\cup Q_2)\right]$ that dominates every edge in H, a contradiction. This implies that (A7) holds. □

By (A5)–(A7), $x_0\in V(Q_1^{\prime }\cup Q_2^{\prime })\setminus (X\cup Y)$ and $y_0\in V\left(Q_3^{\prime }\right)\setminus Z$. Without loss of generality, we assume that $x_0\in V\left(Q_1^{\prime }\right)$. Then, $k_2=2$. Otherwise, Then, $H[V(Q_1\cup Q_3]$ contains a subgraph $F_2\cong T_{2,2,2}$. Then $H[E\left(F_2\right)\cup (E\left(Q_2\right)\setminus \left\{u{y}_1\right\})]$ is a $L^{-1}(N_{1,1,1}\cup K_2)$, a contradiction. Note that $x_0\notin X$ and $y_0\notin Z$. Then there exists at least one path $\widehat{P}$ of length at most two from $x_i$ to $z_j$ for $i\le k_1-2$ and $j\in \{1,2\}$ such that $V\left(\widehat{P}\right)\cap V\left(T\right)=\{x_i,z_j\}$. Note that $k_2=2$. Then, by (A5) and (A6), the edge $u{y}_1$ is a cut edge of H. By Lemma A2, the edge set $\{\left\{x_{k_1-1}{x}_{k_1-2}\right\},\left\{z_2{z}_3\right\}\}$ has at least one element that is not the cut edge of H. Suppose, first, that $x_{k_1-1}{x}_{k_1-2}$ is not the cut edge in H. By Claim 17, (A5) and (A6), $N\left(X\right)\cap (V(Q_2^{\prime }\cup Q_3^{\prime })\cup \left\{u\right\})=\varnothing$. Since H is $K_3$-free, $N\left(x_{k_1-2}\right)\cap X=\varnothing$. Then $k_1=4$ and $N\left(x_{k_1-3}\right)\cap X\ne \varnothing$. By Claims 15,16, we can find a dominating trail that dominates every edge in H, a contradiction. Suppose, now, that $z_2{z}_3$ is not the cut edge in H. By Claim 17, (A7), $N\left(Z\right)\cap (V(Q_1^{\prime }\cup Q_2^{\prime })\cup \left\{u\right\})=\varnothing$. Since H is $K_3$-free, by Claim 16, $z_4{z}_1\in E\left(H\right)$. By Claims 15,16, we can find a dominating trail that dominates every edge in H, a contradiction. These contradictions show that Claim 18 holds. □

By Claim 18, $N_H\left(V\left(Q_i^{\prime }\right)\right)\cap V(H\setminus Q_i^{\prime })=\left\{u\right\}$ for $i\in \{1,2,3\}$. By Claim 17, $N_H\left(u\right)\cap (X\cup Y\cup Z)=\varnothing$. Then, it is not difficult to find that every $D_i^{\prime }$ contains a cut edge of H that is not pendent, contradicting Lemma A2. This contradiction shows that $\{K_{1,3},N_{1,1,1}\cup K_2\}$-free block-chain is traceable. □

Proof of (6):

Let G be $\{K_{1,3},N_{1,1,2}\cup K_1\}$-free block-chain. Then we will show that G is isomorphic to a member of ${\mathcal{G}}_0$.

Note that $k_3\ge 4$. Then $k_3=4$. Otherwise, the subgraph $H\left[\{u{x}_1,x_1{x}_2,u{y}_1,y_1{y}_2,u{z}_1,z_1{z}_2,z_2{z}_3\}\right]\cup H\left[\left\{z_4{z}_5\right\}\right]$ is a $L^{-1}\left(N_{1,1,2}\right)\cup L^{-1}\left(K_1\right)$, a contradiction. This implies that $2\le k_1\le k_2\le k_3=4$. Moreover, $k_1=k_2=2$. Otherwise, $H[V(Q_1\cup Q_2)\cup \{z_1,z_2\}]$ contains a subgraph $F\cong T_{2,2,3}$. Then $H\left[\{E\left(F\right)\cup \left\{z_3{z}_4\right\}\}\right]$ is a $L^{-1}(N_{1,1,2}\cup K_1)$, a contradiction. Then, $T=T_{2,2,4}\left(u\right)$. Furthermore,

$$N\left(z_2\right)\cap (V\left(H\right)\setminus V\left(T_{2,2,4}\left(u\right)\right))=\varnothing .$$

(A8)

Proof of (A8):

By contradiction, suppose that $z_2$ has a neighbor $z_2^{\prime }$ outside $V\left(T_{2,2,4}\left(u\right)\right)$, then the subgraph $H\left[\{u{x}_1,x_1{x}_2,u{y}_1,y_1{y}_2,u{z}_1,z_1{z}_2,z_2{z}_2^{\prime }\}\right]\cup H\left[\left\{z_3{z}_4\right\}\right]$ is a $L^{-1}\left(N_{1,1,2}\right)\cup L^{-1}\left(K_1\right)$, a contradiction. This implies that (A8) holds. □

Claim 19. For any component $D\in \mathcal{D}\left(T\right)$, $D\cong K_1$.

Proof. 

Suppose, by contradiction, that there exists an element $D_0\in \mathcal{D}\left(T\right)$ such that $D_0\ncong K_1$. Then there exist a vertex $v_0$ such that $v_0\in N_H\left(V\left(D_0\right)\right)\cap V\left(T_{2,2,4}\left(u\right)\right)$. Then $v_0\notin \{x_2,y_2,z_4\}$. By (A8), $v_0\ne z_2$. If $v_0=u$, then $H\left[V(Q_1\cup Q_3\cup D_0)\right]$ contains a subgraph $F_1\cong T_{2,2,3}$. Then $H[E\left(F_1\right)\cup \left\{y_1{y}_2\right\}]$ is a $L^{-1}(N_{1,1,2}\cup K_1)$, a contradiction. If $v_0=z_3$, then $H\left[V\left(D_0\right)\right]$ contains a subgraph $F_2\cong K_2$. Then $H[\{u{x}_1,x_1{x}_2,u{y}_1,y_1{y}_2,u{z}_1,z_1{z}_2,z_2{z}_3\}\cup E\left(F_2\right)]$ is a $L^{-1}(N_{1,1,2}\cup K_1)$, a contradiction. If $v_0\in \{x_1,y_1,z_1\}$, then $H[V(Q_1\cup Q_2\cup D_0)\cup \{z_1,z_2\}]$ contains a subgraph $F_3\cong T_{2,2,3}$. Then $H[E\left(F_3\right)\cup \left\{z_3{z}_4\right\}]$ is a $L^{-1}(N_{1,1,2}\cup K_1)$, a contradiction. □

Claim 20.$d\left(v\right)=1$ for any vertex $v\in N_{\mathcal{D}\left(T\right)}\left(V\left(Q_i\right)\right)$ for $i\in \{1,2\}$.

Proof. 

Suppose, by contradiction, that there exists a vertex $v_0\in N_{\mathcal{D}\left(T\right)}\left(V\left(Q_i\right)\right)$ for $i\in \{1,2\}$ with $d\left(v_0\right)>1$. Without loss of generality, suppose that $v_0\in N_{\mathcal{D}\left(T\right)}\left(V\left(Q_1\right)\right)$. By Claim 19, $N\left(v_0\right)\cap (V\left(H\right)\setminus V\left(T_{2,2,4}\left(u\right)\right))=\varnothing$. By (A8), $N\left(v_0\right)\subseteq \{x_1,y_1,u,z_1,z_3\}$. Since H is $K_3$-free, $|N\left(v_0\right)\cap \{x_1,u\}|=1$.

Suppose first that $|N\left(v_0\right)\cap \{z_1,z_3\}|=0$. Then $y_1\in N\left(v_0\right)$. Since H is $K_3$-free, $x_1\in N\left(v_0\right)$. By Claim 19, we can find a dominating trail $T_1=z_4{z}_3{z}_2{z}_{1}u{x}_1{v}_0{y}_1{y}_2$ that dominates every edge in H, a contradiction.

Suppose now that $|N\left(v_0\right)\cap \{z_1,z_3\}|\ne 0$. If $z_1\in N\left(v_0\right)$, then $x_1\in N\left(v_0\right)$. By Claim 19, we can find a dominating trail $T_2=z_4{z}_3{z}_2{z}_1{v}_0{x}_{1}u{y}_1{y}_2$ that dominates every edge in H, a contradiction. This implies that $z_3\in N\left(v_0\right)$. If $u\in N\left(v_0\right)$, then, by Claim 19, we can find a dominating trail $T_3=x_2{x}_{1}u{v}_0{z}_3{z}_2{z}_{1}u{y}_1{y}_2$ that dominates every edge in H, a contradiction. This implies that $x_1\in N\left(v_0\right)$. By Claim 19, we can find a dominating trail $T_4=x_2{x}_1{v}_0{z}_3{z}_2{z}_{1}u{y}_1{y}_2$ that dominates every edge in H, a contradiction. □

Claim 21.$E\left(H\left[V\left(T\right)\right]\right)\setminus E\left(T\right)=\left\{x_1{z}_2\right\}$ or $\left\{y_1{z}_2\right\}$.

Proof. 

First, we will show that

$$N\left(V\left(Q_i\right)\right)\cap \{z_3,z_4\}=\varnothing \mathrm{for}i\in \{1,2\}.$$

(A9)

Proof of (A9):

Suppose, by contradiction, that there exists a $Q_{i_0}$ with $N\left(V\left(Q_{i_0}\right)\right)\cap \{z_3,z_4\}\ne \varnothing$ for $i_0\in \{1,2\}$. Without loss of generality, we suppose that $N\left(V\left(Q_1\right)\right)\cap \{z_3,z_4\}\ne \varnothing$. If $N(V\left(Q_1\right)\setminus \left\{u\right\})\cap \{z_3,z_4\}\ne \varnothing$, then, by Claim 19, a cycle $C_1$ can be found in $Q_1\cup Q_3$ passing through u that dominates $E(Q_1\cup Q_3\cup {\mathcal{D}}_T(Q_1\cup Q_3))$. By Claim 19 again, we can find a dominating trail $H\left[E(Q_2\cup C_1)\right]$ that dominates every edge in H, a contradiction. This implies that $N\left(u\right)\cap \{z_3,z_4\}\ne \varnothing$, then, by Claim 19, a cycle $C_2$ can be found in $Q_3$ passing through u that dominates $E(Q_3\cup {\mathcal{D}}_T\left(Q_3\right))$. By Claim 19 again, we can find a dominating trail $H\left[E(Q_1\cup Q_2\cup C_2)\right]$ that dominates every edge in H, a contradiction. This implies that (A9) holds. □

Next, we will prove that

$$N\left(v\right)\cap \{z_1,z_2\}=\varnothing \mathrm{for}\mathrm{any}\mathrm{vertex}v\in \{x_2,y_2\}.$$

(A10)

Proof of (A10):

Suppose, by contradiction, that there exists a vertex $v_0\in \{x_2,y_2\}$ with $N\left(v_0\right)\cap \{z_1,z_2\}\ne \varnothing$. Without loss of generality, we assume that $N\left(x_2\right)\cap \{z_1,z_2\}\ne \varnothing$. If $x_2{z}_1\in E\left(H\right)$, then, by Claim 19, we can find a dominating trail $T_1=z_4{z}_3{z}_2{z}_1{x}_2{x}_{1}u{y}_1{y}_2$ that dominates every edge in H, a contradiction. This implies that $x_2{z}_2\in E\left(H\right)$. Then $N\left(z_1\right)\cap (V\left(H\right)\setminus V\left(T_{2,2,4}\left(u\right)\right))=\varnothing$. Otherwise, we can find an $L^{-1}(N_{1,1,2}\cup K_1)$. Therefore, we can find a dominating trail $T_2=z_4{z}_3{z}_2{x}_2{x}_{1}u{y}_1{y}_2$ that dominates every edge in H, a contradiction. This implies that (A10) holds. □

Now,

$$N\left(u\right)\cap V\left(T_{2,2,4}\left(u\right)\right)=\{x_1,y_1,z_1\}.$$

(A11)

Proof of (A11):

Suppose, by contradiction, that $N\left(u\right)\cap V\left(T_{2,2,4}\left(u\right)\right)\ne \{x_1,y_1,z_1\}$. Note that $\{x_1,y_1,z_1\}\subseteq N\left(u\right)\cap V\left(T_{2,2,4}\left(u\right)\right)$. Then there exists a vertex $v_0\in V\left(T_{2,2,4}\left(u\right)\right)\setminus \{x_1,y_1,z_1\}$ with $v_0\in N\left(u\right)\cap V\left(T_{2,2,4}\left(u\right)\right)$. Since H is $K_3$-free, $v_0\notin \{x_2,y_2,z_2\}$. This implies that $v_0\in \{z_3,z_4\}$. By Claim 19, a cycle C can be found in $Q_3$ passing through u that dominates $E(Q_3\cup {\mathcal{D}}_T\left(Q_3\right))$. By Claim 19 again, we can find a dominating trail $H\left[E(Q_1\cup Q_2\cup C)\right]$ that dominates every edge in H, a contradiction. This implies that (A11) holds. □

If $|N\left(z_2\right)\cap \{x_1,y_1\}|\ne 1$, then $|N\left(z_2\right)\cap \{x_1,y_1\}|\ge 1$. Otherwise, by Claim 20 and (A9)–(A11), the edges $u{x}_1$, $u{y}_1$ and $u{z}_1$ are cut edges of H that are not pendent, contradicting Lemma A2. This implies that $\{z_2{x}_1,z_2{y}_1\}\subseteq E\left(H\right)$. Then, by Claim 19, we can find a dominating trail $T=z_4{z}_3{z}_2{x}_{1}u{z}_1{z}_2{y}_1{y}_2$ that dominates every edge in H, a contradiction. This implies that Claim 21 holds. □

Claim 22.$d\left(v\right)=1$ for each vertex $v\in N_{\mathcal{D}\left(T\right)}\left(\{z_1,z_2,z_3\}\right)$.

Proof. 

Suppose, by contradiction, that there exists a vertex $v_0\in N_{\mathcal{D}\left(T\right)}\left(\{z_1,z_2,z_3\}\right)$ with $d\left(v_0\right)>1$. By Claim 19, $v_0$ has no neighbor outside $V\left(T_{k_1,k_2,k_3}\left(u\right)\right)$. By Claim 20, $N\left(v_0\right)\cap V(Q_1\cup Q_2)=\varnothing$. By (A8), $N\left(v_0\right)=\{z_1,z_3\}$. By Claim 21, $|N\left(z_2\right)\cap \{x_1,y_1\}|=1$. Without loss of generality, we assume that $z_2{x}_1\in E\left(H\right)$. Then, by Claim 19, there is a dominating trail $T=z_4{z}_3{v}_0{z}_1{z}_2{x}_{1}u{y}_1{y}_2$ that dominates every edge in H, a contradiction. □

${\mathcal{D}}_T\left(z_1\right)\ne \varnothing$. Otherwise, by Claim 19, we can find a dominating trail that dominates every edge in H, a contradiction. Therefore, by (A8) and Claims 19-22, H is isomorphic to a member of ${\mathcal{F}}_0$. That means G is isomorphic to a member of ${\mathcal{G}}_0$.

Appendix A.3. Proofs of Theorem 11

Proof of Theorem 11.

By contradiction, suppose that G is $\{K_{1,3},S\cup P_4\}$-free non-traceable block-chain with $\left|V\right(G\left)\right|$ is as small as possible for $S\in \{P_4,Z_1\}$ such that $\left|V\right(G\left)\right|\ge 212$. We use $Cut\left(G\right)$ to denote the set of vertices which is cut vertex of G. Let F be a subgraph of G and $\mathcal{D}(F,G)$ be the set of all components of $G-F$ and ${\mathcal{D}}_F(v,G)=\{D:D\in \mathcal{D}(F,G),N_G\left(v\right)\cap V\left(D\right)\ne \varnothing \}$ for $v\in V\left(F\right)$.

Suppose that G is 2-connected. Note that G is $S\cup P_4$-free, then G must be $N_{1,1,5}$-free. By Theorem A6, G is traceable. Thus $Cut\left(G\right)\ne \varnothing$ and let $x\in Cut\left(G\right)$.

Claim 23. At least one element of $\mathcal{D}(x,G)$ consists of an isolated vertex if $x\in Cut\left(G\right)$.

Proof. 

Clearly, $\left|\mathcal{D}\right(x,G\left)\right|=2$; otherwise $x\cup \left(N\right(x)\cap V(\mathcal{D}(x,G)\left)\right)$ will induce a claw. Let $\{H_1,H_2\}=\mathcal{D}(x,G)$. Suppose that $\left|V\right(H_1\left)\right|\ge 2$ and $\left|V\right(H_2\left)\right|\ge 2$. For $i=1,2$, let $y_i\in N_{H_i}\left(x\right)$, and let $G_i$ be the subgraph of G induced by $H_i\cup \{x,y_{3-i}\}$. It is not hard to see that $G_i$ is a block-chain, and that $\left\{y_{3-i}\right\}=N_{G_i}\left(x\right)$. By selecting G, $G_i$ contains a Hamilton path $Q_i$ (starting from $y_{3-i}$). Then $H_i\cup \left\{x\right\}$ contains a Hamilton path $Q_i^{\prime }=Q_i-y_{3-i}$ which starts from x. Thus G contains a Hamilton path $Q_1^{\prime }x{Q}_2^{\prime }$, a contradiction. □

Let $x\in Cut\left(G\right)$, and let $y\in \mathcal{D}(x,G)$. It is not hard to see that $\{x,y\}$ induce the subgraph which is an end-block of G. If $\left|Cut\right(G\left)\right|\ge 3$, then there will be at least three end-blocks of G, a contradiction. Thus $\left|Cut\right(G\left)\right|\le 2$.

By Theorem A1, let H be a triangle-free graph with $G=L\left(H\right)$. Recall that G is traceable if and only if H contains a dominating trail. Then by the choice of G, H does not contain a dominating trail. Let $c_v\left(G\right)$ be the length of the longest cycle of G passing through v. Let $G^{\prime }=G-y$ and $H^{\prime }$ be the subgraph of H corresponding to $G^{\prime }$ and let $e,e_0$ be the edges of H corresponding to the vertices $y,x$ of G, respectively. Denote $e=v^{″}{v}^{\prime }$ and $e_0=v^{\prime }{v}_0$. Let $C_{v_0}=v_0{v}_1{v}_2\dots v_{\left|V\right(C_{v_0}\left)\right|-1}{v}_0$ be a longest cycle of H passing through $v_0$.

Fact 1.$c_{v_0}\left(H\right)\le 5$.

Proof. 

By contradiction, suppose that $c_{v_0}\left(H\right)>5$. First, we will prove that

$$\left|V\right(C_{v_0}\left)\right|<8.$$

(A12)

Proof of (A12):

By contradiction, suppose that $\left|V\right(C_{v_0}\left)\right|\ge 8$. Next, we will prove that H includes $S\cup P_4$ as a subgraph, thus arriving a contradiction in all cases. If $S=P_4$, then $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_1,v_1{v}_2\}\right]\cup H\left[\{v_3{v}_4,v_4{v}_5,v_5{v}_6,v_6{v}_7\}\right]$ is a $L^{-1}\left(P_4\right)\cup L^{-1}\left(P_4\right)$. If $S=Z_1$, then there are two paths in $C_{v_0}$ starting $v_0$ of length 1. Let $v_0{v}_1$ and $v_0{v}_{\left|V\right(C_{v_0}\left)\right|-1}$ be such two paths. Note that $\left|V\right(C_{v_0}\left)\right|\ge 8$. Then $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_1,v_0{v}_{\left|V\right(C_{v_0}\left)\right|-1}\}\right]\cup H\left[\{v_2{v}_3,v_3{v}_4,v_4{v}_5,v_5{v}_6\}\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$. This implies that (A12) holds. □

By (A12), $6\le c_{v_0}\left(H\right)\le 7$. Let $X=V\left(C_{v_0}\right)\cup \{v^{\prime },v^{″}\}$.

Suppose, first, that $S=P_4$.

Claim 24.$N\left(u\right)\cap \left(V\right(H)\setminus X)=\varnothing$ for any $u\in N\left(v_i\right)\cap (V\left(H\right)\setminus X)$, for $i\in \{0,1,3\}$.

Proof. 

By contradiction, suppose that there is a vertex $u_0\in N\left(v_i\right)\cap (V\left(H\right)\setminus X)$ with $N\left(u_0\right)\cap (V\left(H\right)\setminus X)\ne \varnothing$ for $i\in \{0,1,3\}$. We assume that $u_1\in N\left(u_0\right)\cap (V\left(H\right)\setminus X)$. Then

$$\begin{array}{c}\left\{\begin{array}{cc}H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{u}_0,u_0{u}_1)\right\}]\cup H\left[\{v_1{v}_2,v_2{v}_3,v_3{v}_4,v_4{v}_5\}\right],\hfill & \mathrm{if}{u}_0=v_0,\hfill \\ H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_{\left|V\right(C_{v_0}\left)\right|-1},v_{\left|V\right(C_{v_0}\left)\right|-1}{v}_{\left|V\right(C_{v_0}\left)\right|-2}\}\right]\cup H\left[\{u_1{u}_0,u_0{v}_1,v_1{v}_2,v_2{v}_3\}\right],\hfill & \mathrm{if}{u}_0=v_1,\hfill \\ H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_{\left|V\right(C_{v_0}\left)\right|-1},v_{\left|V\right(C_{v_0}\left)\right|-1}{v}_{\left|V\right(C_{v_0}\left)\right|-2}\}\right]\cup H\left[\{u_1{u}_0,u_0{v}_3,v_3{v}_2,v_2{v}_1\}\right],\hfill & \mathrm{if}{u}_0=v_3,\hfill \end{array}\right.\hfill \end{array}$$

is a $L^{-1}\left(P_4\right)\cup L^{-1}\left(P_4\right)$, a contradiction. □

Claim 25.$\left|V\right(C_{v_0}\left)\right|=6$.

Proof. 

By contradiction, suppose that $\left|V\right(C_{v_0}\left)\right|\ge 7$. By (A12), $\left|V\right(C_{v_0}\left)\right|=7$. $N\left(u\right)\cap \left(V\right(H)\setminus X)=\varnothing$ for any $u\in N\left(v_2\right)\cap (V\left(H\right)\setminus X)$. Otherwise, suppose that there exist at least one vertex $u_0\in N\left(v_2\right)\cap (V\left(H\right)\setminus X)$ with $N\left(u_0\right)\cap (V\left(H\right)\setminus X)\ne \varnothing$. Then we assume that $u_1\in N\left(u_0\right)\cap (V\left(H\right)\setminus X)$. Then $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_6,v_6{v}_5\}\right]\cup H\left[\{u_1{u}_0,u_0{v}_2,v_2{v}_3,v_3{v}_4\}\right]$ is a $L^{-1}\left(P_4\right)\cup L^{-1}\left(P_4\right)$. Therefore, by symmetry and Claim 24, H contains a dominating trail $T=v^{″}{v}^{\prime }{C}_{v_0}$, a contradiction. □

Claim 26. For every component $D\in {\mathcal{D}}_{H\left[X\right]}(v_2,H)$, D has no $P_3$ as a subgraph such that one of end of $P_3$ is adjacent to $v_2$. Moreover, $H[V\left({\mathcal{D}}_{H\left[X\right]}(v_2,H)\right)\cup \left\{v_2\right\}]$ does not contain subgraph which is isomorphic to $P_5$.

Proof. 

Suppose, by contradiction, that there exists a path $P_3\in {\mathcal{D}}_{H\left[X\right]}(v_2,H)$ such that one of end of $P_3$ is adjacent to $v_2$. Let $P_3=y_1{y}_2{y}_3$ and $y_1{v}_2\in E\left(H\right)$. Then the $H\left[\{y_3{y}_2,y_2{y}_1,y_1{v}_2,v_2{v}_1\}\right]\cup H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_5,v_5{v}_4\}\right]$ is a $L^{-1}\left(P_4\right)\cup L^{-1}\left(P_4\right)$.

Suppose, by contradiction, that $H[V\left({\mathcal{D}}_{H\left[X\right]}(v_2,H)\right)\cup \left\{v_2\right\}]$ contains subgraph $F_1$ (say) which is isomorphic to $P_5$. Then $H\left[E\left(F_1\right)\right]\cup H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_5,v_5{v}_4\}\right)]$ is a $L^{-1}\left(P_4\right)\cup L^{-1}\left(P_4\right)$. □

If either each of element of ${\mathcal{D}}_{H\left[X\right]}(v_2,H)\cup {\mathcal{D}}_{H\left[X\right]}(v_4,H)$ is isomorphic to a subgraph of $P_1$, then by Claim 24, H contains a dominating trail $T=v^{″}{v}^{\prime }{C}_{v_0}$, a contradiction. Then, by Claim 26, there exists one element $D\in {\mathcal{D}}_{H\left[X\right]}(v_2,H)\cup {\mathcal{D}}_{H\left[X\right]}(v_4,H)$ such that D has a $P_2$ as a subgraph such that one of end of $P_2$ is adjacent to $v_2$ or $v_4$. Without loss of generality, we assume that one of end of $P_2$ is adjacent to $v_2$. Let $P_2=v_2^{\prime }{v}_2^{″}$ and $v_2^{\prime }{v}_2\in E\left(H\right)$. We can know that

$$N\left(\{v_1,v_3\}\right)\cap (V\left(H\right)\setminus (X\cup V\left(P_2\right)))=\varnothing$$

(A13)

Otherwise, we can find an $L^{-1}\left(P_4\right)\cup L^{-1}\left(P_4\right)$. Then, $v_4$ has a neighbor $v_4^{\prime }$ outside $X\cup V\left(P_2\right)$ and $v_4^{\prime }$ has a neighbor $v_4^{″}$ outside $X\cup V\left(P_2\right)$. Otherwise, by Claims 24, 26 and (A13), H contains a dominating trail $T=v^{″}{v}^{\prime }{v}_0{v}_5{v}_4{v}_3{v}_2{v}_2^{\prime }{v}_2^{″}$, a contradiction.

By Lemma A2, the number of cut edges in H that is not pendent is at most two and $H^{\prime }$ is the subgraph of H corresponding to $G^{\prime }$. Then, the number of cut edges in $H^{\prime }$ that is not pendent is at most one. Then, by symmetry and Claim 26, (A13), there is either a vertex v in $\{v_2^{\prime },v_4^{\prime }\}$ with $d_{H^{\prime }}\left(v\right)>2$ or a vertex u in $\{v_2^{″},v_4^{″}\}$ with $d_{H^{\prime }}\left(u\right)>1$.

(1)

There is a vertex v in $\{v_2^{\prime },v_4^{\prime }\}$ with $d_{H^{\prime }}\left(v\right)>2$. Without loss of generality, we assume that $d_{H^{\prime }}\left(v_2^{\prime }\right)>2$. By Claim 24, $\{v_0,v_5\}\cap N\left(v_2^{\prime }\right)=\varnothing$. Since $g\left(G\right)\ge 4$, $N\left(v_2^{\prime }\right)\cap \{v_1,v_3\}=\varnothing$. By Claim 26, $\{v_4,v_4^{\prime },v_4^{″}\}\cap N\left(v_2^{\prime }\right)=\varnothing$. Then, $d_{H^{\prime }}\left(v_2^{\prime }\right)=2$, contradicting $d_{H^{\prime }}\left(v_2^{\prime }\right)>2$.

(2)

There is a vertex u in $\{v_2^{″},v_4^{″}\}$ with $d_{H^{\prime }}\left(u\right)>1$. Without loss of generality, we assume that $d_{H^{\prime }}\left(v_2^{″}\right)>1$. By Claim 24, $\{v_0,v_1,v_3,v_5\}\cap N\left(v_2^{″}\right)\ne \varnothing$. By Claim 26, $\{v_4,v_4^{\prime },v_4^{″}\}\cap N\left(v_2^{″}\right)\ne \varnothing$. Then, $d_{H^{\prime }}\left(v_2^{″}\right)=1$, contradicting $d_{H^{\prime }}\left(v_2^{″}\right)>1$.

These contradictions show that $c_{v_0}\left(H\right)\le 5$.

Suppose, now, that $S=Z_1$.

Claim 27.$\left|V\right({\mathcal{D}}_{H\left[X\right]}(v_i,H)\left)\right|\le 4$ for $i\in \{0,1,3\}$.

Proof. 

By contradiction, suppose that $\left|V\right({\mathcal{D}}_{H\left[X\right]}(v_i,H)\left)\right|\ge 5$ for $i\in \{0,1,3\}$.

First, we will show that $|{\mathcal{D}}_{H\left[X\right]}(v_i,H)|\le 1$. Otherwise, $|{\mathcal{D}}_{H\left[X\right]}(v_i,H)|>1$. Then there exist at least two vertices $\{v_i^{\prime },v_i^{″}\}\subseteq N\left(v_i\right)\cap (V\left(H\right)\setminus X)$, the

$$\begin{array}{c}\left\{\begin{array}{cc}H\left[\{v_0{v}^{\prime },v^{\prime }{v}^{″},v_0{v}_0^{\prime },v_0{v}_0^{″}\}\right]\cup H\left[\{v_1{v}_2,v_2{v}_3,v_3{v}_4,v_4{v}_5\}\right],\hfill & \mathrm{if}i=0,\hfill \\ H\left[\{v_1{v}_2,v_2{v}_3,v_1{v}_1^{\prime },v_1{v}_1^{″}\}\right]\cup H\left[\{v_{\left|V\right(C_{v_0}\left)\right|-2}{v}_{\left|V\right(C_{v_0}\left)\right|-1},v_{\left|V\right(C_{v_0}\left)\right|-1}{v}_0,v_0{v}^{\prime },v^{\prime }{v}^{″}\}\right],\hfill & \mathrm{if}i=1,\hfill \\ H[\{v_3{v}_4,v_4{v}_5,v_3{v}_3^{\prime },v_3{v}_3^{″}\}\cup H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_1,v_1{v}_2\}\right)],\hfill & \mathrm{if}i=3,\hfill \end{array}\right.\hfill \end{array}$$

is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. This contradiction implies that $|{\mathcal{D}}_{H\left[X\right]}(v_i,H)|\le 1$.

Let $\left\{D_i\right\}={\mathcal{D}}_{H\left[X\right]}(v_i,H)$. Then

$$d_D\left(u_i\right)\le 2foranyvertex{u}_i\in V\left(D_i\right).$$

(A14)

Proof of (A14):

Otherwise, there exists a vertex $u_{i_0}\in V\left(D_{i_0}\right)$ with $d_{D_{i_0}}\left(u_{i_0}\right)\ge 3$. Then

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}H[V\left(D_0\right)\cup \{v_0,v^{\prime }\}],\hfill & \mathrm{if}i=0,\hfill \\ H[V\left(D_1\right)\cup \{v_1,v_2\}],\hfill & \mathrm{if}i=1,\hfill \\ H[V\left(D_3\right)\cup \{v_3,v_2\}],\hfill & \mathrm{if}i=3,\hfill \end{array}\right.\end{array}$$

contains a subgraph $F\cong T_{1,1,2}$. Then

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}H\left[E\left(F\right)\right]\cup H\left[\{v_1{v}_2,v_2{v}_3,v_3{v}_4,v_4{v}_5\}\right],\hfill & \mathrm{if}i=0,\hfill \\ H\left[E\left(F\right)\right]\cup H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_{\left|V\right(C_{v_0}\left)\right|-1},v_{\left|V\right(C_{v_0}\left)\right|-1}{v}_{\left|V\right(C_{v_0}\left)\right|-2}\}\right],\hfill & \mathrm{if}i\in \{1,3\},\hfill \end{array}\right.\end{array}$$

is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. This implies that (A14) holds. □

$D_i$ does not contain a subgraph $P_5$. Otherwise, $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_1,v_0{v}_{\left|V\right(C_{v_0}\left)\right|-1}\}\right]\cup H\left[E\left(P_5\right)\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. Combining this with (A14), $\left|V\right({\mathcal{D}}_{H\left[X\right]}(v_i,H)\left)\right|\le 4$. □

Claim 28.$\left|V\right(C_{v_0}\left)\right|=6$.

Proof. 

By contradiction, suppose that $\left|V\right(C_{v_0}\left)\right|=7$. First, we will show that

$$N\left(v_i\right)\cap (V\left(H\right)\setminus X)=\varnothing fori\in \{2,5\}.$$

(A15)

Proof of (A15):

By symmetry, it just need to deal with $N\left(v_2\right)\cap (V\left(H\right)\setminus X)=\varnothing$. By contradiction, suppose that there exists at least one vertex $v_2^{\prime }\in N\left(v_2\right)\cap (V\left(H\right)\setminus X)$. Then $H\left[\{v_0{v}^{\prime },v^{\prime }{v}^{″},v_0{v}_1,v_0{v}_6\}\right]\cup H\left[\{v_2^{\prime }{v}_2,v_2{v}_3,v_3{v}_4,v_4{v}_5\}\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. This contradiction implies that (A15) holds. □

By Claim 27 and (A15), $n\left(H\right)\le 29$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 211$ and $n\left(G\right)\le 211$, contradicting $n\left(G\right)\ge 212$.

By Claim 28, $\left|V\right(C_{v_0}\left)\right|=6$. Then $N\left(u\right)\cap \left(V\right(H)\setminus X)=\varnothing$ for any vertex $u\in N\left(v_2\right)\cap (V\left(H\right)\setminus X)$. Otherwise, there exists at least one vertex $v_2^{\prime }\in N\left(v_2\right)\cap (V\left(H\right)\setminus X)$ with $N\left(v_2^{\prime }\right)\cap (V\left(H\right)\setminus X)\ne \varnothing$. We assume that $v_2^{″}\in N\left(v_2^{\prime }\right)\cap (V\left(H\right)\setminus X)$, then $H\left[\{v_2{v}_2^{\prime },v_2^{\prime }{v}_2^{″},v_2{v}_3,v_2{v}_1\}\right]\cup H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_5,v_5{v}_4\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

Suppose first that $\mid N\left(v_2\right)\cap (V\left(H\right)\setminus X)\mid \le 1$ and $\mid N\left(v_4\right)\cap (V\left(H\right)\setminus X)\mid \le 1$. By Claims 27, $n\left(H\right)\le 26$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 169$ and $n\left(G\right)\le 169$, contradicting $n\left(G\right)\ge 212$.

Suppose now that $\mid N\left(v_2\right)\cap (V\left(H\right)\setminus X)\mid >1$ or $\mid N\left(v_4\right)\cap (V\left(H\right)\setminus X)\mid >1$. By symmetry, it suffices to consider that $\mid N\left(v_2\right)\cap (V\left(H\right)\setminus X)\mid >1$. Then $N\left(v_i\right)\cap (V\left(H\right)\setminus X)=\varnothing$ for $i\in \{0,1,3,5\}$. Otherwise, we also can find an $L^{-1}(Z_1\cup P_4)$. Then H contains a dominating trail $T=v^{″}{v}^{\prime }{C}_{v_0}$, a contradiction.

These contradictions show that $c_{v_0}\left(H\right)\le 5$. Therefore, Fact 1 holds. □

Claim 29.$c\left(H\right)\le 5$.

Proof. 

By contradiction, suppose that $c\left(H\right)>5$. Let $C=x_1{x}_2\dots x_{c\left(H\right)-1}{x}_1$ be a longest cycle of H. Note that there are at most two cut vertices in G. Then, by Claim 23, H contains at least a maximal 2-connected subgraph $H_1$ such that $v_0\in V\left(H_1\right)$. It is easy to see that $C\subseteq H_1$. Otherwise we can find a $S\bigcup P_5$ in H for $S\in \{P_5,T_{1,1,2}\}$. By Fact 1, $v_0\notin V\left(C\right)$. By Fan Lemma, there exists a $(v_0,V\left(C\right))$-fan $\{L_1,L_2\}$ of width 2 in $H_1$. Then $\left|V\right(C_{v_0}\left)\right|=5$. Otherwise, by Fact 1, $\left|V\right(C_{v_0}\left)\right|=4$. Then it will produce a cycle of length at least 5 passing through $v_0$, a contradiction.

Note that $\left|V\right(C_{v_0}\left)\right|=5$ and $c\left(H\right)>5$. Then $c\left(H\right)=6$ and $L_i$ is an edge between the vertex $v_0$ and C for $i\in \{1,2\}$. Otherwise, it will produce a cycle of length at least 6 passing through $v_0$, a contradiction. Without loss of generality, we assume that $L_1=v_0{x}_1$ and $L_2=v_0{x}_4$. Let $Z=V\left(C\right)\cup \{v^{″},v^{\prime },v_0\}$.

Suppose, first, that $S=P_4$. We will prove that

$$N\left(V\right(C\left)\right)\cap \left(V\right(H)\setminus Z)=\varnothing .$$

(A16)

Proof of (A16):

Otherwise, there exists a vertex $x\in N\left(V\right(C\left)\right)\cap \left(V\right(H)\setminus Z)$. By symmetry, we just need to consider the case x is the neighbor of $x_1$ or $x_2$. If x is the neighbor of $x_1$, then $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{x}_1,x_{1}x)\right\}]\cup H\left[\{x_2{x}_3,x_3{x}_4,x_4{x}_5,x_5{x}_6\}\right]$ is a $L^{-1}(P_4\cup P_4)$, a contradiction. If x is the neighbor of $x_2$, then $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{x}_1,x_1{x}_6\}\right]\cup H\left[\{x{x}_2,x_2{x}_3,x_3{x}_4,x_4{x}_5\}\right]$ is a $L^{-1}(P_4\cup P_4)$, a contradiction. These imply that (A16) holds. □

$N\left(u\right)\cap \left(V\right(H)\setminus Z)=\varnothing$ for any vertex $u\in N\left(v_0\right)\cap (V\left(H\right)\setminus Z)$. Otherwise, there exists at least one vertex $u_0\in N\left(v_0\right)\cap (V\left(H\right)\setminus Z)$ such that $N\left(u_0\right)\cap (V\left(H\right)\setminus Z)\ne \varnothing$. Let $u_1\in N\left(u_0\right)\cap (V\left(H\right)\setminus Z)$. Then $H\left[\{u_1{u}_0,u_0{v}_0,v_0{v}^{\prime },v^{\prime }{v}^{″}\}\right]\cup H\left[\{x_1{x}_2,x_2{x}_3,x_3{x}_4,x_4{x}_5\}\right]$ is a $L^{-1}(P_4\cup P_4)$. Then, by (A16), H contains a dominating trail $T=v^{″}{v}^{\prime }{v}_{0}C$, a contradiction. This implies that $c\left(H\right)\le 5$.

Suppose, now, that $S=Z_1$. $N\left(v_0\right)\cap (V\left(H\right)\setminus Z)=\varnothing$. Otherwise, there exists at least one vertex $v_0^{\prime }\in N\left(v_0\right)\cap (V\left(H\right)\setminus Z)$, then $H\left[\{v_0{v}^{\prime },v^{\prime }{v}^{″},v_0{v}_0^{\prime },v_0{x}_1\}\right]\cup H\left[\{x_2{x}_3,x_3{x}_4,x_4{x}_5,x_5{x}_6\}\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. Furthermore, $N\left(x_1\right)\cap (V\left(H\right)\setminus Z)=\varnothing$. Otherwise, there exists at least one vertex $x_1^{\prime }\in N\left(x_1\right)\cap (V\left(H\right)\setminus Z)$, then $H\left[\{x_1{x}_1^{\prime },x_1{x}_2,x_1{x}_6,x_6{x}_5\}\right]\cup H\left[\{x_3{x}_4,x_4{v}_0,v_0{v}^{\prime },v^{\prime }{v}^{″}\}\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. Next, $|{\mathcal{D}}_{H\left[Z\right]}(x_2,H)|\le 1$ and ${\mathcal{D}}_{H\left[Z\right]}(x_2,H)$ contains at most one element of $\{P_1,P_2\}$. Otherwise, we also can find a $L^{-1}(Z_1\cup P_4)$. It means that $n\left(H\right)\le 17$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 74$ and $n\left(G\right)\le 74$, contradicting $n\left(G\right)\ge 212$. This implies that $c\left(H\right)\le 5$. □

Note that $\left|Cut\right(G\left)\right|\le 2$. Then we should distinguish the following cases to prove Theorem 11.

Case 1.$\left|Cut\right(G\left)\right|=1$, say $\left\{x\right\}=Cut\left(G\right)$.

If $\left|V\right(G^{\prime }\left)\right|=2$, then the result is trivially true. Thus we suppose that $\left|V\right(G^{\prime }\left)\right|\ge 3$. If $Cut\left(G^{\prime }\right)\ne \varnothing$, say $y\in Cut\left(G^{\prime }\right)$ (note that $x\notin Cut\left(G^{\prime }\right)$), then $y\in Cut\left(G\right)$, a contradiction. So we assume that $G^{\prime }$ is 2-connected. Then $H^{\prime }$ is an essentially 2-edge-connected graph such that $g\left(H\right)\ge 4$. Let $H_0$ be the core of $H^{\prime }$.

If $H_0$ is 2-connected, then, by Fact 1, $c_{v_0}\left(H\right)\le 5$. By Claim 29 and Theorem A7, $H_0$ has a spanning trail that starts from $v_0$. Then H has a dominating trail, a contradiction. Therefore, $H_0$ has cut vertex of H.

We define $\Lambda \left(H^{\prime }\right)$ to be the set of the vertices in $H^{\prime }$ which are also vertices in $H_0$ and adjacent to a vertex of degree 1 in $H^{\prime }$. Let $B_1,B_2,$$\dots ,B_{t^{\prime }}$ be all the blocks of $H_0$ and $H\left(B_i\right)=B_i\cup \{e:e$ is a pendent edge of $H^{\prime }$ and e has one end in $V\left(B_i\right)\cap \Lambda \left(H^{\prime }\right)\}$. $H\left(B_i\right)$ is called a super-block of $H^{\prime }$. Note that $H_0$ is 2-edge-connected graph with $g\left(H\right)\ge 4$. Then $B_i$ is not isomorphic to $K_2$ for $i\in \{1,\dots ,t^{\prime }\}$. Let $\mathcal{B}\left(v_0\right)$ be the set of block of $H_0$ which contain the vertex $v_0$ and $Cut\left(H_0\right)$ be the set of cut vertices of $H_0$. By Fact 1, $4\le c_{v_0}\left(B_i\right)\le 5$ for $i\in \{1,\dots ,t^{\prime }\}$.

Claim 30. If $\left|V\right(C_{v_0}\left)\right|=4$, then $c\left(B_i\right)=4$ for any block $B_i\in \mathcal{B}\left(v_0\right)$. Moreover, $B_i\cong K_{2,t}$ for $t\ge 2$.

Proof. 

By contradiction, suppose that there exists at least one block $B_{i_0}\in \mathcal{B}\left(v_0\right)$ such that $c\left(B_{i_0}\right)\ge 5$. Let $C_{i_0}$ be a longest cycle of $B_{i_0}$. Then $v_0\notin V\left(C_{i_0}\right)$. By Fan Lemma, there exists a $(v_0,V\left(C_{i_0}\right))$-fan $\{L_1,L_2\}$ of width 2. Note that $\left|V\right(C_{v_0}\left)\right|=4$ and $c\left(B_{i_0}\right)\ge 5$. Then it will produce a cycle of length at least 5 passing through $v_0$, a contradiction.

Moreover, if $c\left(B_i\right)=4$, then it easy to check that $B_i\cong K_{2,t}$ for $t\ge 2$. Otherwise it will produce a cycle of length at least 5 in $B_i$, contradicting $c\left(B_i\right)=4$. □

Let ${\mathcal{B}}_1\left(v_0\right)=\{B\in \mathcal{B}\left(v_0\right):c_{v_0}\left(B\right)=4\}$ and ${\mathcal{B}}_2\left(v_0\right)=\{B\in \mathcal{B}\left(v_0\right):c_{v_0}\left(B\right)=5\}$. Then, by Claim 29, $\mathcal{B}\left(v_0\right)={\mathcal{B}}_1\left(v_0\right)\cup {\mathcal{B}}_2\left(v_0\right)$. Then We should tell the following two cases apart.

Case 1.1$S=P_4$.

Suppose first that $\left|\mathcal{B}\right(v_0\left)\right|=1$, say $\mathcal{B}\left(v_0\right)=B_1$. Note that $H_0$ has cut vertex. Then there exists at least one block say $B_2$ such that $B_2\ne B_1$ and $v_0\notin V(B_1\cap B_2)$. Then $c_{v_0}\left(B_1\right)=4$. Otherwise, by Fact 1, $c_{v_0}\left(B_1\right)=5$. Note that $g\left(B_2\right)\ge 4$. Then we can find a $P_5\bigcup P_5$, a contradiction. By Claim 30, $B_1\cong K_{2,t}$ for $t\ge 2$. It is easy to verify that $c\left(B_2\right)\le 5$ and $H_0=B_1\cup B_2$. Otherwise, we can find a $P_5\bigcup P_5$. Let $v\in V\left(B_1\right)\cup V\left(B_2\right)$. Then $v\ne v_0$. Let $C=v_0{v}_1{v}_2{v}_3{v}_0$ be a longest cycle of $B_1$ passing through $v_0$ and v.

$$Ifv\in \{v_1,v_2\},then{v}_3\in V_2\left(H\left(B_1\right)\right).$$

(A17)

Proof of (A17):

By contradiction, suppose that there is at least one vertex $v_3^{\prime }\in V\left(H\left(B_1\right)\right)\setminus \{v_0,v_2\}$ and $v_3{v}_3^{\prime }\in E\left(H\left(B_1\right)\right)$. Note that $g\left(B_2\right)\ge 4$. Then $H[V\left(B_2\right)\cup \{v_1,v_2\}]$ contains a subgraph $F\cong P_5$. Then the subgraph formed by $v^{″}{v}^{\prime }{v}_0{v}_3{v}_3^{\prime }$ and $P_5$ is an $L^{-1}(P_4\cup P_4)$, a contradiction. This implies that (A17) holds. □

We assume that $v\in \{v_1,v_3\}$. Without loss of generality, we assume that $v=v_1$. Note that $B_1\cong K_{2,t}$ for $t\ge 2$. Then, by (A17), there exists a dominating trail $T_1=v_0{v}_3{v}_2{v}_1$ of $H\left(B_1\right)$ from $v_0$ to $v_1$. Note that $c\left(B_2\right)\le 5$. Then by Theorem A7, there exists a dominating trail $T_2$ of $H\left(B_2\right)$ that starts from $v_1$. Since $H_0=B_1\cup B_2$, we can find a dominating trail $v^{″}{v}^{\prime }{T}_1\cup T_2$ of H, a contradiction. This implies that $v=v_2$. Then, by (A17), there exists a dominating trail $T_1=v_0{v}_3{v}_2$ of $H\left(B_1\right)$ from $v_0$ to $v_2$. Note that $c\left(B_2\right)\le 5$ and $H_0=B_1\cup B_2$. Then, by Theorem A7, we can find a dominating trail of H, a contradiction.

Suppose now that $\left|\mathcal{B}\right(v_0\left)\right|\ne 1$. Then there exist at least two block $B_i$, $B_j$ such that $\{B_i,B_j\}\subseteq \mathcal{B}\left(v_0\right)$. It is easy to verify that $Cut\left(G_0\right)=\left\{v_0\right\}$. Otherwise, we can find a $P_5\bigcup P_5$ in H.

Claim 31. For any block $B_i$, $B_i$ has a dominating cycle of $H\left(B_i\right)$ passing through $v_0$.

Proof. 

Note that $Cut\left(G_0\right)=\left\{v_0\right\}$. Then $B_i\in \mathcal{B}\left(v_0\right)$. By Fact 1, $c_{v_0}\left(B_i\right)\le 5$.

Suppose first that $B_i\in {\mathcal{B}}_1\left(v_0\right)$. By Claim 30, $B_i\cong K_{2,t}$. Then $\mid (V_2\left(B_i\right)\setminus \left\{v_0\right\})\cap \Lambda \left(H^{\prime }\right)\mid \le 1$. Otherwise, $H[V\left(H\left(B_i\right)\right)\setminus \left\{v_0\right\}]$ contains a subgraph $F_1\cong P_5$, and $H[V\left(H\left(B_j\right)\right)\cup \{v^{″},v^{\prime }\}]$ contains a subgraph $F_2\cong P_5$. Then we can find $P_5\bigcup P_5$ in H. Therefore, $B_i$ has a dominating cycle of $H\left(B_i\right)$ passing through $v_0$.

Suppose now that $B_i\in {\mathcal{B}}_2\left(v_0\right)$. Let $C=v_0{v}_1{v}_2{v}_3{v}_4{v}_0$ be a longest cycle of $B_i$ passing through $v_0$. By Claim 29, $c\left(B_i\right)=5$.

$$\{v_1,v_4\}\subseteq V_2\left(H\right).$$

(A18)

Proof of (A18):

By contradiction, suppose that $d\left(v_1\right)>2$ or $d\left(v_4\right)>2$. Without loss of generality, we assume that $d\left(v_1\right)>2$. Note that $c\left(B_i\right)=5$ and there exist at least one block $B_j$ such that $V\left(B_j\right)\cap V\left(B_j\right)=\left\{v_0\right\}$. Then there exist one vertex $v_1^{\prime }\in V\left(H\right)\setminus (V(B_i\cup B_j)\cup \{v^{″},v^{\prime }\})$ such that $v_1{v}_1^{\prime }\in E\left(H\right)$. Then $H[V\left(B_j\right)\cup \{v^{″},v^{\prime }\}]$ contains a subgraph $F\cong P_5$. Therefore, $H\left[\{v_1^{\prime }{v}_1,v_1{v}_2,v_2{v}_3,v_3{v}_4\}\right]\cup H\left[E\left(F\right)\right]$ is a $L^{-1}(P_4\cup P_4)$, a contradiction. This indicate that (A18) holds. □

By Claim 29 and (A18), $B\cong S_{m,l}$. By symmetry and (A18) again, $(V\left(B_i\right)\setminus \{v_0,v_2,v_3\})\subseteq V_2\left(H\right)$. Then $B_i$ has a dominating cycle C of $H\left(B_i\right)$ passing through $v_0$.

Note that $H_0=\bigcup B_i$ for $i\in [1,t^{\prime }]$. By Claim 31, H contains a dominating trail T, a contradiction.

Case 1.2$S=Z_1$.

Claim 32.$Cut\left(H_0\right)\ne \left\{v_0\right\}$.

Proof. 

By contradiction, suppose that $Cut\left(H_0\right)=\left\{v_0\right\}$. For any block $B_i$ ($i\in [1,t^{\prime }]$), $B_i\in \mathcal{B}\left(v_0\right)$. By Fact 1, $c_{v_0}\left(B_i\right)\le 5$. We will prove that

$$each{B}_{i}hasadominatingcycleofH\left(B_i\right)passingthrough{v}_0.$$

(A19)

Proof of (A19):

Suppose first that $B_i\in {\mathcal{B}}_1\left(v_{{}_0}\right)$. By Claim 30, $B_i\cong K_{2,t}$. Note that $\left|\mathcal{B}\right(v_0\left)\right|\ne 1$. Then there exist at least one block $B_j$ such that $V\left(B_i\right)\cap V\left(B_j\right)=\left\{v_0\right\}$. Therefore, $H[V\left(B_j\right)\cup \{v^{″},v^{\prime }\}]$ contains a subgraph $F_1\cong T_{1,1,2}$. Then $\mid (V_2\left(B_i\right)\setminus \left\{v_0\right\})\cap \Lambda \left(H^{\prime }\right)\mid \le 1$, otherwise, $\mid (V_2\left(B_i\right)\setminus \left\{v_0\right\})\cap \Lambda \left(H^{\prime }\right)\mid \ge 2$, say $\{u,w\}\subseteq (V_2\left(B_i\right)\setminus \left\{v_0\right\})\cap \Lambda \left(H^{\prime }\right)$. Then there exist at least two vertices $\{u^{\prime },w^{\prime }\}\subseteq V\left(H\right)\setminus (V(B_i\cup B_j)\cup \{v^{\prime },v^{″}\})$ such that $\{u{u}^{\prime },w{w}^{\prime }\}\subseteq E\left(H\right)$. Therefore, $H[(V\left(B_i\right)\cup \{u^{\prime },w^{\prime }\})\setminus \left\{v_0\right\}]$ contains a subgraph $F_2\cong P_5$. Then $H\left[E\left(F_1\right)\right]\cup H\left[E\left(F_2\right)\right]$ is an $L^{-1}(Z_1\cup P_4)$, a contradiction. Therefore, $B_i$ has a dominating cycle of $H\left(B_i\right)$ passing through $v_0$. □

Suppose now that $B_i\in {\mathcal{B}}_2\left(v_{{}_0}\right)$. Let $C=v_0{v}_1{v}_2{v}_3{v}_4{v}_0$ be a longest cycle of B passing through $v_0$. By Claim 29, $c\left(B_i\right)=5$.

$$\{v_1,v_4\}\subseteq V_2\left(H\right).$$

(A20)

Proof of (A20):

By contradiction, suppose that $d\left(v_1\right)>2$ or $d\left(v_4\right)>2$. Without loss of generality, we assume that $d\left(v_1\right)>2$. Note that $c\left(B_i\right)=5$ and there exist at least one block $B_j$ such that $V\left(B_i\right)\cap V\left(B_j\right)=\left\{v_0\right\}$. Then there exist one vertex $v_1^{\prime }\in V\left(H\right)\setminus (V(B_i\cup B_j)\cup \{v^{″},v^{\prime }\})$ such that $v_1{v}_1^{\prime }\in E\left(H\right)$. Then $H[V\left(B_j\right)\cup \{v^{″},v^{\prime }\}]$ contains a subgraph $F\cong T_{1,1,2}$. Therefore, $H\left[\{v_1^{\prime }{v}_1,v_1{v}_2,v_2{v}_3,v_3{v}_4\}\right]\cup H\left[E\left(F\right)\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This implies that (A20) holds. □

By Claim 29 and (A20), $B_i\cong S_{m,l}$. By symmetry and (A20) again, $B_i$ has a dominating cycle C of $H\left(B_i\right)$ passing through $v_0$.

These imply that (A19) holds.

Note that $T\left(H_0\right)=\left\{v_0\right\}$ and $\mathcal{B}\left(v_0\right)={\mathcal{B}}_1\left(v_0\right)\cup {\mathcal{B}}_2\left(v_0\right)$. Then, by (A19), H contains a dominating trail, a contradiction. □

Next, we will show that

$$c_{v_0}\left(B_i\right)=4forany{B}_i\in \mathcal{B}\left(v_0\right).$$

(A21)

Proof of (A21):

Otherwise, there exists at least one block $B_{i_0}\in \mathcal{B}\left(v_0\right)$ such that $c_{v_0}\left(B_{i_0}\right)=5$. By Claim 32, $Cut\left(H_0\right)\ne \left\{v_0\right\}$. Note that $H_0$ has cut vertex. Then we can find a $T_{1,1,2}\bigcup P_5$ in H, a contradiction. This implies that (A21) holds. □

Note that $H_0$ has cut vertex. Then there exists at least two blocks $\{B_1,B_2\}\subseteq H_0$ such that $B_1\in \mathcal{B}\left(v_0\right)$, $B_2\notin \mathcal{B}\left(v_0\right)$ and $B_1\cap B_2=\left\{v\right\}$. By (A21), $c_{v_0}\left(B_1\right)=4$. By Claim A.3, $B_1\cong K_{2,t}$. Let $C_1=v_0{v}_1{v}_2{v}_3{v}_0$ be a longest cycle of $B_1$ passing through $v_0$ and v. Then $v\in \{v_1,v_2,v_3\}$. And $H_0=B_1\cup B_2$ and $c\left(B_2\right)\le 5$, otherwise, we can find a $T_{1,1,2}\bigcup P_5$ in H. Then $t>2$, otherwise, note that $c\left(B_2\right)\le 5$. Then, by Theorem A7, there exists a spanning trail $T^{\prime }$(say) of $B_2$ starts from any given vertex. Therefore, H contains a dominating trail, a contradiction.

Suppose first that $v\in \{v_1,v_3\}$. By symmetry, it suffices to consider that $v=v_1$. Then

$$v_3\in V_2\left(H\right).$$

(A22)

Proof of (A22):

Otherwise, there exist at least one vertex $v_3^{\prime }\in V\left(H\right)\setminus (V(C_1\cup B_2)\cup \{v^{\prime },v^{″}\})$ such that $v_3{v}_3^{\prime }\subseteq E\left(H\right)$. Note that $g\left(B_2\right)\ge 4$. Then $H[V\left(B_2\right)\cup \left\{v_2\right\}]$ contains a subgraph $F_1\cong T_{1,1,2}$. Therefore, $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_3,v_3{v}_3^{\prime }\}\right]\cup H\left[E\left(F_1\right)\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This implies that (A22) holds. □

Note that $B_1\cong K_{2,t}$. Then by (A22), $\{v_1,v_3\}\subseteq V_2\left(B_1\right)$. Note that $H_0=B_1\cup B_2$. Then, by symmetry and (A22), $V_2\left(B_1\right)\setminus \left\{v_1\right\}\subseteq V_2\left(H\right)$. Then $v_0{v}_3{v}_2{v}_1$ is a dominating tail of $H\left(B_1\right)$ from $v_0$ to $v_1$. Note that $c\left(B_2\right)\le 5$. Then, by Theorem A7, there exists a spanning trail $T^{\prime }$(say) of $B_2$ starts from the vertex $v_1$. Therefore, H contains a dominating trail, a contradiction.

Suppose now that $v=v_2$. Then

$$v_1\in V_2\left(H\right)$$

(A23)

Proof of (A23):

Otherwise, there exist at least one vertex $v_1^{\prime }\in V\left(H\right)\setminus (V(C_1\cup B_2)\cup \{v^{\prime },v^{″}\})$ such that $v_1{v}_1^{\prime }\subseteq E\left(H\right)$. Note that $g\left(B_2\right)\ge 4$. Then $H[V\left(B_2\right)\cup \left\{v_3\right\}]$ contains a subgraph $F_1^{\prime }\cong T_{1,1,2}$. Therefore, $H\left[\{v^{″}{v}^{\prime },v^{\prime }{v}_0,v_0{v}_1,v_1{v}_1^{\prime }\}\right]\cup H\left[E\left(F_1^{\prime }\right)\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This implies that (A23) holds. □

By (A23), $\{v_1,v_3\}\subseteq V_2\left(B_1\right)$. Note that $H_0=B_1\cup B_2$. Then, by symmetry and (A23), $V_2\left(B_1\right)\subseteq V_2\left(H\right)$. Then $v_0{v}_3{v}_2$ is a dominating tail of $H_1^{\prime }$ from $v_0$ to $v_2$. Note that $c\left(B_2\right)\le 5$. Then, by Theorem A7, there exists a spanning trail $T^{\prime }$(say) of $B_2$ starts from the vertex $v_2$. Therefore, H contains a dominating trail, a contradiction.

Case 2.$\left|Cut\right(G\left)\right|=2$.

Let $\{r,s\}=Cut\left(G\right)$, and let $r_0\in \mathcal{D}(r,G)$ and $s_0\in \mathcal{D}(s,G)$, respectively. Let $B=G-\{r_0,s_0\}$. If $V\left(B\right)=\{r,s\}$, then obviously G is traceable. Therefore, we suppose that $\left|V\right(B\left)\right|\ge 3$. It can be observed that if $Cut\left(B\right)\ne \varnothing$, say $b\in Cut\left(B\right)$, then $b\in Cut\left(G\right)$(clearly $\{r,s\}\cap Cut\left(B\right)=\varnothing$), a contradiction. Then, we suppose that B is 2-connected.

Let $B^{\prime }$ be the subgraph of H corresponding to B and let $e,f,e_0,f_0$ be the edges of H which correspond to the vertices $r,s,r_0,s_0$ of G, respectively. Denote $e_0=v_1{v}_1^{\prime }$, $e=v_1^{\prime }{v}_1^{″}$, $f_0=v_2{v}_2^{\prime }$ and $f=v_2^{\prime }{v}_2^{″}$.

Note that G is traceable if and only if there is dominating trail of H, and it is obvious that every dominating trail in H is certain to have $v_1/v_1^{\prime }$ and $v_2/v_2^{\prime }$ as end vertices. Let T be a trail in H from $v_1$ to $v_2$ satisfying it dominates a maximum number of edges. By the hypothesis, T is not a dominating trail. Let D be a non-trivial component of $H-V\left(T\right)$.

Claim 33.$\mid N_T\left(D\right)\mid \ge 2$.

Proof. 

By contradiction, suppose that $N_T\left(D\right)=\left\{u\right\}$. If $|N_D\left(u\right)|=1$, say $N_D\left(u\right)=\left\{x\right\}$, then $ux$ is a cut edge of H and the vertex of G which corresponds to $ux$ that belongs to $Cut\left(G\right)\setminus \{r,s\}$, a contradiction. Thus $|N_D\left(u\right)|\ge 2$, say $\{x,y\}\subseteq N_D\left(u\right)$. Let P be a path of D from x and y. Then $T^{\prime }=T\cup uxPyu$ is a trail dominating more edges than T, which is opposite to the choice to T. □

By Claim 33, let $\{u_1,u_2\}\subseteq N_T\left(D\right)$. Let P be a path from $u_1$ to $u_2$ with $\left|V\right(P\left)\right|\ge 3$ and $\{V\left(P\right)\setminus \{u_1,u_2\}\}\subseteq V\left(D\right)$. If $u_1{u}_2\in E\left(T\right)$, then $T^{\prime }=T-u_1{u}_2\cup P$ is a trail dominating more edges than T, a contradiction. Hence we come to a conclusion that $u_1{u}_2\notin E\left(T\right)$. Let Q be a path from $u_1$ to $u_2$ with all edges in T. Note that $u_1{u}_2\notin E\left(T\right)$. Then $\mid E\left(Q\right)\mid \ge 2$. We choose Q as long as possible. Clearly $C=P\cup Q$ is a cycle of H.

Let $Q_1$ be a path from $v_1$ to C, and $Q_2$ be a path from $v_2$ to $C\cup Q_1$. Let $w_1$ and $w_2$ be the end vertices of $Q_1$ and $Q_2$ other than $v_1$ and $v_2$, respectively. Let $Y=V(Q_1\cup Q_2\cup C)$.

Since G is $S\cup P_4$-free, H does not contain copy of $L^{-1}(S\cup P_4)$ as a (not necessarily induced) subgraph. In the below, we prove that H contains $L^{-1}(S\cup P_4)$ as a subgraph, thus deducing a contradiction in all cases.

Case 2.1$S=P_4$.

Case 2.1.1.$w_2\in V\left(Q_1\right)$.

In this case, $Q_1$ is divided by $w_2$ into two subgraphs. Let $P_1^{\prime }$ be the subgraph of $Q_1$ from $v_1$ to $w_2$, and $P_1^{″}$ from $w_2$ to $w_1$ ($P_1^{″}$ consists of only one $w_1$ if $w_1=w_2$). Since $N_H\left(v_1^{\prime }\right)=\{v_1,v_1^{″}\}$, we have $\left|V\right(P_1^{\prime }\left)\right|\ge 3$, and similarly $\left|V\right(Q_2\left)\right|\ge 3$. Let $\left\{x_1\right\}=N_{P_1^{\prime }}\left(w_2\right)$, $\left\{x_1^{\prime }\right\}=N_{P_1^{\prime }}\left(x_1\right)\setminus \left\{w_2\right\}$, and let $\left\{x_2\right\}=N_{Q_2}\left(w_2\right)$, $\left\{x_2^{\prime }\right\}=N_{Q_2}\left(x_2\right)\setminus \left\{w_2\right\}$.

If $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|\ge 5$, then there is a path in $P_1^{″}\cup C$ staring from $w_2$ of length at least 5. Let $w_{2}y{y}_1{y}_2{y}_3$ be such a path. Then $H[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\cup H\{w_{2}y,y{y}_1,y_1{y}_2,y_2{y}_3\}]$ is a $L^{-1}(P_4\cup P_4)$.

If $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|=4$, then $w_1=w_2$ or $w_1{w}_2\in E\left(T\right)$. Suppose first that $w_1{w}_2\in E\left(T\right)$. Note that $u_1{u}_2\notin E\left(C\right)$. Let $C=u_{1}y{u}_{2}z{u}_1$, where y is a vertex of D, and let $y^{\prime }\in N_D\left(y\right)$. Then $H[\{y^{\prime }y,y{u}_2,u_{2}z,z{u}_1\}\cup H\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}]$ is an $L^{-1}(P_4\cup P_4)$. Suppose now that $w_1=w_2$. Note that $u_1{u}_2\notin E\left(C\right)$. Let $C=w_2{y}_{1}zx{y}_2{w}_2$. Then

$$N\left(y_i\right)\cap (V\left(H\right)\setminus Y)=\varnothing ,\mathrm{for}i\in \{1,2\}.$$

(A24)

Proof of (A24):

By contradiction, without loss of generality, suppose that $N\left(y_1\right)\cap (V\left(H\right)\setminus Y)\ne \varnothing$. Then there exists a vertex $y_1^{\prime }\in N\left(y_1\right)\cap (V\left(H\right)\setminus Y)$. Then the $H[\{y_1^{\prime }{y}_1,y_{1}z,zx,x{y}_2\}\cup H\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{x}_2,x_2{x}_2^{\prime }\}]$ is a $L^{-1}(P_4\cup P_4)$. This implies that (A24) holds. □

If $\{y_1,y_2\}\cap V\left(D\right)=\varnothing$, then $u_1=y_1$ or $u_2=y_2$. Without loss of generality, we assume that $u_1=y_1$. Let $u_1^{\prime }\in N_T\left(u_1\right)$ and $u_1^{\prime }\ne w_2$ Since H is triangle-free, $u_1^{\prime }\notin \{x_1,x_2,x,y_2\}$. By (A24), $u_1^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_1,x_2\}$. Then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Then $y_1\in V\left(D\right)$ or $y_2\in V\left(D\right)$. Now we assume that $y_1\in V\left(D\right)$. By (A24), $z\in V\left(D\right)$. Note $u_1{u}_2\notin E\left(C\right)$. Then $u_1=w_2$ and $u_2=x$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne y_2$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{w_2,y_1\}$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_1,x_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{\prime }=x_1$, then $x_1\ne v_1^{\prime }$ and $x_1^{\prime }\ne v_1$. Let $x_1^{″}\in N_{Q_1}\left(x_1^{\prime }\right)$ and $x_1^{″}\ne x_1$. Then $H\left[\{x_1^{″}{x}_1^{\prime },x_1^{\prime }{x}_1,x_{1}x,x{y}_2\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_1,y_{1}z\}\right]$ is a $L^{-1}(P_4\cup P_4)$. If $u_2^{\prime }=x_2$, then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Then $H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{y}_1,y_{1}z\}\right]\cup H\left[\{x_2^{″}{x}_2^{\prime },x_2^{\prime }{x}_2,x_{2}x,x{y}_2\}\right]$ is an $L^{-1}(P_4\cup P_4)$. Thus, $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Let $u_2^{″}\in N_T\left(u_2^{\prime }\right)$ and $u_2^{″}\ne u_2$ ($u_2^{″}$ exists due to the $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{″}\notin \{z,y_2\}$. If $u_2^{″}\in V(Q_1\cup Q_2\cup C)\setminus \{w_2,z,y_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{″}\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2^{″}{u}_2^{\prime },u_2^{\prime }x,xz,z{y}_1\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$. Now we assume that $u_2^{″}=w_2$. Note that $u_2^{\prime }$ has no neighbor outside $V(Q_1\cup Q_2\cup C)$. Then $T^{\prime }=T-\{w_2{u}_2^{\prime },u_2^{\prime }x\}+\{w_2{y}_1,y_{1}z,zx\}$ is a trail dominating more edges than T, which is opposite to the choice to T.

Now we assume that $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|=3$, which implies that $w_1=w_2$ and the length of C is 4. Note $u_1{u}_2\notin E\left(G\right)$. Let $C=u_{1}y{u}_{2}z{u}_1$, where $y\in V\left(D\right)$, and let $y^{\prime }\in N_D\left(y\right)$. Now we assume that $w_1=u_1$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne z$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{u_1,y^{\prime }\}$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_1,x_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{\prime }=x_2$, then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Then $H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_{1}y,y{y}^{\prime }\}\right]\cup H\left[\{x_2^{″}{x}_2^{\prime },x_2^{\prime }{x}_2,x_2{u}_2,u_{2}z\}\right]$ is an $L^{-1}(P_4\cup P_4)$. If $u_2^{\prime }=x_1$, then $x_1\ne v_1^{\prime }$ and $x_1^{\prime }\ne v_1$. Let $x_1^{″}\in N_{Q_1}\left(x_1^{\prime }\right)$ and $x_1^{″}\ne x_1$. Then $H\left[\{x_1^{″}{x}_1^{\prime },x_1^{\prime }{x}_1,x_1{u}_2,u_{2}z\}\right]\cup H\left[\{y^{\prime }y,y{w}_1,w_1{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$. Hence, $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Let $u_2^{″}\in N_T\left(u_2^{\prime }\right)$ and $u_2^{″}\ne u_2$ ($u_2^{″}$ exists due to $d_T\left(u_2^{\prime }\right)$ is even). Since H is $K_3$-free, $u_2^{″}\notin \{z,y\}$. If $u_2^{″}\in V(Q_1\cup Q_2\cup C)\setminus \{w_1,z,y\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{″}\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2^{″}{u}_2^{\prime },u_2^{\prime }{u}_2,u_{2}y,y{y}^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{x}_2,x_2{x}_2^{\prime }\}\right]$ is an $L^{-1}(P_4\cup P_4)$. Now we assume that $u_2^{″}=w_1$. Note that $u_2^{\prime }$ has no neighbor outside $V(Q_1\cup Q_2\cup C)$. Then $T^{\prime }=T-\{w_1{u}_2^{\prime },u_2^{\prime }{u}_2\}+\{w_{1}y,y{u}_2\}$ is a trail dominating more edges than T, which is opposite to the choice to T.

Next we assume that $w_1\ne u_1$, and similarly, $w_1\ne u_2$, which implies that $w_1=z$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne w_1$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{u_1,y^{\prime }\}$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \left\{w_1\right\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Therefore, $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Let $u_2^{″}\in N_T\left(u_2^{\prime }\right)$ and $u_2^{″}\ne u_2$ ($u_2^{″}$ exists due to $d_T\left(u_2^{\prime }\right)$ is even). Since H is $K_3$-free, $u_2^{″}\notin \{w_1,y\}$. If $u_2^{″}\in V(Q_1\cup Q_2\cup C)\setminus \{w_1,y,u_1\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{″}\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2^{″}{u}_2^{\prime },u_2^{\prime }{u}_2,u_{2}y,y{y}^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{x}_2,x_2{x}_2^{\prime }\}\right]$ is an $L^{-1}(P_4\cup P_4)$. Now we assume that $u_2^{″}=u_1$. Note that $N\left(u_2^{\prime }\right)\cap (V\left(H\right)\setminus Y)=\varnothing$. Then $T^{\prime }=T-\{u_1{u}_2^{\prime },u_2^{\prime }{u}_2\}+\{u_{1}y,y{u}_2\}$ is a trail dominating more edges than T, which is opposite to the choice to T.

Case 2.1.2$w_2\notin V\left(Q_1\right)$.

In this case, $\{w_1,w_2\}\in V\left(Q\right)$ and $w_1\ne w_2$. Without loss of generality, suppose that $u_1,w_1,w_2,u_2$ appear along Q in this order (with possibly $w_1=u_1$ or $w_2=u_2$ or both). As in Case 2.1.1, let $x_1\in N_{Q_1}\left(w_1\right)$, and $x_1^{\prime }\in N_{Q_1}\left(x_1\right)$ and $x_1^{\prime }\ne w_1$, and let $x_2\in N_{Q_2}\left(w_2\right)$, and $x_2^{\prime }\in N_{Q_2}\left(x_2\right)$ and $x_2^{\prime }\ne w_2$.

Case 2.1.2.1$w_1{w}_2\in E\left(Q\right)$.

By Claim 29, $c\left(H\right)\le 5$. Then the length of C at most is 5.

We first assume that the length of C is 5. Let $C=y_1{w}_1{w}_2{y}_{2}z$. If $z\in V\left(Q\right)$, then $\mid \{y_1,y_2\}\cap V\left(D\right)\mid =1$. Without loss of generality, suppose that $y_1\in V\left(D\right)$, and let $y_1^{\prime }\in N_D\left(y_1\right)$. Then $H\left[\{z{y}_2,y_2{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_1^{\prime }\}\right]$ is an $L^{-1}(P_4\cup P_4)$. Now, suppose that $z\in V\left(D\right)$. We assert that either $u_1=y_1$ or $u_2=y_2$; otherwise $u_1=w_1$, $u_2=w_2$ and $u_1{u}_2\in E\left(T\right)$. Without loss of generality, suppose that $u_1=y_1$. Let $u_1^{\prime }\in N_T\left(u_1\right)$ and $u_1^{\prime }\ne w_1$ ($u_1^{\prime }$ exists due to $d_T\left(u_1\right)$ is even). If $u_1^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{z{y}_2,y_2{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{u}_1,u_1{u}_1^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$. Then $u_1^{\prime }\in V(Q_1\cup Q_2\cup C)$. Since H is triangle-free, $u_1^{\prime }\notin \{y_2,x_1,w_2\}$. If $u_1^{\prime }\notin V(Q_1\cup Q_2)\setminus \{w_1,w_2,x_2,x_1\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_1^{\prime }=x_2$, then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Then $H\left[\{z{u}_1,u_1{x}_2,x_2{x}_2^{\prime },x_2^{\prime }{x}_2^{″}\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{w}_2,w_2{y}_2\}\right]$ is an $L^{-1}(P_4\cup P_4)$.

As far as the last subcase is concerned, suppose that $\left|V\right(C\left)\right|=4$. This indicates that $\left|V\right(P\left)\right|=\left|V\right(Q\left)\right|=3$. Let $C=y_1{w}_1{w}_2{y}_2{y}_1$. Since $w_1,w_2\notin V\left(D\right)$, without loss of generality, say $y_2\in V\left(D\right)$, which indicates that $u_1=y_1$ and $u_2=w_2$. Let $y_2^{\prime }\in N_D\left(y_2\right)$. Let $u_1^{\prime }\in N_T\left(u_1\right)$ and $u_1^{\prime }\ne w_1$. Since H is triangle-free, $u_1^{\prime }\notin \{w_2,x_1\}$. If $u_1^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_1,w_2,x_2,x_1\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction.

$$u_1^{\prime }\ne x_2.$$

(A25)

Proof of (A25):

By contradiction, suppose that $u_1^{\prime }=x_2$. Then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Let ${\widehat{x}}_2$ be a neighbor of $x_2$ on T other than $w_2$, $x_2^{\prime }$, $u_1$ (${\widehat{x}}_2$ exists due to $d_T\left(x_2\right)$ is even). Since H is triangle-free, ${\widehat{x}}_2\notin \{y_2,x_2^{″},w_1\}$. Then $N\left(x_2^{″}\right)\cap (V\left(H\right)\setminus Y)=\varnothing$, otherwise, there exists a vertex $x_2^{‴}\in N\left(x_2^{″}\right)\cap (V\left(H\right)\setminus Y)$, then $H[\left\{\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_2\}\right]\cup H\left[\{x_2^{‴}{x}_2^{″},x_2^{″}{x}_2^{\prime },x_2^{\prime }{x}_2,x_2{w}_2\}\right]$ is an $L^{-1}(P_4\cup P_4)$, a contradiction. Therefore, ${\widehat{x}}_2\notin V\left(Q_2\right)$. If ${\widehat{x}}_2\in V\left(Q_1\right)\setminus \left\{w_1\right\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Then ${\widehat{x}}_2\notin V(Q_1\cup Q_2\cup C)$. Let ${\widehat{x}}_2^{\prime }\in N_T\left({\widehat{x}}_2\right)$ and ${\widehat{x}}_2^{\prime }\ne x_2$ (${\widehat{x}}_2^{\prime }$ exists due to $d_T\left({\widehat{x}}_2\right)$ is even). Since H is triangle-free, ${\widehat{x}}_2^{\prime }\ne w_2$. Note that $N\left(x_2^{″}\right)\cap (V\left(H\right)\setminus Y)=\varnothing$. Then ${\widehat{x}}_2^{\prime }\notin V\left(Q_2\right)$. If ${\widehat{x}}_2^{\prime }\in V(Q_1\cup C)\setminus \{w_1,y_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If ${\widehat{x}}_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_2\}\right]\cup H\left[\{x_2^{″}{x}_2^{\prime },x_2^{\prime }{x}_2,x_2{\widehat{x}}_2,{\widehat{x}}_2{\widehat{x}}_2^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$, a contradiction. This implies that (A25) holds. □

By (A25), $u_1^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{y_2^{\prime }{y}_2,y_2{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{u}_1,u_1{u}_1^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$.

Case 2.1.2.2$w_1{w}_2\notin E\left(Q\right)$.

In this case, C is divided into two subpath (from $w_1$ to $w_2$), say $R_1$ and $R_2$, by $w_1$ and $w_2$. Clearly the lengths of $R_1$ and $R_2$ are both at least 2. For $i=1,2$, let $l\left(R_i\right)$ be the length of $R_i$. Without loss of generality, suppose that $l\left(R_1\right)\ge l\left(R_2\right)$. By Claim 29, the length of C is at most 5. Then $l\left(R_2\right)=2$. Let $R_2=w_{1}z{w}_2$.

Firstly, suppose that $\left|V\right(C\left)\right|=5$. Let $C=w_1{y}_1{y}_2{w}_{2}z{w}_1$. Then

$$N\left(\{x_1^{\prime },z,x_2^{\prime }\}\right)\cap (V\left(H\right)\setminus Y)=\varnothing$$

(A26)

Proof of (A26):

By contradiction, suppose that there exists a vertex $u\in N\left(\{x_1^{\prime },z,x_2^{\prime }\}\right)\cap (V\left(H\right)\setminus Y)$. By symmetry, we just need to consider the case $u\in N\left(\{x_1^{\prime },z\}\right)\cap (V\left(H\right)\setminus Y)$. Then

$$\begin{array}{c}\left\{\begin{array}{cc}H\left[\{u{x}_1^{\prime },x_1^{\prime }{x}_1,x_1{w}_1,w_{1}z\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_1\}\right],\hfill & \mathrm{if}u\in N\left(x_1^{\prime }\right)\cap (V\left(H\right)\setminus X),\hfill \\ H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_{1}z,zu\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_1\}\right],\hfill & \mathrm{if}u\in N\left(z\right)\cap \left(V\right(H)\setminus X),\hfill \end{array}\right.\hfill \end{array}$$

is a $L^{-1}(P_4\cup P_4)$, a contradiction. This implies that (A26) holds. □

Then $\{y_1,y_2\}\cap V\left(D\right)\ne \varnothing$. If $\{y_1,y_2\}\subseteq V\left(D\right)$, then, by (A26), $T^{\prime }=T-\{w_{1}z,z{w}_2\}+\{w_1{y}_1,y_1{y}_2,y_2{w}_2\}$ is a trail dominating more edges than T, which is opposite to the choice to T. Since $w_1,w_2\notin V\left(D\right)$, without loss of generality, suppose that $y_1\in V\left(D\right)$, which implies that $u_1=w_1$ and $u_2=y_2$. Let $y_1^{\prime }\in N_D\left(y_1\right)$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne w_2$. Since H is triangle-free, $u_2^{\prime }\ne z$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_1,w_2,x_1,x_1^{\prime },z\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{\prime }=x_1$ or $x_1^{\prime }$, then $x_1\ne v_1^{\prime }$ and $x_1^{\prime }\ne v_1$. It means that the vertex $x_1^{\prime }$ has a neighbor outside $V(Q_1\cup Q_2\cup C)$, a contradiction. Then $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2^{\prime }{u}_2,u_2{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_1^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$.

Suppose that $\left|V\right(C\left)\right|=4$. Let $C=w_{1}y{w}_{2}z{w}_1$. Since $w_1,w_2\notin V\left(D\right)$, without loss of generality, say $y\in V\left(D\right)$, which means that $u_1=w_1$ and $u_2=w_2$. Let $y^{\prime }\in N_D\left(y\right)$. Then

$$N\left(z\right)\cap \left(V\right(H)\setminus Y)=\varnothing$$

(A27)

Proof of (A27):

By contradiction, suppose that there exists a vertex $u\in N\left(z\right)\cap \left(V\right(H)\setminus Y)$. Note that D is a non-trivial component of $H-V\left(T\right)$. Then $u\ne y^{\prime }$. Therefore, the $H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_{1}z,zu\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_{2}y,y{y}^{\prime }\}\right]$ is a $L^{-1}(P_4\cup P_4)$, a contradiction. This implies that (A27) holds. □

Then, by (A27), $T^{\prime }=T-\{w_{1}z,z{w}_2\}+\{w_{1}y,y{w}_2\}$ is a trail dominating more edges than T, which is opposite to the choice to T.

Case 2.2$S=Z_1$.

Case 2.2.1$w_2\in V\left(Q_1\right)$.

In this case, $Q_1$ is divided by $w_2$ into two subgraphs. Let $P_1^{\prime }$ be the subgraph of $Q_1$ from $v_1$ to $w_2$, and $P_1^{″}$ from $w_2$ to $w_1$ ($P_1^{″}$ consists of only one $w_1$ if $w_1=w_2$). Since the only neighbors of $v_1^{\prime }$ in H are $v_1$ and $v_1^{″}$, we have $\left|V\right(P_1^{\prime }\left)\right|\ge 3$, and similarly of $\left|V\right(Q_2\left)\right|\ge 3$. Let $\left\{x_1\right\}=N_{P_1^{\prime }}\left(w_2\right)$, $\left\{x_1^{\prime }\right\}=N_{P_1^{\prime }}\left(x_1\right)\setminus \left\{w_2\right\}$, and let $\left\{x_2\right\}=N_{Q_2}\left(w_2\right)$, $\left\{x_2^{\prime }\right\}=N_{Q_2}\left(x_2\right)\setminus \left\{w_2\right\}$.

If $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|\ge 6$, then there exists a path in $P_1^{″}\cup C$ staring from $w_2$ of length at least 5. Let $y{y}_1{y}_2{y}_3{y}_4{y}_5$ be such a path. Then $H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,w_{2}y\}\right]\cup H\left[\{y_1{y}_2,y_2{y}_3,y_3{y}_4,y_4{y}_5\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

If $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|=5$, then the length of $P_1^{″}$ is 0 or 1 or 2. Suppose that the length of $P_1^{″}$ is 2. Let $P_1^{″}=w_{2}z{w}_1$. Then $\left|V\right(C\left)\right|=4$. Let $C=w_{1}y{y}_1{y}_2{w}_1$. Then $H\left[\{w_{1}z,w_1{y}_2,w_{1}y,y{y}_1\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Therefore, the length of $P^{″}$ is 1 or 0. By Claim 29, the length of $P_1^{″}$ is 1. Otherwise, it will produce a cycle of length at least 6 in H, a contradiction. Then $w_1{w}_2\in E\left(T\right)$. Note that $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|=5$. Then $H[V(P_1^{″}\cup C)\setminus \left\{w_2\right\}]$ contains a subgraph $F\cong P_5$ and $H\left[V(P_1^{″}\cup C)\right]$ contains a subgraph $F^{\prime }\cong T_{1,1,2}$.

Claim 34.$\left|V\right({\mathcal{D}}_{H\left[Y\right]}(u,H)\left)\right|\le 2$ for $u\in \{x_1^{\prime },x_1,w_2,x_2,x_2^{\prime }\}$.

Proof. 

By symmetry, we just need to consider the case $\left|V\right({\mathcal{D}}_{H\left[Y\right]}(u,H)\left)\right|\le 2$ for $u\in \{x_1^{\prime },x_1,w_2\}$. Let $P=x_1^{\prime }{x}_1{w}_2{x}_2{x}_2^{\prime }$.

First, we will show that $|{\mathcal{D}}_{H\left[Y\right]}(u,H)\left)\right|\le 1$. Otherwise, $|{\mathcal{D}}_{H\left[Y\right]}(u,H)|>1$. Then $H\left[V\right(P)\cup \{u\left\}\right]$ contains a subgraph $F_1\cong T_{1,1,2}$. Then $H\left[E\left(F_1\right)\right]\cup H\left[E\left(F\right)\right]$ is a $L^{-1}(Z_1\cup P_4)$. This implies that $|{\mathcal{D}}_{H\left[Y\right]}(u,H)|\le 1$.

Suppose that $|{\mathcal{D}}_{H\left[Y\right]}(u,H)|=1$. Let $\left\{D_u\right\}={\mathcal{D}}_{H\left[Y\right]}(u,H)$. Then

$$d_{D_u}\left(v\right)\le 2foranyvertexv\in V\left(D_u\right).$$

(A28)

Proof of (A28):

Otherwise, $H[V\left(D_u\right)\cup V\left(P\right)]$ contains a subgraph $F_2\cong T_{1,1,2}$. Then the subgraph formed by F and $F_2$ is an $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. This implies that (A28) holds. □

$D_u$ does not contain a subgraph $P_3$. Otherwise, $D_u$ contains a subgraph $P_3$. Suppose first that $u=x_1^{\prime }$. By (A28) and $|{\mathcal{D}}_{H\left[Y\right]}(x_1^{\prime },H)\left)\right|\le 1$, $H[V\left(D_{x_1^{\prime }}\right)\cup \{x_1^{\prime },x_1\}]$ contains a subgraph $F_3\cong P_5$. Then $H\left[E\left(F^{\prime }\right)\right]\cup H\left[E\left(F_3\right)\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. Suppose now that $u\in \{x_1,w_2\}$. $H[V\left(D_u\right)\cup \left\{u\right\}]$ contains a subgraph $F_4\cong T_{1,1,2}$. Then $H\left[E\left(F\right)\right]\cup H\left[E\left(F_4\right)\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. □

Note that the length of $P_1^{″}$ is 1. Then $\left|V\right(C\left)\right|=5$. Let $C=y_0{y}_1{y}_2{y}_3{y}_4{y}_0$. If $y_{i\left(mod5\right)}$ has a neighbor $y_i^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{y_i{y}_i^{\prime },y_i{y}_{i+1},y_{i+1}{y}_{i+2},y_i{y}_{i+4}\}\right]\cup$$H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$, $i=0,1,2,3,4$. Therefore, by Claim 34, $n\left(H\right)\le 20$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 100$ and $n\left(G\right)\le 100$, contradicting $n\left(G\right)\ge 212$.

If $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|=4$, then $w_1=w_2$ or $w_1{w}_2\in E\left(T\right)$. Suppose first that $w_1{w}_2\in E\left(T\right)$. Note that $u_1{u}_2\notin E\left(C\right)$. Let $C=u_{1}y{u}_{2}z{u}_1$, where $y\in V\left(D\right)$, and let $y^{\prime }\in N_D\left(y\right)$. Then $H\left[\{y^{\prime }y,y{u}_2,u_{2}z,y{u}_1\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Suppose now that $w_1=w_2$. Note that $u_1{u}_2\notin E\left(C\right)$. Let $C=w_2{y}_{1}zx{y}_2{w}_2$.

If $\{y_1,y_2\}\cap V\left(D\right)=\varnothing$, then $u_1=y_1$ or $u_2=y_2$. Without loss of generality, we suppose that $u_2=y_2$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne w_2$. Since H is triangle-free, $u_2^{\prime }\notin \{x_1,x_2,z,y_1\}$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_1,x_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Therefore, $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Let $u_2^{″}\in N_T\left(u_2^{\prime }\right)$ and $u_2^{″}\ne u_2$ ($u_2^{″}$ exists due to $d_T\left(u_2^{\prime }\right)$ is even). Since H is $K_3$-free, $u_2^{″}\notin \{x,w_2\}$. If $u_2^{″}\in V(Q_1\cup Q_2\cup C)\setminus \{w_2,z,x,y_1\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{″}\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{w_2{y}_1,w_2{x}_1,w_2{x}_2,x_2{x}_2^{\prime }\}\right]\cup H\left[\{zx,x{u}_2,u_2{u}_2^{\prime },u_2^{\prime }{u}_2^{″}\}\right]$ is an $L^{-1}(Z_1\cup P_4)$. If $u_2^{″}=z$, then $H\left[\{z{u}_2^{″},zx,x{u}_2,z{u}_1\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. These imply that $u_2^{″}=u_1$. Note that $N\left(u_2^{\prime }\right)\cap (V\left(H\right)\setminus Y)=\varnothing$. Then $T^{\prime }=T-\{u_2{u}_2^{\prime },u_2^{\prime }{u}_1\}+\{y_{2}x,zx,z{u}_1\}$ is a trail dominating more edges than T, which is opposite to the choice to T.

Then $\{y_1,y_2\}\cap V\left(D\right)\ne \varnothing$. Now we assume that $y_1\in V\left(D\right)$. Note that z has no neighbors outside $V(Q_1\cup Q_2\cup C)$. Then $z\in V\left(D\right)$. Note $u_1{u}_2\notin E\left(C\right)$. Then $u_1=w_2$ and $u_2=x$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne y_2$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{w_2,y_1\}$. If $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2{u}_2^{\prime },u_{2}z,z{y}_1,u_2{y}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_1,x_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{\prime }=x_1$, then $x_1\ne v_1^{\prime }$ and $x_1^{\prime }\ne v_1$. Let $x_1^{″}\in N_{Q_1}\left(x_1^{\prime }\right)$ and $x_1^{″}\ne x_1$. Then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{y}_1,\}\right]\cup H\left[\{x_1^{″}{x}_1^{\prime },x_1^{\prime }{x}_1,x_1{w}_2,w_2{u}_2\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If $u_2^{\prime }=x_2$, then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Then $H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{y}_1,w_2{y}_2\}\right]\cup H\left[\{x_2^{″}{x}_2^{\prime },x_2^{\prime }{x}_2,x_2{u}_2,u_{2}z\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

Now we assume that $|V(P_1^{″}\cup C)\setminus \left\{w_2\right\}|=3$, which implies that $w_1=w_2$ and $\left|V\right(C\left)\right|=4$. Note $u_1{u}_2\notin E\left(G\right)$. Let $C=u_{1}y{u}_{2}z{u}_1$, where $y\in V\left(D\right)$, and let $y^{\prime }\in N_D\left(y\right)$. Now we assume that $w_1=u_1$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne z$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{u_1,y^{\prime }\}$. If $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2{u}_2^{\prime },u_{2}z,u_{2}y,y{y}^{\prime }\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_1,x_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Then $u_2^{\prime }\in \{x_1,x_2\}$. Without loss of generality, we assume that $u_2^{\prime }=x_2$. Then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Then let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}=x_2$.

$$N\left(x_2^{″}\right)\cap (V\left(H\right)\setminus Y)=\varnothing .$$

(A29)

Proof of (A29):

By contradiction, suppose that there exists a vertex $u\in N\left(x_2^{″}\right)\cap (V\left(H\right)\setminus Y)$. Then $H\left[\{w_2{x}_1,x_1{x}_1^{\prime },w_{2}z,w_{2}y\}\right]\cup H\left[\{u{x}_2^{″},x_x^{″}{x}_2^{\prime },x_2^{\prime }{x}_2,x_2{u}_2\}\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This indicates that (A29) holds. □

Let $x_2^1$ be a neighbor of $x_2$ on T other than $u_2$,$x_2^{\prime }$,$w_2$ ($x_2^1$ exists due to $d_T\left(x_2\right)$ is even). Note that D is a non-trivial component of $H-V\left(T\right)$. Then $x_2^1\ne y^{\prime }$. If $x_2^1\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{x_2{x}_2^{\prime },x_2^{\prime }{x}_2^{″},x_{2}u,x_2{u}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_{2}y,y{y}^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Since H is $K_3$-free, by (A29), $x_2^1\in V\left(Q_1\right)\setminus \left\{w_2\right\}$. Then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction.

Next we assume that $w_1\ne u_1$, and similarly, $w_1\ne u_2$, which implies that $w_1=z$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne w_1$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{u_1,y^{\prime }\}$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \left\{w_1\right\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Therefore, $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Note that D is a non-trivial component of $H-V\left(T\right)$. Then $u_2^{\prime }\ne y^{\prime }$. Therefore, the $H\left[\{y{y}^{\prime },y{u}_2,u_2{u}_2^{\prime },y{u}_1\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

Case 2.2.2$w_2\notin V\left(Q_1\right)$.

In this case, $\{w_1,w_2\}\subseteq V\left(Q\right)$ and $w_1\ne w_2$. Without loss of generality, we suppose that $u_1,w_1,w_2,u_2$ appear along Q in this order (with possibly $w_1=u_1$ or $w_2=u_2$ or both). As in Case 2.2.1, let $x_1\in N_{Q_1}\left(w_1\right)$, and $x_1^{\prime }\in N_{Q_1}\left(x_1\right)$ and $x_1^{\prime }\ne w_1$, and let $x_2\in N_{Q_2}\left(w_2\right)$, and $x_2^{\prime }\in N_{Q_2}\left(x_2\right)$ and $x_2^{\prime }\ne w_2$.

Case 2.2.2.1$w_1{w}_2\in E\left(Q\right)$.

By Claim 29, the length of C is at most 5.

We first assume that the length of C is 5. Let $C=y_1{w}_1{w}_2{y}_{2}z{y}_1$.

If $z\in V\left(Q\right)$, then $\mid \{y_1,y_2\}\cap (V\left(C\right)\cap V\left(D\right))\mid =1$. Without loss of generality, we assume that $y_1\in V\left(D\right)$, and let $y_1^{\prime }\in N_D\left(y\right)$. Then $u_1=w_1$ and $u_2=z$. Let $u_2^{\prime }\in N_T\left(u_2\right)$ and $u_2^{\prime }\ne y_2$ ($u_2^{\prime }$ exists due to $d_T\left(u_2\right)$ is even). Since H is $K_3$-free, $u_2^{\prime }\notin \{w_2,w_1\}$. If $u_2^{\prime }\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{u_2{y}_1,y_1{y}_1^{\prime },u_2{u}_2^{\prime },u_2{y}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If $u_2^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,w_1,x_2,x_1,x_1^{\prime }\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_2^{\prime }=x_2$, then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}=x_2$. Then $H\left[\{x_2{x}_2^{\prime },x_2^{\prime }{x}_2^{″},x_2{u}_2,x_2{w}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_1^{\prime }\}\right]$ is an $L^{-1}(Z_1\cup P_4)$. If $u_2^{\prime }=x_1$, then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_1\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{u}_2,u_2{y}_1,y_1{y}_1^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If $u_2^{\prime }=x_1^{\prime }$, then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_1\}\right]\cup H\left[\{x_1{x}_1^{\prime },x_1^{\prime }{u}_2,u_2{y}_1,y_1{y}_1^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

Now suppose that $z\in V\left(D\right)$. We assert that either $u_1=y_1$ or $u_2=y_2$; otherwise $u_1=w_1$, $u_2=w_2$ and $u_1{u}_2\in E\left(T\right)$. Without loss of generality, we suppose that $u_1=y_1$. Let $u_1^{\prime }\in N_T\left(u_1\right)$ and $u_1^{\prime }\ne w_1$ ($u_1^{\prime }$ exists due to $d_T\left(u_1\right)$ is even). Since H is triangle-free, $u_1^{\prime }\notin \{y_2,x_1,w_2\}$. If $u_1^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_1,w_2,x_2,x_1\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction.

$$u_1^{\prime }\ne x_2.$$

(A30)

Proof of (A30):

By contradiction, suppose that $u_1^{\prime }=x_2$. Then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Let ${\widehat{x}}_2$ be a neighbor of $x_2$ on T other than $w_2$, $x_2^{\prime }$, $u_1$ (${\widehat{x}}_2$ exists due to $d_T\left(x_2\right)$ is even). Since H is triangle-free, ${\widehat{x}}_2\notin \{y_2,z,w_1\}$. If ${\widehat{x}}_2\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{x_2{x}_2^{\prime },x_2^{\prime }{x}_2^{″},x_2{w}_2,x_2{\widehat{x}}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_{1}z\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If ${\widehat{x}}_2\in V\left(Q_2\right)$, then $H\left[\{x_2{w}_2,w_2{y}_2,x_2{x}_2^{\prime },x_2{\widehat{x}}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_{1}z\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Therefore, ${\widehat{x}}_2\in V\left(Q_1\right)\setminus \left\{w_1\right\}$. Then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. This implies that (A30) holds. □

By (A30), $u_1^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Then $y_2\in V\left(D\right)$. Otherwise, note $u_1{u}_2\notin E\left(G\right)$ and $z\in V\left(D\right)$. Let $z^{\prime }\in N_D\left(z\right)$. Then $H\left[\{z{z}^{\prime },z{u}_1,u_1{u}_1^{\prime },z{y}_2\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{x}_1,x_1{x}_1^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Therefore, $u_2=w_2$. Let $u_1^{″}\in N_T\left(u_1^{\prime }\right)$ and $u_1^{″}\ne u_1$ ($u_1^{″}$ exists due to $d_T\left(u_1^{\prime }\right)$ is even). If $u_1^{″}\in V(Q_1\cup Q_2)\setminus \{w_1,w_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Since H is triangle-free, $u_1^{″}\ne w_1$. If $u_1^{″}=w_2$, then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{u}_1^{″}\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{u}_1,u_{1}z\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Let $u_1^{‴}\in N_T\left(u_1^{″}\right)$ and $u_1^{‴}\ne u_1^{\prime }$ ($u_1^{‴}$ exists due to $d_T\left(u_1^{″}\right)$ is even). If $u_1^{‴}\in V(Q_1\cup Q_2)$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Since H is triangle-free, $u_1^{‴}\ne u_1$. Then $u_1^{‴}\notin V(Q_1\cup Q_2)\cup \left\{u_1\right\}$. Then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_1\}\right]\cup H\left[\{u_1^{‴}{u}_1^{″},u_1^{″}{u}_1^{\prime },u_1^{\prime }{u}_1,u_{1}z\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

As far as the last subcase is concerned, suppose that $\left|V\right(C\left)\right|=4$. This indicates that $\left|V\right(P\left)\right|=\left|V\right(Q\left)\right|=3$. Let $C=y_1{w}_1{w}_2{y}_2{y}_1$. Since $w_1,w_2\notin V\left(D\right)$, without loss of generality, we assume that $y_2\in V\left(D\right)$, which indicates that $u_1=y_1$ and $u_2=w_2$. Let $y_2^{\prime }\in N_D\left(y_2\right)$. Let $Z=Y\cup \left\{y_2^{\prime }\right\}$.

Claim 35.$\mid N\left(x_i^{\prime }\right)\cap (V\left(H\right)\setminus Z)\mid \le 1$; If $N\left(x_i^{\prime }\right)\cap (V\left(H\right)\setminus Z)=\left\{x_i^{″}\right\}$, then $\mid N\left(x_i^{″}\right)\cap (V\left(H\right)\setminus Z)\mid \le 1$; If $N\left(x_i^{″}\right)\cap (V\left(H\right)\setminus Z)=\left\{x_i^{‴}\right\}$, then $N\left(x_i^{‴}\right)\cap (V\left(H\right)\cup \left\{x_i^{″}\right\}\setminus Z)=\varnothing$ for $i\in \{1,2\}$.

Proof. 

By symmetry, we just need to consider the case $i=1$. By contradiction, suppose that $\mid N\left(x_1^{\prime }\right)\cap (V\left(H\right)\setminus Z)\mid >1$. Then there exists at least two vertices $\{x_1^{\prime 1},x_1^{\prime 2}\}\subseteq N\left(x_1^{\prime }\right)\cap (V\left(H\right)\setminus Z)$. Then $H\left[\{x_1^{\prime }{x}_1^{\prime 1},x_1^{\prime }{x}_1^{\prime 2},x_1^{\prime }{x}_1,x_1{w}_1\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. This means $\mid N\left(x_1^{\prime }\right)\cap (V\left(H\right)\setminus Z)\mid \le 1$.

If $N\left(x_1^{\prime }\right)\cap (V\left(H\right)\setminus Z)=\left\{x_1^{″}\right\}$, then $\mid N\left(x_1^{″}\right)\cap (V\left(H\right)\setminus Z)\mid \le 1$, otherwise, there exists at least two vertices $\{x_1^{″1},x_1^{″2}\}\subseteq N\left(x_1^{″}\right)\cap (V\left(H\right)\setminus Z)$, then $H\left[\{x_1^{″}{x}_1^{″1},x_1^{″}{x}_1^{″2},x_1^{″}{x}_1^{\prime },x_1^{\prime }{x}_1\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. This implies that $\mid N\left(x_1^{″}\right)\cap (V\left(H\right)\setminus Z)\mid \le 1$.

If $N\left(x_1^{″}\right)\cap (V\left(H\right)\setminus Z)=\left\{x_1^{‴}\right\}$, then $N\left(x_1^{‴}\right)\cap (V\left(H\right)\cup \left\{x_1^{″}\right\}\setminus Z)=\varnothing$. Otherwise, there exists at least one vertex $x_1^{‴1}\in N\left(x_1^{‴}\right)\cap (V\left(H\right)\cup \left\{x_1^{″}\right\}\setminus Y)$, then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_1,\}\right]\cup H\left[\{x_1{x}_1^{\prime },x_1^{\prime }{x}_1^{″},x_1^{″}{x}_1^{‴},x_1^{‴}{x}_1^{‴1}\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. □

Let $u_1^{\prime }\in N_T\left(u_1\right)$ and $u_1^{\prime }\ne w_1$ ($u_1^{\prime }$ exists due to $d_T\left(u_1\right)$ is even). Since H is triangle-free, $u_1^{\prime }\notin \{w_2,x_1\}$. If $u_1^{\prime }\in V(Q_1\cup Q_2)\setminus \{w_2,x_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction.

$$u_1^{\prime }\ne x_2.$$

(A31)

Proof of (A31):

By contradiction, suppose that $u_1^{\prime }=x_2$. Then $x_2\ne v_2^{\prime }$ and $x_2^{\prime }\ne v_2$. Let $x_2^{″}\in N_{Q_2}\left(x_2^{\prime }\right)$ and $x_2^{″}\ne x_2$. Let ${\widehat{x}}_2$ be a neighbor of $x_2$ on T other than $w_2$, $x_2^{\prime }$, $u_1$ (${\widehat{x}}_2$ exists due to $d_T\left(x_2\right)$ is even). Since H is triangle-free, ${\widehat{x}}_2\notin \{y_2,x_2^{″},w_1\}$. If ${\widehat{x}}_2\notin V(Q_1\cup Q_2\cup C)$, then $H\left[\{x_2{x}_2^{\prime },x_2^{\prime }{x}_2^{″},x_2{w}_2,x_2{\widehat{x}}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_2\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. If ${\widehat{x}}_2\in V\left(Q_2\right)$, then $H\left[\{x_2{x}_2^{\prime },x_2^{\prime }{x}_2^{″},x_2{w}_2,x_2{\widehat{x}}_2\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_2\}\right]$ is an $L^{-1}(Z_1\cup P_4)$. Then ${\widehat{x}}_2\in V\left(Q_1\right)\setminus \left\{w_1\right\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. This implies that (A31) holds. □

By (A31), $u_1^{\prime }\notin V(Q_1\cup Q_2\cup C)$. Let $u_1^{″}\in N_T\left(u_1^{\prime }\right)$ and $u_1^{″}\ne u_1$ ($u_1^{″}$ exists due to $d_T\left(u_1^{\prime }\right)$ is even). Since H is $K_3$-free, $u_1^{″}\notin \{y_2,w_1\}$. If $u_1^{″}\in V(Q_1\cup Q_2\cup C)\setminus \{w_1,w_2\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction.

Claim 36.$u_1^{″}\ne w_2.$

Proof. 

By contradiction, suppose that $u_1^{″}=w_2$. If $N\left(u_1^{\prime }\right)\cap (V\left(H\right)\setminus Y)=\varnothing$, then $T^{\prime }=T-\{u_1{u}_1^{\prime },u_1^{\prime }{w}_2\}+\{u_1{y}_2,y_2{w}_2\}$ is a trail dominating more edges than T, which is opposite to the choice to T. This implies that $N\left(u_1^{\prime }\right)\cap V\left(H\right)\setminus Y\ne \varnothing$. Let ${\widehat{u}}_1\in N\left(u_1^{\prime }\right)\cap V\left(H\right)\setminus Y$ and $Y^{\prime }=Y\cup \{u_1^{\prime },{\widehat{u}}_1,y_2^{\prime }\}$. Then

$${\widehat{u}}_1\ne y_2^{\prime }.$$

(A32)

Proof of (A32):

By contradiction, suppose that ${\widehat{u}}_1=y_2^{\prime }$. Note that D is a non-trivial component of $H-V\left(T\right)$. Then ${\widehat{u}}_1\notin V\left(T\right)$. Therefore, $T^{\prime }=T-\left\{u_1^{\prime }{w}_2\right\}+\{u_1^{\prime }{y}_2^{\prime },y_2^{\prime }{y}_2,y_2{w}_2\}$ is a trail dominating more edges than T, a which is opposite to the choice to T. This implies that (A32) holds. □

$$N\left(u\right)\cap (V\left(H\right)\setminus Y^{\prime })=\varnothing foranyvertexu\in \{x_1,w_1,w_2,x_2,u_1,u_1^{\prime },y_2\}$$

(A33)

Proof of (A33):

By contradiction, suppose that $u^1\in N\left(u\right)\cap (V\left(H\right)\setminus Y^{\prime })$. Then, by (A32),

$$\begin{array}{c}\left\{\begin{array}{cc}H\left[\{x_1{w}_1,w_1{y}_1,x_1{x}_1^1,x_1{x}_1^{\prime }\}\right]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_2^{\prime }\}\right],\hfill & \mathrm{if}u=x_1,\hfill \\ H[\{x_2{w}_2,w_2{y}_2,x_2{x}_2^1,x_2{x}_2^{\prime }]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{u}_1^{\prime },u_1^{\prime }{\widehat{u}}_1\}\right],\hfill & \mathrm{if}u=x_2,\hfill \\ H[\{w_1{x}_1,x_1{x}_1^{\prime },w_1{y}_1,w_1{w}_1^1]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_2^{\prime }\}\right],\hfill & \mathrm{if}u=w_1,\hfill \\ H[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_2^1]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{u}_1^{\prime }\}\right],\hfill & \mathrm{if}u=w_2,\hfill \\ H[\{y_1{w}_1,w_1{x}_1,y_1{y}_2,y_1{y}_1^1]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{u}_1^{\prime },u_1^{\prime }{\widehat{u}}_1\}\right],\hfill & \mathrm{if}u=y_1,\hfill \\ H[\{y_2{y}_1,y_1{w}_1,y_2{y}_2^{\prime },y_2{y}_2^1]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{u}_1^{\prime },u_1^{\prime }{\widehat{u}}_1\}\right],\hfill & \mathrm{if}u=y_2,\hfill \\ H[\{u_1^{\prime }{u}_1,u_1{w}_1,u_1^{\prime }{\widehat{u}}_1,u_1{u}_1^1]\cup H\left[\{x_2^{\prime }{x}_2,x_2{w}_2,w_2{y}_2,y_2{y}_2^{\prime }\}\right],\hfill & \mathrm{if}u=u_1^{\prime },\hfill \end{array}\right.\hfill \end{array}$$

is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This indicates that (A33) holds. □

$$\left|V\right({\mathcal{D}}_{H\left[Y^{\prime }\right]}(y_2^{\prime },H)\left)\right|\le 1.$$

(A34)

Proof of (A34):

First, we will show that $|{\mathcal{D}}_{H\left[Y^{\prime }\right]}(y_2^{\prime },H)\left)\right|\le 1$. Otherwise, $|{\mathcal{D}}_{H\left[Y^{\prime }\right]}(y_2^{\prime },H)|>1$. Then there exist two vertices $\{y_2^{\prime 1},y_2^{\prime 2}\}\subseteq N\left(y_2^{\prime }\right)\cap (V\left(H\right)\setminus Z)$. Then $H[\{y_2^{\prime }{y}_2,y_2{y}_1,y_2^{\prime }{y}_2^{\prime 1},y_2^{\prime }{y}_2^{\prime 2}]\cup H\left[\{x_1{w}_1,w_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. This indicates that $|{\mathcal{D}}_{H\left[Y^{\prime }\right]}\left(y_2^{\prime }\right),H\left)\right|\le 1$. □

Suppose that $|{\mathcal{D}}_{H\left[Y^{\prime }\right]}(y_2^{\prime },H)|=1$. Let $\left\{y_2^{″}\right\}\in {\mathcal{D}}_{H\left[Y^{\prime }\right]}(y_2^{\prime },H)$ and $y_2^{″}{y}_2^{\prime }\in E\left(H\right)$. Then $N\left(y_2^{″}\right)\cap (V\left(H\right)\setminus Y^{\prime })=\varnothing$. Otherwise, there exists at least one vertex $y_2^{‴}\in N\left(y_2^{″}\right)\cap (V\left(H\right)\setminus Z)$, then $H[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{u}_1^{\prime },w_2{w}_1]\cup H\left[\{y_1{y}_2,y_2{y}_2^{\prime },y_2^{\prime }{y}_2^{″},y_2^{″}{y}_2^{‴}\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. This indicates that (A34) holds. is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This implies that (A34) holds.

$$\left|V\right({\mathcal{D}}_{H\left[Y^{\prime }\right]}({\widehat{u}}_1,H)\left)\right|\le 1.$$

(A35)

Proof of (A35):

First, we will show that $|{\mathcal{D}}_{H\left[Y^{\prime }\right]}({\widehat{u}}_1,H)\left)\right|\le 1$. Otherwise, there exist two vertices $\{u_1^1,u_1^2\}\subseteq N\left({\widehat{u}}_1\right)\cap (V\left(H\right)\setminus Y^{\prime })$. Then $H[\{{\widehat{u}}_1{u}_1^{\prime },u_1^{\prime }{u}_1,{\widehat{u}}_1{u}_1^1,{\widehat{u}}_1{u}_2^1]\cup H\left[\{x_1{w}_1,w_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. This indicates that $\left|V\right({\mathcal{D}}_{H\left[Y^{\prime }\right]}({\widehat{u}}_1,H)\left)\right|\le 1$. □

Suppose that $\left|V\right({\mathcal{D}}_{H\left[Y^{\prime }\right]}({\widehat{u}}_1,H)\left)\right|=1$. Let $\left\{{\widehat{u}}_1^{\prime }\right\}\in {\mathcal{D}}_{H\left[Y^{\prime }\right]}({\widehat{u}}_1,H)$ and ${\widehat{u}}_1{\widehat{u}}_1^{\prime }\in E\left(H\right)$. Then $N\left({\widehat{u}}_1^{\prime }\right)\cap (V\left(H\right)\setminus Y^{\prime })=\varnothing$. Otherwise, there exists at least one vertex ${\widehat{u}}_1^{″}\in N\left({\widehat{u}}_1^{\prime }\right)\cap (V\left(H\right)\setminus Y^{\prime })$, then $H[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_1]\cup H\left[\{u_1{u}_1^{\prime },u_1^{\prime }{\widehat{u}}_1,{\widehat{u}}_1{\widehat{u}}_1^{\prime },{\widehat{u}}_1^{\prime }{\widehat{u}}_1^{″}\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. This indicates that (A35) holds.

By (A33)–(A35) and Claim 35, $n\left(H\right)\le 19$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 91$ and $n\left(G\right)\le 91$, contradicting $n\left(G\right)\ge 212$.

By Claim 36, $u_1^{″}\notin V(Q_1\cup Q_2\cup C)$. Let $u_1^{‴}\in N_T\left(u_1^{″}\right)$ and $u_1^{‴}\ne u_1^{\prime }$ ($u_1^{‴}$ exists due to $d_T\left(u_1^{″}\right)$ is even). If $u_1^{‴}\in V(Q_1\cup Q_2\cup C)$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. Then $u_1^{‴}\notin V(Q_1\cup Q_2\cup C)$. Let $u_1^{″″}\in N_T\left(u_1^{‴}\right)$ and $u_1^{″″}\ne u_1^{″}$ ($u_1^{″″}$ exists due to $d_T\left(u_1^{‴}\right)$ is even). If $u_1^{″″}\in V(Q_1\cup Q_2\cup C)\setminus \left\{u_1\right\}$, then there exists a path from $u_1$ to $u_2$ in T longer than Q, a contradiction. If $u_1^{″″}=u_1$, then $H[\{u_1{u}_1^{\prime },u_1^{\prime }{u}_1^{″},u_1{u}_1^{‴},u_1{y}_2]\cup H\left[\{x_1{w}_1,w_1{w}_2,w_2{x}_2,x_2{x}_2^{\prime }\}\right]$ is a $L^{-1}(Z_1\cup P_4)$. Therefore, $u_1^{″″}\notin V(Q_1\cup Q_2\cup C)$. Then $H[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_2{w}_1]\cup H\left[\{u_1{u}_1^{\prime },u_1^{\prime }{u}_1^{″},u_1^{″}{u}_1^{‴},u_1^{‴}{u}_1^{″″}\}\right]$ is a $L^{-1}(Z_1\cup P_4)$.

Case 2.2.2.2$w_1{w}_2\notin E\left(Q\right)$.

In this case, $w_1$ and $w_2$ divide C into two subpath (from $w_1$ to $w_2$), say $R_1$ and $R_2$. Clearly the lengths of $R_1$ and $R_2$ are both at least 2. For $i=1,2$, let $l\left(R_i\right)$ be the length of $R_i$. Without loss of generality, we suppose that $l\left(R_1\right)\ge l\left(R_2\right)$. By Claim 29, the length of C is at most 5. Then $l\left(R_2\right)=2$. Let $R_2=w_{1}z{w}_2$.

When we refer to the case that the length of C is 4, we assume that $C=w_{1}y{w}_{2}z{w}_1$ and $y\in V\left(D\right)$.

$$ThereisapathPinC\cup D\cup Q_{2}from{x}_2^{\prime }oflengthis4notpassingthrough{w}_{1}andz.$$

(A36)

Proof of (A36):

Suppose first that the length of C is 5. We assume that $C=w_1{y}_1{y}_2{w}_{2}z{w}_1$. Then $P=x_2^{\prime }{x}_2{w}_2{y}_1{y}_2$ is such path. Suppose now that the length of C is 4. Note that $y\in V\left(D\right)$. Then $u_1=w_1$ and $u_2=w_2$. Let $y^{\prime }\in N_D\left(y\right)$. Then $P=x_2^{\prime }{x}_2{w}_{2}y{y}^{\prime }$ is such path. (A36) holds. □

Let $Z=Y\cup V\left(P\right)$

Claim 37.$N\left(u\right)\cap \left(V\right(H)\setminus Z)=\varnothing$ for any vertex $u\in \{x_1,w_1,w_2,x_2\}$.

Proof. 

By symmetry, we just need to consider the case $N\left(u\right)\cap \left(V\right(H)\setminus Z)=\varnothing$ for any vertex $u\in \{x_1,w_1\}$. By contradiction, suppose that $u^1\in N\left(u\right)\cap (V\left(H\right)\setminus Z)$. Then

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}H\left[\{x_1{w}_1,w_{1}z,x_1{x}_1^1,x_1{x}_1^{\prime }\}\right]\cup H\left[E\left(P\right)\right],\hfill & \mathrm{if}u=x_1,\hfill \\ H[w_1{x}_1,x_1{x}_1^{\prime },w_{1}z,w_1{w}_1^1\}]\cup H\left[E\left(P\right)\right],\hfill & \mathrm{if}u=w_1,\hfill \end{array}\right.\end{array}$$

is a $L^{-1}(Z_1\cup P_4)$, a contradiction. □

Claim 38.$\mid V\left({\mathcal{D}}_{H\left[Z\right]}(x_i^{\prime },H)\right)\mid \le 1$ for $i\in \{1,2\}$.

Proof. 

By symmetry, we just need to consider the case $\mid V\left({\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)\right)\mid \le 1$. By contradiction, suppose that $\left|V\right({\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)\left)\right|>1$.

First, we will show that $|{\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)|\le 1$. Otherwise, $|{\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)|>1$. Then there exist at least two vertices $\{x_1^{\prime 1},x_1^{\prime 2}\}\subseteq N\left(x_1^{\prime }\right)\cap (V\left(H\right)\setminus Z)$, then $H\left[\{x_1^{\prime }{x}_1^{\prime 1},x_1^{\prime }{x}_1^{\prime 2},x_1^{\prime }{x}_1,x_1{w}_1\}\right]\cup H\left[E\left(P\right)\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$. This implies that $|{\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)|\le 1$.

Suppose that $|{\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)|=1$. Let $\left\{D_1\right\}={\mathcal{D}}_{H\left[Z\right]}(x_1^{\prime },H)$. Then $D_1$ does not contain a subgraph $P_2$. Otherwise, $H[V\left(D_1\right)\cup \{x_1^{\prime },x_1,w_1\}]$ contains a subgraph $F_1\cong P_5$ and $H[V\left(Z\right)\setminus V\left(Q_1\right)]$ contains a subgraph $F_2\cong T_{1,1,2}$. Then $H\left[E\left(F_1\right)\right]\cup H\left[E\left(F_2\right)\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. □

Claim 39.$\mid N\left(z\right)\cap \left(V\right(H)\setminus Z)\mid \le 1$ and $\mid V\left({\mathcal{D}}_{H\left[Z\right]}(z,H)\right)\mid \le 4$.

Proof. 

By contradiction, suppose that $\left|V\right({\mathcal{D}}_{H\left[Z\right]}(z,H)\left)\right|\ge 5$. First, we will show that $\mid N\left(z\right)\cap \left(V\right(H)\setminus Z)\mid \le 1$. Otherwise, $\mid N\left(z\right)\cap \left(V\right(H)\setminus Z)\mid >1$. Then there exist at least two vertices $\{z^{\prime },z^{″}\}\subseteq N\left(z\right)\cap (V\left(H\right)\setminus Z)$, the $H\left[\{z{w}_1,w_1{x}_1,z{z}^{\prime },z{z}^{″}\}\right]\cup H\left(E\left(P\right)\right]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. This contradiction shows that $|{\mathcal{D}}_{H\left[Z\right]}(z,H)|\le 1$.

Suppose that $|{\mathcal{D}}_{H\left[Z\right]}(z,H)|=1$. Let $\left\{D_z\right\}={\mathcal{D}}_{H\left[Z\right]}(z,H)$. Then

$$d_D\left(u\right)\le 2foranyvertexu\in V\left(D_z\right).$$

(A37)

Proof of (A37):

Otherwise, there exists a vertex $u_0\in V\left(D_z\right)$ such that $d_{D_z}\left(u_0\right)\ge 3$. Then $H[V\left(D_z\right)\cup \left\{w_1\right\}]$ contains a subgraph $F_1\cong T_{1,1,2}$. Then $H[E\left(F_1\right)\cup E\left(P\right)]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. This implies that (A37) holds. □

$D_z$ does not contain a subgraph $P_5$. Otherwise, $H\left[V(Q_2\cup C\cup P)\right]$ contains a subgraph $F_2\cong T_{1,1,2}$. Then $H[E\left(F_2\right)\cup E\left(P_5\right)]$ is a $L^{-1}\left(Z_1\right)\cup L^{-1}\left(P_4\right)$, a contradiction. Combining this with (A37), $\left|V\right({\mathcal{D}}_{H\left[Z\right]}(z,H)\left)\right|\le 4$.

Firstly, suppose that $\left|V\right(C\left)\right|=5$. Let $C=w_1{y}_1{y}_2{w}_{2}z{w}_1$. Then

$$N\left(u\right)\cap V\left(H\right)\setminus Z=\varnothing foranyvertexu\in \{y_1,y_2\}$$

(A38)

Proof of (A38):

By symmetry, we just need to consider the case $N\left(y_1\right)\cap V\left(H\right)\setminus Z=\varnothing$. By contradiction, suppose that $y_1^1\in N\left(u\right)\cap V\left(H\right)\setminus Z$. Then $H\left[\{w_2{x}_2,x_2{x}_2^{\prime },w_2{y}_2,w_{2}z\}\right]\cup H\left[\{x_1^{\prime }{x}_1,x_1{w}_1,w_1{y}_1,y_1{y}_1^1\}\right]$ is a $L^{-1}(Z_1\cup P_4)$, a contradiction. This implies that (A38) holds. □

By Claims 37–39 and (A38), $n\left(H\right)\le 15$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 57$ and $n\left(G\right)\le 57$, contradicting $n\left(G\right)\ge 212$.

As far as the last subcase is concerned, we assume that $\left|V\right(C\left)\right|=4$. Let $C=w_{1}y{w}_{2}z{w}_1$. Since $w_1,w_2\notin V\left(D\right)$, without loss of generality, we suppose that $y\in V\left(D\right)$, which implies that $u_1=w_1$ and $u_2=w_2$. Let $y^{\prime }\in N_D\left(y\right)$.

If $N\left(z\right)\cap \left(V\right(H)\setminus Y)=\varnothing$, then $T^{\prime }=T-\{w_{1}z,z{w}_2\}+\{w_{1}y,y{w}_2\}$ is a trail dominating more edges than T, which is opposite to the choice to T. Therefore, $N\left(z\right)\cap \left(V\right(H)\setminus Y)\ne \varnothing$. Note that D is a non-trivial component of $H-V\left(T\right)$. Then $y^{\prime }\notin N\left(z\right)\cap (V\left(H\right)\setminus Y)$. Combining this with Claim 39, $\mid N\left(z\right)\cap \left(V\right(H)\setminus Y)\mid =1$. Let $\left\{z^{\prime }\right\}=N\left(z\right)\cap (V\left(H\right)\setminus Y)$. By symmetry, $\left\{y^{\prime }\right\}=N\left(y\right)\cap (V\left(H\right)\setminus Y)$. Let $\left\{D_z\right\}={\mathcal{D}}_{H\left[Y\right]}(z,H)$ and $\left\{D_y\right\}={\mathcal{D}}_{H\left[Y\right]}(y,H)$. Then

$$\mid V\left({\mathcal{D}}_{H\left[Y\right]}(u,H)\right)\mid \le 4foranyvertexu\in \{z,y\}.$$

(A39)

Proof of (A39):

By symmetry, we only need to deal with the case $\mid V\left({\mathcal{D}}_{H\left[Y\right]}(z,H)\right)\mid \le 4$ First, we will prove that $D_z\cap D_y=\varnothing$. Otherwise, by Claim 29, $z^{\prime }{y}^{\prime }\in E\left(H\right)$. Then $T^{\prime }=T-\left\{w_{1}z\right\}+\{w_{1}y,y{y}^{\prime },y^{\prime }z\}$ is a trail dominating more edges than T, which is opposite to the choice to T. This implies that $\mid V\left({\mathcal{D}}_{H\left[Y\right]}(z,H)\right)\mid =\mid V\left({\mathcal{D}}_{H\left[Z\right]}(z,H)\right)\mid$. By Claim 39, $\mid V\left({\mathcal{D}}_{H\left[Y\right]}(z,H)\right)\mid \le 4$. (A39) holds. □

By (A39) and Claims 37 and 38, $n\left(H\right)\le 18$. By Theorem A5, since H is $K_3$-free, $e\left(H\right)\le 81$ and $n\left(G\right)\le 81$, contradicting $n\left(G\right)\ge 212$.