1. Introduction
A natural reaction of anyone reading the title of this paper is, “Surely this was all done 100 years ago!”. To which we respond “Yes, but some results that are well established are not well known, and there remain misunderstandings that we want to correct”. Accordingly, our article is a tutorial review. It is addressed to scientists rather than to mathematicians.
We are presently engaged in a program of identifying a basic library of knotted, linked, and woven structures that would provide suitable and interesting candidates for designed realization at the molecular level. We are particularly concerned with both finite and periodic structures in one, two, or three linearly-independent directions. Recent reviews of the synthetic aspects of such structures are provided by Guo et al. on finite structures [
1], and by Di Silvestro and Mayor on weavings of threads [
2]. Symmetry is an important aspect of such structures, yet not many groups explore their molecular symmetry. In our approach, we simplify these structures by regarding them as graphs, or nets, comprising vertices that are connected by straight edges (sticks). In graph theory, edges do not need to be straight, but in molecular synthesis, such edges tend to be rigid, linear, molecular linkers. The woven and linked nature of the structures, along with the constraint of straight edges, imposes strict conditions on the symmetry that such structures can support; many symmetry groups would force straight sticks to intersect. In our explorations of these structures, we have encountered symmetry-related surprises that have delighted and intrigued us, and we have noticed recurrent misunderstandings in the literature. We address some of these issues in this article.
We want to cover all symmetry aspects of materials encountered in chemistry and materials science that can be abstracted as graphs. We specifically exclude objects that are infinitely extended in one or more dimensions, but which are not periodic. These last include objects such as chiral 3
6 tilings of the cylinder. The simplest of these is the Boerdijk–Coxeter helix, which has vertices related by screw rotations of cos
−1(−3/2), which is not a rational fraction of a circle [
3]. The duals of these structures are the structures of chiral carbon nanotubes, surely also lacking translational periodicity. Other excluded structures are quasicrystals [
4], structures with two or more incommensurate periodicities [
5], and non-rigid objects [
6]. We are instead particularly concerned here to make the case (a) for using the ‘international’ system (Hermann–Mauguin notation) to cover systematically
all dimensions and periodicities within three-dimensional Euclidean space: and (b) clearly distinguishing abstract graphs from their realizations as embeddings in Euclidean space.
We have already met our first problem with terminology. Chemists generally use the term n-dimensional to mean “infinitely extended in n dimensions”. However, all chemical materials, from hydrogen atoms to complex crystals, are three-dimensional. On the other hand, mathematicians, when describing things such as knots, use “periodic” to mean “having rotational periodicity” (symmetry!).
2. The Space Groups and Subperiodic Groups
One of the great achievements of human intellect is the enumeration and description of the space groups of Euclidean space brought to completion by Fedorov and Schoenflies at the end of the 19th century. Equally important, in our view, was the subsequent development of the Hermann–Mauguin notation (hereinafter “HM notation”) which provides a unified approach to 0-, 1-, 2-, and 3-periodic objects in 1-, 2-, or 3-dimensions.
The discussion of space groups usually begins with the description of the possible lattices in two- or three-dimensions. The requirement that the shortest distance between lattice points has a lower bound leads to the “crystallographic restriction”—that only rotations of order 1-, 2-, 3-, 4-, or 6-fold can arise, and that there are 230 space groups in three-dimensions. However, in the space of diffraction patterns (reciprocal space or Fourier space), the crystallographic restriction no longer holds and rotations of any order are possible.
Mermin and colleagues have enumerated all space groups without the crystallographic restriction and reported them in the HM notation [
7]. This work is relevant to our discussion because the crystallographic restriction no longer applies to 0- or 1-periodic objects. Thus, the 11 icosahedral space groups of reciprocal space [
7] allow us to include the 2 icosahedral point groups (Schoenflies symbols
, and
) in the system with HM notation
and
. Only missing are the symbols for the spherical groups (Schoenflies symbols
, and
) generally given as
and
in HM notation. The enumeration [
8] of all axial groups, for any order of rotation, directly allows the inclusion of all 0-dimensional (point) groups with HM notation, as is indeed done generally. We note, however, that although the HM notation for point groups is given generally in texts, e.g., [
9], they are very rarely used, and it is commonplace to see HM notation used for space groups and Schoenflies notation for point groups
in the same paper.The crystallographic restriction does not apply to 1-periodic structures, so periodic rods can have any order of rotation axis. Generally, however, the
rod groups are considered to be only those 75 with 1-, 2-, 3-, 4-, or 6-fold rotations [
9,
10,
11]. The groups for any order of rotation are sometimes referred to as
line groups. These can be found readily for any order of rotation using the space group enumeration [
8]. In the list below,
is the order of rotation,
is an integer with
, and
.
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | | |
Note that, here, is the 1-periodic lattice with lattice vector c.
The crystallographic restriction applies to the 2-periodic layer groups, of which there are 80, and these can be obtained readily as a subgroup of the 230 3-periodic groups. Periodicity is taken to be in the
a,
b plane with possible lattices
p and
c, and only those groups with no translations along
c, such as screw and glide operations, are accepted. The layer groups have been known for over 100 years, for references see [
12], and are listed in terms of HM notation in a number of places, e.g., [
9,
10,
11,
12]. We emphasize this last point because, although 2-periodic objects are common in everyday experience (weaving, knitting, chain mail, chain-link fencing) and have occasioned mathematical discussions, we have not found any work prior to our recent work (discussed below) that actually describes their symmetries correctly. A notable exception is an enumeration, and crystallographic description, of bilayers of vertex-transitive sphere packings [
13].
The layer groups should not be confused with the 17 plane (or, “wallpaper”) groups, which apply to periodic structures in two-dimensional space. Although flat periodic structures (such as a single layer of graphite—graphene) can be described by a plane group (p6mm), the layer group (p6/mmm) will usually describe additional symmetry elements—in this case, the additional mirror plane lying in the layer.
3. Symmetries of Embedded Finite Graphs—Knots, Links, and Tangles: Terminology
Discussions of graphs in the context of molecules and crystals lead at once to problems with terminology. For example, in graph theory, a graph with all vertices three-coordinated is called “cubic”. We want to avoid that term in that sense so we use “trivalent”. A “symmetric” graph is vertex- and edge-transitive (one type of vertex, and one type of edge). The “symmetry” of a graph is the automorphism group, which is the group of permutations of vertices that leaves the graph adjacencies unchanged.
We use the term “embedding” to refer to a realization of a graph in space, with symmetry and coordinates. In every case in this paper, the space is the three-dimensional Euclidean space. In every case, the embedding is piecewise linear. In embeddings relevant to materials chemistry, the edges have finite length, are linear, and are non-intersecting. Additionally, two or more vertices do not occupy the same positions (they do not collide).
The symmetries of simple molecules and shapes, such as polyhedra, need little discussion here. However, increasingly, chemists are concerned with molecular structures such as knots, links, and tangles (“chemical topology”) [
14], and their descriptions can be more contentious. We start with simple knots, known as torus knots as they can be drawn on the surface of a torus without edge crossings.
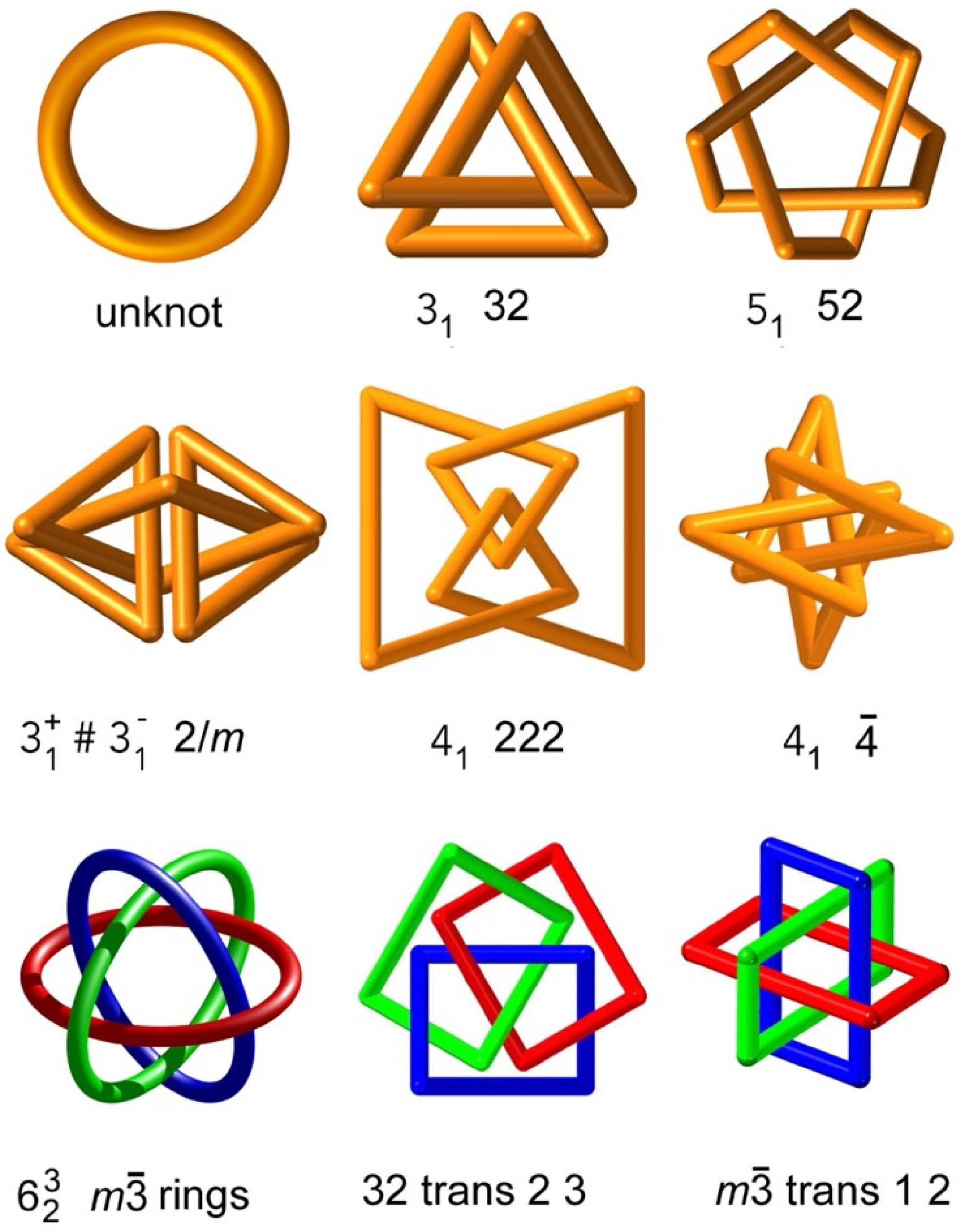
Figure 1 shows the simplest of all, the “trefoil” knot, symbol
, and also the “cinquefoil” knot,
. Note that these symbols are the
Alexander–Briggs notation for knots, and are not related to screw-symmetry operations in crystallography, which are described by similar symbols. The minimal number of edge crossings in a plane drawing of these is three and five, respectively. The torus knots have a piecewise linear embedding with one kind of vertex and two kinds of edge (transitivity 1 2) and are the only knots with vertex-transitive (isogonal) embeddings [
15]. The symmetries of the optimal piecewise linear embeddings are
(
odd) and
(
even), where
is the order of the rotation symmetry, and these are the relevant symmetries for the molecular chemist synthesizing knots. To a knot theorist, all the torus knots have the same “symmetry”,
, the cyclic group of order 2 [
16]. It should be noted that the underlying graph of a knot is just a single loop—the “unknot”, which has the symmetry of a cylinder,
. The possible symmetries of a knot are then the subgroups of this—the triclinic, monoclinic or orthorhombic, or axial symmetries. Knots cannot have icosahedral or cubic symmetry [
17], as these symmetry groups are not subgroups of the cylindrical symmetry of the loop. A further restriction is that
prime knots cannot have embeddings with mirror symmetry; however, a composite knot (a “sum” of two, or more, prime knots), and the unknot, may. We show in
Figure 1 the simplest example, the square knot, which is the sum of two trefoils of opposite handedness, and which has an embedding with a symmetry of
.
Generally, several embeddings of a knot are possible. The “figure-of-eight”,
, is shown in two embeddings in
Figure 1. These have symmetries
and
, and thus the question arises: “Which is ‘the’ symmetry?”. We maintain that this is the wrong question. The question that
can be answered, generally, is: “What is the best piecewise linear embedding?”.
and
are groups of the same order, but the embedding in
has lower vertex transitivity (2 rather than 3). The knot has crossing number 4, as shown in the
embedding. The
embedding cannot be so drawn. Indeed, it is often the case that high-symmetry drawings, and molecular realizations of knots, show more than the minimum number of crossings in any linear piecewise projection, and this can lead to incorrect identifications [
18].
We also show embeddings of the famous Borromean rings. These do have an embedding with cubic symmetry and, as shown in
Figure 1, three non-intersecting loops (not circles!) can be arranged with cubic symmetry. Catenanes (linked molecular loops) can have cubic (
and
) or icosahedral (
) symmetry; self-intersections can now be avoided because the group generates multiple separate copies of a loop. Such catenanes include a small set with vertex- and edge-transitive embeddings [
15]. It is a common error to suppose that objects with
symmetry (or more generally
symmetry, with
a multiple of 4) are chiral, as their symmetries contain neither an inversion center nor a mirror plane. However, that is not correct, and, in particular, the
knot (Alexander–Briggs notation) is not chiral.
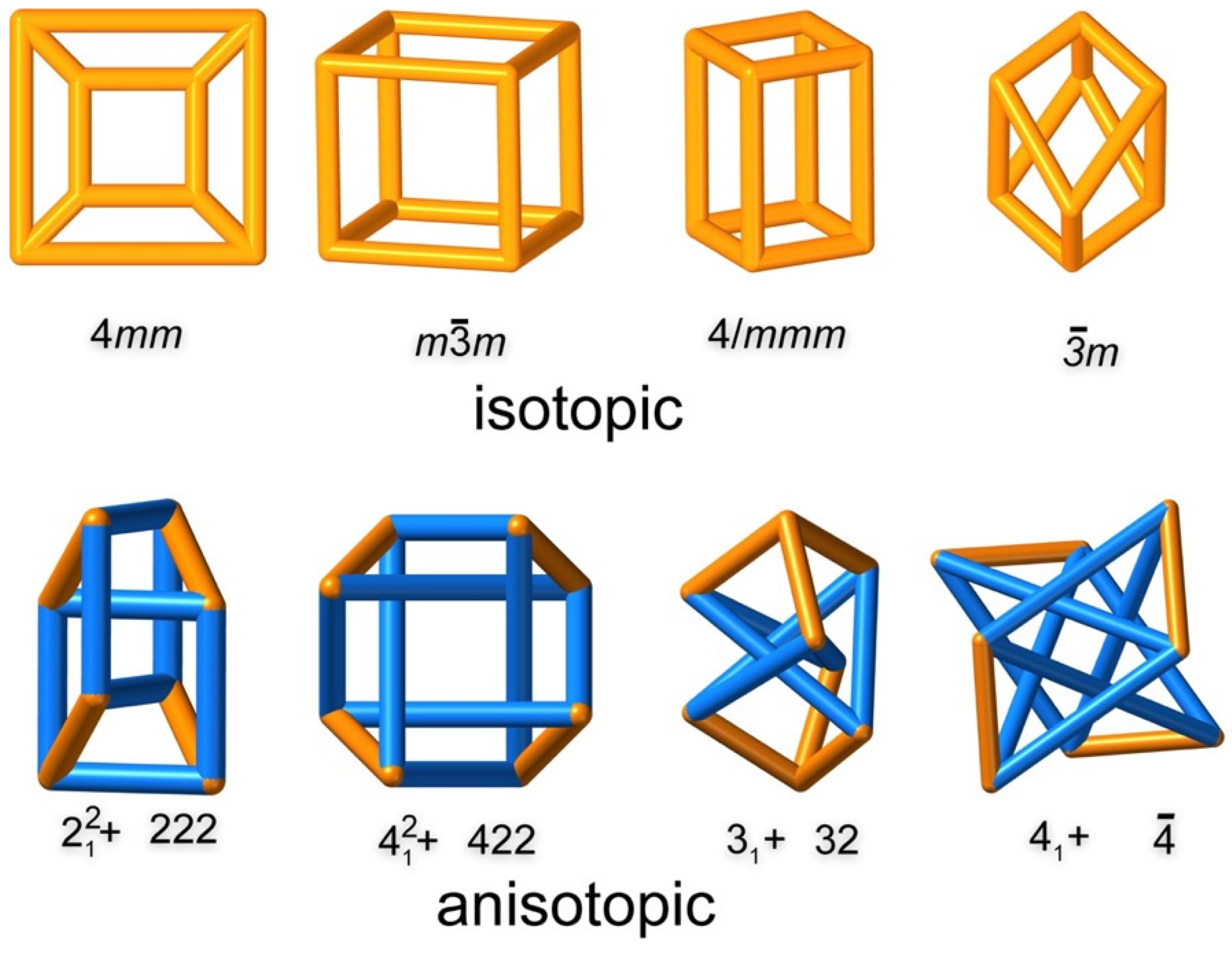
The geometry and symmetry of tangled graphs are also of interest [
19]. In
Figure 2 we show some embeddings with straight non-intersecting edges of the graph of the cube. Their symmetry is not necessarily cubic. The graph, as indeed all graphs of polyhedra, has a planar embedding, meaning that it has an embedding without essential edge crossings. However, many tangles are possible [
20,
21]. The top row of
Figure 2 shows embeddings of the cube graph that are not tangled. In mathematical terms, these are
ambient isotopic. By this, it is meant that one can be deformed into another by simple deformation, not breaking, or making, links. The qualifier “ambient” is necessary mathematically, as knots and links can be unknotted in four-dimensional space. However, we usually drop it, as we are referring here exclusively to structures in three-dimensional Euclidean space.
In addition, shown in
Figure 2 (bottom row) are tangled versions of the embedded cube graph [
21]. These all have knots, or links, as a substructure (shown in blue). Thus, the one on the left contains the Hopf link—the simplest link with crossing number 2. The next contains the Solomon link with crossing number 4. The last two contain the knots
, and
. It should be clear that none of these four are (ambient) isotopic with the top-row embeddings of the cube graph, or with each other, and we label them (ambient)
anisotopic. To be explicit: when we say that two or more structures are anisotopic, we mean that they are not ambient isotopic (to each other). Chemists would call isomeric (same elemental composition) molecules that are anisotopic,
topological isomers [
22]. Tangles with different crossing numbers are anisotopic. Additionally, those with the same crossing number may also be anisotopic—after all, there are more than a million anisotopic knots with 16 or fewer crossings [
23].
The
and
embeddings of the
knot are
isotopic as, by definition, are all embeddings of a given knot. This means that the
embedding of the achiral knot can be deformed into its mirror image without breaking the thread. Another possible source of confusion is that chemists have long used
isotopic in a different sense, e.g., in [
24]. Thus, ordinary water (H
2O) and heavy water (D
2O) are i
sotopic molecules as they contain isotopes (atoms of the same atomic number, but different mass) of the same element.
Anisotopic is also found to refer to an element with only one stable isotope, e.g., fluorine.
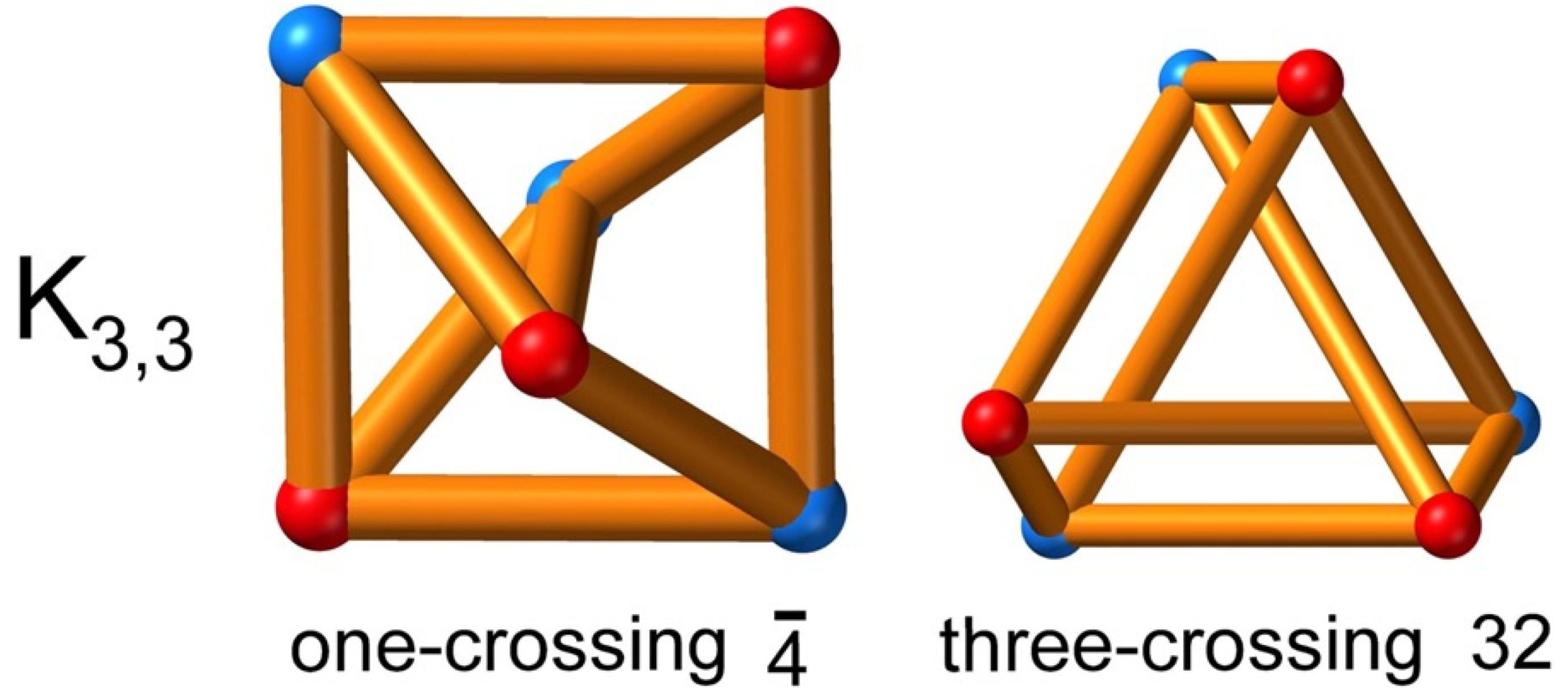
Non-planar graphs have essential crossings and the term “crossing number” is sometimes taken to mean the minimum crossing number of a projection of a three-dimensional embedding, and is thus a property of the graph. We illustrate this point with a simple non-planar graph—the complete bipartite graph K
3,3. This graph contains two sets of three vertices, A and B, with edges linking all A to all B, but no A–A or B–B edges occur. This is also known as the 3-Möbius ladder graph and has occasioned considerable discussion by chemists [
25]. The order of the automorphism group is readily found as follows: permuting the A vertices (3! permutations) or the B vertices (another 3!) does not change the adjacencies. Nor does interchanging A and B. The total number of graph-preserving permutations is then 3! × 3! × 2 = 72. An embedding in three-dimensional Euclidean space with symmetry of that order is impossible. The rotational symmetry would have to be at least 18-fold (in 18/
mmm), which is impossible with only 6 vertices. The highest-symmetry embeddings of the graph we can find have symmetry
(order 6, three crossings) and
(order 4, one crossing) as shown in
Figure 3.
The automorphism groups of graphs are generally given in terms of the basic abstract groups. These are:
, the cyclic groups of order
;
, the dihedral groups of order
;
, the group of
permutations of order
, and
, the alternating group of even permutations of order
. Note that
is the same as
, and
is the same as
. The structure of the cubic and icosahedral groups in terms of these abstract groups are:
where
indicates a group direct product. It should be clear that knowing the abstract structure of the symmetry group does not completely specify the nature of the embedded symmetry; thus, symmetry groups
and
have the same abstract structure,
. This means that knowing the abstract automorphism group of a graph tells us only which symmetries of an embedding are impossible, not which are possible.
We take as a final example of a finite graph the trivalent 12-vertex Franklin graph. This is a non-planar graph with an automorphism group
. This, however, is not
as there are embeddings with symmetry
(which is not a subgroup of
) [
21] and
examples are shown in
Figure 4. The Franklin graph has a minimum of 3 crossings, and an embedding with symmetry
with this property is depicted in
Figure 4. It is easy to show that these three are anisotopic embeddings of the graph. The
embedding contains, as a substructure, the torus link T(6,3) of 3 rings and 12 crossings. The
embedding has, as a substructure, the 6-crossing Borromean rings, and the 32 embedding contains the three 4-rings as not directly linked, but connected through a 3-crossing (trefoil) knot. These three embeddings are anisotopic, but are they the same graph? (These were generated by us from the Franklin graph, so we know they share the same graph. However, the question here is: “how does a third-party reader, looking at the images, confirm this?”). A simple test is provided by the vertex symbol [
26], readily found by the computer program
ToposPro [
27] to be
at each vertex. Agreement between vertex symbols fails to falsify the assertion that they are the same graph. To be sure they are the same, all possible graphs should be checked to make sure that the one with all vertices having that vertex symbol is unique, if indeed it is. However, there are 94 trivalent graphs with 12 vertices and over
with 24 vertices. In the case of the embeddings of the Franklin graph, it is easy to prove that all three graphs are the same by numbering the vertices, as shown in
Figure 4, where the vertices are numbered sequentially around the 4-rings from blue to green to red. It can be verified that, for example, vertex 1 is connected to vertices 2, 4, and 12 in every case. However, the number of labelings of a graph with
vertices is
, so the general problem, the
graph isomorphism problem, is famously difficult. Proving that two knots or tangles are the same is equally challenging.
To summarize the main messages of this section: graphs and their embeddings are very different. There is generally a “one-to-many” correspondence, as graphs can have multiple (ambient) anisotopic embeddings. A graph has an automorphism group, and embeddings have an isomorphous symmetry group or a subgroup. Different embeddings of planar graphs, all without crossings, are isotopic: graph embeddings with a different number of essential crossings are necessarily anisotopic. In particular, it is misleading to refer to a graph as a “topology” or as a “topological type”, as is sometimes done, particularly by chemists. It is the particular embedding of that graph, and the associated set of ambient isotopes, that is “the topology”.
4. Symmetries of 1-Periodic Embedded Graphs and Weavings
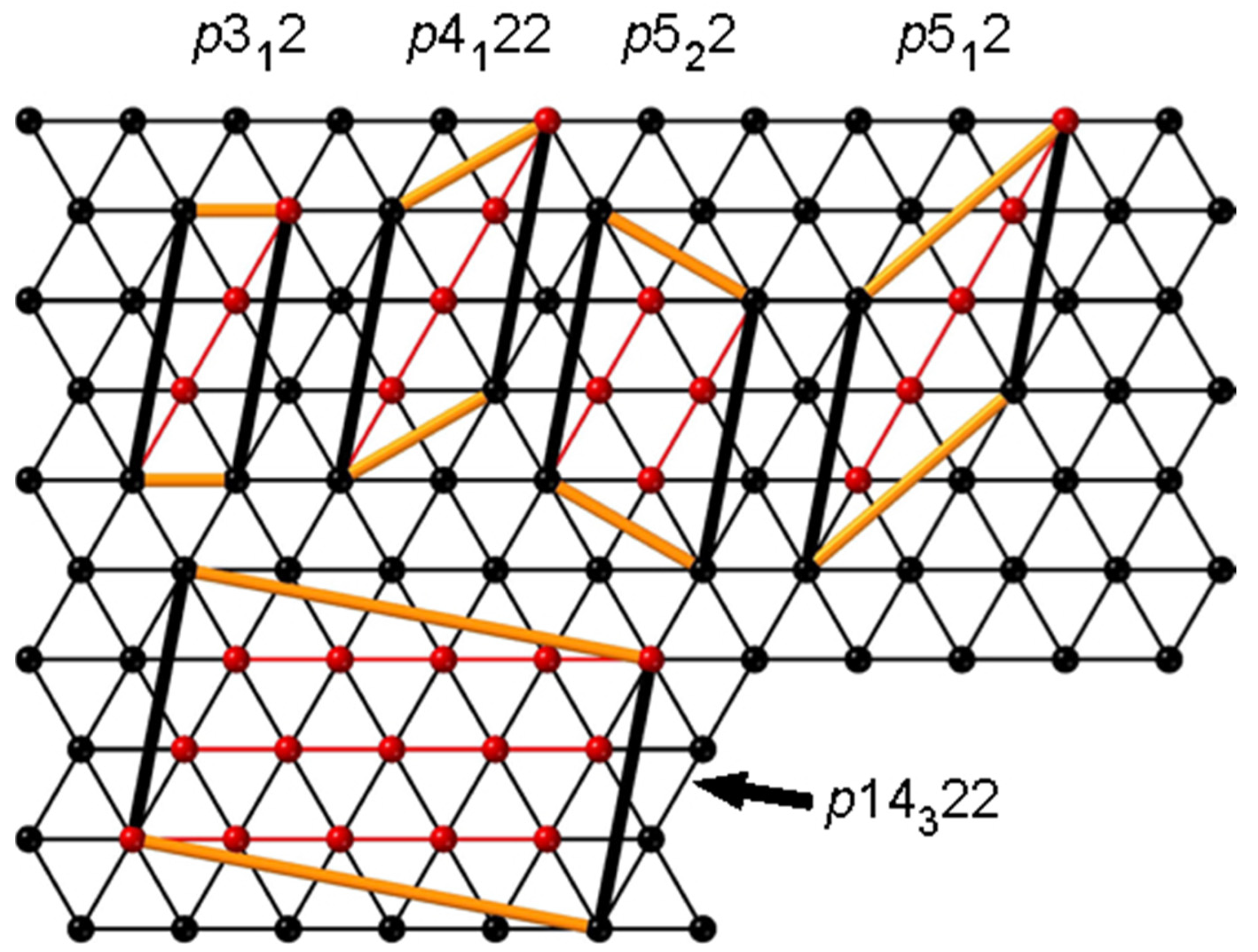
As noted earlier, descriptions of 1-periodic symmetries are generally limited to the 75 groups with 1-, 2-, 3-, 4-, or 6-fold rotation symmetries. However, in general, there is no “crystallographic restriction” and local regions of 1-periodic 5- or 8-fold symmetry have been reported in real crystal structures [
28,
29,
30]. Systematic descriptions have been given of isogonal (vertex-transitive) piecewise linear embeddings of 1-periodic structures and their occurrences in materials [
13,
31,
32]. Here, we just illustrate, with examples of common materials with 1-periodic structures.
We start with structures based on cylindrical tilings—specifically, 3
6 tilings, by triangles and their duals, 6
3 tilings by hexagons. The vertices of 3
6 tilings are the centers of cylindrical close packings of equal spheres, and a detailed account of the geometry of such structures, and their occurrence in biological structure, was given almost 50 years ago [
31]. More recently, the dual structures, 6
3 tilings, have attracted considerable attention as the structures of carbon tubules (“nanotubes”) [
32].
We consider first some embeddings of 36 tilings. The tiling (graph) can be specified by its derivation from the plane tiling. For the plane tiling, the hexagonal cell has axes a and b at 120°. The tilings are specified by the girdle vector , which is orthogonal to, and goes around, the cylinder axis. They fall into two groups. Achiral structures, [u, 0] and [u, 2u], have maximum symmetry with vertices in the unit cell. Chiral tilings by regular triangles (sphere packings with six contacts) are not periodic, but the question of the possible symmetries of the hexavalent graph is of interest. We note that, in the carbon nanotube literature, it is common to use instead axes at 60°, and specify tilings as with , .
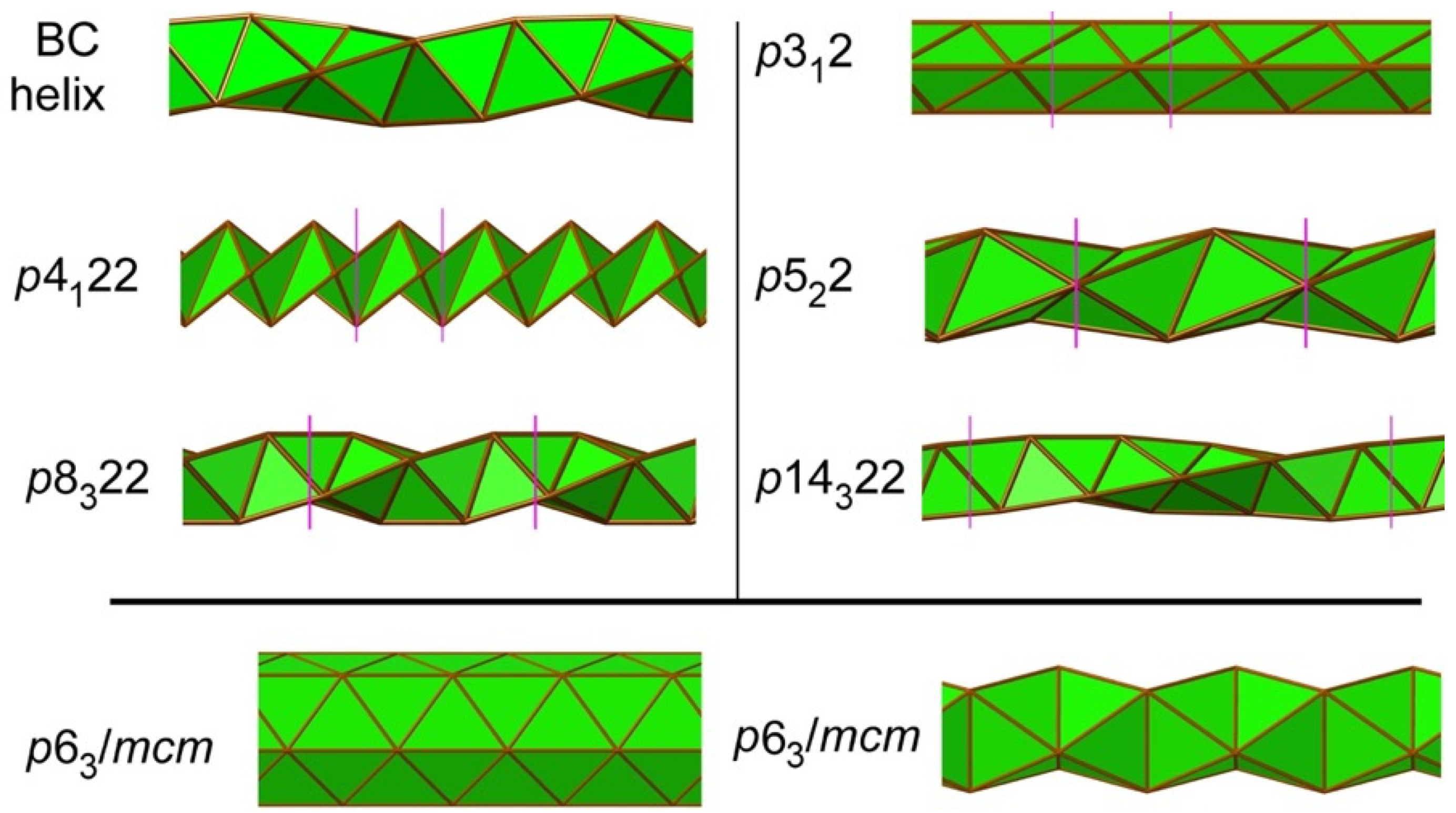
We focus on the simplest chiral structure, [3,1] (or, (2,1)). With regular triangles, this can also be considered a rod of face-sharing regular tetrahedra and is known as the Boerdijk–Coxeter (BC) helix, the terahelix, or the Bernal spiral. In
Figure 5, we show some unit cells for periodic embeddings; these have axes [3,1] and
and contain
vertices. It is straightforward to show that the possible symmetries are
with
and
co-prime (and, of course, their subgroups), so, in contrast to the achiral cases, there is no “best” periodic symmetry. An exactly rectangular planar cell has
(14 vertices) so a
tiling on the surface of the cylinder has equal curved edges. In every case, the vertices are on 2-fold axes normal to the cylinder axis, so in this sense, all periodic embeddings are equally “good”—translations are being replaced by screw operations or
vice versa.
Figure 6 illustrates some of these embeddings.
In the non-periodic sphere packing, centers are related by a rotation of cos
−1(−2/3)
131.8°. In a
embedding, the rotation along the axis is 360
3/8 = 135° so, with that structure, approximately equal edges are possible, and indeed that embedding in the subgroup
is found in structures such as β-Mn [
3], and metal-organic frameworks [
30].
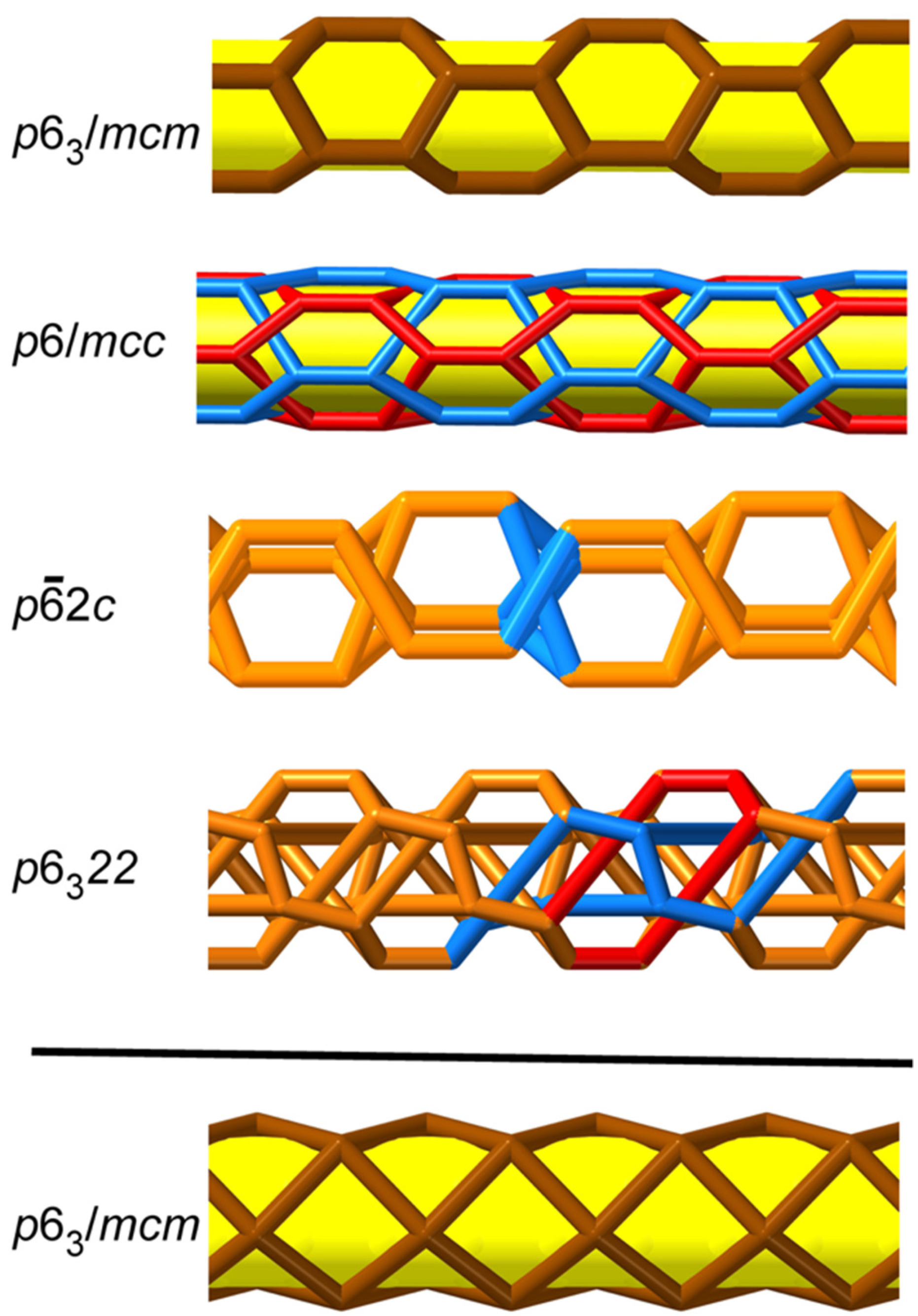
The embeddings of the [3,1] 3
6 tilings given above are all isotopic—one can be transformed into another by a simple twist. In
Figure 7 we show some different embeddings of the [3,0] 6
3 nanotube. These, in contrast, are anisotopic. In one case, a 6-ring is replaced by a 3
1 (trefoil) knot, and in another 6-rings are catenated.
The only
regular (vertex-, edge-, and tile-transitive) cylinder tilings are 4
4 tilings with symmetry
(
); the case
is shown in
Figure 7.
In summary, the difference between the chiral and achiral cylinder tilings is this: the embeddings of the chiral graphs can be twisted to give any order of rotational symmetry; whereas, the achiral graphs have a unique maximum-symmetry achiral embedding.
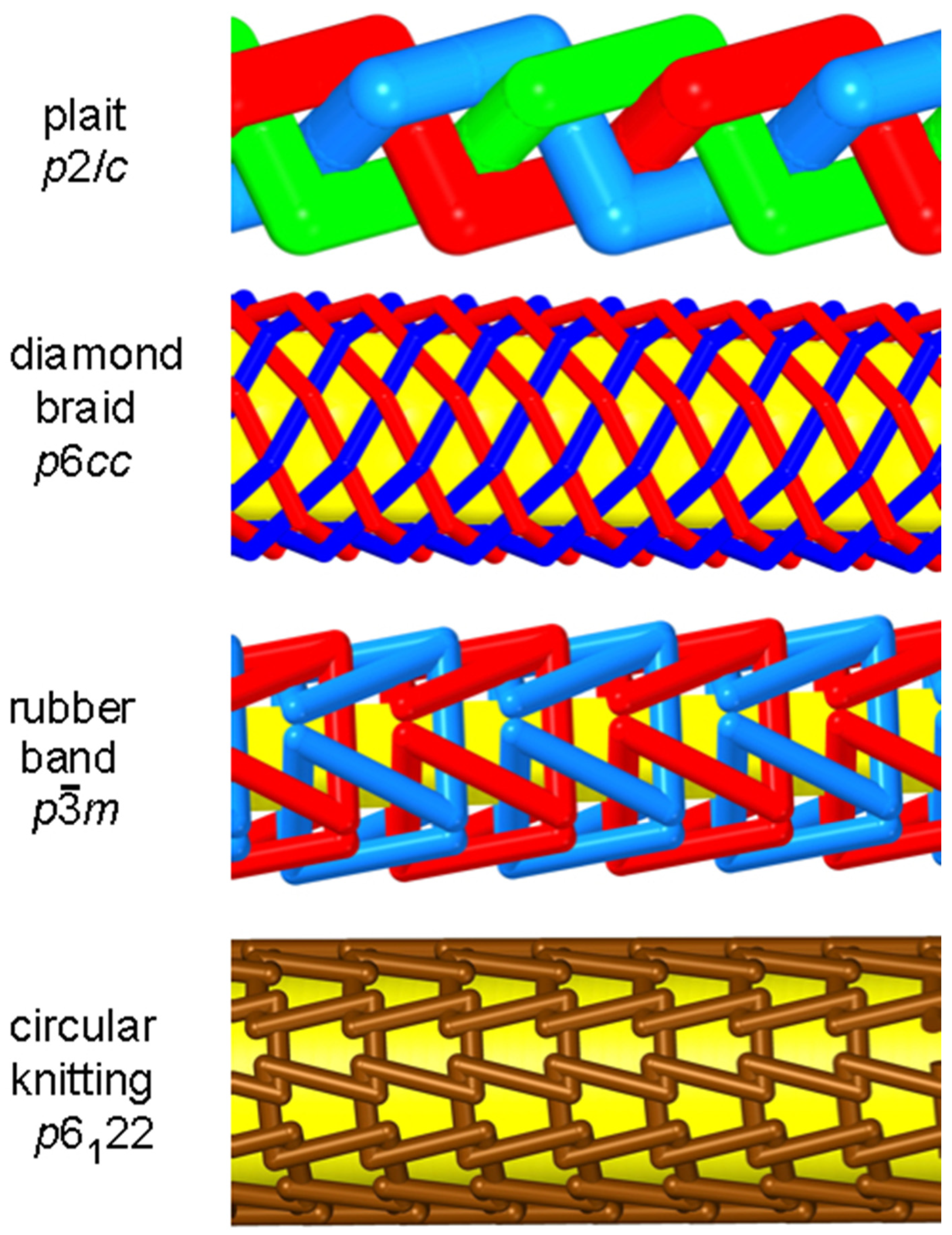
We conclude this section with some other familiar 1-periodic structures.
Figure 8 shows the structure of a plait—a structure commonly found in hairstyling, belts, etc. It is shown with three strands, but structures with any odd number of strands have the same symmetry,
c in piecewise linear embeddings [
33]. Further, shown in
Figure 8 is an example of the structure of “diamond braid” ropes. These have an even number, 2
N, of strands, generally between 4 and 48 [
34], and have piecewise linear embeddings with symmetry
, [
33].
Circular (better, “helical”) knitting has been known for a hundred years and is now commonplace. In this mode, a single thread, and a single curved “needle”, are used to construct a helical pattern. The simplest structure has “knit” stitches with symmetry
(
even) [
35]; the case for
N = 6 is shown in
Figure 8. Finally, in this section (also in
Figure 8), is an example of a 1-periodic link (chain) known as a rubber-band link. A better term might be the true “circular” (rather than helical) knitting. This has the Brunnian property that if one link is removed the rest become unlinked. These have the symmetries
m (
N odd) or
m2 (
N a multiple of 4) [
31]; the case
N = 3 is illustrated in
Figure 8.
6. Symmetries of 3-Periodic Graphs and Their Embeddings
The general topic of 3-periodic graphs is a huge topic [
36], generally ignored by mathematicians. Here, we discuss first the automorphism groups of 3-periodic graphs and the symmetries of their embeddings—again, as is normal, piecewise linear. In a
barycentric embedding, vertices are placed at coordinates that are the average of the coordinates of their neighbors; this is sometimes called an
equilibrium placement. A key result is that if no two vertices have identical coordinates (absence of
collisions) the automorphism group is isomorphic to a crystallographic space group [
37]; such graphs are termed
crystallographic nets. The symmetry of such 3-periodic graphs can be found using the program
Systre of Olaf Delgado-Friedrichs (ODF) [
38]. It was further shown by ODF, and implemented in Systre, that for such nets a unique invariant, the Systre key, can be determined [
38,
39]. The importance of this result is that most of the graphs of interest in chemistry and materials science are crystallographic (some exceptions are noted below), so for these, we can unambiguously determine the identity and maximum symmetry of an embedding. It might be noted that not all periodic graphs with collisions are non-crystallographic. Occurrences in real materials (chemical structures) are rare [
40]. A simple example of a non-crystallographic graph is one in which two vertices have the same neighbors; simply interchanging these two vertices keeping all others fixed is a local (non-rigid-body) symmetry [
40]. At the other extreme are
ladder graphs in which the interchange of two or more components with equal numbers of vertices is a graph automorphism [
40,
41]. The HM notation is now universally used for 3-periodic structures with crystallographic symmetry.
A
net is a simple (no loops or multiple edges), connected graph [
42], generally considered (as herein) to be periodic [
43]. A large library of mainly crystallographic 3-periodic nets has been assembled in the Reticular Chemistry Structure Resource (RCSR) [
44]. These are generally assigned a three-letter symbol such as
xyz, sometimes with an extension as in
xyz-q. It is very common to see, in the chemical literature, statements such as “structures with the
pts topology” [
45], and the RCSR symbols have to be interpreted as referring both to a graph (net) and
also to a particular embedding of that graph (a “topology”). In RCSR, crystallographic nets (graphs) are normally given an embedding (topology) with full symmetry. However, sometimes an alternative embedding is given and identified by an appended
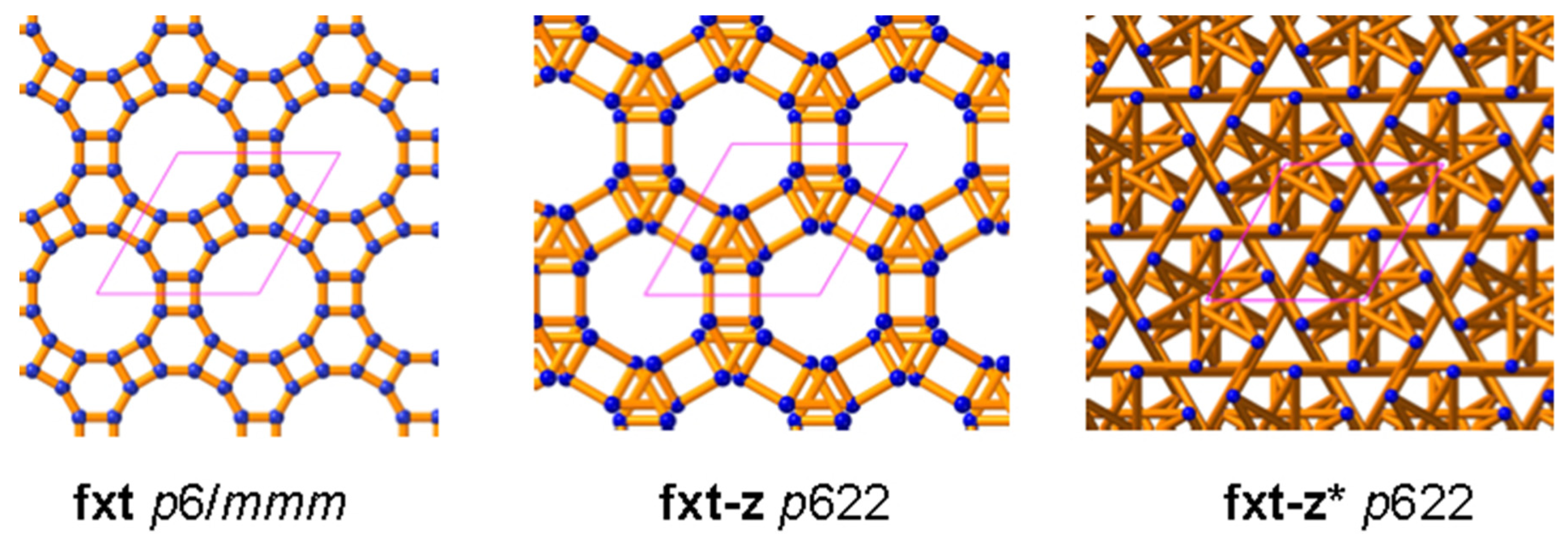
-z. An example is the 5-valent net
gan with symmetry
[
36]. However, in that embedding, all edges cannot have equal length and the five-coordinated sphere packing 5/5/
c1, which has the same net and equal edges, has symmetry
. RCSR assigns that embedding the symbol
gan-z. So far, no problem, but the ubiquitous
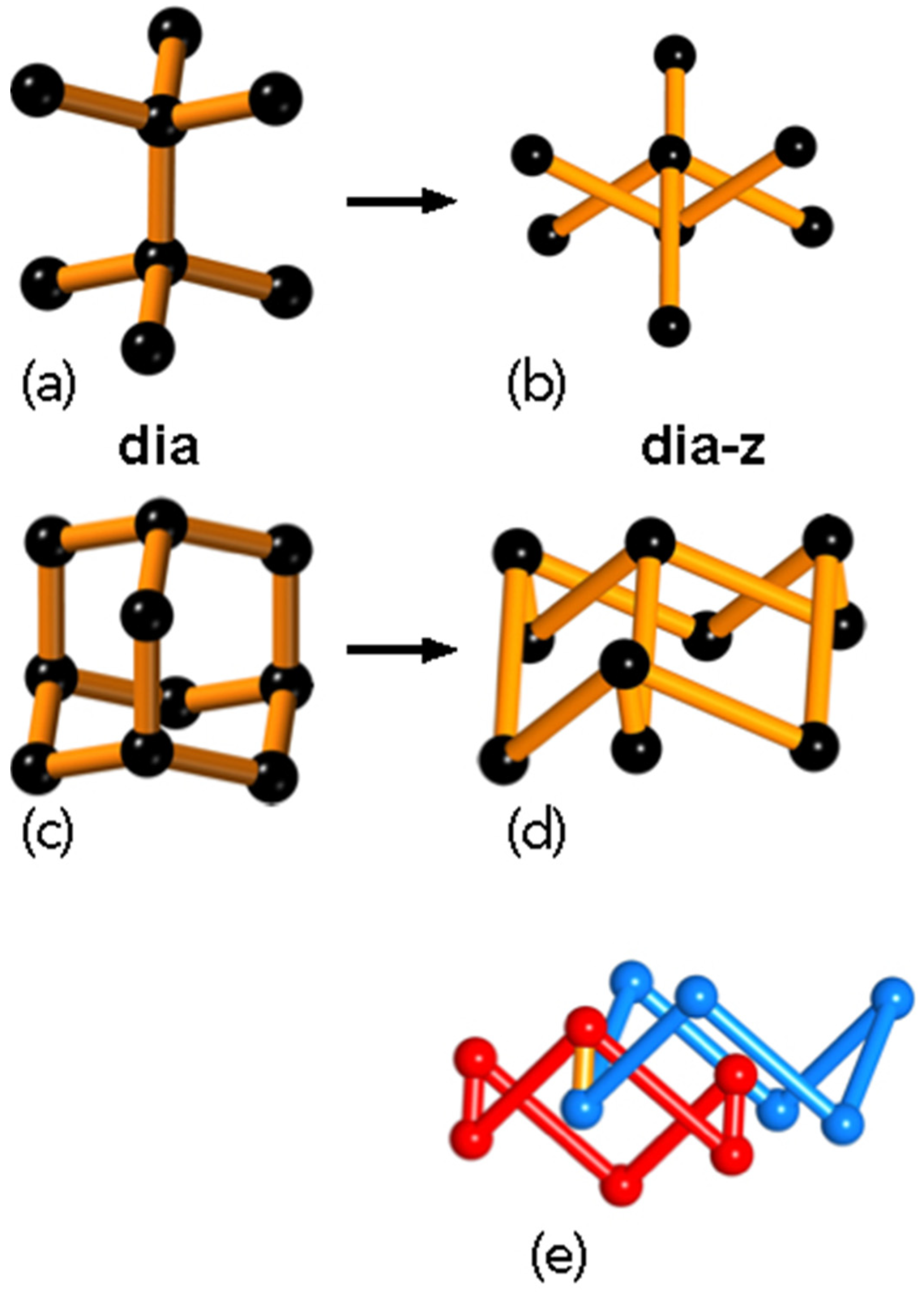
dia net (the net of the diamond structure) with symmetry
, also occurs in a tangled (
not isotopic) version with symmetry
[
46]. The shortest cycles in the
dia net are 6-rings, and in the
dia embedding, they are not catenated with each other as shown in
Figure 11. However, as also shown in
Figure 11, in
dia-z the 6-rings are catenated, so that embedding is topologically distinct (anisotopic) to the
dia embedding. We emphasize that programs such as Systre and ToposPro identify the graph, not the topology of the embedding. ToposPro can often distinguish between two topologically-distinct embeddings of the same graph, such as
dia and
dia-z, based on the catenation of rings. However, not all tangles contain catenated rings.
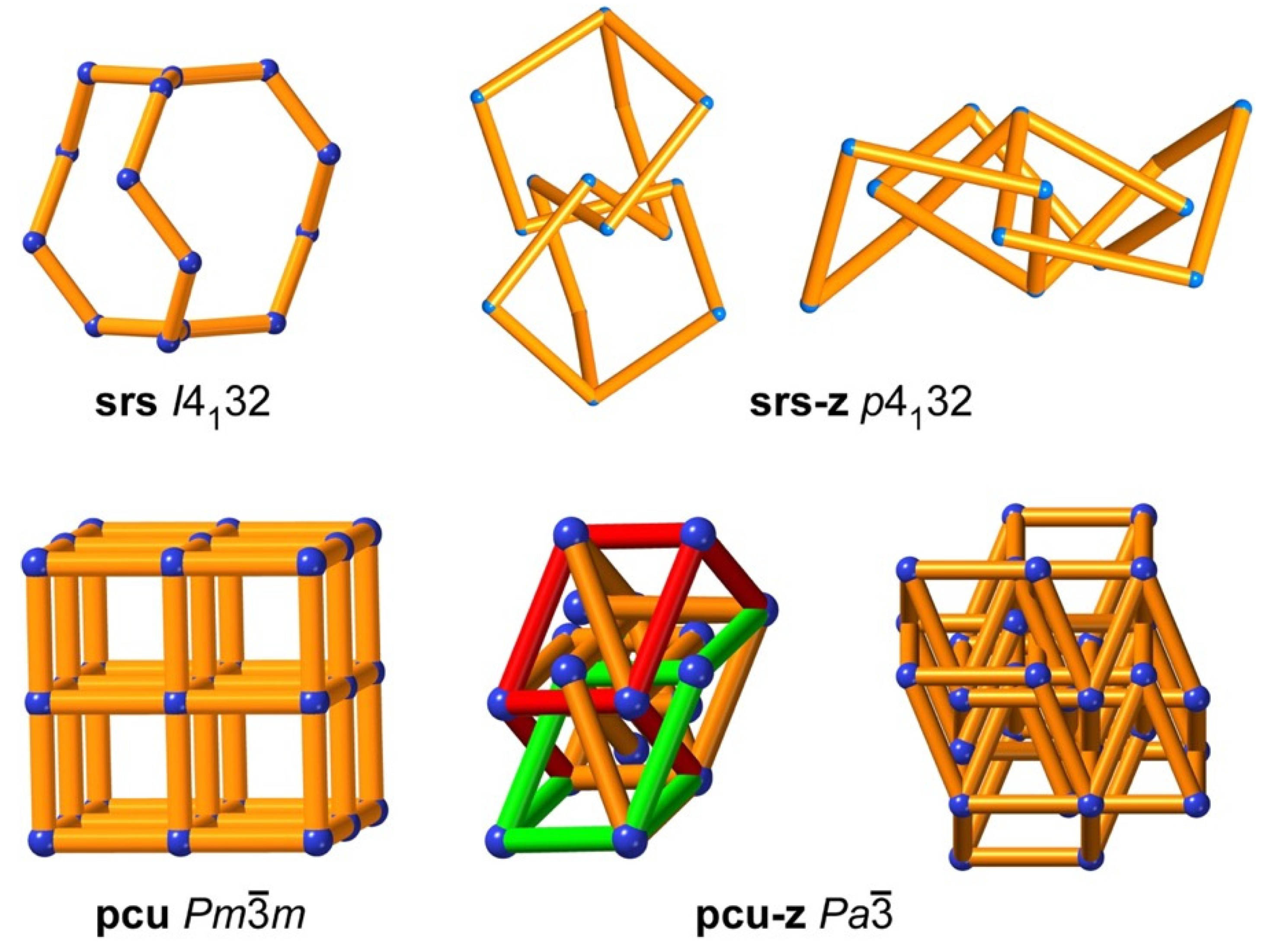
In
Figure 12 we present two further examples of common nets with topologically distinct embeddings. The net,
pcu, of the primitive cubic lattice with symmetry
, has no catenated 4-rings in its maximum-symmetry embedding, but there is a topologically distinct embedding,
pcu-z, with symmetry
in which the 4-rings are catenated. Another commonly occurring net is the trivalent
srs (symmetry
), which contains cages of three 10-rings. In the embedding
srs-z (symmetry
P4
132), the cage graph is entangled, as shown in
Figure 12. Interestingly, both these tangled embeddings are vertex- and edge-transitive.
Although crystal structures based on tangled 3-periodic nets are rare, so far there are many occurrences of two or more nets interpenetrating (catenated) [
47]. The possible symmetries of such structures have attracted some attention [
48,
49]. The question of whether two patterns of interpenetration are isotopic or anisotopic to each other is often solved by examining the pattern of catenation of rings—for example, the “Hopf ring net” (HRN) [
50]. Such catenated patterns are identified in RCSR by symbols such as
dia-c for a pair of interpenetrating diamond nets., and
dia-c3,
dia-c3*, and
dia-c3** for three distinct anisotopic structures comprising three distinct interpenetrating diamond nets.
Reticular chemistry itself is concerned with the designed synthesis of materials such as metal-organic frameworks (MOFs) and covalent organic frameworks (COFs) by linking together symmetrical modules (secondary building units—SBUs) [
51]. The most important nets for materials design are edge-transitive [
52], More generally, nets with minimal transitivity, with given vertex transitivity, are a central topic in theoretical reticular chemistry. Enumerating such structures is a large topic [
53].
7. Nets with Edge-Intersecting, or Vertex-Colliding, Embeddings
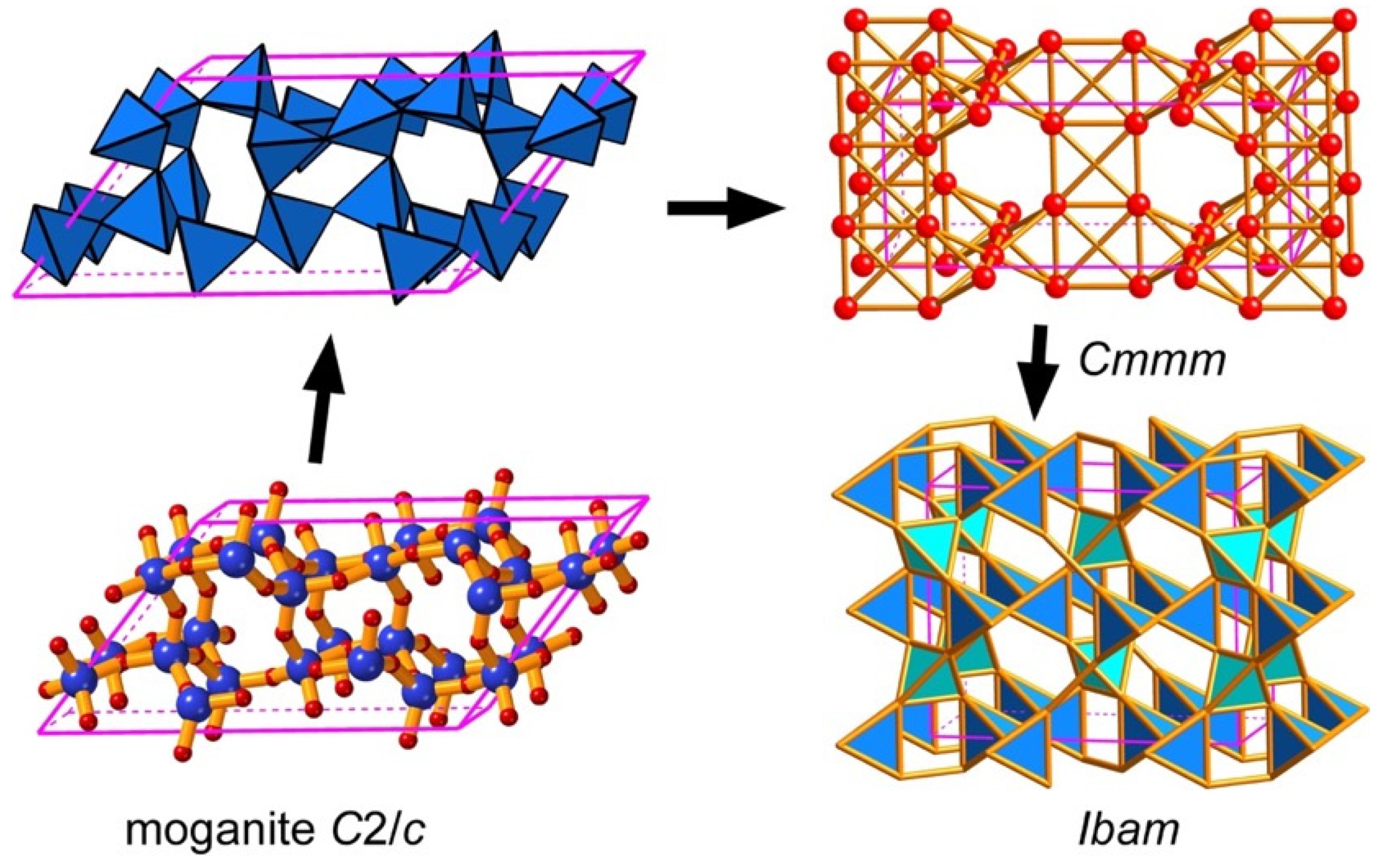
Embedding of nets suitable for serving as the underlying net of a crystal or molecular structure must satisfy some basic conditions. They must, for example, contain no edge intersections. The anion net of the mineral, moganite, a form of silica, SiO
2 provides a good illustration [
38].
Figure 13 shows the structure of the real material, symmetry
C2/
c. and the pattern of anions as a net of corner-connected tetrahedra. In the maximum-symmetry embedding,
Cmmm, some tetrahedra become planar rectangles, and to accommodate tetrahedral shape one must go to a doubled cell with symmetry
Ibam (an order two subgroup of
Cmmm) as shown in
Figure 13. Similar phenomena occur in the anion nets of some zeolite nets [
54].
A good way to think of barycentric coordinates in 3-periodic nets is to consider a realization in which vertices are linked by uniform harmonic springs under the constraint of fixed volume. The vertices will relax to barycentric coordinates (hence the term
equilibrium placement [
37]. It should be clear then that if pairs of vertices have the same neighbors they will collide. A simple example is the net
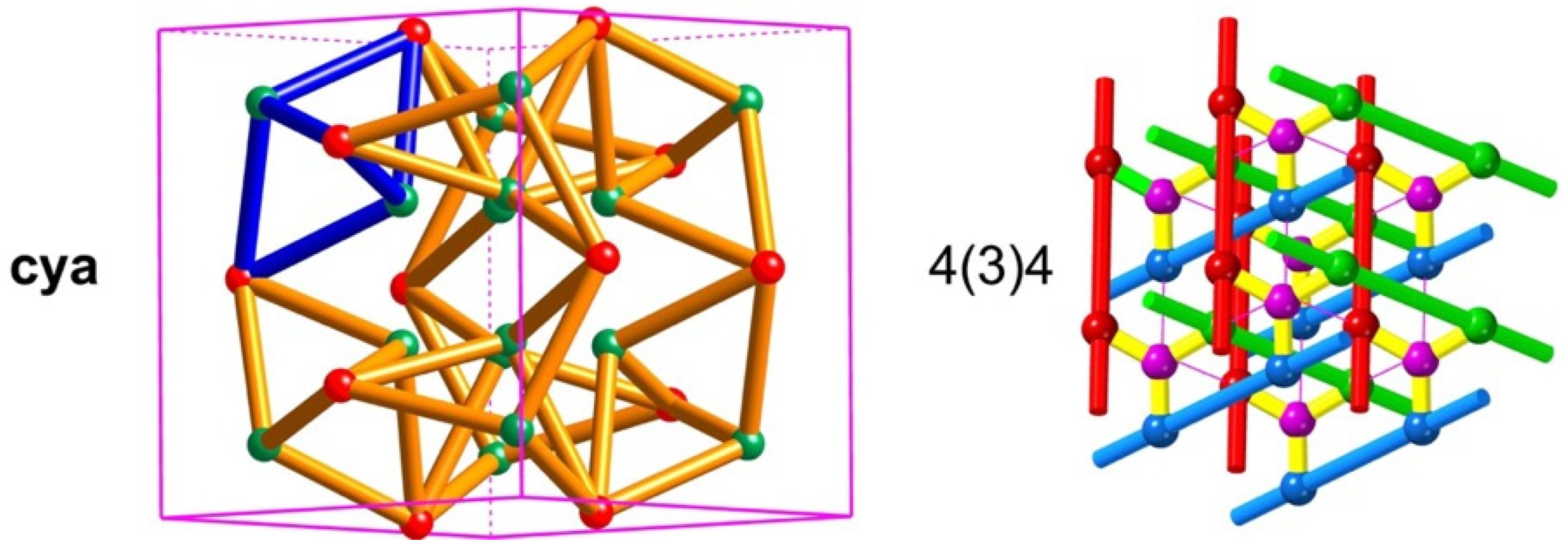
cya illustrated in
Figure 14. This is one of a group of such nets of importance in reticular chemistry [
55]. Clearly, in this case, there are non-rigid-body symmetries (interchanging pairs of vertices) and Systre does not handle such cases. A slightly more complicated case is the
minimal net labeled 4(3)4 [
56]. In this case, in barycentric coordinates, groups of four vertices collide and edges shrink to zero length, [
57].
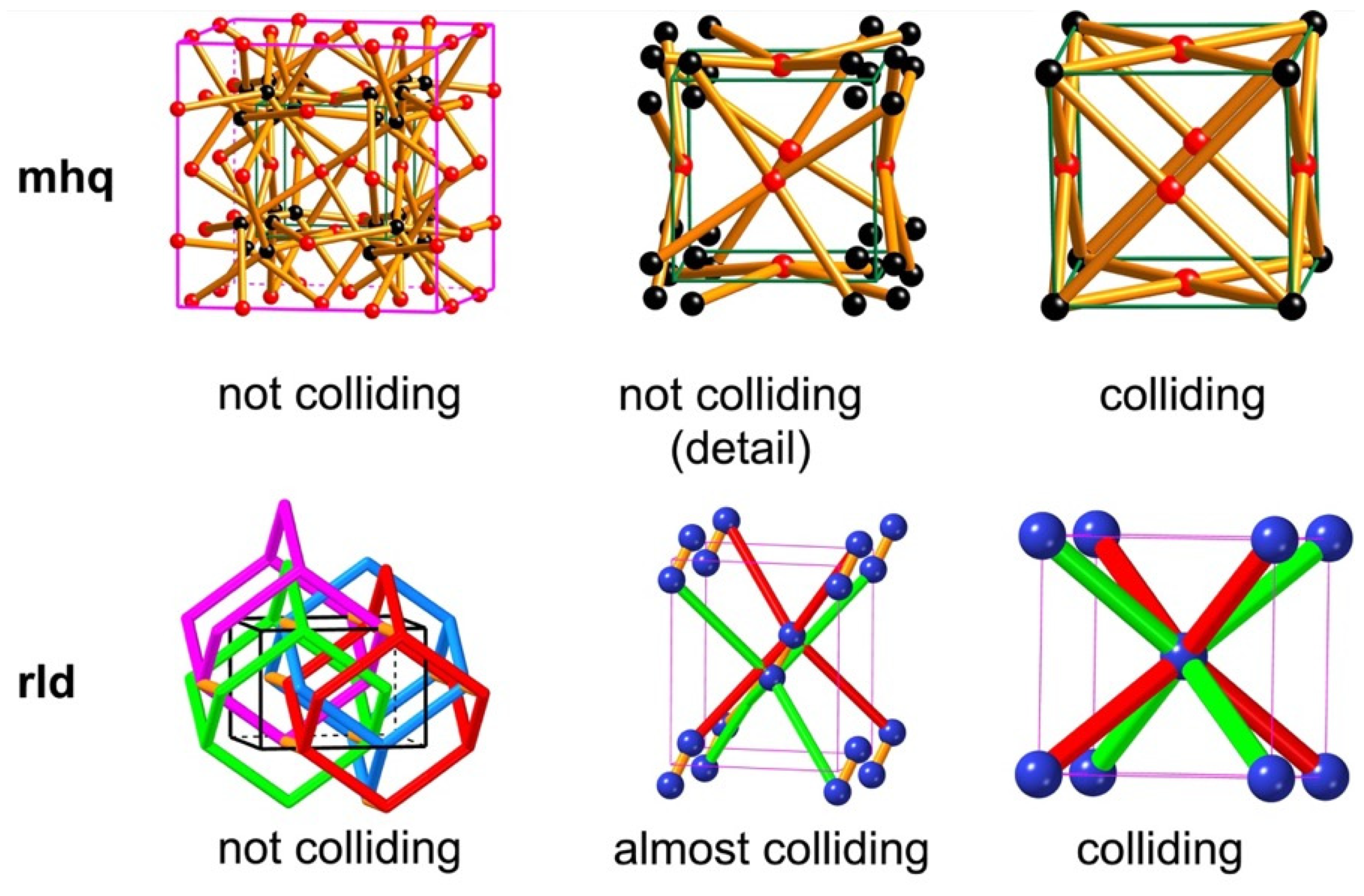
The next two examples of nets with collisions come from crystal structures [
40]. These nets have crystallographic symmetry but, in a maximum-symmetry embedding, vertices collide. In the first case, edges all remain finite; in the second, there are some zero-length edges. In the first example (
Figure 15) the net
mhq is shown in maximum symmetry without collisions:
. In barycentric coordinates groups of four vertices collide, and the symmetry is now
, with half the unit cell edge. The second example here is a remarkable net
rld. In the reported structures it has symmetry
with vertices (eight per cell) falling on four interpenetrating diamond (
dia) nets linked by an extra edge to make a five-coordinated structure (
Figure 15). Upon relaxation of the net to barycentric coordinates, that fifth edge shrinks to zero length, and the symmetry becomes
with just two vertices in the primitive cell.
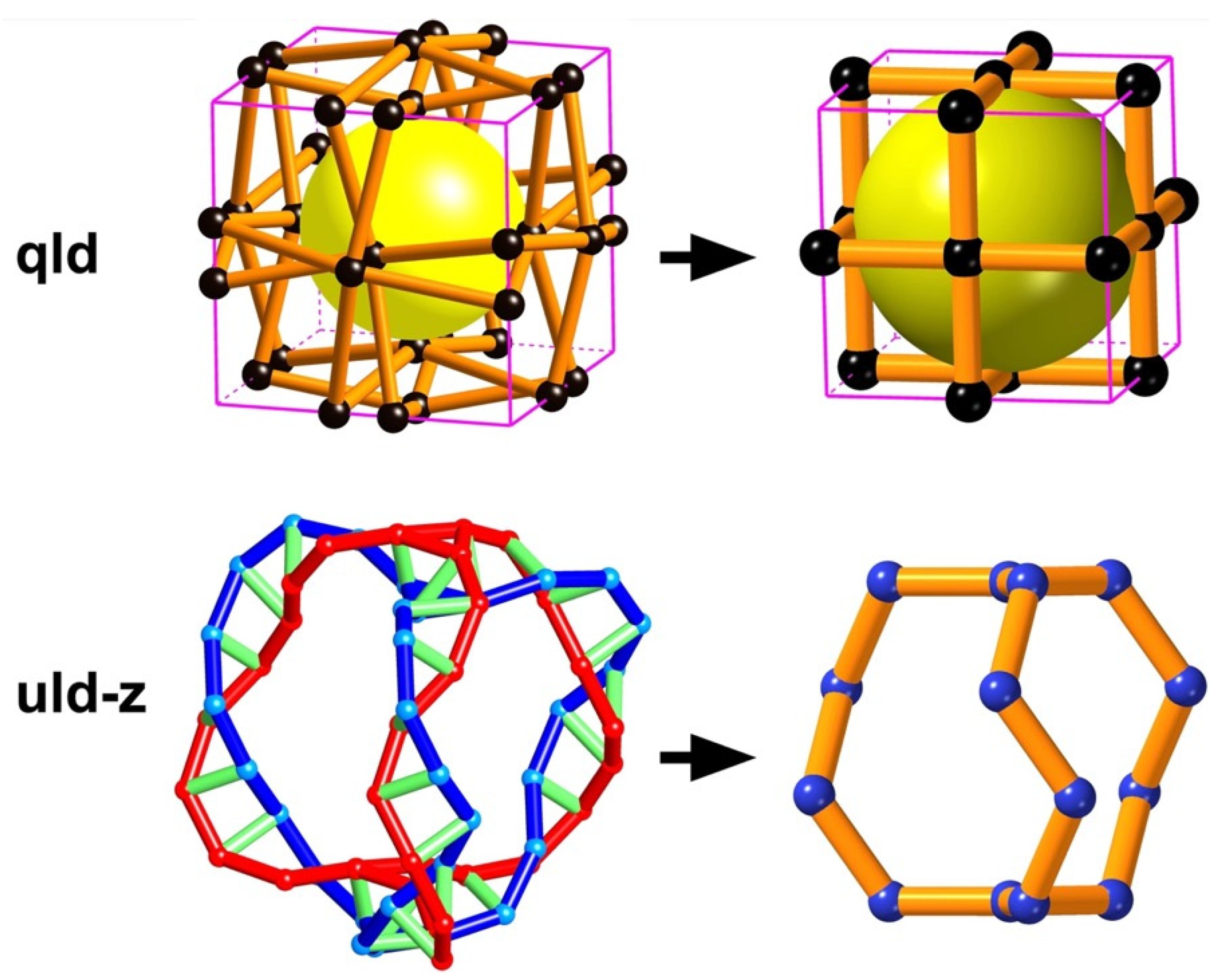
We conclude this section with examples of “ladder” nets [
40,
41]. In these, vertices of two or more equal fractions of the net collide. The collisions may occur either with or without zero-length edges. The first example, shown in
Figure 16, is a simple vertex-and edge-transitive net
qld shown in an embedding with symmetry
. In barycentric coordinates, the vertices come together in pairs, and edges coincide. The full symmetry is
combined with the “ladder” operation of interchanging all pairs of vertices. The second example in
Figure 16,
uld-z, is the net of a vertex-transitive sphere packing with symmetry
. The net contains “ladders” shown with red and blue “risers” and green “rungs”. In barycentric coordinates, the rungs shrink to zero length and the ladder “risers” collide. The symmetry is
, combined with the “ladder” automorphism of interchanging risers. Systre can derive a key for ladder nets so such nets (graphs) can be unambiguously identified.