Nested Polyhedra and Indices of Orbits of Coxeter Groups of Non-Crystallographic Type
Abstract
1. Introduction
2. Even-Degree Indices for Orbits
- the size of an orbit of any Coxeter group is always limited;
- the points of an orbit have only real numbers as their coordinates;
- the product of several orbits can always be decomposed into the sum of orbits of smaller sizes.
3. Odd-Degree Indices for Orbits
- The anomaly numbers
- The odd-order indices , for and .
- For the Coxeter groups and , as any orbit contains the elements with positive and negative signs, the anomaly numbers obtained for any orbit are equal to zero:
4. Embedding Index
- consider the points of an orbit ;
- remove the first coordinate of each point in the case of , and the third one for the crystallographic group ;
- among all the points in select those with non-negative coordinates; such points provide the orbits of in .
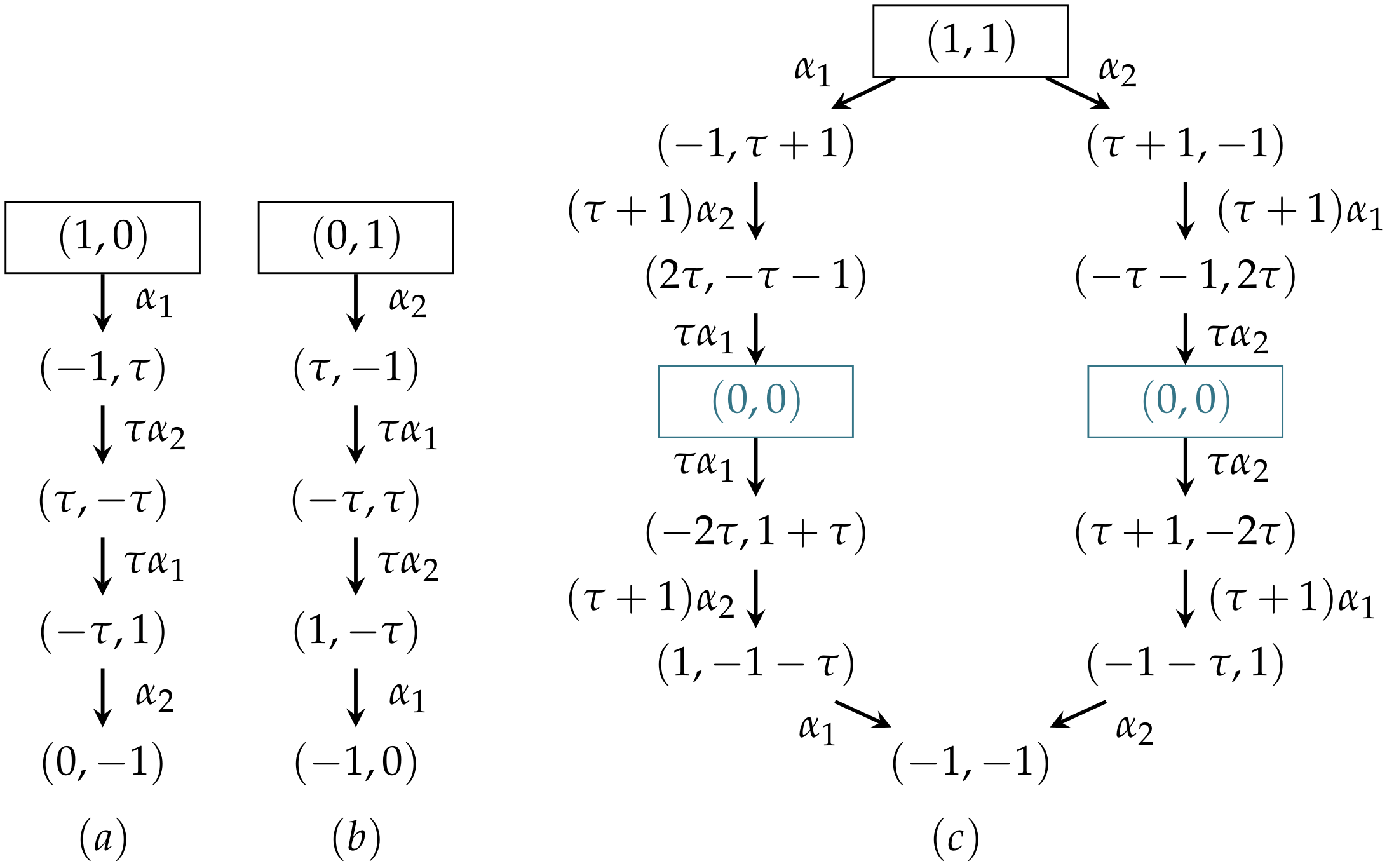
5. Lower Orbits of and
- determination of the highest weight;
- subtraction of simple roots from the highest weight;
- an algorithm that describes the subtraction path.
- determine a dominant point , , ;
- establish a correspondence between the coordinates of a dominant point and the indexof a simple root : ;
- if at least one of , , then proceed the following subtraction:
- if , then ,
- if :
- -
- and , then ,
- -
- and , then ,
- replace a point in with ;
- repeat the steps – until at least one of the coordinates is greater than zero.
6. Concluding Remarks
- The decomposition of a tensor product of representations of a simple Lie algebra into a direct sum of irreducible components given by Young tableaux symmetries plays an essential role in physics. As the indices of the representations help to determine such a decomposition [31], we demonstrate that their definitions can be extended to orbits of the non-crystallographic Coxeter groups. As a result, the notation of the even- and odd-order indices of representations are reformulated for the orbits of , .
- It would be useful to generalize the properties of higher-order indices and anomaly numbers of orbits, similarly to [18,23]. Along with these properties, one could potentially obtain the formulas for the explicit forms of higher even-order indices of a tensor product of orbits. Moreover, the expressions for the even-order indices, anomaly numbers and embedding indices could be reformulated and adapted to orbits of any finite reflection group of crystallographic type.
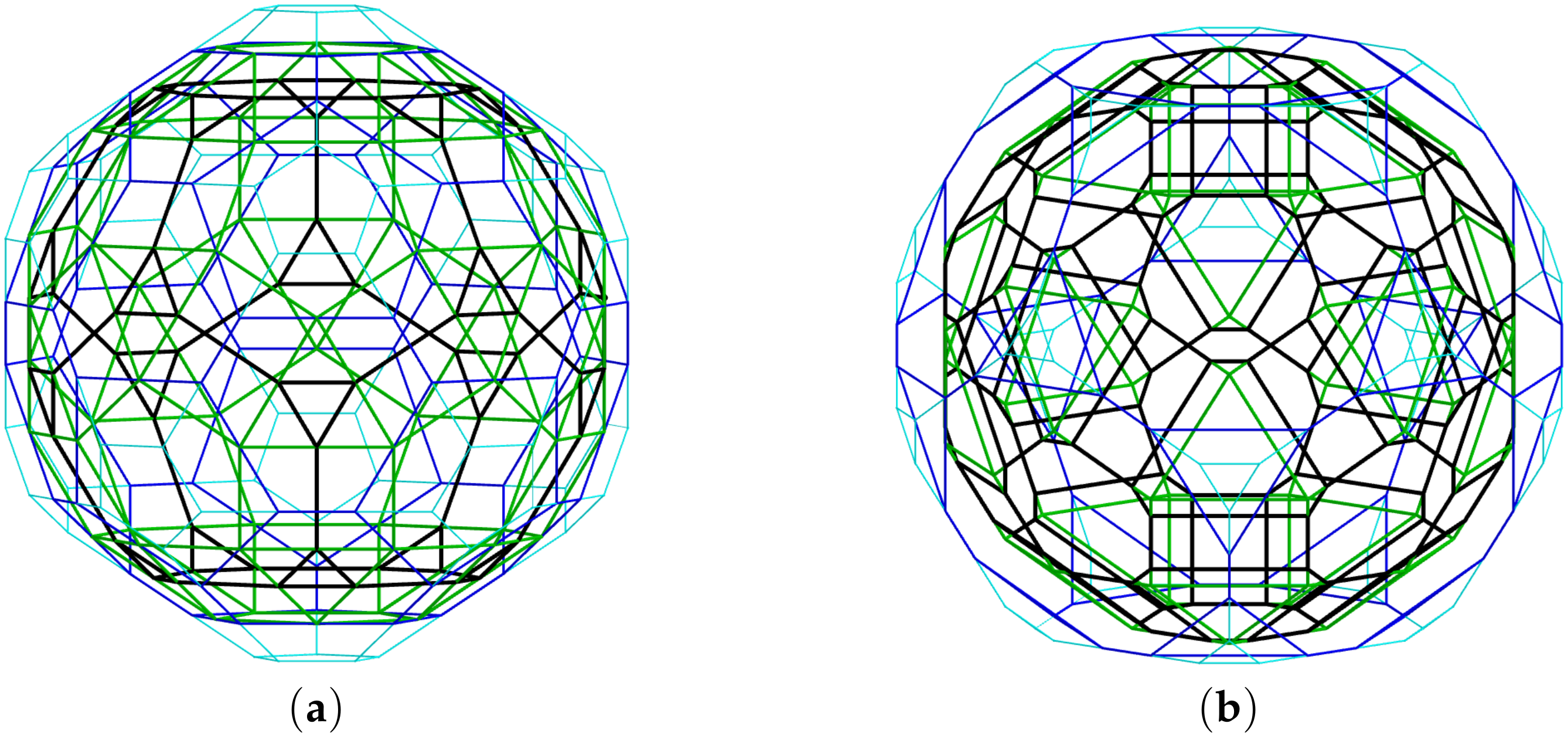
- Even though the Coxeter groups of non-crystallographic types do not have underlying Lie algebras, the recursive algorithm introduced in Section 5 is shown to be similar to the algorithm developed for the weight multiplicities of simple Lie groups [34]. It is important to mention that our algorithm also provides the seed points of orbits that are smaller in radius than an initial orbit (referred to as ‘lower orbits’). The geometrical construction of sets of lower orbits results in the structures of nested polytopes. Since the recursive rules are only applied to a dominant point of the non-crystallographic groups and , one could consider applying them to any seed point of the group as well. As the size of an orbit , for , the generalization of the formulas for the coordinates of the seed points of lower orbits is considered as future research. Moreover, it would be an interesting task to generalize the formulas given in Table 4 for any , as it was done for the case.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Talis, A.L.; Kraposhin, V.S.; Kondrat’ev, S.Y.; Nikolaichik, V.I.; Svyatysheva, E.V.; Everstov, A.A. Non-crystallographic symmetry of liquid metal, flat crystallographic faults and polymorph transformation of the M7C3 carbide. Acta Cryst. A 2017, 73, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Nespolo, M.; Souvignier, B.; Litvin, D. About the concept and definition of noncrystallographic symmetry. Z. Kristallogr. Cryst. Mater. 2008, 223, 605–606. [Google Scholar] [CrossRef]
- Terwilliger, T.C. Finding non-crystallographic symmetry in density maps of macromolecular structures. J. Struct. Funct. Genom. 2013, 14, 91–95. [Google Scholar] [CrossRef]
- Levitov, L.S.; Rhyner, J. Crystallography of quasicrystals; application to icosahedral symmetry. J. Phys. France 1988, 49, 1835–1849. [Google Scholar] [CrossRef]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Dover Publications, Inc.: New York, NY, USA, 2007; ISBN 9780486453620. [Google Scholar]
- Dechant, P.-P.; Wardman, J.; Keef, T.; Twarock, R. Viruses and fullerenes—Symmetry as a common thread? Acta Cryst. A 2014, 70, 162–167. [Google Scholar] [CrossRef]
- Indelicato, G.; Cermelli, P.; Salthouse, D.G.; Racca, S.; Zanzotto, G.; Twarock, R. A crystallographic approach to structural transitions in icosahedral viruses. J. Math. Biol. 2011, 64, 745–773. [Google Scholar] [CrossRef]
- Salthouse, D.G.; Indelicato, G.; Cermelli, P.; Keef, T.; Twarock, R. Approximation of virus structure by icosahedral tilings. Acta Cryst. A 2015, 71, 410–422. [Google Scholar] [CrossRef]
- Twarock, R. Mathematical virology: A novel approach to the structure and assembly of viruses. Philos. Trans. R. Soc. A 2006, 364, 3357–3373. [Google Scholar] [CrossRef]
- Chen, L.; Moody, R.V.; Patera, J. Non-crystallographic root systems. In Quasicrystals and Discrete Geometry; Patera, J., Ed.; American Mathematical Society: Providence, RI, USA, 1998; Volume 10, pp. 135–178. ISBN 978-0-8218-0682-1. [Google Scholar]
- Shcherbak, O.P. Wavefronts and reflection groups. Russ. Math. Surv. 1988, 43, 149–194. [Google Scholar] [CrossRef]
- Champagne, B.; Kjiri, M.; Patera, J.; Sharp, R.T. Description of reflection-generated polytopes using decorated Coxeter diagrams. Can. J. Phys. 1995, 73, 566–584. [Google Scholar] [CrossRef]
- Kirillov, A., Jr. An Introduction to Lie Groups and Lie Algebras; Cambridge University Press: Cambridge, UK, 2008; ISBN 9780511755156. [Google Scholar]
- Ramond, P. Group Theory: A Physicist’s Survey; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780521896030. [Google Scholar]
- Braden, H.W. Integral Pairings and Dynkin Indices. J. London Math. Soc. 1991, s2-43, 313–323. [Google Scholar] [CrossRef]
- Panyushev, D.I. On the Dynkin index of a principal sl2-subalgebra. Adv. Math. 2009, 221, 1115–1121. [Google Scholar] [CrossRef][Green Version]
- Dynkin, E.B. Semisimple subalgebras of semisimple Lie algebras. Trans. Am. Math. Soc. 1957, 6, 111–244. [Google Scholar] [CrossRef]
- Patera, J.; Sharp, R.T.; Winternitz, P. Higher indices of group representations. J. Math. Phys. 1976, 17, 1972–1979. [Google Scholar] [CrossRef]
- Okubo, S.; Patera, J. General indices of simple Lie algebras and symmetrized product representations. J. Math. Phys. 1983, 24, 2722–2733. [Google Scholar] [CrossRef]
- Okubo, S.; Patera, J. General indices of representations and Casimir invariants. J. Math. Phys. 1984, 25, 219–227. [Google Scholar] [CrossRef]
- Okubo, S. Gauge groups without triangular anomaly. Phys. Rev. D 1977, 16, 3528–3534. [Google Scholar] [CrossRef]
- Okubo, S.; Patera, J. Cancellation of higher-order anomalies. Phys. Rev. D 1985, 31, 2669–2671. [Google Scholar] [CrossRef]
- Patera, J.; Sharp, R.T. On the triangle anomaly number of SU(n) representations. J. Math. Phys. 1981, 22, 2352–2356. [Google Scholar] [CrossRef]
- Zhang, H.; Okubo, S.; Tosa, Y. Global gauge anomaly for simple Lie algebras. Phys. Rev. D 1988, 37, 2946–2957. [Google Scholar] [CrossRef]
- Larouche, M.; Nesterenko, M.; Patera, J. Branching rules for the Weyl group orbits of the Lie algebra An. J. Phys. A 2009, 42, 485203. [Google Scholar] [CrossRef]
- Larouche, M.; Patera, J. Branching rules for Weyl group orbits of simple Lie algebras Bn, Cn and Dn. J. Phys. A 2011, 44, 115203. [Google Scholar] [CrossRef]
- Grabowiecka, Z.; Patera, J.; Szajewska, M. Reduction of orbits of finite Coxeter groups of non-crystallographic type. J. Math. Phys. 2018, 59, 101705. [Google Scholar] [CrossRef]
- Janner, A. Alternative approaches to onion-like icosahedral fullerenes. Acta Cryst. A 2014, 70, 168–180. [Google Scholar] [CrossRef]
- Thomas, B.G.; Twarock, R.; Valiunas, M.; Zappa, E. Nested Polytopes with Non-crystallographic Symmetry Induced by Projection. In Proceedings of the Bridges: Mathematical Connections in Art, Music and Science 2015, Baltimore, MD, USA, 29 July–2 August 2015; Tessellations Publishing: Phoenix, AZ, USA, 2015; pp. 167–174. [Google Scholar]
- Zelevinsky, A. Nested complexes and their polyhedral realizations. Pure Appl. Math. Q. 2006, 2, 655–671. [Google Scholar] [CrossRef]
- Háková, L.; Larouche, M.; Patera, J. The rings of n-dimensional polytopes. J. Phys. A 2008, 41, 495202. [Google Scholar] [CrossRef]
- Okubo, S. Branching index sum rules for simple Lie algebras. J. Math. Phys. 1985, 26, 2127–2137. [Google Scholar] [CrossRef]
- McKay, W.G.; Patera, J. Tables of Dimensions, Indices, and Branching Rules for Representations of Simple Lie Algebras; Marcel Dekker, Inc.: New York, NY, USA, 1981; ISBN 0824712277. [Google Scholar]
- Bremner, M.R.; Moody, R.V.; Patera, J. Tables of Dominant Weight Multiplicities for Representations of Simple Lie Algebras; Marcel Dekker, Inc.: New York, NY, USA, 1985; ISBN 0824772709. [Google Scholar]
- Moody, R.V.; Patera, J. Fast recursion formula for weight multiplicities. Bull. Am. Math. Soc. 1982, 7, 237–242. [Google Scholar] [CrossRef]
- Bremner, M.R. Fast computation of weight multiplicities. J. Symb. Comput. 1986, 2, 357–362. [Google Scholar] [CrossRef][Green Version]





| 5 | |
| 5 | |
| 10 | |
| 12 | |
| 30 | |
| 20 | |
| 60 | |
| 60 | |
| 60 | |
| 120 | |
| 120 | |
| 720 | |
| 1200 | |
| 600 | |
| 1440 | |
| 3600 | |
| 2400 | |
| 3600 | |
| 3600 | |
| 2400 | |
| 7200 | |
| 7200 | |
| 7200 | |
| 7200 | |
| 14,400 |
| G | ||
|---|---|---|
| 2 | ||
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | ||
| 1 |
| : | |
| any a | |
| even a | |
| odd | |
| : | |
| any a | |
| even a | |
| odd | |
| : | |
| any a, | |
| even a | |
| odd | |
| : | |
| any a | |
| even a | |
| odd | |
| : | |
| any a | |
| , | |
| even a | |
| odd | |
| odd | |
| even | |
| odd | |
| : | |
| any a | |
| even a | |
| even a | |
| odd | |
| odd |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myronova, M.; Patera, J.; Szajewska, M. Nested Polyhedra and Indices of Orbits of Coxeter Groups of Non-Crystallographic Type. Symmetry 2020, 12, 1737. https://doi.org/10.3390/sym12101737
Myronova M, Patera J, Szajewska M. Nested Polyhedra and Indices of Orbits of Coxeter Groups of Non-Crystallographic Type. Symmetry. 2020; 12(10):1737. https://doi.org/10.3390/sym12101737
Chicago/Turabian StyleMyronova, Mariia, Jiří Patera, and Marzena Szajewska. 2020. "Nested Polyhedra and Indices of Orbits of Coxeter Groups of Non-Crystallographic Type" Symmetry 12, no. 10: 1737. https://doi.org/10.3390/sym12101737
APA StyleMyronova, M., Patera, J., & Szajewska, M. (2020). Nested Polyhedra and Indices of Orbits of Coxeter Groups of Non-Crystallographic Type. Symmetry, 12(10), 1737. https://doi.org/10.3390/sym12101737





