Abstract
In many application fields (closed curve noise data reconstruction, time series data fitting, image edge smoothing, skeleton extraction, etc.), curve reconstruction based on noise data has always been a popular but challenging problem. In a single domain, there are many methods for curve reconstruction of noise data, but a method suitable for multi-domain curve reconstruction has received much less attention in the literature. More importantly, the existing methods have shortcomings in time consumption when dealing with large data and high-density point cloud curve reconstruction. For this reason, we hope to propose a curve fitting algorithm suitable for many fields and low time consumption. In this paper, a curve reconstruction method based on clustering and point cloud principal component analysis is proposed. Firstly, the point cloud is clustered by the K++ means algorithm. Secondly, a denoising method based on point cloud principal component analysis is proposed to obtain the interpolation nodes of curve subdivision. Finally, the fitting curve is obtained by the parametric curve subdivision method. Comparative experiments show that our method is superior to the classical fitting method in terms of time consumption and effect. In addition, our method is not constrained by the shape of the point cloud, and can play a role in time series data, image thinning and edge smoothing.
1. Introduction
1.1. Context
Curve reconstruction of planar cloud is an important research issue in reverse engineering. Reverse engineering technology is a new discipline and technology developed with the development of computer technology and the progress of data measurement technology. Curve reconstruction technology has important applications in the field of virtual cultural relic restoration, image edge smoothing, image refinement and 3D point cloud reconstruction. Curve reconstruction methods are generally divided into the curve reconstruction of an ordered set or a disordered set of points. The reconstruction of ordered points refers to constructing a curve to interpolate or approximate these sampling points in turn. For this reconstruction, there have been many mature methods, such as the B-spline method [,], the rational interpolation or approximation method [,], the subdivision method [,] etc. However, in reverse engineering, due to the different data sampling methods, the obtained data point set is a disordered discrete data point cloud. There are many methods for curve reconstruction of unordered point cloud, such as the least square method [,,,], the clustering method [,,,,] and principal component analysis [,,,].
1.2. Analysis of Existing Methods and Research Objectives
The least square (LS) method is one of the most widely used methods at present, mainly because it can find the best matching function of data by minimizing the square of error, and get displayed expression. In 1998, Levin [] proposed a moving least square (MLS) method, which was applied to the field of curve reconstruction, and used this method to refine the scattered point cloud. In 2017, Mustafa [] used the dynamic weighted iterative least squares method to propose a nonlinear subdivision scheme based on one-variable cubic polynomial, which is used to deal with the fitting of scattered data with noise and outliers. MLS plays a good role in curve reconstruction on small data sets or open curve data sets; however, on large data sets, this method needs to calculate the coefficients of polynomials. If the condition number of the matrix is large, the equations may be ill conditioned. On the other hand, the MLS method is a technique based on polynomial fitting. If the values of large data sets (such as stock prices) change sharply, the fitting process is prone to over fitting; that is, the fitting curve is too smooth, ignoring some details of the data, and making insufficient contribution to the maintenance of the shape of curve, as shown in Figure 1. At the same time, in the fitting process of large data sets, the number of compact supported sets is directly proportional to the running time, and there are also deficiencies in the fitting efficiency of the MLS method.
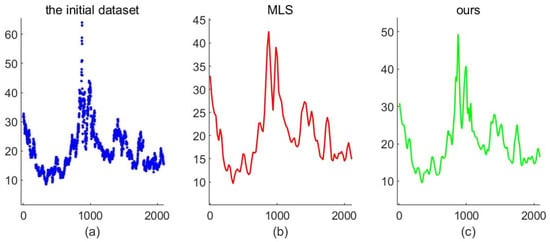
Figure 1.
A stock price fitting by moving least square (MLS) and ours. (a) The price data of a stock. The abscissa represents the time (day) and the ordinate represents the price; there are 2130 data points. (b) The fitting curve obtained by MLS. The number of nodes is 100, the weight function is cubic spline function, and the basis function is . (c) The fitting curve obtained by the method proposed in this paper; the number of control points is 100.
The clustering method is a widely used and effective classification method, which is mainly used in image segmentation [,,,], statistical analysis [,,], and industrial design [,]. The goal of point cloud clustering is to identify clusters with the same characteristics from a group of point clouds. K-means algorithm is one of the oldest and most commonly used clustering algorithms, it is best suited to create the desired shape curve, such as the approximate optimal shape of the scanned data point set. In point cloud reconstruction, this method is mainly used to deal with outliers and has achieved good results. In 2021, using the clustering and B-spline method, Chen [] presented an automatic approach to generating a fitting curve to a set of unorganized points generated randomly from a closed curve; unfortunately, this method can only solve the fitting of noisy data on closed curves. In 2021, Gu [] proposed a novel moving total least squares (MTLS)-based reconstruction method combined with k-means clustering to enhance the robustness and accuracy of MTLS in handling the measurement data with outliers. The algorithm first adopts LS for pre-fitting, and then uses MTLS to generate the fitting curve. Although it can well remove the outliers, two matrix operations are performed in each support domain, which has high computational complexity and reduces the fitting efficiency. For example, when processing the point cloud curve reconstruction of more than 6000 data points, if the classical fitting method MLS is used, it generally takes more than 20 s.
Principal component analysis (PCA) is a classical point cloud normal vector calculation method which was proposed by Hoppe []. The method constructs the covariance matrix through the neighborhood information of the point, so as to obtain the geometric information of the point. In 2011, Furferi [] provided a method of using PCA to detect the local main direction of the point cloud and fit the disordered data. The method was applied to image thinning, and proved to be effective in preserving the original shape. In 2020, Yang [] proposed a point cloud simplification algorithm based on PCA and cluster. Its main purpose was to obtain the normal vector, angle entropy, curvature, and density information of the point cloud. In 2021, Neuville [] proposed a method to segment tree stems in a deciduous forest stand that does not rely on any site-specific parameters. In this paper, the clustering algorithm is used to segment the trunk, and the PCA method is used to extract the trunk direction. In the above literatures, PCA is used to determine the direction (curve) or normal vector (surface) of a point cloud. In fact, this method can also be adopted for noise processing in data processing; however, it is not reflected in the above literature.
For this reason, we propose a point cloud curve reconstruction method based on point cloud clustering and principal component analysis. Firstly, the K-means++ clustering method is used to segment the point cloud into several clusters. Secondly, point cloud principal component analysis (PCPCA) is proposed on each cluster to remove the outliers, and detect the main control point and the principal direction of the point. Thirdly, by non-uniform curve subdivision, a limit curve is obtained. The main contributions of this paper are as follows:
- PCPCA is proposed to find the projection line and main direction of each cluster, and -principle is adopted to remove the outliers.
- For complex point clouds with self-intersection, using the main direction of each cluster, we can divide all main control points into two groups and sort the points in groups.
- The method proposed in this paper has wider application fields than state-of-the-art methods, including planar point cloud curve reconstruction, time series data fitting, image refinement and image edge smoothing.
- In the curve reconstruction of high-density point cloud, our method takes 20% of the time of classical methods (such as MLS).
In the following, we first review K-means clustering and K-means++ clustering in Section 2. In Section 3, PCPCA is proposed, the method of removing outliers and the determination of main control points and main directions are introduced. In Section 4, we review the non-uniform curve subdivision method. Section 5 gives a series of numerical examples to show the effectiveness and robustness of the method proposed in this paper. The conclusions and discussion about this paper are in Section 6.
2. K-Means Clustering
The K-means clustering algorithm was proposed independently by Steinhaus (1955), Lloyed (1957), Ball and Hall (1965), and McQueen (1967), in different scientific fields. The K-means clustering algorithm has been widely studied and applied in different disciplines since it was proposed.
2.1. Classical K-Means Clustering
The K-means clustering algorithm is an iterative clustering algorithm, which is to randomly divide all the points into clusters , then randomly select points as the initial clustering center . The distance from to each clustering center , is noted as:
Then, based on the minimum value , is assigned to the cluster . After assigning all points to constitute the first clusters, we can generate a new cluster center according to the points in each cluster as:
Next, all data points are redistributed according to the previous method to obtain the second clusters. Continuing in the same way, the K-means clustering algorithm stops until the points in each cluster do not change.
2.2. Improved K-Means Clustering (K-Means++)
In 2007, D. Arthur [] improved the K-means clustering method and the proposed K-means++ clustering method, which randomly selected an initial data point as the initial clustering center in the initial data set . The distance between the other points, and , is calculated as:
The probability is introduced. is randomly selected as the second clustering center , according to the probability . Assuming that initial clustering centers have been selected , when selecting the clustering center, the point farther away from the current clustering centers will have a higher probability to be selected as the clustering center. K-means++ can significantly improve the final error of classification results. The clustering method used in this paper is the K-means++ clustering method. Figure 2 shows the difference between two clustering methods for the same point cloud. Under different clustering methods and different numbers of clusters, Table 1 shows the average distance from the point in each cluster to the cluster center of the point cloud in Figure 2a.
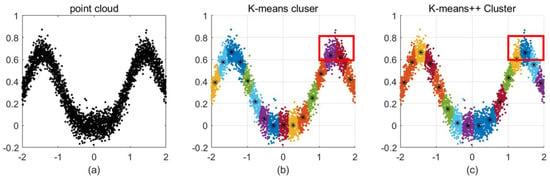
Figure 2.
Point cloud clustering using the K-means (b), and K-means++ (c) methods. (a) shows the point cloud composed of 6248 data points. (b,c) shows the 16 clusters of the same point cloud by the two methods. It can be seen from the two figures that the red rectangular area is an extreme region of the point cloud; the K-means clustering method divides the region into two clusters and generates two cluster centers, but the K-means++ method generates a cluster in the region and forms a cluster center, which can better protect the shape of the point cloud.

Table 1.
Comparison with the K-means method and the K-means++ method. The value in the first row is the number of clusters. The values in the second and third rows are the average distance from the point in each cluster to the cluster center.
3. Point Cloud Principal Component Analysis (PCPCA)
3.1. The Main Line and the Main Control Point of Points Cloud
PCA is a statistical method that converts multiple related variables into a few independent variables (principal components) through dimension reduction technology, and is one of the most important dimension reduction methods. It can reduce the dimension of high dimensional data and remove noise by dimension reduction.
In this paper, we propose a point cloud principal component analysis (PCPCA). The main idea of this method is as follows:
- (1)
- The abscissa and ordinate of each point in the point cloud are used to form two -dimensional columnvectors and ;
- (2)
- A -order square matrix is obtained by using the formula , and eigenvalues and eigenvectors of are found;
- (3)
- The eigenvector corresponding to the maximum eigenvalue is recorded as , and the projection vector set is obtained from the formula .
Definition 1.
Letbe a point cloud set,be any straight line, andbe the projected point of. If
is called the main line of the point cloud,is named the main control point of the point cloud, and the direction of is called the principal direction of the point cloud, denoted by .
Assume is the set of all points in a cluster. Let
then and are -dimensional vectors, is a projected point set on a straight line , denoted:
The main control point is defined as:
Since (and ) is -dimensional vector, the dimension reduction of the initial -dimensional data vector (and )is needed, so that the idea of the PCA method can be used.
First of all, let be the transform unit vector for dimensionality reduction, so that
Suppose
The minimization principle (1) implies that the projected points are sufficiently near to the data points . Let
Then
Substituting and into the above expression yields
So
Constructing Lagrange functions
For the first item of is a quadratic form, the partial derivative over is
Let
Then
which implies that is the eigenvector of the matrix corresponding to the eigenvalue .
Theorem 1.
Letbe a point cloud set, andbe the eigenvector corresponding to the maximum eigenvalueof matrix. If
then the line where the point setis located is the main line, and the direction of the line is the principal direction of the control point.
Proof of Theorem 1.
According to Equations (2) and (3), the point set is generated by:
then all the points are located in a straight line.
The rank of matrix is
The matrix is a symmetric matrix, so the matrix has at most two non-zero eigenvalues, denoted as . Suppose , the corresponding eigenvectors are , and are the orthogonal unit vectors.
Substituting into , respectively, we get
The eigenvector corresponding to the eigenvalue can minimize the distance between the projected point and . The straight line where is located at is the main straight line of the cluster, and the direction of the straight line is the principal direction, as shown in Figure 3. □
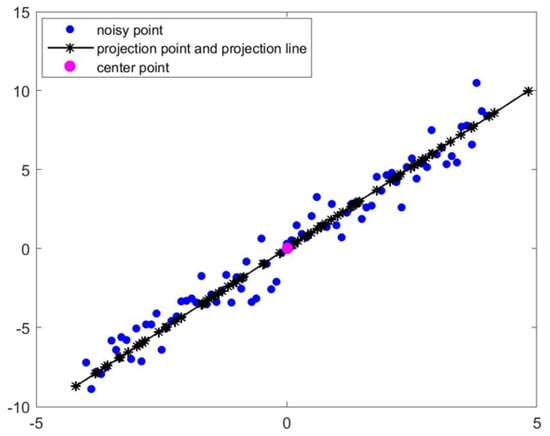
Figure 3.
The noisy points are indicated by blue dots (81 in total), the black stars are the projection points obtained through point cloud principal component analysis, and the black solid line is the main straight line of the point cloud, and the pink dot is the center point of all noisy points.
3.2. Processing of Point Cloud Outliers
The main function of the PCA method in data processing includes two aspects: dimensionality reduction and noise reduction. In Section 3.1, we indirectly use the dimensionality reduction function of the PCPCA method to obtain the projection points and projection lines of noisy data. In the traditional PCA method, we will treat these projection points as real points, so as to achieve the function of noise reduction. However, these noisy data may contain some outliers, which will have some impact on the projection points. Therefore, we hope to add a step of removing outliers in the PCPCA method.
In statistical analysis, we often use the principle to denoise. That is, in a group of test data, the data contains random error. The mean and standard deviation can be obtained by calculating the data. The probability of the data in the interval is . Accordingly, the data not in this interval is not the data generated by random error, but outliers, which should be eliminated. This paper adopts principle to delete outliers.
principle: Let is the distance from the point in the cluster and the projection line, the mean and standard deviation of the distance are and , respectively. If the distance from a point and the line satisfies the condition
is the outlier, and will be deleted from the point cloud, where the and are calculated by the following formula:
Next, we continue to use the method in Section 3.1 to recalculate the main line and main control point of the point cloud, as shown in Figure 4; (a) presents the noisy data (blue dots), its projection points (black asterisks), and the projection line; (b) shows the projection line and projection points after removing the outliers by principle. The points not connected by solid red lines represent the outliers. Compared with (a), we find that the projection points in (b) are more concentrated, and the points far away from the projection line are removed.
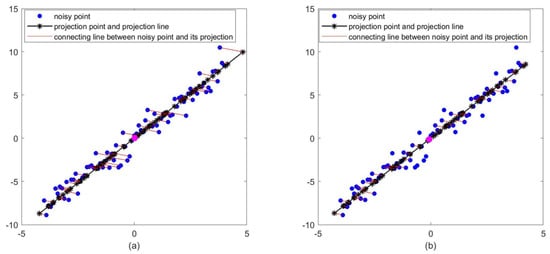
Figure 4.
(a) The point cloud with outliers and its projection line. (b) The point cloud and its projection line after removing outliers. In (b), some noisy points are not connected with their projection points because they are judged as outliers (13 in total). It can also be seen from the figure that these outliers obviously deviate from the projection line. Therefore, these points will be removed when calculating the control points.
The reason for not adopting the -principle commonly used in statistics is because when the first PCPCA is used, if there is an outlier in the point cloud, the projection line has shifted to the point , and the distance from the outlier to the line has been reduced. If adopting the -principle, it will be difficult for us to delete the outlier.
4. The Subdivision of the Main Control Points
In Section 3 of this paper, we introduce the generation method of main control points of the point cloud. Next, we need to use these points as interpolation nodes to fit the curve. In the previous literature, most of them generate fitting curves by the polynomial or B-spline method. We know that polynomial interpolation is prone to the Runge phenomenon, while the B-spline method needs to calculate the control vertices, which will increase a lot of computation. In 2013, Beccari [] proposed a four-point binary non-uniform parametric curve subdivision method, and gave a non-uniform parameterized surface subdivision method on regular quadrilateral meshes, and proved the continuity of the limit surface.
Since non-uniform curve subdivision has a good interpolation or approximation effect on control polygons with arbitrary topology, the method is used in this paper to generate the fitting curve.
Let be the vertices after the th refinement, and denote by the distance between and . Then, by means of the parameterized Lagrange interpolation basis functions, the subdivision mask can be obtained as:
The four-point binary non-uniform curve subdivision scheme is:
5. Numerical Examples
5.1. Curve Fitting of the Planar Point Clouds
The function is taken as the benchmark for our method and MLS. The point cloud distribution after adding Gaussian noise is shown separately as the black points on the left in Figure 5a. In Figure 5a, there are 6284 initial data points. A large number of data points can be removed through our method. The number of retained data points is 4532 is shown by the cyan dots, the removal rate is 28%, of which black data is the removed point. From Figure 5b, we find that the limit curve generated by our method is closer to the real curve near the extreme point than the MLS method, as shown in the red and blue boxes in the figure. In addition, in terms of running time, due to the large number of data points, the running time of our method is 4.0098 s, while that of the MLS method is 21.6411 s.
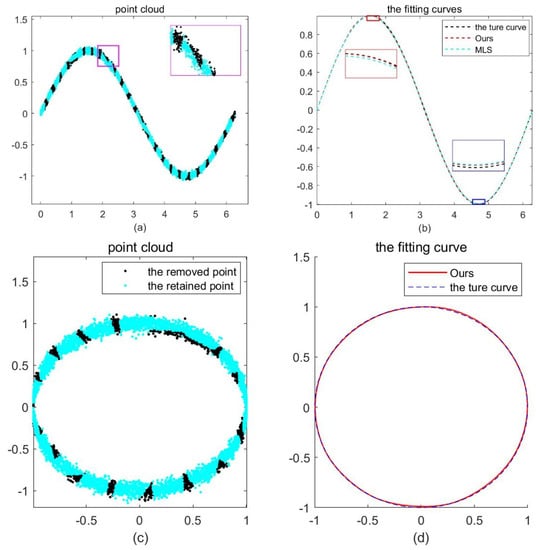
Figure 5.
Curve reconstruction of the planar point clouds. (a,c) show the planar point clouds, respectively, and the number of the points in each point cloud is 6284. The black dots in the figures are removal points, and the removal rates are 28% and 12%. The black dotted line in (b) and the blue dotted line in (d) represent the real curve, and the red line represents the fitting curve. Because MLS cannot fit the parameter curve, only the fitting curve generated by our method is shown in (d).
Figure 5c is a closed curve point cloud generated by function . There are 6284 data points. The removal rate of the point cloud is 12%, and the cyan points are reserved points. The MLS method cannot generate the fitting curve of the closed curve. Figure 5d shows the fitting curve generated by our method, which basically coincides with the original curve.
5.2. Curve Reconstruction of the Complex Point Clouds
Figure 6a,c shows the curve fitting of -type and -type point clouds. For the fitting of these two types of point clouds, we first cluster the point cloud into several clusters, and then find the main control points and main directions through PCA. Combined with the main directions, we divide the main control points into two groups and sort each group of points. Finally, the limit curves are obtained by the subdivision method for two main control points, as shown in Figure 6b,d; the two real curves (red and blue) in the figure correspond to the two curves fitted by the two main control point sets, respectively.
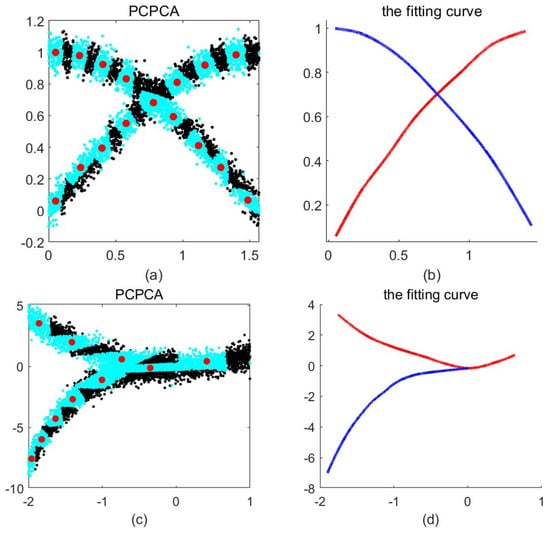
Figure 6.
(a) The curve reconstruction of the type point cloud; (c) the curve reconstruction of the type point cloud. The two real curves (red and blue) in (b,d), respectively, correspond to the two curves fitted by the two main control point sets in each point cloud.
5.3. Curve Reconstruction of the Time Series
Time series (or dynamic series) refers to the series formed by arranging the values of the same statistical index according to the time sequence of occurrence. The main purpose of time series analysis is to predict the future according to the existing historical data. Most of the economic data are given in the form of time series. According to the different observation time, the time in the time series can be year, quarter, month or any other form of time, such as stock price movements shown in Figure 1a. If regression analysis, MLS and other methods are used for data fitting, the imitative effect shown in Figure 1b is not so good; the reason for this is that polynomials are not very sensitive to the processing of mutation data. For this kind of data, we use the method proposed in this paperto get a continuous limit curve for the data points, and the trend of the curve has high similarity with the change trend of the original data. Figure 1c shows the results of reconstruction.
5.4. Image Refinement
Refinement refers to the process of reducing the lines of an image from multi-pixel width to unit pixel width, which is also called skeleton extraction of the image. The refined images in this paper are from MNIST digital image sets, as shown in Figure 7a. The pixel values of each point in these images are distributed in [0, 30] or [240, 255]. The refinement method of this paper is divided into the following steps. Firstly, the pixels with pixel values between 240–255 in the digital image are regarded as point clouds, the coordinates of each pixel are recorded as , and the point cloud dataset . Next, for the dataset , the method in this paper is used to obtain the fitting curve through clustering, PCPCA and subdivision methods, and the curve is used as the thinning result of the image, as shown in Figure 7b.

Figure 7.
Image refinement: (a) is the initial image from MNIST digital image sets, and (b) is the image refinement by the method in this paper.
5.5. Image Edge Smoothing
Image enlargement is one of the important digital image processing technologies. When the image is enlarged, the edge of the image will appear with sawtooth distortion. In order to suppress this distortion, it is necessary to refine the edge of the image. The commonly used image edge processing methods include bilinear interpolation, spline interpolation, and so on. We use the method proposed in this paper to process the edge of the image (the images are from the MNIST digital image set, as shown in the left column of Figure 8). Firstly, the Canny algorithm is used to extract the image edge, as shown in the middle column of Figure 8, and the pixels of the image edge are transformed into double precision. The double precision of white pixels is and the double precision of black pixels is . The point set with double precision of is used as the point cloud. Next, the fitting point set is generated by using the methods of clustering, PCPCA and subdivisions. The coordinate of the points in are rounded to obtain a new coordinate with image double precision of , and the double precision of other points is defined as . The last edge of the generated image, as shown in the right column of Figure 8. From the experimental results, our method can effectively smooth the image edge.

Figure 8.
Image edge smoothing. The first column is two images from the digital image set MNIST. The second column is the edges of the two images obtained by the Canny algorithm. The third column is the smoothed image edge.
6. Conclusions and Discussion
In order to further improve the performance of curve reconstruction algorithm of a point cloud, and ensure the fitting efficiency, a point cloud curve reconstruction method based on K-means++ clustering and PCA is proposed. By clustering the point cloud, the point cloud is divided into several clusters, then the outliers of each cluster are removed by PCPCA, and the projection line and main control points of the points in the cluster are found. Finally, the main control points are interpolated by the curve subdivision method to obtain the fitting curve of the point cloud. Compared with the classical curve reconstruction methods, as shown in Table 2, our method can be well adapted to the fitting of the open curve, closed curve and self-intersection curve. At the same time, in the curve reconstruction of high-density point cloud, our method takes 20% of the time of classical methods (such as MLS). Finally, we extend this method to image refinement and image edge smoothing, and the experimental results are also satisfactory.

Table 2.
Comparison of curve reconstruction methods in different types of point clouds.
However, the method in this paper is to be further improved in the following aspects. The cluster of the point cloud uses a method of taking random starting points, so the results of clustering are not unique, and the k-means++ clustering method is not sensitive to the density of the point cloud. On the other hand, extending this method to the surface reconstruction is also the work we are studying at present. Finally, when extending our method to image processing, the image type is digital. How to extend this method to other image types is also a problem we need to consider later.
Author Contributions
Conceptualization, K.P. and J.T.; methodology, K.P. and J.T.; software, G.Z.; validation, J.T., formal analysis, K.P. and J.T.; resources, K.P. and G.Z.; data curation, K.P. and G.Z.; writing—original draft preparation, K.P.; writing—review and editing, J.T.; visualization, K.P. and G.Z.; supervision, J.T.; project administration, J.T.; funding acquisition, J.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, under Grant No. 62172135.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gordon, W.J.; Riesenfeld, R.F. B-spline curves and surfaces. Comput. Aided Geom. Des. 1974, 23, 95–126. [Google Scholar]
- Gao, M.; Feng, L. Improved B-spline curve fitting algorithm based on genetic algorithm. Appl. Res. Comput. 2019, 36, 2480–2485. [Google Scholar]
- Piegl, L.A.; Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Tan, J. Interpolating multivariate rational splines of special forms. J. Math. Res. Expo. 1993, 13, 111–115. [Google Scholar]
- Dyn, N.; Levin, D.; Gregory, J.A. A 4-point interpolatory subdivision scheme for curve design. Comput. Aided Geom. Des. 1987, 4, 257–268. [Google Scholar] [CrossRef]
- Peng, K.; Tan, J.; Li, Z.; Zhang, L. Fractal behavior of a ternary 4-Point rational interpolation subdivision scheme. Math. Comput. Appl. 2018, 23, 65. [Google Scholar] [CrossRef] [Green Version]
- Levin, D. Mesh-Independent Surface Interpolation; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Lee, I.-K. Curve reconstruction from unorganized points. Comput. Aided Geom. Des. 1999, 17, 161–177. [Google Scholar] [CrossRef] [Green Version]
- Dyn, N.; Heard, A.; Hormann, K.; Sharon, N. Univariate subdivision schemes for noisy data with geometric applications. Comput. Aided Geom. Des. 2015, 37, 85–104. [Google Scholar] [CrossRef]
- Mustafa, G.; Hameed, R. Families of non-linear subdivision schemes for scattered data fitting and their non-tensor product extensions. Appl. Math. Comput. 2019, 359, 214–240. [Google Scholar] [CrossRef]
- Wang, W.; Pottmann, H.; Liu, Y. Fitting B-spline curves to point clouds by curvature-based squared distance minimization. ACM Trans. Graph. 2006, 25, 214–238. [Google Scholar] [CrossRef]
- Fang, L.; Wang, G. Shapes of point clouds and curves reconstruction. J. Comput. Aided Des. Comput. Graph. 2009, 21, 1558–1562. [Google Scholar]
- Mingyang, G.; Chongjun, L. Curve reconstruction algorithm based on discrete data points and normal vectors. J. Math. Res. Appl. 2020, 40, 87–100. [Google Scholar]
- Chen, L.; Ghosh, S.K. Uncertainty quantification and estimation of closed curves based on noisy data. Comput. Stat. 2021, 36, 2161–2176. [Google Scholar] [CrossRef]
- Furferi, R.; Governi, L.; Palai, M.; Volpe, Y. From unordered point cloud to weighted B-spline: A novel PCA-based method. In Proceedings of the American Conference on Applied Mathematics, Puerto Moleros, Mexico, 29–31 January 2011. [Google Scholar]
- Yang, Y.; Li, M.; Ma, X. A Point Cloud Simplification Method Based on Modified Fuzzy C-Means Clustering Algorithm with Feature Information Reserved. Math. Probl. Eng. 2020, 2020, 5713137. [Google Scholar] [CrossRef]
- Chen, Y. PointSCNet: Point Cloud Structure and Correlation Learning Based on Space-Filling Curve-Guided Sampling. Symmetry 2021, 14, 8. [Google Scholar] [CrossRef]
- Mustafa, M.S. An Improvised SIMPLS Estimator Based on MRCD-PCA Weighting Function and Its Application to Real Data. Symmetry 2021, 13, 2211. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Xu, X.; Li, H.; Yin, F.; Xi, L.; Qiao, H.; Ma, Z.; Shen, S.; Jiang, B.; Ma, X. Wheat ear counting using K-means clustering segmentation and convolutional neural network. Plant Methods 2020, 16, 106. [Google Scholar] [CrossRef]
- Chen, W.; He, C.; Ji, C.; Zhang, M.; Chen, S. An improved K-means algorithm for underwater image background segmentation. Multimed. Tools Appl. 2021, 80, 21059–21083. [Google Scholar] [CrossRef]
- Karuppanagounder, S.; Kalaiselvi, N. Feature identification in satellite images using K-Means segmentation. In Proceedings of the National Conference on Signal and Image Processing, Gandhigram, India, 9–10 February 2012. [Google Scholar]
- Xu, T.S.; Chiang, H.D.; Liu, G.Y.; Tan, C.-W. Hierarchical K-means method for clustering large-scale advanced metering infrastructure data. IEEE Trans. Power Deliv. 2017, 32, 609–616. [Google Scholar] [CrossRef]
- Rajendran, S.; Khalaf, O.I.; Alotaibi, Y.; Alghamdi, S. MapReduce-based big data classification model using feature subset selection and hyperparameter tuned deep belief network. Sci. Rep. 2021, 11, 24138. [Google Scholar] [CrossRef]
- Le, T.; Son, L.H.; Vo, M.T.; Lee, M.Y.; Baik, S.W. A Cluster-Based Boosting Algorithm for Bankruptcy Prediction in a Highly Imbalanced Dataset. Symmetry 2018, 10, 250. [Google Scholar] [CrossRef] [Green Version]
- Gu, T.; Lin, H.; Tang, D.; Lin, S.; Luo, T. Curve and surface reconstruction based on MTLS algorithm combined with k-means clustering. Measurement 2021, 182, 109737. [Google Scholar] [CrossRef]
- Hoppe, H. Surface Reconstruction from Unorganized Points. ACM SIGGRAPH Comput. Graph. 1992, 26, 71–78. [Google Scholar] [CrossRef]
- Neuville, R.; Bates, J.S.; Jonard, F. Estimating Forest Structure from UAV-Mounted LiDAR Point Cloud Using Machine Learning. Remote. Sens. 2021, 13, 352. [Google Scholar] [CrossRef]
- Beccari, C.; Casciola, G.; Romani, L. Non-uniform non-tensor product local interpolatory subdivision surfaces. Comput. Aided Geom. Des. 2013, 30, 357–373. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).