Studying Massive Suction Impact on Magneto-Flow of a Hybridized Casson Nanofluid on a Porous Continuous Moving or Fixed Surface
Abstract
:1. Introduction
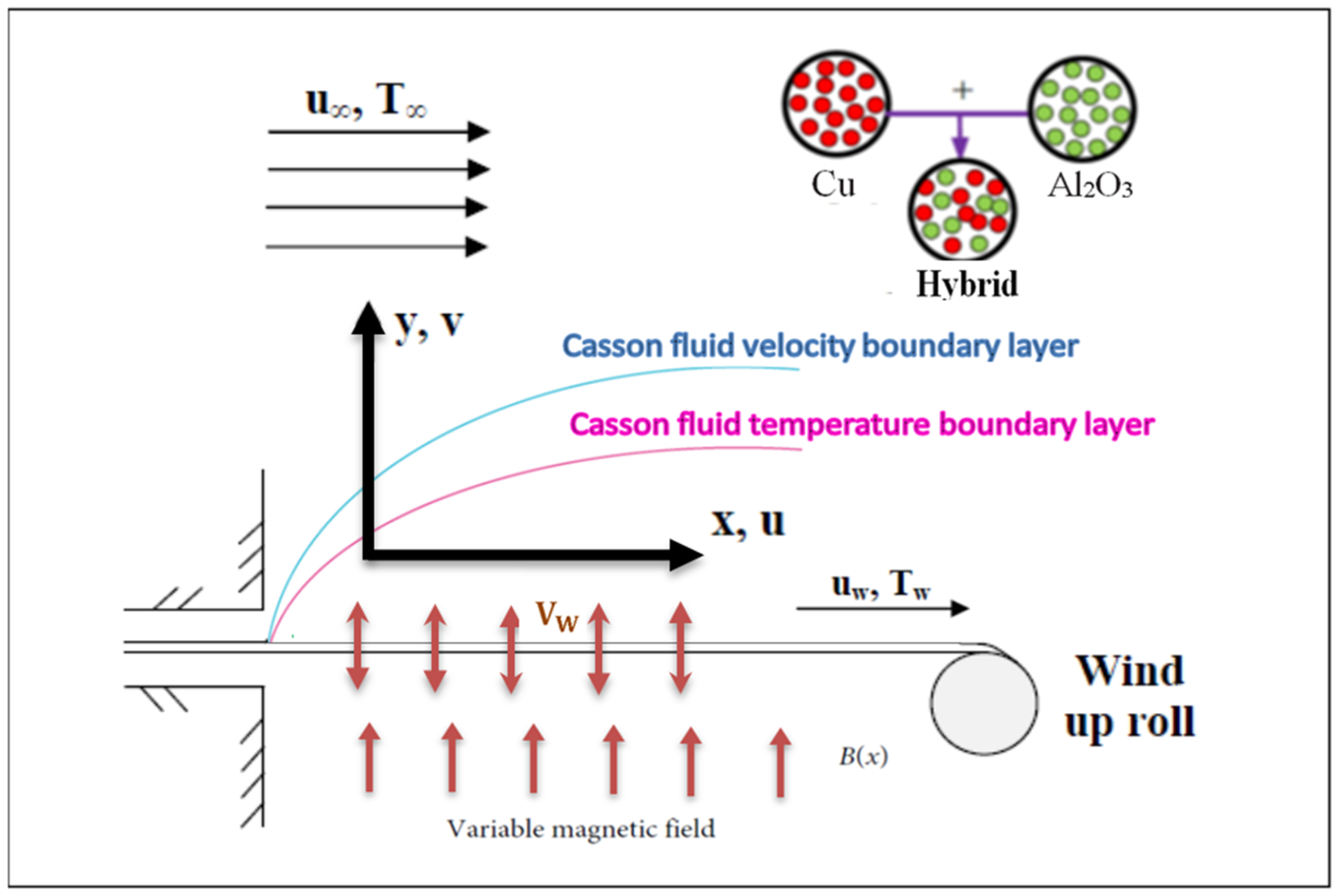
2. Modeling
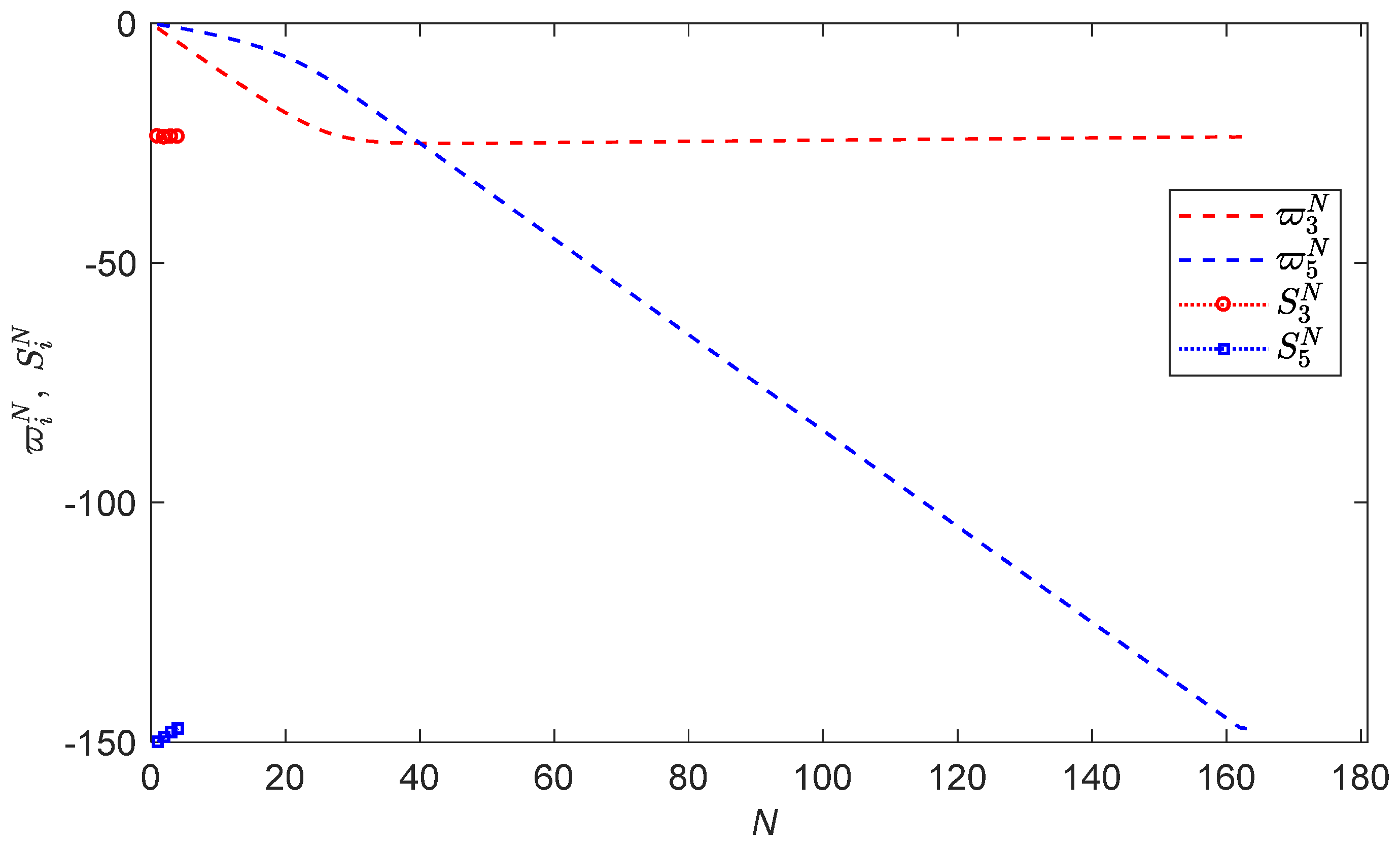
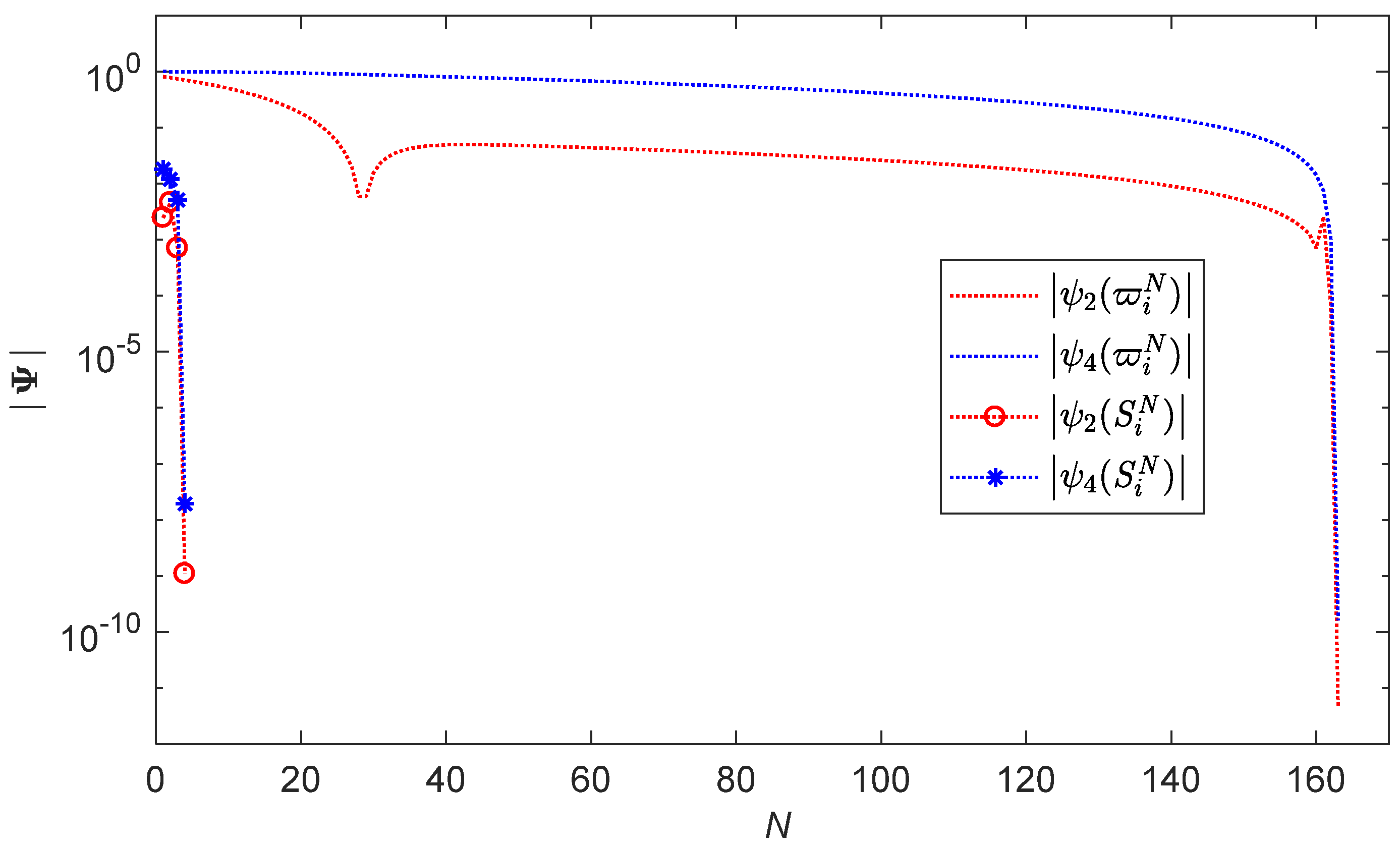
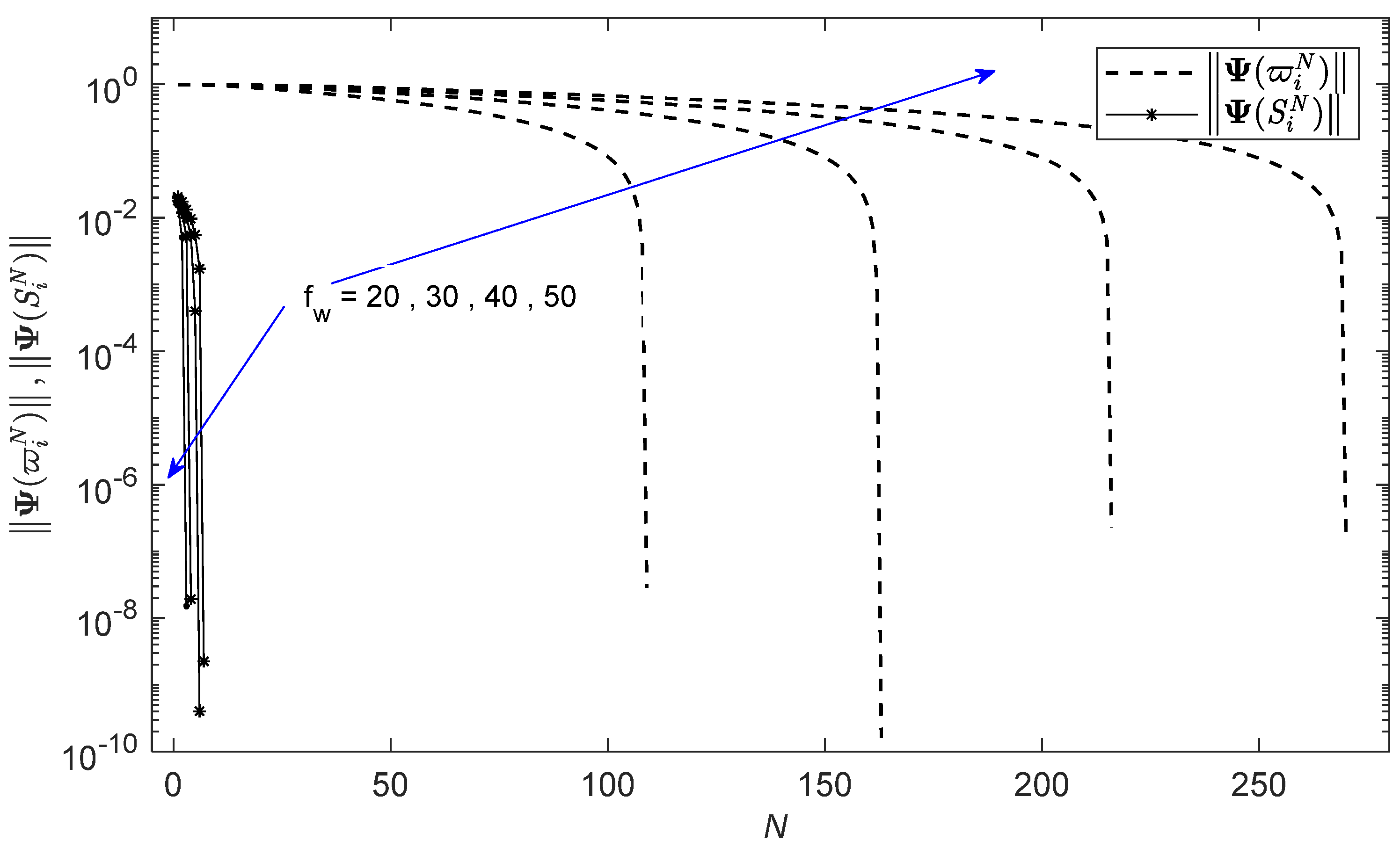
3. An Improved Shooting Method
Asymptotic Approximation for the Missing Initial Conditions
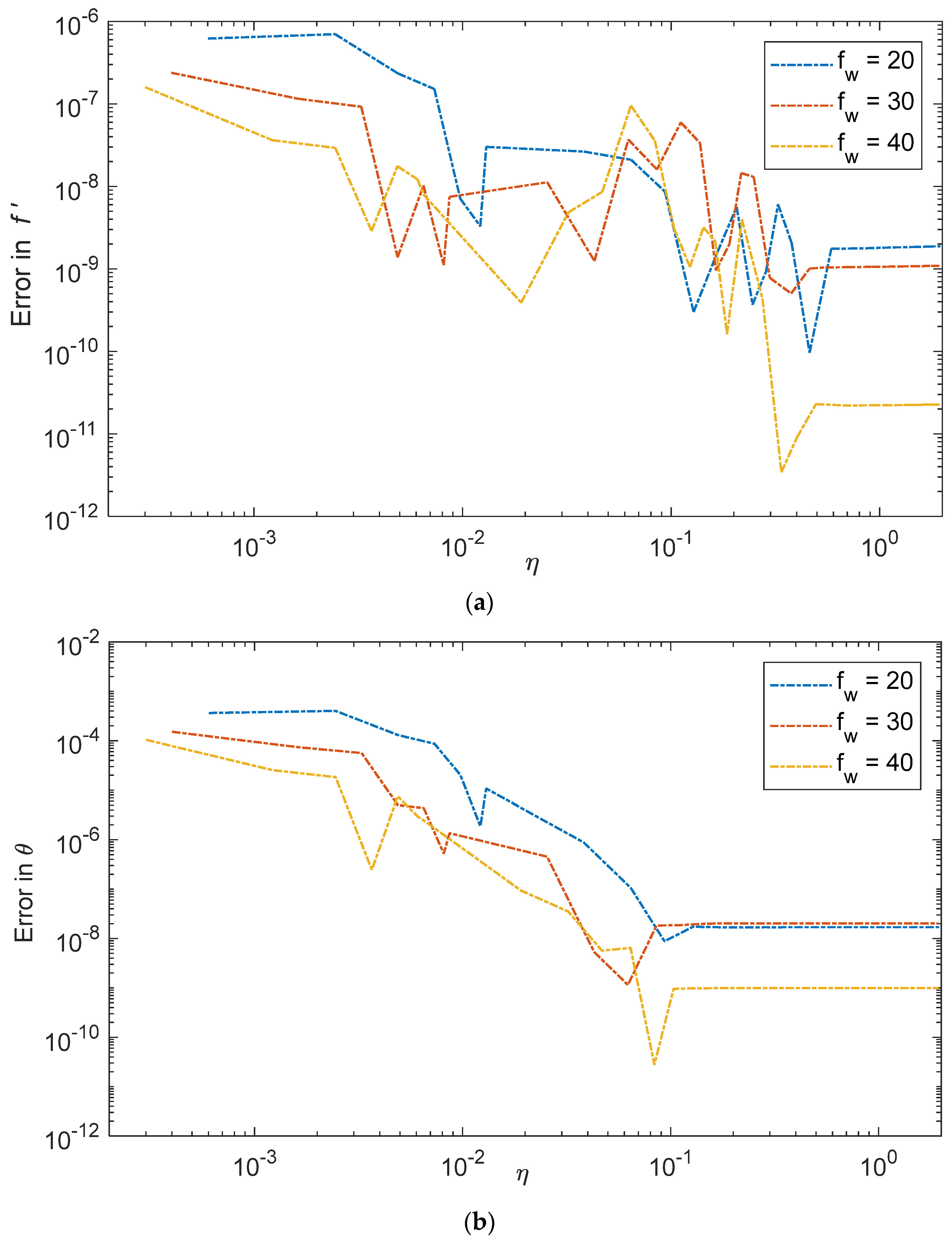
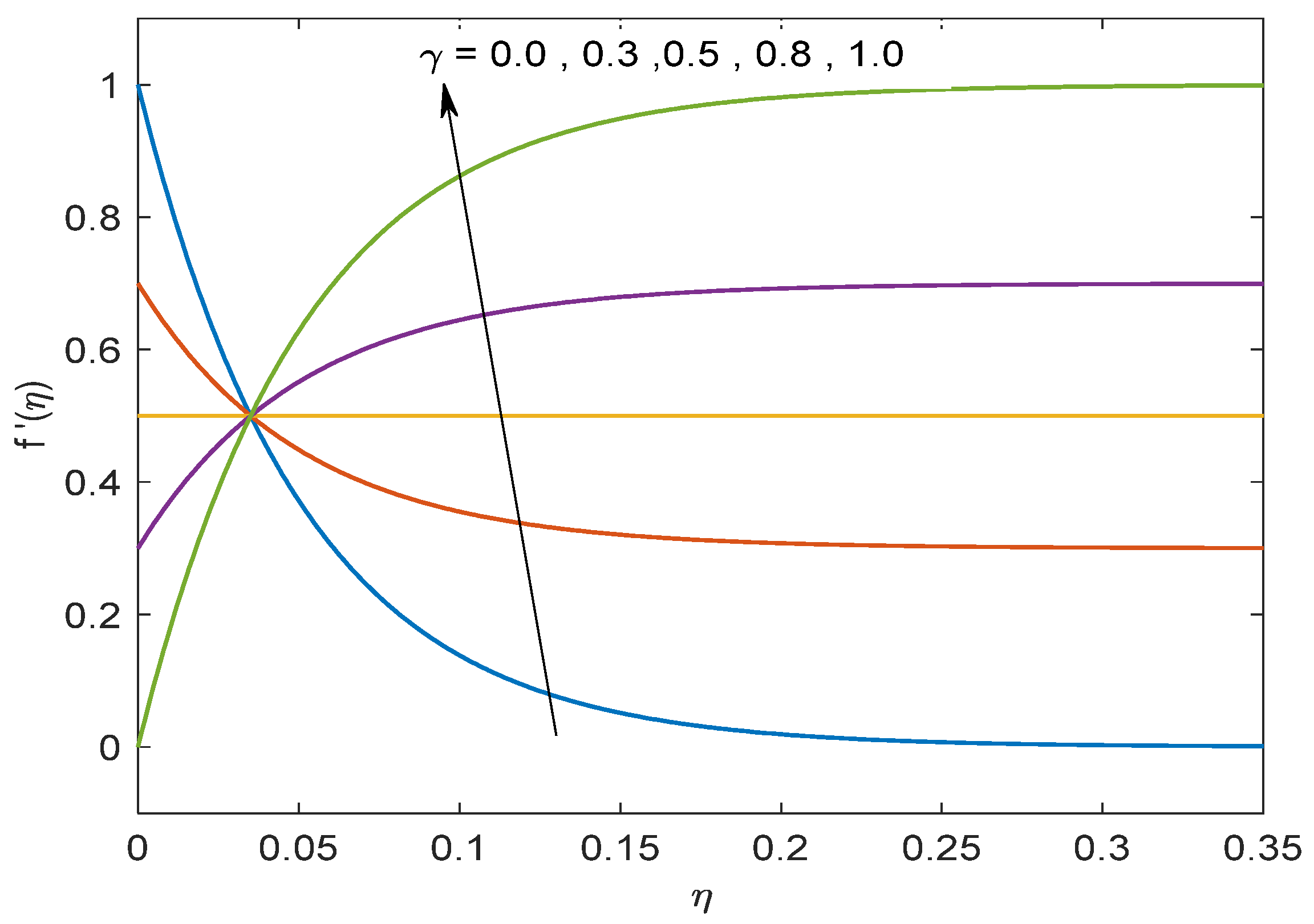
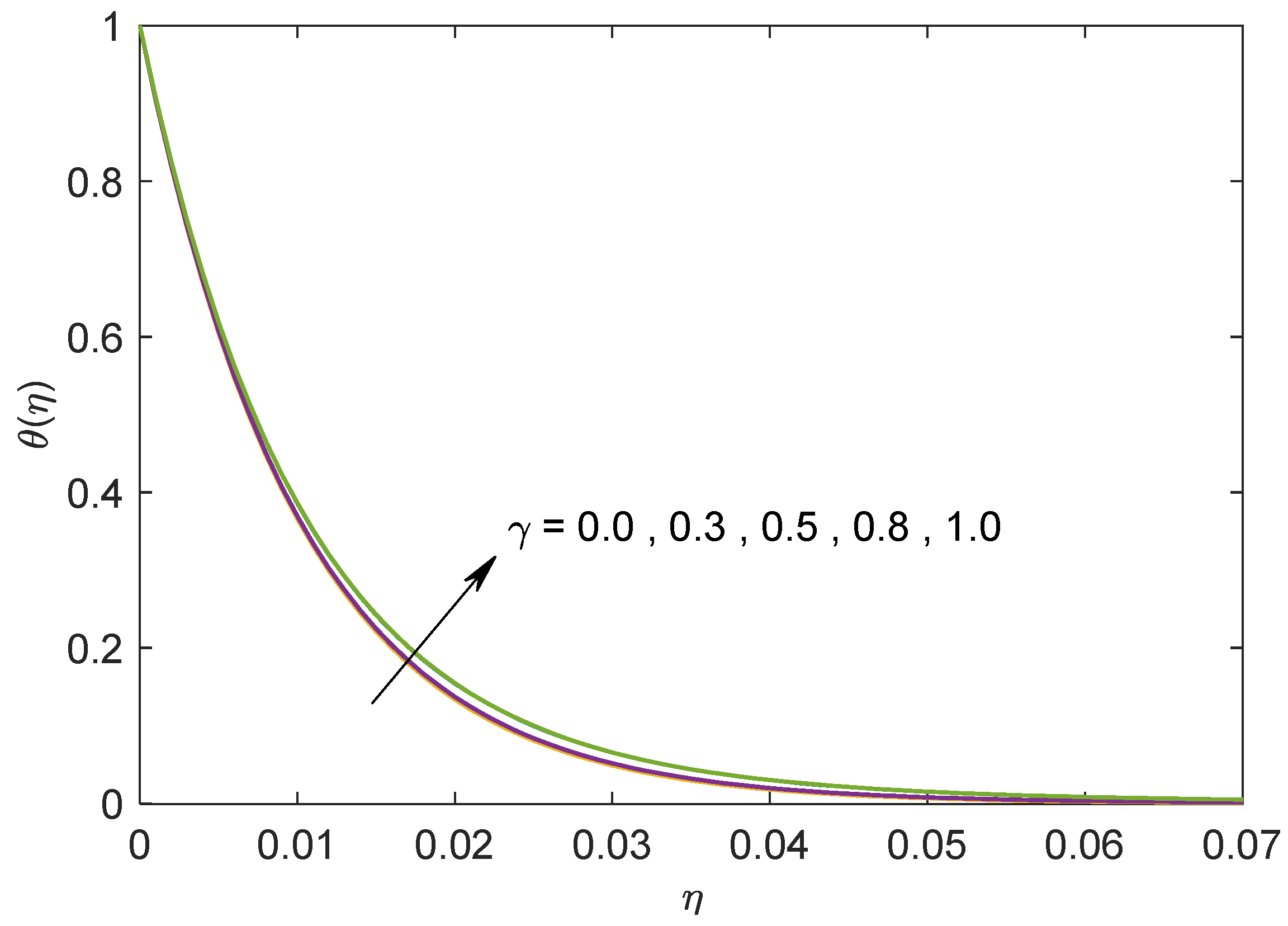
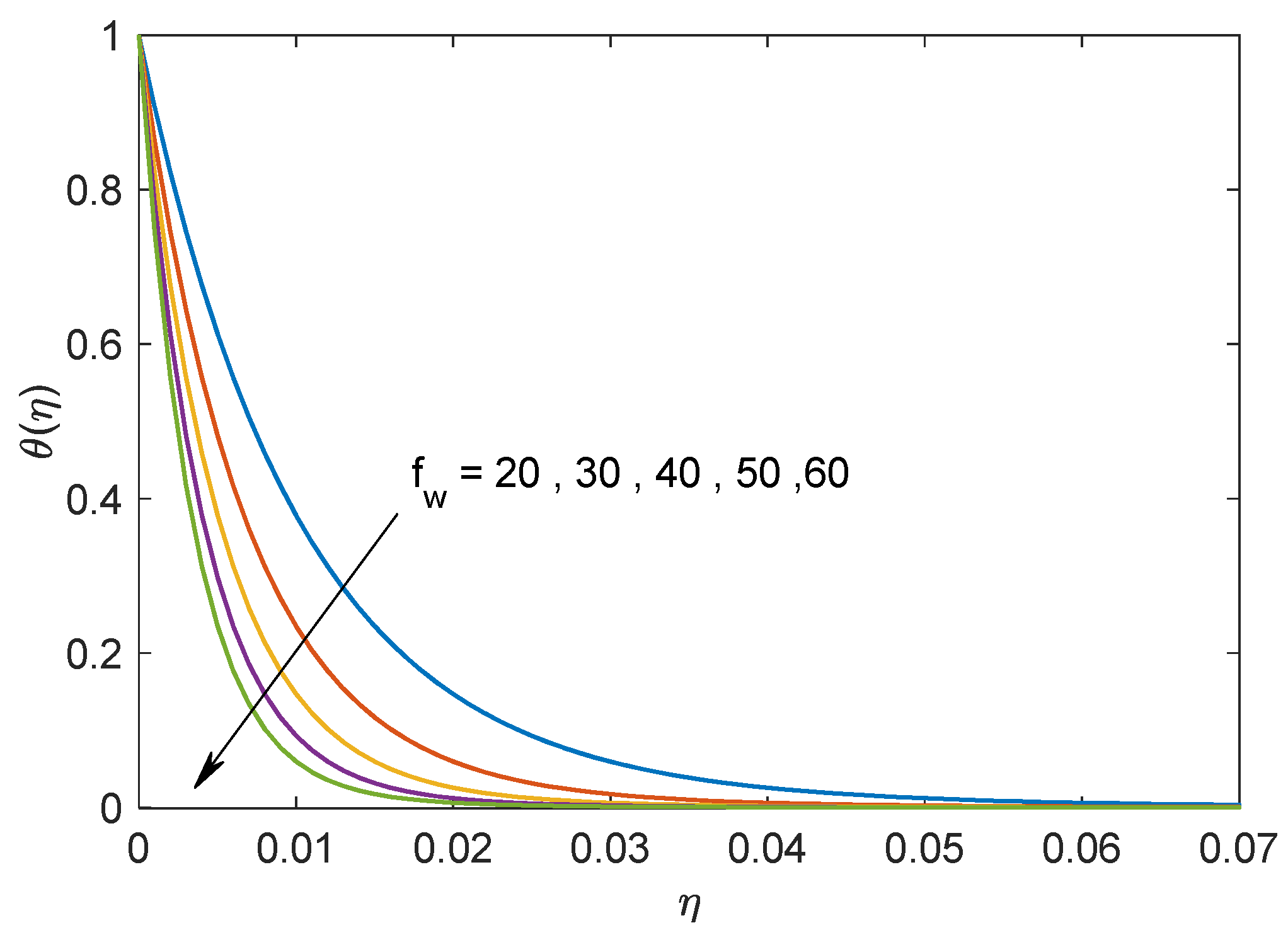
4. Outputs and Discussion
5. Conclusions
- -
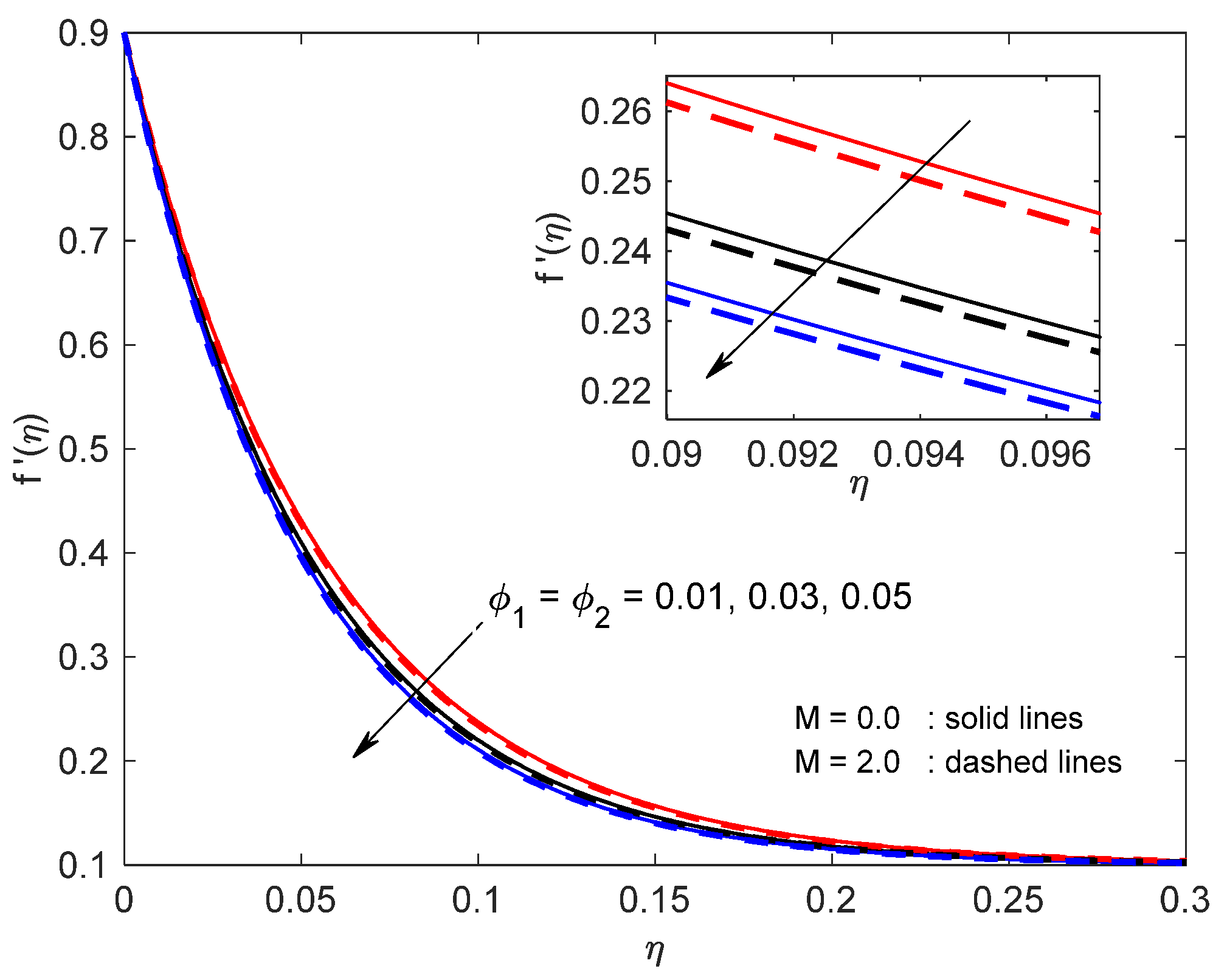
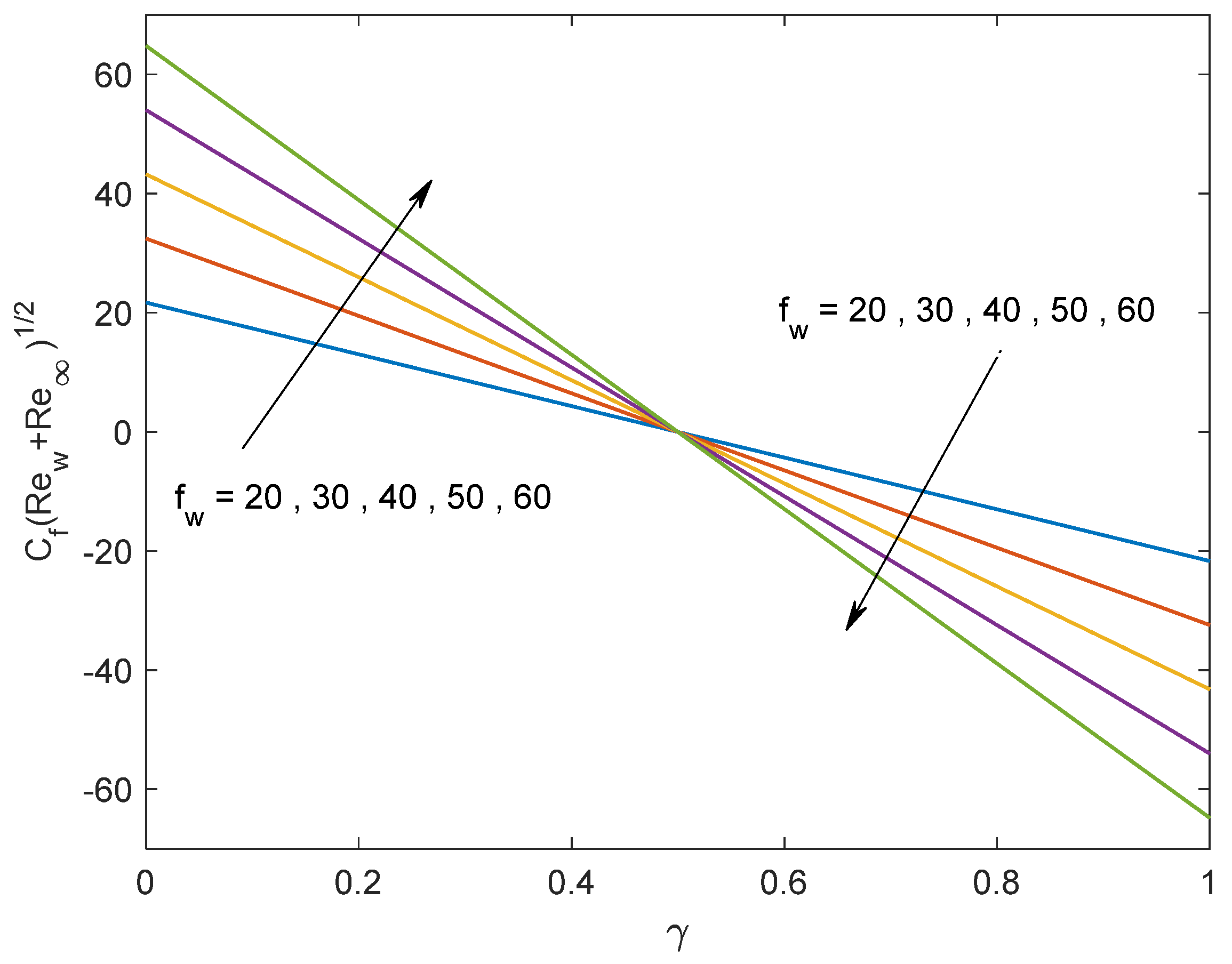
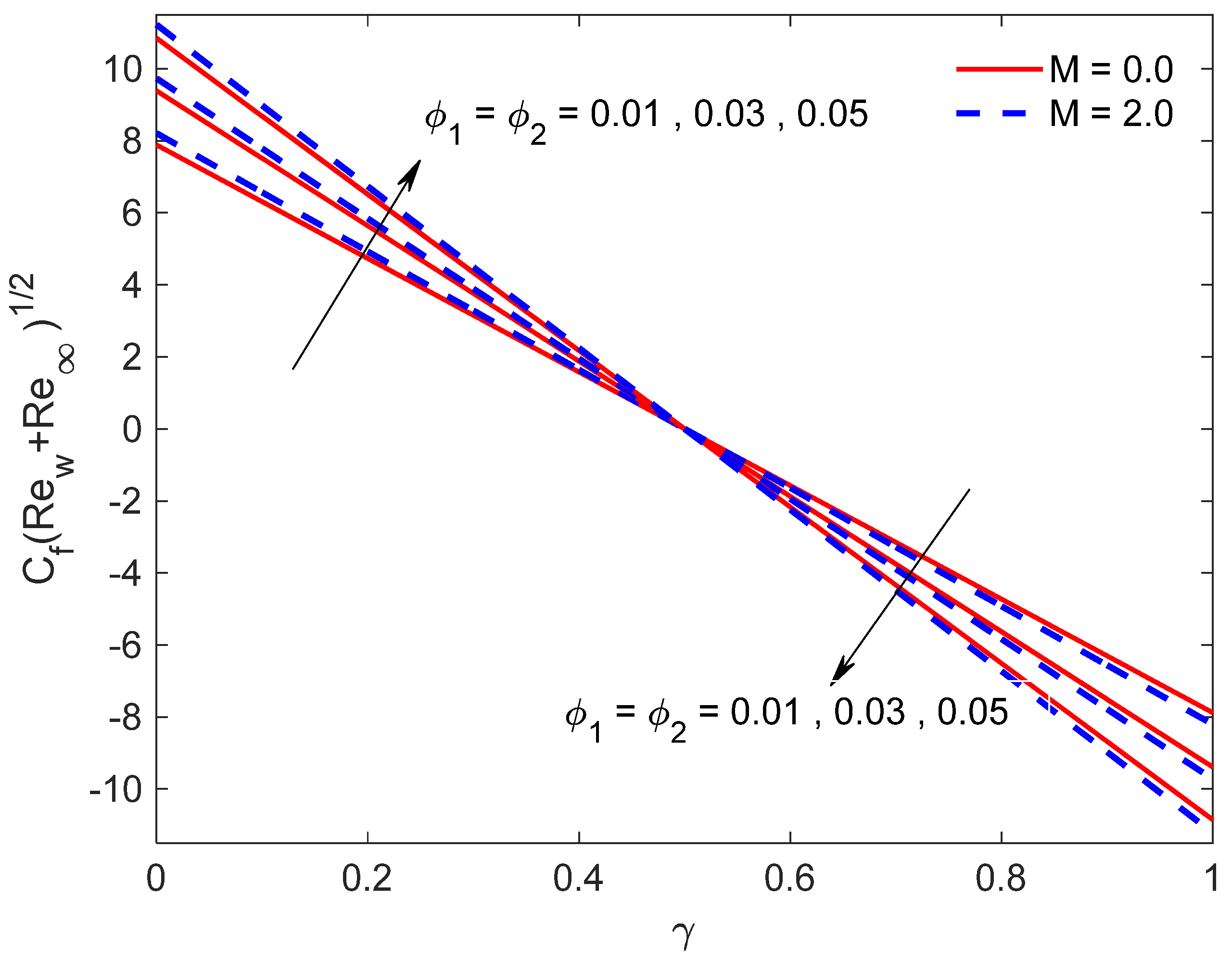
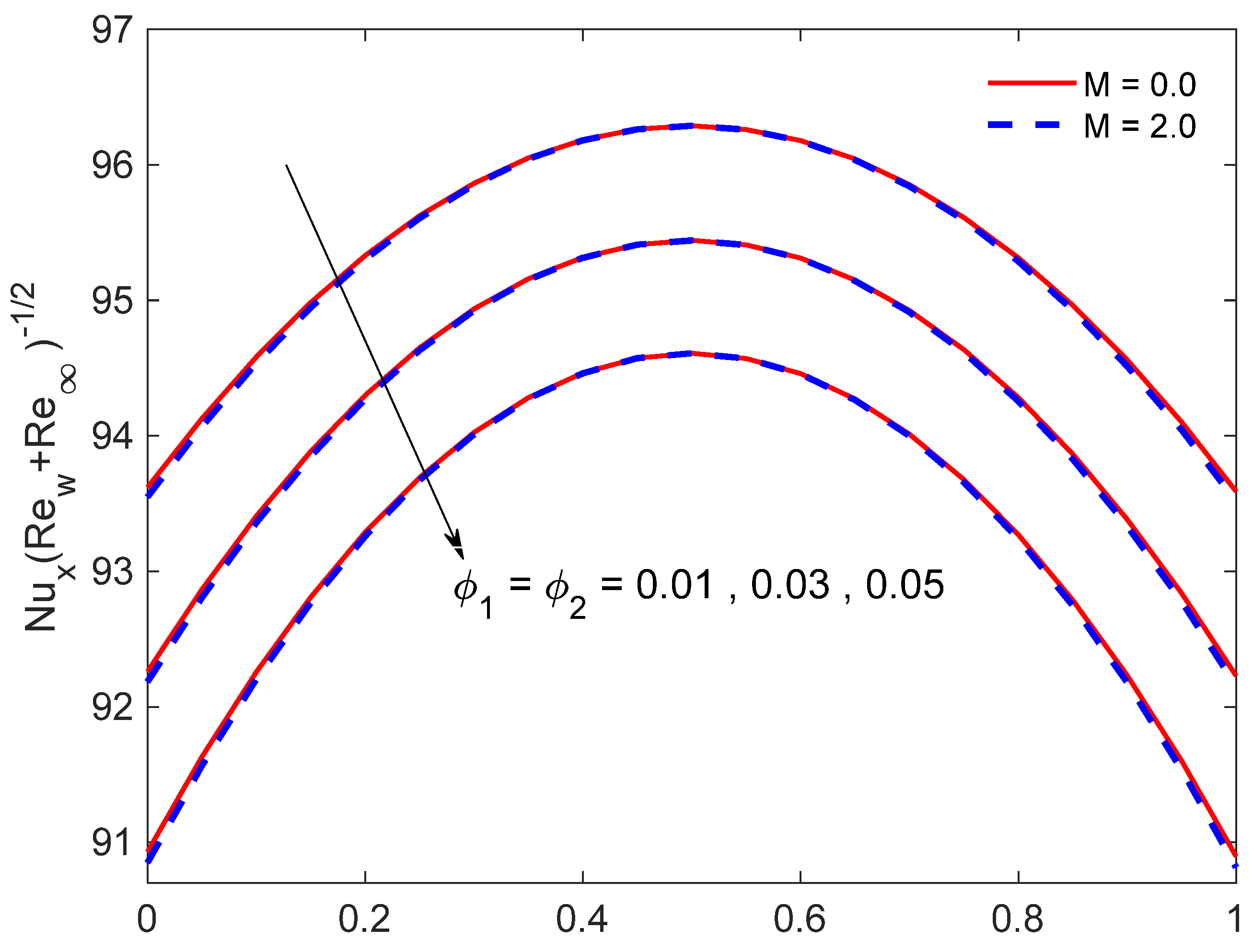
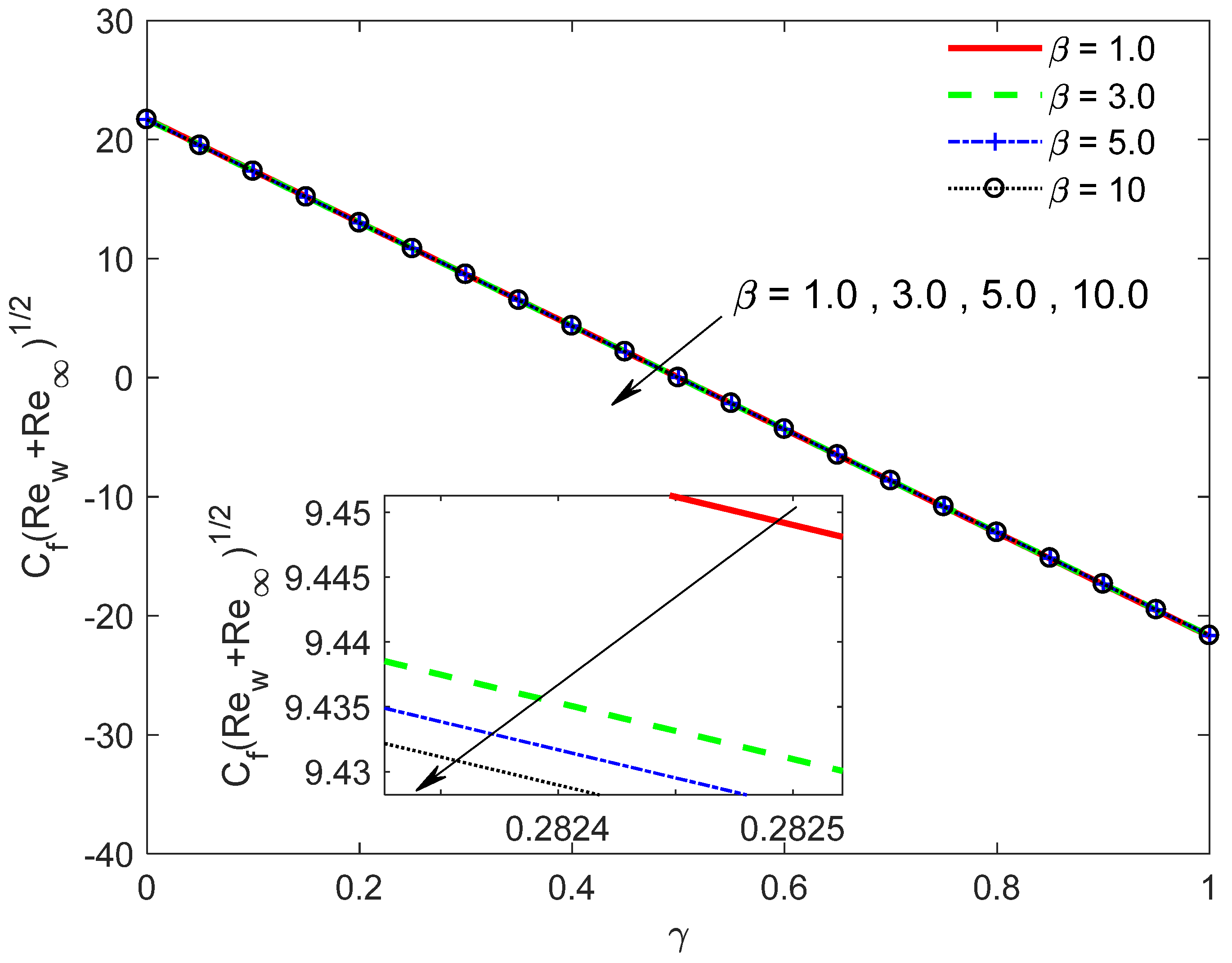
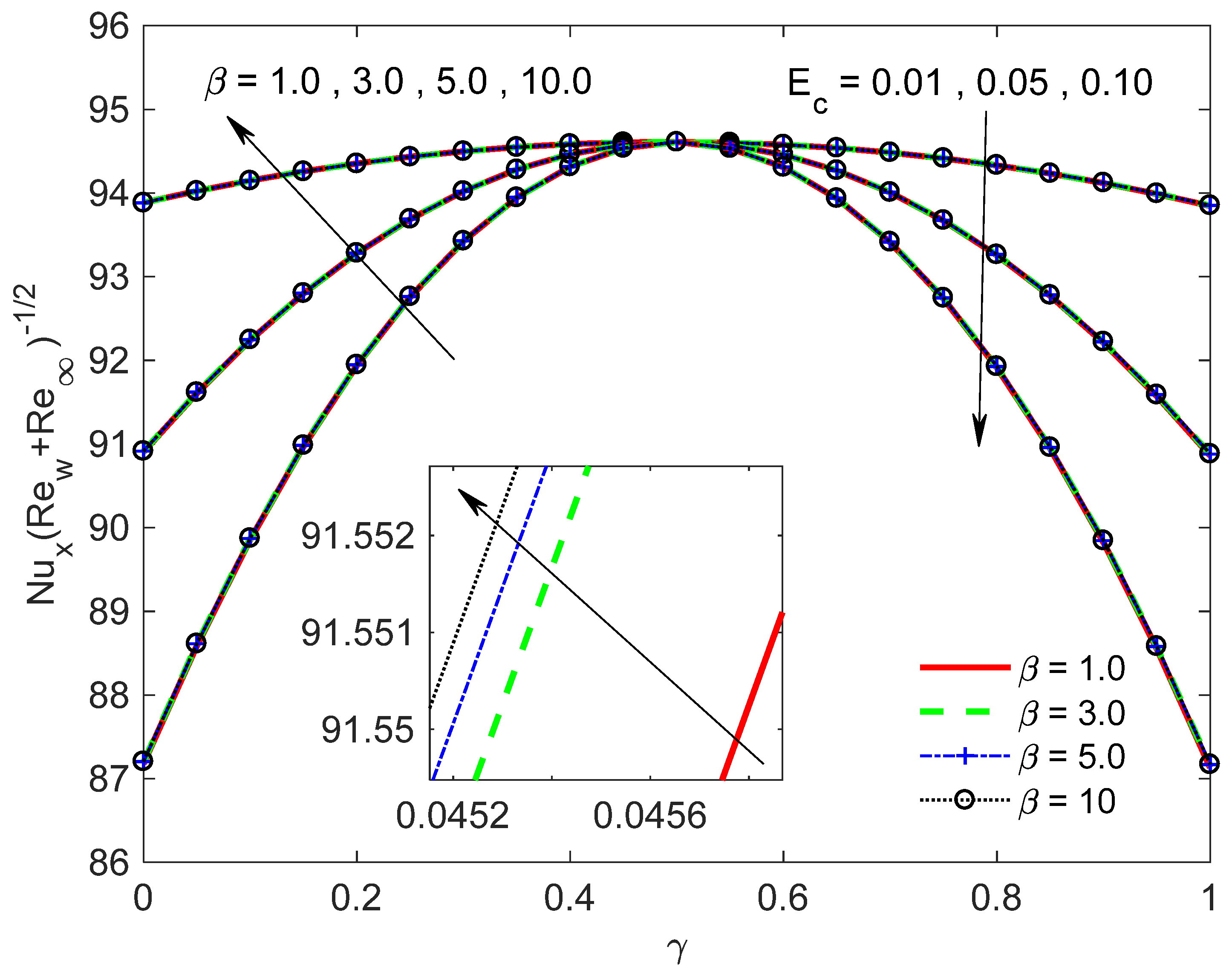
- Enhancing the suction parameter yields an improvement in both the skin friction coefficient and the Nusselt number.
- -
- An augmentation in the volume fraction parameters has a tendency to diminish the skin friction coefficient for velocity ratio γ > 0.5 and, conversely, an impact is uncovered for γ < 0.5, and causes a reduction in the Nusselt number.
- -
- Surface friction coefficient decreases with a rise in Casson parameter and, conversely, an impact is uncovered for the local Nusselt number.
- -
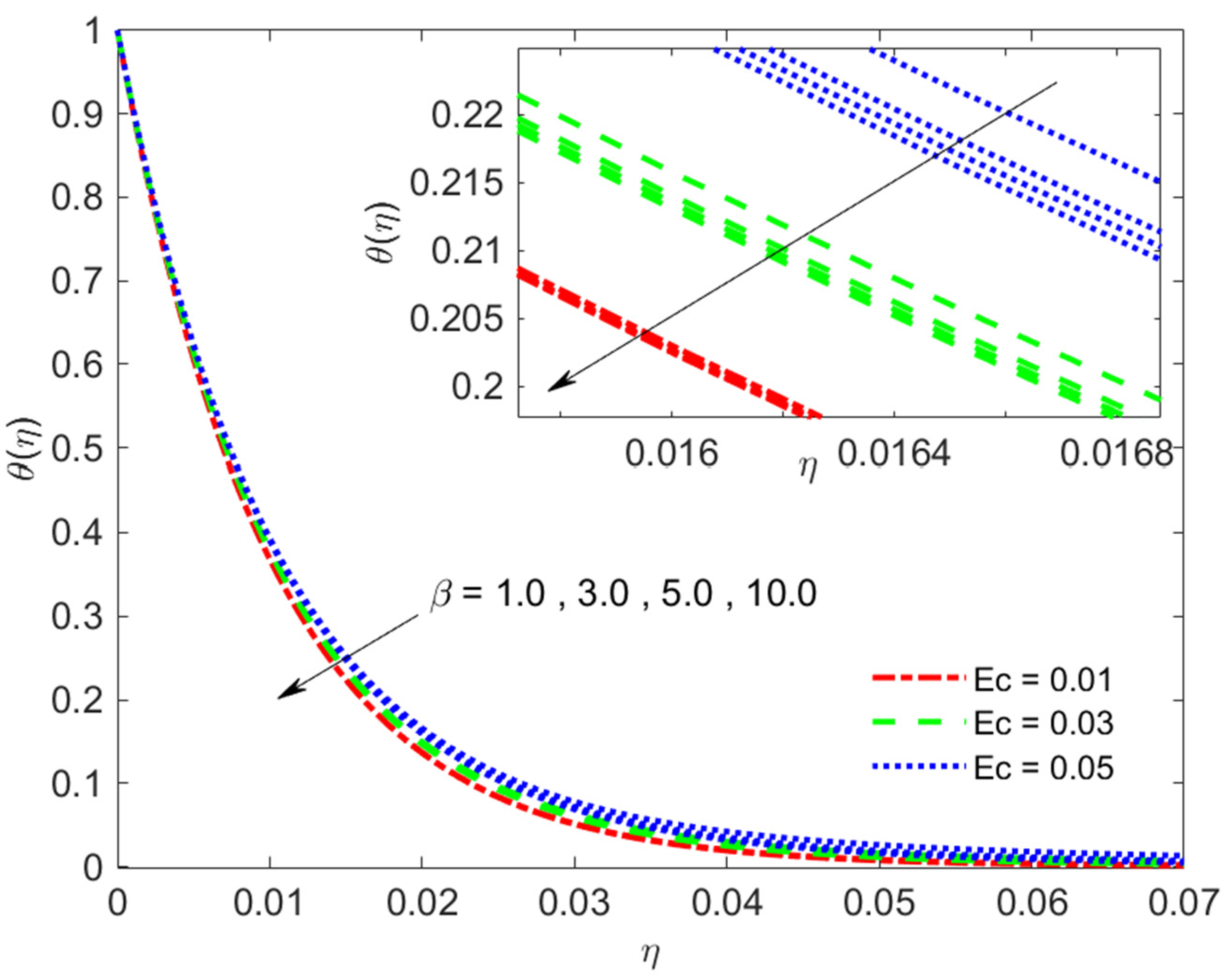
- Both the magnetic parameter and Eckert number Ec have caused a decline behavior in the Nusselt number and skin friction coefficient.
- -
- After the successful numerical struggle of parametric effectiveness on the fluid dynamics, this investigation can be extended in future for Maxwell hybrid nanofluid, Oldroyd-B hybrid nanofluid, and comparative analysis between Maxwell hybrid nanofluid, tangent-hyperbolic, and Jeffrey’s hybrid nanofluids.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| B | magnetic field strength |
| Cp | specific heat at constant pressure (J·kg−1·K−1) |
| Cf | local skin-friction coefficient |
| Ec | Eckert number |
| fw | suction parameter |
| f′ | dimensionless velocity |
| K | thermal conductivity (m2 s−1) |
| M | magnetic field parameter |
| Nux | local Nusselt number |
| Pr | Prandtl number |
| Rew, Re∞ | Reynolds numbers |
| T | Temperature (K) |
| u, v | Velocity components along and axes (m/s) |
| Uw, U∞ | The plate velocity and free stream velocity, respectively (m/s) |
| X | coordinate in flow direction (m) |
| Y | coordinate perpendicular to flow direction (m) |
| Vw | Transpiration velocity (m/s) |
| Greek Symbols | |
| α | Thermal diffusivity (m2 s−1) |
| β | Casson parameter |
| γ | velocity ratio parameter |
| η | similarity variable |
| θ | Dimensionless temperature |
| φ | solid volume fraction parameter |
| ψ | dimensional stream function |
| μ | Dynamic viscosity (kgm−1 s−1) |
| υ | kinematic viscosity (m2 s−1) |
| ρCp | Heat capacity (J·kg−3·K−1) |
| ρ | density (kg/m3) |
| σ | electric conductivity (Sm−1) |
| Subscripts | |
| 1 | Copper (Cu) |
| 2 | Alumina (Al2O3) |
| Bf | base fluid |
| hbnf | hybrid nanofluid |
| F | Fluid |
| Nf | Nanofluid |
| S | Nanoparticle |
| W | condition at the wall |
| ∞ | condition at infinity |
References
- Chen, S.-B.; Shahmir, N.; Ramzan, M.; Sun, Y.-L.; Aly, A.A.; Malik, M.Y. Thermophoretic particle deposition in the flow of dual stratified Casson fluid with magnetic dipole and generalized Fourier’s and Fick’s laws. Case Stud. Therm. Eng. 2021, 26, 101186. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Tran. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. Effect of thermophysical properties models on the predicting of the convective heat transfer coefficient for low concentration nanofluid. Int. Commun. Heat Mass Tran. 2008, 35, 1320–1326. [Google Scholar] [CrossRef]
- Choi, S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Developments and Applications of Non-Newtonian Flows; ASME: New York, NY, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Tran. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Sun, C.; Bai, B.; Lu, W.Q.; Liu, J. Shear-rate dependent effective thermal conductivity of H2Oþ SiO2. Nanofluids 2013, 25, 052002. [Google Scholar]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina-copper/water hybrid nanofluid flow over a stretching cylinder. J. Therm. Anal. Calorim. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- EL-Zahar, E.R.; Rashad, A.M.; Saad, W.; Seddek, L.F. Magneto-Hybrid Nanofluids Flow via Mixed Convection past a Radiative Circular Cylinder. Sci. Rep. 2020, 10, 10494. [Google Scholar] [CrossRef]
- Mabood, F.; Ashwinkumar, G.P.; Sandeep, N. Effect of nonlinear radiation on 3D unsteady MHD stagnancy flow of Fe3O4/ graphene–water hybrid nanofluid. Int. J. Ambient. Energy 2020. [CrossRef]
- Tlili, I.; Nabwey, H.A.; Samrat, N.; Sandeep, N. 3D MHD nonlinear radiative flow of CuO-MgO/methanol hybrid nanofluid beyond an irregular dimension surface with slip effect. Sci. Rep. 2020, 10, 9181. [Google Scholar] [CrossRef]
- Taghreed, H.; Alarabi, A.M.; Rashad, A. Homogeneous–heterogeneous chemical reactions of radiation hybrid nanofluid flow on a cylinder with joule heating: Nanoparticles shape impact. Coatings 2021, 11, 1490. [Google Scholar]
- Casson, N. A Flow Equation for Pigment-Oil Suspensions of the Printing Ink Type, Rheology of Disperse Systems; Pergamon Press: London, UK, 1959. [Google Scholar]
- Ahmad, S.; Nadeem, S. Cattaneo-Christov-based study of SWCNT–MWCNT/EG Casson hybrid nanofluid flow past a lubricated surface with entropy generation. Appl. Nanosci. 2020, 10, 5449–5458. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gowda, R.J.P.; Gireesha, B.J.; Prasannakumara, B.C. Non-Newtonian hybrid nanofluid flow over vertically upward/downward moving rotating disk in a Darcy-Forchheimer porous medium. Eur. Phys. J. Spec. Top. 2021, 230, 1227–1237. [Google Scholar] [CrossRef]
- Essam, R.; El-Zahar, A.R.; Mahdy, A.E.N.; Rashad, A.M.; Saad, W.; Seddek, L.F. Unsteady MHD Mixed Convection Flow of Non-Newtonian Casson Hybrid Nanofluid in the Stagnation Zone of Sphere Spinning Impulsively. Fluids 2021, 6, 197. [Google Scholar]
- Chalavadi, S.; Madde, P.; Naramgari, S.; Poojari, A.G. Effect of variable heat generation/absorption on magneto-hydrodynamic Sakiadis flow of Casson/Carreau hybrid nanoliquid due to a persistently moving needle. Heat Transf. 2021, 50, 8354. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahammad, N.A.; Chamkha, A.J. Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Stud. Therm. Eng. 2021, 27, 101229. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Alhadhrami, A.; Kumar, R.N.; Gowda, R.J.P.; Prasannakumara, B.C.; Kumar, R.S.V. Physical insights into the heat and mass transfer in Casson hybrid nanofluid flow induced by a Riga plate with thermophoretic particle deposition. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 095440892110393. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Rashad, A.M.; Gelany, A.M. Studying High Suction Effect on Boundary-Layer Flow of a Nanofluid on Permeable Surface via Singular Perturbation Technique. J. Comput. Theor. Nanosci. 2015, 12, 4828–4836. [Google Scholar] [CrossRef]
- El-Zahar, E.R. Applications of Adaptive Multi step Differential Transform Method to Singular Perturbation Problems Arising in Science and Engineering. Appl. Math. Inf. Sci. 2015, 9, 223–232. [Google Scholar] [CrossRef]
- El-Zahar, E.R.; Habib, H.M. Mathematical Modeling of Heat-Transfer for a Moving Sheet in a Moving Fluid. J. Appl. Fluid Mech. 2013, 6, 369–373. [Google Scholar]
- El-Zahar, E.R. Approximate analytical solutions of singularly perturbed fourth order boundary value problems using differential transform method. J. King Saud Univ. (Sci.) 2013, 25, 257–265. [Google Scholar] [CrossRef] [Green Version]
- El-Zahar, E.R.; El-Kabeir, S.M.M. A new method for solving singularly perturbed boundary value problems. Appl. Math. Inf. Sci. 2013, 7, 927–938. [Google Scholar] [CrossRef]
- Habib, H.M.; El-Zahar, E.R. Variable step size initial value algorithm for singular perturbation problems using locally exact integration. Appl. Math. Comput. 2008, 200, 330–340. [Google Scholar] [CrossRef]
- Habib, H.M.; El-Zahar, E.R. An algorithm for solving singular perturbation problems with mechanization. Appl. Math. Comput. 2007, 188, 286–302. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; Volume 1. [Google Scholar]
- Vulanović, R. A uniform numerical method for quasilinear singular perturbation problems without turning points. Computing 1989, 41, 97–106. [Google Scholar] [CrossRef]
- Doolan, E.P.; Miller, J.J.H.; Schilders, W.H.A. Uniform Numerical Methods for Singular-Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions; World Scientific: Singapore, 1996. [Google Scholar]
- Fehlberg, E. Low-Order Classical Runge-Kutta Formulas with Stepsize Control and Their Application to Some Heat Transfer Problems; National Aeronautics and Space Administration: Washington, DC, USA, 1969; Volume 315. [Google Scholar]
- Richard, L.B.; Faires, J.D. Numerical Analysis, 8th ed.; Thomson Brooks/Cole: Belmont, CA, USA, 2005. [Google Scholar]
- Morrison, D.D.; Riley, J.D.; Zancanaro, J.F. Multiple shooting method for two-point boundary value problems. Commun. ACM 1962, 5, 613–614. [Google Scholar] [CrossRef]
- Al-Juaydi, H.S. On Approximate Solutions of Singular Perturbation Boundary Value Problems. Master’s Thesis, PSAU University, Al-Kharj, Saudi Arabia, 2022, unpublished. [Google Scholar]
- El-Kabeir, S.M.M.; Rashad, A.M.; Gorla, R.S.R. Heat transfer in a micropolar fluid flow past a permeable continuous moving surface. J. Appl. Math. Mech. 2011, 92, 360–370. [Google Scholar] [CrossRef]




| Properties | Hybrid Nanofluid | Nanofluid |
|---|---|---|
| Dynamic viscosity | ||
| Density | ||
| Heat capacity | ||
| Thermal conduc. | ||
| Electrical conduc. |
| Property | Pure Water | Copper (Cu) | Alumina Al2O3 |
|---|---|---|---|
| ρ (kg m−3) | 997.1 | 8933 | 3970 |
| Cp (Jkg−1 K−1) | 4179 | 385 | 765 |
| k (W m−1 K−1) | 0.613 | 401 | 40 |
| 0.05 | 5.96 × 107 | 1 × 10−10 |
| ASM | IASM | ASM | IASM | ASM | IASM | ASM | IASM | |
|---|---|---|---|---|---|---|---|---|
| 2 | 9.91 × 10−1 | 1.74 × 10−2 | 9.94 × 10−1 | 1.53 × 10−1 | 9.95 × 10−1 | 1.20 × 10−2 | 9.96 × 10−1 | 5.05 × 10−3 |
| 4 | 9.86 × 10−1 | 9.70 × 10−3 | 9.91 × 10−1 | 5.41 × 10−3 | 9.93 × 10−1 | 1.92 × 10−10 | 9.94 × 10−1 | 1.51 × 10−12 |
| 6 | 9.80 × 10−1 | 1.72 × 10−3 | 9.87 × 10−1 | 4.01 × 10−10 | 9.90 × 10−1 | 9.92 × 10−1 | ||
| 8 | 9.72 × 10−1 | 2.25 × 10−10 | 9.82 × 10−1 | 9.87 × 10−1 | 9.90 × 10−1 | |||
| 10 | 9.62 × 10−1 | 9.77 × 10−1 | 9.84 × 10−1 | 9.87 × 10−1 | ||||
| 60 | 4.78 × 10−1 | 6.74 × 10−1 | 7.72 × 10−1 | 8.31 × 10−1 | ||||
| 80 | 2.80 × 10−1 | 5.42 × 10−1 | 6.72 × 10−1 | 7.51 × 10−1 | ||||
| 100 | 8.29 × 10−2 | 4.10 × 10−1 | 5.73 × 10−1 | 6.72 × 10−1 | ||||
| 120 | 2.87 × 10−10 | 2.78 × 10−1 | 4.74 × 10−1 | 5.92 × 10−1 | ||||
| 140 | 1.46 × 10−1 | 3.75 × 10−1 | 5.13 × 10−1 | |||||
| 160 | 1.42 × 10−2 | 2.76 × 10−1 | 4.34 × 10−1 | |||||
| 180 | 1.60 × 10−10 | 1.77 × 10−1 | 3.55 × 10−1 | |||||
| 200 | 7.89 × 10−2 | 2.76 × 10−1 | ||||||
| 220 | 2.28 × 10−7 | 1.96 × 10−1 | ||||||
| 240 | 1.17 × 10−1 | |||||||
| 260 | 3.85 × 10−2 | |||||||
| 280 | 1.71 × 10−7 | |||||||
| CPU Time (s) | Number of Iterations (N) | |||
|---|---|---|---|---|
| ASM | IASM | ASM | IASM | |
| 15 | 12.5632 | 0.2766 | 82 | 2 |
| 20 | 17.8714 | 0.5015 | 109 | 3 |
| 25 | 25.9999 | 0.7556 | 136 | 4 |
| 30 | 46.8376 | 0.8388 | 163 | 4 |
| 35 | 46.8376 | 1.1532 | 190 | 5 |
| 40 | 58.5254 | 1.5102 | 216 | 6 |
| 45 | 86.0195 | 1.6364 | 243 | 6 |
| 50 | 78.9723 | 2.0545 | 270 | 7 |
| 55 | 93.2497 | 2.5722 | 297 | 8 |
| 60 | 108.9572 | 2.7534 | 324 | 8 |
| γ | EL-Kabeir et al. [34] | Present Results |
|---|---|---|
| 0.0 | 0.33206 | 0.3322903 |
| 0.1 | 0.27828 | 0.2783955 |
| 0.2 | 0.21734 | 0.2174451 |
| 0.3 | 0.15017 | 0.1501433 |
| 0.4 | 0.07753 | 0.07728752 |
| 0.5 | 0 | 0 |
| 0.6 | −0.08190 | −0.08195239 |
| 0.7 | −0.16772 | −0.1678250 |
| 0.8 | −0.25703 | −0.2568486 |
| 0.9 | −0.34944 | −0.3494589 |
| 1.0 | −0.44455 | −0.4440279 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
EL-Zahar, E.R.; Rashad, A.M.; Al-Juaydi, H.S. Studying Massive Suction Impact on Magneto-Flow of a Hybridized Casson Nanofluid on a Porous Continuous Moving or Fixed Surface. Symmetry 2022, 14, 627. https://doi.org/10.3390/sym14030627
EL-Zahar ER, Rashad AM, Al-Juaydi HS. Studying Massive Suction Impact on Magneto-Flow of a Hybridized Casson Nanofluid on a Porous Continuous Moving or Fixed Surface. Symmetry. 2022; 14(3):627. https://doi.org/10.3390/sym14030627
Chicago/Turabian StyleEL-Zahar, Essam R., Ahmed M. Rashad, and Haifa S. Al-Juaydi. 2022. "Studying Massive Suction Impact on Magneto-Flow of a Hybridized Casson Nanofluid on a Porous Continuous Moving or Fixed Surface" Symmetry 14, no. 3: 627. https://doi.org/10.3390/sym14030627
APA StyleEL-Zahar, E. R., Rashad, A. M., & Al-Juaydi, H. S. (2022). Studying Massive Suction Impact on Magneto-Flow of a Hybridized Casson Nanofluid on a Porous Continuous Moving or Fixed Surface. Symmetry, 14(3), 627. https://doi.org/10.3390/sym14030627







