Abstract
In this paper, multi-channel active noise control systems subjected to narrowband disturbances with close frequencies are investigated. Instead of controlling each frequency separately, a mixed-reference signal is assumed and thus a transversal controller is utilized. First, the convergent behaviors of a generalized FxLMS-based algorithm are theoretically analyzed in the mean sense, from which the influence of the controller structure on the convergence rate is revealed. A novel narrowband algorithm is then proposed, in which a decimated transversal controller is used to alleviate the computational burden. Simulations based on a 4 × 8 active-noise-control system are carried out to verify the proposed method. The results show that a good convergence rate can be obtained, and the computational complexity can also be greatly reduced.
1. Introduction
Active noise control (ANC) [1,2] is an effective method to attenuate noise in low-frequency bands where traditional passive strategies are generally considered to be bulky and inefficient. The basic principle of an ANC system is the superposition, where an unwanted primary noise could be cancelled by a secondary noise with the same amplitude but the opposite phase. In many industrial applications, the rotating machine is one of the most common sources of the unwanted noise or vibration. The disturbance generated by such machines generally consists of multiple sinusoidal components, and thus are narrowband in nature. Although adaptive algorithms such as the filtered-x least-mean-square (FxLMS) algorithm can be directly used to deal with such narrowband disturbances, the ANC system would exhibit characteristics that are different from the general case with the broadband inputs [3]. As a result, a variety of FxLMS-based narrowband algorithms have been proposed and well analyzed [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23], which can also be used in the area of active vibration control (AVC) of the narrowband disturbances, such as in the case of vibration isolation (VI) [9,10].
Vicente et al. [4] presented a detailed convergence analysis of the FxLMS algorithm with the narrowband inputs. It has been shown that the global behavior of the ANC system is linear and time-invariant (LTI), provided that the controller length is sufficiently long, in which case the time-varying terms become negligible. Haarnoja et al. [5] presented an exact linear time-periodic (LTP) state-space representation of the multi-channel FxLMS algorithm. It has been confirmed that the ANC system has an LTI behavior if the controller length is suitably chosen. In order to get rid of the influence of the time-varying terms corresponding to the controller length, Xiao et al. [6,7] proposed FxLMS-based narrowband algorithms in which two orthogonal reference signals (sine and cosine) are used for the control of each disturbance frequency. Compared with the original FxLMS algorithm, the computational load is reduced since each controller only has two taps. With such a controller structure, the computational complexity could be further reduced since the control for the different disturbance frequencies is separated and hence low-order local secondary path models could be used [8]. Based on this two-tapped controller with the orthogonal references, Li et al. [9,10] further proposed the FxNewton algorithms, in which the inverse of the frequency response matrix of the secondary path model is used so that the multi-channel control system can be completely decoupled, and an optimal convergence rate can then be obtained. In addition, variable stepsize algorithms [11,12], filtered-x weighted accumulated LMS algorithms [13,14] as well as decentralized control algorithms [15,16] have also been proposed with similar controller structures.
Although Xiao’s methods have the advantages of a lowered complexity and an accelerated convergence rate, an external synchronization signal is generally necessary for the synthetization of the orthogonal reference signals. If this signal is not available, then frequency estimation algorithms should be used. Since the noise reduction performance is rather sensitive to the frequency estimation error [17], different algorithms [18,19,20,21,22,23] have been proposed to provide an accurate disturbance frequency. This frequency can not only be adaptively adjusted according to the error signal [18,19], but it can also be estimated using a reconstructed disturbance signal (with the help of the internal model control) [20,21,22] or even a reference signal [23]. If a reference signal is available for the system, another approach to generate the orthogonal references is to use an extra reference filter corresponding to the Hilbert transformation [9,10]. However, with this method, the computational complexity is enhanced, and an extra delay is also imposed on the reference signals.
In the ANC/AVC applications where multiple primary sources exist, some harmonic components from different devices might have very close disturbance frequencies, such as the case for the VI system, where different machines operate with rather close rotating speeds [10]. In these cases, the design of the narrowband ANC/AVC systems would become more challenging. A multi-reference algorithm is proposed in [10], in which different reference signals could be obtained directly from the primary sources and the control of the different disturbance frequencies could then be separated. However, the references corresponding to the different frequencies might not be able to be obtained in some practical implementations, such as when designing a general-purpose VI system without any knowledge of its loading equipment. In this situation, how to generate the reference signals remains a problem since the frequency estimation methods mentioned above would lose their efficiency if the disturbance frequencies were rather close.
In this paper, the multi-channel narrowband control system with close disturbance frequencies is discussed with the assumption that only a mixed-reference signal is available. Instead of separating the reference signals for the different frequencies with the usage of high-order bandpass filters, which are not efficient or even feasible for practical implementations, the mixed-reference signal is used directly as the input of a set of transversal controllers. First, a frequency-domain convergence analysis is presented in the mean sense. A characteristic matrix is constructed based on the symmetry of the controller’s responses on the positive and negative disturbance frequencies, from which the influence of the controller structure on the convergent behaviors is revealed. An insight view on the degradation of the convergence rate with an insufficient controller length is also provided. Based on the theoretical analyses, a narrowband FxLMS-based algorithm is then proposed, in which a decimated FIR controller is used in order to accelerate the convergence rate and lower the computational burden as much as possible. Simulations based on a realistic multi-channel (4 × 8) ANC system are carried out, and the results demonstrate the effectiveness of the proposed algorithm.
2. Methods
2.1. Frequency-Domain Convergence Analysis
In order to analyze the convergent behaviors with different controller structures, the narrowband FxLMS-based algorithms can be given with the following equations:
where y(n), e(n) and d(n) are the vectors of the output, error and disturbance signals, respectively. The controller has N coefficient vectors wi(n) (i = 0, …, N−1), which correspond to the N reference signals xi(n), respectively. Sl, Cl are the l-th coefficient matrices of the impulse responses of the secondary path as well as its model, and Ls, L are the corresponding lengths. Thus, Ri(n) is the matrix of the filtered reference signal which corresponds to xi(n). In Equation (4), the controller coefficient vectors are updated with a stepsize μ. The algorithm shown by Equations (1)–(4) can be considered as a generalization of the narrowband FxLMS-based algorithms mentioned in Section 1. For the original FxLMS algorithm, since the controllers are the transversal FIR filters, N is the controller length and xi(n) = x(n−i), where x(n) is the input reference signal. For Xiao’s methods [6,7], we have N = 2, and x0(n), x1(n) are the orthogonal references cos(ωn), sin(ωn).
Without a loss of generality, the reference signal x(n) is assumed to consist of two close frequencies in this paper:
where ω1, ω2 are the disturbance frequencies, A1, A2 and φ1, φ2 are the corresponding amplitudes and initial phases, respectively. The initial phases are assumed to be uniformly distributed within (0, 2π) and independent with respect to each other. Thus, xi(n) can be written as:
where χk, (k = 1, 2) are the complex amplitudes and θki is an extra phase shift corresponding to the controller’s structure. We have θki = −ωki for the FIR controllers and θk0 = 0, θk1 = −0.5π for Xiao’s methods. Similarly, the disturbance vector can also be written as:
where z(n) is a zero-mean additive noise vector.
Substitute Equations (6) and (7) into Equations (1)–(3), then
where
are the frequency response vectors of the controller at ωk as well as at −ωk, and
are the frequency response matrices of the secondary path and its model at ωk. It is noted that Ck varies in different algorithms. With a perfect secondary path model, we have Ck = Sk for the FxLMS algorithm and for the FxNewton algorithm [9,10]. Ck can also be a diagonal matrix in decentralized control whose elements should be optimized [16].
In the derivation of Equation (9), a slow convergence is assumed, i.e., Wk(n) ≈ Wk(n − l) for all l = 0, …, Ls−1. This approximation indicates that the controller would not change significantly during the timescale of the impulse response of the secondary path. Since the stepsize is usually small, this assumption is common in the ANC literature [1].
Next, by substituting Equation (4) into Equation (11), the update equations for the frequency responses of the controller at ±ωk can be obtained:
Define
as the error vector of the controller’s frequency responses with respect to their optimal values, substitute Equations (9) and (10) into Equations (13) and (14) for k = 1,2 and take the expectation on both sides, then we have
where
are parameters only corresponding to the controller’s structure. In the derivation of Equations (16) and (17), the error vectors defined in Equation (15) are assumed to be independent with respect to the initial phases φ1, φ2 as well as the noise vector z(n). As a result, all of the terms corresponding to φ1, φ2 and z(n) would be zero when taking this expectation.
Equations (16) and (17) can be further combined as follows:
where
The convergent behaviors of Equation (19) are mainly determined by the specific eigenvalues of the characteristic matrix (I−H) [1,16]. It can be seen that both the controller structure and the secondary path as well as its model contribute to the convergence rate. It can also be observed that the convergent behaviors for different disturbance frequencies are coupled together, provided that the parameters defined in Equation (18) are non-negligible, which generally indicates a slow convergence rate.
If the FxNewton algorithm is used with accurate models (i.e., P1,2 = I), H would be a Hermitian matrix with real eigenvalues:
where is a diagonal matrix with all of the eigenvalues of H, and Q is the orthogonal-transformation matrix. With Equation (21), the convergence process can further be written as:
From Equation (22), it can be found that the algorithm converges exponentially with the different modes, each of which corresponds to a specific eigenvalue of H. The convergence rate of the algorithm is determined by the slowest mode with respect to the minimum eigenvalue λmin. In the logarithmic domain, this mode decreases linearly, and the decreasing slope is
Thus, the time constant of this mode is approximately
within which, the mode amplitude would decrease to e−1 of its initial value. This time constant can be seen as a benchmark of the convergence rate and should be depressed as much as possible. As a result, in order to obtain the fastest convergence rate, the minimum eigenvalue of H must be maximized. This occurs when μ1 = μ2 and all of the parameters in Equation (18) are equal to 0. Since the parameters in Equation (18) are only determined by the controller, its structure should be carefully designed.
2.2. The Proposed Algorithm
Since it is assumed that only a mixed-reference x (n) can be obtained, whose components at different frequencies can hardly be separated in applications, transversal filters are used as the controllers in this paper. For the FIR controllers with length N, Equation (18) would become
which should be kept as small as possible so that the influence of the controller structure on the convergent process can be eliminated and the convergence rate can then be enhanced. Since the disturbance frequencies are close, the first two parameters in Equation (25) decrease more rapidly as N increases, which generally makes the third parameter dominant. Meanwhile, as the difference between the two disturbance frequencies is rather small, the controller length N should be rather large to reduce this dominant parameter. Precisely, N should be set to one entire cycle corresponding to the difference frequency so that can be reduced to 0. This is in accordance with the results in [4,5]. However, the computational complexity would be greatly enhanced with such a large controller length.
In order to lower the computational burden, a decimated transversal controller is proposed in this paper. The i-th coefficient vector wi (n) corresponds to a down-sampled reference signal:
where M is the decimation factor. With this decimated controller, the phase-shift parameter would be θki = −Mωki and Equation (18) would reduce to
It can be observed that in order to force to 0, the controller length N and the decimation factor M should satisfy
where fs is the sampling frequency. Equation (28) still indicates that the time scale T of the controller should cover one entire cycle of the difference frequency. However, the filter length N can be reduced by a factor of M in this case, which means that the computational complexity can also be greatly reduced.
With Equation (26), the filtered reference matrices in Equation (3) can further be simplified as:
Since the disturbance frequencies are close, a local secondary path model [8] is used in this paper. Theoretically, L = 2 is sufficient to give the accurate frequency responses of the model filters.
It is further noted that the decimation factor M is not limited by the Nyquist–Shannon sampling theorem, which means that half of the actual sampling frequency of the decimated controller can be even lower than the disturbance frequencies. However, the aliasing of the disturbance frequencies should be avoided, i.e., M (ω1 + ω2) should never be an integer multiple of 2π. Otherwise, the controller would lose the ability to differentiate the two disturbance frequencies and hence the noise reduction performance would be greatly deteriorated. It can also be observed from Equation (27) that would be 1 in this case, which indicates that half of the eigenvalues of the characteristic matrix (I−H) would be 1 and the frequency responses of the controller would never converge to its optimal value. Besides, N and M should be chosen to keep all of the 3 parameters in Equation (27) small enough when M becomes relatively large, since in this case, might no longer be dominant.
3. Simulation Validation
In this section, simulations based on a realistic multi-channel ANC system [16] are carried out to validate the effectiveness of the proposed methods. The ANC system, as shown in Figure 1, is mainly constituted with an acrylic box, two primary noise sources, four secondary noise sources as well as eight error microphones. The primary sources are placed inside the box, while the secondary sources are mounted on the opening top of the box. The error microphones are placed above the secondary speakers as a 4 × 2 array. All of the primary and secondary paths are identified with the FIR models, which are used in simulations. A more detailed description as well as some of the identified acoustic responses of the ANC system can be found in [16].

Figure 1.
The multi-channel ANC system, based on which simulations are carried out.
In the simulations, an 8 kHz sampling frequency is used and two sinusoidal disturbances with f1 = 99 Hz and f2 = 101 Hz are generated by the two primary sources, respectively, as shown in Figure 1. Meanwhile, Gaussian white noises are added in the disturbance signals as z(n), whose variance is set to 0.0001. A mixed reference is used in the control algorithm, as shown by Equation (5), where the amplitudes of the two components are set to be equal. A set of two-order filters (L = 2) are used as the reference filters in Equation (29), whose coefficient matrices C0 and C1 are calculated so that is satisfied at 100 Hz. With these reference filters, P1 and P2 would approximately reduce to identity matrices, and the influence of the secondary path responses on the convergence rate can be eliminated [16]. Hence, the influence of the controller structure on the convergent behaviors can be shown more clearly. Since the normalized stepsize μk is affected by the controller length N, the stepsize μ in Equation (4) is chosen to satisfy μ1 = μ2 = 0.0001 for all of the simulations. For each combination of N and M, the convergent trajectories are obtained by the ensemble average of 30 simulations, where the initial phases φ1, φ2 are independently chosen from a uniform distribution within (0,2π). The control algorithm is started at 1 s in the simulations.
First, the parameters in Equation (27) are calculated with different combinations of N and M, whose absolute values are illustrated in Figure 2a–d. It can be seen that the parameters corresponding to the controller’s structure are mainly determined by the controller’s time scale T = NM. When M is not significant, the absolute values of κ1,2 and decrease rapidly as T increases. However, the decrease in is much slower since the corresponding difference frequency is much smaller. When M gets larger, κ1,2 and could also exhibit some non-negligible values even if T is relatively high, in which case N should be carefully chosen so that all of the parameters in Equation (27) are small enough. It can also be observed that equals 1 and κ1,2 also exhibit abnormal values when M = 40. This is the case in which M (ω1 + ω2) = 2π and the two disturbance frequencies are aliased together.
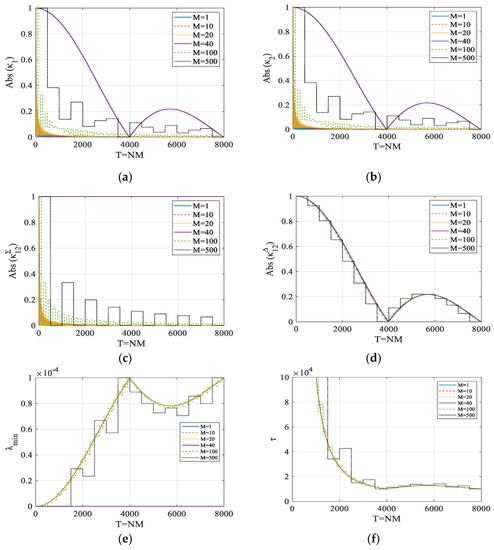
Figure 2.
The absolute values of (a) ; (b) ; (c) ; (d) ; (e) the minimum eigenvalues of H and (f) the time constant τ corresponding to the slowest modes with different N and M.
The minimum eigenvalues of H as well as the time constants defined in Equation (24) corresponding to the slowest modes are further calculated, whose results are shown in Figure 2e,f, respectively. It can be observed that, generally, λmin gets larger and the convergence rate gets faster as T increases when T < 4000, which mainly results from the decreasing values of . However, when T > 4000, λmin decreases and the convergence rate also decreases slightly. It can be found that the fastest convergence rate can be obtained with T = 4000 for all rational M. Thus, T = 4000 is the best choice for the controller, with which all of the parameters in Equation (27) exhibit very small values and the fastest convergence rate could then be expected. This value just corresponds to one cycle of a difference frequency of 2 Hz.
Next, the proposed algorithm is simulated with different combinations of N and M. The resultant convergent behaviors of the total error energy, which is the summation of all squared error signals, is shown in Figure 3 and Figure 4. The total error energy is normalized in these figures with respect to its initial value before the control. Figure 3 shows the averaged convergent trajectories with a different T while M is fixed to 20. It can be found that the controller’s time scale T is a key issue for the convergence rate. When T is small in this case, has a relatively large value, and hence a slow convergence process is observed. The convergence rate can be enhanced as T gets larger and the value of gets smaller. The fastest convergence rate can be obtained when T = 4000, just as predicted by Figure 2, in which case is exactly 0. However, the convergence rate is slightly reduced as T increases to 6000. This is because also increases in this case, as shown in Figure 2. The results of Figure 3 illustrate that an inappropriate controller structure would degrade the convergence rate of the ANC system, just as analyzed in Section 2 and predicted by Figure 2. In order to control the disturbances with the close frequencies efficiently, the controller’s time scale T must be sufficiently large.
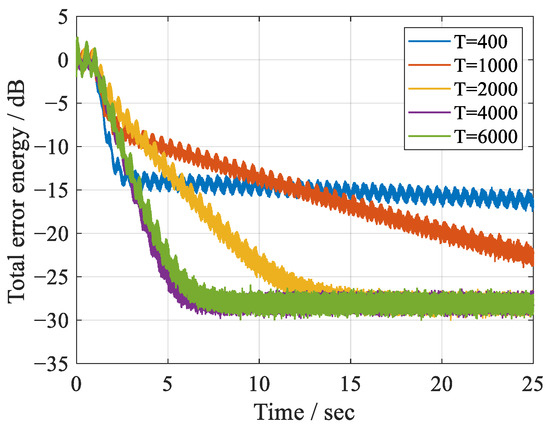
Figure 3.
Averaged convergent trajectories of the normalized total error energy with M = 20 and different time scales T of the controller.
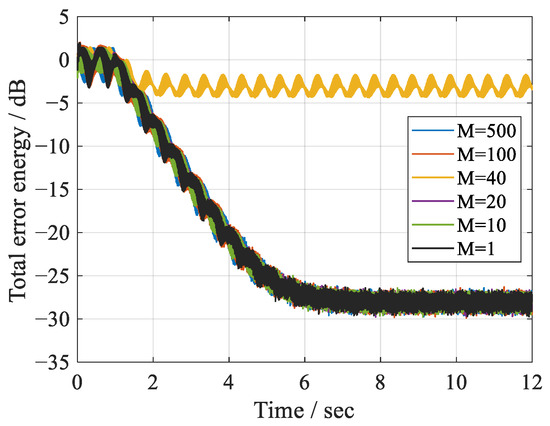
Figure 4.
Averaged convergent trajectories of the normalized total error energy with T = 4000 and different decimation factors M.
Figure 4 shows the averaged convergent trajectories with a different M. Here, T is set to 4000 so that the optimal convergence rate can be expected. It can be observed that with a different M, the proposed algorithm exhibits almost the same convergent behaviors. The only exception is the case of M = 40, with which the aliasing of the two disturbance frequencies happens, and hence the noise reduction performance is significantly deteriorated. It is also shown that the maximum stepsizes of the proposed algorithm with a different M are almost the same. These results indicate that the decimation of the controller would not affect the performance of the ANC system, provided that the decimation factor is carefully chosen so that the aliasing of the disturbance frequencies is avoided. However, the decimation of the controller can greatly reduce the computational burden. In this case, the controller length N is reduced to 8 with a decimation factor of 500, while this value is as large as 4000 for the original FxLMS algorithm. Thus, with a decimated controller, the proposed algorithm could still be computationally efficient even with a very large T. Figure 5 shows the total power spectrum of the error signals, which is the summation of the individual power spectrums over all of the error signals. It can be found that the tonal disturbances with the close frequencies can be effectively attenuated.
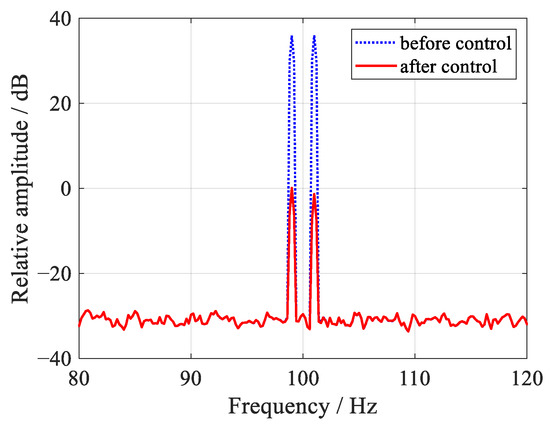
Figure 5.
The total power spectrum of the error signals before and after control.
Finally, the convergent behaviors of the frequency responses of the controllers are compared with the theoretical ones predicted by Equation (19). Figure 6 shows the averaged and theoretical convergent trajectories of the controller’s frequency responses corresponding to all of the four output channels at both f1 and f2. In this case, T and M are set to 1000 and 20, respectively. It can be seen that the averaged results can match well with the theoretical ones. The errors might mainly result from the independence assumption of the initial phases and the controller, especially when the stepsize is relatively large.
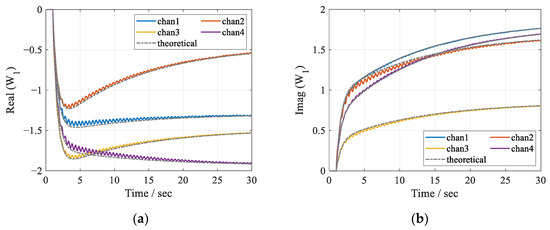
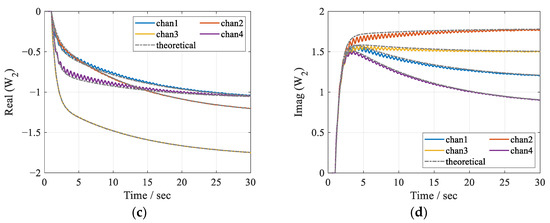
Figure 6.
Averaged convergent trajectories of the frequency responses of the controllers, with T = 1000 and M = 20: (a) real; (b) imaginary parts for W1; (c) real; (d) imaginary parts for W2. Colored solid lines for simulation results and gray dashed lines for theoretical results.
4. Conclusions
The design of the narrowband ANC system becomes challenging if the disturbance frequencies are rather close to each other, especially when the reference signals corresponding to each disturbance frequency cannot be directly obtained from the primary sources. In this paper, the control of the narrowband disturbances with two close frequencies is discussed, in which only a mixed-reference signal is assumed to be available. Based on the symmetry of the controller’s frequency responses, the convergent behaviors of a generalized FxLMS-based algorithm are theoretically analyzed, through which a characteristic matrix is constructed to reveal the influence of the controller structure on the convergence rate. A novel narrowband algorithm is further proposed with a decimated transversal controller. Simulations based on a 4 × 8 ANC system are carried out, and the results show that the time scale of the controller should cover one entire cycle of the difference frequency in order to obtain the fastest convergence rate. With the help of the decimation of the controller, the proposed algorithm can maintain its fastest convergence rate with much less computational complexity.
Author Contributions
Conceptualization, F.A.; Methodology, F.A.; Software, F.A.; Validation, F.A.; Formal Analysis, F.A.; Investigation, F.A.; Data Curation, F.A.; Writing—Original Draft Preparation, F.A.; Writing—Review and Editing, F.A. and B.L.; Supervision, B.L.; Project Administration, B.L.; Funding Acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant # 11404367, 11874034), the Taishan Scholar Program of Shandong (# ts201712054) and the Shandong Science and Technology Enterprise Innovation Capacity Enhancement Project (# 2021TSGC1036).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elliott, S.J. Signal Processing for Active Control; Academic Press: London, UK, 2001. [Google Scholar]
- Hansen, C.; Snyder, S.; Qiu, X.; Brooks, L.; Moreau, D. Active Control of Noise and Vibration; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Bermudez, J.C.M.; Bershad, N.J. Non-Wiener behavior of the filtered LMS algorithm. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1999, 46, 1110–1113. [Google Scholar] [CrossRef]
- Vicente, L.; Masgrau, E. Novel FxLMS convergence condition with deterministic reference. IEEE Trans. Signal Process. 2006, 54, 3768–3774. [Google Scholar] [CrossRef]
- Haarnoja, T.; Tammi, K.; Zenger, K. Exact LTP representation of the generalized periodic reference FxLMS algorithm. IEEE Trans. Signal Process. 2014, 62, 121–130. [Google Scholar] [CrossRef]
- Xiao, Y. A new efficient narrowband active noise control system and its performance analysis. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 1865–1874. [Google Scholar] [CrossRef]
- Xiao, Y.; Ikuta, A.; Ma, L.; Khorasani, K. Stochastic analysis of the FXLMS-based narrowband active noise control system. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 1000–1014. [Google Scholar] [CrossRef]
- Delega, R.; Bernasconi, G.; Piroddi, L. A novel cost-effective parallel narrowband ANC system with local secondary-path estimation. J. Sound Vib. 2017, 401, 311–325. [Google Scholar] [CrossRef]
- Li, Y.; He, L.; Shuai, C.; Wang, F. Time-domain filtered-x-Newton narrowband algorithms for active isolation of frequency-fluctuating vibration. J. Sound Vib. 2016, 367, 1–21. [Google Scholar] [CrossRef]
- Wang, C.; He, L.; Li, Y.; Shuai, C. A multi-reference filtered-x-Newton narrowband algorithm for active isolation of vibration and experimental investigations. Mech. Syst. Signal Process. 2018, 98, 108–123. [Google Scholar] [CrossRef]
- Huang, B.; Xiao, Y.; Sun, J.; Wei, G. A variable step-size FXLMS algorithm for narrowband active noise control. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 301–312. [Google Scholar] [CrossRef]
- Gong, C.; Wu, M.; Guo, J.; Cao, Y.; Zhang, Z.; Yang, J. Modified narrowband active noise control system with frequency mismatch tolerance. Appl. Acoust. 2022, 189, 108598. [Google Scholar] [CrossRef]
- Bo, Z.; Yang, J.; Sun, C.; Jiang, S. A filtered-x weighted accumulated LMS algorithm: Stochastic analysis and simulations for narrowband active noise control system. Signal Process. 2014, 104, 296–310. [Google Scholar] [CrossRef]
- Bo, Z.; Sun, C.; Xu, Y.; Jiang, S. A variable momentum factor filtered-x weighted accumulated LMS algorithm for narrowband active noise control systems. Measurement 2014, 48, 282–291. [Google Scholar] [CrossRef]
- An, F.; Cao, Y.; Liu, B. Optimized decentralized adaptive control of noise and vibration for periodic disturbances. J. Acoust. Soc. Am. 2018, 144, EL275–EL280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- An, F.; Cao, Y.; Liu, B. Optimized decentralized filtered-x least mean square algorithm for over-determined systems with periodic disturbances. J. Sound Vib. 2021, 491, 115763. [Google Scholar] [CrossRef]
- Jeon, H.J.; Chang, T.G.; Kuo, S.M. Analysis of frequency mismatch in narrowband active noise control. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1632–1642. [Google Scholar] [CrossRef]
- Xiao, Y.; Ma, L.; Khorasani, K.A. Ikuta, A new robust narrowband active noise control system in the presence of frequency mismatch. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 2189–2200. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, L.; Gao, J.; Zhang, X. Analysis and compensation of reference frequency mismatch in multiple-frequency feedforward active noise and vibration control system. J. Sound Vib. 2017, 409, 145–164. [Google Scholar] [CrossRef]
- Jeon, H.J.; Chang, T.G.; Yu, S.; Kuo, S.M. A narrowband active noise control system with frequency corrector. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 990–1002. [Google Scholar] [CrossRef]
- Wang, H.; Sun, H.; Sun, Y.; Wu, M.; Yang, J. A narrowband active noise control system with a frequency estimation algorithm based on parallel adaptive notch filter. Signal Process. 2019, 154, 108–119. [Google Scholar] [CrossRef]
- Han, R.; Wu, M.; Liu, F.; Sun, H.; Yang, J. A narrowband active noise control system with a frequency estimator based on Bayesian inference. J. Sound Vib. 2019, 455, 299–311. [Google Scholar] [CrossRef]
- Gong, C.; Wu, M.; Guo, J.; Zhang, Z.; Cao, Y.; Yang, J. Multichannel narrowband active noise control system with a frequency estimator based on DFT coefficients. J. Sound Vib. 2022, 521, 116660. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).