Abstract
We employ the extended Nambu-Jona-Lasinio (NJL), linear- models, and the density-dependent model with chiral limits to work out the mean fields and relevant properties of nuclear matter. To have the constraint from the data, we re-examine the Dirac optical potentials and symmetry potential based on the relativistic impulse approximation (RIA). Unlike the extended NJL and the density-dependent models with the chiral limit in terms of the vanishing scalar density, the extended linear- model with a sluggish changing scalar field loses the chiral limit at the high-density end. The various scalar fields can characterize the different Schrödinger-equivalent potentials and kinetic symmetry energy in the whole density region and the symmetry potential in the intermediate density region. The drop in the scalar field due to the chiral restoration results in a clear rise of the kinetic symmetry energy. The chiral limit in the models gives rise to the softening of the symmetry potential and thereof the symmetry energy at high densities.
1. Introduction
Besides the development of the various many-body theories based on the boson exchanges in the quantum field theory, e.g., see Ref. [1], the gauge invariance is regarded to be important to construct the model for strong interacting systems. However, the zero-mass gauge bosons are required by the gauge invariance, which becomes a puzzle of the Yang–Mills fields when applying to the realistic interacting systems. The success of the Bardeen–Cooper–Schrieffer theory for superconducting electrons [2] brings the enlightenment that the ground state or vacuum of the interacting systems is not necessary to respect the gauge symmetry. The symmetry invariant models can possess charges, the temporal component of the currents, that break the vacuum (the vacuum is not annihilated by the charge). By early 1960s, it comes to a surge of such model constructions. The typical models are the linear- [3,4] and Nambu–Jona–Lasinio (NJL) [5] models where the order parameters for the chiral symmetry are the scalar condensate <> or the scalar field . In these models, the potentials are characteristic of the field term of the fourth power that ensures a double-well potential, and the chiral parter is the so-called Nambu–Goldstone boson, the pion that is the fundamental and unique boson in the effective field theory [6]. These models provide some clue to the solution of zero-mass puzzle of the Yang–Mills fields. It is interesting to note that Schwinger has the view that the gauge boson does not necessarily have zero mass for the special vacuum [7], and soon later Anderson adds that the gauge boson and Nambu–Golstone boson can cancel each other to leave the finite mass boson only [8]. These are, in fact, the looming prelude for the Higgs mechanism. This is seemly digressive but, instead, restates the importance of the vacuum. Since the original linear- and NJL models fail to fit nuclear matter saturation, a dozen of extended models have been developed to fit nuclear matter saturation and properties of finite nuclei [9,10,11,12,13,14,15,16,17,18,19,20]. In addition, the chiral symmetry can also be manifest by virtue of the vector channel in the hidden local symmetry [21]. The example of such a vector manifestation of chiral symmetry is the model based on the Brown–Rho (BR) scaling [22,23,24]. In this work, we single out three models from these categories that feature the partial restoration of the chiral symmetry in nuclear matter to expose the role of the chiral symmetry in the nuclear and symmetry potentials relevant to the symmetry energy in the relativistic impulse approximation (RIA). Though the chiral symmetry plays a fundamental role in the strong interaction systems, it has various realizations and forms in various chiral models where the scalar field (or equivalently, the chiral condensate) is taken as the order parameter of the chiral symmetry. In this work, we thus aim to check the specific or common in-medium characteristics of the scalar field in a variety of the chiral models and their effects on nuclear potentials. Here, we should mention that the scalar field, related to the scalar density, plays an imperative role in obtaining the optical potentials in the RIA. Note that the chiral effective field theory (EFT) is another kind of the chiral model based on the nonlinear realization of the chiral symmetry and has achieved the quantitative successes in the low-energy non-perturbative hadron physics in past decades. Since no dynamics of the scalar field is given by the chiral EFT [25], we do not include the chiral EFT in our work that also involves the energy region beyond the validity of the chiral EFT.
Recently, the uncertainty of the symmetry energy has been again a hot issue, since the accurate measurement of Pb neutron skin thickness ( fm) through the weak-interaction electron scattering gives a large span of the symmetry energy slope MeV [26,27]. At the same time, a large span of the MeV is deduced from the spectra of charged pions [28]. These results seem to shake off the previous constraints on the symmetry energy. In the past, the globally average of 28 independent analyses of various data has led to the value of MeV [29]. With inclusion of the lower ranges either extracted from data [30,31] or obtained from the ab initio results of neutron matter [32], an average of the L values gives a larger range of MeV [33]. In addition, the measurement of electron dipole polarizability in finite nuclei even gives a lower limit of MeV [34]. The rising uncertainty of the symmetry energy and the inconsistency in different extractions pose the challenge and meantime the opportunity to study the symmetry energy from multiple angles. We aim to seek a possible hint and/or constraint on the symmetry energy by revisiting the ingredients of the symmetry energy in terms of nuclear potentials in the relativistic chiral models that in general exhibit the broken vacuum, associated tightly with the symmetry energy through the scalar potential.
We will be interested in the RIA that combines the Dirac decomposition of scattering amplitudes with the nuclear scalar and vector densities. The direct combination with the scattering data ensures the simplification in the analysis of tangled factors in the strong interaction. It is known that the optical potentials obtained from the RIA can reproduce the analyzing power and spin-rotation parameter in proton-nucleus (pA) scatterings successfully [35,36,37], in stark contrast with the standard nonrelativistic optical models [38,39]. In the past, the RIA has also been used to study the symmetry potentials [40,41,42,43] and in-medium nucleon-nucleon (NN) cross sections [44,45]. In this work, we study the effects of the chiral symmetry on the symmetry potential in the RIA. The chiral models will be solved in the mean-field approximation, and also present the result with the usual relativistic mean-field (RMF) model for comparison.
2. Brief Formalism
2.1. Models with Chiral Symmetry
The chiral symmetry plays very important roles in the strong interaction systems. In the quantum chromodynamics (QCD), the chiral symmetry is cooperated by the gauge symmetry to resolve the axial anomaly and then point to the more fundamental structure of quarks and leptons [46,47]. The chiral symmetry also seems to be a probe to the composite structure of hadrons, which is manifest in the NJL model. In particular, the chiral phase transition would generally coincide with the color deconfinement [48].
As for nuclear physics with the broken chiral symmetry, our attention is on the order parameter (the non-vanishing vacuum of the scalar field or condensate) in chiral models that brings the effects on nuclear potentials, as mentioned in the Introduction. In the following, we interpret simply the extended NJL, linear- models and the density-dependent model with chiral limits that are used in this work. The extended NJL model includes the additional interaction terms with the scalar-vector, scalar-isovector couplings (, ) to fit the saturation and density dependence of the symmetry energy. Here, the additional terms are given by [20,45,49]
In the mean-field approximation, the gap equation reads
where is the scalar coupling, and is the bare nucleon mass which is determined by the Gell-Mann-Oakes-Reinner relation on the hadron level [20].
The linear- model with additional scalar-vector coupling can have the saturation that leads to a stiff equation of state (EOS) with a very large incompressibility [9]. Among a large collection of extended models, we choose the one with the following potential obtained from the QCD lattice calculation in the strong coupling limit (SCL) [16]
where the coefficients , , and . The potential is symmetric about the axis with the minimum of the potential at . The potential in Equation (3), instead of the original potential in the fourth power of the , avoids the bifurcation that leads to chiral collapse at the lower chiral condensate. Note that the similar term also appears in a scheme that includes the coupling to the field of the glueball [10].
The density-dependent models with the chiral limit are similar to the simple Walecka model and the density-dependent parameters are based on the BR scaling [22,23,24]. The mean-field potential energy is given by [50]
where the asterisk on the meson mass denotes the density dependence according to the BR scaling [23,24]. The parametrization SLCd used in this work, detailed in Ref. [24], is characterized by the density dependent hadron masses and meson-nucleon coupling constants and respects the chiral limit in terms of the vanishing scalar density and nucleon effective mass at high densities. For usual RMF models, we choose the parametrization FSUGold that contains the nonlinear self-interactions of the and mesons [51].
2.2. Relativistic Impulse Approximation
In the pA scattering, the scattering process can be approximately treated as the incident proton scattered by each of the nucleons of the target nucleus, regardless of the impact of the incident particle on the mean fields. The Dirac optical potential in the RIA is given in a familiar form [35,36]:
where the forward NN elastic scattering amplitudes and are determined directly from the experimental NN phase shifts [52]. The RIA optical potential was used to reproduce the pA elastic scattering data at the incident energies above 400 MeV successfully [37]. and are the spatial scalar and vector densities of infinite nuclear matter,
The scalar density with various models given in the above can give the distinct difference at high densities, as shown in Figure 1. This will give rise to subsequent effects on the optical potentials and relevant quantities. The Dirac optical potential can be expressed in terms of scalar and vector optical potentials
where , , and are real scalar, imaginary scalar, real vector and imaginary vector optical potentials, respectively. Note that these potentials are obtained from the nucleon-nucleon scattering amplitudes, since the Dirac potentials in the RMF models do not have the imaginary part.
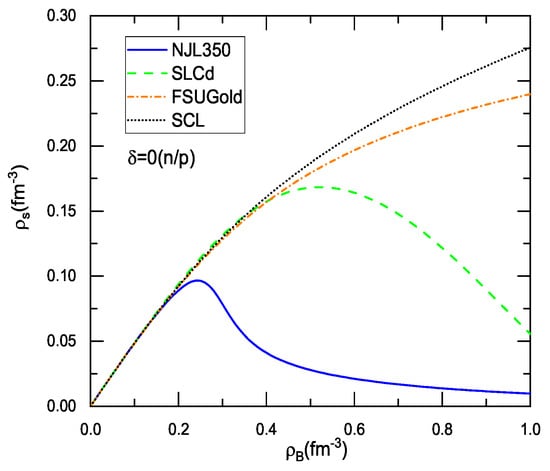
Figure 1.
The proton and neutr on scalar densities as a function of density in the NJL350, SCL, SLCd, and FSUGold models in symmetric matter.
One can recombine the terms in the relativistic dispersion relation into a non-relativistic form , where with being the kinetic energy, and the Schrödinger-equivalent potential (SEP) is given by [44]
where . With the SEP, the symmetry potential is written as
with being the isospin asymmetry parameter. The is also known as the Lane potential [53].
3. Results and Discussions
The models to be used are the extended NJL model (NJL350) with a momentum cutoff 350 MeV [20,45,49], SLCd that is a density-dependent relativistic model with chiral limit [24,54], the extended linear- model in the strong coupling limit (denoted by SCL) [16], and the RMF model FSUGold [51]. The RMF model FSUGold can reproduce the properties of finite nuclei well [51], while it produces the maximum mass of neutron stars below the 2 constraint. The SLCd can simultaneously reproduce the properties of finite nuclei [24] and neutron star properties with and without hyperonization [55]. In addition, the neutron star deformability obtained with the SLCd fits the data fairly well [50]. The progress to describe the properties of finite nuclei and neutron stars is also made with the SCL [16,56]. The NJL model, developed to have the saturation property, is used to constrain the symmetry energy and describe the properties of neutron stars including the glitches of the Vela pulsar [20,49]. In Table 1, we tabulate some properties of saturation, symmetry energy and neutron stars with these four models.

Table 1.
Properties given by the various models. Tabulated from left to right are, in turn, the incompressibility, saturation density, symmetry energy and its slope parameter at saturation density, and the maximum mass and corresponding radius of neutron stars.
Figure 2 shows the scalar and vector fields for these models in the mean-field approximation. As shown in Figure 2, the scalar field with various models can group into two categories: one of which (NJL350 and SLCd) has a fast dropping in the medium, while the other (SCL and FSUGold) has a sluggish decrease. For the chiral models or models with the chiral limit, the scalar field plays a role of the order parameter that reflects the breaking vacuum and probes the chiral restoration in the medium. For the NJL model, the scalar field is, in fact, equivalent to the scalar condensate <>. A clear decrease of the scalar field with the NJL350 and SLCd indicates that these two models have the chiral limit in terms of the vanishing of the scalar field or scalar density (see Figure 1). The in-medium scalar field with the SCL behaves like that of the RMF model FSUGold, which means that the SCL that respects the chiral symmetry at the vacuum degenerates into a usual RMF model in the medium. As a result, the SCL is not able to restore the chiral symmetry in dense matter even at the sufficiently high density. This is also true for other extended linear- models, as it is not able to bring the scalar field down to vanishing in the medium [16]. The slowly varying scalar field also provides considerable attraction that softens the EOS at high density. Together with rather soft vector potential, the SCL and FSUGold are not able to meet the constraint of neutron stars. The situation with the NJL350 and SLCd is quite different by owning the stiff EOS’s at high densities and fitting the constraint of neutron stars [20,50,55].
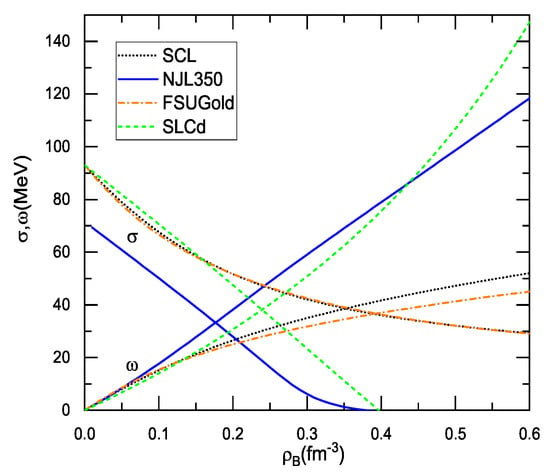
Figure 2.
The scalar and vector fields in symmetric matter. The scalar field is redefined for models SLCd and FSUGold as .
The scalar field that dictates the nucleon effective mass changes the kinetic symmetry energy (the kinetic part of the symmetry energy) which in the relativistic formulation is with being the Fermi energy. The decreasing nucleon effective mass in dense matter increases the clearly. As shown in Figure 3, the difference in the kinetic symmetry energy develops beyond saturation density, and it is the most appreciable for the NJL350. With the increase in density, the kinetic symmetry energy with the SLCd comes closer to that with the NJL350 because of the chiral limit of the SLCd. This is a direct evidence that the (partial) restoration of the chiral symmetry has a characteristic contribution to the symmetry energy, which stiffens the kinetic symmetry energy.
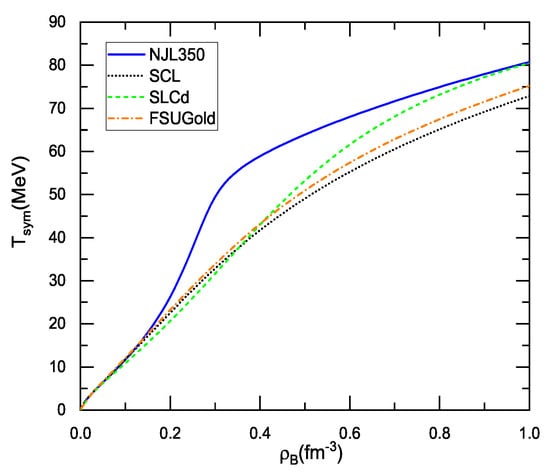
Figure 3.
The kinetic symmetry energy as a function of density with various models.
Within the framework of the RIA, the nucleon SEP is derived as in Equation (8). Figure 4 shows the nucleon SEP of symmetric matter with increasing the density at the two given kinetic energies and 800 MeV, which are two typical energies within the RIA valid region to fit the data of the pA scattering [37]. The attribution of the difference in various curves is similar to that in Figure 3 due to the different scalar density. As shown in Figure 4, the concrete content of the chiral restoration, such as that reflected by the departure in the NJL350 and SLCd, decides the density dependent behavior of the SEP. With the increase in density, the SEP with the SLCd approaches that with NJL350 due to the increasing eclipse of the nucleon mass. For the models SCL and FSUGold that have a sluggish descent of the nucleon mass, the SEP stays away from those with the models that own the chiral limit. Note that the RIA may not work as well at high densities, and the SEP at the high density end would just be referential.
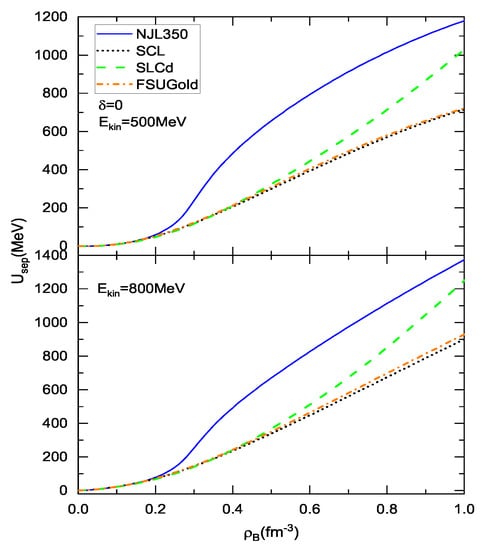
Figure 4.
The SEP as a function of density at the kinetic energy 500 and 800 MeV.
With Equation (9), we can carry out the symmetry potential as functions of the density or kinetic energy. The symmetry potential is tightly related to the potential part of the symmetry energy [43,57]. Figure 5 shows the symmetry potential based on various models at and 800 MeV. Let us first focus on the result at MeV. We see again that the effect of the chiral restoration at the intermediate densities (by the NJL350) gives a very clear rise in the symmetry potential. As shown in the upper panel of Figure 5, the symmetry potential bends downwards at high densities, which occurs coincidentally in the models NJL350 and SLCd which share the chiral limit. As inferred from Figure 3 and Figure 5, the symmetry energy appears to be stiffer around saturation density with a larger slope parameter L for the chiral model which owns the chiral limit. It should be pointed out that the symmetry potential at high densities does not follow in a homeomorphic way the difference in the scalar density as those in Figure 3 and Figure 4. At high densities, there are trespassing between the symmetry potential curves that are subject to the different scalar densities or nucleon effective masses. The reason for this lies in the fact that the variation of the nucleon effective mass against the isospin asymmetry can be alternating in various regions of the nucleon effective mass, yielding the disorder in the SEP and symmetry potential for the nonzero isospin asymmetry. Such a disorder also appears in the higher density region ( fm) for the case of MeV. The difference between the lower and upper panels of Figure 5 in the depicted density region is attributed to the energy dependence of the NN scattering amplitudes. In particular, the RIA results with MeV actually include some contributions of the inelastic nucleon-nucleon scattering [45].
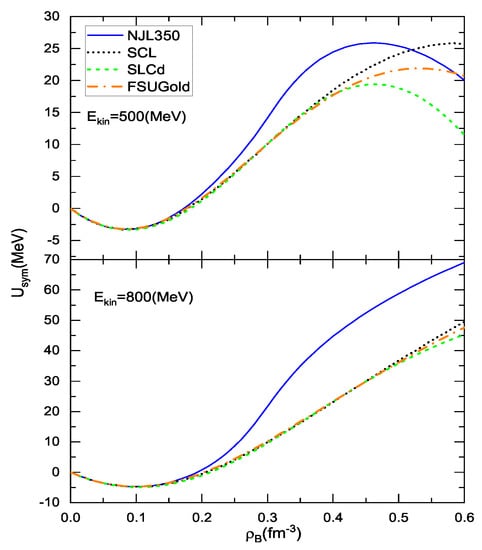
Figure 5.
The symmetry potential as a function of density at kinetic energy and 800 MeV.
Note that the symmetry potential obtained with the models SCL and FSUGold is similar and also close at high densities, as shown in Figure 5. This is due to the fact that two models have similar nucleon scalar density (or, the nucleon effective mass). In the early time when the non-linear terms of the -meson self-interactions are introduced, it is known that the sign of the coefficient of the quartic term in non-linear RMF models is opposite to that of the models with the Mexican-hat potential. The situation has changed in the RMF models by including the non-linear self-interaction, which is the case of the FSUGold. The resembling model facet makes, at least partially, of the similarity in the symmetry potentials of the models SCL and FSUGold. It is also shown in Figure 5 that the symmetry potential obtained from various models overlaps around and below saturation density. The similar situation also occurs in the SEP (), shown in Figure 4. In the local density approximation, these optical potentials can, in principle, be translated into those for describing the high-energy proton-nucleus scattering, as the success of the RIA at high energies over that of the non-relativistic one is characterized by the spin dynamics specific in the RMF models [35,36,37]. The reasonable incompressibility in the current models, compared to the stiff one in the Walecka model, is important to produce the correct spin–orbit splitting of finite nuclei, which would lead to a better data fit in the RIA.
At last, it is necessary to explain the relation between the symmetry potential in the RIA and the symmetry energy. According to the thermodynamic consistency in non-relativistic models, the symmetry energy is given as [57], where with and being the k-mass and E-mass, respectively. Since there is no momentum dependence of the potentials in the RIA (), the E-mass alone is not able to give the quantitative symmetry energy based on the SEP. If one uses the relativistic kinetic symmetry energy instead of the non-relativistic one, the has to be supplemented with additional terms [58]. Since the additional terms are not given by the RMF model itself, it is not straightforward to calculate the symmetry energy based on the symmetry potential in the RIA. Nevertheless, the chiral models with faster dropping of the nucleon effective mass bring the symmetry potential up in a certain large density span as shown in Figure 5, leading to the stiffening of the symmetry energy. This trend is roughly consistent with that in Table 1 by connecting the relative difference in the slope of the symmetry energy to the dropping of the nucleon effective mass in various models.
4. Summary
The chiral symmetry and its breaking define the vacuum and the Goldstone particles, the pion mesons, for the non-perturbative strong interaction system and can add restrictions on the nuclear potentials in the medium. We have revisited the extended NJL and linear- models which have a nonzero order parameter, the scalar field or the chiral condensate that plays an important role in the properties of bulk matter. Together with the usual RMF model and the density-dependent model with the chiral limit, we have made a comparative study on the nuclear potentials that are relevant to the symmetry energy. It is found that the chiral limit in whatever models, chiral or not, ensures a significant reduction of the scalar field and consequently the stiffening of the EOS. Such a stiffening due to the chiral limit is also observed in the Schrödinger-equivalent potentials and the kinetic symmetry energy. In addition, we find that the models with the chiral limit bring the coincident softening of the symmetry potential at high densities, which suggests the softening of the symmetry energy at high densities. On the contrary, the sluggish descent of the scalar field makes the extended linear- model to be absent from the chiral limit in the finite density region and accordingly degenerate into the usual RMF model at high densities.
Author Contributions
Conceptualization, methodology, software, investigation, N.L., S.-N.W. and W.-Z.J.; data curation, N.L. and S.-N.W.; writing—original draft preparation, writing—review and editing, N.L. and W.-Z.J.; supervision, W.-Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported in part by the National Natural Science Foundation of China under Grant No. 11775049.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Jing Ye for the useful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brockmann, R.; Machleidt, R. Reletivistic nuclear structure. I. Nuclear matter. Phys. Rev. C 1990, 42, 1965–1980. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic Theory of Superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Schwinger, J. A theory of the fundamental interactions. Ann. Phys. (N. Y.) 1957, 2, 407–434. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Lévy, M. The axial vector current in beta decay. Nuovo Cimento 1960, 16, 705–720. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–348. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological lagrangians. Phys. A 1979, 96, 327–340. [Google Scholar] [CrossRef]
- Schwinger, J. Gauge invariance and mass. Phys. Rev. 1962, 125, 397–398. [Google Scholar] [CrossRef]
- Anderson, P.W. Plasmons, Gauge Invariance, and Mass. Phys. Rev. 1963, 130, 439–442. [Google Scholar] [CrossRef]
- Boguta, J. A saturating chiral field theory of nuclear matter. Phys. Lett. B 1983, 120, 34–38. [Google Scholar] [CrossRef][Green Version]
- Heide, E.K.; Rudaz, S.; Ellis, P.J. An effective lagrangian with broken scale and chiral symmetry applied to nuclear matter and finite nuclei. Nucl. Phys. A 1994, 571, 713–732. [Google Scholar] [CrossRef]
- Furnstahl, R.J.; Serot, B.D.; Tang, H. A chiral effective lagrangian for nuclei. Nucl. Phys. A 1997, 615, 441–482. [Google Scholar] [CrossRef]
- Sahu, P.K.; Ohnishi, A. SU(2) Chiral Sigma Model and Properties of Neutron Stars. Prog. Theor. Phys. 2000, 104, 1163–1171. [Google Scholar] [CrossRef][Green Version]
- Mishustin, I. How far is normal nuclear matter from the chiral symmetry restoration? Phys. Rep. 2004, 391, 363–380. [Google Scholar] [CrossRef][Green Version]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Zschiesche, D.; Tolos, L.; Schaffner-Bielich, J.; Pisarski, R.D. Cold, dense nuclear matter in a SU(2) parity doublet model. Phys. Rev. C 2007, 75, 055202. [Google Scholar] [CrossRef]
- Tsubakihara, K.; Ohnishi, A. A chiral symmetric relativistic mean field model with a logarithmic sigma potential. Prog. Theor. Phys. 2007, 117, 903–921. [Google Scholar] [CrossRef][Green Version]
- Jha, T.K.; Mishra, H. Constraints on nuclear matter parameters of an effective chiral model. Phys. Rev. C 2008, 78, 065802. [Google Scholar] [CrossRef]
- Hu, J.; Ogawa, Y.; Toki, H.; Hosaka, A. Variational multiparticle-multihole configuration mixing method applied to pairing correlations in nuclei. Phys. Rev. C 2009, 78, 024305. [Google Scholar] [CrossRef]
- Janowski, S.; Parganlija, D.; Giacosa, F.; Rischke, D.H. Glueball in a chiral linear sigma model with vector mesons. Phys. Rev. D 2011, 84, 054007. [Google Scholar] [CrossRef]
- Wei, S.N.; Jiang, W.Z.; Yang, R.Y.; Zhang, D.R. Symmetry energy and neutron star properties in the saturated Nambu-Jona-Lasinio model. Phys. Lett. B 2016, 763, 145–150. [Google Scholar] [CrossRef]
- Brown, G.E.; Rho, M. Matching the QCD and hadron sectors and medium-dependent meson masses; hadronization in relativistic heavy ion collisions. Phys. Rep. 2004, 398, 301–325. [Google Scholar] [CrossRef][Green Version]
- Song, C. Dense nuclear matter: Landau Fermi-liquid theory and chiral Lagrangian with scaling. Phys. Rep. 2001, 347, 289. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Li, B.A.; Chen, L.W. Equation of state of isospin-asymmetric nuclear matter in relativistic mean-field models with chiral limits. Phys. Lett. B 2007, 653, 184–189. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Li, B.A.; Chen, L.W. Neutron-skin thickness of finite nuclei in relativistic mean-field models with chiral limits. Phys. Rev. C 2007, 76, 054314. [Google Scholar] [CrossRef]
- Koch, V. Aspects of chiral symmetry. arXiv 1997, arXiv:nucl-th/9706075. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Anio, K.; Armstrong, D.S.; Averett, T.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; Benesch, J.F.; et al. Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2021, 126, 172502. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Estee, J.; Lynch, W.G.; Tsang, C.Y.; Barney, J.; Jhang, G.; Tsang, M.B.; Wang, R.; Kaneko, M.; Lee, J.W.; Isobe, T.; et al. Probing the Symmetry Energy with the Spectral Pion Ratio. Phys. Rev. Lett. 2021, 126, 162701. [Google Scholar] [CrossRef]
- Li, B.A.; Han, X. Constraining the neutron proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys. Lett. B 2013, 727, 276–281. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the Symmetry Parameters of the Nuclear Interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur. Phys. J. A 2014, 50, 40. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11–24. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Agrawal, B.K.; Colὸ, G.; Paar, N.; Piekarewicz, J.; Vretenar, D. Neutron skin thickness from the measured electric dipole polarizability in 68Ni, 120Sn, and 208Pb. Phys. Rev. C 2015, 92, 064304. [Google Scholar] [CrossRef]
- McNeil, J.A.; Ray, L.; Wallace, S.J. Impulse approximation NN amplitudes for proton-nucleus interactions. Phys. Rev. C 1983, 27, 2123–2133. [Google Scholar] [CrossRef]
- McNeil, J.A.; Shepard, J.R.; Wallace, S.J. Impulse-Approximation Dirac Optical Potential. Phys. Rev. Lett. 1983, 50, 1439–1442. [Google Scholar] [CrossRef]
- Ray, L.; Hoffmann, G.W. Relativistic and nonrelativistic impulse approximation descriptions of 300–1000 MeV proton + nucleus elastic scattering. Phys. Rev. C 1985, 31, 538–560. [Google Scholar] [CrossRef]
- Auger, J.P.; Gillespie, J.; Lombard, R.J. Proton-4He elastic scattering at intermediate energies. Nucl. Phys. A 1976, 212, 372–388. [Google Scholar] [CrossRef]
- Klem, B.; Igo, G.; Talaga, R.; Wriekat, A.; Courant, H.; Einsweiler, K.; Joyce, T.; Kagan, H.; Makdisi, Y.; Marshak, M.; et al. Polarization in p-4He Elastic Scattering at 0.56, 0.80, 1.03, 1.27, and 1.73 GeV. Phys. Rev. Lett. 1977, 38, 1272–1275. [Google Scholar] [CrossRef]
- Chen, R.; Cai, B.J.; Chen, L.W.; Li, B.A.; Li, Z.H.; Xu, C. Single-nucleon potential decomposition of the nuclear symmetry energy. Phys. Rev. C 2012, 85, 024305. [Google Scholar] [CrossRef]
- Wang, R.; Chen, L.W.; Zhou, Y. Extended Skyrme interactions for transport model simulations of heavy-ion collisions. Phys. Rev. C 2018, 98, 054618. [Google Scholar] [CrossRef]
- Li, Z.H.; Chen, L.W.; Ko, C.M.; Li, B.A.; Ma, H.R. Nuclear symmetry potential in the relativistic impulse approximation. Phys. Rev. C 2006, 74, 044613. [Google Scholar] [CrossRef]
- Chen, L.W.; Ko, C.M.; Li, B.A. High-energy behavior of the nuclear symmetry potential in asymmetric nuclear matter. Phys. Rev. C 2005, 72, 064606. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Li, B.A.; Chen, L.W. Mean free paths and in-medium scattering cross sections of energetic nucleons in neutron-rich nucleonic matter within the relativistic impulse approximation. Phys. Rev. C 2007, 76, 044604. [Google Scholar] [CrossRef]
- Wei, S.N.; Yang, R.Y.; Ye, J.; Li, N.; Jiang, W.Z. Symmetry potentials and in-medium nucleon-nucleon cross sections within the Nambu Jona Lasinio model in relativistic impulse approximation. Phys. Rev. C 2021, 103, 064604. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A.; Strathdee, J. Are quarks composite? Phys. Lett. B 1975, 59, 265–268. [Google Scholar] [CrossRef]
- Huang, K. Quarks, Leptons, and Gauge Fields; World Scientific: London, UK, 1992; pp. 1–348. [Google Scholar]
- Coleman, S.; Witten, E. Chiral-Symmetry Breakdown in Large-N Chromodynamics. Phys. Rev. Lett. 1980, 45, 100–102. [Google Scholar] [CrossRef]
- Wei, S.N.; Yang, R.Y.; Jiang, W.Z. Crust-core properties of neutron stars in the Nambu Jona Lasinio model. Chin. Phys. C 2018, 42, 054103. [Google Scholar] [CrossRef]
- Shangguan, W.Z.; Huang, Z.Q.; Wei, S.N.; Jiang, W.Z. Neutron star deformability with hyperonization in density-dependent relativistic mean-field models. Phys. Rev. D 2021, 104, 063035. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J. Neutron-Rich Nuclei and Neutron Stars: A New Accurately Calibrated Interaction for the Study of Neutron-Rich Matter. Phys. Rev. Lett. 2005, 95, 122501. [Google Scholar] [CrossRef]
- Arndt, R.A.; Roper, L.D.; Bryan, R.A.; Clark, R.B.; VerWest, B.J.; Signell, P. Nucleon-nucleon partial-wave analysis to 1 GeV. Phys. Rev. D 1983, 28, 97–122. [Google Scholar] [CrossRef]
- Lane, A.M. Isobaric spin dependence of the optical potential and quasi-elastic (p, n) reactions. Nucl. Phys. 1962, 35, 676–685. [Google Scholar] [CrossRef]
- Jiang, W.Z. Rearrangement term with relativistic density-dependent hyperon potentials. Chin. Phys. C 2013, 37, 064101. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Li, B.A.; Chen, L.W. Large-mass neutron stars with hyperonization. Astrophys. J. 2012, 756, 609–612. [Google Scholar] [CrossRef]
- Tsubakihara, K.; Maekawa, H.; Matsumiya, H.; Ohnishi, A. Lambda hypernuclei and neutron star matter in a chiral SU(3) relativistic mean field model with a logarithmic potential. Phys. Rev. C 2010, 81, 065206. [Google Scholar] [CrossRef]
- Xu, C.; Li, B.A.; Chen, L.W. Symmetry energy, its density slope, and neutron-proton effective mass splitting at normal density extracted from global nucleon optical potentials. Phys. Rev. C 2010, 82, 106–146. [Google Scholar] [CrossRef]
- Li, B.A.; Cai, B.J.; Chen, L.W.; Xu, J. Nucleon effective masses in neutron-rich matter. Prog. Part. Nucl. Phys. 2018, 99, 29–119. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).