Abstract
Abstract symmetric patterns are generally preferred to less regular patterns. Here, we studied 2D patterns presented as 2D images in the plane, and therefore producing a symmetric pattern on the retina, and the same patterns seen in perspective. This perspective transformation eliminates the presence of perfect symmetry in terms of retinotopic coordinates. Stimuli were abstract patterns of local coplanar elements, or irregular polygons. In both cases they can be understood as 2D patterns on a transparent glass pane. In the first study we found that perspective increased reaction time and errors in a classification task, even when the viewing angle was kept constant over many images. In a second study we tested a large sample (148 participants) and asked for a rating of beauty for the same images. In addition, we used the Cognitive Reflection Test (CRT) to test the hypothesis that people who tend to give the more immediate and intuitive answer would also show a stronger preference for the symmetry presented in the frontoparallel plane (in the image and on the retina). Preference for symmetry was confirmed, and there was a cost for perspective viewing. CRT scores were not related to preference, thus not supporting the hypothesis of a stronger preference for symmetry in the image when people follow a more immediate and intuitive gut response.
1. Introduction
Symmetry is often cited as a fundamental principle of aesthetics. There is extensive evidence that participants tend to like symmetry in familiar objects, e.g., faces and body, in addition to abstract patterns [1,2,3,4].
In this study, we asked to what extent perspective distortions affect perception of symmetry, and in turn preference for symmetry. The first research question we posed is about perception, and it has been asked before; it can be considered a classic aspect of the problem. For instance, Syzlk Rock and Fisher write “Does the spontaneous impression of symmetry about a vertical axis depend upon the perception of the slant of the figure and the achievement of veridical perception of the size of its two halves?” (p. 124) [5]. Under conditions that allow optimal shape constancy, perception of symmetry should be unaffected by slant. However, often constancy processes are less than perfect, and the difficulty in extracting information from an image may affect the perception of symmetry and preference for symmetry. This is our second research question: the relationship, for a specific set of stimuli, between perception and beauty judgments. We expect that when symmetry is more salient it would also be judged as more beautiful. Importantly, to answer this question we employed the same stimuli in the two tasks. We were also interested in individual differences because people may vary in how they are affected by task difficulty.
1.1. Symmetry and Shape Constancy
Perceptual constancy is a fundamental aspect of human vision: the size and shape of objects remain constant despite large changes in local image properties due to changes in viewing distance and angle. For instance, we perceive the wheels of our bicycle as round even though from most viewpoints they are subject to foreshortening (so ovals are projected on the retina). Perceptual constancy is so powerful that studies have shown a difficulty of observers in extracting properties of the projected image. For example, participants match the image of a slanted circle with an elliptical shape closer to a circle (less foreshortened) than to the retinal image. Thouless called this effect a “phenomenal regression” to the real shape [6,7].
What our visual system achieves is remarkable because that there are countless possible sources (i.e., distal objects) of a given retinal image. Starting from the arrangement of objects and light sources, we can determine the image projected on screen (the forward problem). However, given an image, we do not know the arrangement of objects and light sources (the inverse problem). From as early as Berkeley and Helmholtz’s work, we understand that the inverse problem in vision is ill posed. Some have argued that our conscious visual experience is a stream of unconsciously-computed, best-guess solutions to this problem, and that object-level representation is the hallmark of conscious visual experience [8]. In solving the inverse problem, observers move from ego-centric (image level) representations to allocentric (view-invariant, object level) representations [9,10,11].
Symmetry is a spatial property that can be computed on the basis of rigid transformations that match one part of an object to another. In the plane, these transformations are reflection, rotation, translation, and glide reflection. However, symmetry is also a property of objects that may be seen in perspective. For instance, a human face has approximate bilateral symmetry (one reflection). However, this reflection is not present in the image from any non-arbitrary viewpoints [12]. Our processing of faces is minimally affected by perspective. Indeed, most portraits show faces as a three-quarters view and this pose has even a slight advantage in recognition tasks [13].
There have been several studies of the effect of perspective and skew on perception of symmetry (Figure 1). In a famous study by Wagemans et al. [14], skewed symmetry was used to assess the importance of higher order structures called colinear quadrangles in symmetry detection. Some forms of skewing preserve parallelism and midpoint collinearity, while disrupting higher order structure. The fact that this skewing has a performance cost suggests higher order structure is important for symmetry perception. The skewing in Wagemans et al. is an orthographic projection, which approximates a perspective projection [15]. In another study, Wagemans [16] asked people to judge whether two patterns were the same or different. Changing view angle impaired performance, but less so when the patterns were symmetrical. Symmetry in the distal stimulus facilitates construction of allocentric representations. This is consistent with results from [17,18]. The second and third columns in Figure 1 show images used by Szlyk et al. [5]. They found that the presence of depth cues allows respondents to identify the objective (i.e., allocentric) symmetry.
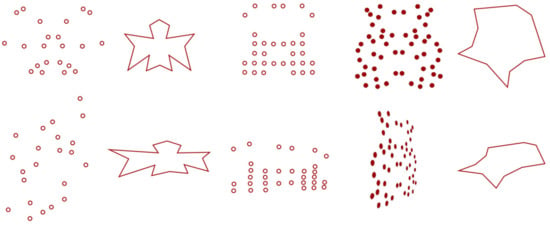
Figure 1.
Illustration of stimuli based on previous studies on symmetry perception: Wagemans et al. [13] Szlyk et al. [5] van der Vloed et al. [18], and Sawada and Pizlo [14]. This list is not exhaustive and some of these papers used more than one type; for instance, van der Vloed et al. [20] also tested blob patterns. See [15] for a discussion of some of the limitations of the stimuli used in the literature.
In summary, the literature shows that it is easier to discriminate symmetry when depth cues are available, allowing an object-based representation and judgment. In this sense, symmetry perception is dependent on depth perception [5]. Moreover, it is difficult to process an object’s shape across changes in viewpoint. However, this trans-viewpoint matching is easier when objects are symmetrical [17,18]. Therefore, allocentric representation helps find symmetry [5] whereas planes and axes of symmetry may help with allocentric representation [18,19].
1.2. Brain Responses to Symmetry and Slant
Many behavioural studies have shown that the human visual system is very sensitive to symmetry in the image. For example, symmetry can be detected with very brief presentations [21,22,23]. More recently, neurophysiological studies have documented the brain response to symmetry (for a review see [24]). Converging evidence from fMRI and EEG found symmetry-related activity in bilateral extrastriate regions of the occipital cortex. The extrastriate regions include V3A, V4, V7, and the lateral occipital complex (LOC) [25,26,27,28]. In the case of EEG, presence of symmetry in the image generated an Event Related Potential (ERP) known as the Sustained Posterior Negativity (SPN, [29,30,31,32]). Activation of this symmetry network is automatic in the sense that it is independent of the task that the observers are performing [33].
More relevant for this study, the question of brain responses to symmetry not present in the retinal image has been studied in a few papers. Makin et al. [34] compared the SPN produced by image-level and object-level symmetry. The image-level SPN was automatic, in the sense that it was the same when participants were attending to symmetry or to the colour of the stimuli. However, object-level SPN was only present when observers were attending to symmetry. This finding was confirmed later by an fMRI study using different stimuli [35]. It seems that the brain always responds to symmetry in the image, but it can sometimes go beyond this, and respond to symmetry in the object [36,37].
1.3. The Current Study
We conducted two experiments online. Experiment 1 addressed the effect of perspective on symmetry perception, and Experiment 2 addressed the effect of perspective on preference. In Experiment 1a we measured response times for perception of symmetry using abstract patterns. The task was to discriminate between two types of shape. In one type there was a correlation between positions of elements (or vertices) on the two sides of each axis (two orthogonal axes were present). The other type of shape was identical except that the correlations were absent because the positions were chosen independently; for short we use the term “random” for this condition. Note that the participants were different in Experiments 1 and 2, but the set of stimuli was the same.
To make the difference between the symmetry and random conditions salient, our symmetric stimuli had two axes of reflection. If the rotation of the surface with respect to the line of sight is orthogonal to one of the symmetry axes, symmetry is preserved in the image. For example, assuming a human face has perfect vertical symmetry, a rotation around the horizontal axis would lead to foreshortening but vertical symmetry is still present. Therefore, in creating our stimuli, the perspective transformation did not correspond to either axis of reflection, thus ensuring that no symmetry was preserved after the transformation. Examples of stimuli can be seen in Figure 2.

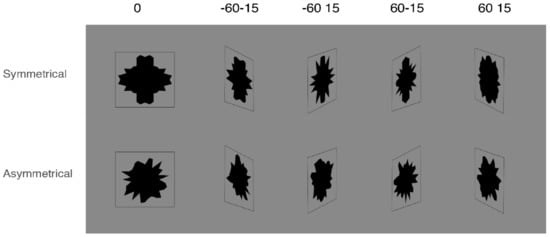
Figure 2.
Examples of stimuli. Top panel, Gabor elements within a square frame. Bottom panel polygon within a square frame. The white stimuli are not shown but were similar except for the change in colour. The full set of stimuli is available at https://osf.io/8vhwe/ (accessed on 30 June 2021).
We predicted an advantage for symmetry in the frontoparallel plane (symmetry present in the retinotopic frame of reference), compared to a perspective view (we used four different transformations, described later). Because of the additional information from internal axes, we also predicted that this perspective cost would be reduced for solid polygons compared to a configuration of individual elements. In a second version of this experiment (Experiment 1b), we tested whether having the images in perspective presented all together in a block would help observers adjust to one consistent view angle and therefore eliminate or reduce the perspective cost.
Experiment 2 used the same stimuli as Experiment 1. We asked participants to rate the beauty of the images. Different theories in empirical aesthetics make different predictions here. The influential fluency-attribution model [38] claims people are sensitive to the fluency (i.e., speed and efficiency) of their own perceptual and cognitive operations. Fluent operations have a positive hedonic tone, and people often attribute this to inherent qualities of the stimuli. The fluency account predicts that people will like the symmetries that are detected fastest (as found by [39,40]). In the current study, perspective costs on symmetry detection should translate into perspective costs on symmetry preference. However, other accounts make different predictions. For example, perspective symmetry is more likely to lead to a positive “Aha” moment, when a post-constancy representation is completed following computation in the visual brain ([41,42].
Despite the robust preference for symmetry observed in many studies, there are exceptions. Some authors have found that attractiveness of symmetric faces may be weaker for perfect symmetry, obtained using computer generated faces [43]. Leder et al. [44] recently claimed that symmetry is not a universal law of beauty. They found that while most people do indeed like symmetry, artists and art historians cultivate a preference for asymmetry. Bertamini et al. [45] interleaved faces, polygons, flowers, and landscapes. For each category there were symmetric and asymmetric stimuli. Landscapes that were artificially made to appear symmetric were liked less than the original landscapes, probably because symmetry is expected to belong to individual objects and not to scenes. Finally, and perhaps most importantly, Graf and Landwehr introduced the Pleasure-Interest Model of Aesthetic Liking [46]. They suggest that there is a first stimulus-driven response upon encountering an aesthetic stimulus, linked to pleasure or displeasure. However, with sufficient motivation there is also a second, more elaborate perceiver-driven response. This model extends the processing fluency theory and turns it into a dual-process theory.
In [45], despite the fact that observers liked the symmetric landscapes less than the asymmetric landscapes, an analysis within these modified landscapes revealed an interesting pattern. For beauty ratings of just the unnatural symmetric landscapes, preference was correlated with the rating of symmetry salience. Symmetry was therefore still affecting responses, but differently for natural and artificial stimuli.
The evidence about neural responses to symmetry has highlighted that a strong and automatic activation of ventral visual areas is produced automatically when symmetry is present in the image [24]. To recover symmetry information under other conditions, for example from a generic view of an object, observers may require cognitive processing. Based on the idea that there is a first, immediate and image-driven response, and a second, reflexive and object-based response, we made the additional hypothesis that preference for symmetry may depend on how an individual approaches the task, and in particular on a bias to report the first response that comes to mind. The idea is that the first response is based on the more automatic processing of visual information. Therefore, we included in this experiment the Cognitive Reflection Test (CRT, [47]). This test has been used in many studies. It is intended to measure whether an individual is able to override an apparently logical but incorrect response, and arrive at the correct one ([48,49].
The CRT test consists of three questions:
- A bat and a ball cost £1.10 in total. The bat costs £1.00 more than the ball. How much does the ball cost? (incorrect answer 10, correct answer 5).
- If it takes 5 machines 5 min to make 5 widgets, how long would it take 100 machines to make 100 widgets? (incorrect answer 100, correct answer 5).
- In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake? (incorrect answer 24, correct answer 47).
The CRT score can vary from 0 (no correct answer) to 3. The ability to avoid an intuitive answer requires effort, and this type of deliberate reasoning may be important to deal with difficult problems [50,51]. However, CRT has only a moderate overlap with measures of cognitive ability [47,52]. It is debated whether the CRT measures a trait. Some authors have suggested that this is a measure of openness, or open-minded thinking [53].
For the purpose of this study, we focus on the intuitive versus the deliberate distinction. We reasoned that individuals with low CRT scores will be less inclined to rely on allocentric representations. Their preferences will be guided by image-level properties, and their preference for symmetry will be greatly reduced in perspective conditions. This corresponds to the stimulus-driven response in Graf and Landwehr’s model [46]. Conversely, more deliberative individuals (high CRT) may take time to form allocentric representations. Their preferences will be guided by object-level representations, and their preference for symmetry will be similar in frontoparallel and perspective conditions.
All studies were conducted online using the GorillaTM app. In the case of Experiment 2, in which we were also interested in individual differences, we decided that a large sample was necessary, and therefore tested 148 participants. This sample provided an 80% chance of detecting modest correlations of r > 0.23.
2. Experiment 1. Materials and Methods
In Experiment 1 we tested whether a symmetrical pattern seen in perspective would be harder to recognise as symmetrical. We used two types of abstract patterns; one was a configuration of elements (2D Gaussian-filtered patches) and the other was a closed and filled polygon (Figure 2). Although these are not technically Gabors, we use this label for this class of stimuli. We reasoned that the closed contour of the polygon may help observers perceive the symmetry of the object [19].
There were two versions of Experiment 1, with 64 participants in each. In the first (Experiment 1a) the factors were symmetry (present or absent), perspective distortion (present or absent), and type (Polygon or Gabor). When the surface was shown in perspective, the transformation was a change of viewpoint in one of four possible directions (see Figure 2 and methods for details). We also had a between-subjects factor: whether the stimuli were black or white (always against a grey background). We had no specific hypothesis about colour, and we did not include this factor in the analyses. Design and analyses were pre-registered (see https://osf.io/8vhwe/ (accessed on 30 June 2021)).
The design of Experiment 1b was similar to that of Experiment 1a but with two important differences. The first was that we used only polygons. The second is that there was a new factor, called Block. In one condition all viewing angles were presented interleaved (as in Experiment 1a) but in another condition they were fixed, so that all images appeared together as seen from a particular angle. We predicted that blocking by angle would reduce perspective cost.
2.1. Participants
Sixty-four participants took part in Experiment 1a and 64 in Experiment 1b (total 128). Participants were naive with respect to the specific hypothesis of the study.
2.2. Design
In Experiment 1A, there were three within-subjects factors: Regularity (symmetry, asymmetry), Stimulus Type (Gabors, Solid Polygons), and Angle. There were 5 different viewing angles, constructed by changing viewpoint along the horizontal and vertical meridians ([0,0], [−60,−15], [−60,15], [60,−15], [60,15]). This design (2 × 2 × 5) gives 20 combinations, but to maintain an equal number of trials between frontoparallel and perspective conditions, frontoparallel ([0,0]) was presented 4 times as often. This produced 32 trials that were repeated 16 times for a total of 512 trials. However, we collapsed the four angles to obtain two levels (frontoparallel, perspective). Finally, there was a between-subjects factor, the colour of the stimuli (black, white). In Experiment 1b there were three within-subjects factors: Regularity (symmetry, asymmetry), Block (randomized, blocked), and Angle (frontoparallel, perspective).
2.3. Stimuli and Procedure
Stimuli were generated with a Python script, using the Psychopy software [54]. The Gabor arrays were constructed from a 10 × 10 virtual grid. For one quarter of the grid, 40% of cells were occupied with a Gabor. For the random patterns, the other three quarters were generated independently according to the same algorithm. For the reflectional symmetry patterns, the other 3 quarters were mirrored, producing horizontal and vertical reflection. All patterns had 40 Gabor elements in total. The size of individual Gabors was 0.33 degrees in diameter, but modulated with a SD of 0.5, so the visible dot was approximately 0.16 degrees in diameter. Gabors could be either black (as in Figure 2) or white.
The solid polygons were constructed by setting 36 vertices at a random +/− 0.8 degree distance from a circle with a radius of 2.4 degrees. The radial spacing (increments around the circumference) was uniform. The vertices were connected to form a polygon, and the central region filled either black or white.
Four different transformations were used, constructed by rotating a virtual camera +/− 60 degrees around the equator (left and right) and +/− 15 degrees around the meridian (up and down). There parameters were designed to be optically correct when viewed from 57 cm. In other words, we used a perspective projection rather than an orthographic projection [15]. We moved the virtual camera in two dimensions, because otherwise image symmetry is not substantially distorted [15,55]. The 60-degree view angle change was also based on recommendations in [15]. The full set of images is available on Open Science Framework: https://osf.io/8vhwe/ (accessed on 30 June 2021).
The presentation to the participants was controlled by Gorilla (www.gorilla.sc (accessed on 30 June 2021)). Each trial began with a fixation cross for 700 ms, then a pattern was shown that was approximately 6 × 6 cm in an 8 × 8 cm frame, as shown in Figure 3. To ensure that size was approximately equal for all participants before the start of the study, they adjusted a rectangle on the screen to match the size of a credit card, and were asked to sit approximately 60 cm from the screen. Stimuli were presented in random order. Before the start of the experimental trials there were eight practice trials.
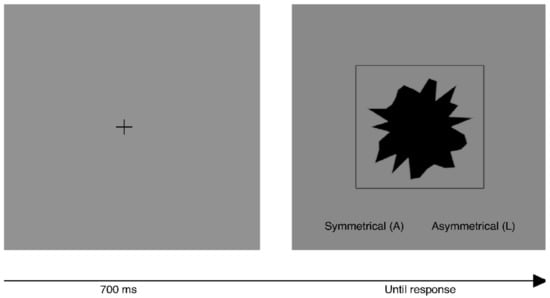
Figure 3.
Description of a trial sequence for Experiments 1a and 1b. In this example the image is an asymmetrical polygon.
Responses were entered via the keyboard. Text in the lower part of the screen reminded participants of the buttons. If participants pressed the correct key, the word ‘correct’ appeared for 200 ms. If participants pressed the wrong key, the word ‘incorrect’ appeared and the participant had to press the correct key.
3. Experiment 1 Results
Results of Experiment 1 are shown in Figure 4. There was a perspective cost on response time in all conditions, which was not abolished by using solid polygons in Experiment 1a, or by blocking by view angle in Experiment 1b.
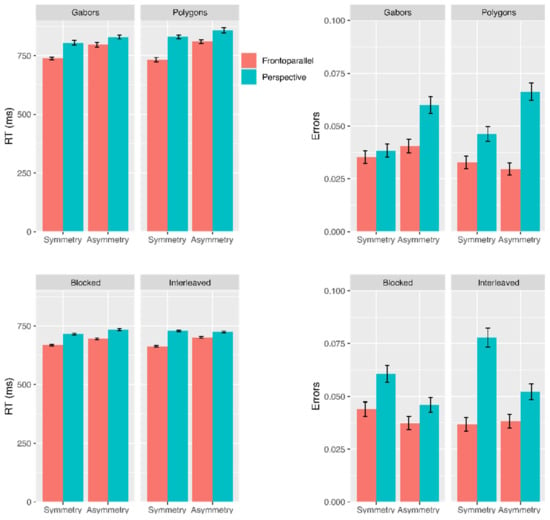
Figure 4.
Results from Experiments 1a (first row) and 1b (second row). Error bars are ±1 SE of the mean (based on [56]).
We analysed response time for correct trials in Experiment 1a with a repeated measures ANOVA. Errors overall were 4.4%. No subject was replaced on the basis of excessive rate of errors (20% as per pre-registration). Responses more than 4 standard deviations from the mean were removed (less than 1%).
The analysis confirmed faster responses to symmetry (F(1,63) = 27.97, p < 0.001, ηp2 = 0.31) and faster responses to images not shown in perspective (F(1,63) = 89.91, p < 0.001, ηp2 = 0.58). There was also an interaction between these two factors (F(1,63) = 12.42, p < 0.001, ηp2 = 0.16). As shown in Figure 4 this interaction is not a reversal in the pattern but rather it shows a stronger effect of symmetry in the frontoparallel condition. The frequency of errors was low, and the pattern of errors was consistent with the pattern of latency (therefore a speed accuracy trade-off cannot explain our results). With respect to the non-significant effects, there was no effect of stimulus type (F(1,63) = 0.55, p = 0.462, ηp2 < 0.01), and no significant interaction between type and symmetry (F(1,63) = 0.62, p = 0.432, ηp2 < 0.01), between type and perspective (F(1,63) = 3.47, p = 0.067, ηp2 = 0.05), or between type, symmetry and perspective (F(1,63) = 0.46, p = 0.462, ηp2 < 0.01).
We repeated the same analysis for Experiment 1b. However, here there was no factor type because only polygons were used. Instead, there was a new important factor, i.e., whether the perspective angle was interleaved or blocked.
Errors overall were 4.9%. Responses more than 4 standard deviations from the mean were removed (less than 1%). One participant was replaced due to errors >20%. The analysis confirmed faster responses to symmetry (F(1,63) = 11.85, p = 0.001, ηp2 = 0.16) and faster responses to images not shown in perspective (F(1,63) = 109.11, p < 0.001, ηp2 = 0.63). As for Experiment 1a, there was an interaction between these factors (F(1,63) = 17.20, p < 0.001, ηp2 = 0.21) and finally a three-way interaction including the block order (F(1,63) = 14.38, p < 0.001, ηp2 = 0.19). The frequency of errors was low, and the pattern of errors was consistent with the pattern of latency (therefore a speed accuracy trade-off cannot explain our findings). See Figure 4. With respect to the non-significant effects, there was no effect of block (F(1,63) = 0.01, p = 0.914, ηp2 < 0.01), and no significant interaction between block and symmetry (F(1,63) = 0.91, p = 0.343, ηp2 = 0.01), or between block and perspective (F(1,63) = 0.07, p = 0.786, ηp2 < 0.01).
In summary, the prediction that viewing angle affects detection of symmetry was confirmed. Observers were slower when the image was not in the frontoparallel plane in both Experiment 1a and Experiment 1b. The interaction between symmetry and perspective is driven by larger differences in the symmetry compared to the asymmetry case. However, responses were also faster overall for symmetry, and the effect of perspective angle was in the same direction. Similarly, the interaction involving block in Experiment 1b seems of little theoretical interest to the present investigation as it is due to a small difference in response time within a pattern that is consistent across all conditions (i.e., faster responses for frontoparallel stimuli compared to perspective stimuli).
The prediction that it should be easier to extract symmetry information from polygon stimuli, as opposed to Gabors, was not confirmed. In neither Exp1a nor Exp1b there was an interaction between angle and type.
4. Experiment 2. Materials and Methods
In Experiment 2, we asked participants to express how much they liked each pattern. The stimuli were the same as those used in Experiment 1a. Experiment 2 also tested whether preference for symmetry in perspective depends on individual differences, and in particular on a bias present in some individuals to report the first response that comes to mind. To test this hypothesis, we included in this experiment the Cognitive Reflection Test (CRT, [47]).
4.1. Participants
One hundred and forty-eight participants took part in Experiment 2 (twenty-two males). They were naive with respect to the specific hypothesis of the study, and had not taken part in Experiment 1.
4.2. Design and Procedure
There were four within-subjects factors: Regularity (symmetry, asymmetry), Stimulus Type (Gabors, Solid Polygons), Angle (frontoparallel, perspective), and Colour (black, white). Stimuli were generated with a Python script as in Experiment 1. They were presented in random order for a total of 64 trials. Before the start of the experiment, there was a practice session of eight trials. The whole experiment lasted approximately ten to fifteen minutes. On each trial, the participant saw a pattern on the screen and was asked to decide how much they liked it using an analogue scale. The two poles of the scale were labelled “not at all” and “very much”. For the purpose of data analysis this distance was recorded as a number between 0 and 100.
After this part of the study, each participant was also asked to answer three questions (CRT test). These were presented on the screen and for each there was a text box in which participants could type their answer.
5. Experiment 2. Results
Preference scores from Experiment 2 are shown in Figure 5. On average, participants liked symmetry more than asymmetry, in both frontoparallel and perspective conditions. Symmetry preference was slightly reduced in the perspective conditions, particularly with solid polygons.
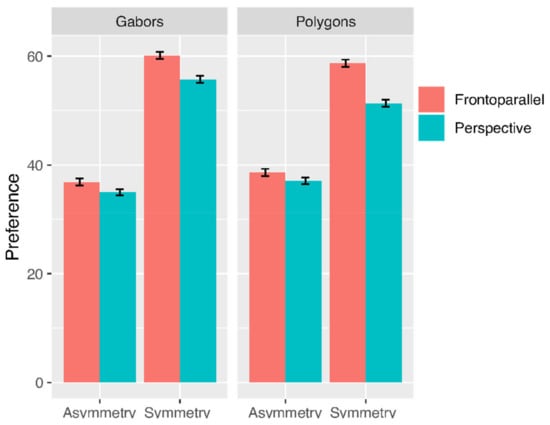
Figure 5.
Results from Experiment 2. Mean preference rating on a scale from 0 to 100. Error bars are ±1 SE of the mean (based on [56]).
We analysed preference scores as recorded using the analogue scale with a repeated measures ANOVA. The analysis confirmed higher scores for symmetry (F(1,147) = 173.29, p < 0.001, ηp2 = 0.54) and for frontoparallel images (F(1,147) = 30.99, p < 0.001, ηp2 = 0.17). There was also an interaction between these two factors (F(1,147) = 29.22, p < 0.001, ηp2 = 0.17). The factor Type (Gabors and Polygons) interacted with Regularity (F(1,147) = 12.72, p < 0.001, ηp2 = 0.08). Finally, there was a three-way interaction between these factors (F(1,147) = 5.65, p < 0.05, ηp2 = 0.04). See Figure 5. With respect to the non-significant effects, there was no effect of stimulus type (F(1,147) = 0.10, p = 0.755, ηp2 < 0.01), and no significant interaction between stimulus type and perspective (F(1,147) = 3.64, p = 0.058, ηp2 = 0.02).
The lower scores for images in perspective were expected. It is also interesting that the perspective cost was specific to symmetric images, and was not present, or smaller, for asymmetrical patterns, thus producing an interaction between these two factors. Unlike Experiment 1, in Experiment 2 there was an interaction between regularity and type. Preference was particularly low (reduced) for polygon stimuli seen in perspective.
We turn now to the analysis of the Cognitive Reflection Test. Here, each participant could score zero (wrong answer for all three questions), one, two or three (correct answer to all three questions). On average the score was 1.169 out of 3 (sd = 1.174). In the original study, undergraduate students in the USA produced means between 0.5 to 1, whereas students at elite American Universities averaged between 1.5 and 2 [47]. Our results are therefore in line with predictions.
To the best of our knowledge, the CRT score has never been used before in the context of beauty judgements. We were first interested in the correlation between CRT and preference for symmetry. Therefore, for each participant we computed a preference for symmetry as a difference score (mean rating for symmetry minus mean rating for asymmetry). There was no correlation between preference for symmetry and CRT score (r = 0.010, p = 0.86, Figure 6 left panel). This is in line with expectations; symmetry is always a strong predictor of preference, in any subgroup of the population [40].
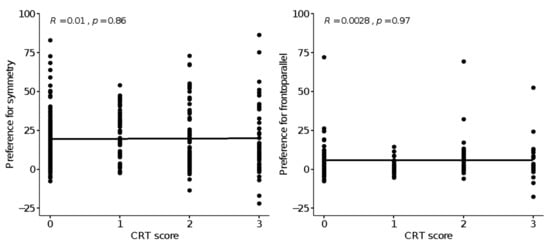
Figure 6.
The relationship between CRT score and preference for symmetry (left) and between CRT score and preference for images shown in the frontoparallel plane (right). In this latter case, only symmetry images are included. Each dot is one participant.
Next, we computed a preference for the frontoparallel view, by taking the difference from the perspective view. In this case we only used the symmetry data because, as we have seen, the preference for the frontoparallel view was specific to symmetry. We expected a negative correlation because individuals with lower scores on the CRT may be less sensitive to symmetry when this is harder to see, or less salient. There was no correlation between preference for frontoparallel view and CRT score (r = 0.003, p = 0.97, Figure 6 right panel). Overall, we could find no strong evidence that a measure of a tendency to follow the more obvious and intuitive solution had anything to do with image- or object-level symmetry preferences.
6. Discussion
Preference for symmetry in familiar and abstract shapes is a well-established phenomenon. It has been confirmed in cross-cultural studies (for a review see [57]), and using implicit measures of affect [39]. The perceived beauty of symmetry may also be related to the fact that human visual system is very sensitive to the presence of symmetry in an image [24].
In our study, patterns were presented as images in the 2D frontoparallel plane or in perspective. The perspective transformation meant that perfect symmetry was absent in terms of image or retinal coordinates. That is, for a non-arbitrary viewpoint, object-level symmetry is lost at the image level. Although it is possible to detect the presence of symmetry at the object level, taking view angle into account, this is a challenge for the visual system. Previous studies have demonstrated how perspective or skew impairs perception of symmetry [5,15,16,20,55]. Experiment 1 confirmed that perspective increased reaction time and errors in a classification task. There was a perspective cost even when stimuli were solid polygons (Experiment 1a) and even when the viewing angle was kept constant over many trials (Experiment 1b). (In one ERP study, Makin et al. [34] found a nearly identical response for frontoparallel and perspective symmetry when participants were attending to symmetry. Assuming that our observers were engaged with the task, they were attending to symmetry and the brain response to symmetry would have been similar in the frontoparallel and perspective trials of Experiment 1. In general, factors that influence RT and SPN amplitude are tightly coupled [32]. However, the stimuli used in [34] were different: only one slant angle was used, and there was one axis of symmetry orthogonal to the rotation).
Experiment 2 was also conducted online. Each participant rated the beauty of the images used in Experiment 1. In addition, participants completed the Cognitive Reflection Test (CRT, [47]). We predicted that people who tend to give the more immediate and intuitive answer on the CRT would show preference for image-level symmetry. Conversely, people who give more deliberative answers may take the time to form allocentric representations and show equivalent preferences for image- and object-level symmetry. Preference for symmetry was confirmed in Experiment 2. This symmetry preference was present for frontoparallel and perspective images but it was reduced in the perspective condition. This is in line with the prediction that visual salience, in this case the salience of symmetry, is related to visual preference. However, we could not confirm any relationship between CRT scores and preference.
In general, our preference results are consistent with the fluency hypothesis [38]. Participants like symmetry most when it can be perceived most efficiently, in the frontoparallel condition. However, as discussed in the introduction, it is possible to make an alternative prediction. If preference formation is a process that develops over time, and given that observers were able in all cases to detect the presence of symmetry in our images, then one would expect the opposite pattern. That is, based on the idea of a discovery process, and possibly a “Aha” experience, after shape constancy was achieved, we predicted higher beauty ratings for symmetry in perspective. Here, the observer has found the presence of regularity in the image with effort, and pleasure may follow from this discovery [41]. Note also that some authors have suggested that perfect symmetry can be too regular and slight deviations from it may be better at driving preference [58]. This hypothesis, however, does not have empirical support [59].
With respect to the effect of the perspective transformation, we also made an additional prediction. Specifically we hypothesised a difference at the individual level, reflecting a more direct and a more reflexive approach [46]. To test this hypothesis, we used the Cognitive Reflection Test (CRT) in a sample of 148 participants (Experiment 2). Overall, considering the results from both experiments, there was no evidence that achieving perceptual constancy added significantly to the aesthetic experience, nor that this process varies at an individual level.
Animals are often attracted to phenotypic symmetry during mate selection [60,61]. Swaddle [62] points out that evolved symmetry attraction must be directed at object-level symmetry, not image-level symmetry, given that perfectly symmetrical images are the exception in natural viewing conditions. Given this, it is not surprising that our participants liked symmetry in frontoparallel and perspective conditions. However, it is not clear that aesthetic preference for abstract symmetry has anything to do with evolved preference for symmetrical mates. Preference for symmetry may be a more general and universal principle, as proposed by [63]. Another possibility is that preference for symmetry emerges from learning about image properties. Neural network modelling has shed light on the possible dynamics of evolved symmetry preference [64,65]. Symmetrical objects will project many non-symmetrical images depending on view angle. However, the average of all these images may still be symmetrical, even though few of the exemplars are. For a trained visual system, image symmetry becomes a super-stimulus or prototype, which may generate the strongest response.
In summary, we report evidence in line with many other studies in which observers show a preference for images containing symmetry, over less symmetrical images. Distortions due to perspective reduced the salience of the symmetry (as shown by longer response times) and also reduced preference. This pattern was consistent and was not modulated by differences in measures of intuitive/reflexive biases at the individual level.
Author Contributions
Conceptualization, M.B.; A.D.J.M.; methodology, M.B.; A.D.J.M.; formal analysis and investigation, M.B.; A.D.J.M.; J.T.-C.; writing, M.B.; A.D.J.M.; visualization, M.B.; A.D.J.M.; funding acquisition, M.B.; A.D.J.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by an ESRC grant award (ES/S014691/1). We thank Giulia Rampone and Silvia Ajao for assisting with data collection.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The full set of stimuli is available at https://osf.io/8vhwe/ (accessed on 30 November 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bertamini, M.; Byrne, C.; Bennett, K.M. Attractiveness is Influenced by the Relationship between Postures of the Viewer and the Viewed Person. i-Perception 2013, 4, 170–179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eisenman, R. Complexity-simplicity: I. Preference for symmetry and rejection of complexity. Psychon. Sci. 1967, 8, 169–170. [Google Scholar] [CrossRef]
- Höfel, L.; Jacobsen, T. Temporal Stability and Consistency of Aesthetic Judgments of Beauty of Formal Graphic Patterns. Percept. Mot. Ski. 2003, 96, 30–32. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, G.; Proffitt, F.; Grady, J.M.; Sumich, A. Facial symmetry and the perception of beauty. Psychon. Bull. Rev. 1998, 5, 659–669. [Google Scholar] [CrossRef] [Green Version]
- Szlyk, J.P.; Rock, I.; Fisher, C.B. Level of processing in the perception of symmetrical forms viewed from different angles. Spat. Vis. 1995, 9, 139–150. [Google Scholar] [CrossRef]
- Thouless, R.H. PHENOMENAL REGRESSION TO THE REAL OBJECT. I. Br. J. Psychol. Gen. Sect. 1931, 21, 339–359. [Google Scholar] [CrossRef]
- Lawson, R.; Bertamini, M.; Liu, D. Overestimation of the projected size of objects on the surface of mirrors and windows. J. Exp. Psychol. Hum. Percept. Perform. 2007, 33, 1027–1044. [Google Scholar] [CrossRef] [Green Version]
- Seth, A.K.; Baars, B.J. Neural Darwinism and consciousness. Conscious. Cogn. 2005, 14, 140–168. [Google Scholar] [CrossRef]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; W. H. Freeman: San Francisco, CA, USA, 1982; ISBN 978-0-262-51462-0. [Google Scholar]
- Ullman, S. High-Level Vision: Object Recognition and Visual Cognition; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Hoffman, D.D. Visual Intelligence: How We Create What We See; WW Norton & Company: New York, NY, USA, 2000. [Google Scholar]
- Chen, C.-C.; Kao, K.-L.C.; Tyler, C.W. Face Configuration Processing in the Human Brain: The Role of Symmetry. Cereb. Cortex 2006, 17, 1423–1432. [Google Scholar] [CrossRef] [Green Version]
- Logie, R.H.; Baddeley, A.D.; Woodhead, M.M. Face Recognition, Pose and Ecological Validity. Appl. Cogn. Psychol. 1987, 1, 53–69. [Google Scholar] [CrossRef]
- Wagemans, J.; VanGool, L.; d’ Ydewalle, G. Detection of Symmetry in Tachistoscopically Presented Dot Patterns: Effects of Multiple Exes and Skewing. Percept. Psychophys. 1991, 50, 413–427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sawada, T.; Pizlo, Z. Detection of skewed symmetry. J. Vis. 2008, 8, 14–18. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J. Skewed Symmetry: A Nonaccidental Property Used to Perceive Visual Forms. J. Exp. Psychol. Hum. Percept. Perform. 1993, 19, 364–380. [Google Scholar] [CrossRef] [PubMed]
- Tarr, M.J.; Pinker, S. When Does Human Object Recognition Use a Viewer-Centered Reference Frame? Psychol. Sci. 1990, 1, 253–256. [Google Scholar] [CrossRef]
- Koning, A.; van Lier, R. No symmetry advantage when object matching involves accidental viewpoints. Psychol. Res. 2006, 70, 52–58. [Google Scholar] [CrossRef]
- Li, Y.; Pizlo, Z.; Steinman, R.M. A computational model that recovers the 3D shape of an object from a single 2D retinal representation. Vis. Res. 2009, 49, 979–991. [Google Scholar] [CrossRef]
- Van der Vloed, G.; Csatho, A.; van der Helm, P.A. Symmetry and Repetition in Perspective. Acta Psychol. 2005, 120, 74–92. [Google Scholar] [CrossRef]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vis. Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Julesz, B. Foundations of Cyclopean Perception; University of Chicago Press: Chicago, IL, USA, 1971. [Google Scholar]
- Carmody, D.P.; Nodine, C.F.; Locher, P.J. Global Detection of Symmetry. Percept. Mot. Ski. 1977, 45, 1267–1273. [Google Scholar] [CrossRef]
- Bertamini, M.; Silvanto, J.; Norcia, A.M.; Makin, A.D.; Wagemans, J. The neural basis of visual symmetry and its role in mid- and high-level visual processing. Ann. New York Acad. Sci. 2018, 1426, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, Y.; Vanduffel, W.; Knutsen, T.; Tyler, C.W.; Tootell, R. Symmetry Activates Extrastriate Visual Cortex in Human and Nonhuman Primates. Proc. Natl. Acad. Sci. USA 2005, 102, 3159–3163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tyler, C.W.; Baseler, H.A.; Kontsevich, L.L.; Likova, L.T.; Wade, A.R.; Wandell, B.A. Predominantly extra-retinotopic cortical response to pattern symmetry. NeuroImage 2005, 24, 306–314. [Google Scholar] [CrossRef] [PubMed]
- Kohler, P.J.; Clarke, A.; Yakovleva, A.; Liu, Y.; Norcia, A.M. Representation of Maximally Regular Textures in Human Visual Cortex. J. Neurosci. 2016, 36, 714–729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Meel, C.; Baeck, A.; Gillebert, C.R.; Wagemans, J.; de Beeck, H.P.O. The representation of symmetry in multi-voxel response patterns and functional connectivity throughout the ventral visual stream. NeuroImage 2019, 191, 216–224. [Google Scholar] [CrossRef]
- Jacobsen, T.; Höfel, L. Descriptive and evaluative judgment processes: Behavioral and electrophysiological indices of processing symmetry and aesthetics. Cogn. Affect. Behav. Neurosci. 2003, 3, 289–299. [Google Scholar] [CrossRef]
- Höfel, L.; Jacobsen, T. Electrophysiological Indices of Processing Aesthetics: Spontaneous or Intentional Processes? Int. J. Psychophysiol. 2007, 65, 20–31. [Google Scholar] [CrossRef]
- Makin, A.D.J.; Wilton, M.M.; Pecchinenda, A.; Bertamini, M. Symmetry perception and affective responses: A combined EEG/EMG study. Neuropsychologia 2012, 50, 3250–3261. [Google Scholar] [CrossRef]
- Makin, A.D.; Wright, D.; Rampone, G.; Palumbo, L.; Guest, M.; Sheehan, R.; Cleaver, H.; Bertamini, M. An Electrophysiological Index of Perceptual Goodness. Cereb. Cortex 2016, 26, 4416–4434. [Google Scholar] [CrossRef] [Green Version]
- Makin, A.D.J.; Rampone, G.; Morris, A.; Bertamini, M. The Formation of Symmetrical Gestalts Is Task-Independent, but Can Be Enhanced by Active Regularity Discrimination. J. Cogn. Neurosci. 2020, 32, 353–366. [Google Scholar] [CrossRef]
- Makin, A.D.J.; Rampone, G.; Bertamini, M. Conditions for view invariance in the neural response to visual symmetry. Psychophysiology 2015, 52, 532–543. [Google Scholar] [CrossRef]
- Keefe, B.D.; Gouws, A.D.; Sheldon, A.A.; Vernon, R.J.W.; Lawrence, S.J.D.; McKeefry, D.J.; Wade, A.R.; Morland, A.B. Emergence of symmetry selectivity in the visual areas of the human brain: fMRI responses to symmetry presented in both frontoparallel and slanted planes. Hum. Brain Mapp. 2018, 39, 3813–3826. [Google Scholar] [CrossRef] [PubMed]
- Rampone, G.; Makin, A.D.J.; Tatlidil, S.; Bertamini, M. Representation of symmetry in the extrastriate visual cortex from temporal integration of parts: An EEG/ERP study. NeuroImage 2019, 193, 214–230. [Google Scholar] [CrossRef] [PubMed]
- Rampone, G.; Makin, A.D.J.; Tyson-Carr, J.; Bertamini, M. Spinning objects and partial occlusion: Smart neural responses to symmetry. Vis. Res. 2021, 188, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Reber, R. Processing Fluency, Aesthetic Pleasure, and Culturally Shared Taste. In Aesthetic Science: Connecting Mind, Brain, and Experience; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Makin, A.D.J.; Pecchinenda, A.; Bertamini, M. Implicit affective evaluation of visual symmetry. Emotion 2012, 12, 1021–1030. [Google Scholar] [CrossRef] [Green Version]
- Makin, A.D.; Helmy, M.; Bertamini, M. Visual cortex activation predicts visual preference: Evidence from Britain and Egypt. Q. J. Exp. Psychol. 2018, 71, 1771–1780. [Google Scholar] [CrossRef]
- De Cruys, S.; Wagemans, J. Putting Reward in Art: A Tentative Prediction Error Account of Visual Art. i-Perception 2011, 2, 1035–1062. [Google Scholar] [CrossRef] [Green Version]
- Muth, C.; Carbon, C.-C. The Aesthetic Aha: On the pleasure of having insights into Gestalt. Acta Psychol. 2013, 144, 25–30. [Google Scholar] [CrossRef]
- Zaidel, D.W.; Deblieck, C. Attractiveness of Natural Faces Compared to Computer Constructed Perfectly Symmetrical Faces. Int. J. Neurosci. 2007, 117, 423–431. [Google Scholar] [CrossRef]
- Leder, H.; Tinio, P.P.L.; Brieber, D.; Kröner, T.; Jacobsen, T.; Rosenberg, R. Symmetry Is Not a Universal Law of Beauty. Empir. Stud. Arts 2019, 37, 104–114. [Google Scholar] [CrossRef] [Green Version]
- Bertamini, M.; Rampone, G.; Makin, A.D.J.; Jessop, A. Symmetry preference in shapes, faces, flowers and landscapes. PeerJ 2019, 7, e7078. [Google Scholar] [CrossRef]
- Graf, L.K.M.; Landwehr, J.R. A Dual-Process Perspective on Fluency-Based Aesthetics: The Pleasure-Interest Model of Aesthetic Liking. Pers. Soc. Psychol. Rev. 2015, 19, 395–410. [Google Scholar] [CrossRef] [PubMed]
- Frederick, S. Cognitive Reflection and Decision Making. J. Econ. Perspect. 2005, 19, 25–42. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.; Frankish, K. Two Minds: Dual Processes and Beyond; Oxford University Press: Oxford, UK, 2009; ISBN 978-0-19-923016-7. [Google Scholar]
- Welsh, M.; Burns, N.; Delfabbro, P. The Cognitive Reflection Test: How Much More than Numerical Ability? In Proceedings of the Annual Meeting of the Cognitive Science Society, Berlin, Germany, 31 July–3 August 2013; Volume 35. Available online: https://escholarship.org/uc/item/68n012fh (accessed on 30 November 2021).
- Kahneman, D.; Frederick, S. Representativeness Revisited: Attribute Substitution in Intuitive Judgment. Heuristics Biases Psychol. Intuitive Judgm. 2002, 49, 81. [Google Scholar] [CrossRef] [Green Version]
- Stanovich, K.E.; West, R.F. The rationality debate as a progressive research program. Behav. Brain Sci. 2003, 26, 531–533. [Google Scholar] [CrossRef]
- Obrecht, N.A.; Chapman, G.B.; Gelman, R. An encounter frequency account of how experience affects likelihood estimation. Mem. Cogn. 2009, 37, 632–643. [Google Scholar] [CrossRef] [PubMed]
- Campitelli, G.; Labollita, M. Correlations of Cognitive Reflection with Judgments and Choices. Judgm. Decis. Mak. 2010, 5, 182–191. [Google Scholar]
- Peirce, J.W. PsychoPy—Psychophysics Software in Python. J. Neurosci. Methods 2007, 162, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Locher, P.; Smets, G. The influence of stimulus dimensionality and viewing orientation on detection of symmetry in dot patterns. Bull. Psychon. Soc. 1992, 30, 43–46. [Google Scholar] [CrossRef] [Green Version]
- Morey, R.D. Confidence Intervals from Normalized Data: A correction to Cousineau (2005). Tutorials Quant. Methods Psychol. 2008, 4, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Che, J.; Sun, X.; Gallardo, V.; Nadal, M. Cross-Cultural Empirical Aesthetics. In Progress in Brain Research; Elsevier: London, UK, 2018; Volume 237, pp. 77–103. ISBN 978-0-12-813981-3. [Google Scholar]
- McManus, I.C. Symmetry and asymmetry in aesthetics and the arts. Eur. Rev. 2005, 13, 157–180. [Google Scholar] [CrossRef]
- Gartus, A.; Leder, H. The Small Step toward Asymmetry: Aesthetic Judgment of Broken Symmetries. i-Perception 2013, 4, 361–364. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P. Bumblebee Preference for Symmetrical Flowers. Proc. Natl. Acad. Sci. USA 1995, 92, 2288–2292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grammer, K.; Fink, B.; Møller, A.P.; Thornhill, R. Darwinian aesthetics: Sexual selection and the biology of beauty. Biol. Rev. 2003, 78, 385–407. [Google Scholar] [CrossRef] [PubMed]
- Swaddle, J.P. Visual signalling by asymmetry: A review of perceptual processes. Philos. Trans. R. Soc. B Biol. Sci. 1999, 354, 1383–1393. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, V.S.; Hirstein, W. The Science of Art: A Neurological Theory of Aesthetic Experience. J. Conscious. Stud. 1999, 6, 15–51. [Google Scholar]
- Enquist, M.; Arak, A. Symmetry, Beauty and Evolution. Nature 1994, 372, 169–172. [Google Scholar] [CrossRef]
- Enquist, M.; Johnstone, R.A. Generalization and the Evolution of Symmetry Preferences. Proc. R. Soc. Lond. B Biol. Sci. 1997, 264, 1345–1348. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).