The Mechanistic Integration and Thermodynamic Optimality of a Nanomotor
Abstract
:1. Introduction
2. Theoretical Model and Methods
2.1. The Motor-Track System
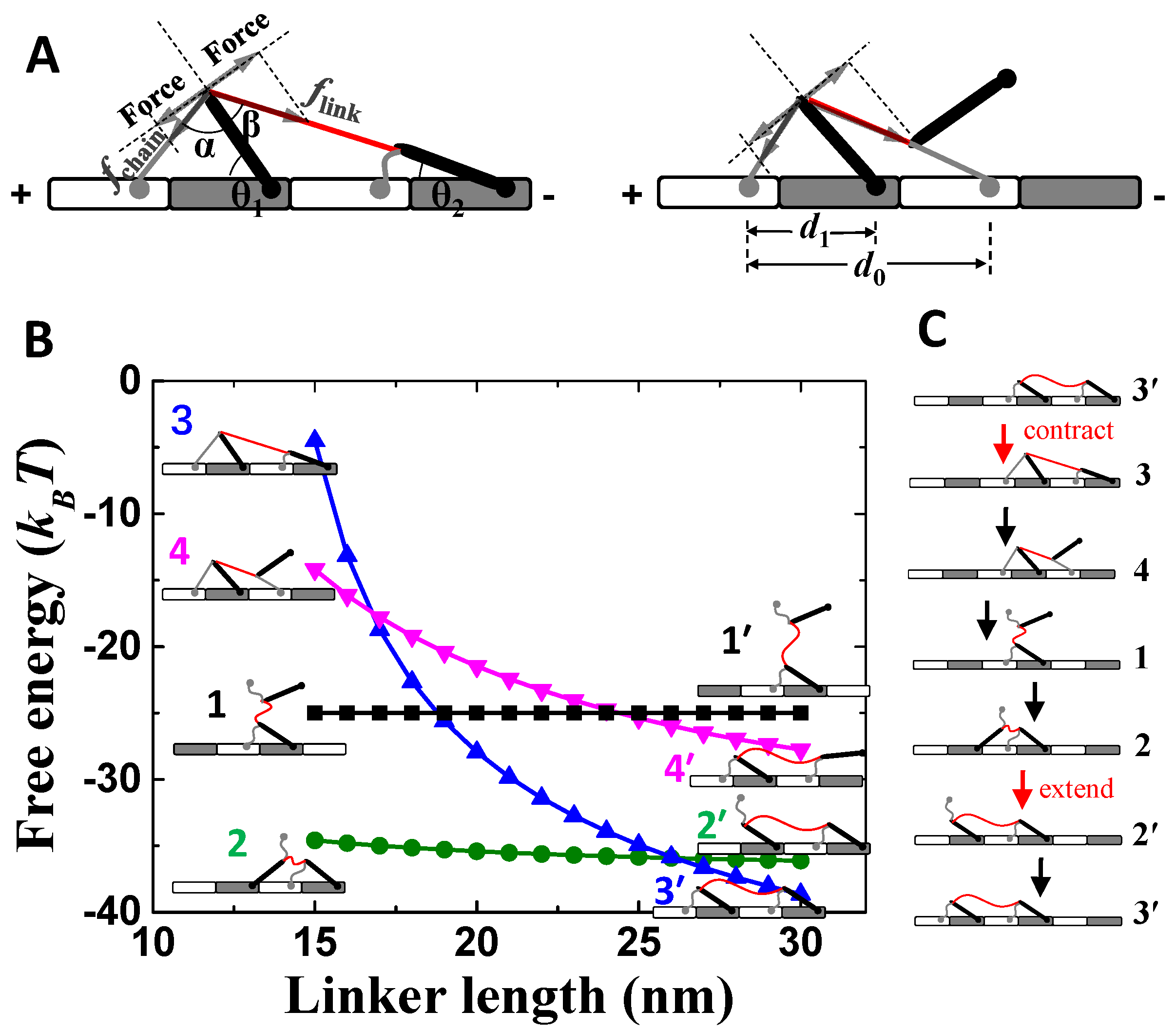
2.2. Free Energy of Motor-Track Binding State
2.3. Mechanical–Kinetic Model
3. Results
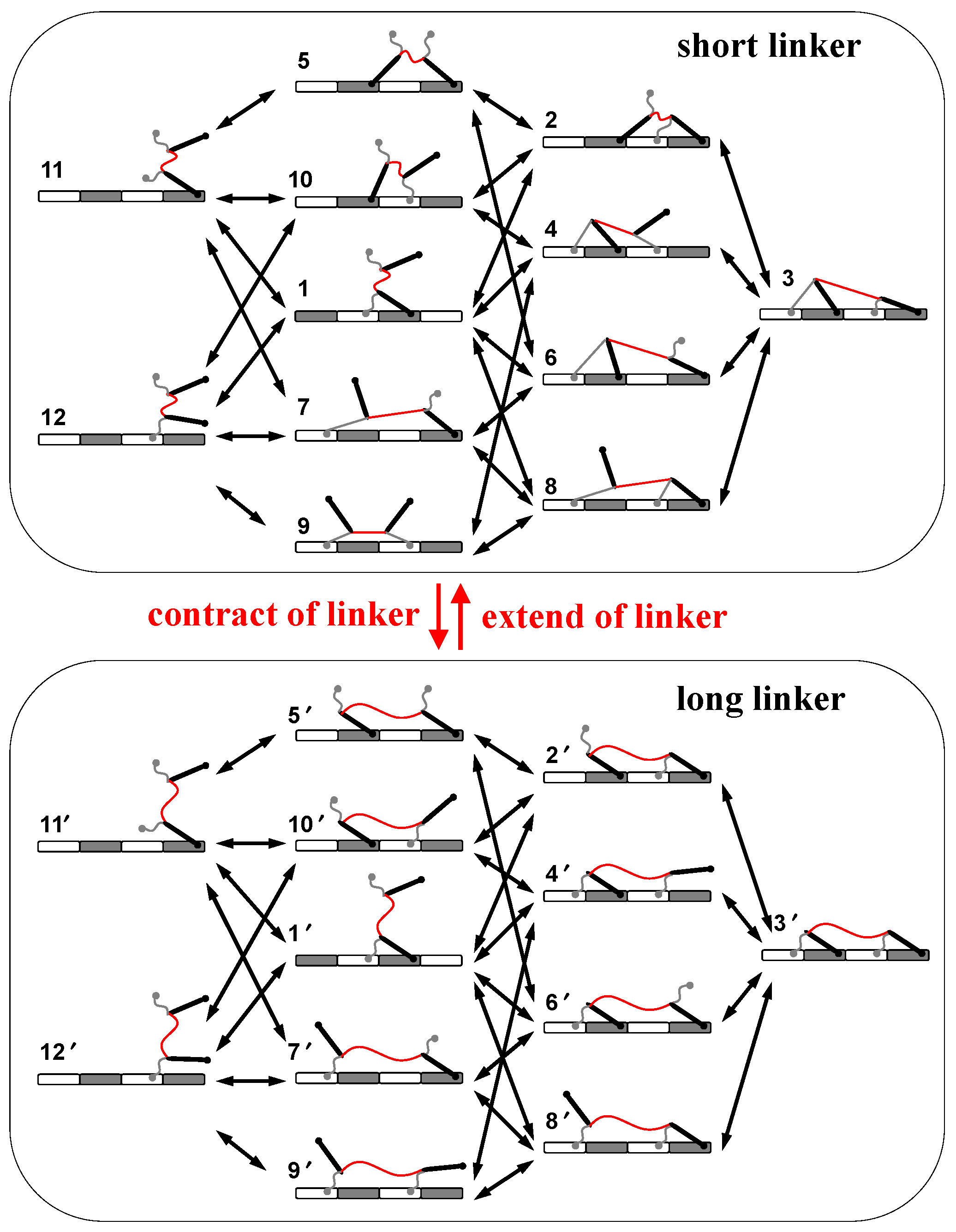
3.1. Selective Foot Detachment and Biased Binding
3.2. Mechanistic Integration of Selective Foot Detachment and Biased Binding
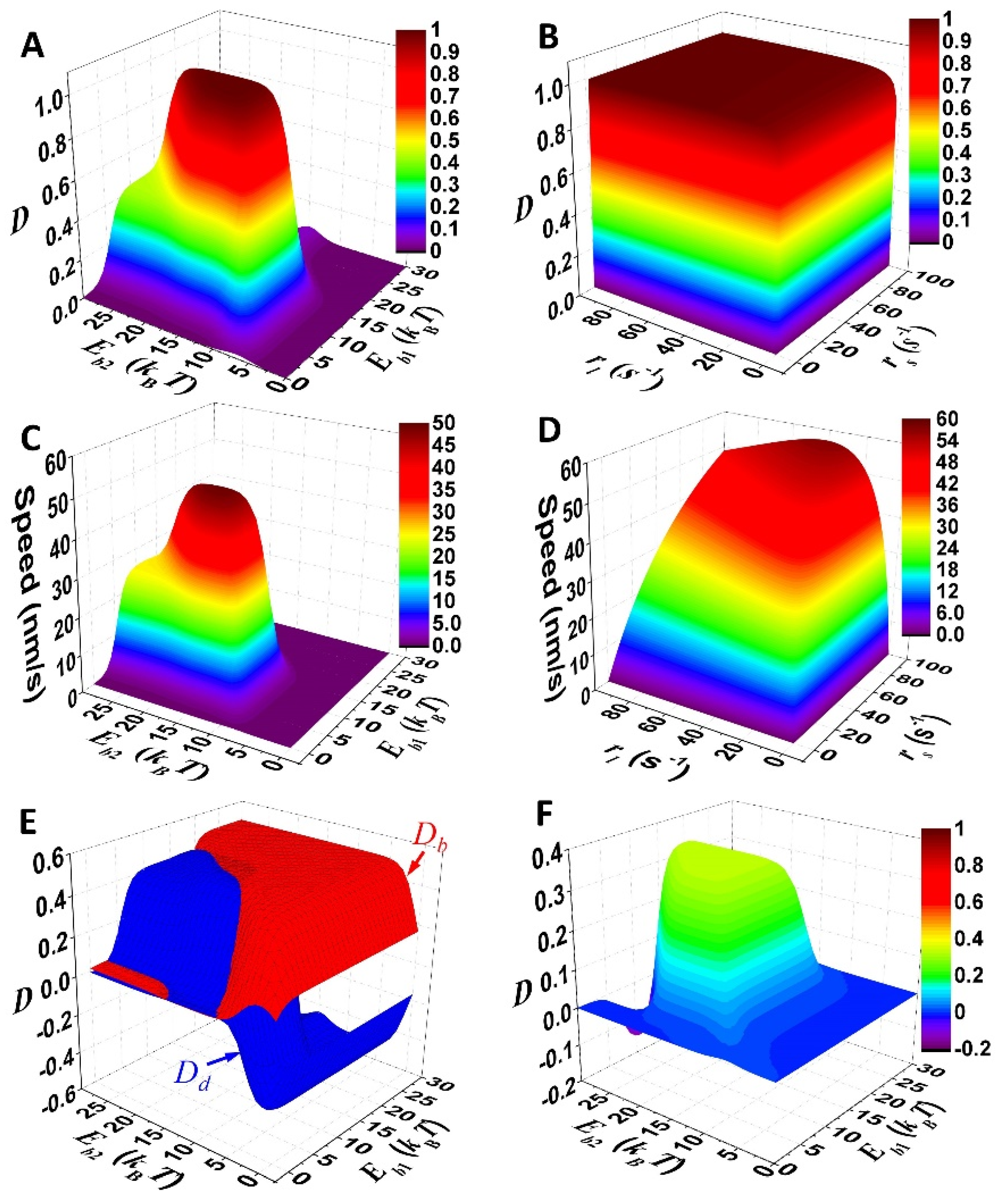
3.3. Optimization of the Motor
3.4. Speed-Directional Fidelity Tradeoff
4. Discussion
4.1. Implementation of the Motor-Track System
4.2. Motor Optimality
5. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Simmel, F.C.; Yurke, B.; Singh, H.R. Principles and Applications of Nucleic Acid Strand Displacement Reactions. Chem. Rev. 2019, 119, 6326–6369. [Google Scholar] [CrossRef] [PubMed]
- Feringa, B.L. The Art of Building Small: From Molecular Switches to Motors (Nobel Lecture). Angew. Chem.-Int. Ed. 2017, 56, 11059–11078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kassem, S.; van Leeuwen, T.; Lubbe, A.S.; Wilson, M.R.; Feringa, B.L.; Leigh, D.A. Artificial molecular motors. Chem. Soc. Rev. 2017, 46, 2592–2621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilson, M.R.; Sola, J.; Carlone, A.; Goldup, S.M.; Lebrasseur, N.; Leigh, D.A. An autonomous chemically fuelled small-molecule motor. Nature 2016, 534, 235. [Google Scholar] [CrossRef] [Green Version]
- Erbas-Cakmak, S.; Fielden, S.D.P.; Karaca, U.; Leigh, D.A.; McTernan, C.T.; Tetlow, D.J.; Wilson, M.R. Rotary and linear molecular motors driven by pulses of a chemical fuel. Science 2017, 358, 340–343. [Google Scholar] [CrossRef] [Green Version]
- Omabegho, T.; Sha, R.; Seeman, N.C. A bipedal DNA Brownian motor with coordinated legs. Science 2009, 324, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Green, S.J.; Bath, J.; Turberfield, A.J. Coordinated chemomechanical cycles: A mechanism for autonomous molecular motion. Phys. Rev. Lett. 2008, 101, 238101. [Google Scholar] [CrossRef] [Green Version]
- Yin, P.; Choi, H.M.T.; Calvert, C.R.; Pierce, N.A. Programming biomolecular self-assembly pathways. Nature 2008, 451, 318–322. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; He, Y.; Chen, Y.; Yin, P.; Mao, C. A DNAzyme that walks processiviely and autonomously along a one-dimensional track. Angew. Chem. Int. Ed. 2005, 44, 4355–4358. [Google Scholar] [CrossRef]
- Cheng, J.; Sreelatha, S.; Hou, R.Z.; Efremov, A.; Liu, R.C.; van der Maarel, J.R.C.; Wang, Z.S. Bipedal Nanowalker by Pure Physical Mechanisms. Phys. Rev. Lett. 2012, 109, 238104. [Google Scholar] [CrossRef] [Green Version]
- Loh, I.Y.; Cheng, J.; Tee, S.R.; Efremov, A.; Wang, Z. From Bistate Molecular Switches to Self-Directed Track-Walking Nanomotors. Acs Nano 2014, 8, 10293–10304. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.H.; Cheng, J.; Tee, S.R.; Sreelatha, S.; Loh, I.Y.; Wang, Z.S. Biomimetic Autonomous Enzymatic Nanowalker of High Fuel Efficiency. Acs Nano 2016, 10, 5882–5890. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Zhao, X.; Loh, I.Y.; Yan, J.; Wang, Z. Single-molecule mechanical study of an autonomous artificial translational molecular motor beyond bridge-burning design. Nanoscale 2021, 13, 13195–13207. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Chao, J.; Xiao, S.J.; Seeman, N.C. A proximity-based programmable DNA nanoscale assembly line. Nature 2010, 465, 202–206. [Google Scholar] [CrossRef]
- Thubagere, A.J.; Li, W.; Johnson, R.F.; Chen, Z.; Doroudi, S.; Lee, Y.L.; Izatt, G.; Wittman, S.; Srinivas, N.; Woods, D.; et al. A cargo-sorting DNA robot. Science 2017, 357, eaan6558. [Google Scholar] [CrossRef] [Green Version]
- Lund, K.; Manzo, A.J.; Dabby, N.; Michelotti, N.; Johnson-Buck, A.; Nangreave, J.; Taylor, S.; Pei, P.; Stojanovic, M.N.; Walter, N.G.; et al. Molecular robots guided by prescriptive landscapes. Nature 2010, 465, 206–210. [Google Scholar] [CrossRef] [Green Version]
- Wickham, S.F.J.; Bath, J.; Katsuda, Y.; Endo, M.; Hidaka, K.; Sugiyama, H.; Turberfield, A.J. A DNA-based molecular motor that can navigate a network of tracks. Nat. Nanotechnol. 2012, 7, 169–173. [Google Scholar] [CrossRef]
- He, Y.; Liu, D.R. Autonomous multistep organic synthesis in a single isothermal solution mediated by a DNA walker. Nat. Nanotechnol. 2010, 5, 778–782. [Google Scholar] [CrossRef] [Green Version]
- Meng, W.; Muscat, R.A.; McKee, M.L.; Milnes, P.J.; El-Sagheer, A.H.; Bath, J.; Davis, B.G.; Brown, T.; O’Reilly, R.K.; Turberfield, A.J. An autonomous molecular assembler for programmable chemical synthesis. Nat. Chem. 2016, 8, 542–548. [Google Scholar] [CrossRef]
- De Bo, G.; Gall, M.A.Y.; Kuschel, S.; De Winter, J.; Gerbaux, P.; Leigh, D.A. An artificial molecular machine that builds an asymmetric catalyst. Nat. Nanotechnol. 2018, 13, 381. [Google Scholar] [CrossRef]
- Clancy, B.E.; Behnke-Parks, W.M.; Andreasson, J.O.L.; Rosenfeld, S.S.; Block, S.M. A universal pathway for kinesin stepping. Nat. Struct. Mol. Biol. 2011, 18, 1020–1027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Efremov, A.; Wang, Z.S. Maximum directionality and systematic classification of molecular motors. Phys. Chem. Chem. Phys. 2011, 13, 5159–5170. [Google Scholar] [CrossRef] [PubMed]
- Efremov, A.; Wang, Z. Universal optimal working cycles of molecular motors. Phys. Chem. Chem. Phys. 2011, 13, 6223–6233. [Google Scholar] [CrossRef] [PubMed]
- Hou, R.; Wang, Z. Role of directional fidelity in multiple aspects of extreme performance of the F-1-ATPase motor. Phys. Rev. E 2013, 88, 022703. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.S.; Makarov, D.E. Rate of intramolecular contact formation in peptides: The loop length dependence. J. Chem. Phys 2002, 117, 4591–4593. [Google Scholar] [CrossRef]
- Wang, Z.S.; Plaxco, K.W.; Makarov, D.E. Influence of local and residual structures on the scaling behavior and dimensions of unfolded proteins. Biopolymers 2007, 86, 321–328. [Google Scholar] [CrossRef]
- Hill, T.L. Free Energy Transduction and Biochemical Cycle Kinetics; Springer: New York, NY, USA, 1989. [Google Scholar]
- Seifert, U. Entropy Production along a Stochastic Trajectory and an Integral Fluctuation Theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef] [Green Version]
- Schnakenberg, J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys 1976, 48, 571–585. [Google Scholar] [CrossRef]
- Visscher, K.; Schnitzer, M.J.; Block, S.M. Single kinesin molecules studied with a molecular force clamp. Nature 1999, 400, 184–189. [Google Scholar] [CrossRef]
- Hou, R.; Loh, I.Y.; Li, H.; Wang, Z. Mechanical-Kinetic Modeling of a Molecular Walker from a Modular Design Principle. Phys. Rev. Appl. 2017, 7, 024020. [Google Scholar] [CrossRef]
- Alberti, P.; Mergny, J.L. DNA duplex-quadruplex exchange as the basis for a nanomolecular machine. Proc. Natl. Acad. Sci. USA 2003, 100, 1569–1573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lubrich, D.; Lin, J.; Yan, J. A contractile DNA machine. Angew. Chem. Int. Ed. 2008, 47, 7026–7028. [Google Scholar] [CrossRef] [PubMed]
- Hamad-Schifferli, K.; Schwartz, J.J.; Santos, A.T.; Zhang, S.; Jacobson, J.M. Remote electronic control of DNA hybridization through inductive coupling to an attached metal nanocrystal antenna. Nature 2002, 415, 152–155. [Google Scholar] [CrossRef] [PubMed]
- Liedl, T.; Simmel, F.C. Switching the conformation of a DNA molecule with a chemical oscillator. Nano Lett. 2005, 5, 1894–1898. [Google Scholar] [CrossRef]
- Xiao, X.; Plakos, K.J.I.; Lou, X.; White, R.J.; Qian, J.; Plaxco, K.W.; Soh, H.T. Fluorescence detection of single-nucleotide polymorphisms with a single self-complementary, triple-stem DNA probe. Angew. Chem. Int. Ed. 2009, 48, 4354–4358. [Google Scholar] [CrossRef] [Green Version]
- Vallee-Belisle, A.; Ricci, F.; Plaxco, K.W. Thermodynamic basis for the optimization of binding-induced biomolecular switches and structure-switching biosensors. Proc. Natl. Acad. Sci. USA 2009, 106, 13802–13807. [Google Scholar] [CrossRef] [Green Version]
- Hugel, T.; Holland, N.B.; Cattani, A.; Moroder, L.; Seitz, M.; Gaub, H.E. Single-molecule optomechanical cycle. Science 2002, 296, 1103–1106. [Google Scholar] [CrossRef]
- Liang, X.; Mochizuki, T.; Asanuma, H. A supra-photoswitch involving sandwiched DNA base pairs and azobenzenes for light-driven nanostructures and nanodevices. Small 2009, 5, 1761–1768. [Google Scholar] [CrossRef]
- Sherman, W.B.; Seeman, N.C. A precisely controlled DNA biped walking device. Nano Lett. 2004, 4, 1203–1207. [Google Scholar] [CrossRef]
- Tee, S.R.; Hu, X.; Loh, I.Y.; Wang, Z. Mechanosensing Potentials Gate Fuel Consumption in a Bipedal DNA Nanowalker. Phys. Rev. Appl. 2018, 9, 034025. [Google Scholar] [CrossRef]
- Ouldridge, T.E.; Hoare, R.L.; Louis, A.A.; Doye, J.P.K.; Bath, J.; Turberfield, A.J. Optimizing DNA Nanotechnology through Coarse-Grained Modeling: A Two-Footed DNA Walker. ACS Nano 2013, 7, 2479–2490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ouldridge, T.E.; Louis, A.A.; Doye, J.P.K. Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys. 2011, 134, 085101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Astumian, R.D. Thermodynamics and kinetics of a Brownian motor. Science 1997, 276, 917–922. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Size parameters | length of linker | 15.5 nm after contract 30 nm after extend |
| length of foot chain | 4 nm | |
| length of foot bone | 5 nm | |
| lattice constant (d0) | 14nm | |
| separation distance (d1) | 5 nm | |
| Mechanical parameters | persistence length of soft chains lp | 0.8 nm |
| Kinetic parameters | zero-load dissociation rate (kd0) | 0.1 s−1 for both foot bone and chain |
| force-coupling length (ld) | 1 nm for both foot bone and chain |
| Mechanical parameters | binding energies | 25 kBT for foot bone 24 kBT for foot chain |
| Kinetic parameters | zero-load dissociation rate (kd0) | 0.1 s−1 for foot bone 0.9 s−1 for foot chain |
| force-coupling length (ld) | 1.0 nm for foot bone 0.1 nm for foot chain | |
| operation rate | 3.6 × 106 s−1 for contract 5.9 × 106 s−1 for extend |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, R. The Mechanistic Integration and Thermodynamic Optimality of a Nanomotor. Symmetry 2022, 14, 416. https://doi.org/10.3390/sym14020416
Hou R. The Mechanistic Integration and Thermodynamic Optimality of a Nanomotor. Symmetry. 2022; 14(2):416. https://doi.org/10.3390/sym14020416
Chicago/Turabian StyleHou, Ruizheng. 2022. "The Mechanistic Integration and Thermodynamic Optimality of a Nanomotor" Symmetry 14, no. 2: 416. https://doi.org/10.3390/sym14020416
APA StyleHou, R. (2022). The Mechanistic Integration and Thermodynamic Optimality of a Nanomotor. Symmetry, 14(2), 416. https://doi.org/10.3390/sym14020416






