Double Diffusive Magneto-Free-Convection Flow of Oldroyd-B Fluid over a Vertical Plate with Heat and Mass Flux

Abstract

The purpose of this research is to analyze the general equations of double diffusive magneto-free convection in an Oldroyd-B fluid flow based on the fundamental symmetry that are presented in non-dimensional form and are applied to a moving heated vertical plate as the boundary layer flow up, with the existence of an external magnetic field that is either moving or fixed consistent with the plate. The thermal transport phenomenon in the presence of constant concentration, coupled with a first order chemical reaction under the exponential heating of the symmetry of fluid flow, is analyzed. The Laplace transform method is applied symmetrically to tackle the non-dimensional partial differential equations for velocity, mass and energy. The contribution of mass, thermal and mechanical components on the dynamics of fluid are presented and discussed independently. An interesting property regarding the behavior of the fluid velocity is found when the movement is observed in the magnetic intensity along with the plate. In that situation, the fluid velocity is not zero when it is far and away from the plate. Moreover, the heat transfer aspects, flow dynamics and their credence on the parameters are drawn out by graphical illustrations. Furthermore, some special cases for the movement of the plate are also studied.

1. Introduction

Double diffusive convection is a mixing process due to the interaction of different components of fluid having different density gradients and rates of diffusion [1]. Oceanography is the simplest example of this phenomena, in which the concentration of salt and heat exist with distinct gradients, and they diffuse with different rates. For more details, refer to [2,3,4].

Moreover, over the years, the study of mass and the thermal transport phenomenon for the magneto-hydrodynamic (MHD) natural convective flow of fluids under the impact of electrical conduction has gained much popularity in view of their applications in meteorology, chemical engineering geophysics, solar physics and performance motion, which leads to symmetrical aspects in both the structure and the physical process. The results for this type of motions for the case of viscous fluids over vertical planes are developed for diversified boundary conditions. For example, for an impulsively moving plate with the radiation effects and ramp wall temperature [5], dynamics of a fluid of heat absorbing type with mass transfer [6], analytical study with a random unsteady shear stress boundary condition [7]. The MHD free convective flow passing through a micro channel along with the conditions of temperature and velocity slip on the boundary has been studied in [8]. Hussain et al. [9] performed an analysis of the MHD flow and heat transfer of ferrofluid in a channel with non-symmetrical cavities. They investigated and addressed the thermal transport properties of ferrofluid in the non-symmetric cavity in the channel with a magnetic field enforced on it. For other related and useful investigations, see [10,11,12] and the references therein.

In all these investigations, it is remarkable to confer that the uniform magnetic flux in the fluid is unyielding. Narahari and Debnath [13] conducted a useful analysis of MHD-natural convective flow by way of a fixed heat flux with two cases, namely, either the intensity of magnetic field is fixed respective to the fluid (MFFRF) or the area around the magnet is fixed in respect to the plate (MFFRP). Later, results were obtained by Shah et al. [14,15] for an MHD natural convective flowing up an erected plate through chemical reaction with the varying temperature of the plate in the cases for MFFRF and MFFRP.

Furthermore, in the existing literature, the investigations are carried out only for viscous fluid. There are few efforts performed for the case of rate type fluid, for example, some work related to free convective flow for MHD Maxwell fluid up a perpendicular plate can be found in [16,17,18], but they only correspond for the case of MFFRF.

In this paper, we explore a general study of double diffusive magneto-free-convection flow for a rate type fluid over a plate that is not fixed in the existence of chemical reaction, with a constant concentration and exponential heating of the plate. Nonetheless, our aim is not only to generalize the results by considering rate type fluids and heat–mass transfer, but to produce contemporary results for both oscillating and general motions of the plate. It is important to mention that, in case of MFFRP, the velocity of the fluid does not vanish outlying from the plate. Furthermore, expressions for the thermal boundary layer and velocity of fluid expressed in terms of the thermal and mechanical concentration contributions to the fluid motion are obtained. The solutions relating to the swaying movements of the plate are also discussed and demonstrated, resulting in the sum of transient and parts and steady state. Additionally, the influence of the involved parameters in the velocity of the fluid are graphically highlighted for the slow accelerating motions of the plate. Finally, the effective Prandtl number of impacts on the viscous of thermal boundary face is graphically determined.

This paper is structured as follows. In Section 2, the mathematical model with appropriate initial and boundary conditions is established. The exact analytic expressions for the velocity field is computed in Section 3. In Section 4, some special cases concerning the motion of the plate are discussed as well as expressions derived from obtained solutions by using different physical parameters. In Section 5, the results and discussion are presented and graphs are shown to analyze the impacts of various system parameters on the flow. Finally, in Section 6, some important conclusions are presented.

2. Experimental Procedure

We are considering the time-dependent, incompressible, electrically conductive natural convective movement of an Oldroyd-B fluid over an erected plate, which is also nonconductive and has infinite length. An unvarying magnetic intensity with strength $B$ is placed transversally on the plate along with the assumptions asserted that the magnetic intensity is supposed to be fixed for the plate or to the fluid. Initially, it was supposed that fluid and plate are static and have fixed species concentration $C_{\infty }$ and temperature $T_{\infty }$. As time $t=0^{+}$, the plate starts to excel in opposition of the gravitational pull with certain $Vf(t)$. Moreover, the temperature is stabilized at the expense of a relation in the form $T_{\infty }+T_w(1-a{e}^{-bt})$, whereas the concentration is maintained at the value $C_w.$ Here, $f(\cdot )$ is a continuous piecewise function that dies out at $t=0$. $V$ is assumes as a constant having dimension of velocity, and $a$, $b$, $T_w$ and $C_w$ are also constants.

The following assumptions are introduced:

(i)

Except for the variations in density with temperature in the body force, all other physical properties are constant;

(ii)

Comparing to the applied magnetic field, the magnetic field induced is insignificant;

(iii)

Except for the effects of radiation along the chemical process (in between the species concentration and the fluid), the Joule heating and viscous dissipation are neglected.

With the choice of an appropriate Cartesian coordinate system $Oxyz$ and using the Boussinesq and Rosseland approximations, the principal equations of Oldroyd-B fluid are governed as [19,20]:

$$\frac{\partial v\left(y,t\right)}{\partial t}=\frac{1}{\rho }\frac{\partial \tau \left(y,t\right)}{\partial y}+g\left(T-T_{\infty }\right){\beta }_T+g\left(C-C_{\infty }\right){\beta }_C-\frac{\sigma B_0^2}{\rho }\left(v\left(y,t\right)-\epsilon Vf(t)\right);\hspace{0.17em}\hspace{0.17em}y,\hspace{0.17em}\hspace{0.17em}t\hspace{0.17em}>0,$$

(1)

$$\frac{\tau \left(y,t\right)}{\mu }\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)=\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\frac{\partial v\left(y,t\right)}{\partial y}.$$

(2)

Solving Equations (1) and (2) to eliminate $\tau$ from Equation (1), we obtain:

$$\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\partial v}{\partial t}=v\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\frac{{\partial }^{2}v}{\partial y^2}+\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\left(g\left(T-T_{\infty }\right){\beta }_T+g{\beta }_C\left(C-C_{\infty }\right)-\frac{\sigma B_0^2}{\rho }\left(v-\epsilon Vf(t)\right)\right).$$

(3)

Additionally, heat and concentration equations are:

$$\rho c_p\frac{\partial T}{\partial t}=k\frac{{\partial }^{2}T}{\partial y^2}-\frac{\partial q_r}{\partial y},$$

(4)

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial y^2}-R\left(C-C_{\infty }\right),$$

(5)

with initial/boundary conditions for all $y,\hspace{0.17em}\hspace{0.17em}t\hspace{0.17em}>0$,

$$v(\iota ,t)=Vf(t),C(\iota ,t)=C_w,T(\iota ,t)=T_{\infty }-T_w(a{e}^{-bt}-1);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\ge 0,$$

(6)

$$v(y,t)<\infty ,C(y,t)\to C_{\infty },T(y,t)\to T_{\infty },\mathrm{as}y\to \infty ,$$

(7)

$$v(y,\iota )=0,C(y,\iota )=C_{\infty },T(y,\iota )=T_{\infty };\hspace{0.17em}\hspace{0.17em}\iota =0\mathrm{and}y\ge 0,$$

(8)

where $v(y,t)$, $C(y,t)$ and $T(y,t)$ denotes the velocity, the species concentration and temperature, respectively. $D,$ and $R$ are mass diffusivity and chemical reaction parameters, respectively, whereas ${\beta }_T,$ ${\beta }_C,$ ${\lambda }_1,$ $g,$ $\nu ,$ $\rho ,$ ${\lambda }_2,$ $k,$ $q_r,$ $\sigma ,$ and $c_p$ are thermal expansion coefficient (it can be positive or negative), concentration expansion coefficient (it is always positive), relaxation time, gravitational acceleration, kinematic viscosity, fluid density, retardation time, thermal conductivity, radiative heat flux, electrical conductivity and specific heat at constant pressure, respectively.

It is pertinent to mention that the parameter $\epsilon$ is 0 when MFFRF and 1 when MFFRP.

By adaptation (for an optically viscous fluid), then the Rosseland diffusion approach [11,21,22] is:

$$q_r=-\frac{4}{3}\frac{\mathsf{\sigma }}{k_R}\frac{\partial T^4}{\partial y},$$

(9)

where $k_R$ denotes the Rosseland mean attenuation coefficient and $\mathsf{\sigma }$ represents the Stefan–Boltzmann constant. In the case when the disparity between T (fluid temperature) and $T_{\infty }$ (free stream temperature) is small, Equation (4) changes into the following simpler expression [21]:

$$\frac{{\partial }^{2}T(y,t)}{\partial y^2}={\mathrm{Pr}}_{eff}\frac{\partial T(y,t)}{\partial t};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\mathrm{all}t,y\hspace{0.17em}>0,$$

(10)

where ${\mathrm{Pr}}_{eff}=\frac{\mathrm{Pr}}{1+N_r}$, which is known as effective Prandtl number [23], is the transport parameter regarding the diffusion (thermal and mass). Moreover, $\hspace{0.17em}\hspace{0.17em}{N}_r$ and $\mathrm{Pr}$ are denoted as the radiation–conduction parameter and the Prandtl number, respectively, where, $\hspace{0.17em}\hspace{0.17em}{N}_r=\frac{16}{3}\frac{\mathsf{\sigma }}{k{k}_R}{T}_{\infty }^3$ and $\mathrm{Pr}=\frac{\mu c_p}{k}.$

Introducing the following dimensionless quantities

$$\begin{array}{l}{t}^{\ast }=\frac{V^2}{\nu }t,\hspace{0.17em}{y}^{\ast }=\frac{V}{\nu }y,v^{\ast }=\frac{v}{V},\hspace{0.17em}{b}^{\ast }=\frac{\nu }{V^2}b,T^{\ast }=\frac{T-T_{\infty }}{T_w},\hspace{0.17em}{\lambda }_2{}^{*}=\frac{V^2}{\nu }{\lambda }_2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ C^{\ast }=\frac{C-C_{\infty }}{C_w-C_{\infty }},R^{\ast }=\frac{\nu }{V^2}R,\hspace{0.17em}{\lambda }_1{}^{*}=\frac{V^2}{\nu }{\lambda }_1,\hspace{0.17em}\hspace{0.17em}{f}^{*}(t)=f\left(\frac{\nu }{v^2}{t}^{*}\right).\end{array}$$

(11)

into (3)—(8), (10) and drop the $\ast$, our problem is transformed into the following non-dimensional form and can be written as:

$$\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\frac{\partial v(y,t)}{\partial t}=\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)·\frac{{\partial }^{2}v(y,t)}{\partial y^2}+\left(1+{\lambda }_1\frac{\partial }{\partial t}\right)\left(T(y,t)-M\left(v(y,t)-\epsilon f(t)\right)+NC(y,t)\right),\hspace{0.17em}\hspace{0.17em}$$

(12)

$$\frac{{\partial }^{2}T(y,t)}{\partial y^2}={\mathrm{Pr}}_{eff}\left(\frac{\partial T(y,t)}{\partial t}\right),$$

(13)

$$\frac{{\partial }^{2}C(y,t)}{\partial y^2}=Sc·\left(\frac{\partial C(y,t)}{\partial t}+RC(y,t)\right).$$

(14)

for $t,y>0$ and with the boundary and initial conditions

$$v(\iota ,t)=f(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C(\iota ,t)=1,T(\iota ,t)=1-a{e}^{-bt};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(15)

$$v(y,t)<\infty ,\hspace{0.17em}C(y,t),\hspace{0.17em}T(y,t)\to 0\mathrm{as}y\to \infty ,$$

(16)

$$v(y,\iota )=T(y,\iota )=C(y,\iota )=0\mathrm{for}\iota =0\hspace{0.17em}\mathrm{and}y\ge 0,$$

(17)

where $N$ is the ratio of buoyancy forces, while $M$, $Sc$ and $R$ denote the magnetic parameter, Schmidt number and dimensionless chemical reaction parameter, respectively. Moreover, they are defined as $N=\frac{{\beta }_C(C_w-C_{\infty })}{{\beta }_T{T}_w},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}M=\frac{\sigma B^2}{\rho }\frac{\nu }{V^2}\mathrm{and}\hspace{0.17em}Sc=\frac{\nu }{D}.$ The Schmidt number is a transport parameter with respect to the mass diffusivity, whereas $N$, calibrating the comparative contribution for the mass transportation on the natural convective flow [20], can have a negative or positive value. In the absence of the buoyancy force impact from the mass diffusion, we have $N=0$.

3. Solution of the Problem

It is extremely essential to point out that the expressions for the temperature and concentration commensurate to the similar problem can be found in the existing literature; in this paper, our target is to establish the fluid velocity expressions. We applied the standard Laplace transform method. Now, the Laplace transformed derived equations for $T(y,\tau )$ and $C(y,\tau )$, namely Equation (15) in [23] and Equation (20) in [14], respectively, yield

$$\overline{T}(y,q)=\frac{e^{-y\sqrt{{\mathrm{Pr}}_{eff}q}}}{q}-\frac{a{e}^{-y\sqrt{{\mathrm{Pr}}_{eff}q}}}{q+b},\hspace{0.17em}$$

(18)

$$\overline{C}(y,q)=\frac{e^{-y\sqrt{Sc(q+R)}}}{q}.$$

(19)

where $q$ is the Laplace transform parameter.

3.1. Calculation of Thermal Boundary Layer Thickness

When a fluid flows over a heated surface, then, due to the difference in temperature of surface and fluid, heat transfer takes place till an equilibrium temperature is attained. This heat transfer supervenes at plate surface as there is no relative motion noticed between the fluid and fluid’s surface. During the process of attaining the stabilization state, the fluid transmits heat to the leftover layers of fluid until it attains ambient temperature. As a result, a layer is settled (where the temperature down gradually) called thermal boundary layer. It is significant that, as the thermal outline layer becomes thicker, the convective energy transfer coefficient decreases. So, it is favorable to minimize the thickness of the thermal outline layer in order to enhance the convective thermal coefficient. Considering that ${\delta }_T(t)$ denotes the measure of thermal boundary layer, if ${\delta }_{1T}$ is the thermal boundary layer thickness, then ${\delta }_T(t)={\displaystyle \underset{0}{\overset{{\delta }_{1T}}{\int }}T(y,t)dy}$ and the differential equation of the thermal boundary layer thickness are obtained by integration.

Equation (13), with respect to $y$ from 0 to $\infty$ using the fact that $\underset{y\to \infty }{\lim }T(y,t)=\underset{y\to \infty }{\lim }\frac{\partial T(y,t)}{\partial y}=0$ and introducing the measure of thermal layer, can be written as follow

$${\mathrm{Pr}}_{eff}\frac{d{\delta }_T(t)}{dt}=-{\left.\frac{\partial T(y,t)}{\partial y}\right|}_{y=0}$$

(20)

Solving Equation (20) by employing the Laplace transform with the concerned initial conditions and ${\delta }_T(0)=0$, we obtain

$${\overline{\delta }}_T(q)=\frac{1}{\sqrt{{\mathrm{Pr}}_{eff}q}}\left(\frac{1}{q}-\frac{a}{q+b}\right).$$

(21)

or equivalently

$${\overline{\delta }}_T(q)=\frac{1}{\sqrt{{\mathrm{Pr}}_{eff}}}\left(\frac{1}{q^{3/2}}-\frac{a}{(q+b)\sqrt{q}}\right).$$

(22)

Now, employing the inverse Laplace transform to Equation (22) yields

$${\delta }_T(t)=\frac{2}{\sqrt{{\mathrm{Pr}}_{eff}\pi }}\left(\sqrt{t}-\frac{a{e}^{-bt}\sqrt{\pi }erf\left(i\sqrt{bt}\right)}{\sqrt{b}}\right).$$

(23)

3.2. Calculation of the Velocity Field

Implementing the Laplace transform on Equation (12) and making use of the concerned initial conditions, the ordinary differential equation obtained is

$$\left(q+{\lambda }_1{q}^2\right)\overline{v}(y,q)=\left(1+{\lambda }_{2}q\right)\frac{d^2\overline{v}(y,q)}{d{y}^2}+\left(1+{\lambda }_{1}q\right)\left(N\overline{C}(y,q)+\overline{T}(y,q)+M\left(\epsilon F(q)-\overline{v}(y,q)\right)\right).$$

(24)

with boundary conditions

$$\overline{v}(\iota ,q)=F(q),\overline{v}(y,q)<\infty \mathrm{as}y\to \infty \mathrm{and}\iota =0.$$

(25)

where the Laplace transforms of $f(t)$ and $v(y,t)$ are denoted by $F(q)$ and $\overline{v}(y,q)$ respectively. Introducing Equations (18) and (19) into (24), it yields

$$\begin{array}{l}\left(1+{\lambda }_{2}q\right)\frac{{\partial }^2\overline{v}(y,q)}{\partial y^2}-\left(M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q\right)\overline{v}(y,q)\\ =-\left(1+{\lambda }_{1}q\right)\left(\epsilon M\hspace{0.17em}F(q)+\left(\frac{1}{q}-\frac{a}{q+b}\right)e^{-y\sqrt{{\mathrm{Pr}}_{eff}\hspace{0.17em}q}}+N\frac{1}{q}{\mathrm{e}}^{-y\sqrt{Sc·(R+q)}}\right).\end{array}$$

(26)

The obtained solution of (26), with the boundary conditions (25), is

$$\begin{gathered} \overline{v}(y,q)=F(q){\mathrm{e}}^{-y\sqrt{\frac{M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q}{1+{\lambda }_{2}q}}}+\frac{\epsilon M·\left(1+{\lambda }_{1}q\right)·F(q)}{M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)·q}·\left(1-{\mathrm{e}}^{-y\sqrt{\frac{M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q}{1+{\lambda }_{2}q}}}\right) \\ +\frac{\left(1+{\lambda }_{1}q\right)\left(\frac{1}{q}-\frac{a}{q+b}\right)}{\left(q+{\lambda }_2{q}^2\right){\mathrm{Pr}}_{eff}-\left(M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q\right)}\left({\mathrm{e}}^{-y\sqrt{{\mathrm{Pr}}_{eff}}\sqrt{q}}-{\mathrm{e}}^{-y\sqrt{\frac{M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q}{1+{\lambda }_{2}q}}}\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{1}{q}·\frac{N}{\left((q+R)\left(1+{\lambda }_{2}q\right)Sc-\left(M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q\right)\right)}\left({\mathrm{e}}^{-y\sqrt{Sc}\sqrt{(q+R)}}-{\mathrm{e}}^{-y\sqrt{\frac{M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q}{1+{\lambda }_{2}q}}}\right). \end{gathered}$$

(27)

By introducing the relations (A1) and (A2) from the Appendix A into Equation (27), implementing the inverse Laplace transform and with the use of Equations (A3) and (A4), as defined in Appendix A, the equation for velocity field can be written as:

$$v(y,t)=v_T(y,t)+v_m(y,t)+v_C(y,t).$$

(28)

where

$$\begin{array}{l}{v}_m(y,t)={\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(y,s;M,{\lambda }_1,{\lambda }_2)·f\left(t-s\right)ds}\\ +\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_2(s;M,{\lambda }_1)·f(t-s)ds}-\epsilon M·{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{s}{\int }}{\omega }_2(u;M,{\lambda }_1)}}{\omega }_1(y,s-u;M,{\lambda }_1,{\lambda }_2)f\left(t-s\right)duds,\end{array}$$

(29)

$$\begin{array}{l}{v}_T(y,t)=-{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_3(s;M,{\lambda }_1,{\lambda }_2,{\mathrm{Pr}}_{eff})}erfc\left(\frac{y}{2\sqrt{t-s}}\right)ds\\ +a{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_3(s;M,{\lambda }_1,{\lambda }_2,{\mathrm{Pr}}_{eff})}\varphi \left(y\sqrt{{\mathrm{Pr}}_{eff}},t-s;0,-b\right)ds\\ +{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{s}{\int }}{\omega }_1(y,u;M,{\lambda }_1,{\lambda }_2){\omega }_3(t-s;M,{\lambda }_1,{\lambda }_2,{\mathrm{Pr}}_{eff})duds}}\\ -a{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{s}{\int }}{\omega }_3(t-s;M,{\lambda }_1,{\lambda }_2,{\mathrm{Pr}}_{eff})e^{-bu}{\omega }_1(y,s-u;M,{\lambda }_1,{\lambda }_2)duds}},\end{array}$$

(30)

$$v_C(y,t)=N\left({\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{s}{\int }}{\omega }_1(y,u;{\lambda }_1,{\lambda }_2,M){\omega }_4(t-s;{\lambda }_1,{\lambda }_2,S_c,R,M)duds-}}\varphi \left(y\sqrt{Sc},t;R,0\right)\right).$$

(31)

stands for its mechanical component, thermal component and concentration component, respectively.

Furthermore, in the above expressions

$$\begin{array}{l}{\omega }_1(y,t;M,{\lambda }_1,{\lambda }_2)=L^{-1}\left\{{\mathrm{e}}^{-y\sqrt{\frac{M+{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q}{1+{\lambda }_{2}q}}}\right\}\\ ={\displaystyle \sum _{k=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }\frac{{(-y)}^k·{(M)}^{\frac{k}{2}-l}·{({\lambda }_1)}^m·{(1+{\lambda }_{1}M)}^{l-m}·\Gamma (\frac{k}{2}+1)}{k!m!(l-m)!·{({\lambda }_2)}^{\frac{k}{2}}·\Gamma (\frac{k}{2}-l+1)}}}}·G_{1,l+m,\frac{k}{2}}(-\frac{1}{{\lambda }_2},t),\\ {\omega }_2(t;{\lambda }_1,M)=L^{-1}\left\{\frac{1+{\lambda }_{1}q}{{\lambda }_1{q}^2+\left(1+{\lambda }_{1}M\right)q+M}\right\}\\ ={\displaystyle \sum _{\alpha =0}^{\infty }\frac{{(-M)}^{\alpha }}{{({\lambda }_1)}^{\alpha +1}}}·\left(G_{1,-\alpha -1,\alpha +1}(-(M+\frac{1}{\lambda 1}),t)+{\lambda }_1{G}_{1,-\alpha ,\alpha +1}(-(M+\frac{1}{\lambda 1}),t)\right),\\ {\omega }_3(t;{\lambda }_1,{\lambda }_2,{\mathrm{Pr}}_{eff},M)=L^{-1}\left\{\frac{1+{\lambda }_{1}q}{({\lambda }_2{\mathrm{Pr}}_{eff}-{\lambda }_1)q^2+\left({\mathrm{Pr}}_{eff}-1-{\lambda }_{1}M\right)q-M}\right\}\\ ={\displaystyle \sum _{\beta =0}^{\infty }\frac{{(M)}^{\beta }}{{({\lambda }_2{\mathrm{Pr}}_{eff}-{\lambda }_1)}^{\beta +1}}}·\left(G_{1,-\beta -1,\beta +1}(-\frac{{\mathrm{Pr}}_{eff}-1-{\lambda }_{1}M}{{\lambda }_2{\mathrm{Pr}}_{eff}-{\lambda }_1},t)+{\lambda }_1{G}_{1,-\beta ,\beta +1}(-\frac{{\mathrm{Pr}}_{eff}-1-{\lambda }_{1}M}{{\lambda }_2{\mathrm{Pr}}_{eff}-{\lambda }_1},t)\right),\\ {\omega }_4(t;{\lambda }_1,{\lambda }_2,S_c,R,M)=L^{-1}\left\{\frac{1+{\lambda }_{1}q}{({\lambda }_2{S}_c-{\lambda }_1)q^2+\left(S_c(1+{\lambda }_{2}R)-(1+{\lambda }_{1}M)\right)q+(S_{c}R-M)}\right\}\\ ={\displaystyle \sum _{\eta =0}^{\infty }\frac{{(M-S_{c}R)}^{\eta }}{{({\lambda }_2{S}_c-{\lambda }_1)}^{\eta +1}}}·\left(G_{1,-\eta -1,\eta +1}(-\frac{S_c(1+{\lambda }_{2}R)-(1+{\lambda }_{1}M)}{{\lambda }_2{S}_c-{\lambda }_1},t)+{\lambda }_1{G}_{1,-\eta ,\eta +1}(-\frac{S_c(1+{\lambda }_{2}R)-(1+{\lambda }_{1}M)}{{\lambda }_2{S}_c-{\lambda }_1},t)\right).\end{array}$$

where $\varphi (y,t;a,b)$ and $G_{a,b,c}(.,t)$ are written in the Appendix A (A4) and (A12), respectively.

It can be verified easily that the solution of $v(y,t)$ expressed in Equation (28) satisfies the imposed boundary and initial conditions.

Regarding the limit of velocity as $y\to \infty$, we have

$$\underset{y\to \infty }{\lim }\hspace{0.17em}v(y,t)=\left\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\epsilon =0\\ M{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_2(s;M,{\lambda }_1)f(t-s)ds}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\epsilon =1.\end{array}\right.$$

(32)

Eventually, for the case when magnetic flux is fixed with respect to plate (MFFRP), the fluid does not stay at rest when it is very far from the plate.

Next, for the validation of our results, we take ${\lambda }_1=0$ and ${\lambda }_2=0$ in Equations (29)–(31), and then recover the corresponding equations Equation (27)–(29) in [15], as Shah et al. obtained for the viscous fluid case. Furthermore, when $f(t)=H(t)$ (the Heaviside unit step function) and ${\lambda }_1=0$ and ${\lambda }_2=0$ in relation to (29), we can use Equations (A5) and (A6) from the Appendix A. The achieved solution expressions are the same as those derived by Narahari and Debnath (Equation (11-A) in [13]), taking $a_o=0$, and also Tokis (Equation (12) in [24]), for the case when thermal and concentration effects ignored. Evidently, by adjusting $f(\cdot )$ in different appropriate forms, the exact solution of fluid motion of these types is recovered.

In the next section, we explore the fluid dynamics under the effect of oscillating motion or the slow acceleration of the plate coupled with the objective for the deep understanding of the physical aspects of the acquired results.

4. Various Cases Concerning the Motion of the Plate

Notice that the mass and thermal parts of velocity are independent of the movement of the plate. However, thermal and mass transport can impact the fluid flow, due to the fact that it is logically needed to perceive that if their control is ignored or prominent in some fluid motions with desirable applications in modern technology.

Now, we will establish the solution expression relative to motions generated due to the oscillation of the plate and the slow acceleration in the plate (when $\alpha <1$).

4.1. Case-I: Variably Accelerating Plate

In this case, Equation (29) becomes, after substituting $f(t)=H(t)t^{\alpha },$ with $\alpha >0$

$$\begin{array}{l}{v}_{\alpha m}(y,t)={\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(y,s;M,{\lambda }_1,{\lambda }_2)·{(t-s)}^{\alpha }ds}\\ +\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_2(s;M,{\lambda }_1)·{(t-s)}^{\alpha }ds}-\epsilon M·{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{s}{\int }}{(t-s)}^{\alpha }{\omega }_2(u;M,{\lambda }_1)}}·{\omega }_1(y,s-u;M,{\lambda }_1,{\lambda }_2)duds.\end{array}$$

(33)

which represents the motion of fluid caused by highly, slowly or constantly accelerating the plate.

Additionally, considering the case for $\alpha =0,$ i.e., when $f(t)=H(t)$, we obtain

$$\begin{array}{l}{v}_{0m}(y,t)={\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(y,s;{\lambda }_1,{\lambda }_2,M)ds}\\ +\epsilon M·{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_2(s;{\lambda }_1,M)ds}-\epsilon M·{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{s}{\int }}{\omega }_2(u;{\lambda }_1,M)}}{\omega }_1(y,s-u;{\lambda }_1,{\lambda }_2,M)duds.\end{array}$$

(34)

Further, by taking the limit ${\lambda }_1,{\lambda }_2\to 0$ for Equation (33), we obtain

$$v_m(y,t)=\frac{y}{2\sqrt{\pi }}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{{(t-s)}^{\alpha }}{s\sqrt{s}}\exp \left(-\frac{y^2}{4s}-Ms\right)ds+\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}{(t-s)}^{\alpha }{e}^{-Ms}erf\left(\frac{y}{2\sqrt{s}}\right)ds}}.$$

(35)

the solutions for the viscous fluid [15] case.

4.2. Case-II: Oscillating Plate

Inserting $f(t)=\cos (\omega t)\hspace{0.17em}H(t)\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}\sin (\omega t)H(t)$ into Equation (29), we obtain

$$\begin{array}{l}{v}_{cm}(y,t)={\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(y,s;{\lambda }_1,{\lambda }_2,M)\cos \left(\omega \left(t-s\right)\right)ds+\epsilon M\left(\frac{M{e}^{-Mt}}{M^2+{\omega }^2}+\frac{\cos \left(\omega t+\theta \right)}{\sqrt{M^2+{\omega }^2}}\right)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{M{e}^{-Ms}}{M^2+{\omega }^2}+\frac{\cos \left(\omega s+\theta \right)}{\sqrt{M^2+{\omega }^2}}\right)}{\omega }_1(y,t-s;{\lambda }_1,{\lambda }_2,M)ds,\end{array}$$

(36)

$$\begin{array}{l}{v}_{sm}(y,t)={\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(y,s;{\lambda }_1,{\lambda }_2,M)\sin \left[\omega (t-s)\right]ds+\epsilon M\left(\frac{\omega e^{-Mt}}{M^2+{\omega }^2}+\frac{\sin \left(\omega t-\theta \right)}{\sqrt{M^2+{\omega }^2}}\right)}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{\omega e^{-Ms}}{M^2+{\omega }^2}+\frac{\sin \left(\omega s-\theta \right)}{\sqrt{M^2+{\omega }^2}}\right)}{\omega }_1(y,t-s;{\lambda }_1,{\lambda }_2,M)ds.\end{array}$$

(37)

Again, the limit ${\lambda }_1,{\lambda }_2\to 0$ yields the appropriate results for the viscous fluid [15] case, as follows:

$$v_{cm}(y,t)=\frac{y}{2\sqrt{\pi }}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{\cos \left[\omega (t-s)\right]}{s\sqrt{s}}\exp \left(-\frac{y^2}{4s}-Ms\right)ds+\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}\cos \left[\omega (t-s)\right]e^{-Ms}erf\left(\frac{y}{2\sqrt{s}}\right)ds}},$$

(38)

$$v_{sm}(y,t)=\frac{y}{2\sqrt{\pi }}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{\sin \left[\omega (t-s)\right]}{s\sqrt{s}}\exp \left(-\frac{y^2}{4s}-Ms\right)ds+\epsilon M{\displaystyle \underset{0}{\overset{t}{\int }}\sin \left[\omega (t-s)\right]e^{-Ms}erf\left(\frac{y}{2\sqrt{s}}\right)ds.}}$$

(39)

It can be noticed that the non-dimensional velocities $v_{cm}(y,t)$ and $v_{sm}(y,t)$(as given in Equations (36) and (37)) represent the movement of the fluid starting sometime later. Finally, when the transients depart, Equations (36) and (37) become

$$\begin{array}{l}{v}_{cmp}(y,t)={\displaystyle \underset{0}{\overset{\infty }{\int }}{\omega }_1(y,s;M,{\lambda }_1,{\lambda }_2)·\cos \left(\omega \left(t-s\right)\right)ds+\frac{\epsilon M}{\sqrt{{\omega }^2+M^2}}·\cos \left(\omega t+\theta \right)}\\ -\frac{\epsilon M}{\sqrt{{\omega }^2+M^2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}\cos \left(\omega s+\theta \right)}\hspace{0.17em}{\omega }_1(y,t-s;M,{\lambda }_1,{\lambda }_2)ds,\end{array}$$

(40)

$$\begin{array}{l}{v}_{smp}(y,t)={\displaystyle \underset{0}{\overset{\infty }{\int }}{\omega }_1(y,s;M,{\lambda }_1,{\lambda }_2)·\sin \left[\omega (t-s)\right]ds+\frac{\epsilon M}{\sqrt{{\omega }^2+M^2}}·\sin \left(\omega t-\theta \right)}\\ -\frac{\epsilon M}{\sqrt{{\omega }^2+M^2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}\sin \left(\omega s-\theta \right)\hspace{0.17em}}{\omega }_1(y,t-s;M,{\lambda }_1,{\lambda }_2)ds,\end{array}$$

(41)

which are the required steady-state solution expressions.

Moreover, it can be easily verified that the acquired results also fulfill the involving conditions at the boundary, also governing Equation (12) by ignoring the concentration and effects caused by heat. Over a certain specific time, fluids flow in accordance with Equations (40) and (41), with the exception of thermal and mass effects. Applying the limit on Equations (40) and (41) as $y\to \infty$, then we have

$$v_{cmp}(\infty ,t)=\left\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\epsilon =0\\ \frac{M}{\sqrt{M^2+{\omega }^2}}\cos (\omega t-\theta )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\epsilon =1,\end{array}\right.$$

(42)

$$v_{smp}(\infty ,t)=\left\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\epsilon =0\\ \frac{M}{\sqrt{M^2+{\omega }^2}}\sin (\omega t-\phi )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\epsilon =1.\end{array}\right.$$

(43)

For good analogy, if we replace $f(t)=H(t)\cos (\omega t)\hspace{0.17em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}\hspace{0.17em}f(t)=\mathrm{H}\left(t\right)\sin (\omega t)$ into Equation (32), then, we obtain

$$v_c(\infty ,t)=\left\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\epsilon =0\\ -\frac{M^2}{M^2+{\omega }^2}{e}^{-Mt}+\frac{M}{\sqrt{M^2+{\omega }^2}}\cos (\omega t-\theta )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\epsilon =1,\end{array}\right.$$

(44)

$$v_c(\infty ,t)=\left\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\epsilon =0\\ \frac{M\omega }{M^2+{\omega }^2}{e}^{-Mt}+\frac{M}{\sqrt{M^2+{\omega }^2}}\sin (\omega t-\theta )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\epsilon =1.\end{array}\right.$$

(45)

which are in agreement with Equations (42) and (43). Equations (44) and (45) also involve the transient elements of velocity at infinity for the case MFFRP.

5. Results and Discussion

In this paper, the general equations of double diffusive magneto-free convection in a Oldroyd-B fluid are represented in non-dimensional form and are applied to the flow at the boundary of unsteady fluids past a moving upright heating plate subject to the availability of an external magnetic flux that either moves or is fixed coupled with the plate. The thermal transport phenomenon was discussed in the presence of constant concentration along with a first order chemical reaction under exponential heating. The Laplace transform method was applied to interpret the dimensionless differential equations for velocity, mass and energy. The contribution of mass, thermal and mechanical components on the dynamics of fluid are presented and discussed independently. For the sake of exploring the physical perspective of the analytically accomplished results, two particular cases are considered in this paper to examine the effects of the system parameters $N,$ $Sc,$ $R$, ${\mathrm{Pr}}_{eff}$, ${\lambda }_1$, ${\lambda }_2$ and variables on fluid motion. Additionally, the motion of a slowly accelerating plate is discussed and displayed graphically.

Figure 1 demonstrates the effect of time on the velocity profile at distinct times. It is observed that velocity increases as a function of time. Figure 2 shows the plot of the mechanical term of velocity $v_m(y,t)$ versus $y$ at varying values of times. The same trend is observed as in Figure 1. Moreover, the velocities corresponding to MFFRP are considerably larger in comparison to the case of MFFRF. In both situations, we see the smooth decline in velocity from definite large values at the endpoint to an asymptotical value as $y$ enlarge. Furthermore, it can be seen from these figures that, when y approaches to infinity, the values that exist asymptotically for both velocities are non-zero for the case of MFFRP.

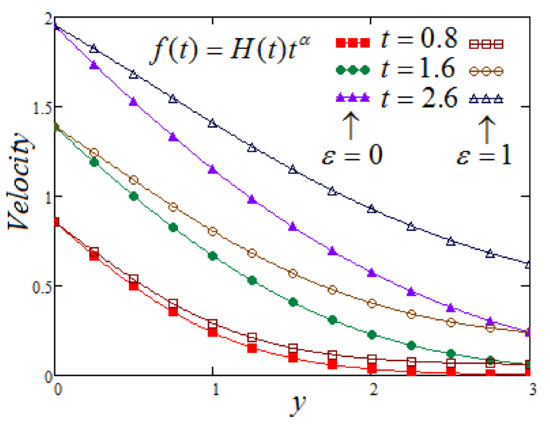
Figure 1. Trace of $v(y,t)$ versus $y$ for ${\mathrm{Pr}}_{eff}=4.5,$ $Sc=0.8,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $\alpha =0.7,$ $N=2.5,$ $R=0.7$ and varying of $t$.

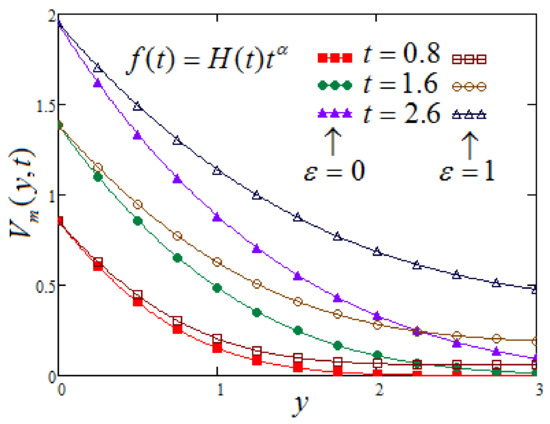
Figure 2. Trace of $V_m(y,t)$ versus $y$ for ${\mathrm{Pr}}_{eff}=4.5,$ $Sc=0.8,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $\alpha =0.7,$ $N=2.5,$ $R=0.7$ and varying of $t$.

Figure 3 represents the effects of $N$ on the fluid’s velocity, at time $t=0.8$ and $t=1.4$ for both aiding and opposing flows. For adding flow $N>0$, the thermal buoyancy force is supported by the buoyancy force (caused by species diffusion), which, as a result, causes the rise in velocity and a rise in the values of $N.$ For opposing flow $N<0$, the buoyancy force results in a reversal flow effect and, hence, resists the flow of fluid.

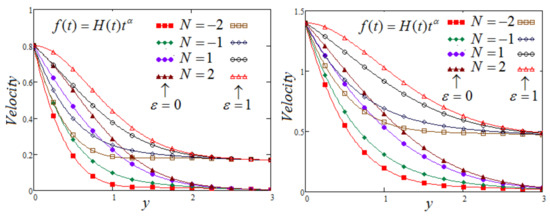
Figure 3. Trace of $v(y,t)$ versus $y$ at $t=0.8$ and $t=1.4$ for ${\mathrm{Pr}}_{eff}=4.5,$ $Sc=0.8,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $\alpha =0.7,$ $R=0.7$ and varying of $N$.

The $Sc$ (Schmidt number) and $R$ (the chemical reaction) influence on a fluid’s velocity can be noticed in Figure 4 and Figure 5. It can be observed that velocity is in a decreasing trend, corresponding to the increase in the values of both of these parameters. Furthermore, we should point out that, for the case of MFFRP, the momentum profiles are superior.

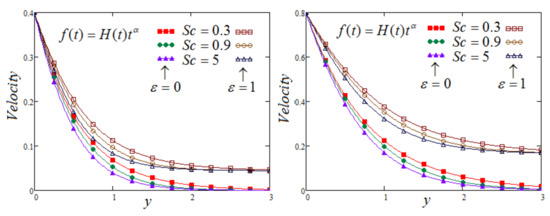
Figure 4. Trace of $v(y,t)$ versus $y$ at $t=0.4$ and $t=0.8$ for $N=2.5,$ ${\mathrm{Pr}}_{eff}=4.5,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $\alpha =0.7,$ $R=0.7$ and varying of $Sc$.

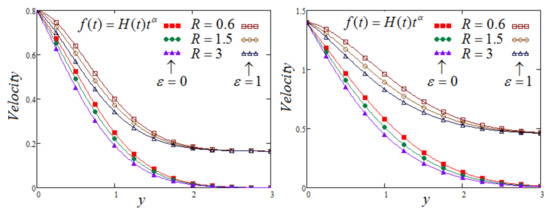
Figure 5. Trace of $v(y,t)$ versus $y$ at $t=0.8$ and $t=1.4$ for $N=2.5,$ ${\mathrm{Pr}}_{eff}=4.5,$ $Sc=0.8,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $\alpha =0.7$ and varying of $R$.

As expected, Figure 6 and Figure 7 represent the fluid velocity in both cases (when MFFRF or MFFRP), showing a decreasing trend for the relaxation time but showing a reverse trend for retardation time. So, the relaxation time serves as the shear thickening parameter. It can be observed that the effect of ${\lambda }_1$ vanishes along time, but velocity rises due to the increase in the value of ${\lambda }_2$. Figure 8 depicts the decay in velocity due to the increase in the values of ${\mathrm{Pr}}_{eff}$. Moreover, the three components of the velocity contributions on the movement of the fluid are plotted in Figure 9 for both cases, i.e., MFFRP and MFFRF. These figures depict the contribution of each component and the appreciable impact on the fluid’s velocity, which cannot be ignored. Finally, as displayed in Figure 10, the thickness of thermic boundary layer reduces, corresponding to the raising values of effective Prandtl number parameter. It can be noted that we have set $a=0.70,\hspace{0.17em}\hspace{0.17em}b=0.10,$ $M=0.6$, in all Figures (1–10).

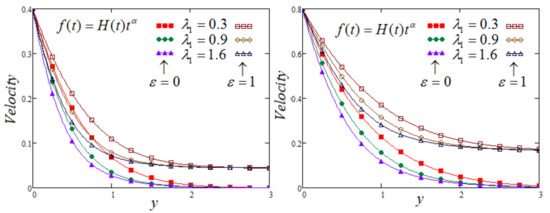
Figure 6. Trace of $v(y,t)$ versus $y$ at $t=0.4$ and $t=0.8$ for $N=2.5,$ ${\mathrm{Pr}}_{eff}=4.5,$ $R=0.7$ ${\lambda }_2=0.3,$ $\alpha =0.7$$Sc=0.8$ and varying of ${\lambda }_1$.

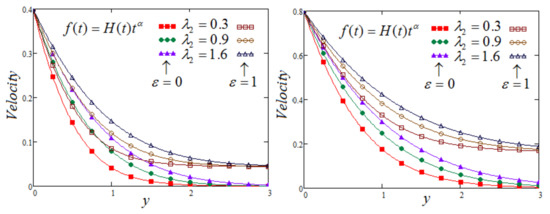
Figure 7. Trace of $v(y,t)$ versus $y$ at $t=0.4$ and $t=0.8$ for $R=0.7,$ $N=2.5,$ ${\mathrm{Pr}}_{eff}=4.5,$ ${\lambda }_1=0.7,$ $\alpha =0.7$ $Sc=0.8,$ and varying of ${\lambda }_2$.

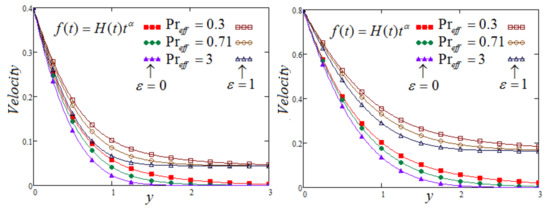
Figure 8. Trace of $v(y,t)$ versus $y$ at $t=0.4$ and $t=0.8$ for $N=2.5,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $\alpha =0.7$, $R=0.7,$ $Sc=0.8$ and varying of ${\mathrm{Pr}}_{eff}$.

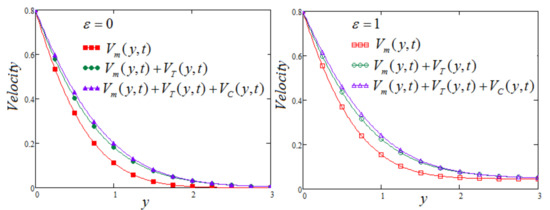
Figure 9. Behavior of velocities $V_m(y,t),$ $V_T(y,t)+V_m(y,t)$ and $V_T(y,t)+V_m(y,t)+V_C(y,t)$ versus $y$ at $t=0.8$ for ${\mathrm{Pr}}_{eff}=0.71,$ $Sc=0.8,$ ${\lambda }_1=0.7,$ ${\lambda }_2=0.3,$ $R=0.7$ and $N=2.5$.

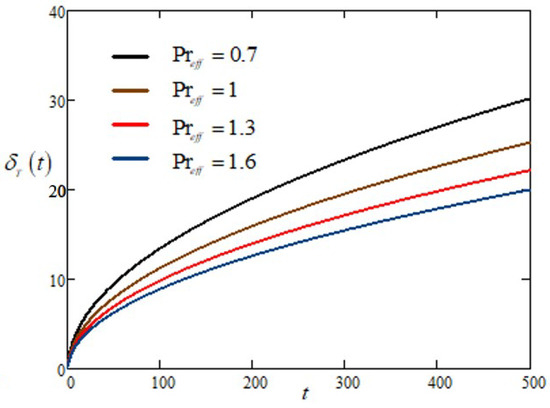
Figure 10. Behavior of the thermal boundary layer thickness for the varying values of ${\mathrm{Pr}}_{eff}$.

6. Conclusions

The thermal transport phenomenon was discussed in the presence of a constant concentration along with a first order chemical reaction, thermal conductivity with exponential heating. The Laplace transform method was applied to tackle the non-dimensional partial differential equations for velocity, mass and energy. The contribution of mass, thermal and mechanical components on the dynamics of fluid were presented and discussed independently. For the sake of exploring and understanding the physical perspective of the analytically accomplished results, in this paper, two particular cases were considered, the slowly accelerating or oscillating motion of the plate. Furthermore, the impact of variables and pertinent parameters, such as $N,$ ${\lambda }_1,$ $Sc,$ ${\mathrm{Pr}}_{eff},$ $R$ and ${\lambda }_2$, on the motion of the fluid is illustrated graphically and examined for the slowly accelerating movement in the plate. We can conclude that:

• It can be noticed that, at infinity for the fixed magnetic field relative to the plate, the fluid velocity does not settle to zero.
• It can be perceived that, in the case of MFFRP, the velocity is significantly larger as we compare with the case of MFFRF.
• The fluid velocity decreases in relation to the relaxation time and its impact dies out with time, but shows the reverse behavior of retardation time.
• For $N>0$, there is an increase in velocity graphically for the values of $N.$ An opposite trend was observed for $N<0$.
• The contributions of velocity components (mechanical, thermal and concentration) are considerable and cannot be ignored.
• The thickness of thermal boundary layer and velocity decline, corresponding to the increase in the effective Prandtl number.