Coaxiality Optimization Analysis of Plastic Injection Molded Barrel of Bilateral Telecentric Lens
Abstract
:1. Introduction
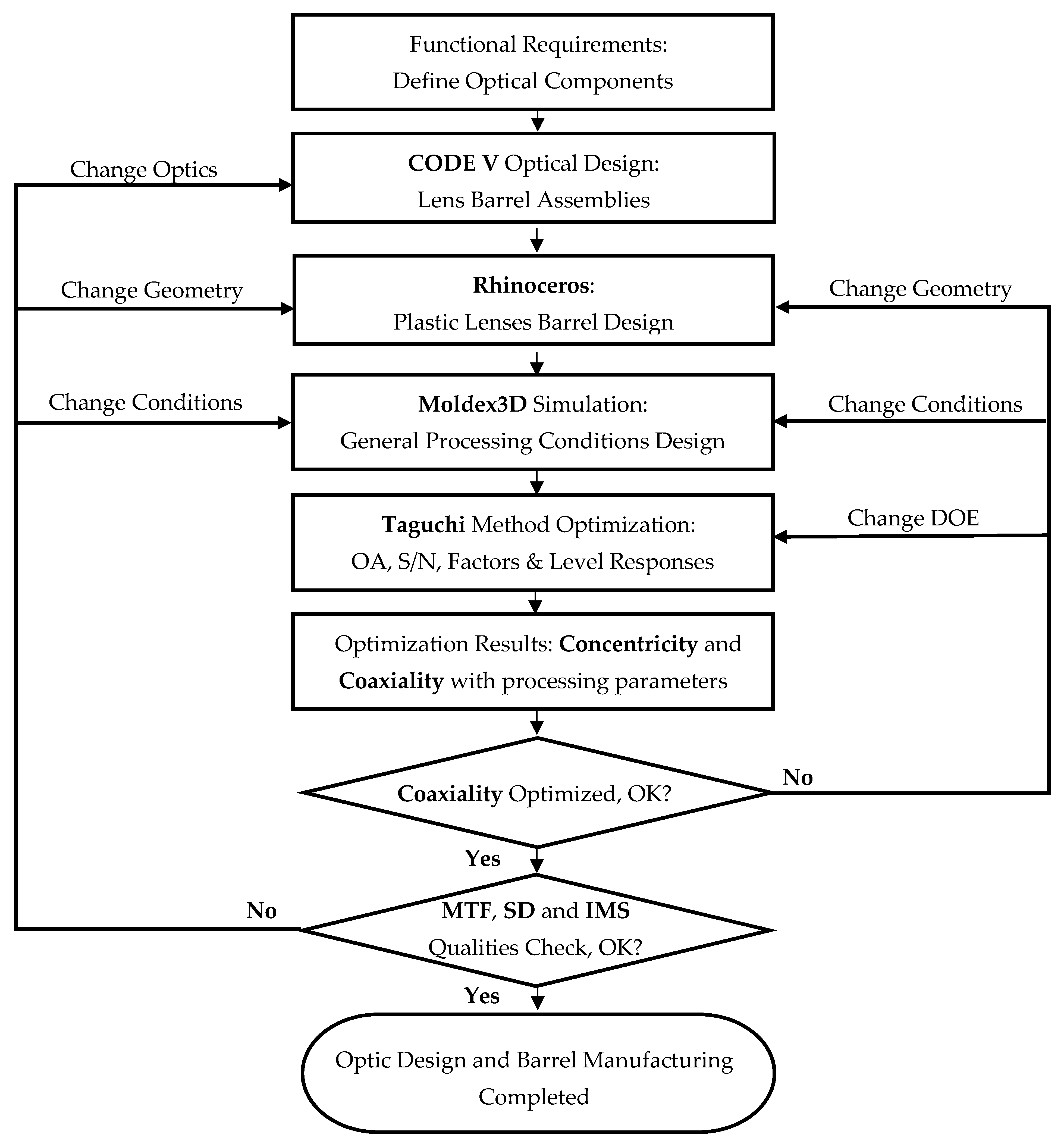
2. Method and Procedures
2.1. Materials and Geometry Model
2.2. Mold Flow Analysis and Taguchi Experimental Method
2.3. Roundness, Concentricity, and Coaxiality Measures
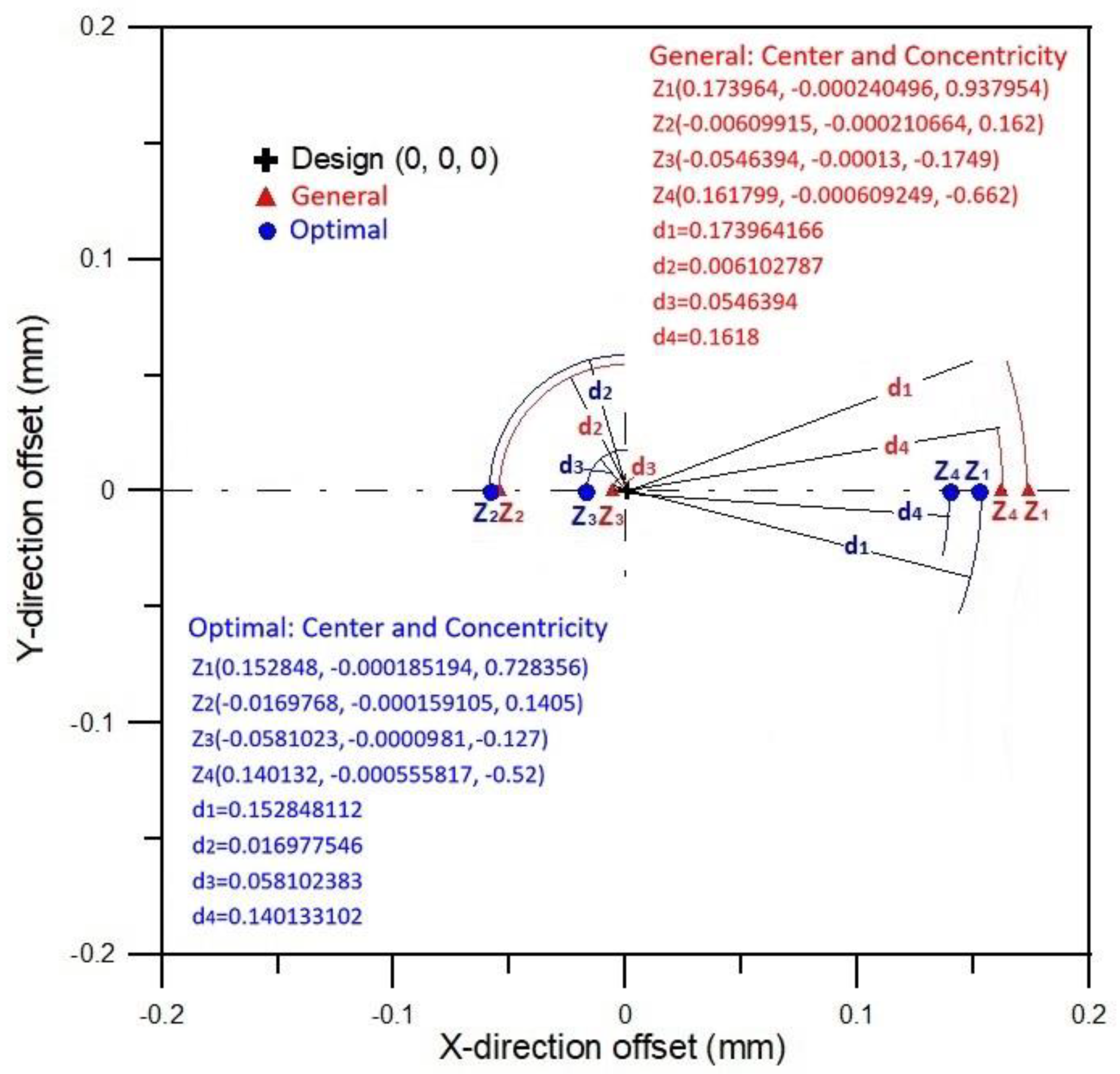
2.4. CODE V Optical Evaluation Using Eccentric Coordinates (xc, yc, zc)
3. Results and Discussion
3.1. Taguchi Optimization Results
3.2. Geometry Analysis
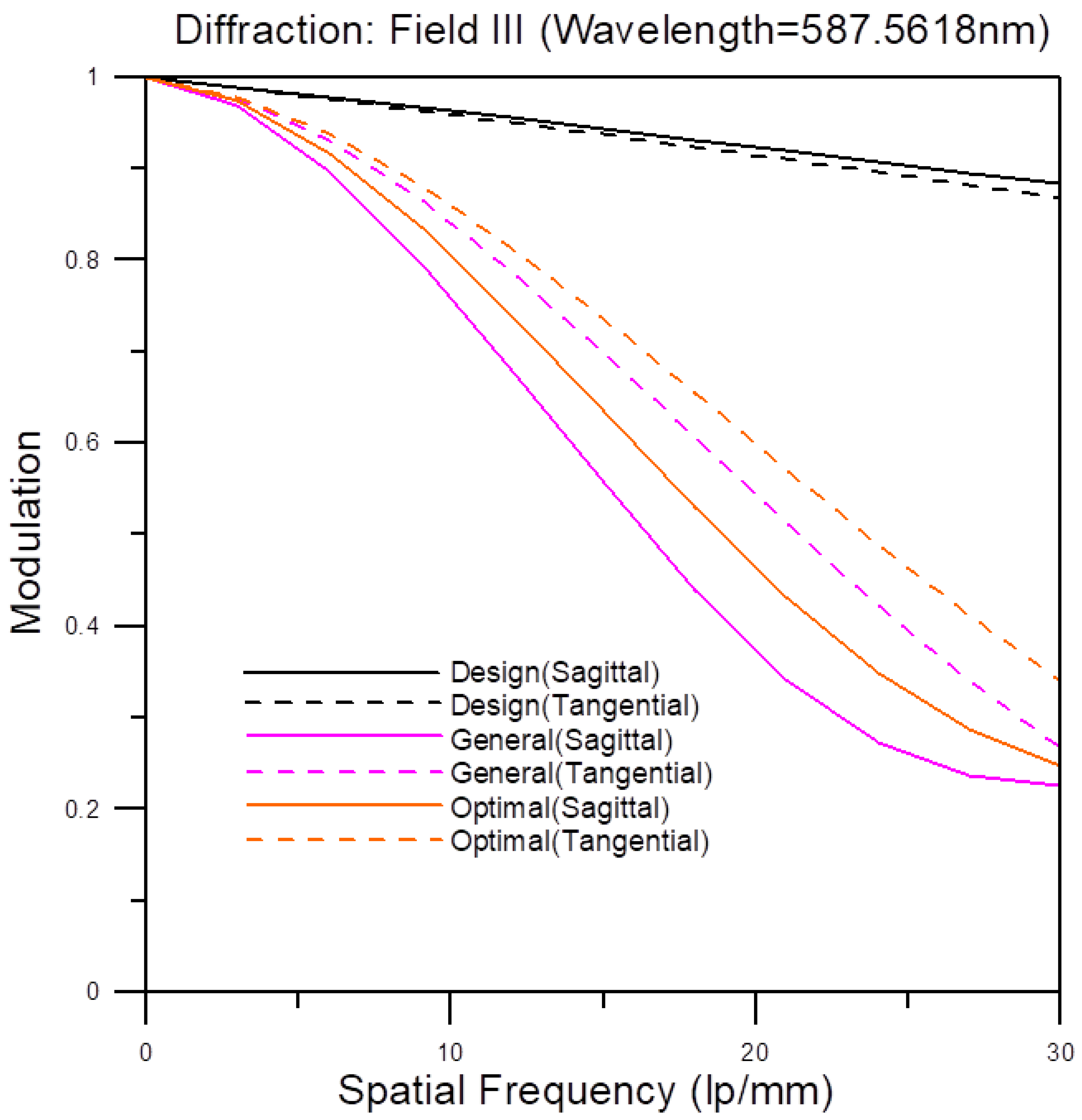
3.3. Optical Performance
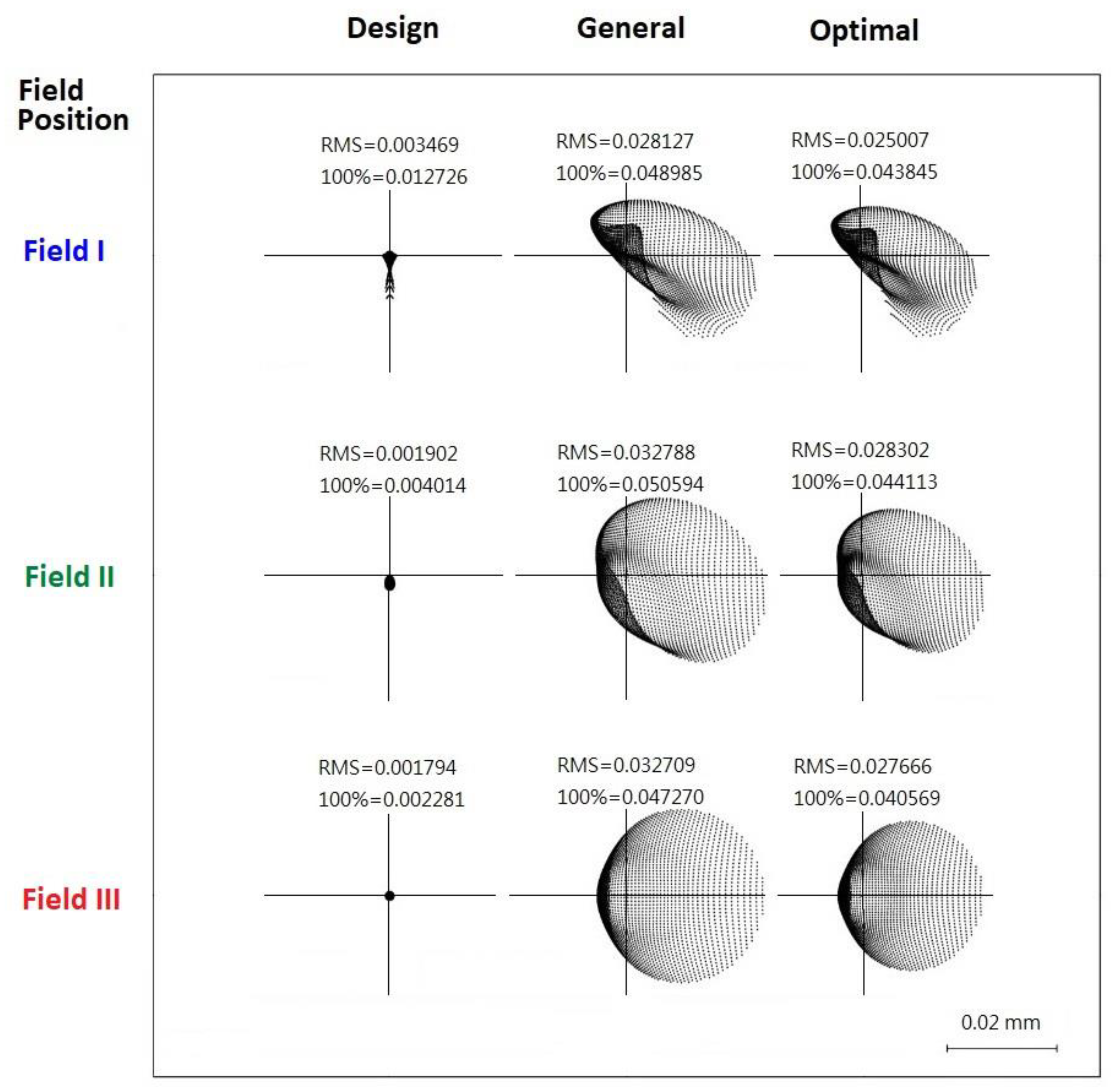
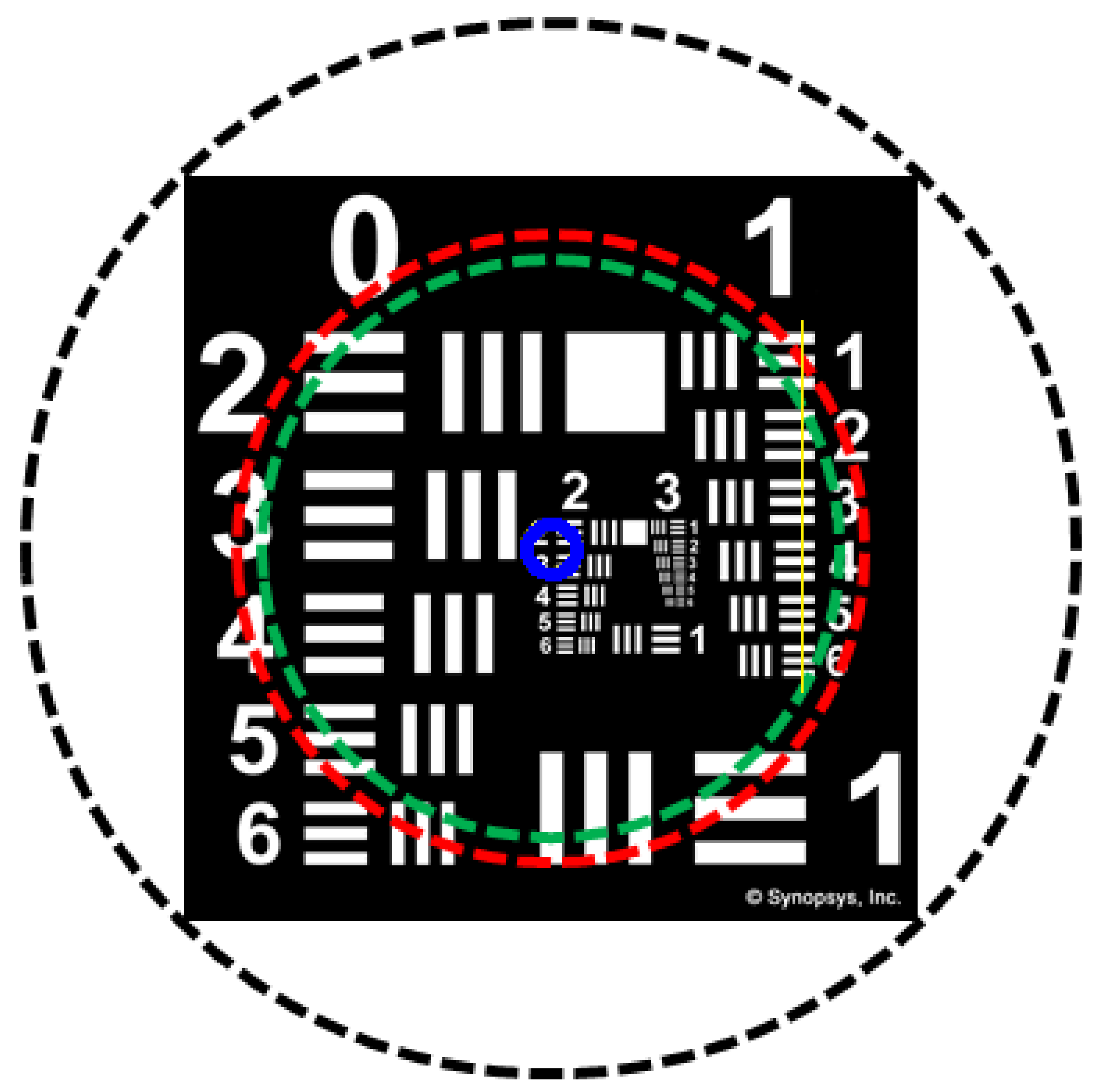
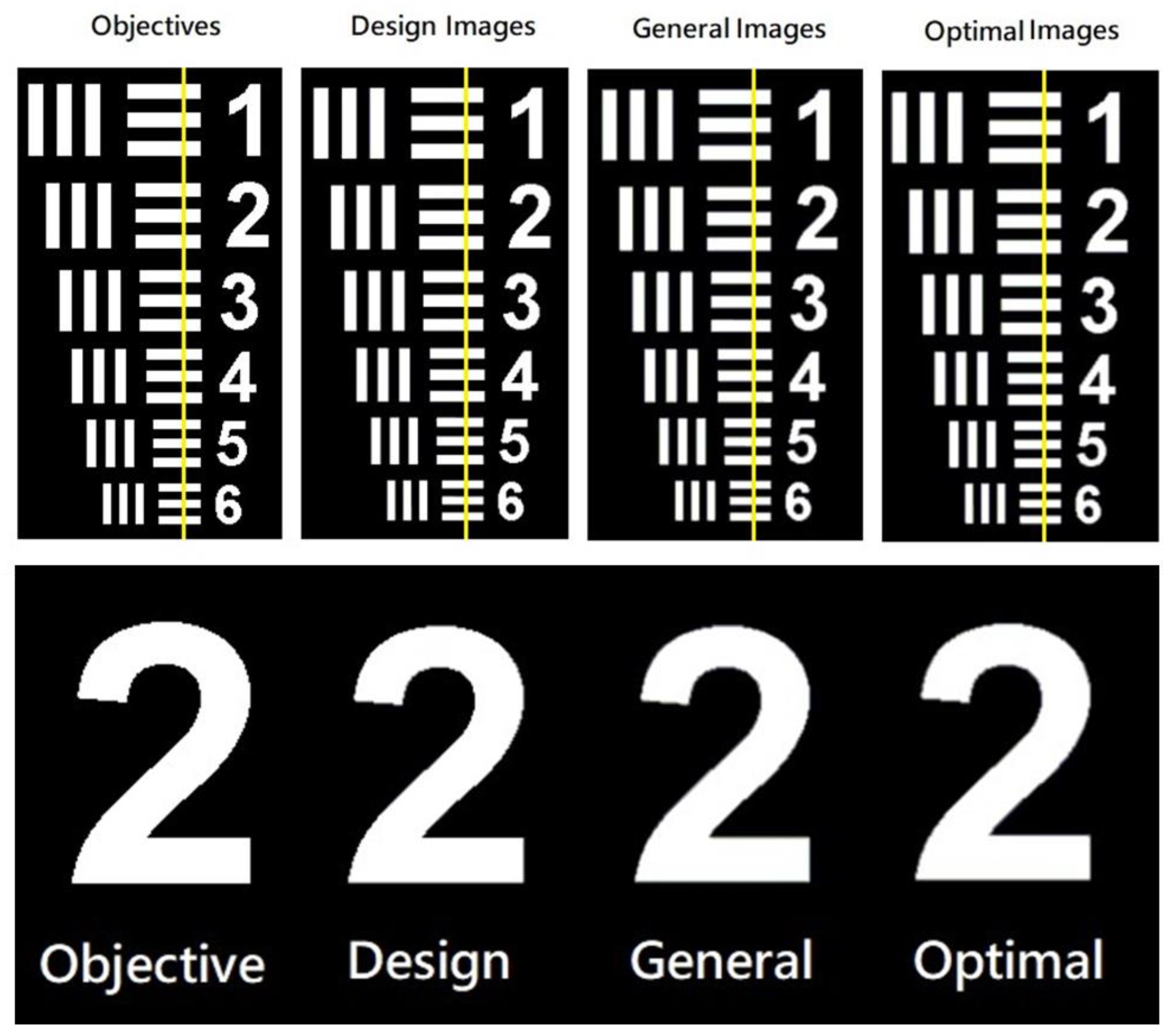
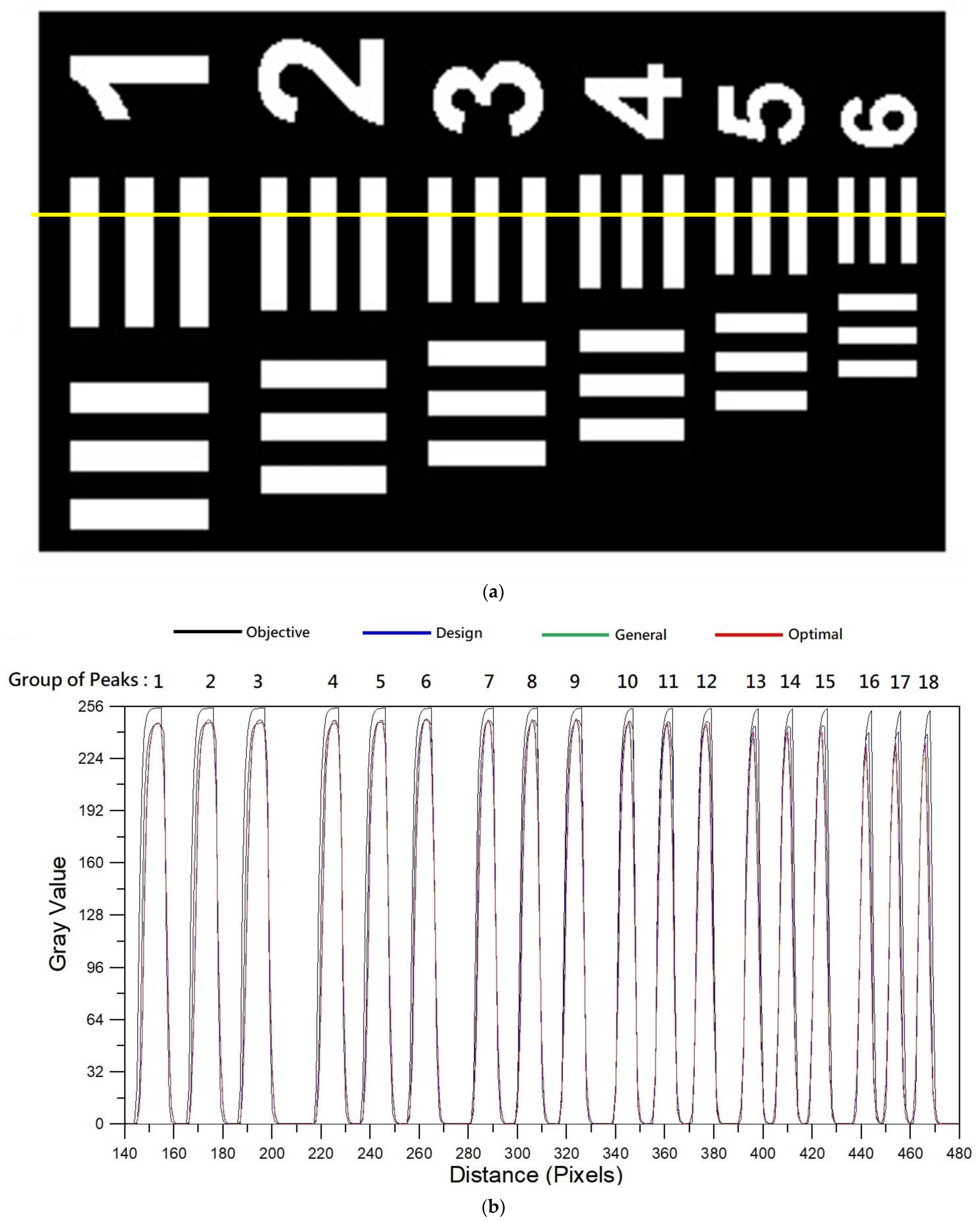
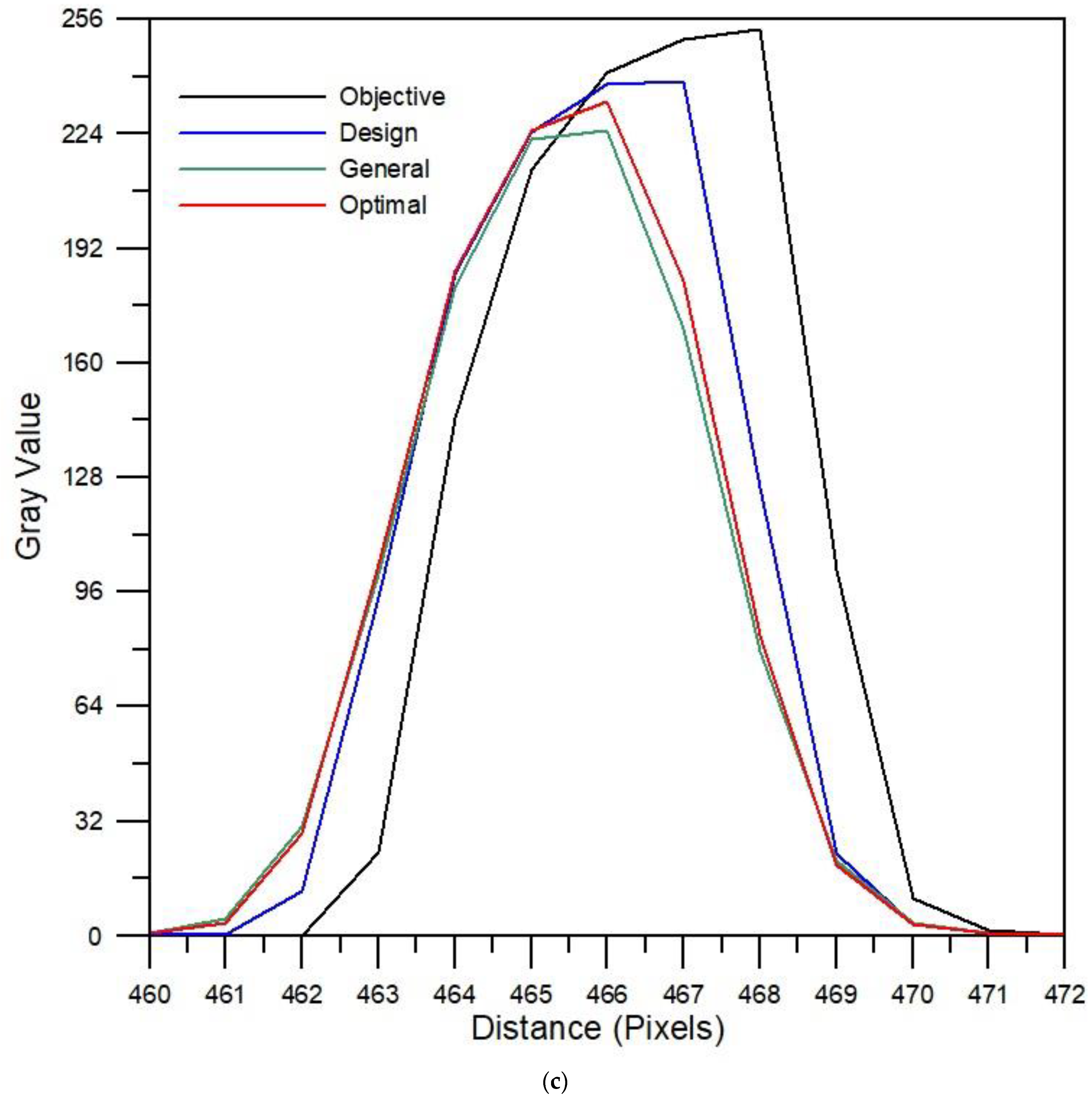
3.4. D Imaging Simulation: Grayscale Analysis of Imaging Quality
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Lin, C.M.; Tan, C.M.; Wang, C.K. Gate design optimization in the injection molding of the optical lens. Optoelectron. Adv. Mater. Rapid Commun. 2013, 7, 580–584. [Google Scholar]
- Lin, C.M.; Hsieh, H.K. Processing optimization of Fresnel lenses manufacturing in the injection molding considering birefringence effect. Microsyst. Technol. 2017, 23, 5689–5695. [Google Scholar] [CrossRef]
- Lin, C.M.; Chen, Y.W. Grey optimization of injection molding processing of plastic optical lens based on joint consideration of aberration and birefringence effects. Microsyst. Technol. 2019, 25, 621–631. [Google Scholar] [CrossRef]
- Lu, X.; Khim, L.S. A statistical experimental study of the injection molding of optical lenses. J. Mater. Process. Technol. 2001, 113, 189. [Google Scholar] [CrossRef]
- Lee, Y.B.; Kwon, T.H.; Yoon, K. Numerical prediction of residual stresses and birefringence in injection/compression molded center-gated disk. Part I: Basic modeling and results for injection molding. Polym. Eng. Sci. 2002, 42, 2246–2272. [Google Scholar] [CrossRef]
- Shyu, G.D.; Isayyev, A.I.; Lee, H.S. Numerical simulation of flow-induced birefringence in injection molded disk. Jpn. Korea Plast Process Jt. Semin. 2003, 4, 41–47. [Google Scholar]
- Fan, B.; Kazmer, D.O.; Bushko, W.C.; Theriault, R.P.; Poslinski, A.J. Birefringence prediction of optical media. Polym. Eng. Sci. 2004, 44, 814–824. [Google Scholar] [CrossRef]
- Liao, S.J.; Chang, D.Y.; Chen, H.J.; Tsou, L.S.; Ho, J.R.; Yau, H.T.; Hsieh, W.H.; Wang, J.T.; Su, Y.C. Optimal process conditions of shrinkage and warpage of thin-wall parts. Polym. Eng. Sci. 2004, 44, 917–928. [Google Scholar] [CrossRef]
- Tang, S.H.; Tan, Y.J.; Sapuan, S.M.; Sulaiman, S.; Ismail, N.; Samin, R. The use of Taguchi method in the design of plastic injection mould for reducing warpage. J. Mater. Process. Technol. 2007, 182, 418–426. [Google Scholar] [CrossRef]
- Bociaga, E.; Jaruga, T.; Lubczynska, K.; Gnatowski, A. Warpage of injection moulded parts as the result of mould temperature difference. Arch. Mat. Sci. Eng. 2010, 44, 28–34. [Google Scholar]
- Shayfull, Z.; Ghazali, M.F.; Azaman, M.; Nasir, S.M.; Faris, N.A. Effect of differences core and cavity temperature on injection molded part and reducing the warpage by Taguchi method. Int. J. Eng. Technol. 2010, 10, 125–132. [Google Scholar]
- Fischer, R.E.; Tadic-Galeb, B.; Yoder, P.R. Optical System Design, 2nd ed.; McGraw-Hill: New York, NY, USA, 2008; pp. 179–198. [Google Scholar]
- Dilworth, D.C. New tools for the lens designer, Current Developments in Lens Design and Optical Engineering IX. Int. Soc. Opt. Photonics 2008, 7060, 70600B. [Google Scholar]
- Sahin, F.E. Lens design for active alignment of mobile phone cameras. Opt. Eng. 2017, 56, 065102. [Google Scholar] [CrossRef]
- Grabarnik, S. Optical design method for minimization of ghost stray light intensity. Appl. Opt. 2015, 54, 3083–3089. [Google Scholar] [CrossRef]
- Sahin, F.E. Open-source optimization algorithms for optical design. Optik 2019, 178, 1016–1022. [Google Scholar] [CrossRef]
- Houllier, T.; Lépine, T. Comparing optimization algorithms for conventional and freeform optical design: Erratum. Opt. Express 2019, 27, 28383. [Google Scholar] [CrossRef]
- Lin, C.M.; Chen, Y.J. Taguchi Optimization of Roundness and Concentricity of a Plastic Injection Molded Barrel of a Telecentric Lens. Polymers 2021, 13, 3419. [Google Scholar] [CrossRef]
- Sui, W.; Zhang, D. Four Methods for Roundness Evaluation. Phys. Procedia 2012, 24, 2159–2164. [Google Scholar] [CrossRef] [Green Version]
- Ahn, S.J. Least Squares Orthogonal Distance Fitting of Curves and Surfaces in Space; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Srinivasan, V.; Shakarji, C.M.; Morse, E.P. On the enduring appeal of least-squares fitting in computational coordinate metrology. J. Comput. Inf. Sci. Eng. 2011, 12, 011008. [Google Scholar] [CrossRef]
- Kim, N.H.; Kim, S.W. Geometrical tolerances: Improved linear approximation of least-squares evaluation of circularity by minimum variance International. J. Mach. Tools Manuf. 1996, 36, 355–366. [Google Scholar] [CrossRef]
- Hichem, N.; Pierre, B. Evaluation of roundness error using a new method based on a small displacement screw. Meas. Sci. Technol. 2014, 25, 25. [Google Scholar]
- O’Shea, D.C.; Bentley, J.L. Designing Optics Using CODE V; SPIE PRESS: Bellingham, WA, USA, 2018. [Google Scholar]
- MIL-STD-150A; Military Standard: Photographic Lenses. EverySpec LLC: Gibsonia, PA, USA, 12 May 1959.

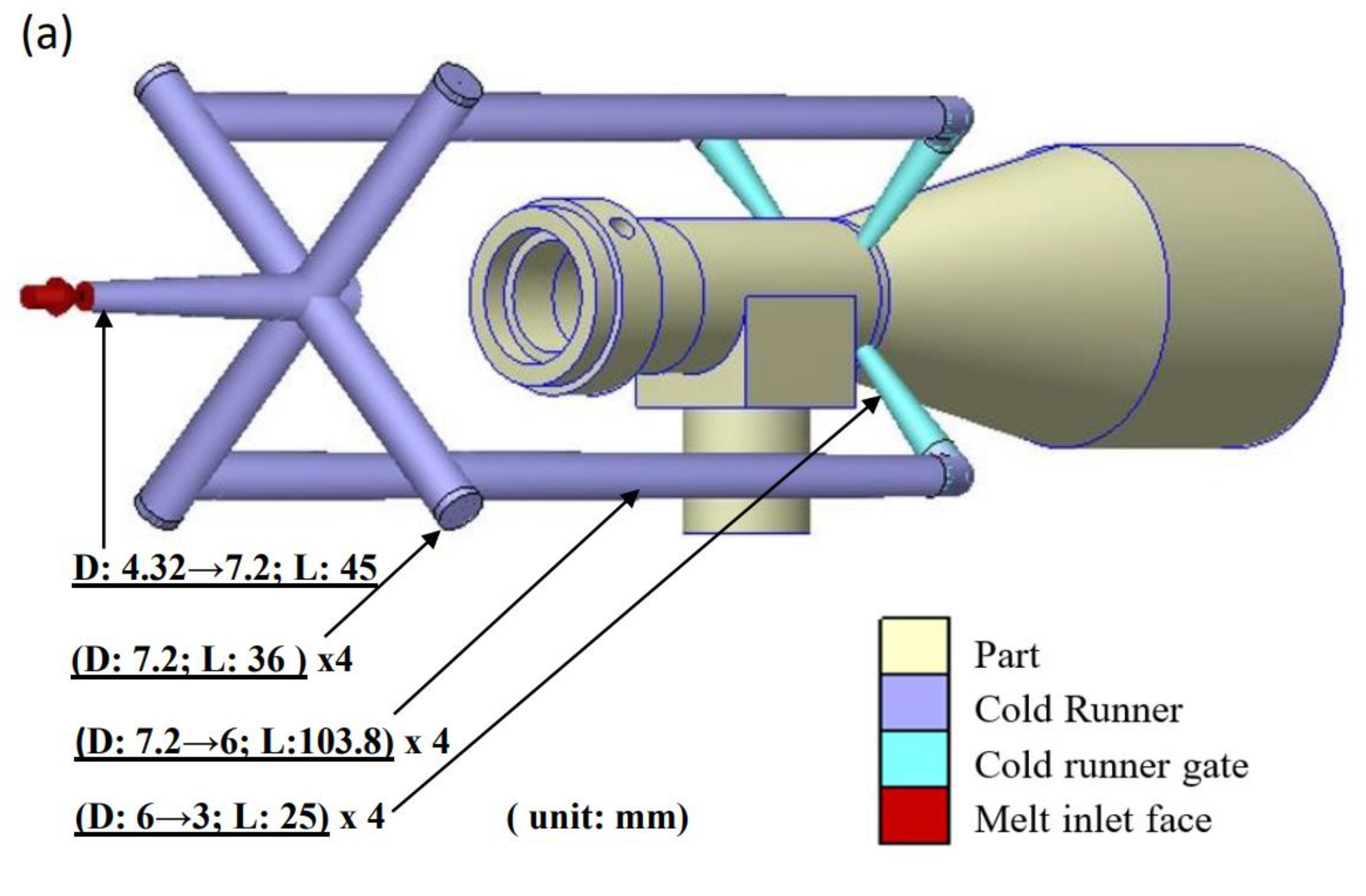
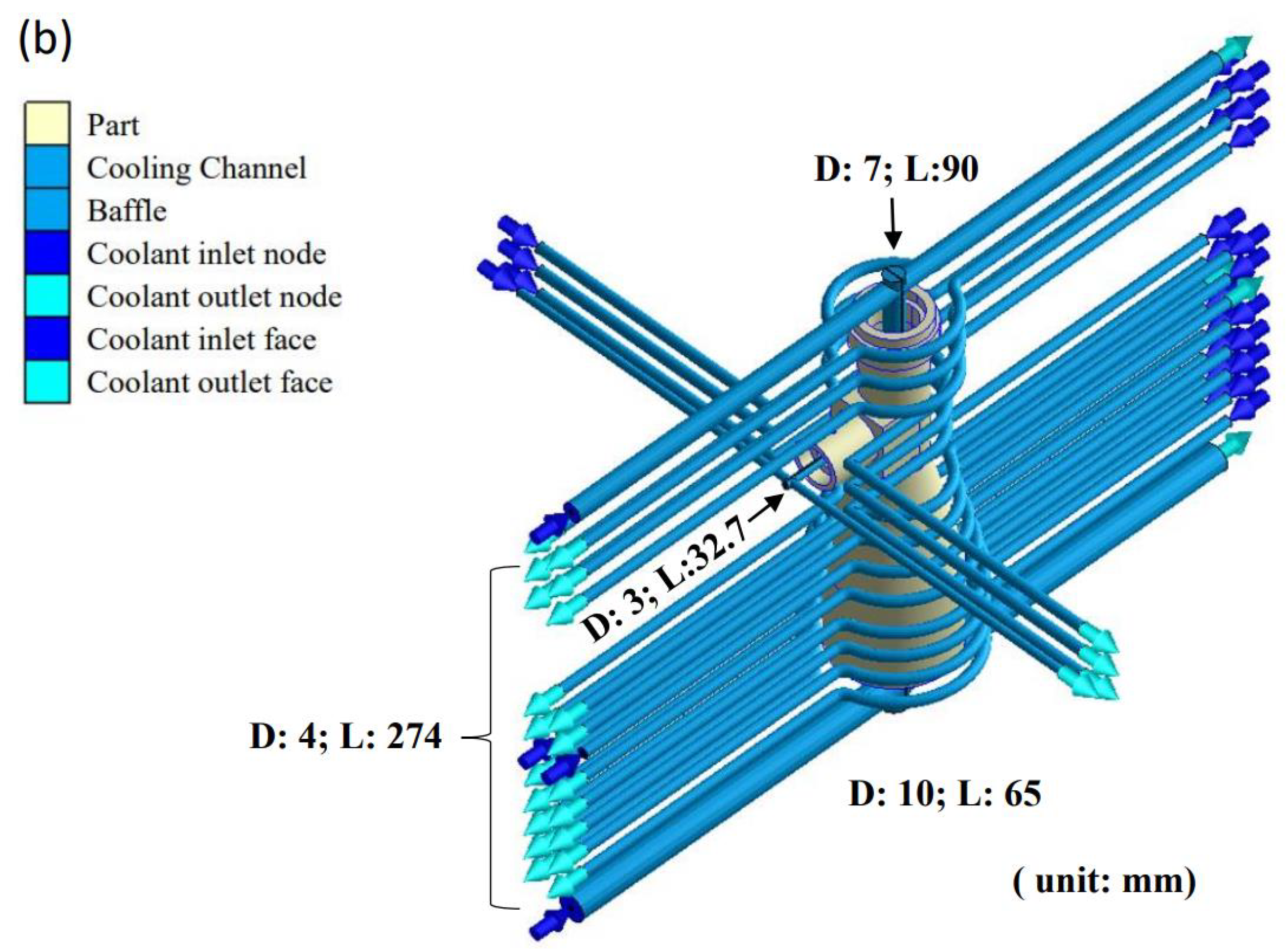







| Material Properties | Values | Unit |
| Density | 1140 | Kg/m3 |
| Specific heat | 2 × 10−11 | J/Kg. °C |
| Heat conduction coefficient | 0.25 | J/s.m. °C |
| Mold shrinkage | 1.90 | % |
| Tensile modulus | 3000 | MPa |
| Melt temperature | 263 | °C |
| Coefficient of linear thermal expansion (23–85 °C) | 7 × 10−5 | °C |
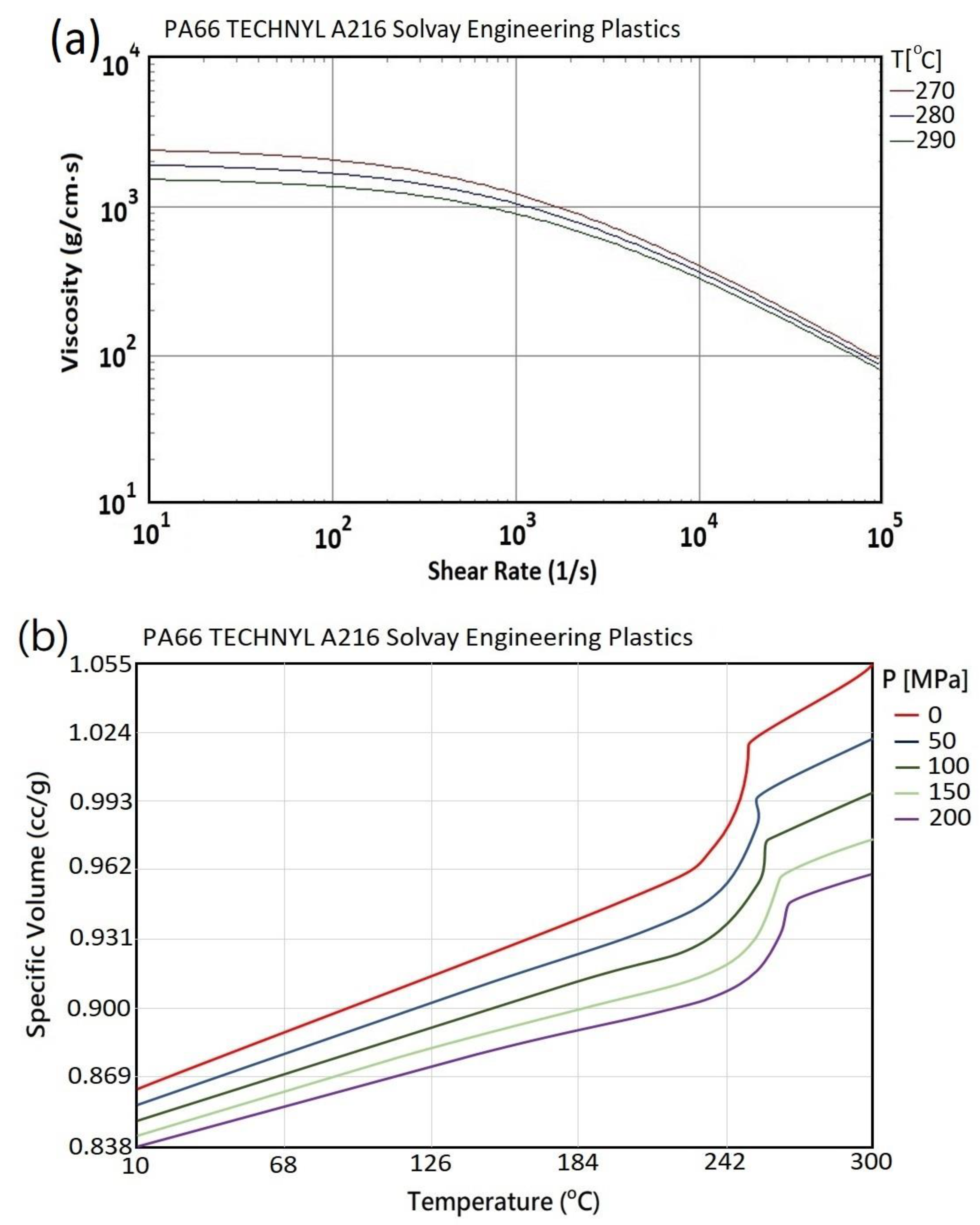
| Viscosity vs. shear rate under different temperatures | shown in Figure 3a | |
| P-v-T | shown in Figure 3b | |
| Processing Conditions in Injection Molding (Recommended) | Values | Unit |
| Maximum injection pressure | 180–240 | MPa |
| Maximum packaging pressure | 180–240 | MPa |
| Melt temperature | 270–290 | °C |
| Mold temperature | 60–100 | °C |
| Cooling time | 11–17 | s |
| Ejection temperature | 190 | °C |
| Curing temperature | 210 | °C |
| Lens No. | Glass/SCHOTT | Curvature Radius (mm) | Thickness (mm) | Refractive Index (-) | Abbe Value (-) | Partial Dispersion (-) | Dispersion (NL-N1) (-) |
|---|---|---|---|---|---|---|---|
| Len 1 | NLAK33A | 109.2083 | 5.0065 | 1.75393 | 52.271 | 0.30323 | 0.01442 |
| −786.0770 | |||||||
| Len 2 | NLAK33B | 38.8283 | 5.0044 | 1.75500 | 52.300 | 0.30321 | 0.01444 |
| 137.9732 | |||||||
| Len 3 | FK5HTI | −67.9914 | 18.1944 | 1.48748 | 70.470 | 0.30977 | 0.00692 |
| 15.3674 | |||||||
| Len 4 | LAFN7 | 427.9534 | 17.2165 | 1.74950 | 34.951 | 0.29414 | 0.02144 |
| −33.0637 |
| Trials | Processing Factors | ||||
|---|---|---|---|---|---|
| A Maximum Injection Pressure (MPa) | B Maximum Packing Pressure (MPa) | C Melt Temperature (°C) | D Mold Temperature (°C) | E Cooling Time (s) | |
| General Parameters | 200 | 200 | 280 | 80 | 13 |
| 1 | 180 | 180 | 275 | 70 | 11 |
| 2 | 180 | 200 | 280 | 80 | 13 |
| 3 | 180 | 220 | 285 | 90 | 15 |
| 4 | 180 | 240 | 290 | 100 | 17 |
| 5 | 200 | 180 | 280 | 90 | 17 |
| 6 | 200 | 200 | 275 | 100 | 15 |
| 7 | 200 | 220 | 290 | 70 | 13 |
| 8 | 200 | 240 | 285 | 80 | 11 |
| 9 | 220 | 180 | 285 | 100 | 13 |
| 10 | 220 | 200 | 290 | 90 | 11 |
| 11 | 220 | 220 | 275 | 80 | 17 |
| 12 | 220 | 240 | 280 | 70 | 15 |
| 13 | 240 | 180 | 290 | 80 | 15 |
| 14 | 240 | 200 | 285 | 70 | 17 |
| 15 | 240 | 220 | 280 | 100 | 11 |
| 16 | 240 | 240 | 275 | 90 | 13 |
| Optimal Parameters | 220 | 240 | 275 | 90 | 17 |
| Factor | Control Factors | |||||
|---|---|---|---|---|---|---|
| Level/ Range/Rank | A | B | C | D | E | |
| Level 1 (dB) | 18.42426 | 17.93074 | 18.64934 | 18.4332 | 18.38978 | |
| Level 2 (dB) | 18.44004 | 18.29598 | 18.51562 | 18.45852 | 18.36406 | |
| Level 3 (dB) | 18.4714 | 18.63066 | 18.3822 | 18.45247 | 18.44444 | |
| Level 4 (dB) | 18.4491 | 18.92741 | 18.23765 | 18.44061 | 18.58652 | |
| S/N Range (dB) | 0.047142 | 0.996663 | 0.41169 | 0.025322 | 0.22246 | |
| Influence Rank | 4 | 1 | 2 | 5 | 3 | |
| General Design | Optimal Design | |
|---|---|---|
| Filling | ||
| Filling time (s) | 2.13 | 2.13 |
| Melt temperature (°C) | 280 | 275 |
| Mold temperature (°C) | 80 | 90 |
| Maximum injection pressure (MPa) | 200 | 220 |
| Injection volume (cm3) | 68.1 | 68.1 |
| Packing | ||
| Packing time (s) | 7 | 7 |
| Maximum packing pressure (MPa) | 200 | 240 |
| Cooling | ||
| Cooling time (s) | 13 | 17 |
| Mold-open time (s) | 5 | 5 |
| Eject temperature (°C) | 190 | 190 |
| Air temperature (°C) | 25 | 25 |
| Miscellaneous | ||
| Cycle time (s) | 27.13 | 27.13 |
| Unit: mm | Design | General | Optimal |
|---|---|---|---|
| Planes | |||
| Z1 = 0 | (0, 0, 0) 0 | Z1(0.173964, −0.000240496, 0.937954) d1 = 0.173964166 | Z1(0.152848, −0.000185194, 0.728356) d1 = 0.152848112 |
| Z2 = 57.75 | (0, 0, 0) 0 | Z2(−0.00609915, −0.000210664, 0.162) d2 = 0.006102787 | Z2(−0.0169768, −0.000159105, 0.1405) d2 = 0.016977546 |
| Z3 = 82.3 | (0, 0, 0) 0 | Z3(−0.0546394, −0.00013, −0.1749) d3 = 0.0546394 | Z3(−0.0581023, −0.0000981, −0.127) d3 = 0.058102383 |
| Z4 = 117.7 | (0, 0, 0) 0 | Z4(0.161799, −0.000609249, −0.662) d4 = 0.1618 | Z4(0.140132, −0.000555817, −0.52) d4 = 0.140133102 |
| Coaxiality | 0 | 0.014866 | 0.011666 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-M.; Chen, Y.-J. Coaxiality Optimization Analysis of Plastic Injection Molded Barrel of Bilateral Telecentric Lens. Symmetry 2022, 14, 200. https://doi.org/10.3390/sym14020200
Lin C-M, Chen Y-J. Coaxiality Optimization Analysis of Plastic Injection Molded Barrel of Bilateral Telecentric Lens. Symmetry. 2022; 14(2):200. https://doi.org/10.3390/sym14020200
Chicago/Turabian StyleLin, Chao-Ming, and Yun-Ju Chen. 2022. "Coaxiality Optimization Analysis of Plastic Injection Molded Barrel of Bilateral Telecentric Lens" Symmetry 14, no. 2: 200. https://doi.org/10.3390/sym14020200
APA StyleLin, C.-M., & Chen, Y.-J. (2022). Coaxiality Optimization Analysis of Plastic Injection Molded Barrel of Bilateral Telecentric Lens. Symmetry, 14(2), 200. https://doi.org/10.3390/sym14020200







