Convective Heat Transfer of a Pseudoplastic Nanosuspension within a Chamber with Two Heated Wall Sections of Various Heat Fluxes

Abstract

Cooling of heat-generating elements in different engineering fields is a very important and crucial topic. The present research is devoted to numerical analysis of thermogravitational convection of a pseudoplastic nanosuspension in a chamber with two heated bottom wall sections of various heat fluxes and isothermally cooling vertical walls. A mathematical model formulated employing the time-dependent Oberbeck–Boussinesq equations with non-primitive variables has been worked out by the finite difference technique. It has been revealed that a mixture of 1% carboxymethylcellulose with water can be the most effective medium to cool the heat-generating elements. At the same time, aluminum oxide nano-sized solid particles have a more essential cooling impact on the heated sections.

1. Introduction

The use of liquids in various mechanical and industrial tools, as well as in heat exchangers, is common. The most popular working media are air, water, ethylene glycol and engine oil, which have very low heat conductivity. However, in order to save energy and costs, it is necessary to use media with higher thermal characteristics. As a result, many studies, theoretical and practical experiments have been carried out aimed at increasing the thermal conductivity of working fluids. One of the ways to solve the problem was the addition of millimeter- and micrometer-sized particles. However, this approach showed many disadvantages, such as a high pressure drop, erosion of details, and settling of particles. All these difficulties led Choi [1] to pioneer the study of nanometer-sized particles in base fluids and achieve improved thermal performance. Such liquids became known as nanofluids and they consist of a base medium and nanoadditives, which are metal or metal oxide particles, single-walled or multi-walled carbon nanotubes. Hybrid nanofluids, which use two types of nanoparticles, have also become widespread. The obtained improved working media are used in many technical applications, including cooling equipment, nuclear reactors, imaging and sensing, drug delivery, fuel cells, and microchips [2,3,4,5].

Many authors have devoted their research to studying the properties of liquids with nanoparticles. For example, Akhter et al. [6] have studied the convective energy transport of a Cu-Al₂O₃/water hybrid nanosuspension inside a porous cavity, on the walls of which there are heated and cooling sections. A heat-conducting cylinder is placed in the center of the chamber. The outcomes have demonstrated that an increase in the Rayleigh number and the Darcy number intensifies the convective flow. The work of Ibrahim et al. [7] deals with the study of natural convective heat transfer of Al₂O₃/water nanoliquid in a square chamber inclined by 45°. On the lower wall, there are two semicircular isothermal heat sources, and the upper wall is cold. During the study, it has been found that an increase in Ra from 10³ to 10⁶ increases the energy transport rate by almost six times. Additionally, a square cavity has been used for analysis by Al-Farhany et al. [8]. The convective flow has been formed due to the temperature difference of the side walls, while the right wall is characterized by a variable heat generation. A vertical partition is located on the bottom border of the cavity. Using numerical simulations, it has been revealed that an increase in Ra and a baffle length L_b = 0.3 provide better heat transfer characteristics. Al-Maliki et al. [9] has performed research on experimental analysis of the hybrid nanofluid natural convection in a rectangular differentially heated cavity. A special feature is the presence of a partition filled with a phase change material. The results have shown that an increase in the concentration of nanoparticles enhances convective heat exchange. The influence of the magnetic field and temperature gradient on the natural convection of a hybrid nanofluid in a square cavity is estimated by Ghali et al. [10]. This case had two sections of the wall with different temperatures and a porous insert. The authors have found that an increase in the Rayleigh number and the volume fraction of nanoparticles enhances heat transfer inside the cavity. A numerical study of MHD natural convection of a hybrid H₂O/Ag-MgO nanosuspension in a triangular porous cavity has been carried out by Redouane et al. [11]. The cathetuses are maintained at a high temperature, and the hypotenuse has a wavy shape and is maintained at a low temperature. A rotating cylinder is inside the cavity. Modeling has shown that the strength of energy transfer can be enhanced by increasing the size of the solid particles.

Comparison of the efficiency of using a CuO/H₂O nanofluid and water in the process of natural convective heat exchange in a vacuum tube solar collector has been carried out by Tabarhoseini and Sheikholeslami [12]. The authors have found that when using a nanofluid, the heat transfer coefficient is higher than when using water. Additionally, the solar collector has been studied analytically by Panda et al. [13], where a CuO/H₂O nanosuspension has also been used as a working medium. The authors have evaluated the effects of the Grashof number and the nanoparticle concentration, resulting in a strengthening of convective heat transfer with an increase in these parameters. A combination of active (electric field) and passive (adding carbon nanotube nanoparticles) approaches to enhance heat transfer in a dielectric oil filling a concentric cavity has been evaluated by Rejeb et al. [14]. The inner cylinder is hot and the outer one is cold. The results have shown that the application of an electric field can improve heat transfer by up to 3% to 77%, and the addition of 0.5% volume fraction of carbon nanotubes provides an improvement in heat transfer of approximately 27%. A numerical study of MHD nanofluid convection in a channel immersed in a porous medium has been carried out by Khan and Alqahtani [15]. The channel walls have different temperatures and are permeable. The authors have revealed a significant influence of the volume fraction of nanoparticles on both velocity profiles and temperature patterns. Nabwey et al. [16] have studied the MHD convection of a Cu/H₂O nanosuspension in a tilted U-shaped chamber, where a source of fixed volumetric energy production has been located on the bottom border. In the course of the study, an increase in the mean Nu has been obtained with an increment of nanoparticle concentration, as well as when the source moved towards the right boundary of the cavity. A comparison of the thermal characteristics of two nanofluids, γAl₂O₃-C₂H₆O₂ and γAl₂O₃-H₂O, has been carried out by Asifa et al. [17]. Liquids are filled in the differentially heated channel and the flow occurs due to natural convection. The analysis has shown that a mixture of water and γAl₂O₃ nanoparticles improves heat transfer more efficiently than dispersion of γAl₂O₃ in ethylene glycol.

Algehyne et al. [18] have also compared a hybrid and a trihybrid nanofluid with a pseudoplastic base medium in the problem of convective energy transport over a heated stretching plate under the magnetic field impact. The main conclusion is that the thermal conductivity of the base fluid rises with the addition of hybrid and trihybrid nanocomposites to 32% and 61%, respectively. Rahman et al. [19] have investigated the thermal convection of a micropolar non-Newtonian hybrid nanofluid, MWCNT-Fe₃O₄/water, in an inclined ⊥-shaped cavity. A semicircular source of constant temperature has been placed on the bottom boundary. The authors have found that an increase in the microrotation parameter, the chamber inclination angle and the Hartmann parameter leads to a decrease in the mean Nu. Additionally, a ⊥-shaped porous cavity has been studied by Abderrahmane et al. [20], where the natural convective flow of a nano-enhanced phase change material has been simulated. The lower wall of the cavity is trapezoidal and it has been maintained at a constant high temperature. Modeling has shown that convective heat transfer can be increased with increasing Rayleigh and Darcy numbers. The work of Reddy and Panda [21] is devoted to the MHD natural convection of a non-Newtonian nanofluid in a trapezoidal chamber, and the lower boundary of this region has a wavy shape and it is maintained at a high temperature. The side walls are cooled down. The authors have ascertained that the energy transport rate augments significantly with increasing Hartmann number. Thermal and hydrodynamic characteristics of non-Newtonian nanofluid have been studied by Ganesh et al. [22]. The cavity is a square shell with wavy horizontal boundaries, the lower of which is partially heated and a cylindrical partition is placed within the chamber. The boundary conditions of the insert have been changed between thermal insulation, heating, and cooling effects. As a result, regardless of the type of obstacle, the intensification of convective heat transfer can be achieved with an increase in the Casson parameter, Rayleigh number, nanoadditive concentration, and the radiation parameter. The convective flow of a nanoencapsulated material with a phase transition inside a porous differentially heated cavity with a wavy top wall has been studied by Hussain et al. [23]. The performed simulations have shown that an increase in the Darcy and Rayleigh numbers intensifies the convective heat transfer within the cavity. Additionally, Hussain et al. [24,25,26] have conducted a detailed study on the bioconvection of oxytactic microorganisms with nanoencapsulated materials with a phase transition in porous cavities of various shapes. The authors have found that an increase in the Darcy number improves the oxygen isoconcentration and the isoconcentration of microorganisms.

The performed analysis of published studies has shown that the chosen topic has a high popularity due to huge practical application and fundamental interest. However, there is still much to be learned to fill in the gaps. That is why the purpose of this study is to simulate the transient regimes of thermogravitational transport of a pseudoplastic nanosuspension in a closed chamber with two heated sections of the bottom wall.

2. Formulation of the Problem

In this paper, a study of the pseudoplastic nanofluid natural convective heat transfer in a closed chamber with two thermally generating sections of the bottom wall has been performed. The convective flow is unsteady and laminar. The cavity is a square with a characteristic size of L. The horizontal boundaries are completely thermally insulated, while the vertical ones are maintained at a minimum temperature T_c. Gravity force is directed vertically down. The geometry of the analyzed region is presented in Figure 1. It is supposed that viscous dissipation and thermal radiation are neglected due to weak convective flow within the chamber and non-diathermal nature of the working liquid, where thermal radiation has a weak influence on the total heat transfer rate. Moreover, the single-phase nanofluid model and local thermal equilibrium approach are used for mathematical description of the considered phenomenon.

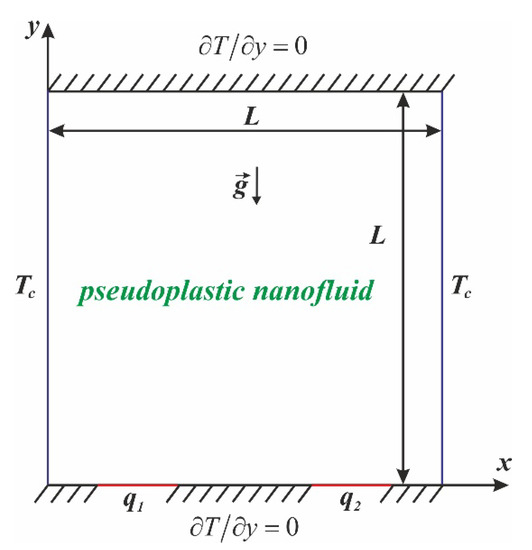
Figure 1. Geometry of the analyzed domain.

A nanofluid is used as a working medium, the base fluid of which is a mixture of 0.1% carboxymethylcellulose (CMC) with water. The following materials are employed for nanoadditives: Cu, Al₂O₃, CuO, and TiO₂. All properties of the materials used are presented in Table 1 [27].

Table 1. Thermal characteristics of materials.

Properties	cp, J·kg−1·K−1	ρ, kg·m−3	k, W·m−1·K−1
CMC/water (0.0–0.3%)	4179	997.1	0.613
Cu	385	8933	400
Al2O3	765	3970	40
CuO	535.6	6500	20
TiO2	686.2	4250	8.9538

The resulting suspension of the base medium and nanoparticles is a pseudoplastic liquid that satisfies the Boussinesq approximation. Such substances are effective in cooling tasks, as they have a viscosity that reduces with an increase in the strain rate. The pseudoplastic nature of the fluid flow is described by the Ostwald–de Waele power law [28]:

$${\mathsf{\tau }}_{ij}=2{\mathsf{\mu }}_{nf}{D}_{ij}$$

(1)

Here, τ_ij is the deviatoric portion of the stress tensor, $D_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$ are the components of the strain rate tensor, and u_i, u_j are the velocity vector components; μ_nf is the effective coefficient of viscosity of the nanosuspension, which has been calculated using the experimental Corcione correlation [29]:

$${\mathsf{\mu }}_{nf}=\frac{{\mathsf{\mu }}_{bf}}{1-34.87{\left(d_p/d_{bf}\right)}^{-0.3}{\mathsf{\varphi }}^{1.03}}$$

(2)

The viscosity of the host liquid taking into account the Ostwald–de Waele law is defined by the following relationship: ${\mathsf{\mu }}_{bf}=K{\left(2D_{kl}{D}_{kl}\right)}^{\frac{n-1}{2}}$, where K is the consistency and n is an indicator of liquid nature. Considering that the fluid behavior index is n < 1, we can conclude that the medium has pseudoplastic rheology. Table 2 presents the variants of the fluid behavior indicator that will be considered in this work [27].

Table 2. Host liquid rheology characteristics.

Properties	n	K/Nsn, M−2	Pr
CMC/water (0.0%)	1	0.000855	5.85
CMC/water (0.1%)	0.91	0.006319	26.8
CMC/water (0.2%)	0.85	0.017540	299.05
CMC/water (0.3%)	0.81	0.0313603	669.87

The nanosuspension heat conductivity is also defined using the experimental data [29]

$$k_{nf}=\left(1+4.4R{e}^{0.4}P{r}^{0.66}{\left(\frac{T}{T_{fr}}\right)}^{10}{\left(\frac{k_p}{k_{bf}}\right)}^{0.03}{\mathsf{\varphi }}^{0.66}\right)\cdot k_{bf}$$

(3)

The flow structure and energy transport of the liquid in the chamber are defined employing a single-phase approach with effective properties and primitive variables [30,31,32]:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(4)

$${\mathsf{\rho }}_{nf}\left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)=-\frac{\partial p}{\partial x}+\frac{\partial {\mathsf{\tau }}_{xx}}{\partial x}+\frac{\partial {\mathsf{\tau }}_{xy}}{\partial x}$$

(5)

$${\mathsf{\rho }}_{nf}\left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=-\frac{\partial p}{\partial y}+\frac{\partial {\mathsf{\tau }}_{xy}}{\partial x}+\frac{\partial {\mathsf{\tau }}_{yy}}{\partial y}+g{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{nf}\left(T-T_c\right)$$

(6)

$${\left(\mathsf{\rho }c\right)}_{nf}\left(\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=\frac{\partial }{\partial x}\left(k_{nf}\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k_{nf}\frac{\partial T}{\partial y}\right)$$

(7)

The correlations for nanosuspension properties are [33,34]

$$\begin{array}{l}{\mathsf{\rho }}_{nf}={\mathsf{\rho }}_{bf}\left(1-\mathsf{\varphi }\right)+{\mathsf{\rho }}_p\mathsf{\varphi },\\ {\left(\mathsf{\rho }\mathsf{\beta }\right)}_{nf}={\left(\mathsf{\rho }\mathsf{\beta }\right)}_{bf}\left(1-\mathsf{\varphi }\right)+{\left(\mathsf{\rho }\mathsf{\beta }\right)}_p\mathsf{\varphi },\\ {\left(\mathsf{\rho }c\right)}_{nf}={\left(\mathsf{\rho }c\right)}_{bf}\left(1-\mathsf{\varphi }\right)+{\left(\mathsf{\rho }c\right)}_p\mathsf{\varphi }.\end{array}$$

(8)

To reduce the mathematical difficulties, the stream function ψ $\left(u=\partial \mathsf{\psi }/\partial y,v=-\partial \mathsf{\psi }/\partial x\right)$ and vorticity ω $\left(\mathsf{\omega }=\partial v/\partial x-\partial u/\partial y\right)$, as well as reference parameters presented in Table 3 [32], are introduced into Equations (4)–(7). L is chosen as the length scale; $\mathsf{\Delta }T=qL/k_{bf}$ is used for the temperature difference.

Table 3. Reference parameters.

Parameters	Formula
Velocity	$\sqrt{g\mathsf{\beta }L\mathsf{\Delta }T}$
Time	$\sqrt{L/\left(g\mathsf{\beta }\mathsf{\Delta }T\right)}$
Stream function	$\sqrt{g\mathsf{\beta }{L}^3\mathsf{\Delta }T}$
Vorticity	$\sqrt{g\mathsf{\beta }\mathsf{\Delta }T/L}$
Temperature	$\mathsf{\Theta }=\left(T-T_c\right)/\mathsf{\Delta }T$

As a result of this mentioned transformation, we have obtained the following system of time-dependent partial differential equations including the conservation equations for mass, momentum and energy based on non-primitive variables [30,31,32]

$$\frac{{\partial }^2\mathsf{\Psi }}{\partial X^2}+\frac{{\partial }^2\mathsf{\Psi }}{\partial Y^2}=-\mathsf{\Omega }$$

(9)

$$\frac{\partial \mathsf{\Omega }}{\partial \mathsf{\tau }}+\frac{\partial \mathsf{\Psi }}{\partial Y}\frac{\partial \mathsf{\Omega }}{\partial X}-\frac{\partial \mathsf{\Psi }}{\partial X}\frac{\partial \mathsf{\Omega }}{\partial Y}=H_1\left(\mathsf{\varphi }\right){\left(\frac{Ra}{\mathrm{Pr}}\right)}^{\frac{n-2}{2}}\left[{\nabla }^2\left(\overline{M}\mathsf{\Omega }\right)+S_{\mathsf{\Omega }}\right]+H_2\left(\mathsf{\varphi }\right)\frac{\partial \mathsf{\Theta }}{\partial X}$$

(10)

$$\frac{\partial \mathsf{\Theta }}{\partial \mathsf{\tau }}+\frac{\partial \mathsf{\Psi }}{\partial Y}\frac{\partial \mathsf{\Theta }}{\partial X}-\frac{\partial \mathsf{\Psi }}{\partial X}\frac{\partial \mathsf{\Theta }}{\partial Y}=\frac{H_3\left(\mathsf{\varphi }\right)}{\sqrt{Ra\cdot \mathrm{Pr}}}\left[\frac{\partial }{\partial X}\left(\frac{k_{nf}}{k_{bf}}\cdot \frac{\partial \mathsf{\Theta }}{\partial X}\right)+\frac{\partial }{\partial Y}\left(\frac{k_{nf}}{k_{bf}}\cdot \frac{\partial \mathsf{\Theta }}{\partial Y}\right)\right]$$

(11)

Non-dimensional viscosity $\overline{M}$ and source term S_Ω from Equation (10) are [31,32]

$$\begin{array}{c}\overline{M}={\left[4{\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial X\partial Y}\right)}^2+{\left(\frac{{\partial }^2\mathsf{\Psi }}{\partial Y^2}-\frac{{\partial }^2\mathsf{\Psi }}{\partial X^2}\right)}^2\right]}^{\frac{n-1}{2}},\\ S_{\mathsf{\Omega }}=2\left[\frac{{\partial }^2\overline{M}}{\partial X^2}\frac{{\partial }^2\mathsf{\Psi }}{\partial Y^2}+\frac{{\partial }^2\overline{M}}{\partial Y^2}\frac{{\partial }^2\mathsf{\Psi }}{\partial X^2}-2\frac{{\partial }^2\overline{M}}{\partial X\partial Y}\frac{{\partial }^2\mathsf{\Psi }}{\partial X\partial Y}\right]\end{array}$$

The formulated set of Equations (9)–(11) includes the Rayleigh number $Ra=g\mathsf{\beta }\mathsf{\Delta }T{L}^3/\left(\overline{\mathsf{\nu }}\mathsf{\alpha }\right)$ and the Prandtl number $\mathit{Pr}=\overline{\mathsf{\nu }}/\mathsf{\alpha }$. The kinetic viscosity is defined as $\overline{\mathsf{\nu }}={\left(\frac{K}{\mathsf{\rho }}\right)}^{\frac{1}{2-n}}\cdot L^{\frac{2-2n}{2-n}}$. Additional dimensionless complexes are

$$\begin{array}{l}{H}_1\left(\mathsf{\varphi }\right)=\frac{{\mathsf{\rho }}_{bf}}{{\mathsf{\rho }}_{nf}}=\frac{1}{\left(1-\mathsf{\varphi }+\mathsf{\varphi }{\mathsf{\rho }}_p/{\mathsf{\rho }}_{bf}\right)}\\ H_2\left(\mathsf{\varphi }\right)=\frac{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{nf}}{{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{bf}}\frac{{\mathsf{\rho }}_{bf}}{{\mathsf{\rho }}_{nf}}=\frac{1-\mathsf{\varphi }+\mathsf{\varphi }{\left(\mathsf{\rho }\mathsf{\beta }\right)}_p/{\left(\mathsf{\rho }\mathsf{\beta }\right)}_{bf}}{1-\mathsf{\varphi }+\mathsf{\varphi }{\mathsf{\rho }}_p/{\mathsf{\rho }}_{bf}}\\ H_3\left(\mathsf{\varphi }\right)=\frac{{\left(\mathsf{\rho }c\right)}_{bf}}{{\left(\mathsf{\rho }c\right)}_{nf}}=\frac{1}{1-\mathsf{\varphi }+\mathsf{\varphi }{\left(\mathsf{\rho }c\right)}_p/{\left(\mathsf{\rho }c\right)}_{bf}}\end{array}$$

(12)

The additional restrictions for the considered Equations (9)–(11) can be formulated as Equation (13), where $q_r=\frac{q_2}{q_1}$ is the thermal flux density ratio.

$$\begin{array}{ccc}\hfill \mathsf{\tau }=0\to & \mathsf{\Psi }=\mathsf{\Omega }=0,\mathsf{\Theta }=0.5;\hfill & \\ \hfill \mathsf{\tau }>0\to & \\ & X=0\mathrm{and}X=1,0\le Y\le 1,\mathsf{\Psi }=0,\frac{\partial \mathsf{\Psi }}{\partial X}=0,\mathsf{\Theta }=0;\\ & Y=0,0\le X\le 0.2\mathrm{and}0.4\le X\le 0.6\mathrm{and}0.8\le X\le 1,\mathsf{\Psi }=0,\frac{\partial \mathsf{\Psi }}{\partial Y}=0,\frac{\partial \mathsf{\Theta }}{\partial Y}=0;\\ & Y=0,0.2\le X\le 0.4,\mathsf{\Psi }=0,\frac{\partial \mathsf{\Psi }}{\partial Y}=0,\frac{\partial \mathsf{\Theta }}{\partial Y}=-\frac{k_{bf}}{k_{nf}};\\ & Y=0,0.6\le X\le 0.8,\mathsf{\Psi }=0,\frac{\partial \mathsf{\Psi }}{\partial Y}=0,\frac{\partial \mathsf{\Theta }}{\partial Y}=-\frac{k_{bf}}{k_{nf}}{q}_r;\\ & Y=1,0\le X\le 1,\mathsf{\Psi }=0,\frac{\partial \mathsf{\Psi }}{\partial Y}=0,\frac{\partial \mathsf{\Theta }}{\partial Y}=0.\end{array}$$

(13)

3. Numerical Technique

To approximate and solve the described system of time-dependent differential Equations (9)–(11), various difference schemes have been used based on the finite difference method. The method of successive under relaxation has been applied to solve the Poisson Equation (9). The dimensionless viscosity has been approximated using regularization scheme. The Samarskii locally one-dimensional scheme has been used to write the equations of motion and energy (10) and (11) in one-dimensional form. Next, the convective terms have been discretized based on the pattern with donor cells, and the diffusion members have been approximated using mean differences, while for an approximation of time-dependent terms, the Euler scheme of the first order has been used. The resulting set of linear equations has been worked out by the Thomas algorithm.

The developed algorithm for solving the problem and the resulting program code have been tested using simple problems. Figure 2 shows the geometric statement of the test problem. A non-Newtonian power-law liquid fills a closed differentially heated chamber. The horizontal surfaces are adiabatic. Comparisons of the results have been made on the basis of the normalized values of the mean Nu calculated on the heated boundary, depending on time and the liquid nature parameter n according to the formula $N{u}_{avg}={\displaystyle \underset{0}{\overset{1}{\int }}\left(-\frac{\partial \mathsf{\Theta }}{\partial X}\right)}dY$. The comparison is shown in Figure 3. Our data are indicated by white points; the data of Turan et al. [35] are indicated by black points. It can be seen that the agreement is good, which indicates the performance of our code.

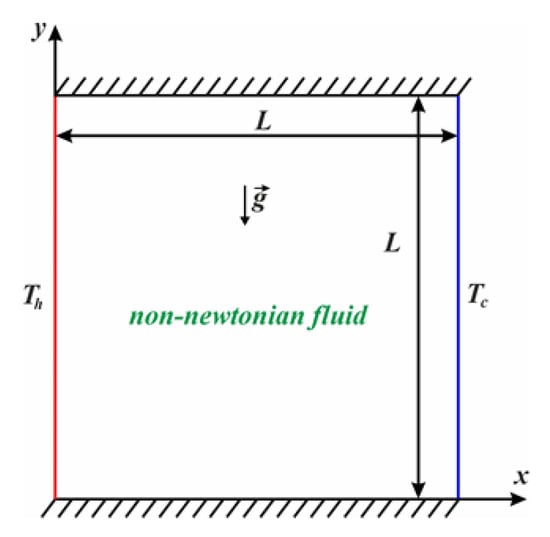
Figure 2. Domain for the benchmark.

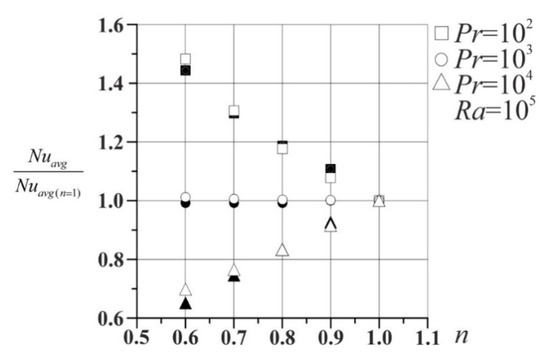
Figure 3. Comparison with [35].

Separately, an analysis has been conducted for the impact of mesh parameters on solution convergence according to the profiles of the average Nu and average temperature calculated on the left heater, which are shown in Figure 4 for Al₂O₃ at Ra = 10⁵, ϕ = 0.01, q_r = 1. The average Nusselt number is calculated by the relation: $N{u}_{avg}=\frac{1}{0.2}{\displaystyle \underset{0.2}{\overset{0.4}{\int }}\left(\frac{1}{{\mathsf{\Theta }}_{Y=0}}\right)}dX$. It can be seen that the grids of 100 × 100 and 150 × 150 elements did not lead to essential differences, so the subsequent calculations have been carried out for a mesh of 100 × 100 cells to diminish the calculation time.

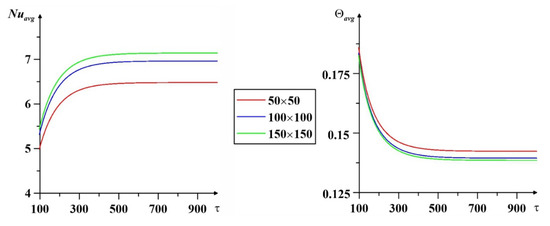
Figure 4. Influence of grid parameters for Ra = 10⁵, ϕ = 0.01, and q_r = 1.

4. Results

In this work, mathematical modeling of the time-dependent modes of laminar thermal convection of a pseudoplastic nanosuspension CMC/water + nanoparticles of Cu, Al₂O₃, CuO, TiO₂ has been carried out.

An analysis of the impact of the properties of the base medium on the process of convective heat transfer has been conducted. Note that the behavior index n < 1 characterizes the pseudoplastic nature of the liquid, while n = 1 is for the Newtonian liquid. Thus, Figure 5 shows a comparison of the mean Nu and average temperature for various n at Al₂O₃, Ra = 10⁵, ϕ = 0.01, and q_r = 1. It can be seen that at n = 0.91, the convective heat transfer is the most intense, since Nu_avg in this case has the maximum values, with an advantage even over the Newtonian medium. At the same time, the mean temperature of the right heater has low magnitudes, which indicates effective heat removal. Thus, these results confirm the effectiveness of using a pseudoplastic base fluid for cooling a heated element.

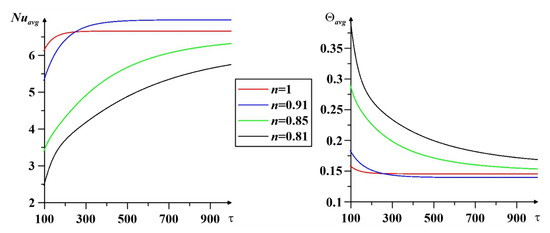
Figure 5. Effect of base fluid properties at Al₂O₃, Ra = 10⁵, ϕ = 0.01, and q_r = 1.

Separately, a study has been conducted of the influence of the nanoparticle material on the process at Ra = 10⁵ and ϕ = 0.01. Figure 6 demonstrates the profiles of the mean Nu and mean temperature with time and the substance of which the nanoparticles are composed. Nu_avg and Θ_avg values have been calculated using the second source at q_r = 2. It can be seen that the maximum Nu_avg and minimum Θ_avg values correspond to the use of aluminum oxide nanoparticles. The results of calculations using titanium oxide almost coincide with the curves for aluminum oxide, but are still less efficient. Thus, Al₂O₃ nanoparticles have been used for further calculations. Moreover, it is interesting to note that the distributions of the average Nu are directly proportional to the heat capacity of the considered nanoparticle material and inversely proportional to its density, while one can find the opposite influence for the average heater temperature.

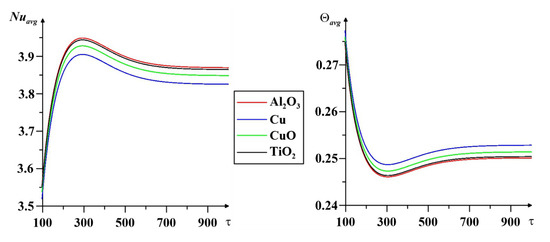
Figure 6. Influence of nanoparticle material for Ra = 10⁵, ϕ = 0.01, and q_r = 2.

Figure 7 presents the isoline patterns of stream function and temperature with the volume fraction of Al₂O₃ nanoparticles dispersed in the base medium. The distributions are built for Ra = 10⁵ and q_r = 1. The streamlines reflect the structure of the liquid motion within the chamber. Two convective cells are apparent, the right of which has a clockwise direction, and the left one has a counterclockwise direction. The flow pattern practically does not change with ϕ—only a change in the shape of the cells and a decrease in cores are noticeable. In this case, if one pays attention to the numerical values of the stream functions, one can notice a decrease in the flow velocity with an increase in the nanoparticle concentration. The second line of the figure illustrates the change in the distribution of isotherms depending on ϕ. The origin of a two-dimensional heat plume can be observed in the absence of nanoadditives. However, with an increase in ϕ, a degradation of the plume occurs, which reflects the attenuation of convective energy transport.

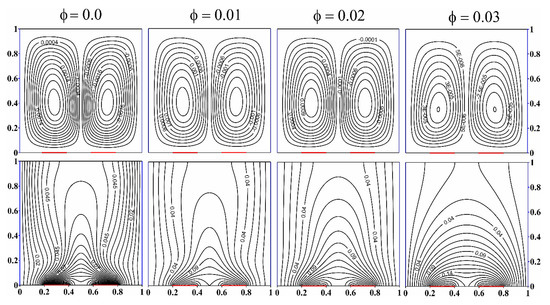
Figure 7. Impact of the nanoadditive concentration on streamlines and isotherms at Al₂O₃, Ra = 10⁵, q_r = 1.

The conclusions obtained for Figure 7 confirm the profiles of the mean Nu and temperature in Figure 8 at Ra = 10⁵ and q_r = 1. Convective energy transport is weakened with an increase in nanoadditive concentration, while the average source temperature increases. It should be noted that an increase in ϕ also results in an increment of the required time to reach the steady-state regime. This result can be explained by an increase in the viscosity of the working medium with an increase in the volume fraction of nanoparticles.

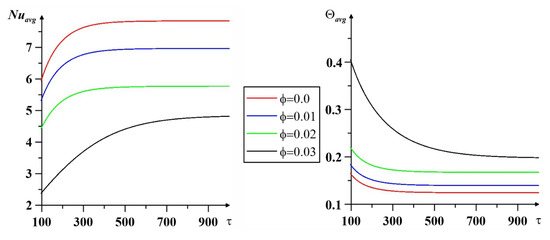
Figure 8. Impact of the nanoadditive concentration on Nu_avg and Θ_avg at Al₂O₃, Ra = 10⁵, and q_r = 1.

Separately, the influence of the thermal flux density ratio on the structure of the fluid flow and heat transfer has been analyzed for Al₂O₃ nanoparticles at Ra = 10⁵ and ϕ = 0.01. It can be seen from Figure 9 that an ascending flow is formed over a more heated source in all cases; but at q_r = 0.5 and q_r = 2, this flow is directed towards the center of the cavity at an angle, and not straight up, as when q_r = 1. Such a flow forms two convective cells of different power, and a less powerful one is located almost above the source, which has a higher heat flux density. In the case when the heat flow of both sources is the same, symmetrical circulation zones are located in the cavity. If we pay attention to the isotherms, we again see a symmetrical distribution at q_r = 1. At other values of q_r, a heat plume forms over a heated element in the central part of the domain. We can also note a more essential warming of the chamber for q_r = 2.

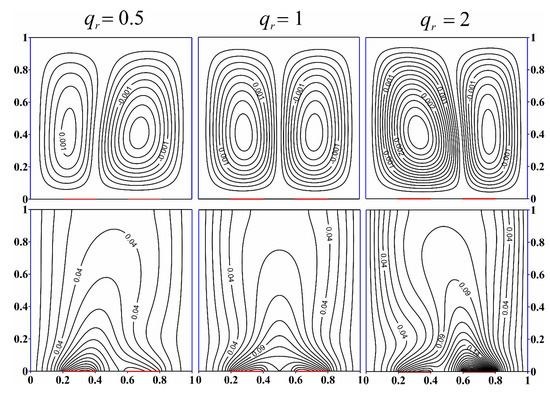
Figure 9. Effect of heat flux density on streamlines and isotherms for Al₂O₃ at Ra = 10⁵ and ϕ = 0.01.

Figure 10 reflects the integral characteristics depending on the heat flux density ratio calculated for both heaters when Al₂O₃ nanoparticles are at Ra = 10⁵ and ϕ = 0.01. Solid lines refer to the first source; dashed lines deal with the second one. If we consider the values of the average Nusselt number, we can note that the values on the first source are in the range from 6 to 8. The values for the second source have a wider range, from 4 to 12. A similar trend is observed for the mean temperature of the heaters. Note that the magnitudes of Nu_avg and Θ_avg at equal heat flux q_r = 1 coincide at both sources. It is also worth noting that the most intense convective flow corresponds to the case when q_r = 0.5 and the Nu_avg values are calculated on the second source. The same case corresponds to the most efficient cooling of the heated element, since Θ_avg has minimum values for these parameters.

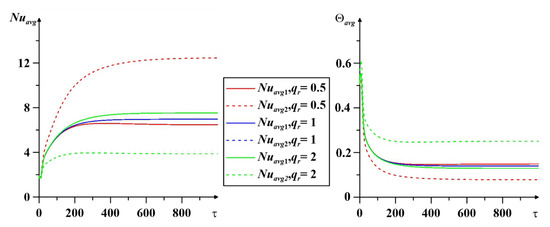
Figure 10. Effect of heat flux density ratio on Nu_avg and Θ_avg for Al₂O₃ at Ra = 10⁵ and ϕ = 0.01.

5. Conclusions

The process of thermogravitational energy transport of a pseudoplastic nanosuspension inside a chamber with two heated sections of the bottom wall has been studied in this work. An investigation on the influence of the key parameters, including the index of the behavior of the base medium (n), material of nanoparticles (Cu, Al₂O₃, CuO, and TiO₂), nanoadditive concentration (ϕ) and the thermal flux density ratio (q_r) has been conducted. A feature of this research is the use of experimental relations for nanoliquid physical properties.

It has been found that a mixture of 1% carboxymethylcellulose and water can be the most effective medium for the cooling process. Comparing the composition of nanoparticles, it has been found that the use of aluminum oxide particles characterizes more active cooling of the heated element. Within the framework of the described problem, an increase in nanoadditive concentration is not efficient, since the lowest source temperature is observed in the absence of nanoadditives. An assessment of the influence of the thermal flux density ratio has shown that with more active heating of one element, more efficient heat removal occurs from the second one.