Long-Wave Anti-Plane Motion in a Pre-Stressed Compressible Elastic Laminate with One Fixed and One Free Face
Abstract
1. Introduction
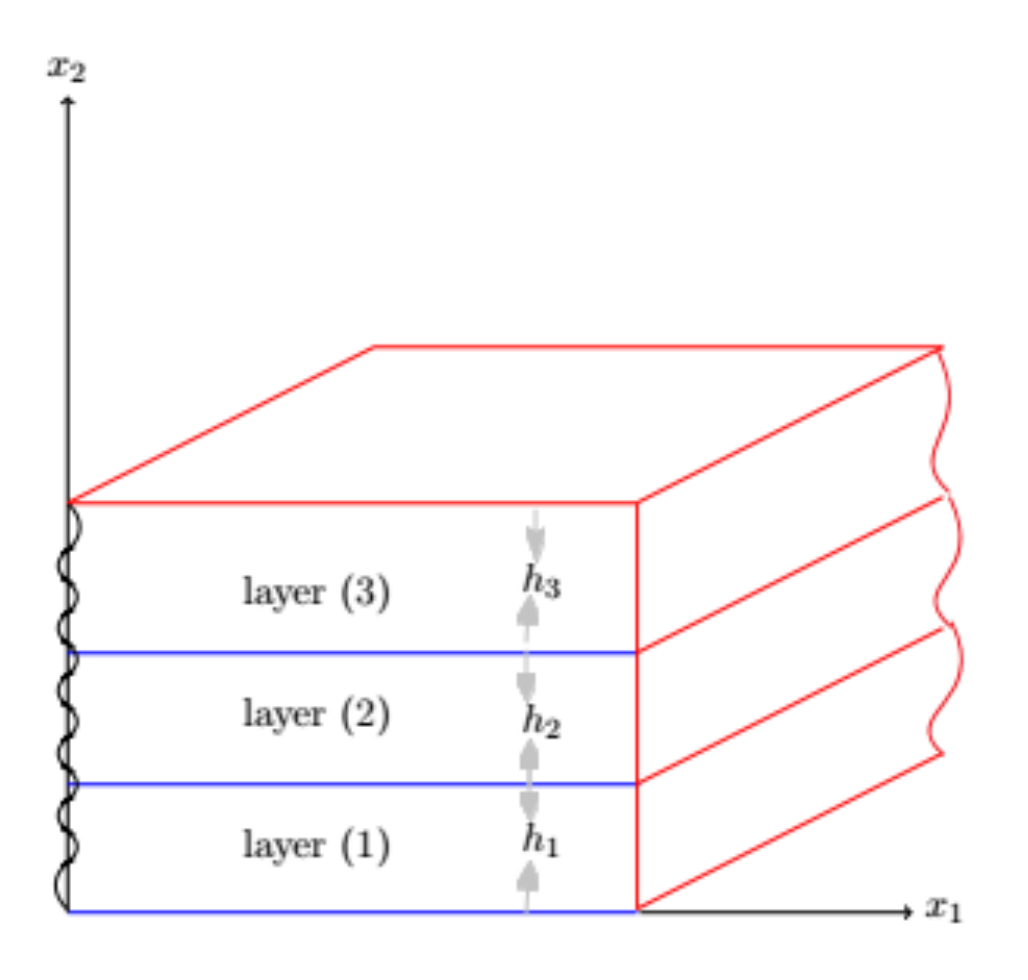
2. Statement of the Problem
3. Exact Dispersion Relation
4. Asymptotic Approach of Pre-Stressed Materials
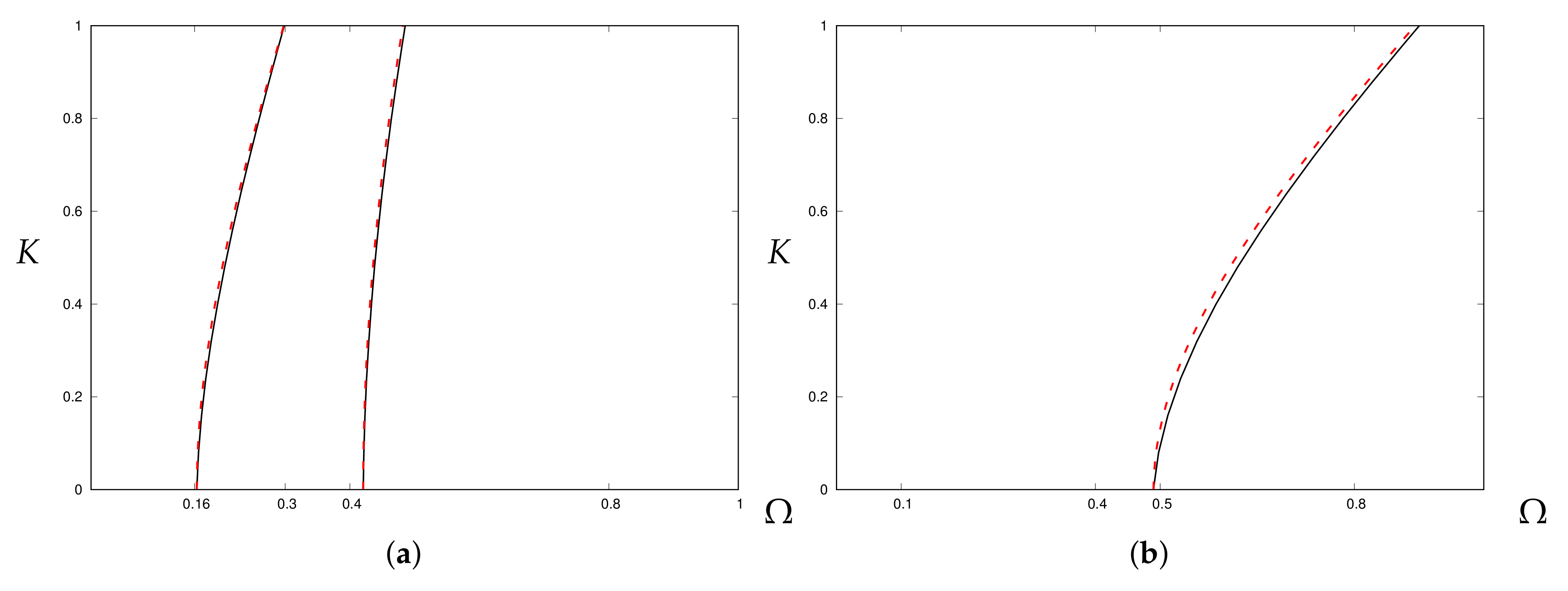
4.1. 2-Layered Laminate
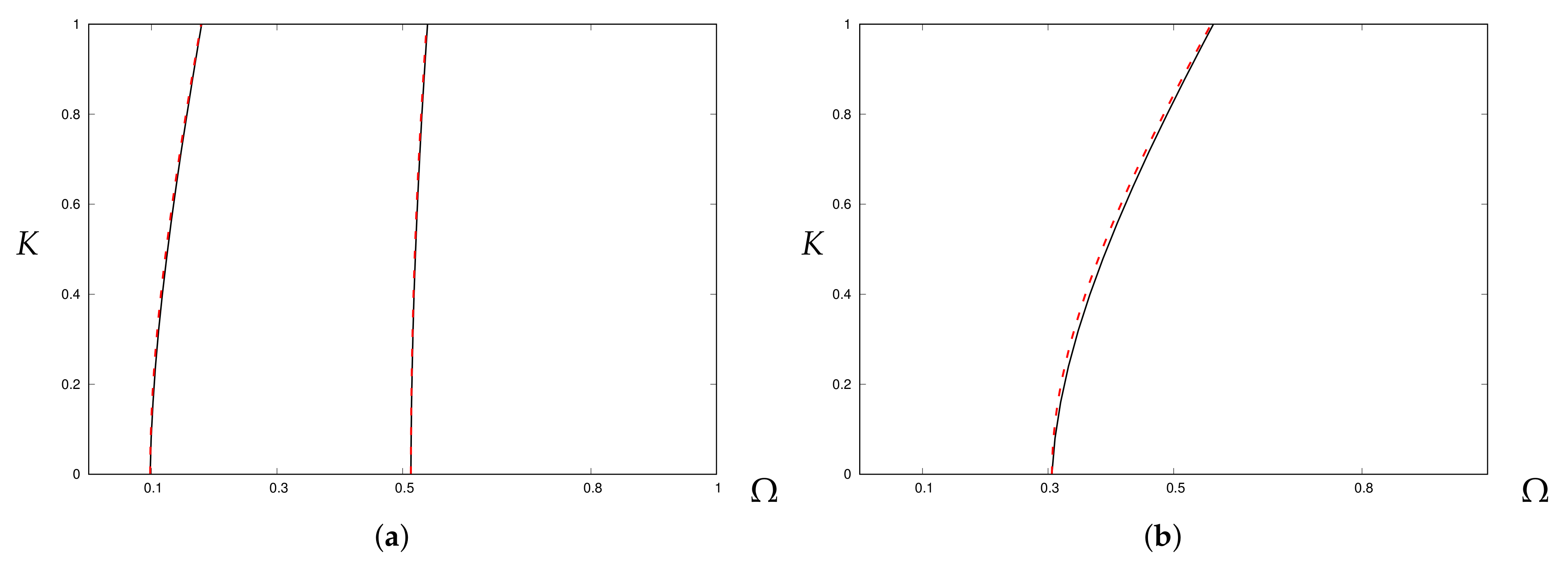
4.2. 3-Layered Laminate
4.3. Special Cases
4.3.1. 2-Layered Isotropic Laminate
4.3.2. 3-Layered Isotropic Laminate
5. Some Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lamb, H. On waves in an elastic plate. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1917, 93, 114–128. [Google Scholar]
- Daniel, I.M.; Ishai, O.; Daniel, I.M.; Daniel, I. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Reiss, E.L.; Locke, S. On the theory of plane stress. Quar. Appl. Math. 1961, 19, 195–203. [Google Scholar] [CrossRef]
- Reissner, E. On the derivation of the theory of thin elastic shells. J. Math. Phys. 1963, 42, 263–277. [Google Scholar] [CrossRef]
- Green, A.E. On the linear theory of thin elastic shells. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1962, 266, 143–160. [Google Scholar]
- Vinson, J. The Behavior of Sandwich Structures of Isotropic and Composite Materials; Routledge: London, UK, 2018. [Google Scholar]
- Rogerson, G.A.; Sandiford, K.J. Flexual waves in incompressible pre-stressed elastic composites. Quar. J. Mech. Appl. Math. 1997, 50, 597–624. [Google Scholar] [CrossRef]
- Rogerson, G.A.; Sandiford, K.J. The effect of finite primary deformations on harmonic waves in layered elastic media. Int. J. Solids Struct. 2000, 37, 2059–2087. [Google Scholar] [CrossRef]
- Rogerson, G.A.; Sandiford, K.J. Some comments on the dispersion relation for periodically layered pre-stressed elastic media. Int. J. Eng. Sci. 2002, 40, 23–49. [Google Scholar] [CrossRef]
- Willson, A.J. Surface and plate waves in biaxially-stressed elastic media. Pure Appl. Geophys. 1973, 102, 182–192. [Google Scholar] [CrossRef]
- Ogden, R.W.; Roxburgh, D.G. The effect of pre-stress on vibration and stability of elastic plates. Int. J. Eng. Sci. 1993, 31, 1611–1639. [Google Scholar] [CrossRef]
- Peter, C.; Jarvis, D.A. Surface waves in a pre-stressed elastic body. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1979, 366, 517–536. [Google Scholar]
- Roxburgh, D.G.; Ogden, R.W. Stability and vibration of pre-stressed compressible elastic plates. Int. J. Eng. Sci. 1994, 32, 427–454. [Google Scholar] [CrossRef]
- Helmi, M.M.; Rogerson, G.A. Long-Wave Motion in Pre-stressed Layered Media. In Proceedings of the 14th International Conference on Vibration Problems, Crete, Greece, 1–4 September 2019; pp. 1105–1115. [Google Scholar]
- Chattopadhyay, A.; Rogerson, G.A. Wave reflection in slightly compressible, finitely deformed elastic media. Arch. Appl. Mech. 2001, 71, 307–316. [Google Scholar] [CrossRef]
- Sun, T.; Yuan, Y. Mixed finite element method and the characteristics-mixed finite element method for a slightly compressible miscible displacement problem in porous media. Math. Comput. Simul. 2015, 107, 24–45. [Google Scholar] [CrossRef]
- Chatterjee, M.; Chattopadhyay, A. Propagation, reflection, and transmission of SH-waves in slightly compressible, finitely deformed elastic media. Appl. Math. Mech. 2015, 36, 1045–1056. [Google Scholar] [CrossRef]
- Chaki, M.S.; Guha, S.; Singh, A.K. Impact of Rectangular/Parabolic Shaped Irregularity on the Propagation of Shear Horizontal Wave in a Slightly Compressible Layered Structure. In Proceedings of the International Conference on Mathematical Modelling and Scientific Computation, Indore, India, 19–21 July 2018; pp. 61–74. [Google Scholar]
- Singh, A.K.; Agarwalla, S.; Chaki, M.S.; Chattopadhyay, A. Shear wave propagation in a slightly compressible finitely deformed layer over a foundation with pre-stressed fibre-reinforced stratum and dry sandy viscoelastic substrate. Waves Random Complex Media 2021, 31, 847–866. [Google Scholar] [CrossRef]
- Kaplunov, J.D.; Kossovitch, L.Y.; Nolde, E.V. Dynamics of ThinWalled Elastic Bodies; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Rogerson, G.A.; Kaplunov, J.D.; Nolde, E.V. An asymptotic analysis of initial-value problems for thin elastic plates. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 2541–2561. [Google Scholar] [CrossRef]
- Andrianov, I.V.; Bolshakov, V.I.; Danishevskyy, V.V.; Weichert, D. Higher-order asymptotic homogenization and wave propagation in periodic composite materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 1181–1201. [Google Scholar] [CrossRef]
- Daya, E.M.; Potier-Ferry, M. Vibrations of long repetitive structures by a double scale asymptotic method. Struct. Eng. Mech. 2001, 12, 215–230. [Google Scholar] [CrossRef]
- Helmi, M.M.; Mubaraki, A.M.; Nuruddeen, R.I. Analysis of horizontally polarized shear waves on a highly inhomogeneous loaded bi-material plate. AIMS Math. 2022. accepted. [Google Scholar] [CrossRef]
- Mubaraki, A.M.; Almalki, F.M. Surface waves on a coated homogeneous half-space under the effects of external forces. Symmetry 2022, 14, 2241. [Google Scholar] [CrossRef]
- Asif, M.; Nawaz, R.; Nuruddeen, R.I. Dispersion of elastic waves in an inhomogenous multilayered plate over a Winkler elastic foundation with imperfect interfacial conditions. Phys. Scr. 2021, 96, 125026. [Google Scholar] [CrossRef]
- Mubaraki, A.M.; Helmi, M.M.; Nuruddeen, R.I. Surface wave propagation in a rotating doubly coated nonhomogeneous half space with application. Symmetry 2022, 14, 1000. [Google Scholar] [CrossRef]
- Nolde, E.V.; Prikazchikova, L.A.; Rogerson, G.A. Dispersion of small amplitude waves in a pre-stressed compressible elastic plate. J. Elast. 2004, 75, 1–29. [Google Scholar] [CrossRef]
- Kaplunov, J.D.; Nolde, E.V.; Rogerson, G.A. A low-frequency model for dynamic motion in pre-stressed incompressible elastic structures. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2000, 456, 2589–2610. [Google Scholar] [CrossRef]
- Kaplunov, J.D.; Nolde, E.V. Long-wave vibrations of a nearly incompressible isotropic plate with fixed faces. Quart. J. Mech. Appl. Math. 2002, 55, 345–356. [Google Scholar] [CrossRef][Green Version]
- Rogerson, G.A.; Fu, Y.B. An asymptotic analysis of the dispersion relation of a pre-stressed incompressible elastic plate. Acta Mech. 1995, 111, 59–74. [Google Scholar] [CrossRef]
- Nolde, E.V.; Rogerson, G.A. Long wave asymptotic integration of the governing equations for an incompressible elastic layer with fixed faces. Wave Motion 2002, 36, 287–304. [Google Scholar] [CrossRef]
- Pichugin, A.V.; Rogerson, G.A. An asymptotic membrane-like theory for long-wave motion in a pre-stressed elastic plate. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2002, 458, 1447–1468. [Google Scholar] [CrossRef]
- Knowles, J.K. A note on anti-plane shear for compressible materials in finite elastostatics. J. Aust. Math. Soc. 1977, 20, 1–7. [Google Scholar] [CrossRef]
- Rogerson, G.A. Some asymptotic expansions of the dispersion relation for an incompressible elastic plate. Int. J. Solids Struct. 1997, 34, 2785–2802. [Google Scholar] [CrossRef]
- Yang, F. Asymptotic solution to axisymmetric indentation of a compressible elastic thin film. Thin Solid Films 2006, 515, 2274–2283. [Google Scholar] [CrossRef]
- Goldenveizer, A.L.; Kaplunov, J.D.; Nolde, E.V. On Timoshenko-Reissner type theories of plates and shells. Int. J. Solids Struct. 1993, 30, 675–694. [Google Scholar] [CrossRef]
- Alibeigloo, A. Free vibration analysis of nano-plate using three-dimensional theory of elasticity. Acta Mech. 2011, 222, 149. [Google Scholar] [CrossRef]
- Aksentian, O.K.; Vorovich, I.I. The state of stress in a thin plate. J. Appl. Math. Mech. 1963, 27, 1621–1643. [Google Scholar] [CrossRef]
- Lutianov, M.; Rogerson, G.A. Long wave motion in layered elastic media. Int. J. Eng. Sci. 2010, 48, 1856–1871. [Google Scholar] [CrossRef]
- Danishevs, V.V.; Kaplunov, J.; Rogerson, G.A. Anti-plane shear waves in a fibre-reinforced composite with a non-linear imperfect interface. Int. J. Nonlinear Mech. 2015, 76, 223–232. [Google Scholar] [CrossRef]
- Alzaidi, A.S.M.; Mubaraki, A.M.; Nuruddeen, R.I. Effect of fractional temporal variation on the vibration of waves on elastic substrates with spatial non-homogeneity. AIMS Math. 2022, 7, 13746–13762. [Google Scholar] [CrossRef]
- Horgan, C.O. Anti-plane shear deformations in linear and nonlinear solid mechanics. SIAM Rev. 1995, 37, 53–81. [Google Scholar] [CrossRef]
- Kaplunov, J.; Prikazchikova, L.; Alkinidri, M. Antiplane shear of an asymmetric sandwich plate. Contin. Mech. Thermodyn. 2021, 33, 1247–1262. [Google Scholar] [CrossRef]
- Alkinidri, M.; Kaplunov, J.; Prikazchikova, L. A two mode non-uniform approximation for an elastic asymmetric sandwich. In Proceedings of the XI International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020. [Google Scholar]
- Nuruddeen, R.I.; Nawaz, R.; Zia, Z.Q.M. Asymptotic approach to anti-plane dynamic problem of asymmetric three-layered composite plate. Math. Meth. Appl. Sci. 2021, 44, 10933–10947. [Google Scholar] [CrossRef]
- Nuruddeen, R.I.; Nawaz, R.; Zia, Z.Q.M. Asymptotic analysis of an anti-plane shear dispersion of an elastic five-layered structure amidst contrasting properties. Arch. Appl. Mech. 2020, 90, 1875–1892. [Google Scholar] [CrossRef]
- Prikazchikov, L.A.; Aydin, Y.E.; Erbas, B.; Kaplunov, J. Asymptotic analysis of anti-plane dynamic problem for a three-layered strongly inhomogeneous laminate. Math. Mech. Solids 2018, 56, 189. [Google Scholar] [CrossRef]
- Erbas, B.; Kaplunov, J.; Nobili, A.; Kilic, G. Dispersion of elastic waves in a layer interacting with a Winkler foundation. J. Acoust. Soc. Am. 2018, 144, 2918–2925. [Google Scholar] [CrossRef] [PubMed]
- Kaplunov, J.; Prikazchikov, D.A.; Prikazchikova, L.A. Dispersion of elastic waves in a strongly inhomogeneous three-layered plate. Int. J. Solids Struct. 2017, 113, 169–179. [Google Scholar] [CrossRef]
- Lashhab, M.I.; Rogerson, G.A.; Prikazchikova, L.A. Small amplitude waves in a pre-stressed compressible elastic layer with one fixed and one free face. Z. Angew. Math. Phys. 2015, 66, 741–2757. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helmi, M.M. Long-Wave Anti-Plane Motion in a Pre-Stressed Compressible Elastic Laminate with One Fixed and One Free Face. Symmetry 2022, 14, 2516. https://doi.org/10.3390/sym14122516
Helmi MM. Long-Wave Anti-Plane Motion in a Pre-Stressed Compressible Elastic Laminate with One Fixed and One Free Face. Symmetry. 2022; 14(12):2516. https://doi.org/10.3390/sym14122516
Chicago/Turabian StyleHelmi, Maha M. 2022. "Long-Wave Anti-Plane Motion in a Pre-Stressed Compressible Elastic Laminate with One Fixed and One Free Face" Symmetry 14, no. 12: 2516. https://doi.org/10.3390/sym14122516
APA StyleHelmi, M. M. (2022). Long-Wave Anti-Plane Motion in a Pre-Stressed Compressible Elastic Laminate with One Fixed and One Free Face. Symmetry, 14(12), 2516. https://doi.org/10.3390/sym14122516