A New Numerical Approach for Variable-Order Time-Fractional Modified Subdiffusion Equation via Riemann–Liouville Fractional Derivative
Abstract
1. Introduction
2. Preliminaries
- (i)
- (ii)
- (iii)
- There exists a positive constantsuch that
- (vi)
3. Implicit Difference Scheme
3.1. Stability Analysis
3.2. Consistency
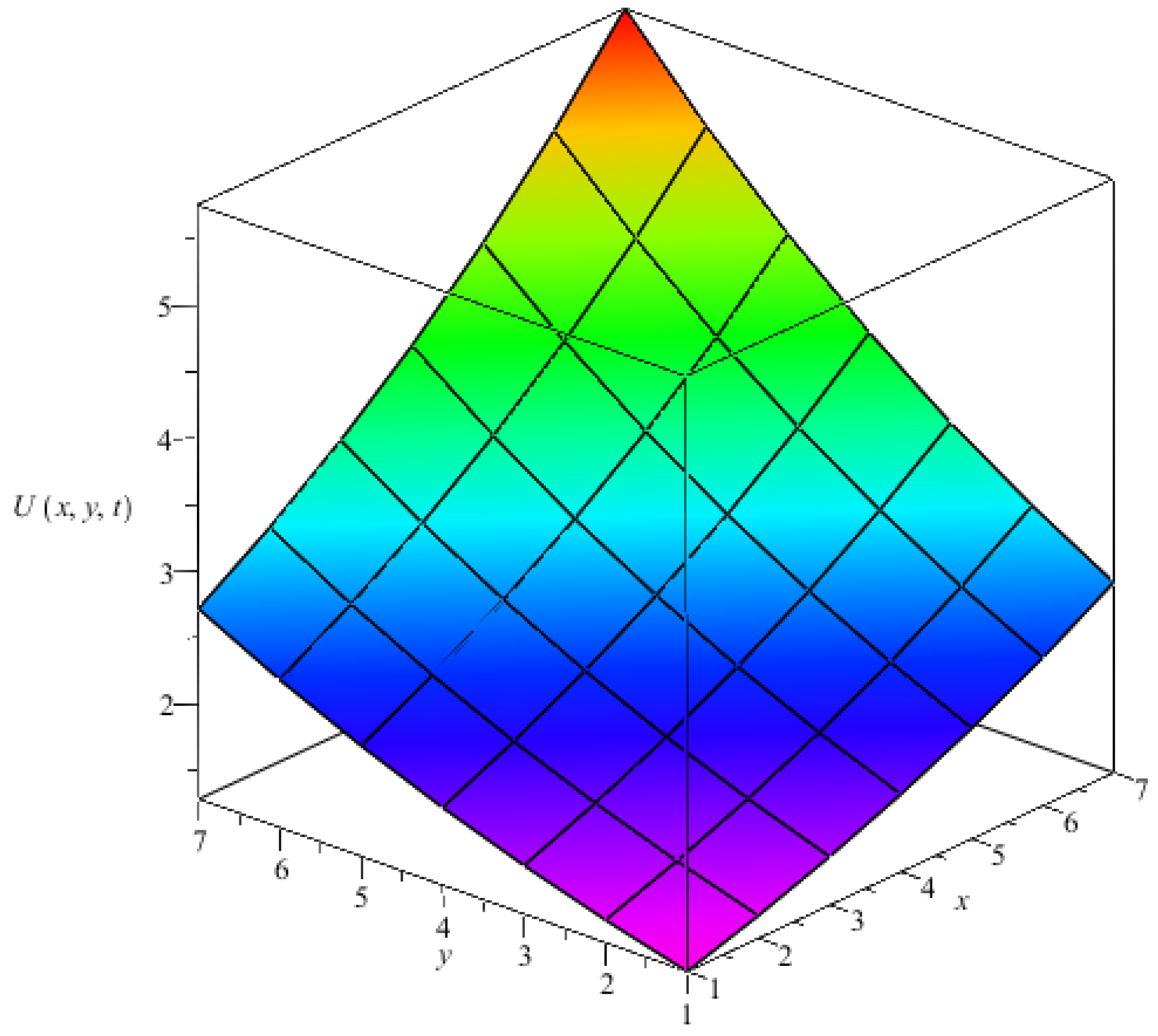
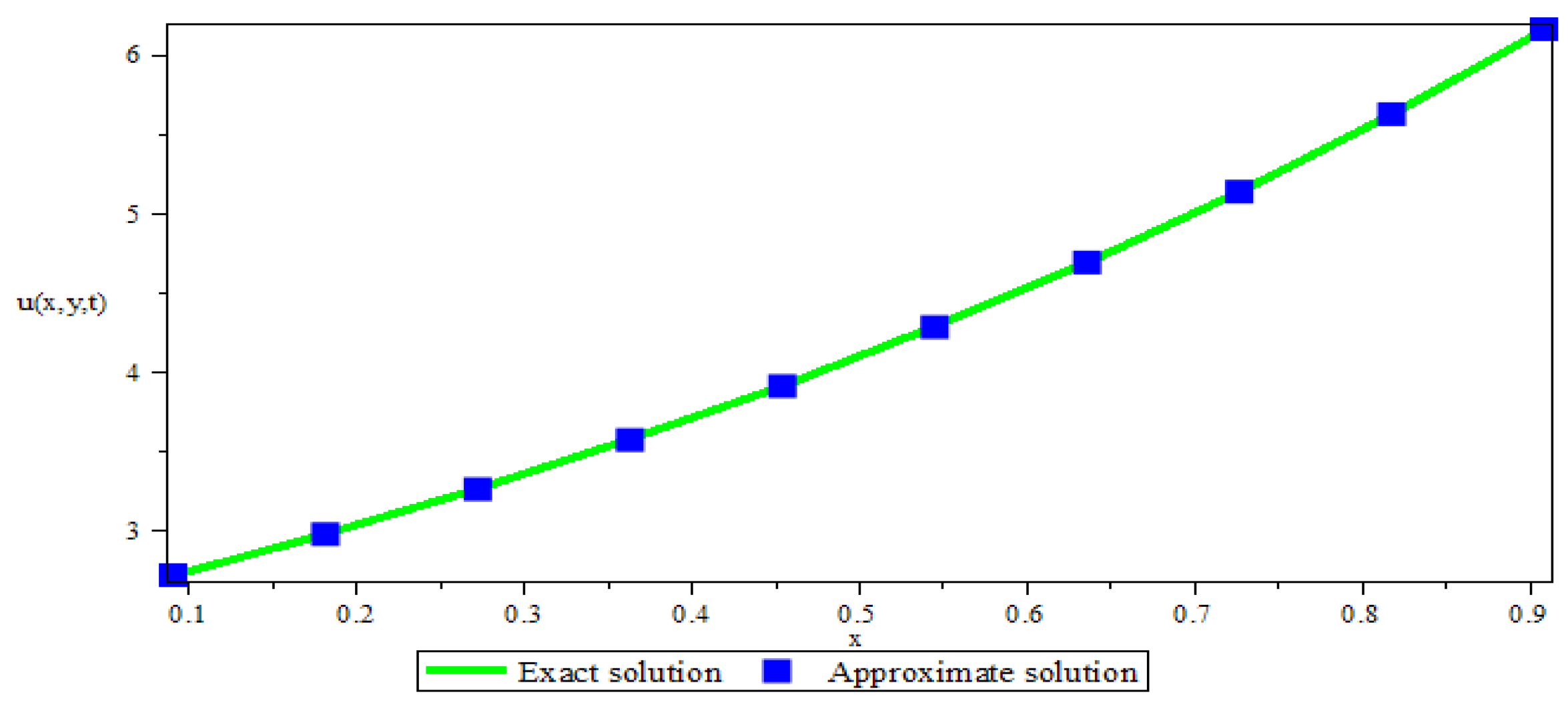
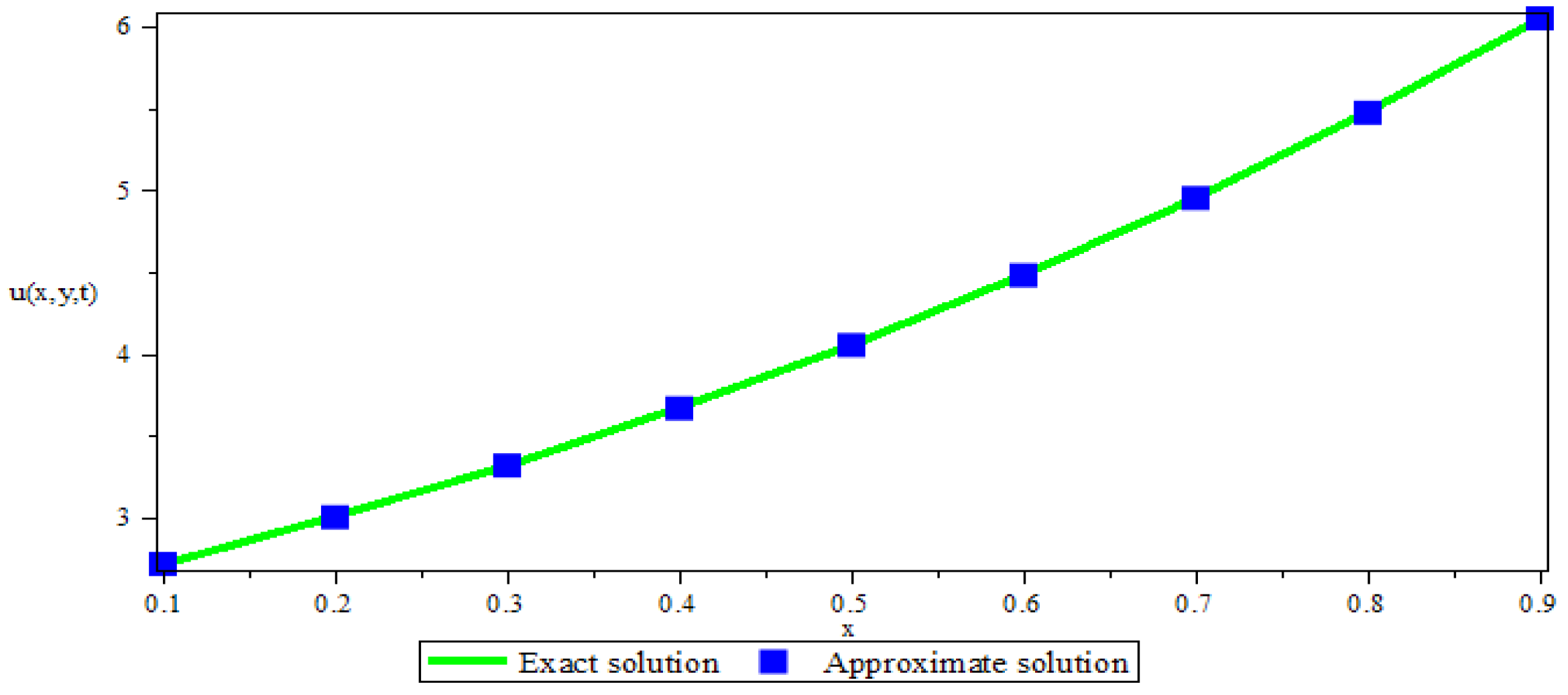
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, J.; Qiu, Y.; Song, G. A compact fnite difference scheme for variable order subdiffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 140–149. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Chen, Y. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A Stat. Mech. Its Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Shekari, Y.; Tayebi, A.; Heydari, M.H. A meshfree approach for solving 2D variable-order fractional nonlinear diffusion-wave equation. Comput. Methods Appl. Mech. Eng. 2019, 350, 154–168. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Anh, V.; Turner, I. Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equation. SIAM J. Sci. Comput. 2010, 32, 1740–1760. [Google Scholar] [CrossRef]
- Xu, T.; Lü, S.; Chen, W.; Chen, H. Finite difference scheme for multi-term variable-order fractional diffusion equation. Adv. Differ. Equ. 2018, 2018, 103. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Li, G.; Wang, Y. A simultaneous inversion problem for the variable-order time fractional differential equation with variable coefficient. Math. Probl. Eng. 2019, 2019, 13. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2015, 80, 101–116. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z.; Karniadakis, G.E. Second-order approximations for variable order fractional derivatives: Algorithms and applications. J. Comput. Phys. 2015, 293, 184–200. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Chen, J.; Turner, I.; Anh, V. Numerical techniques for the variable order time fractional diffusion equation. Appl. Math. Comput. 2012, 218, 10861–10870. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Avazzadeh, Z.; Heydari, M.H.; Mahmoudi, M.R. An approximate approach for the generalized variable-order fractional pantograph equation. Alex. Eng. J. 2020, 59, 2347–2354. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Fractional spectral collocation methods for linear and nonlinear variable order FPDEs. J. Comput. Phys. 2015, 293, 312–338. [Google Scholar] [CrossRef]
- Ali, U. Numerical Solutions for Two Dimensional Time-Fractional Differential Sub-Diffusion Equation. Ph.D. Thesis, University Sains Malaysia, Gelugor, Malaysia, 2019; pp. 1–200. [Google Scholar]
- Ma, S.; Xu, Y.; Yue, W. Numerical solutions of a variable-order fractional financial system. J. Appl. Math. 2012, 2012, 417942. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. Numerical solution of variable order fractional differential equations. arXiv 2018, arXiv:1802.00519. [Google Scholar]
- Akgül, A.; Baleanu, D. On solutions of variable-order fractional differential equations. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2017, 7, 112–116. [Google Scholar] [CrossRef]
- Jia, Y.T.; Xu, M.Q.; Lin, Y.Z. A numerical solution for variable order fractional functional differential equation. Appl. Math. Lett. 2017, 64, 125–130. [Google Scholar] [CrossRef]
- Dehghan, R. A numerical solution of variable order fractional functional differential equation based on the shifted Legendre polynomials. SeMA J. 2019, 76, 217–226. [Google Scholar] [CrossRef]
- Chen, C.M. Numerical methods for solving a two-dimensional variable-order modified diffusion equation. Appl. Math. Comput. 2013, 225, 62–78. [Google Scholar] [CrossRef]
- Ali, U.; Sohail, M.; Abdullah, F.A. An Efficient Numerical Scheme for Variable-Order Fractional Sub-diffusion Equation. Symmetry 2020, 12, 1437. [Google Scholar] [CrossRef]
- Ahmad, H.; Akgül, A.; Khan, T.A.; Stanimirović, P.S.; Chu, Y.M. New Perspective on the Conventional Solutions of the Nonlinear Time-Fractional Partial Differential Equations. Complexity 2020, 2020, 8829017. [Google Scholar] [CrossRef]
- Sweilam, N.H.; AL-Mrawm, H.M. On the numerical solutions of the variable order fractional heat equation. Stud. Nonlinear Sci. 2011, 2, 31–36. [Google Scholar]
- Babaei, A.; Jafari, H.; Banihashemi, S. Numerical solution of variable order fractional nonlinear quadratic integro-differential equations based on the sixth-kind Chebyshev collocation method. J. Comput. Appl. Math. 2020, 377, 112908. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, X. Analysis and numerical solution of a nonlinear variable-order fractional differential equation. Adv. Comput. Math. 2019, 45, 2647–2675. [Google Scholar] [CrossRef]
- Kaur, S.; Kumar, A.; Pathak, A.K. October. A new computational procedure for the solution of the time-fractional advection problem. AIP Conf. Proc. 2022, 2451, 020058. [Google Scholar]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, H.; Thounthong, P.; Chu, Y.M.; Cesarano, C. Solution of multi-term time-fractional PDE models arising in mathematical biology and physics by local meshless method. Symmetry 2020, 12, 1195. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A. December. Modified implicit difference method for one-dimensional fractional wave equation. AIP Conf. Proc. 2019, 2184, 060021. [Google Scholar]
- Ahmad, I.; Khan, M.N.; Inc, M.; Ahmad, H.; Nisar, K.S. Numerical simulation of simulate an anomalous solute transport model via local meshless method. Alex. Eng. J. 2020, 59, 2827–2838. [Google Scholar] [CrossRef]
- Mahmood, A.; Md Basir, M.F.; Ali, U.; Mohd Kasihmuddin, M.S.; Mansor, M. Numerical Solutions of Heat Transfer for Magnetohydrodynamic Jeffery-Hamel Flow Using Spectral Homotopy Analysis Method. Processes 2019, 7, 626. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, H.; Abouelregal, A.E.; Thounthong, P.; Abdel-Aty, M. Numerical study of integer-order hyperbolic telegraph model arising in physical and related sciences. Eur. Phys. J. Plus 2020, 135, 759. [Google Scholar] [CrossRef]
- Srivastava, M.H.; Ahmad, H.; Ahmad, I.; Thounthong, P.; Khan, N.M. Numerical simulation of three-dimensional fractional-order convection-diffusion PDEs by a local meshless method. Therm. Sci. 2020, 25, 347–358. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A.; Ismail, A.I. Crank-Nicolson finite difference method for two-dimensional fractional sub-diffusion equation. J. Interpolat. Approx. Sci. Comput. 2017, 2017, 18–29. [Google Scholar] [CrossRef]
- Ali, U.; Abdullah, F.A.; Mohyud-Din, S.T. Modified implicit fractional difference scheme for 2D modified anomalous fractional sub-diffusion equation. Adv. Differ. Equ. 2017, 2017, 185. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann-Liouville derivative and fractional Taylor series of non-differentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Ali, U.; Sohail, M.; Usman, M.; Abdullah, F.A.; Khan, I.; Nisar, K.S. Fourth-Order Difference Approximation for Time-Fractional Modified Sub-Diffusion Equation. Symmetry 2020, 12, 691. [Google Scholar] [CrossRef]
- Aslefallah, M.; Rostamy, D.; Hosseinkhani, K. Solving time-fractional differential diffusion equation by theta-method. Int. J. Appl. Math. Mech. 2014, 2, 1–8. [Google Scholar]
- Sanz-Serna, J.; Palencia, C. A general equivalence theorem in the theory of discretization methods. Math. Comput. 1985, 45, 143–152. [Google Scholar] [CrossRef]

| [20] | Scheme | [20] | Scheme | ||
|---|---|---|---|---|---|
| 8.0355 × | 5.8320 × | 2.0696 × | 1.2832 × | ||
| 8.0183 × | 6.2580 × | 2.0640 × | 1.3293 × | ||
| 8.1723 × | 5.0709 × | 2.1095 × | 9.6731 × | ||
| 8.2124 × | 4.8675 × | 2.1195 × | 6.3245 × | ||
| 8.0406 × | 3.2527 × | 2.0718 × | 4.6502 × | ||
| 8.1988 × | 5.4178 × | 2.1130 × | 2.3773 × |
| 3.7765 × | 9.2040 × | 1.9846 × | ||
| 3.9540 × | 9.8408 × | 2.1700 × | ||
| 2.3184 × | 8.2456 × | 2.1890 × | ||
| 2.2517 × | 7.9011 × | 2.0444 × | ||
| 3.5056 × | 8.1540 × | 1.6455 × | ||
| 3.4383 × | 7.8799 × | 1.5577 × | ||
| 2.7685 × | 6.1931 × | 1.1278 × | ||
| 2.7378 × | 5.5218 × | 8.9180 × | ||
| 3.0216 × | 7.0405 × | 4.1117 × |
| 2.7906 × | 8.0080 × | 2.0703 × | 1.3204 × | |
| 2.6989 × | 6.1874 × | 4.8372 × | 3.5197 × | |
| 6.0945 × | 7.6964 × | 1.0488 × | 2.1621 × | |
| 5.2639 × | 3.7005 × | 1.8890 × | 2.0941 × | |
| 5.6529 × | 5.3719 × | 2.0541 × | 1.6042 × | |
| 5.5681 × | 5.2462 × | 1.8347 × | 1.4969 × | |
| 4.3292 × | 3.1150 × | 2.7668 × | 9.3363 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathima, D.; Naeem, M.; Ali, U.; Ganie, A.H.; Abdullah, F.A. A New Numerical Approach for Variable-Order Time-Fractional Modified Subdiffusion Equation via Riemann–Liouville Fractional Derivative. Symmetry 2022, 14, 2462. https://doi.org/10.3390/sym14112462
Fathima D, Naeem M, Ali U, Ganie AH, Abdullah FA. A New Numerical Approach for Variable-Order Time-Fractional Modified Subdiffusion Equation via Riemann–Liouville Fractional Derivative. Symmetry. 2022; 14(11):2462. https://doi.org/10.3390/sym14112462
Chicago/Turabian StyleFathima, Dowlath, Muhammad Naeem, Umair Ali, Abdul Hamid Ganie, and Farah Aini Abdullah. 2022. "A New Numerical Approach for Variable-Order Time-Fractional Modified Subdiffusion Equation via Riemann–Liouville Fractional Derivative" Symmetry 14, no. 11: 2462. https://doi.org/10.3390/sym14112462
APA StyleFathima, D., Naeem, M., Ali, U., Ganie, A. H., & Abdullah, F. A. (2022). A New Numerical Approach for Variable-Order Time-Fractional Modified Subdiffusion Equation via Riemann–Liouville Fractional Derivative. Symmetry, 14(11), 2462. https://doi.org/10.3390/sym14112462









