Graphical Views of Intuitionistic Fuzzy Double-Controlled Metric-Like Spaces and Certain Fixed-Point Results with Application

Abstract

In this article, we establish the concept of intuitionistic fuzzy double-controlled metric-like spaces by “assuming that the self-distance may not be zero”; if the value of the metric is zero, then it has to be “a self-distance”. We derive numerous fixed-point results for contraction mappings. In addition, we provide several non-trivial examples with their graphical views and an application of integral equations to show the validity of the proposed results.

1. Introduction

In 1965, Zadeh [1] developed “fuzzy notion” to contrast imprecise terms, in which the membership function is used. Atanassov [2] introduced the concept of intuitionistic fuzzy sets in which membership and non-membership functions are used. Fuzzy sets presented in [1] and metric spaces are combined to establish the concept of fuzzy metric spaces, in which the notion of the continuous t-norm is used, which was introduced by Schweizer and Sklar [3]. The notion of fuzzy metric spaces was first introduced by Kramosil and Michalak [4] in 1975 and then George and Veeramani [5,6] updated it in 1994. Garbiec [7] established the fuzzy version of the Banach fixed-point result.

Harandi [8] established the concept of metric-like spaces and proved several fixed-point theorems for contraction mappings. The notion of metric-like spaces is a generalization of metric space. Mlaiki [9] established the concept of controlled metric-type spaces. Mlaiki et al. [10] established the notion of controlled metric-like spaces as a generalization of controlled-type metric spaces. Shukla and Abbas [11] established the notion of fuzzy metric-like spaces as a generalization of fuzzy metric spaces. Recently, Javed et al. [12] introduced the notion of fuzzy b-metric-like spaces as a generalization of fuzzy b-metric spaces and fuzzy metric-like spaces and proved several fixed-point results for contraction mappings.

In 2004, Park [13] established the notion of intuitionistic fuzzy metric spaces and discussed the topological structure. Konwar [14] established the concept of intuitionistic fuzzy b-metric spaces as a generalization of intuitionistic fuzzy metric spaces. Shatanawi et al. [15] used an E.A property and the common E.A property for coupled maps to obtain new results on generalized intuitionistic fuzzy metric spaces, and Gupta et al. [16] obtained some coupled fixed-point results on modified intuitionistic fuzzy metric spaces and applied them to the integral-type contraction. Recently, Sezen [17] established the concept of controlled fuzzy metric spaces and derived several fixed-point results. Saleem et al. [18] established the concept of fuzzy double-controlled metric spaces as a generalization of controlled fuzzy metric spaces and proved several fixed-point results for contraction mappings with an application of integral equations. Itoh [19] derived several random fixed-point theorems with an application of random differential equations in Banach spaces. Numerous fixed-point results of generalizations of fuzzy metric spaces were established by the authors [20,21,22,23,24]. Recently, Farheen et al. [25] introduced the concept of intuitionistic fuzzy double-controlled metric spaces and proved some fixed-point results. The authors in [26,27,28,29,30] worked on different interesting applications of the fixed-point theory.

In this manuscript, we introduce the concept of intuitionistic fuzzy double-controlled metric-like spaces by replacing the following properties of intuitionistic fuzzy double-controlled metric spaces:

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=1\mathrm{for}\mathrm{all}\upsilon >0,\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\varpi =\varrho ,$$

$$\aleph \left(\varpi ,\varrho ,\upsilon \right)=0\mathrm{for}\mathrm{all}\upsilon >0,\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\varpi =\varrho ,$$

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=1\mathrm{for}\mathrm{all}\upsilon >0,\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\varpi =\varrho ,$$

with

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=1\mathrm{for}\mathrm{all}\upsilon >0,\mathrm{implies}\varpi =\varrho ,$$

$$\aleph \left(\varpi ,\varrho ,\upsilon \right)=0\mathrm{for}\mathrm{all}\upsilon >0,\mathrm{implies}\varpi =\varrho .$$

We assume that the self-distance may not be zero; if the value of the metric is zero, then it has to be a self-distance and several fixed-point results for contraction mappings must be proven. Additionally, we establish a number of non-trivial examples with their graphs and an application for integral equations.

2. Preliminaries

In the section, we give some basic notions that are helpful for readers to understand the main section.

Definition 1

 ([1]). A fuzzy set $F$ defined in a space $X$ is a non-empty set of 2-tuple elements:

$$F=\left\{\langle x,\mu \left(x\right)\rangle ,x\in X\right\},\forall x\in X,$$

where $\mu :X\to \left[0,1\right]$ is a membership function of a set $S$, which for every element $x\in X$ assigns its membership degree $\mu \left(x\right)\in \left[0,1\right]$ to the fuzzy set $F$. The set $X$ is called a domain of discourse and we write $F\mathit{\subseteq }X$.

Definition 2

 ([2]). Let $X$ be a non-empty set. An intuitionistic fuzzy set $A$ in $X$ is an object having the form $A=\left\{\langle \mu \left(x\right),\nu \left(x\right)\rangle :x\in X\right\},$ where the functions $\mu ,\nu :X\to \left[0,1\right]$ define, respectively, the degree of membership and degree of non-membership of the element $x\in X$ to the set $A,$ which is the subset of $X,$ and for all $x\in X,$ $0\le \mu \left(x\right)+\nu \left(x\right)\le 1$. Furthermore, we have $\pi \left(x\right)=1-\mu \left(x\right)-\nu \left(x\right)$, called the index of the intuitionistic fuzzy set or the hesitation margin of $x\in A.$ $\pi \left(x\right)$ is the degree of indeterminacy of $x\in X$ to the intuitionistic fuzzy set $A$ and $\pi \left(x\right)\in \left[0,1\right]$ for every $x\in X.$

Definition 3

 ([13]). A binary operation $\ast$: [0, 1]$\times$ [0, 1] $\to$ [0, 1] is said to be a CTN if it satisfies the following conditions:

1. 

$\varsigma \ast \mathrm{ɷ}=\mathrm{ɷ}\ast \varsigma ,(\forall )\varsigma ,\mathrm{ɷ}\in \left[0,1\right];$

2. 

$\ast$is continuous;

3. 

$\varsigma \ast 1=\varsigma ,(\forall )\varsigma \in \left[0,1\right];$

4. 

$\left(\varsigma \ast \mathrm{ɷ}\right)\ast \rho =\varsigma \ast \left(\mathrm{ɷ}\ast \rho \right),(\forall )\varsigma ,\mathrm{ɷ},\rho \in \left[0,1\right];$

5. 

If$\varsigma \le \rho$and$\mathrm{ɷ}\le \Delta ,$with$\varsigma ,\mathrm{ɷ},\rho ,\Delta \in \left[0,1\right],$then$\varsigma \ast \mathrm{ɷ}\le \rho \ast \Delta .$

Definition 4

 ([13]). A binary operation $○$: [0, 1] $\times$ [0, 1] $\to$ [0, 1] is said to be a CTCN if it satisfies the following conditions:

1. 

$\varsigma ○\mathrm{ɷ}=\mathrm{ɷ}○\varsigma ,forall\varsigma ,\mathrm{ɷ}\in \left[0,1\right];$

2. 

$○$is continuous;

3. 

$\varsigma ○0=0,forall\varsigma \in \left[0,1\right];$

4. 

$\left(\varsigma ○\mathrm{ɷ}\right)○\rho =\varsigma ○\left(\mathrm{ɷ}○\rho \right),forall\varsigma ,\mathrm{ɷ},\rho \in \left[0,1\right];$

5. 

If$\varsigma \le \rho$and$\mathrm{ɷ}\le \Delta ,$with$\varsigma ,\mathrm{ɷ},\rho ,\Delta \in \left[0,1\right],$then$\varsigma ○\mathrm{ɷ}\le \rho ○\Delta .$

Definition 5

 ([14]). Suppose $\Xi \ne \varnothing$. Let $\ast$ be a CTN, $○$ be a CTCN and $b\ge 1$. Let $\wp ,\aleph$ be FSs on$\Xi \times \Xi \times \left(0,\infty \right)$, If they satisfy the following conditions for all $\varpi ,\varrho \in \Xi and\varrho ,\upsilon >0:$

• (IFB1)$\wp \left(\varpi ,\varrho ,\upsilon \right)+\aleph \left(\varpi ,\varrho ,\upsilon \right)\le 1;$
• (1FB2)$\wp \left(\varpi ,\varrho ,\upsilon \right)>0;$
• (IFB3)$\wp \left(\varpi ,\varrho ,\upsilon \right)=1\iff \varpi =\varrho ;$
• (IFB4)$\wp \left(\varpi ,\varrho ,\upsilon \right)=\wp \left(\varrho ,\varpi ,\upsilon \right);$
• (IFB5)$\wp \left(\varpi ,\lambda ,b\left(\upsilon +\varrho \right)\right)\ge \wp \left(\varpi ,\varrho ,\upsilon \right)\ast \wp \left(\varrho ,\lambda ,\varrho \right);$
• (IFB6)$\wp \left(\varpi ,\varrho ,·\right)$is a non-decreasing function of${ℝ}^{+}and\underset{\upsilon \to \infty }{lim}\wp \left(\varpi ,\varrho ,\upsilon \right)=1$;
• (IFB7)$\aleph \left(\varpi ,\varrho ,\upsilon \right)>0;$
• (IFB8)$\aleph \left(\varpi ,\varrho ,\upsilon \right)=0$ $\iff \varpi =\varrho ;$
• (IFB9)$\aleph \left(\varpi ,\varrho ,\upsilon \right)=\aleph \left(\varrho ,\varpi ,\upsilon \right);$
• (IFB10)$\aleph \left(\varpi ,\lambda ,b\left(\upsilon +\varrho \right)\right)\le \aleph \left(\varpi ,\varrho ,\upsilon \right)○\aleph \left(\varrho ,\lambda ,\varrho \right);$
• (IFB11)$\aleph \left(\varpi ,\varrho ,·\right)$is a non-increasing function of${ℝ}^{+}$and$\underset{\upsilon \to \infty }{lim}\aleph \left(\varpi ,\varrho ,\upsilon \right)=0;$
• then$(\Xi ,\wp ,\aleph ,*,○)$is said to be IFBMS.

Definition 6

 ([25]). Let $\Xi \ne \varnothing$. Suppose $\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$ are non-comparable functions. Let $\ast$ be a CTN and $○$ be a CTCN. Let $\wp ,\aleph$ be FSs on $\Xi \times \Xi \times \left(0,\infty \right)$. If they satisfy the following conditions for all $\varpi ,\varrho ,\lambda \in \Xi$:

• (IFD1)$\wp \left(\varpi ,\varrho ,\upsilon \right)+\aleph \left(\varpi ,\varrho ,\upsilon \right)\le 1;$
• (IFD2)$\wp \left(\varpi ,\varrho ,\upsilon \right)>0;$
• (IFD3)$\wp \left(\varpi ,\varrho ,\upsilon \right)=1forall\upsilon >0,ifandonlyif\varpi =\varrho ;$
• (IFD4)$\wp \left(\varpi ,\varrho ,\upsilon \right)=\wp \left(\varrho ,\varpi ,\upsilon \right);$
• (IFD5)$\wp \left(\varpi ,\lambda ,\upsilon +\varrho \right)\ge \wp \left(\varpi ,\varrho ,\frac{\upsilon }{\mathrm{П}\left(\varpi ,\varrho \right)}\right)\ast \wp \left(\varrho ,\lambda ,\frac{\varrho }{\mathrm{Ƹ}\left(\varrho ,\lambda \right)}\right);$
• (IFD6)$\wp \left(\varpi ,\varrho ,·\right):\left(0,\infty \right)\to \left[0,1\right]$is left continuous;
• (IFD7)$\aleph \left(\varpi ,\varrho ,\upsilon \right)>0;$
• (IFD8)$\aleph \left(\varpi ,\varrho ,\upsilon \right)=0forall\upsilon >0,ifandonlyif\varpi =\varrho ;$
• (IFD9)$\aleph \left(\varpi ,\varrho ,\upsilon \right)=\aleph \left(\varrho ,\varpi ,\upsilon \right);$
• (IFD10)$\aleph \left(\varpi ,\lambda ,\upsilon +\varrho \right)\le \aleph \left(\varpi ,\varrho ,\frac{\upsilon }{\mathrm{П}\left(\varpi ,\varrho \right)}\right)○\aleph \left(\varrho ,\lambda ,\frac{\varrho }{\mathrm{Ƹ}\left(\varrho ,\lambda \right)}\right);$
• (IFD11)$\aleph \left(\varpi ,\varrho ,·\right):\left(0,\infty \right)\to \left[0,1\right]$is left continuous;
• then$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is said to be IFDCMS.

3. Main Results

In this section, we introduce the concept of IFDCMLSs and prove some FP results for contraction mappings.

Definition 7.

Let$\Xi \ne \varnothing$. Suppose$\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$are non-comparable functions. Let$\ast$be a CTN and$○$be a CTCN. Let$\wp and\aleph$be FSs on$\Xi \times \Xi \times \left(0,\infty \right)$. If they satisfy the following conditions for all$\varpi ,\varrho ,\lambda \in \Xi :$

• (IFDL1)$\wp \left(\varpi ,\varrho ,\upsilon \right)+\aleph \left(\varpi ,\varrho ,\upsilon \right)\le 1;$
• (IFDL2)$\wp \left(\varpi ,\varrho ,\upsilon \right)>0;$
• (IFDL3)$\wp \left(\varpi ,\varrho ,\upsilon \right)=1forall\upsilon >0,implies\varpi =\varrho ;$
• (IFDL4)$\wp \left(\varpi ,\varrho ,\upsilon \right)=\wp \left(\varrho ,\varpi ,\upsilon \right);$
• (IFDL5)$\wp \left(\varpi ,\lambda ,\upsilon +\varrho \right)\ge \wp \left(\varpi ,\varrho ,\frac{\upsilon }{\mathrm{П}\left(\varpi ,\varrho \right)}\right)\ast \wp \left(\varrho ,\lambda ,\frac{\varrho }{\mathrm{Ƹ}\left(\varrho ,\lambda \right)}\right);$
• (IFDL6)$\wp \left(\varpi ,\varrho ,·\right):\left(0,\infty \right)\to \left[0,1\right]$is left continuous;
• (IFDL7)$\aleph \left(\varpi ,\varrho ,\upsilon \right)>0;$
• (IFDL8)$\aleph \left(\varpi ,\varrho ,\upsilon \right)=0forall\upsilon >0,implies\varpi =\varrho ;$
• (IFDL9)$\aleph \left(\varpi ,\varrho ,\upsilon \right)=\aleph \left(\varrho ,\varpi ,\upsilon \right);$
• (IFDL10)$\aleph \left(\varpi ,\lambda ,\upsilon +\varrho \right)\le \aleph \left(\varpi ,\varrho ,\frac{\upsilon }{\mathrm{П}\left(\varpi ,\varrho \right)}\right)○\aleph \left(\varrho ,\lambda ,\frac{\varrho }{\mathrm{Ƹ}\left(\varrho ,\lambda \right)}\right);$
• (IFDL11)$\aleph \left(\varpi ,\varrho ,·\right):\left(0,\infty \right)\to \left[0,1\right]$is left continuous;
  then$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is said to be an IFDCMLS.

Example 1.

Suppose$\Xi =\left[0,10\right]and\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$ are non-comparable functions given by$\mathrm{П}\left(\varpi ,\varrho \right)=\varpi +\varrho +1and\mathrm{Ƹ}\left(\varpi ,\varrho \right)={\varpi }^2+{\varrho }^2+1$. Define$\wp ,\aleph :\Xi \times \Xi \times \left(0,\infty \right)\to \left[0,1\right]$by

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=\frac{\upsilon }{\upsilon +max\left\{\varpi ,\varrho \right\}}$$

and

$$\aleph \left(\varpi ,\varrho ,\upsilon \right)=\frac{max\left\{\varpi ,\varrho \right\}}{\upsilon +max\left\{\varpi ,\varrho \right\}}.$$

Then,$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is an IFDCMLS with CTN$\varsigma \ast \mathrm{ɷ}=\varsigma \mathrm{ɷ}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$

Remark 1.

In IFDCMLS, the self-distance may be not equal to 1 for the membership function or 0 for non-membership function. So, every IFDCMS is an IFDCMLS, but the converse is not true.

Consider Example 1, and let$\varpi =\varrho =1$. Then

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=\frac{\upsilon }{\upsilon +max\left\{1,1\right\}}\ne 1$$

and

$$\aleph \left(\varpi ,\varrho ,\upsilon \right)=\frac{max\left\{1,1\right\}}{\upsilon +max\left\{1,1\right\}}\ne 0$$

.

Remark 2.

Example 2 is also fulfilled for CTN$\varsigma \ast \mathrm{ɷ}=min\left\{\varsigma ,\mathrm{ɷ}\right\}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$

Example 2.

Let$\Xi =\left[0,1\right]and\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$ be two NCFs given by$\mathrm{П}\left(\varpi ,\varrho \right)=\varpi +\varrho +1and\mathrm{Ƹ}\left(\varpi ,\varrho \right)={\varpi }^2+{\varrho }^2+1$.

Define$\wp ,\aleph :\Xi \times \Xi \times \left(0,\infty \right)\to \left[0,1\right]$as

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=\frac{\upsilon }{\upsilon +max{\left\{\varpi ,\varrho \right\}}^2},\aleph \left(\varpi ,\varrho ,\upsilon \right)=\frac{max{\left\{\varpi ,\varrho \right\}}^2}{\upsilon +max{\left\{\varpi ,\varrho \right\}}^2}.$$

Then$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is an IFDCMLS with CTN$\varsigma \ast \mathrm{ɷ}=\varsigma \mathrm{ɷ}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$The graphical behavior of functions$Pand\aleph$is shown inFigure 1.

Remark 3.

The above example also holds for

$$\mathrm{П}\left(\varpi ,\varrho \right)=\{\begin{array}{c}1if\varpi =\varrho ,\\ \frac{1+max\left\{\varpi ,\varrho \right\}}{min\left\{\varpi ,\varrho \right\}}if\varpi \ne \varrho \end{array}$$

and

$$\mathrm{Ƹ}\left(\varpi ,\varrho \right)=\{\begin{array}{c}1if\varpi =\varrho ,\\ \frac{1+max\left\{{\varpi }^2,{\varrho }^2\right\}}{min\left\{{\varpi }^2,{\varrho }^2\right\}}if\varpi \ne \varrho \end{array}.$$

Remark 4.

Example 3 is also fulfilled for CTN$\varsigma \ast \mathrm{ɷ}=min\left\{\varsigma ,\mathrm{ɷ}\right\}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$

Example 3.

Let$\Xi =\left[0,3\right]and\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$ be two NCFs given by$\mathrm{П}\left(\varpi ,\varrho \right)=\varpi +\varrho +1and\mathrm{Ƹ}\left(\varpi ,\varrho \right)={\varpi }^2+{\varrho }^2-1$. Define$\wp ,\aleph :\Xi \times \Xi \times \left(0,\infty \right)\to \left[0,1\right]$as

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=\frac{\upsilon +min\left\{\varpi ,\varrho \right\}}{\upsilon +max\left\{\varpi ,\varrho \right\}}$$

and

$$\aleph \left(\varpi ,\varrho ,\upsilon \right)=1-\frac{\upsilon +min\left\{\varpi ,\varrho \right\}}{\upsilon +max\left\{\varpi ,\varrho \right\}}.$$

Then$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is an IFDCMLS with CTN$\varsigma \ast \mathrm{ɷ}=\varsigma \mathrm{ɷ}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$The graphical behavior of functions$Pand\aleph$is shown inFigure 2.

Remark 5.

In the above example, if we let$\varsigma \ast \mathrm{ɷ}=min\left\{\varsigma ,\mathrm{ɷ}\right\}$,$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}$,$\varpi =1,\varrho =2,\lambda =3,\upsilon =0.01,\varrho =0.02with\mathrm{П}\left(\varpi ,\varrho \right)=\varpi +\varrho +1and\mathrm{Ƹ}\left(\varpi ,\varrho \right)={\varpi }^2+{\varrho }^2-1$. Then, it is not an IFDCMLS.

Proposition 1.

Let$\Xi =\left[0,1\right]$and$\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$be two NCFs given by$\mathrm{П}\left(\varpi ,\varrho \right)=2\left(\varpi +\varrho +1\right)and\mathrm{Ƹ}\left(\varpi ,\varrho \right)=2\left({\varpi }^2+{\varrho }^2+1\right).$Define$\aleph ,\wp$as

$$\wp \left(\varpi ,\varrho ,{\upsilon }^n\right)={\vartheta }^{-\frac{max{\left\{\varpi ,\varrho \right\}}^2}{{\upsilon }^n}},\aleph \left(\varpi ,\varrho ,{\upsilon }^n\right)=1-{\vartheta }^{-\frac{max{\left\{\varpi ,\varrho \right\}}^2}{{\upsilon }^n}}forall\varpi ,\varrho \in \Xi ,\upsilon >0$$

Then, let$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$be an IFDCMLS with$\varsigma \ast \mathrm{ɷ}=\varsigma \mathrm{ɷ}$and$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$The graphical behavior of functions$Pand\aleph$is shown inFigure 3.

Remark 6.

Proposition 1 is also satisfied for CTN$\varsigma \ast \mathrm{ɷ}=min\left\{\varsigma ,\mathrm{ɷ}\right\}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$

Proposition 2.

Let$\Xi =\left[0,1\right]$and$\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$be two NCFs given by$\mathrm{П}\left(\varpi ,\varrho \right)=2\left(\varpi +\varrho +1\right)and\mathrm{Ƹ}\left(\varpi ,\varrho \right)=2\left({\varpi }^2+{\varrho }^2+1\right).$Define$\aleph ,\wp$as

$$\wp \left(\varpi ,\varrho ,{\upsilon }^n\right)={\left[{\vartheta }^{\frac{max{\left\{x,y\right\}}^2}{{\upsilon }^n}}\right]}^{-1},\aleph \left(\varpi ,\varrho ,{\upsilon }^n\right)=1-{\left[{\vartheta }^{\frac{max{\left\{x,y\right\}}^2}{{\upsilon }^n}}\right]}^{-1}forall\varpi ,\varrho \in \Xi ,\upsilon >0$$

.

Then$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is an IFDCMLS with CTN$\varsigma \ast \mathrm{ɷ}=\varsigma \mathrm{ɷ}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$The graphical behavior of functions$Pand\aleph$is shown inFigure 4.

Remark 7.

The above proposition is also satisfied for CTN$\varsigma \ast \mathrm{ɷ}=min\left\{\varsigma ,\mathrm{ɷ}\right\}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$

Definition 8.

Let an open ball$B\left(\varpi ,r,\upsilon \right)$in an IFDCMLS$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$with center$\varpi ,$radius$r,0<r<1$and$\upsilon >0$be defined as follows:

$$B\left(\varpi ,r,\upsilon \right)=\left\{\varrho \in \Xi :\wp \left(\varpi ,\varrho ,\upsilon \right)>1-r,\aleph \left(\varpi ,\varrho ,\upsilon \right)<r\right\}.$$

Definition 9.

Suppose$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is an IFDCMLS. Let$\left\{{\varpi }_n\right\}$be a sequence in$\Xi$. Then

(i) 

$\left\{{\varpi }_n\right\}$is said to be a convergent sequence if there exists$\varpi \in \Xi$such that

$$\underset{n\to \infty }{lim}\wp \left({\varpi }_n,\varpi ,\upsilon \right)=\wp \left(\varpi ,\varpi ,\upsilon \right),\underset{n\to \infty }{lim}\aleph \left({\varpi }_n,\varpi ,\upsilon \right)=\aleph \left(\varpi ,\varpi ,\upsilon \right),forall\upsilon >0$$

.

(ii) 

$\left\{{\varkappa }_n\right\}$is said to be a Cauchy sequence (CS) if for every$\upsilon >0$there exists$n_0\in \mathbb{N}$such that$\underset{n\to \infty }{lim}\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right),and\underset{n\to \infty }{lim}\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)$exists and is finite.

(iii) 

An IFDCMLS$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is said to be complete if every CS is convergent in$\Xi ,$that is

$$\underset{n\to \infty }{lim}\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)=\underset{n\to \infty }{lim}\wp \left({\varpi }_n,\varpi ,\upsilon \right)=\wp \left(\varpi ,\varpi ,\upsilon \right),$$

$$\underset{n\to \infty }{lim}\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)=\underset{n\to \infty }{lim}\aleph \left({\varpi }_n,\varpi ,\upsilon \right)=\aleph \left(\varpi ,\varpi ,\upsilon \right).$$

Lemma 1.

Let$\varpi and\varrho$be any two points in an IFDCMLS$\left(\Xi ,\wp ,\aleph ,\ast ,○\right).$If for any$\tau \in \left(0,1\right),$we have

$$\wp \left(\varpi ,\varrho ,\tau \upsilon \right)\ge \wp \left(\varpi ,\varrho ,\upsilon \right),\aleph \left(\varpi ,\varrho ,\tau \upsilon \right)\le \aleph \left(\varpi ,\varrho ,\upsilon \right),$$

then$\varpi =\varrho .$

Theorem 1.

Let$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$be a complete IFDCMLS with$\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left(0,1\right)$and$0<\tau <1,$assume that

$$\underset{\upsilon \to \infty }{lim}\wp \left(\varpi ,\varrho ,\upsilon \right)=1and\underset{\upsilon \to \infty }{lim}\aleph \left(\varpi ,\varrho ,\upsilon \right)=0$$

(1)

for all$\varpi ,\varrho \in \Xi$and$\upsilon >0$. Let$\xi :\Xi \to \Xi$be a mapping satisfying

$$\wp \left(\xi \varpi ,\xi \varrho ,\tau \upsilon \right)\ge \wp \left(\varpi ,\varrho ,\upsilon \right)and\aleph \left(\xi \varpi ,\xi \varrho ,\tau \upsilon \right)\le \aleph \left(\varpi ,\varrho ,\upsilon \right)$$

(2)

for all$\varpi ,\varrho \in \Xi$and$\upsilon >0$. Then$\xi$has a unique FP.

Proof. 

Suppose ${\mathsf{\varpi }}_0$ is an arbitrary point in $\mathsf{\Xi }$ and define a sequence ${\mathsf{\varpi }}_{\mathrm{n}}$ by ${\mathsf{\varpi }}_{\mathrm{n}}={\mathsf{\xi }}^{\mathrm{n}}{\mathsf{\varpi }}_0=\mathsf{\xi }{\mathsf{\varpi }}_{\mathrm{n}-1}$, $\mathrm{n}\in \mathbb{N}$. By utilizing $\left(1\right)$ for all $\mathsf{\upsilon }>0,$ we deduce

$$\wp \left({\varpi }_n,{\varpi }_{n+1},\tau \upsilon \right)=\wp \left(\xi {\varpi }_{n-1},\xi {\varpi }_n,\tau \upsilon \right)\ge \wp \left({\varpi }_{n-1},{\varpi }_n,\upsilon \right)\ge \wp \left({\varpi }_{n-2},{\varpi }_{n-1},\frac{\upsilon }{\tau }\right)$$

$$\ge \wp \left({\varpi }_{n-3},{\varpi }_{n-2},\frac{\upsilon }{{\tau }^2}\right)\ge \cdots \ge \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\tau }^{n-1}}\right)$$

and

$$\aleph \left({\varpi }_n,{\varpi }_{n+1},\tau \upsilon \right)=\aleph \left(\xi {\varpi }_{n-1},\xi {\varpi }_n,\tau \upsilon \right)\le \aleph \left({\varpi }_{n-1},{\varpi }_n,\upsilon \right)\le \aleph \left({\varpi }_{n-2},{\varpi }_{n-1},\frac{\upsilon }{\tau }\right)$$

$$\le \aleph \left({\varpi }_{n-3},{\varpi }_{n-2},\frac{\upsilon }{{\tau }^2}\right)\le \cdots \le \aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\tau }^{n-1}}\right)$$

We obtain

$$\wp \left({\varpi }_n,{\varpi }_{n+1},\tau \upsilon \right)\ge \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\tau }^{n-1}}\right)\mathrm{and}\aleph \left({\varpi }_n,{\varpi }_{n+1},\tau \upsilon \right)\le \aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\tau }^{n-1}}\right)$$

(3)

for any $\lambda \in \mathbb{N},\mathrm{using}\left(\mathrm{IFDL}5\right)\mathrm{and}\left(\mathrm{IFDL}10\right)$,

$$\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+\lambda },\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+2},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+3},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+3},{\varpi }_{n+4},\frac{\upsilon }{{\left(2\right)}^4\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+3},{\varpi }_{n+4}\right)\right)}\right)\ast \cdots \ast$$

$$\wp \left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1},\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

and

$$\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+\lambda },\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+2},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+3},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+3},{\varpi }_{n+4},\frac{\upsilon }{{\left(2\right)}^4\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+3},{\varpi }_{n+4}\right)\right)}\right)○\cdots ○$$

$$\aleph \left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1},\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

Using inequalities in (3), we have

$$\ge \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{2{\left(\tau \right)}^{n-1}\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^2{\left(\tau \right)}^n\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^3{\left(\tau \right)}^{n+1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^4{\left(\tau \right)}^{n+2}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+3},{\varpi }_{n+4}\right)\right)}\right)\ast \cdots \ast$$

$$\wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}{\left(\tau \right)}^{n+\lambda -2}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}{\left(\tau \right)}^{n+\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

and

$$\le \aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{2{\left(\tau \right)}^{n-1}\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^2{\left(\tau \right)}^n\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^3{\left(\tau \right)}^{n+1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^4{\left(\tau \right)}^{n+2}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+3},{\varpi }_{n+4}\right)\right)}\right)○\cdots ○$$

$$\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}{\left(\tau \right)}^{n+\lambda -2}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}{\left(\tau \right)}^{n+\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

Utilizing equations in (1) and for $n\to \infty ,$ we obtain

$$\underset{n\to \infty }{\lim }\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)=1\ast 1\ast \cdots \ast 1=1$$

$\mathrm{and}$

$$\underset{n\to \infty }{\lim }\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)=0○0○\cdots ○0=0$$

.

That is, $\left\{{\varpi }_n\right\}$ is a CS. Therefore, $\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$ is a complete IFDCMLS, and there exists $\varpi$ in $\Xi$.

Now investigate that $\varpi$ is an FP of ξ, using $\left(\mathrm{IFDL}5\right),\left(\mathrm{IFDL}10\right)\mathrm{and}\left(2\right)$ of Definition 7, we obtain

$$\wp \left(\varpi ,\xi \varpi ,\upsilon \right)\ge \wp \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},\xi \varpi ,\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)\right)}\right)$$

$$\wp \left(\varpi ,\xi \varpi ,\upsilon \right)\ge \wp \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left(\xi {\varpi }_n,\xi \varpi ,\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)\right)}\right)$$

$$\wp \left(\varpi ,\xi \varpi ,\upsilon \right)\ge \wp \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_n,\varpi ,\frac{\upsilon }{2\tau \left(\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)\right)}\right)\to 1\ast 1=1$$

$\mathrm{as}n\to \infty ,$ and

$$\aleph \left(\varpi ,\xi \varpi ,\upsilon \right)\le \aleph \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},\xi \varpi ,\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)\right)}\right)$$

$$\aleph \left(\varpi ,\xi \varpi ,\upsilon \right)\le \aleph \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left(\xi {\varpi }_n,\xi \varpi ,\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)\right)}\right)$$

$$\aleph \left(\varpi ,\xi \varpi ,\upsilon \right)\le \aleph \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_n,\varpi ,\frac{\upsilon }{2\tau \left(\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)\right)}\right)\to 0○0=0$$

$\mathrm{as}n\to \infty .$ Hence, $\xi \varpi =\varpi$.

Uniqueness: Given another FP, i.e., $\xi \rho =\rho$ for some $\rho \in \Xi$, then

$$1\ge \wp \left(\rho ,\varpi ,\upsilon \right)=\wp \left(\xi \rho ,\xi \varpi ,\upsilon \right)\ge \wp \left(\rho ,\varpi ,\frac{\upsilon }{\tau }\right)=\wp \left(\xi \rho ,\xi \varpi ,\frac{\upsilon }{\tau }\right)$$

$$\ge \wp \left(\rho ,\varpi ,\frac{\upsilon }{{\tau }^2}\right)\ge \cdots \ge \wp \left(\rho ,\varpi ,\frac{\upsilon }{{\tau }^n}\right)\to 1\mathrm{as}n\to \infty ,$$

and

$$0\le \aleph \left(\rho ,\varpi ,\upsilon \right)=\aleph \left(\xi \rho ,\xi \varpi ,\upsilon \right)\le \aleph \left(\rho ,\varpi ,\frac{\upsilon }{\tau }\right)=\aleph \left(\xi \rho ,\xi \varpi ,\frac{\upsilon }{\tau }\right)$$

$$\le \aleph \left(\rho ,\varpi ,\frac{\upsilon }{{\tau }^2}\right)\le \cdots \le \aleph \left(\rho ,\varpi ,\frac{\upsilon }{{\tau }^n}\right)\to 0\mathrm{as}n\to \infty ,$$

by utilizing $\left(\mathrm{IFDL}3\right)\mathrm{and}\left(\mathrm{IFDL}8\right),\mathrm{we}\mathrm{obtain}\varpi =\rho$. □

Definition 10.

Suppose$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is an IFDCMLS. A mapping$\xi :\Xi \to \Xi$is said to be a D-controlled intuitionistic fuzzy-like contraction if there exists$0<\tau <1$, such that

$$\frac{1}{\wp \left(\xi \varpi ,\xi \varrho ,\upsilon \right)}-1\le \tau \left[\frac{1}{\wp \left(\varpi ,\varrho ,\upsilon \right)}-1\right]$$

(4)

and

$$\aleph \left(\xi \varpi ,\xi \varrho ,\upsilon \right)\le \tau \aleph \left(\varpi ,\varrho ,\upsilon \right),$$

(5)

for all$\varpi ,\varrho \in \Xi and\upsilon >0$.

Theorem 2.

Let$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$be a complete IFDCMLS with$\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$and suppose that

$$\underset{\upsilon \to \infty }{lim}\wp \left(\varpi ,\varrho ,\upsilon \right)=1and\underset{\upsilon \to \infty }{lim}\aleph \left(\varpi ,\varrho ,\upsilon \right)=0$$

(6)

for all$\varpi ,\varrho \in \Xi$and$\upsilon >0$. Suppose$\xi :\Xi \to \Xi$is a D-controlled intuitionistic fuzzy-like contraction. Moreover, assume that for a random point${\varpi }_0\in \Xi ,forn,\lambda \in \mathbb{N},$with${\varpi }_n={\xi }^n{\varpi }_0=\xi {\varpi }_{n-1}$. Then$\xi$has a unique FP.

Proof. 

Suppose ${\mathsf{\varpi }}_0$ is an arbitrary point in $\mathsf{\Xi }$ and define a sequence ${\mathsf{\varpi }}_{\mathrm{n}}$ by ${\mathsf{\varpi }}_{\mathrm{n}}={\mathsf{\xi }}^{\mathrm{n}}{\mathsf{\varpi }}_0=\mathsf{\xi }{\mathsf{\varpi }}_{\mathrm{n}-1}$, $\mathrm{n}\in \mathbb{N}$. By utilizing $\left(4\right)$ and $\left(5\right)$ for all $\mathsf{\upsilon }>0,$ $\mathrm{n}>\mathsf{\lambda },$ we deduce

$$\frac{1}{\wp \left({\varpi }_n,{\varpi }_{n+1},\upsilon \right)}-1=\frac{1}{\wp \left(\xi {\varpi }_{n-1},\xi {\varpi }_n,\upsilon \right)}-1$$

$$\le \tau \left[\frac{1}{\wp \left({\varpi }_{n-1},{\varpi }_n,\upsilon \right)}-1\right]=\frac{\tau }{\wp \left({\varpi }_{n-1},{\varpi }_n,\upsilon \right)}-\tau$$

$$\Rightarrow \frac{1}{\wp \left({\varpi }_n,{\varpi }_{n+1},\upsilon \right)}\le \frac{\tau }{\wp \left({\varpi }_{n-1},{\varpi }_n,\upsilon \right)}+\left(1-\tau \right)$$

$$\le \frac{{\tau }^2}{\wp \left({\varpi }_{n-2},{\varpi }_{n-1},\upsilon \right)}+\tau \left(1-\tau \right)+\left(1-\tau \right)$$

Similarly, we deduce

$$\frac{1}{\wp \left({\varpi }_n,{\varpi }_{n+1},\upsilon \right)}\le \frac{{\tau }^n}{\wp \left({\varpi }_0,{\varpi }_1,\upsilon \right)}+{\tau }^{n-1}\left(1-\tau \right)+{\tau }^{n-2}\left(1-\tau \right)+\cdots +\tau \left(1-\tau \right)+\left(1-\tau \right)$$

$$\le \frac{{\tau }^n}{\wp \left({\varpi }_0,{\varpi }_1,\upsilon \right)}+\left({\tau }^{n-1}+{\tau }^{n-2}+\cdots +1\right)\left(1-\tau \right)\le \frac{{\tau }^n}{\wp \left({\varpi }_0,{\varpi }_1,\upsilon \right)}+\left(1-{\tau }^n\right)$$

We obtain

$$\frac{1}{\frac{{\tau }^n}{\wp \left({\varpi }_0,{\varpi }_1,\upsilon \right)}+\left(1-{\tau }^n\right)}\le \wp \left({\varpi }_n,{\varpi }_{n+1},\upsilon \right)$$

(7)

and

$$\aleph \left({\varpi }_n,{\varpi }_{n+1},\upsilon \right)=\aleph \left(\xi {\varpi }_{n-1},\xi {\varpi }_n,\upsilon \right)\le \tau \aleph \left({\varpi }_{n-1},{\varpi }_n,\upsilon \right)=\tau \aleph \left(\xi {\varpi }_{n-2},\xi {\varpi }_{n-1},\upsilon \right)$$

$$\le {\tau }^2\aleph \left({\varpi }_{n-2},{\varpi }_{n-1},\upsilon \right)\le \cdots \le {\tau }^n\aleph \left({\varpi }_0,{\varpi }_1,\upsilon \right)$$

(8)

for any $\lambda \in \mathbb{N},\mathrm{using}\left(\mathrm{IFDL}5\right)\mathrm{and}\left(\mathrm{IFDL}10\right)$, we deduce

$$\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+\lambda },\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+2},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+3},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)\ast \wp \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+3},{\varpi }_{n+4},\frac{\upsilon }{{\left(2\right)}^4\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+3},{\varpi }_{n+4}\right)\right)}\right)\ast \cdots \ast$$

$$\wp \left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1},\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$\ast \wp \left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

and

$$\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+\lambda },\frac{\upsilon }{2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+2},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+3},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○\aleph \left({\varpi }_{n+1},{\varpi }_{n+2},\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+2},{\varpi }_{n+3},\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+3},{\varpi }_{n+4},\frac{\upsilon }{{\left(2\right)}^4\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+3},{\varpi }_{n+4}\right)\right)}\right)○\cdots ○$$

$$\aleph \left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1},\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$○\aleph \left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda },\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

$$\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)\ge \frac{1}{\frac{{\tau }^n}{\wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)}+\left(1-{\tau }^n\right)}\ast \frac{1}{\frac{{\tau }^{n+1}}{\wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)}+\left(1-{\tau }^{n+1}\right)}$$

$$\ast \frac{1}{\frac{{\tau }^{n+2}}{\wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)}+\left(1-{\tau }^{n+2}\right)}\ast \cdots \ast$$

$$\frac{1}{\frac{{\tau }^{n+\lambda -2}}{\wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)}+\left(1-{\tau }^{n+\lambda -2}\right)}$$

$$\ast \frac{1}{\frac{{\tau }^{n+\lambda -1}}{\wp \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)}+\left(1-{\tau }^{n+\lambda -1}\right)}$$

and

$$\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)\le {\tau }^n\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{2\left(\mathrm{П}\left({\varpi }_n,{\varpi }_{n+1}\right)\right)}\right)○{\tau }^{n+1}\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^2\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+1},{\varpi }_{n+2}\right)\right)}\right)$$

$$○{\tau }^{n+2}\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^3\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+2},{\varpi }_{n+3}\right)\right)}\right)○\cdots ○$$

$${\tau }^{n+\lambda -2}\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda }\right)\mathrm{П}\left({\varpi }_{n+\lambda -2},{\varpi }_{n+\lambda -1}\right)\right)}\right)$$

$$○{\tau }^{n+\lambda -1}\aleph \left({\varpi }_0,{\varpi }_1,\frac{\upsilon }{{\left(2\right)}^{\lambda -1}\left(\mathrm{Ƹ}\left({\varpi }_{n+1},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+2},{\varpi }_{n+\lambda }\right)\mathrm{Ƹ}\left({\varpi }_{n+3},{\varpi }_{n+\lambda }\right)\cdots \mathrm{Ƹ}\left({\varpi }_{n+\lambda -1},{\varpi }_{n+\lambda }\right)\right)}\right)$$

Therefore,

$$\underset{n\to \infty }{\lim }\wp \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)=1\ast 1\ast \cdots \ast 1=1$$

$\mathrm{and}$

$$\underset{n\to \infty }{\lim }\aleph \left({\varpi }_n,{\varpi }_{n+\lambda },\upsilon \right)=0○0○\cdots ○0=0$$

.

That is, $\left\{{\varpi }_n\right\}$ is a CS. Therefore, let $\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$ be a complete IFDCMLS, so there exists $\varpi$ in $\Xi .$ Now investigate that $\varpi$ is an FP of ξ, using $\left(\mathrm{IFDL}5\right)\mathrm{and}\left(\mathrm{IFDL}10\right),$ we have

$$\frac{1}{\wp \left(\xi {\varpi }_n,\xi \varpi ,\upsilon \right)}-1\le \tau \left[\frac{1}{\wp \left({\varpi }_n,\varpi ,\upsilon \right)}-1\right]=\frac{\tau }{\wp \left({\varpi }_n,\varpi ,\upsilon \right)}-\tau$$

$$\Rightarrow \frac{1}{\frac{\tau }{\wp \left({\varpi }_n,\varpi ,\upsilon \right)}+\left(1-\tau \right)}\le \wp \left(\xi {\varpi }_n,\xi \varpi ,\upsilon \right).$$

Using the above inequality,

$$\wp \left(\varpi ,\xi \varpi ,\upsilon \right)\ge \wp \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)}\right)\ast \wp \left({\varpi }_{n+1},\xi \varpi ,\frac{\upsilon }{2\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)}\right)$$

$$\ge \wp \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)}\right)\ast \wp \left(\xi {\varpi }_n,\xi \varpi ,\frac{\upsilon }{2\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)}\right)$$

$$\ge \wp \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{\left(2\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)\right)}\right)\ast \frac{1}{\frac{\tau }{\wp \left({\varpi }_n,\varpi ,\frac{\upsilon }{2\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)}\right)}+\left(1-\tau \right)}\to 1\ast 1=1$$

$\mathrm{as}n\to \infty$, and

$$\aleph \left(\varpi ,\xi \varpi ,\upsilon \right)\le \aleph \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)}\right)○\aleph \left({\varpi }_{n+1},\xi \varpi ,\frac{\upsilon }{2\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)}\right)$$

$$\le \aleph \left(\varpi ,{\varpi }_{n+1},\frac{\upsilon }{2\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)}\right)○\aleph \left(\xi {\varpi }_n,\xi \varpi ,\frac{\upsilon }{2\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)}\right)$$

$$\le \aleph \left({\varpi }_n,{\varpi }_{n+1},\frac{\upsilon }{2\mathrm{П}\left(\varpi ,{\varpi }_{n+1}\right)}\right)○\tau \aleph \left({\varpi }_n,\varpi ,\frac{\upsilon }{2\mathrm{Ƹ}\left({\varpi }_{n+1},\xi \varpi \right)}\right)\to 0○0=0\mathrm{as}n\to \infty$$

That is $\xi \varpi =\varpi$.

Uniqueness: Suppose another FP, i.e., $\xi \rho =\rho$ for some $\rho \in \Xi$, then we have

$$\frac{1}{\wp \left(\varpi ,\rho ,\upsilon \right)}-1=\frac{1}{\wp \left(\xi \varpi ,\xi \rho ,\upsilon \right)}-1$$

$$\le \tau \left[\frac{1}{\wp \left(\varpi ,\rho ,\upsilon \right)}-1\right]<\frac{1}{\wp \left(\varpi ,\rho ,\upsilon \right)}-1$$

a contradiction, and

$$\aleph \left(\varpi ,\rho ,\upsilon \right)=\aleph \left(\xi \varpi ,\xi \rho ,\upsilon \right)\le \tau \aleph \left(\varpi ,\rho ,\upsilon \right)<\aleph \left(\varpi ,\rho ,\upsilon \right)$$

a contradiction. Therefore, we must have $\wp \left(\varpi ,\rho ,\upsilon \right)=1\mathrm{and}\aleph \left(\varpi ,\rho ,\upsilon \right)=0$, hence $\varpi =\rho$. □

Example 4.

Let$\Xi =\left[0,1\right]and\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$ be non-comparable functions defined by

$$\mathrm{П}\left(\varpi ,\varrho \right)=\{\begin{array}{c}1if\varpi =\varrho ,\\ \frac{1+max\left\{\varpi ,\varrho \right\}}{min\left\{\varpi ,\varrho \right\}}if\varpi \ne \varrho \end{array}$$

and

$$\mathrm{Ƹ}\left(\varpi ,\varrho \right)=\{\begin{array}{c}1if\varpi =\varrho ,\\ \frac{1+max\left\{{\varpi }^2,{\varrho }^2\right\}}{min\left\{{\varpi }^2,{\varrho }^2\right\}}if\varpi \ne \varrho .\end{array}$$

Define$\wp ,\aleph :\Xi \times \Xi \times \left(0,\infty \right)\to \left[0,1\right]$as

$$\wp \left(\varpi ,\varrho ,\upsilon \right)=\frac{\upsilon }{\upsilon +max{\left\{\varpi ,\varrho \right\}}^2},\aleph \left(\varpi ,\varrho ,\upsilon \right)=\frac{max{\left\{\varpi ,\varrho \right\}}^2}{\upsilon +max{\left\{\varpi ,\varrho \right\}}^2}.$$

Then,$\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$is a complete IFDCMS with CTN$\varsigma \ast \mathrm{ɷ}=\varsigma \mathrm{ɷ}$and CTCN$\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$

Define$\xi :\Xi \to \Xi by\xi \left(\varpi \right)=\frac{1-2^{-\varpi }}{3}$and take$\tau \in \left[\frac{1}{2},1\right),$then

$$\wp \left(\xi \varpi ,\xi \varrho ,\tau \upsilon \right)=\wp \left(\frac{1-2^{-\varpi }}{3},\frac{1-2^{-\varrho }}{3},\tau \upsilon \right)$$

$$=\frac{\tau \upsilon }{\tau \upsilon +max{\left\{\frac{1-2^{-\varpi }}{3},\frac{1-2^{-\varrho }}{3}\right\}}^2}\ge \frac{\upsilon }{\upsilon +max{\left\{\varpi ,\varrho \right\}}^2}=\wp \left(\varpi ,\varrho ,\upsilon \right)$$

and

$$\aleph \left(\xi \varpi ,\xi \varrho ,\tau \upsilon \right)=\aleph \left(\frac{1-2^{-\varpi }}{3},\frac{1-2^{-\varrho }}{3},\tau \upsilon \right)$$

$$=\frac{max{\left\{\frac{1-2^{-\varpi }}{3},\frac{1-2^{-\varrho }}{3}\right\}}^2}{\tau \upsilon +max{\left\{\frac{1-2^{-\varpi }}{3},\frac{1-2^{-\varrho }}{3}\right\}}^2}\le \frac{max{\left\{\varpi ,\varrho \right\}}^2}{\upsilon +max{\left\{\varpi ,\varrho \right\}}^2}=\aleph \left(\varpi ,\varrho ,\upsilon \right).$$

This is seen in Figure 5 and Figure 6, which depict the behavior of contraction mapping.

Hence, all conditions of Theorem 1 are satisfied and $0$ is a unique FP for $\xi$ as shown in Figure 7.

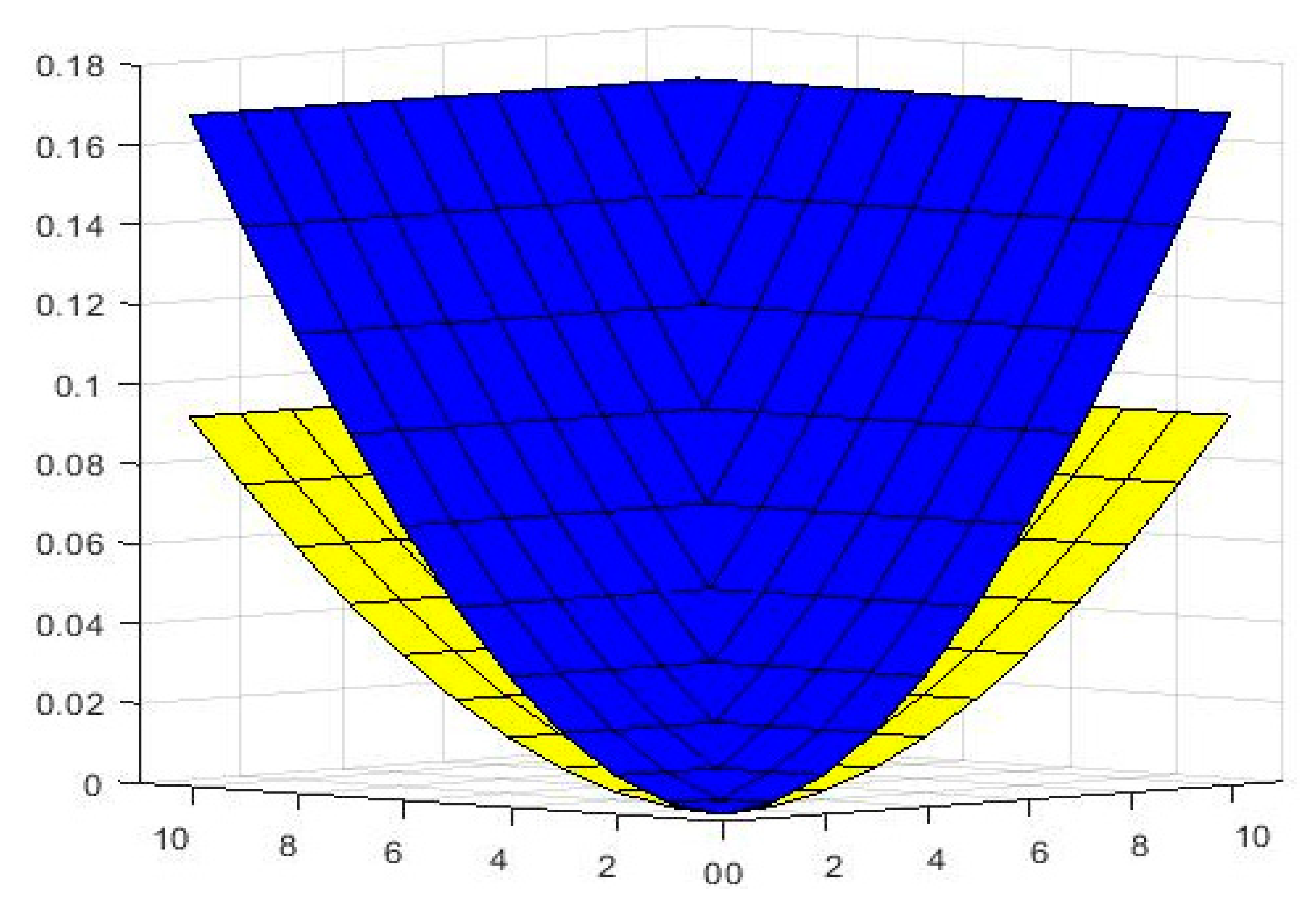
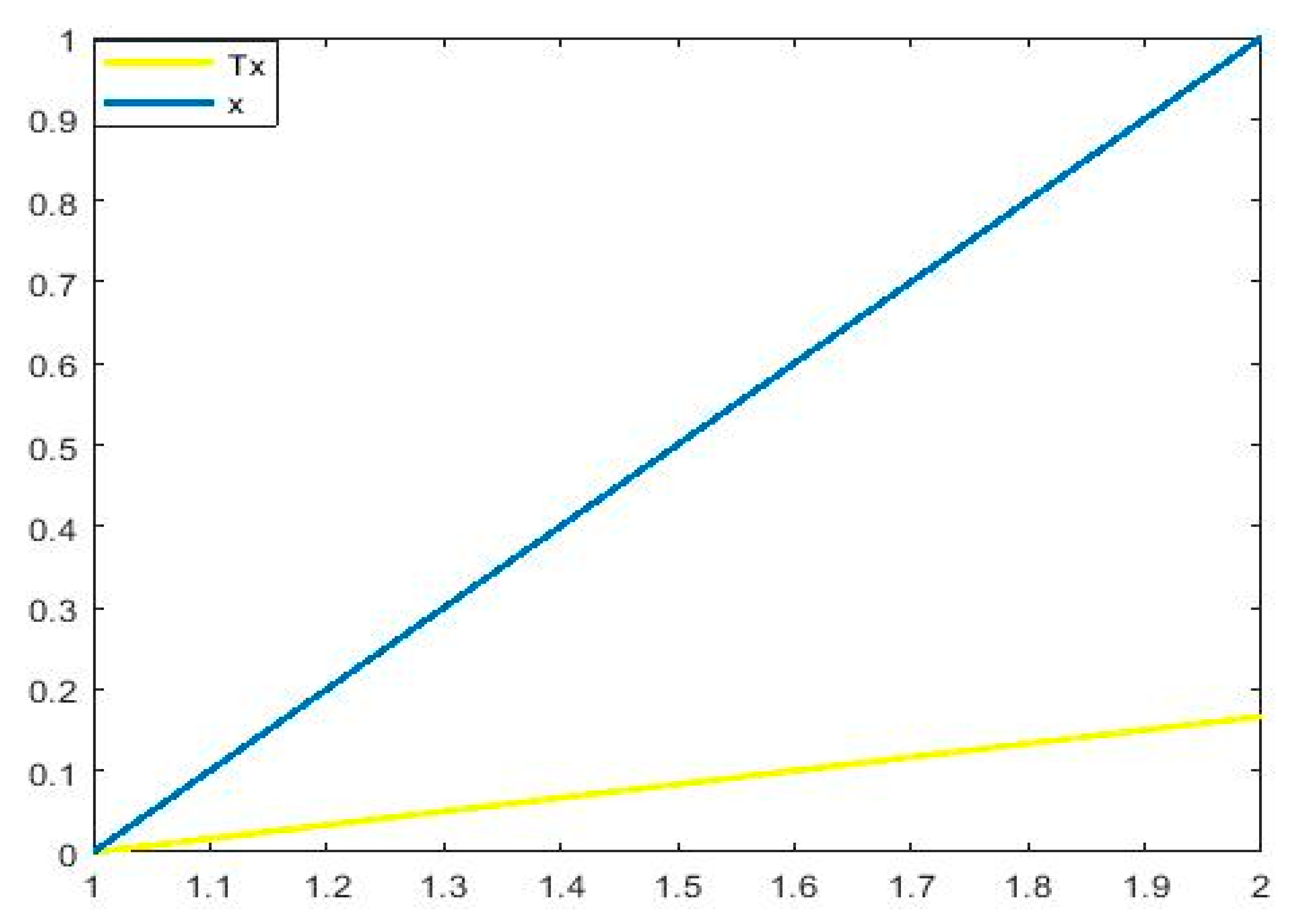
4. Application to an Integral Equation

Suppose $\Xi =C\left(\left[\vartheta ,\mu \right],ℝ\right)$ is a set of all the real-valued continuous functions on the closed interval $\left[\vartheta ,\mu \right]$.

Suppose the following integral equation:

$$\varpi \left(\gamma \right)=\eta \left(j\right)+\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\varpi \left(\gamma \right)\Delta j\mathrm{for}\gamma ,j\in \left[\vartheta ,\mu \right]$$

(9)

where $\delta >0,$ $F\in \Xi$ and $\eta \left(j\right)$ is a fuzzy function of $j:j\in \left[\vartheta ,\mu \right]$. Now, we define $\wp \mathrm{and}\aleph$ by

$$\wp \left(\varpi \left(\gamma \right),\varrho \left(\gamma \right),\upsilon \right)=\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\upsilon }{\upsilon +\max {\left\{\varpi \left(\gamma \right),\varrho \left(\gamma \right)\right\}}^2}\mathrm{for}\mathrm{all}\varpi ,\varrho \in \Xi \mathrm{and}\upsilon >0$$

and

$$\aleph \left(\varpi \left(\gamma \right),\varrho \left(\gamma \right),\upsilon \right)=1-\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\upsilon }{\upsilon +\max {\left\{\varpi \left(\gamma \right),\varrho \left(\gamma \right)\right\}}^2}\mathrm{for}\mathrm{all}\varpi ,\varrho \in \Xi \mathrm{and}\upsilon >0$$

with CTN and CTCN defined by $\varsigma \ast \mathrm{ɷ}=\varsigma .\mathrm{ɷ}\mathrm{and}\varsigma ○\mathrm{ɷ}=max\left\{\varsigma ,\mathrm{ɷ}\right\}.$ Define $\mathrm{П},\mathrm{Ƹ}:\Xi \times \Xi \to \left[1,\infty \right)$ as

$$\mathrm{П}\left(\varpi ,\varrho \right)=\{\begin{array}{c}1\mathrm{if}\varpi =\varrho ;\\ \frac{1+\max \left\{\varpi ,\varrho \right\}}{\min \left\{\varpi ,\varrho \right\}}\mathrm{if}\varpi \ne \varrho \ne 0\end{array};$$

$$\mathrm{Ƹ}\left(\varpi ,\varrho \right)=\{\begin{array}{c}1\mathrm{if}\varpi =\varrho ,\\ \frac{1+\max \left\{{\varpi }^2,{\varrho }^2\right\}}{\min \left\{{\varpi }^2,{\varrho }^2\right\}}\mathrm{if}\varpi \ne \varrho \end{array}.$$

Then, let $\left(\Xi ,\wp ,\aleph ,\ast ,○\right)$ be a complete IFDCMLS.

Let $\max {\left\{F\left(\gamma ,j\right)\varpi \left(\gamma \right),F\left(\gamma ,j\right)\varrho \left(\gamma \right)\right\}}^2\le \max {\left\{\varpi \left(\gamma \right),\varrho \left(\gamma \right)\right\}}^2$ for all $\varpi ,\varrho \in \Xi$, $\tau \in \left(0,1\right)$ and for all $\gamma ,j\in \left[\vartheta ,\mu \right]$. Additionally, suppose ${\left(\delta {{\displaystyle \int }}_{\vartheta }^{\mu }\Delta j\right)}^2\le \tau <1$. Then, integral Equation (9) has a unique solution.

Proof. 

Define $\mathsf{\xi }:\mathsf{\Xi }\to \mathsf{\Xi }$ by

$$\xi \varpi \left(\gamma \right)=\eta \left(j\right)+\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j\mathrm{for}\mathrm{all}\gamma ,j\in \left[\vartheta ,\mu \right]$$

For all $\varpi ,\varrho \in \Xi$, we obtain

$$\wp \left(\xi \varpi \left(\gamma \right),\xi \varrho \left(\gamma \right),\tau \upsilon \right)=\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{\xi \varpi \left(\gamma \right),\xi \varrho \left(\gamma \right)\right\}}^2}$$

$$=\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{\eta \left(j\right)+\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j,\eta \left(j\right)+\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j\right\}}^2}$$

$$=\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j,\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j\right\}}^2}$$

$$=\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{F\left(\gamma ,j\right)\varpi \left(\gamma \right),F\left(\gamma ,j\right)\varrho \left(\gamma \right)\right\}}^2{\left(\delta {{\displaystyle \int }}_{\vartheta }^{\mu }\Delta j\right)}^2}$$

$$\ge \underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\upsilon }{\upsilon +\max {\left\{\varpi \left(\gamma \right),\varrho \left(\gamma \right)\right\}}^2}$$

$$\ge \wp \left(\varpi \left(\gamma \right),\varrho \left(\gamma \right),\upsilon \right).$$

$$\aleph \left(\xi \varpi \left(\gamma \right),\xi \varrho \left(\gamma \right),\tau \upsilon \right)=1-\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{\xi \varpi \left(\gamma \right),\xi \varrho \left(\gamma \right)\right\}}^2}$$

$$=1-\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{\eta \left(j\right)+\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j,\eta \left(j\right)+\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j\right\}}^2}$$

$$=1-\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j,\delta {{\displaystyle \int }}_{\vartheta }^{\mu }F\left(\gamma ,j\right)\vartheta \left(\gamma \right)\Delta j\right\}}^2}$$

$$=1-\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\tau \upsilon }{\tau \upsilon +\max {\left\{F\left(\gamma ,j\right)\varpi \left(\gamma \right),F\left(\gamma ,j\right)\varrho \left(\gamma \right)\right\}}^2{\left(\delta {{\displaystyle \int }}_{\vartheta }^{\mu }\Delta j\right)}^2}$$

$$\le 1-\underset{\gamma \in \left[\vartheta ,\mu \right]}{\sup }\frac{\upsilon }{\upsilon +\max {\left\{\varpi \left(\gamma \right),\varrho \left(\gamma \right)\right\}}^2}$$

$$\le \aleph \left(\varpi \left(\gamma \right),\varrho \left(\gamma \right),\upsilon \right).$$

Observe that all the conditions of Theorem 1 are satisfied. Hence, the integral Equation (9) has a unique solution. □

5. Conclusions

In this paper, we introduced the notion of an IFDCMLS. In this new setting, we established a number of new types of FP theorems. In order to demonstrate the viability of the suggested methods, we provided non-trivial examples together with their graphs. This research is supported by an application that demonstrates how the created methodology outperforms the methods that are based on the literature, since our structure is more general than the class of previously published results. It is easy to extend this research to the structure of intuitionistic fuzzy triple-controlled metric-like spaces, neutrosophic double-controlled metric-like spaces, and neutrosophic triple-controlled metric-like spaces. In the future, we will work on more than one self-mapping to find the existence and uniqueness of a fixed point in different generalized fuzzy metric structures.